Some Iterative Approximation Results of F Iteration Process in Banach Spaces

Abstract

In this research, we suggest some convergence results for operators having $\left(RCSC\right)$ condition in Banach space setting under F iterative scheme. We establish weak convergence under Opials condition and also establish some important strong convergence results under some appropriate assumptions on the domain or on the mapping. We furnish a non-trivial example of mappings having $\left(RCSC\right)$ condition and show that its F iterative scheme is more effective than the corresponding well known iterative schemes on this particular example.

1. Introduction

Many problems in applied sciences can not solved by ordinary analytical methods even the problem has known to have a solution. In such situations, we first rewrite such problems in the form of fixed point problems and then suggest some iterative methods to obtain approximate solutions for such type of problems. The well known and important facts due to Banach [1] asserts the existence and uniqueness of fixed point for contractions in metric spaces and suggest the Picard iterative method [2] to find this fixed point. However, in the case of nonexpansive mappings, the well known result of Browder-Gohde-Kirk [3,4,5] asserts the existence of fixed point for nonexpansive mappings in Banach spaces but the Picard iterative method [2] does not converge to this fixed point in general (see for details [6]). The class of nonexpansive mappings is properly more general then the notion of contraction mappings and has many fruitful applications in many areas of applied mathematics [7,8,9].

On the other hand, Suzuki suggested the notion of generalized nonexpansive mappings. A self-map T of a subset D of a Banach space is said to have Suzuki $\left(C\right)$ condition (also called Suzuki nonexpansive) if every two elements $v,v^{\prime }\in D$, follow that

$$\frac{1}{2}\left|\right|v-Tv\left|\right|\le \left|\right|v-v^{\prime }\left|\right|\Rightarrow \left|\right|Tv-T{v}^{\prime }\left|\right|\le \left|\right|v-v^{\prime }\left|\right|.$$

Since the above definition requires the inequality $\left|\right|Tv-T{v}^{\prime }\left|\right|\le \left|\right|v-v^{\prime }\left|\right|$ only for those $v,v^{\prime }\in D$ which satisfy $\frac{1}{2}\left|\right|v-Tv\left|\right|\le \left|\right|v-v^{\prime }\left|\right|$. Hence it is obvious that if T is any nonexpansive mapping, that is, $\left|\right|Tv-T{v}^{\prime }\left|\right|\le \left|\right|v-v^{\prime }\left|\right|$ for each two element $v,v^{\prime }\in D$, then T enjoys the Suzuki $\left(C\right)$ condition. On the other hand, an example in [10] clearly shows that the converse is not valid in general. In the current literature, lot of papers have been published by the both of the topics nonexpansive and Suzuki nonexpansive (see, e.g., refs. [11,12,13] and references cited therein).

In 2012, keeping Suzuki $\left(C\right)$ condition in mind, Karapinar [14] introduced the notion of $\left(RCSC\right)$ condition. A self-map T of a subset D of a Banach space is said to have $\left(C\right)$ condition (some-times called Reich-Chatterjea-Suzuki $\left(C\right)$ condition) if every two elements $v,v^{\prime }\in D$, follow that

$$\frac{1}{2}\left|\right|v-Tv\left|\right|\le \left|\right|v-v^{\prime }\left|\right|\Rightarrow \left|\right|Tv-T{v}^{\prime }\left|\right|\le \frac{1}{3}\left(\right||v-v^{\prime }\left|\right|+\left|\right|v^{\prime }-Tv\left|\right|+\left|\right|v-T{v}^{\prime }\left|\right|).$$

One of the interesting and important fields of research is the iterative construction of fixed points under the appropriate assumptions on the operator or on the domain. The well known result of the so-called Banach Contraction Principle uses Picard iteration for computations of fixed points of contraction. But the fixed points of nonexpansive and generalized nonexpansive mappings we can not compute by using Picard iteration in general. To compute fixed points of nonexpansive and generalized nonexpansive operators and to find a relatively better speed of convergence to the desired fixed point, one can deal with the different steps of iterative processes in the current literature (see e.g., Mann [15], Ishikawa [16], Noor [17], Agarwal [18], Abbas [7], Thakur et al. [12] and others).

In 2018, Ullah and Arshad were the first who suggested the well-known M iteration scheme as provided below and noted that this scheme is more better than the schemes mentioned above for mappings with Suzuki $\left(C\right)$ condition. The scheme reads as follows:

$$\left.\begin{array}{c}{x}_1=x\in D,\hfill \\ z_k=(1-{\alpha }_k)x_k+{\alpha }_{k}T{x}_k,\hfill \\ y_k=T{z}_k,\hfill \\ x_{k+1}=T{y}_k,\hfill \end{array}\right\}$$

(1)

where ${\alpha }_k\in (0,1)$.

However, very recently, Ali and Ali [19] introduced an up-to-date iterative method, and call it F iteration: which reads as follows:

$$\left.\begin{array}{c}{x}_1=x\in D,\hfill \\ z_k=T((1-{\alpha }_k)x_k+{\alpha }_{k}T{x}_k),\hfill \\ y_k=T{z}_k,\hfill \\ x_{k+1}=T{y}_k,\hfill \end{array}\right\}$$

(2)

where ${\alpha }_k\in (0,1)$. In [19], Ali and Ali observed that the F iteration (2) is stable with respect to any generalized contraction operator and converges to the solution of delay differential equations. Recently, Abdeljawad et al. [20] used M iteration process (1) for finding fixed points of mappings having (RCSC) condition. In this paper, we re-analyze F iteration with the connection of mappings having $\left(RCSC\right)$ condition. We also construct an example of a self-map T which has $\left(RCSC\right)$ condition but not $\left(C\right)$. By using this example, we suggest some numerical observations and commutations in the form of graphs and tables. This will validate the provided theoretical outcome of this research. Our results generalizes the idea of Ali and Ali [19] from the setting of contraction operators to the more general setting of operators having $\left(RCSC\right)$ condition. Our results also improve and extend the corresponding results of Abdeljawad et al. [20] and many other well known results of the current literature.

2. Preliminaries

Let D be a subset of a Banach space X. An element u in a set D is called fixed point of $T:D\to D$ whenever $u=Tu$. The well known notation $F\left(T\right)$ will throughout in the research represent the fixed point set of T. A Banach space $X=(X,||.|\left|\right)$ is said to satisfy Opial property (see for details [21]) if any given sequence $\left\{x_k\right\}\subseteq X$ having weak limit $w^{*}\in X$ is such that

$$\underset{k\to \infty }{lim\; inf}\left|\right|x_k-w^{*}\left|\right|<\underset{k\to \infty }{lim\; inf}\left|\right|x_k-v\left|\right|\mathrm{for}\mathrm{every}\mathrm{element}v\in X-\left\{w^{*}\right\}.$$

Moreover, a given self-map T on a subset D of a Banach space is said to satisfy Condition I [22] if some one find a nondecreasing map $n:[0,\infty )\to [0,\infty )$ such that $n\left(0\right)=0$, $n\left(s\right)>0$ for every choice of $s>0$ and $\left|\right|v-Tv\left|\right|\ge n\left(d\right(v,F\left(T\right))$ for every element v of D. Notice that, $d(v,F(T\left)\right)=inf\left\{\right||v-u||:u\in F(T\left)\right\}$.

Definition 1.

Assume that D is a nonempty subset of Banach space X and $\left\{x_k\right\}$ any bounded sequence in X. If we fix $s\in X$, then

($a_1$)

the asymptotic radius r of the sequence $\left\{x_k\right\}$ at the point s is the real number $r(s,\left\{x_k\right\}):={lim\; sup}_{k\to \infty }\left|\right|s-x_k\left|\right|$;

($a_2$)

the asymptotic radius of the sequence $\left\{x_k\right\}$ in the connection with D is given by $inf\{r(s,\left\{x_k\right\}):s\in D\}=r(D,\left\{x_k\right\})$

($a_3$)

the asymptotic center A of the sequence $\left\{x_k\right\}$ in the connection with D is given by $\{s\in D:r(s,\left\{x_k\right\})=r(D,\left\{x_k\right\})\}=A(D,\left\{x_k\right\})$.

One of the well-known characterization of the set, $A(D,\left\{x_k\right\})$ is that its cardinality is equal to one if the underlying space X is uniformly convex [23]. We also know from [24,25]) that $A(D,\left\{x_k\right\})$ is nonempty and convex in the case when D is weakly compact and convex.

We now collect some very useful and important characterizations of (RCSC) conditions which are established one by one in [14].

Proposition 1.

Suppose a self map T of D subset of a Banach space X and assume that T has (RCSC) condition. Then

(i)

For every choice of $v\in D$ and $u\in F\left(T\right)$, follow that $\left|\right|Tv-Tu\left|\right|\le \left|\right|v-u\left|\right|$.

(ii)

The set $F\left(T\right)$ is always closed. However if X is strictly convex and the domain D is convex, then the set $F\left(T\right)$ also enjoys convexity.

(iii)

For every choice of $v,v^{\prime }$ in D, it follows that

$$\left|\right|v-T{v}^{\prime }\left|\right|\le 9\left|\right|v-Tv\left|\right|+\left|\right|v-v^{\prime }\left|\right|.$$

(iv)

If we assume that X has Opial property, and $\left\{x_k\right\}$ is a weakly convergent to some element u with ${lim}_{k\to \infty }\left|\right|T{x}_k-x_k\left|\right|=0$, then u is the point of of the set $F\left(T\right)$.

We also state the following characterizations of uniform convexity, which is needed for our main outcome.

Lemma 1.

[26] Assume that ${\zeta }_k\in [i,j]\subset (0,1)$ for every natural number k. Suppose that $\left\{v_k\right\}$ and $\left\{w_k\right\}$ are two sequences in a uniformly convex Banach space X with ${lim\; sup}_{k\to \infty }\left|\right|v_k\left|\right|\le \zeta$, ${lim\; sup}_{k\to \infty }\left|\right|w_k\left|\right|\le \zeta$ and ${lim}_{k\to \infty }\left|\right|{\zeta }_k{v}_k+(1-{\zeta }_k)w_k\left|\right|=\zeta$ for some $\zeta \ge 0$, then ${lim}_{k\to \infty }\left|\right|v_k-w_k\left|\right|=0$.

3. Approximation Results

In this section, we state and prove several important iterative approximation results concerning F iterative scheme (2) for the class of maps with $\left(RCSC\right)$ property. For the sake of simplicity, throughout the section, we will write only X instead of uniformly convex Banach space.

We begin the main outcome by state and prove a lemma, which will play a significant roll in every main result.

Lemma 2.

Suppose T is a self-map on a nonempty convex closed subset D of X satisfying $\left(RCSC\right)$ condition. Assume that $F\left(T\right)\ne \varnothing$ and $\left\{x_k\right\}$ be a sequence of F iteration (2). Then ${lim}_{k\to \infty }\left|\right|x_k-u\left|\right|$ exists for every choice of $u\in F\left(T\right)$.

Proof. 

Choose any $u\in F\left(T\right)$ and $k\in \mathbb{N}$. By Proposition 1(i), we have

$$\begin{array}{ccc}\hfill \left|\right|z_k-u\left|\right|& =& \left|\right|T(1-{\alpha }_k)x_k+{\alpha }_{k}T{x}_k)-u||\hfill \\ & \le & \left|\right|(1-{\alpha }_k)x_k+{\alpha }_{k}T{x}_k-u\left|\right|\hfill \\ & \le & (1-{\alpha }_k)\left|\right|x_k-u\left|\right|+{\alpha }_k\left|\right|T{x}_k-u\left|\right|\hfill \\ & \le & (1-{\alpha }_k)\left|\right|x_k-u\left|\right|+{\alpha }_k\left|\right|x_k-u\left|\right|\hfill \\ & =& \left|\right|x_k-u\left|\right|.\hfill \end{array}$$

(3)

Which implies that

$$\begin{array}{ccc}\hfill \left|\right|x_{k+1}-u\left|\right|& =& \left|\right|T{y}_k-u\left|\right|\le \left|\right|y_k-u\left|\right|\hfill \\ & =& \left|\right|T{z}_k-u\left|\right|\le \left|\right|z_k-u\left|\right|\hfill \\ & \le & \left|\right|x_k-u\left|\right|.\hfill \end{array}$$

(4)

Thus, from the above, we obtained $\left|\right|x_{k+1}-u\left|\right|\le \left|\right|x_k-u\left|\right|$ for every choice of $k\in \mathbb{N}$ and $u\in F\left(T\right)$. Hence in particular, $\left\{\right||x_k-u|\left|\right\}$ is bounded and nonincreasing, and ${lim}_{k\to \infty }\left|\right|x_k-u\left|\right|$ exists for every chosen $u\in F\left(T\right)$. □

We now establish an important result as follows which will play key roll in establishing the weak and strong convergence results.

Theorem 1.

Suppose T is a self-map of a closed convex subset D of X satisfying $\left(RCSC\right)$ condition. Assume that $\left\{x_k\right\}$ be a sequence of F iteration (2). Then, $\left\{x_k\right\}$ is bounded and ${lim}_{k\to \infty }\left|\right|x_k-T{x}_k\left|\right|=0$ if and only if $F\left(T\right)\ne \varnothing$.

Proof. 

We consider ${lim}_{k\to \infty }\left|\right|x_k-T{x}_k\left|\right|=0$ and $\left\{x_k\right\}$ be bounded and prove $F\left(T\right)\ne \varnothing$. Choose any $u\in A(D,\left\{x_k\right\})$. Then by Proposition 1(iii), we have

$$\begin{array}{ccc}\hfill r(Tu,\left\{x_k\right\})& =& \underset{k\to \infty }{lim\; sup}\left|\right|x_k-Tu\left|\right|\hfill \\ & \le & 9\underset{n\to \infty }{lim\; sup}\left|\right|T{x}_k-x_k\left|\right|+\underset{k\to \infty }{lim\; sup}\left|\right|x_k-u\left|\right|\hfill \\ & =& \underset{k\to \infty }{lim\; sup}\left|\right|x_k-u\left|\right|\hfill \\ & =& r(u,\left\{x_k\right\}).\hfill \end{array}$$

From the above, one can conclude that $Tu$ is also the element of $A(D,\left\{x_k\right\}$. But in uniformly convex Banach spaces, $A(D,\left\{x_k\right\})$ is always singleton and thus $Tu=u$. Hence $u\in F\left(T\right)$, which now shows that $F\left(T\right)\ne \varnothing$.

Next we consider the set $F\left(T\right)\ne \varnothing$ and try to show that $\left\{x_k\right\}$ is bounded and ${lim}_{n\to \infty }\left|\right|x_k-T{x}_k\left|\right|=0$. Boundedness of $\left\{x_k\right\}$ follows from the proof of Lemma 2. Moreover, since $F\left(T\right)$ is nonempty, we can choose any element p in $F\left(T\right)$. Hence, by Lemma 2, ${lim}_{k\to \infty }\left|\right|x_k-u\left|\right|$ exists. Let this limit be equal to some real number $\zeta$. That is,

$$\zeta =\underset{k\to \infty }{lim}\left|\right|x_k-u\left|\right|.$$

(5)

Keeping (3) in mind, we have

$$\left|\right|z_k-u\left|\right|\le \left|\right|x_k-u\left|\right|$$

$$\Rightarrow \underset{k\to \infty }{lim\; sup}\left|\right|z_k-u\left|\right|\le \underset{k\to \infty }{lim\; sup}\left|\right|x_k-u\left|\right|=\zeta .$$

(6)

By Proposition 1(i), we have

$$\left|\right|T{x}_k-u\left|\right|\le \left|\right|x_k-u\left|\right|$$

$$\Rightarrow \underset{k\to \infty }{lim\; sup}\left|\right|T{x}_k-u\left|\right|\le \underset{k\to \infty }{lim\; sup}\left|\right|x_k-u\left|\right|=\zeta .$$

(7)

Similarly, from (4), we have

$$\left|\right|x_{k+1}-u\left|\right|\le \left|\right|z_k-u\left|\right|$$

$$\Rightarrow \zeta =\underset{k\to \infty }{lim\; inf}\left|\right|x_{k+1}-u\left|\right|\le \underset{k\to \infty }{lim\; inf}\left|\right|z_k-u\left|\right|.$$

(8)

By combining (6) and (8), we obtain

$$\zeta =\underset{k\to \infty }{lim}\left|\right|z_k-u\left|\right|.$$

(9)

From (9), we have

$$\begin{array}{ccc}\hfill \zeta & =& \underset{k\to \infty }{lim}\left|\right|z_k-u\left|\right|\hfill \\ & =& \underset{k\to \infty }{lim}\left|\right|T((1-{\alpha }_k)x_k+{\alpha }_{k}T{x}_k)-u\left|\right|\hfill \\ & \le & \underset{k\to \infty }{lim}\left|\right|(1-{\alpha }_k)x_k+{\alpha }_{k}T{x}_k-u\left|\right|\hfill \\ & =& \underset{k\to \infty }{lim}\left|\right|(1-{\alpha }_k)(x_k-u)+{\alpha }_k(T{x}_k-u)\left|\right|\hfill \\ & \le & \underset{k\to \infty }{lim}(1-{\alpha }_k)\left|\right|x_k-u\left|\right|+\underset{k\to \infty }{lim}{\alpha }_k\left|\right|T{x}_k-u\left|\right|\hfill \\ & \le & \underset{k\to \infty }{lim}(1-{\alpha }_k)\left|\right|x_k-u\left|\right|+\underset{k\to \infty }{lim}{\alpha }_k\left|\right|x_k-u\left|\right|\hfill \\ & =& \underset{k\to \infty }{lim}\left|\right|x_k-u\left|\right|\hfill \\ & =& \zeta .\hfill \end{array}$$

⇔

$$\zeta =\underset{k\to \infty }{lim}\left|\right|(1-{\alpha }_k)(x_k-u)+{\alpha }_n(T{x}_k-u)\left|\right|.$$

(10)

If we apply Lemma 1, we must have

$$\underset{k\to \infty }{lim}\left|\right|T{x}_k-x_k\left|\right|=0.$$

This completes the proof. □

First we suggest a weak convergence result under the assumption that the ground space satisfies Opial’s property.

Theorem 2.

Suppose T is a self-map on a nonempty convex closed subset D of X satisfying $\left(RCSC\right)$ condition. Assume that $F\left(T\right)\ne \varnothing$ and $\left\{x_k\right\}$ be a sequence of F iteration (2). In addition, if X has the Opial’s property then $\left\{x_k\right\}$ converges weakly to a fixed point of T.

Proof. 

Keeping the uniform convexity of X in mind, we can say that X is reflexive. By Theorem 1, the sequence $\left\{x_k\right\}$ is bounded and ${lim}_{k\to \infty }\left|\right|T{x}_k-x_k\left|\right|=0$ for every natural number k. By the reflexivity of X, a weakly convergent subsequence $\left\{x_{k_i}\right\}$ of $\left\{x_k\right\}$ with limit $u\in D$ exists. By Proposition 1(iv), the element u is the fixed point of T. Thus, it is remaining to show that u is the unique weak limit of sequence $\left\{x_k\right\}$. Contrary assume that the element u is not a weak limit of $\left\{x_k\right\}$, that is, there exists another weakly convergent subsequence $\left\{x_{k_j}\right\}$ of $\left\{x_k\right\}$ having weak limit say v such that $u\ne v$. Again by Proposition 1(iv), $v\in F\left(T\right)$. Keeping Opial’s property in mind and Lemma 2, we have

$$\begin{array}{ccc}\hfill \underset{k\to \infty }{lim}\left|\right|x_k-u\left|\right|& =& \underset{i\to \infty }{lim}\left|\right|w_{k_i}-u\left|\right|<\underset{i\to \infty }{lim}\left|\right|x_{k_i}-v\left|\right|\hfill \\ & =& \underset{k\to \infty }{lim}\left|\right|x_k-v\left|\right|=\underset{j\to \infty }{lim}\left|\right|x_{k_j}-v\left|\right|\hfill \\ & <& \underset{j\to \infty }{lim}\left|\right|x_{k_j}-u\left|\right|=\underset{k\to \infty }{lim}\left|\right|x_k-u\left|\right|.\hfill \end{array}$$

The strict inequality above provides a contradiction. We thus conclude that the element u is a weak limit of $\left\{x_k\right\}$. □

Now we suggest a strong convergence result under the assumption that the domain is compact.

Theorem 3.

Suppose T is a self-map on a nonempty convex compact subset D of X satisfying $\left(RCSC\right)$ condition. Assume that $F\left(T\right)\ne \varnothing$ and $\left\{x_k\right\}$ be a sequence of F iteration (2). Then $\left\{x_k\right\}$ converges strongly to a fixed point of T.

Proof. 

By compactness assumption, a strongly convergent subsequence $\left\{x_{k_j}\right\}$ of $\left\{x_k\right\}$ with a strong limit say $v\in D$ exists. By Proposition 1(iii), we have

$$\left|\right|x_{k_j}-Tv\left|\right|\le 9\left|\right|x_{k_j}-T{x}_{k_j}\left|\right|+\left|\right|x_{k_j}-v\left|\right|⟶0.$$

Because in the view of Theorem 1, ${lim}_{j\to \infty }\left|\right|T{x}_{k_j}-x_{k_j}\left|\right|=0$. By uniqueness of limits of convergent sequences in Banach spaces, we conclude that $v=Tv$. By Lemma 2, ${lim}_{k\to \infty }\left|\right|x_k-v\left|\right|$ exists. Thus v is also a strong limit of $\left\{x_k\right\}$. □

A strong convergence result without compactness assumption is stated below. The proof is elementary and therefore omitted.

Theorem 4.

Suppose T is a self-map on a nonempty convex closed subset D of X satisfying $\left(RCSC\right)$ condition. Assume that $F\left(T\right)\ne \varnothing$ and $\left\{x_k\right\}$ be a sequence of F iteration (2). Then $\left\{x_k\right\}$ converges strongly to a fixed point of T whenever ${lim}_{k\to \infty }d(x_k,F\left(T\right))=0$.

Now we suggest a strong convergence result under the assumption that the mapping satisfies condition $\left(I\right)$.

Theorem 5.

Suppose T is a self-map on a nonempty convex closed subset D of X satisfying $\left(RCSC\right)$ condition. Assume that $F\left(T\right)\ne \varnothing$ and $\left\{x_k\right\}$ be a sequence of F iteration (2). Then $\left\{x_k\right\}$ converges strongly to a fixed point of T whenever T satisfies condition $\left(I\right)$.

Proof. 

In the view of Theorem 1, we can write ${lim\; inf}_{k\to \infty }\left|\right|x_k-T{x}_k\left|\right|=0$. Now the condition I, suggests ${lim\; inf}_{k\to \infty }d(x_k,F\left(T\right))=0$. By Theorem 4, $\left\{x_k\right\}$ converges strongly to a fixed point of T. □

4. Example

Now we give an example of mappings having $\left(RCSC\right)$ condition but not $\left(C\right)$. We shall use this example, to support the main outcome. We show by many different choices of starting points and by choosing different values of parameters that F iteration is better than the many other well known iterative processes in the frame work of mappings having $\left(RCSC\right)$ condition.

Example 1.

Suppose $D=[3,6]$ and define $T:D\to D$ by $Tv=3$ if $v=6$ and $Tv=\frac{v+3}{2}$ if $v\ne 6$. Then

Case(a):when $v,v^{\prime }\in [3,6)$. Then $Tv=\frac{v+3}{2}$ and $T{v}^{\prime }=\frac{v^{\prime }+3}{2}$. Keeping triangle inequality in mind, we have

$$\begin{array}{ccc}\hfill \frac{1}{3}\left(|v-v^{\prime }|+|v-T{v}^{\prime }|+|v^{\prime }-Tv|\right)& =& \frac{1}{3}|v-v^{\prime }|+\frac{1}{3}|v-T{v}^{\prime }|+\frac{1}{3}|v^{\prime }-Tv|\hfill \\ & =& \frac{1}{3}|v-v^{\prime }|+\frac{1}{3}|v-\left(\frac{3+v^{\prime }}{2}\right)|+\frac{1}{3}|v^{\prime }-\left(\frac{3+v}{2}\right)|\hfill \\ & \ge & \frac{1}{3}|v-v^{\prime }|+\frac{1}{3}|\left(\frac{3v+3}{2}\right)-\left(\frac{3v^{\prime }+3}{2}\right)|\hfill \\ & =& \frac{1}{3}|v-v^{\prime }|+\frac{1}{3}|\frac{3v}{2}-\frac{3v^{\prime }}{2}|\hfill \\ & =& \frac{1}{3}|v-v^{\prime }|+\frac{1}{2}|v-v^{\prime }|\hfill \\ & \ge & \frac{1}{2}|v-v^{\prime }|\hfill \\ & \ge & |Tv-T{v}^{\prime }|.\hfill \end{array}$$

Case(b):when $v\in [3,6)$ and $v^{\prime }\in \left\{6\right\}$. Then $Tv=\frac{v+3}{2}$ and $T{v}^{\prime }=3$. Now

$$\begin{array}{ccc}\hfill \frac{1}{3}\left(|v-v^{\prime }|+|v-T{v}^{\prime }|+|v^{\prime }-Tv|\right)& =& \frac{1}{3}|v-v^{\prime }|+\frac{1}{3}|v-T{v}^{\prime }|+\frac{1}{3}|v^{\prime }-Tv|\hfill \\ & =& \frac{1}{3}|v-v^{\prime }|+\frac{1}{3}|v-3|+\frac{1}{3}|v^{\prime }-\left(\frac{v+3}{2}\right)|\hfill \\ & \ge & \frac{1}{3}|(v-v^{\prime })+(v^{\prime }-\left(\frac{v+3}{2}\right))|+\frac{1}{3}|v-3|\hfill \\ & =& \frac{1}{3}|(v-\left(\frac{v+3}{2}\right))|+\frac{1}{3}|v-3|\hfill \\ & =& \frac{1}{3}|\frac{v-3}{2}|+\frac{1}{3}|v-3|\hfill \\ & \ge & \frac{1}{3}|\left(\frac{v-3}{2}\right)+(v-3)|\hfill \\ & =& \frac{1}{3}\left|\frac{3v-9}{2}\right|\hfill \\ & =& \frac{1}{2}|v-3|=|Tv-T{v}^{\prime }|.\hfill \end{array}$$

Case(c):finally, for $v=v^{\prime }=6$. Then $Tv=T{v}^{\prime }=3$. Now

$$\begin{array}{c}\hfill \frac{1}{3}\left(|v-v^{\prime }|+|v-T{v}^{\prime }|+|v-T{v}^{\prime }|\right)>0=|Tv-T{v}^{\prime }|.\end{array}$$

The above cases suggest that the self map T has $\left(RCSC\right)$ condition. Nevertheless, T does not satisfy Suzuki $\left(C\right)$-condition. Because, if $v=5.2$ and $v^{\prime }=6$, then $\frac{1}{2}|v-Tv|<|v-v^{\prime }|$ and $|Tv-T{v}^{\prime }|>|v-v^{\prime }|$. Suppose ${\alpha }_k=0.70,{\beta }_k=0.65\mathrm{and}{\gamma }_k=0.90$. The Table 1 shows the strong convergence of F [19], M [13], Thakur [12], Abbas [7], Agarwal [18], Noor [17], Ishikawa [16] and Mann [15] iteration processes to a fixed point $v=3$ of the mapping T.

Table 1. Some values generated by F, M, Thakur, Abbas, S, Noor, Ishikawa and Mann iterations for the mapping T of Example 1.

k	F	M	Thakur	Abbas	Agarwal	Noor	Ishikawa	Mann
1	4	4	4	4	4	4	4	4
2	3.0813	3.1625	3.1931	3.2456	3.3863	3.4851	3.5363	3.6500
3	3.0066	3.0264	3.0373	3.0603	3.1492	3.2353	3.2876	3.4225
4	3.0005	3.0043	3.0072	3.0148	3.0576	3.1141	3.1542	3.2746
5	3	3.0007	3.0014	3.0036	3.0223	3.0554	3.0827	3.1785
6	3	3.0001	3.0003	3.0009	3.0086	3.0269	3.0443	3.1160
7	3	3	3.0001	3.0002	3.0033	3.0130	3.0238	3.0754
8	3	3	3	3.0001	3.0013	3.0063	3.0123	3.0490
9	3	3	3	3	3.0005	3.0031	3.0068	3.0318
10	3	3	3	3	3.0002	3.0015	3.0037	3.0207
11	3	3	3	3	3.0001	3.0007	3.0020	3.0134
12	3	3	3	3	3	3.0003	3.0011	3.0088
13	3	3	3	3	3	3.0002	3.0006	3.0057
14	3	3	3	3	3	3.0001	3.0003	3.0037
15	3	3	3	3	3	3	3.0002	3.0024
16	3	3	3	3	3	3	3.0001	3.0016
17	3	3	3	3	3	3	3	3.0010
18	3	3	3	3	3	3	3	3.0007
19	3	3	3	3	3	3	3	3.0004
20	3	3	3	3	3	3	3	3.0003
21	3	3	3	3	3	3	3	3.0002
22	3	3	3	3	3	3	3	3.0001
23	3	3	3	3	3	3	3	3

Remark 1.

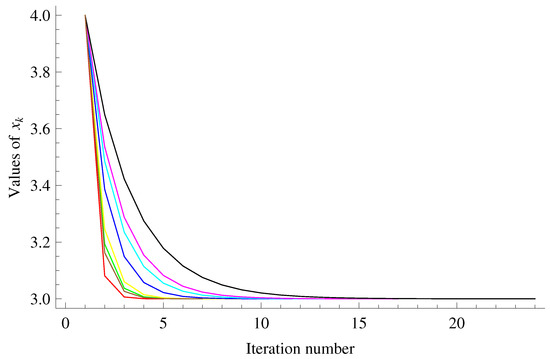
The Table 1 and Figure 1, suggest that F iterative process converges faster to a fixed point $v=3$ of the mapping T than the other iterations.

Figure 1. Convergence behaviors of F (red), M (brown), Thakur (green), Abbas (yellow), Agarwal (blue), Noor (cyan), Ishikawa (magenta) and Mann (black) iterative schemes.

Now we further show the effectiveness of F iterative process by choosing different values of parameters and starting points. Assume that $\left|\right|x_k-v\left|\right|<{10}^{-10}$ be the stopping criterion where $v=3$ is a fixed point of the mapping T. The iteration numbers to get fixed point 3 for the iteration process F [19] are compared with leading three-steps M [13] and Agarwal [18] iterations. The Bold numbers in the Table 2, Table 3 and Table 4 suggests that F iteration is better than both of the Thakur and Agarwal.

Table 2. ${\alpha }_k=\frac{k}{{(k+7)}^{\frac{11}{9}}}$ and ${\beta }_k=\frac{1}{{(k+2)}^{\frac{2}{5}}}$.

Number of Iterates for Obtaining Fixed Point.
Starting Points	Agarwal	M	F
$3.2$	28	14	$\mathbf{10}$
$3.7$	30	14	$\mathbf{10}$
$4.3$	30	15	$\mathbf{10}$
$4.8$	31	15	$\mathbf{10}$
$5.3$	31	15	$\mathbf{11}$
$5.8$	32	15	$\mathbf{11}$

Table 3. ${\alpha }_k=\frac{k}{{(k+6)}^{\frac{17}{14}}}$ and ${\beta }_k=\frac{k}{k+3}$.

Number of Iterates for Obtaining Fixed Point.
Starting Points	Agarwal	M	F
$3.2$	24	13	$\mathbf{9}$
$3.7$	26	14	$\mathbf{10}$
$4.3$	26	15	$\mathbf{10}$
$4.8$	27	15	$\mathbf{10}$
$5.3$	27	15	$\mathbf{11}$
$5.8$	27	15	$\mathbf{11}$

Table 4. ${\alpha }_k=\frac{1}{{(3k+5)}^{\frac{1}{5}}}$ and ${\beta }_k=\frac{k}{7k+9}$.

Number of Iterates for Obtaining Fixed Point.
Starting Points	Agarwal	M	F
$3.2$	28	12	$\mathbf{9}$
$3.7$	29	13	$\mathbf{9}$
$4.3$	30	13	$\mathbf{9}$
$4.8$	31	13	$\mathbf{10}$
$5.3$	31	14	$\mathbf{10}$
$5.8$	31	14	$\mathbf{10}$