Abstract
The ongoing COVID-19 pandemic has caused a paradigm shift in all aspects of contemporary human life. Everyday activities such as shopping have shifted from traditional methods to the ever-more growing online variants, allowing for an increase in electronic commerce (e-commerce) industry. As more services become available online, consumers often rely on trusted services, which are often reflected on the web and mobile platforms they are presented on. In this paper, we study the factors for successful e-commerce platform design in the Western Balkans region using Fuzzy Analytical Hierarchy Process (FAHP) with triangular fuzzy numbers. After an extensive literature overview, interviews with representatives of top-ranking e-commerce companies in the region, and the analysis of experts’ opinions, we select a number of factors and sub-factors for prioritization, taking into account pre-pandemic factors, as well as the ones of the pandemic itself. We extend the FAHP model, which now consists of five (instead of three) points of view. Finally, we present and discuss the results in the form of tables and graphs, as well as an overall recommendation of what should be taken into account when designing an e-commerce platform. Our results rank service quality and security factors first and criteria such as multilingual support last.
1. Introduction
In the last 20 years, in the era of new technologies and modernization, Internet use has increased significantly, especially for the purposes of communication, marketing, and electronic commerce (e-commerce) [1,2]. Business of marketing has always been fluid, continuously adapting to ever-evolving consumer preferences. The migration from traditional to electronic commerce was going on long before the events caused by the COVID-19 pandemic, which has only hastened this transition. Indeed, the need for commerce digitization rapidly graduated for many businesses into means for survival once the pandemic hit. Within a matter of weeks to months, brands without online options were hastily implementing new e-commerce platforms, and those already using digital infrastructures were bracing their servers’ capacities for the impact of increased online traffic. E-commerce is defined as a type of Internet use mainly to carry out business transactions in which parties communicate electronically instead of in person. These transactions significantly reduce costs, save time, increase profits, and simplify business activities, involving manufacturers, consumers, and service providers that use the Internet [3,4]. There is a clear expectation from consumers that companies should do their part to help them in their daily lives and to keep them informed. Brands must be able to meet consumers where they are and offer personalized services for their specific needs. According to Shaw [5], considering the nature of transactions, there are five major categories of e-commerce: Business to Business (B2B), where e-commerce is done exclusively between companies; Business to Customer (B2C), in which company offers services to consumers; Business to Government (B2G), where companies offer government agencies products and services through online marketing and bidding for projects; Consumer to Business (C2B), where companies tender for projects posted by consumers; and Consumer to Consumer (C2C), where consumers sell their products to consumers online.
Knowing that B2C websites, where consumers directly buy products, present the lifeblood of B2C e-commerce, companies strive to design a successful B2C website and to ultimately make business considerably practical and effective. Amazon and Alibaba, followed by eBay, Walmart, Priceline, and Rakuten, are the most dominant and significant B2C e-commerce companies [6]. The popularity and expeditious advancement of B2C e-commerce make these sorts of transactions the leading retailing channel for ordinary customers [7], and therefore Internet-based commerce in general raises the question of awareness and vulnerability of consumers’ privacy and security on B2C platforms [8,9,10]. Security and privacy of information provided by customers are very important, especially in risky and unpredictable ambiance [11]. Factors such as transaction confidentiality, integrity, and authentication imply trust at the technology level. For the continual performance of B2C online commerce, customer relationship management plays an important role [12] and trust becomes an inevitable factor [13,14].
In recent years, multi-criteria decision-making (MCDM) has been applied in various fields of scientific research in cases where it is desirable to restructure a multi-criteria problem. At the end of this process, the most optimal choice, or an alternative one, is selected. A formal framework for modeling multidimensional decision-making problems is therefore provided by applying MCDM, especially for problems that require systems analysis, the analysis of decision complexity, the relevance of consequences, and the need for the accountability of decisions made [15]. Utilizing Fuzzy MCDM (F-MCDM), an efficient approach for evaluating multiple criteria, can be achieved to support managers, experts, and other decision makers with the goal of balancing and measuring different factors, simplifying and clarifying decisions [16].
In this paper, we study the factors for successful e-commerce platform design using Fuzzy Analytical Hierarchy Process (FAHP) based on triangular fuzzy numbers [17]. In many real-world situations, when applying decision-making approaches, human judgment alone is often insufficient and not reliable. Therefore, the use of triangular fuzzy numbers presents a viable alternative for expert judgment regarding the qualitative factors and their importance. Similarly, trapezoidal, Pythagorean, z-numbers, and the recently introduced Spherical fuzzy numbers [18] may also be considered when applying the FAHP method. Although our research is based solely on triangular fuzzy numbers, we present an extension to the current model of optimism indexes. Firstly, we conduct a literature overview, and afterwards we select a number of factors and sub-factors for prioritization, taking into account factors during the COVID-19 pandemic. As a starting point, we include FAHP with three points of view and further extend to a novel, five-points-of-view ranking of sub-criteria.
The advances in this paper are summarized in the following:
- New sub-criteria influencing e-commerce websites are introduced.
- The FAHP method is extended by introducing two new points of view for the decision-maker, namely, semi-pessimistic and semi-optimistic views, with corresponding optimism indexes and , respectively.
- The estimation and analysis of ranking similarities in the extended model is conducted and discussed.
As of writing this paper, the authors have not found any article or study regarding e-commerce platform design using FAHP in the region of the Western Balkans. Therefore, our main goal is to provide insights to the decision-making process and further extend one of the well-known MCDM methods. According to this goal, we formulated four research questions (RQs).
RQ1: Can the results presented in our paper help e-commerce companies of the Western Balkans region?
RQ2: Does a highly influencing sub-factor during the COVID-19 pandemic exist?
RQ3: Are there significant changes in the sub-factors ranking when the three values of an optimism index in the FAHP method are expanded to the finite or countable set of values?
RQ4: Do we have complete insight into the interrelations of sub-criteria using Extended FAHP?
2. Criteria for Evaluation of B2C Websites
In this Section, we firstly give a literature overview on the application of MCDM. Afterwards, we identify the main factors for the design of B2C e-commerce websites.
2.1. Literature Overview
In the past two decades, the application of MCDM and some other approaches in the process of evaluation of B2C e-commerce-website-related tasks has led to a number of published works. These approaches include but are not limited to Analytical Hierarchy Process (AHP) [14,19,20,21], Analytical Network Process (ANP) and Grey Relational Analysis (GRA) [22], fuzzy Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) [23], VIsekriterijumska optimizacija i KOmpromisno Resenje (VIKOR) [15], fuzzy VIKOR [24], Preference Ranking Organization METHod for Enrichment Evaluation (PROMETHEE) [25], and PROMETHEE for Sustainability Assessment (PROSA) [26]. In addition, the Decision-making Trial and Evaluation Laboratory (DEMATEL) [27,28] is also a very convenient method for assessing the B2C websites criteria. Service quality has been the main aim of the majority of online platforms [29], with emphasis on the difference between levels of perceived and expected service [30]. Customer orientation, marketing, and security have been the most important factors in evaluation of five-star hotel websites in Mashhad, according to the research conducted by Ostovare and Shahraki [25], while price saving, awareness, and security took precedence in the assessment of the website quality of the Turkish e-business market [31]. In [32,33,34], content quality, service quality, and system availability, followed by security, ease usage, privacy, efficiency, and appearance, have been influence factors in the prioritization of B2C e-commerce websites. Similar investigations of the influence and relevance of each website quality factor have been discussed by Del Vasto-Terrientes et al. [35], Dey et al. [36], and Chou and Cheng [37]. However, there have been other relevant papers with a different viewpoint. For example, Ashraf et al. [7] have dealt with the connection between e-commerce business and their customers; Kang et al. [38] have introduced new E-S-QUAL based TOPSIS approach for evaluation of e-commerce websites; and Ong and Teh [39] have focused on consumer expectations, complaints, and compensations.
Recent studies have dealt with applying MCDM methods for better decision making. For instance, in [16], the authors deal with delivery time, order fulfillment, convenience of payment, and real-time tracking, and their influence on Last Mile Delivery companies utilizing FAHP with triangular fuzzy numbers. They conclude that utilizing MCDM techniques can be valuable for both researchers and decision-makers themselves. In [40], the authors combine data envelopment analysis and Grey model, with the goal of predicting and assessing future efficiency in e-commerce marketplaces. Finally, in [41], the authors apply triangular fuzzy numbers for FAHP, coupled with TOPSIS-Grey techniques to, respectively, determine factors and access alternatives for B2C e-commerce websites.
2.2. Main Factors for B2C e-Commerce Websites
In this paper, we have identified five major factors with corresponding sub-factors for the design of B2C e-commerce websites. The initial factors and sub-factors were obtained from the extensive literature overview given in Section 2.1. Furthermore, we have selected the top-ranking companies from the Western Balkans Region and interviewed their representatives from sales, management, and IT support sectors [42]. These companies’ activities mainly deal with consumer products, with a couple of them having an e-Bay like business model. A total of 23 persons representing both companies’ points of view, and customers’ experience, responded to our interviews. Finally, four experts in the fields of mathematics, artificial intelligence, digital marketing, and management have acknowledged all given answers, and have, in consensus with the authors, obtained the final list of factors and their respective sub-factors.
The opinions we have collected from the representatives of e-commerce companies, professionals, and ourselves as the authors, as well as the selection and ranking of criteria and sub-criteria, will be useful to the managerial part of companies in meeting various challenges posed by the ongoing COVID-19 pandemic, as well as the challenges that will come after.
The summary of each of the main factors with corresponding sub-factors is given in Figure 1, while the detailed descriptions of each are presented below.
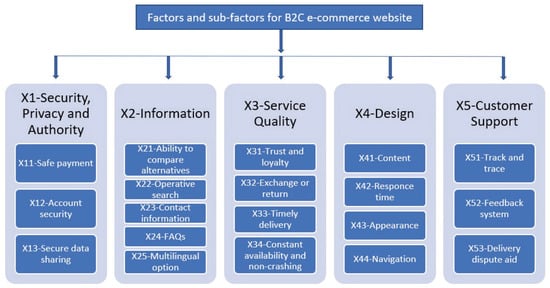
Figure 1.
Factors and sub-factors for B2C website.
2.2.1. : Security, Privacy and Authority
Security is a dominant concern for all types of e-business web sites [43]. The presence of the somewhat insecure networks and/or servers can lead to the corruption and exploitation of customers’ personal data. A company’s reputation heavily relies on this type of vulnerability, and potential attackers should not be able to have access to customers’ information by accessing their databases or websites. When customers have to worry about the process of collection and maltreatment of personal information, trust towards online shops decreases [44]; Conversely, if the impression of being secure while browsing a B2C website persists, confidence and trust towards the website increases. When dealing with online payment, companies should accept well-known payment methods as well as globally recognized credit cards, in order to preserve customers’ credit card information to an online account and ultimately ensure safety [10]. As soon as the pandemic shopping trends started [42], website security became paramount.
2.2.2. : Information
Every customer on the e-commerce website should be able to contact the company for any necessary information and/or regarding disputes [45]. The existence of company contact details also helps in solving problems and contributes to the level of confidence [46]. It is important to have correct and updated information of item availability, a search by keyword options, and the option to compare multiple items’ characteristics [34,47]. Having a version of the website in other languages is mandatory nowadays, especially for those websites trading on a global scale. A section for Frequently Asked Questions or similar step-by-step guides can also be useful, especially for new shopper influx due to the pandemic.
2.2.3. : Service Quality
Every e-commerce website should be trustworthy. Since e-trust has a positive affect on e-loyalty, and a pleased customer often refers new potential buyers to shops, trust is essential for continual success in long-term online business [48,49]. The constant availability of websites, especially well-known ones, is recommended, with no down-time. In addition, a B2C website’s significance and influence are also determined by the purchased items’ delivery time, and multiple delivery options should exist [50], with a no-contact delivery option as well. There should be no delays in the process of delivery, nor should delivery schedules change often, as they have a negative influence on e-satisfaction [51]. The opportunity for item replacement or return enhances the number of customers and helps to solve any potential conflicts between the buyer and the company [39].
2.2.4. : Design
Online shops’ long-term profitability will be strengthened by their content [52]. If the customer is bored by the content of the site, its non-creativeness; or the lack of applications, images, and/or data, or they have difficulties in finding necessary information, the sales potential will be significantly reduced [25,34]. Therefore, according to Ivory [53], good navigation is fundamental, and it should consist of clear and helpful links. Additionally, the appearance on the B2C e-commerce website must be attractive and well-organized, always keeping the customer’s attention and encouraging them to come back [32]. Page load and response times should be as short as possible, because if it takes long to load or download the page (e.g., due to many graphic elements), the site’s performance will suffer [54]. Customers’ satisfaction will increase if the company’s staff is responsible, enthusiastic, and happy to give quick responses to queries and provide help [55].
2.2.5. : Customer Support
It would be desirable for the B2C e-commerce website to include a customer support service as people need to know the status of the purchased item, whether their order is still in the warehouse, or whether it is being delivered [33,50]. The option of product reviews should be available to customers, and they should include realistic feedback about the negative and/or positive aspects of the service [32,56]. Reimbursement is often a subject of discussion or dispute, so B2C e-commerce should provide a help service for these types of situations [57]. One of the essential factors for a successful business is its communication method with online consumers, meaning that quick and adequate information should be provided by the company in order to increase the return visits by customers [58].
3. Methodology
The fuzzy set theory has been known for over half a century, ever since its proposal by Zadeh in 1965. Even then, it has been employed as guidance for fuzzy decision-making problems. Their original inception was intended for linguistics, and it has enabled uncertainty and imprecision to be represented, and, more importantly, constructed in a deterministic manner [59,60]. Sets defined in such a manner could therefore be identified as a generalization of the well-known set theory, enabling a decision-maker to include incomplete or partially unknown information in the decision model [61].
Whereas in the classic set theory, an element can either belong to a set or not belong at all, in fuzzy sets, the membership of an element can be described by a number from the interval . Each element of this set can hence be mapped on this interval with a membership function (MF), denoted by . In addition, a fuzzy set can have an infinite number of different MFs.
Let all fuzzy sets defined on the set of real numbers be represented as . The number is a fuzzy number if there exists so condition holds, and is a closed interval for every (see [17,62]). The membership function, a component of a triangular fuzzy number (TFN) A, is a function , defined as
where inequality holds. Variables l, m, and u are the lower, middle, and upper value, respectively, and when , TFN becomes a crisp number. In the sequel, the triangular fuzzy number will be denoted by .
Assume two TFNs, , , and scalar , . The arithmetic operation properties are defined as [63,64,65]:
Addition:
Subtraction:
Multiplication:
Reciprocal:
Scalar multiplication:
Left and right side of the membership function of triangular number , as shown in Figure 2, are denoted by and , and their matching inverse functions are
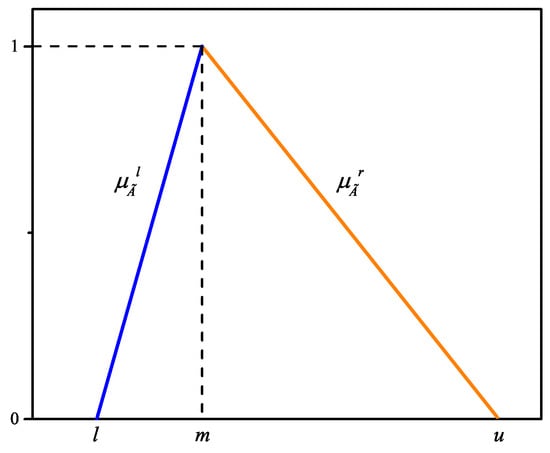
Figure 2.
The representation of a triangular membership function.
Left and right integral values of the triangular fuzzy number , according to [66], are defined as
and
and the total integral value, according to [66] as a combination of left and right integral values, is
where represents an optimism index. The pessimistic, semi-pessimistic, balanced, semi-optimistic, and optimistic points of view of the decision-maker are, respectively, expressed by the values 0, , , , and 1.
Fuzzy AHP
Since its creation [67], the AHP had a respectable application in MCDM, enabling the decision makers to solve complex problems by decomposing them into a hierarchical structure, creating the comparison matrix and determining the importance of one indicator above others. The specified level of uncertainty of a team of experts (or even one expert) [68] due to the inability to express the significance of some criteria has led to the introduction of FAHP [69,70] enabling conversion of linguistic statements into mathematical expressions.
The summarized steps in FAHP are as follows [17,71]:
Step 1. Establishing the main goal and hierarchical appearance of criteria. In general, the hierarchical structure has been organized vertically: the main goal is, as the most important component, at the top; the criteria that contribute to the goal are at the intermediate levels; and the sub-criteria are at the lowest level.
Step 2. Determining the pairwise comparison matrix in terms of TFNs. In this step, a positive fuzzy reciprocal comparison matrix with a total of comparisons of elements from a higher level with elements from a lower level is developed. The fuzzy value represents the degree of relative importance between criteria; , , and , otherwise. Table 1 shows the fuzzy scale for constructing pairwise comparisons.

Table 1.
Marks, linguistic terms, and denotation of TFNs.
As it was recommended in [72], a fuzzy distance of 2 and odd values as boundaries for all non-intermediate values are applied in order to achieve better consistency. There are also different scales of triangular fuzzy numbers applicable in the previous case [73,74,75].
The graphic representation of the used FAHP scale with all three values (lower, median, and upper) is presented in Figure 3.
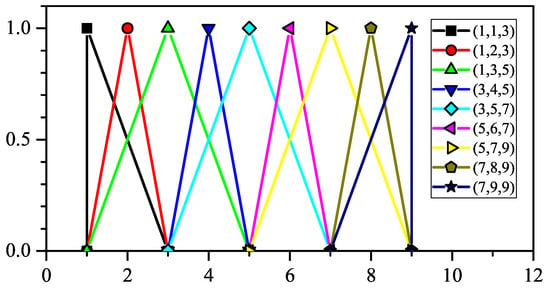
Figure 3.
Graphic representation of TFNs.
Step 3. Matrix consistency review.
For a matrix , the consistency index and consistency ratio are calculated using eqs. from [76]:
where corresponds to a maximal eigenvalue of matrices D and is a random index, as shown in Table 2.

Table 2.
The table of Random Index numbers.
The value confirms the comparison matrix consistency, while otherwise the reason for inconsistency should be found and calculations repeated [77].
Step 4. The fuzzification process.
Using the triangular fuzzy numbers from the comparison matrix , applying
and
the value of the fuzzy synthetic extent is obtained as follows [64]:
Step 5. The defuzzification process.
Next, in this step, using
the total integral value for the TFNs is calculated [78].
Step 6. Normalization of weight vector w and obtaining the vector for each criterion.
Using
the weights for all criteria are obtained.
Step 7. Ranking the weights for all sub-criteria.
The weights for each sub-criterion are obtained by multiplying the weights of the criteria and sub-criteria. Then, arranging the obtained weights, the sub-criteria ranking is received.
These steps can also be presented in algorithm form [79], shown below in Algorithm 1.
| Algorithm 1 Steps in the FAHP process. |
|
One of the main general drawbacks of the AHP methods (FAHP included) is the existence of incomparable criteria. This shortcoming may be overcome using the network-like presented ANP, where all the criteria, sub-criteria, and alternatives are presented as nodes, grouped in clusters, enabling them to be compared to each other as long as an interrelation exists there. In this paper, we have chosen the FAHP method only, due to the fact that it enables the expert to decompose a complex problem into a few simplified steps. We have, however, extended the model to include five points of view instead of the usual three. The decision maker can hence easily express their opinion using descriptive grades, and these linguistic values can be further explained with a mathematical approach.
4. Results and Discussion
We firstly discuss the main criteria ranking, both for AHP and FAHP, with three points of view (pessimistic, balanced, and optimistic). Afterwards, we rank individual sub-criteria. Finally, we conduct the ranking of all nineteen sub-criteria using the extended FAHP, with semi-pessimistic and semi-optimistic points of view, and test our ranking using the Spearman rank correlation coefficient [80].
In the FAHP process, we have firstly calculated a fuzzy comparison matrix and weights for the main five criteria, as shown in Table 3, and since , the matrix is consistent.

Table 3.
Fuzzy comparison matrix and weights for the criteria. (, ).
In addition, the ranking of main criteria for both AHP and pessimistic, balanced, and optimistic FAHP points of view (with corresponding , and , respectively) is presented in Figure 4. In both AHP and all three FAHP cases, criteria -Service Quality ranked highest, while criteria (customer support) ranked lowest. This is somewhat expected, as Quality of Service, and its superset Quality of Experience, are increasing factors in the Internet presence of B2C websites. This corresponds to the finding of [42] for the pandemic shopping trends. In AHP ranking, our results show that and have the same rank, while in all three cases of FAHP, no two criteria are ranked the same. Using FAHP, a decision-maker can fine-tune their actions to increase an aspect of their B2C website.
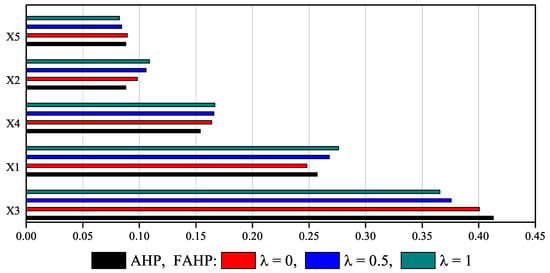
Figure 4.
Ranking of main criteria.
Comparing points of view for main criteria, we can observe that a optimistic point of view (i.e., ) does not always yield a higher rank when compared to the pessimistic view. For instance, for and , the highest and lowest criteria, the pessimistic point of view ranked higher when compared to the corresponding optimistic view.
The ranking of sub-criteria is firstly conducted in the same manner as the ranking of the main criteria, and fuzzy comparison matrices are given in Table 4, Table 5, Table 6, Table 7 and Table 8. The results show that all matrices are consistent. Similar to the main criteria comparison, the AHP method yields equal ranking in some cases, namely, in -Information. Out of five sub-criteria, we have two pairs of equal rankings, in the highest and second highest rank. This can also be observed in the triangular fuzzy numbers for in Figure 5. Sub-criteria and , corresponding to Comparison and Search functions, respectively, have equal ranking. These two sub-criteria both require customer input, and a B2C website with a better user-friendly design would most certainly aid in these functions. The second highest ranking pair, and , referring to contact information and multilingual options, respectively, do not require user input like the previous case but rather serve to increase customers’ trust in the company. Both groups are very important in the post-COVID world as e-trust, as stated in the introductory section, is an ever-increasing factor for B2C websites.

Table 4.
Fuzzy comparison matrix for the sub-criteria X1. (, ).

Table 5.
Fuzzy comparison matrix for the sub-criteria X2. (, ).

Table 6.
Fuzzy comparison matrix for the sub-criteria X3. (, ).

Table 7.
Fuzzy comparison matrix for the sub-criteria X4. (, ).

Table 8.
Fuzzy comparison matrix for the sub-criteria X5. (, ).
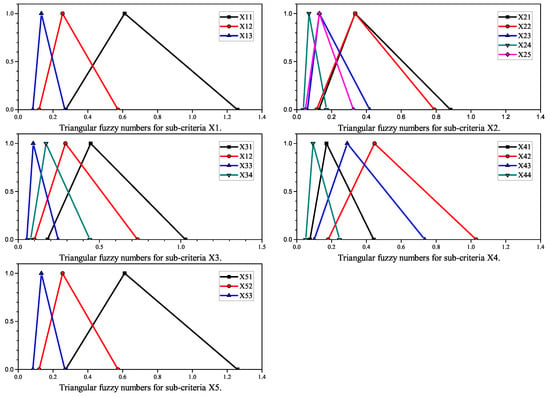
Figure 5.
Triangular fuzzy numbers for criteria X.
Similar to the main criteria case, FAHP distinguishes between sub-criteria; their rankings are unique, regardless of point of view.
Finally, we extend the process of FAHP by adding the semi-pessimistic () and semi-optimistic () points of view. The final ranking sub-criteria is given in Figure 6. We observe that while the sub-criteria from , namely , still ranked highest; however, the remaining sub-criteria from Service Quality, , , and ranked third, fifth, and eleventh, respectively. Furthermore, the highest ranked sub-criteria from customer support, namely, , corresponding to item tracking, ranked seventh overall, is times higher than and times higher for the AHP case and about and times higher in the FAHP case (averaged over all points of view). The high overall ranking of tracking and tracing reflects the shift in online transactions, which includes item delivery during the pandemic and, more importantly, in the post-COVID world.
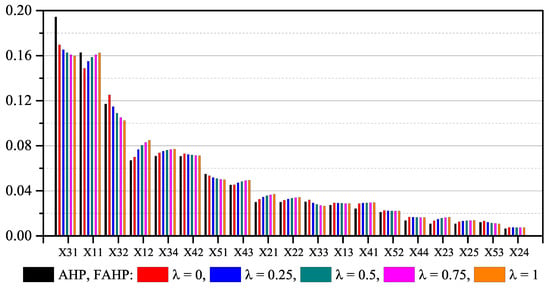
Figure 6.
Final ranking of sub-criteria.
We have applied different solving techniques in this paper, which can, in general, lead to inconsistencies or disagreement. For the purpose of estimation and analysis of ranking similarities applying the AHP and the Extended FAHP to all sub-criteria influencing e-commerce platforms, we have conducted fifteen different rankings using the Spearman rank correlation coefficient: [80]:
where n is the number of elements in the ranking and and represent the ranks of the k-th element in the compared rankings. By applying Equation (17), all compared results are presented in Figure 7, and since , it can be concluded that all rankings have high similarity [81].
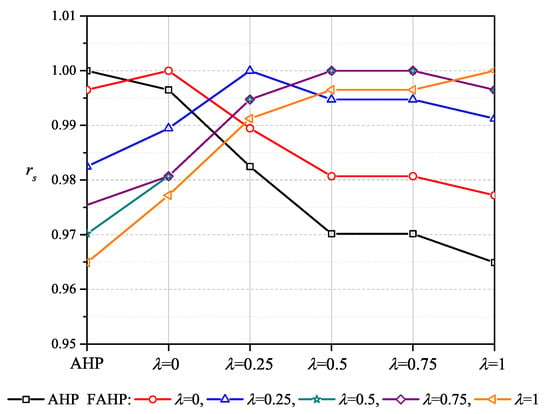
Figure 7.
Ranking similarity.
5. Conclusions
Due to the ongoing pandemic, the previous two years have made a significant impact in all aspects of life—everyday activities, education, healthcare, security, economy, and trade, and have hence acclimated people to a new form of reality. Certain situations, such as lockdowns, paved the way for the ever-growing online presence. The struggle of small and medium enterprises to compete on the market therefore heavily relied on their shift towards online commerce. Reports that show multiple increments of online sales are an indicator that the trend of online commerce will continue to exist and grow in the post-COVID world.
The paper has investigated the problem of e-commerce management and the influence of various different factors. Indicators associated with digital platforms have been divided into five groups, involving security, information, quality, design, and support aspects. Using AHP and Extended FAHP, nineteen sub-criteria were ranked to determine the preferred ones in the process of e-commerce evaluation. The obtained results indicated that the proposed methods are entirely capable of estimating the influence of factors and sub-factors on online trade commerce. Considering the obtained weights for each sub-criteria and all five values of in the FAHP case, factors such as trust and loyalty, safe payment, exchange or return, and account security have the most significant effect on successful e-commerce platform design, while the FAQs, multilingual option, and contact information deemed the least significant. In the AHP case, the same sub-criteria from the service quality and security, privacy, and authority are ranked highest, while those from the information sector are of least importance.
Although our proposed method gives insight into several advantages and potentials in the field of B2C e-commerce, there are limitations to this work. However, these limitations might lead to future possibilities and steps forwards in our future research. Our use of AHP, because of its top-down direction structure and comparisons of criteria from one level with all criteria from the upper level, can lead to incomparable sub-criteria. This challenge can be overcome utilizing ANP, which allows clusters and elements, as well as interactions between the elements of hierarchy. This approach can further lead to more accurate results in the sub-criteria comparisons.
Another limitation presents the impossibility to examine the market solely from the customers’ point of view, which was the main reason for conducting interviews with experts in management and sales from companies with a range of up to two million clients. Based on their experience in e-commerce companies, we have obtained the requirements and experts’ judgments related to e-commerce businesses similar to those given by their clients.
The findings in this paper present a starting point for our continual research in the e-business area. Depending on the type of e-business and/or e-trade, we plan to add or remove certain factors or sub-factors. Furthermore, an extension to this research could focus on the practical application for the ranking of the alternatives of given websites. Finally, various MCDM methods, such as AHP, TOPSIS, and VIKOR, could be applied with fuzzy logic, Pythagorean fuzzy numbers, Intuitionictic fuzzy numbers, z-Numbers, and/or Spherical fuzzy numbers.
Author Contributions
Conceptualization: D.J.S. and N.Z., Methodology: D.J.S. and N.Z. and N.O.V., Software: D.J.S., Validation: N.O.V. and N.Z., Formal analysis: N.Z. and D.J.S., Investigation D.J.S. and N.O.V., Resources: N.O.V. and D.J.S., Data curation: N.Z. and D.J.S., Writing—Original draft preparation: N.Z. and N.O.V., Writing—Review and editing: N.O.V. and D.J.S., Visualization: D.J.S. and N.Z., Supervision: N.Z., N.O.V. and D.J.S., Project administration: D.J.S. and N.O.V., Funding acquisition: N.Z., N.O.V. and D.J.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data sharing not applicable.
Acknowledgments
The first author would like to express his sincere gratitude to Mimica R. Milošević and Dušan M. Milošević for introducing him to the field of MCDM and for their constant advice and support. This paper was supported in part by the Blockchain Technology Laboratory at Belgrade Metropolitan University, Belgrade, Serbia and in part by the Serbian Ministry of Education, Science and Technological Development through Mathematical Institute of the Serbian Academy of Sciences and Arts.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hoffman, D.; Novak, T.P. A new marketing paradigm for electronic commerce. Inf. Soc. 1997, 13, 43–54. [Google Scholar]
- DeLone, W.H.; McLean, E.R. Measuring e-commerce success: Applying the DeLone & McLean information systems success model. Int. J. Electron. Commer. 2004, 9, 31–47. [Google Scholar]
- Liang, T.P.; Turban, E. Introduction to the special issue social commerce: A research framework for social commerce. Int. J. Electron. Commer. 2011, 16, 5–14. [Google Scholar] [CrossRef] [Green Version]
- E-Commerce and E-Business. Information and Communication Technology in Organizations: Adoption, Implementation, Use and Effects; Saga Publications: London, UK, 2012; pp. 139–162. [Google Scholar]
- Shaw, M.J. Electronic commerce: State of the art. In Handbook on Electronic Commerce; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2000; pp. 3–24. [Google Scholar]
- Bhasin, H. Top E-Commerce Companies in the World; Marketing 91: Mumbai, India, 2019. [Google Scholar]
- Ashraf, A.R.; Thongpapanl, N.T.; Spyropoulou, S. The connection and disconnection between e-commerce businesses and their customers: Exploring the role of engagement, perceived usefulness, and perceived ease-of-use. Electron. Commer. Res. Appl. 2016, 20, 69–86. [Google Scholar] [CrossRef]
- Ribbink, D.; Van Riel, A.C.; Liljander, V.; Streukens, S. Comfort your online customer: Quality, trust and loyalty on the internet. Manag. Serv. Qual. Int. J. 2004, 14, 446–456. [Google Scholar] [CrossRef] [Green Version]
- Hong, I.B.; Cho, H. The impact of consumer trust on attitudinal loyalty and purchase intentions in B2C e-marketplaces: Intermediary trust vs. seller trust. Int. J. Inf. Manag. 2011, 31, 469–479. [Google Scholar] [CrossRef]
- Gurung, A.; Raja, M. Online privacy and security concerns of consumers. Inf. Comput. Secur. 2016, 24, 348–371. [Google Scholar] [CrossRef]
- Ratnasingam, P.; Pavlou, P.A. Technology trust in internet-based interorganizational electronic commerce. J. Electron. Commer. Organ. (JECO) 2003, 1, 17–41. [Google Scholar] [CrossRef] [Green Version]
- Choi, Y.; Mai, D.Q. The sustainable role of the e-trust in the B2C e-commerce of Vietnam. Sustainability 2018, 10, 291. [Google Scholar] [CrossRef] [Green Version]
- Kim, D.J.; Song, Y.I.; Braynov, S.B.; Rao, H.R. A multidimensional trust formation model in B-to-C e-commerce: A conceptual framework and content analyses of academia/practitioner perspectives. Decis. Support Syst. 2005, 40, 143–165. [Google Scholar] [CrossRef]
- Holsapple, C.W.; Sasidharan, S. The dynamics of trust in B2C e-commerce: A research model and agenda. Inf. Syst.-Bus. Manag. 2005, 3, 377–403. [Google Scholar] [CrossRef]
- Aydin, S.; Kahraman, C. Evaluation of e-commerce website quality using fuzzy multi-criteria decision making approach. IAENG Int. J. Comput. Sci. 2012, 39, 64–70. [Google Scholar]
- Wang, C.N.; Dang, T.T.; Hsu, H.P.; Nguyen, N.A.T. Evaluating sustainable last-mile delivery (LMD) in B2C E-commerce using two-stage fuzzy MCDM approach: A case study from Vietnam. IEEE Access 2021, 9, 146050–146067. [Google Scholar] [CrossRef]
- Milošević, D.M.; Milošević, M.R.; Simjanović, D.J. Implementation of adjusted fuzzy AHP method in the assessment for reuse of industrial buildings. Mathematics 2020, 8, 1697. [Google Scholar] [CrossRef]
- Kutlu Gündoğdu, F.; Kahraman, C. Spherical fuzzy sets and spherical fuzzy TOPSIS method. J. Intell. Fuzzy Syst. 2019, 36, 337–352. [Google Scholar] [CrossRef]
- Zhang, Y.; Deng, X.; Wei, D.; Deng, Y. Assessment of E-Commerce security using AHP and evidential reasoning. Expert Syst. Appl. 2012, 39, 3611–3623. [Google Scholar] [CrossRef]
- Lee, Y.; Kozar, K.A. Investigating the effect of website quality on e-business success: An analytic hierarchy process (AHP) approach. Decis. Support Syst. 2006, 42, 1383–1401. [Google Scholar] [CrossRef]
- Chen, C.F. Applying the analytical hierarchy process (AHP) approach to convention site selection. J. Travel Res. 2006, 45, 167–174. [Google Scholar] [CrossRef]
- Chiu, W.Y.; Tzeng, G.H.; Li, H.L. Developing e-store marketing strategies to satisfy customers’ needs using a new hybrid gray relational model. Int. J. Inf. Technol. Decis. Mak. 2014, 13, 231–261. [Google Scholar] [CrossRef]
- Triantaphyllou, E.; Lin, C.T. Development and evaluation of five fuzzy multiattribute decision-making methods. Int. J. Approx. Reason. 1996, 14, 281–310. [Google Scholar] [CrossRef] [Green Version]
- Sanayei, A.; Mousavi, S.F.; Yazdankhah, A. Group decision making process for supplier selection with VIKOR under fuzzy environment. Expert Syst. Appl. 2010, 37, 24–30. [Google Scholar] [CrossRef]
- Ostovare, M.; Shahraki, M.R. Evaluation of hotel websites using the multicriteria analysis of PROMETHEE and GAIA: Evidence from the five-star hotels of Mashhad. Tour. Manag. Perspect. 2019, 30, 107–116. [Google Scholar] [CrossRef]
- Chmielarz, W.; Zborowski, M. The Selection and Comparison of the Methods Used to Evaluate the Quality of E-Banking Websites: The Perspective of Individual Clients. Procedia Comput. Sci. 2020, 176, 1903–1922. [Google Scholar] [CrossRef]
- Abdullah, L.; Ramli, R.; Bakodah, H.O.; Othman, M. Developing a causal relationship among factors of e-commerce: A decision making approach. J. King Saud-Univ.-Comput. Inf. Sci. 2020, 32, 1194–1201. [Google Scholar] [CrossRef]
- Wu, W.W.; Lee, Y.T. Developing global managers’ competencies using the fuzzy DEMATEL method. Expert Syst. Appl. 2007, 32, 499–507. [Google Scholar] [CrossRef]
- Nisar, T.M.; Prabhakar, G. What factors determine e-satisfaction and consumer spending in e-commerce retailing? J. Retail. Consum. Serv. 2017, 39, 135–144. [Google Scholar] [CrossRef]
- Zameer, H.; Wang, Y.; Yasmeen, H. Reinforcing green competitive advantage through green production, creativity and green brand image: Implications for cleaner production in China. J. Clean. Prod. 2020, 247, 119119. [Google Scholar] [CrossRef]
- Kaya, T. Multi-attribute evaluation of website quality in E-business using an integrated fuzzy AHPTOPSIS methodology. Int. J. Comput. Intell. Syst. 2010, 3, 301–314. [Google Scholar]
- Aggarwal, A.G.; Aakash. Multi-criteria-based prioritisation of B2C e-commerce website. Int. J. Soc. Syst. Sci. 2018, 10, 201–222. [Google Scholar] [CrossRef]
- Yu, X.; Guo, S.; Guo, J.; Huang, X. Rank B2C e-commerce websites in e-alliance based on AHP and fuzzy TOPSIS. Expert Syst. Appl. 2011, 38, 3550–3557. [Google Scholar] [CrossRef]
- Liang, R.; Wang, J.; Zhang, H. Evaluation of e-commerce websites: An integrated approach under a single-valued trapezoidal neutrosophic environment. Knowl.-Based Syst. 2017, 135, 44–59. [Google Scholar] [CrossRef]
- Del Vasto-Terrientes, L.; Valls, A.; Slowinski, R.; Zielniewicz, P. ELECTRE-III-H: An outranking-based decision aiding method for hierarchically structured criteria. Expert Syst. Appl. 2015, 42, 4910–4926. [Google Scholar] [CrossRef]
- Dey, S.; Jana, B.; Gourisaria, M.K.; Mohanty, S.; Chatterjee, R. Evaluation of Indian B2C E-shopping websites under multi criteria decision-making using fuzzy hybrid technique. Int. J. Appl. Eng. Res. 2015, 10, 24551–24580. [Google Scholar]
- Chou, W.C.; Cheng, Y.P. A hybrid fuzzy MCDM approach for evaluating website quality of professional accounting firms. Expert Syst. Appl. 2012, 39, 2783–2793. [Google Scholar] [CrossRef]
- Kang, D.; Jang, W.; Park, Y. Evaluation of e-commerce websites using fuzzy hierarchical TOPSIS based on ES-QUAL. Appl. Soft Comput. 2016, 42, 53–65. [Google Scholar] [CrossRef]
- Ong, C.E.; Teh, D. Redress procedures expected by consumers during a business-to-consumer e-commerce dispute. Electron. Commer. Res. Appl. 2016, 17, 150–160. [Google Scholar] [CrossRef]
- Wang, C.N.; Dang, T.T.; Nguyen, N.A.T.; Le, T.T.H. Supporting better decision-making: A combined grey model and data envelopment analysis for efficiency evaluation in e-commerce marketplaces. Sustainability 2020, 12, 10385. [Google Scholar] [CrossRef]
- Li, R.; Sun, T. Assessing Factors for Designing a Successful B2C E-Commerce Website Using Fuzzy AHP and TOPSIS-Grey Methodology. Symmetry 2020, 12, 363. [Google Scholar] [CrossRef] [Green Version]
- E-Commerce Rising Stars of the Western Balkans. Available online: https://www.intellinews.com/e-commerce-rising-stars-of-the-western-balkans-205556/ (accessed on 8 August 2021).
- Badre, A.N. Shaping Web usability: Interaction design in context. Ubiquity 2002, 2002, 1. [Google Scholar] [CrossRef]
- Eastlick, M.A.; Lotz, S.L.; Warrington, P. Understanding online B-to-C relationships: An integrated model of privacy concerns, trust, and commitment. J. Bus. Res. 2006, 59, 877–886. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, W.; Xu, J.D.; Liu, T.; Gu, J. Perceived information transparency in B2C e-commerce: An empirical investigation. Inf. Manag. 2018, 55, 912–927. [Google Scholar] [CrossRef]
- Zhang, P.; Von Dran, G.M. Satisfiers and dissatisfiers: A two-factor model for website design and evaluation. J. Am. Soc. Inf. Sci. 2000, 51, 1253–1268. [Google Scholar] [CrossRef] [Green Version]
- Özkan, B.; Özceylan, E.; Kabak, M.; Dağdeviren, M. Evaluating the websites of academic departments through SEO criteria: A hesitant fuzzy linguistic MCDM approach. Artif. Intell. Rev. 2020, 53, 875–905. [Google Scholar] [CrossRef]
- SEVİM, N. The Effect of E-service Quality, E-trust and E-satisfaction on Formation Online Customer Loyalty. Bus. Manag. Stud. Int. J. 2018, 6, 107. [Google Scholar] [CrossRef]
- Zhu, D.S.; Kuo, M.J.; Munkhbold, E. Effects of e-customer satisfaction and e-trust on e-loyalty: Mongolian online shopping behavior. In Proceedings of the 2016 5th IIAI International Congress on Advanced Applied Informatics (IIAI-AAI), Kumamoto, Japan, 10–14 July 2016; pp. 847–852. [Google Scholar]
- Leung, K.; Choy, K.L.; Siu, P.K.; Ho, G.T.; Lam, H.; Lee, C.K. A B2C e-commerce intelligent system for re-engineering the e-order fulfilment process. Expert Syst. Appl. 2018, 91, 386–401. [Google Scholar] [CrossRef]
- Kim, J.; Jin, B.; Swinney, J.L. The role of etail quality, e-satisfaction and e-trust in online loyalty development process. J. Retail. Consum. Serv. 2009, 16, 239–247. [Google Scholar] [CrossRef]
- Cunningham, M. Smart Things to Know about E-Commerce; Capstone: Oxford, UK, 2002. [Google Scholar]
- Ivory, M. Automated Web Site Evaluation: Researchers’ and Practitioners’ Perspectives; Kluwer Academic Publishers: London, UK, 2003. [Google Scholar]
- Oppenheim, C.; Ward, L. Evaluation of web sites for B2C e-commerce. In Aslib Proceedings; Emerald Group Publishing Limited: Bingley, UK, 2006. [Google Scholar]
- Rahhal, W. The effects of service quality dimensions on customer satisfaction: An empirical investigation in Syrian mobile telecommunication services. Int. J. Bus. Manag. Invent. 2015, 4, 81–89. [Google Scholar]
- Lin, H.F. The impact of website quality dimensions on customer satisfaction in the B2C e-commerce context. Total Qual. Manag. Bus. Excell. 2007, 18, 363–378. [Google Scholar] [CrossRef]
- Abedi, F.; Zeleznikow, J.; Bellucci, E. Universal standards for the concept of trust in online dispute resolution systems in e-commerce disputes. Int. J. Law Inf. Technol. 2019, 27, 209–237. [Google Scholar] [CrossRef]
- Van der Merwe, R.; Bekker, J. A framework and methodology for evaluating e-commerce web sites. Internet Res. 2003, 13, 330–341. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning—I. Inf. Sci. 1975, 8, 199–249. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning—II. Inf. Sci. 1975, 8, 301–357. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning—III. Inf. Sci. 1975, 9, 43–80. [Google Scholar] [CrossRef]
- Dimić, V.; Milošević, M.; Milošević, D.; Stević, D. Adjustable model of renewable energy projects for sustainable development: A case study of the Nišava district in Serbia. Sustainability 2018, 10, 775. [Google Scholar] [CrossRef] [Green Version]
- Sun, C.C. A performance evaluation model by integrating fuzzy AHP and fuzzy TOPSIS methods. Expert Syst. Appl. 2010, 37, 7745–7754. [Google Scholar] [CrossRef]
- Chang, D.Y. Applications of the extent analysis method on fuzzy AHP. Eur. J. Oper. Res. 1996, 95, 649–655. [Google Scholar] [CrossRef]
- Wang, W.M.; Lee, A.H.; Chang, D.T. An integrated FA-FEAHP approach on the social indicators of Taiwan’s green building. Glob. Bus. Econ. Rev. 2009, 11, 304–316. [Google Scholar] [CrossRef]
- Kulak, O.; Durmuşoğlu, M.B.; Kahraman, C. Fuzzy multi-attribute equipment selection based on information axiom. J. Mater. Process. Technol. 2005, 169, 337–345. [Google Scholar] [CrossRef]
- Satty, T.L. The Analytic Hierarchy Process; McGraw-Hill International: New York, NY, USA, 1980. [Google Scholar]
- Waas, T.; Hugé, J.; Block, T.; Wright, T.; Benitez-Capistros, F.; Verbruggen, A. Sustainability assessment and indicators: Tools in a decision-making strategy for sustainable development. Sustainability 2014, 6, 5512–5534. [Google Scholar] [CrossRef] [Green Version]
- Yager, R.R. Uncertainty modeling using fuzzy measures. Knowl.-Based Syst. 2016, 92, 1–8. [Google Scholar] [CrossRef]
- Li, D.F. An approach to fuzzy multiattribute decision making under uncertainty. Inf. Sci. 2005, 169, 97–112. [Google Scholar] [CrossRef]
- Kahraman, C.; Cebeci, U.; Ruan, D. Multi-attribute comparison of catering service companies using fuzzy AHP: The case of Turkey. Int. J. Prod. Econ. 2004, 87, 171–184. [Google Scholar] [CrossRef]
- Srdjevic, B.; Medeiros, Y.D.P. Fuzzy AHP assessment of water management plans. Water Resour. Manag. 2008, 22, 877–894. [Google Scholar] [CrossRef]
- Miloševic, D.; Miloševic, M.; Stanojevic, A.; Dimic, V.; Miloševic, A. Application of FAHP Method in the Process of Building Construction from the Aspect of Energy Efficiency. In Proceedings of the 4th International Conference Mechanical Engineering in XXI Century, Niš, Serbia, 19–20 April 2018; pp. 19–20. [Google Scholar]
- Chou, T.Y.; Chen, Y.T. Applying fuzzy AHP and TOPSIS method to identify key organizational capabilities. Mathematics 2020, 8, 836. [Google Scholar] [CrossRef]
- Ghorui, N.; Ghosh, A.; Algehyne, E.A.; Mondal, S.P.; Saha, A.K. AHP-TOPSIS inspired shopping mall site selection problem with fuzzy data. Mathematics 2020, 8, 1380. [Google Scholar] [CrossRef]
- Milošević, M.R.; Milošević, D.M.; Stević, D.M.; Stanojević, A.D. Smart city: Modeling key indicators in Serbia using IT2FS. Sustainability 2019, 11, 3536. [Google Scholar] [CrossRef] [Green Version]
- Milošević, M.R.; Milošević, D.M.; Stanojević, A.D.; Stević, D.M.; Simjanović, D.J. Fuzzy and Interval AHP Approaches in Sustainable Management for the Architectural Heritage in Smart Cities. Mathematics 2021, 9, 304. [Google Scholar] [CrossRef]
- Liou, T.S.; Wang, M.J.J. Ranking fuzzy numbers with integral value. Fuzzy Sets Syst. 1992, 50, 247–255. [Google Scholar] [CrossRef]
- Milošević, A.; Milošević, M.; Milošević, D.; Selimi, A. AHP multi-criteria method for sustainable development in construction. In Proceedings of the 4th International Conference Contemporary Achievements in Civil Engineering, Građevinski Fakultet Subotica, Subotica, Srbija, 22 April 2016; pp. 929–938. [Google Scholar]
- Ceballos, B.; Lamata, M.T.; Pelta, D.A. A comparative analysis of multi-criteria decision-making methods. Prog. Artif. Intell. 2016, 5, 315–322. [Google Scholar] [CrossRef]
- Vinogradova-Zinkevič, I.; Podvezko, V.; Zavadskas, E.K. Comparative Assessment of the Stability of AHP and FAHP Methods. Symmetry 2021, 13, 479. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).