A Randomized Distributed Kaczmarz Algorithm and Anomaly Detection

Abstract

The Kaczmarz algorithm is an iterative method for solving systems of linear equations. We introduce a randomized Kaczmarz algorithm for solving systems of linear equations in a distributed environment, i.e., the equations within the system are distributed over multiple nodes within a network. The modification we introduce is designed for a network with a tree structure that allows for passage of solution estimates between the nodes in the network. We demonstrate that the algorithm converges to the solution, or the solution of minimal norm, when the system is consistent. We also prove convergence rates of the randomized algorithm that depend on the spectral data of the coefficient matrix and the random control probability distribution. In addition, we demonstrate that the randomized algorithm can be used to identify anomalies in the system of equations when the measurements are perturbed by large, sparse noise.

1. Introduction

The Kaczmarz method [1] is an iterative algorithm for solving a system of linear equations $A\overrightarrow{x}=\overrightarrow{b}$, where A is an $m\times k$ matrix. Written out, the equations are ${\overrightarrow{a}}_i^{*}\overrightarrow{x}=b_i$ for $i=1,\dots ,m$, where ${\overrightarrow{a}}_i^{*}$ is the ith row of the matrix A. Given a solution guess ${\overrightarrow{x}}^{(n-1)}$ and an equation number i, we calculate $r_i=b_i-{\overrightarrow{a}}_i^{*}{\overrightarrow{x}}^{(n-1)}$ (the residual for equation i), and define

$${\overrightarrow{x}}^{\left(n\right)}={\overrightarrow{x}}^{(n-1)}+\frac{r_i}{\parallel {\overrightarrow{a}}_i{\parallel }^2}{\overrightarrow{a}}_i.$$

(1)

This makes the residual of ${\overrightarrow{x}}^{\left(n\right)}$ in equation i equal to 0. Here and elsewhere, $\parallel ·\parallel$ is the usual Euclidean (${\ell }^2$) norm. We iterate repeatedly through all equations (i.e., we consider ${lim}_{n\to \infty }{\overrightarrow{x}}^{\left(n\right)}$ where $n\equiv imodm$, so the equations are repeated cyclically). Kaczmarz proved that if the system of equations has a unique solution, then ${\overrightarrow{x}}^{\left(n\right)}$ converges to that solution. Later, it was proved in [2] that if the system is consistent (but the solution is not unique), then the sequence converges to the solution of minimal norm. Likewise, it was proved in [3,4] that if inconsistent, a relaxed version of the algorithm can provide approximations to a weighted least-squares solution.

A protocol was introduced in [5] to utilize the Kaczmarz algorithm to solve a system of equations that are distributed across a network; each node on the network has one equation, and the equations are indexed by the nodes of the network. We consider the network to be a graph and select from the graph a minimal spanning tree. The iteration begins with a single estimate of the solution at the root of the tree. The root updates this estimate using the Kaczmarz update as in Equation (1) according to its equation then passes that updated estimate to its neighbors. Each of these nodes in turn updates the estimate it receives using its equation then passes that updated estimate to it neighbors (except its predecessor). This recursion continues until the estimates reach the leaves of the tree. The multiple estimates are then aggregated by each leaf passing its estimate to its predecessor; each of these nodes then take weighted averages of all of its inputs. This second recursion continues until reaching the root; the single estimate at the root then becomes the input for the next iteration. To formalize this, we first introduce some notation.

1.1. Notation

A tree is a connected graph with no cycles. We denote arbitrary nodes (vertices) of a tree by v, u. Let V denote the collection of all nodes in the tree. Our tree will be rooted; the root of the tree is denoted by r. Following the notation from MATLAB, when v is on the path from r to u, we will say that v is a predecessor of u and write $u\prec v$. Conversely, u is a successor of v. By immediate successor of v we mean a successor u such that there is an edge between v and u (this is referred to as a child in graph theory parlance [6]); similarly, v is an immediate predecessor (i.e., parent) if v is a predecessor of u. We denote the set of all immediate successors of node v by $\mathcal{C}\left(v\right)$; we will also use $\mathcal{P}\left(u\right)$ to denote the parent (i.e., immediate predecessor) of node u. A node without a successor is called a leaf; leaves of the tree are denoted by ℓ. We will denote the set of all leaves by $\mathcal{L}$. Often we will have need to enumerate the leaves as ${\ell }_1,\dots ,{\ell }_t$, hence t denotes the number of leaves.

A weight w is a nonnegative function on the edges of the tree; we denote this by $w(u,v)$, where u and v are nodes that have an edge between them. We assume $w(u,v)=w(v,u)$, though we will typically write $w(u,v)$ when $u\prec v$. When $u\prec v$, but u is not a immediate successor, we write

$$w(u,v):=\prod _{j=1}^{J-1}w(u_{j+1},u_j)$$

(2)

where $v=u_1,\dots ,u_J=u$ is a path from v to u.

We let $\mathrm{\Pi }$ denote the affine orthogonal projection onto the solution space of the matrix equation $A\overrightarrow{x}=\overrightarrow{b}$. For a positive semidefinite matrix C, ${\lambda }_{max}\left(C\right)$ denotes the largest eigenvalue, and ${\lambda }_{min}^{nz}\left(C\right)$ denotes the smallest nonzero eigenvalue.

1.2. The Distributed Kaczmarz Algorithm

The iteration begins with an estimate, say ${\overrightarrow{x}}^{\left(n\right)}$ at the root of the tree (we denote this by ${\overrightarrow{x}}_r^{\left(n\right)}$). Each node u receives from its immediate predecessor v an input estimate ${\overrightarrow{x}}_v^{\left(n\right)}$ and generates a new estimate via the Kaczmarz update:

$${\overrightarrow{x}}_u^{\left(n\right)}={\overrightarrow{x}}_v^{\left(n\right)}+{\displaystyle \frac{r_u\left({\overrightarrow{x}}_v^{\left(n\right)}\right)}{\parallel {\overrightarrow{a}}_u{\parallel }^2}}{\overrightarrow{a}}_u,$$

(3)

where the residual is given by

$$r_u\left({\overrightarrow{x}}_v^{\left(n\right)}\right):=b_u-{\overrightarrow{a}}_u^{*}{\overrightarrow{x}}_v^{\left(n\right)}.$$

(4)

Node u then passes this estimate to all of its immediate successors, and the process is repeated recursively. We refer to this as the dispersion stage. Once this process has finished, each leaf ℓ of the tree now possesses an estimate: ${\overrightarrow{x}}_{\ell }^{\left(n\right)}$.

The next stage, which we refer to as the pooling stage, proceeds as follows. For each leaf, set ${\overrightarrow{y}}_{\ell }^{\left(n\right)}={\overrightarrow{x}}_{\ell }^{\left(n\right)}$. Each node v calculates an updated estimate as:

$${\overrightarrow{y}}_v^{\left(n\right)}=\sum _{u\in \mathcal{C}\left(v\right)}w(u,v){\overrightarrow{y}}_u^{\left(n\right)},$$

(5)

subject to the constraints that $w(u,v)>0$ when $u\in \mathcal{C}\left(v\right)$ (the set of all immediate successors of v) and ${\sum }_{u\in \mathcal{C}\left(v\right)}w(u,v)=1$. This process continues until reaching the root of the tree, resulting in the estimate ${\overrightarrow{y}}_r^{\left(n\right)}$.

We set ${\overrightarrow{x}}^{(n+1)}={\overrightarrow{y}}_r^{\left(n\right)}$, and repeat the iteration. The updates in the dispersion stage (Equation (3)) and pooling stage (Equation (5)) are illustrated in Figure 1.

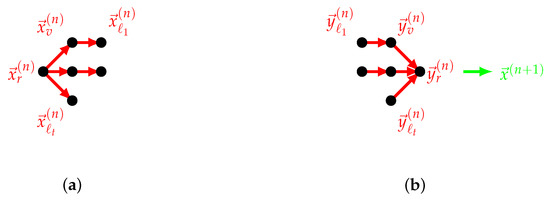
Figure 1. Illustration of updates in the distributed Kaczmarz algorithm with measurements indexed by nodes of the tree. (a) Updates disperse through nodes, (b) updates pool and pass to next iteration.

1.3. Related Work

Recent variations on the Kaczmarz method allowed for relaxation parameters [2], re-ordering equations to speed up convergence [7], or considering block versions of the Kaczmarz method with relaxation matrices ${\mathrm{\Omega }}_i$ [3]. Relatively recently, choosing the next equation randomly has been shown to improve the rate of convergence of the algorithm [8,9,10]. Moreover, this randomized version of the Kaczmarz algorithm has been shown to be comparable to the gradient descent method [11]. The randomized version we present in the present article is similar to the Cimmino method [12], which was extended in [13] and is most similar to the greedy method given in [14]. Both of these methods involve averaging estimates, in addition to applying the Kaczmarz update, as we do here. In addition, a special case of our randomized variant is found in [15]. There, the authors analyze a randomized block Kaczmarz algorithm with averaging, as we do; however, they assume that the size of the block is the same for every iteration, which we do not, and they also assume that the weights associated to the averaging and the probabilities for selecting the blocks are proportional to the inverse of the norms of the row vectors of the coefficient matrix, which we also do not do. See Remark 2 for further details.

The situation we consider in the present article can be considered a distributed estimation problem. Such problems have a long history in applied mathematics, control theory, and machine learning. At a high level, similar to our approach, they all involve averaging local copies of the unknown parameter vector interleaved with update steps [16,17,18,19,20,21,22,23,24,25]. Recently, a number of protocols for gossip methods, including a variation of the Kaczmarz method, was analyzed in [26].

However, our version of the Kaczmarz method differs from previous work in a few aspects: (i) we assume an a priori fixed tree topology (which is more restrictive than typical gossip algorithms); (ii) there is no master node as in parallel algorithms, and no shared memory architecture; (iii) as we will emphasize in Theorem 2, we make no strong convexity assumptions (which is typically needed for distributed optimization algorithms, but see [27,28] for a relaxation of this requirement); and (iv) we make no assumptions on the matrix A, in particular we do not assume that it is nonnegative.

On the other end of the spectrum are algorithms that distribute a computational task over many processors arranged in a fixed network. These algorithms are usually considered in the context of parallel processing, where the nodes of the graph represent CPUs in a highly parallelized computer. See [29] for an overview.

The algorithm we are considering does not really fit either of those categories. It requires more structure than the gossip algorithms, but each node depends on results from other nodes, more than the usual distributed algorithms.

This was pointed out in [29]. For iteratively solving a system of linear equations, a Successive Over-Relaxation (SOR) variant of the Jacobi method is easy to parallelize; standard SOR, which is a variation on Gauss-Seidel, is not. The authors also consider what they call the Reynolds method, which is similar to a Kaczmarz method with all equations being updated simultaneously. Again, this method is easy to parallelize. A sequential version called Reynolds Gauss–Seidel (RGS) can only be parallelized in certain settings, such as the numerical solution of PDEs.

A distributed version of the Kaczmarz algorithm was introduced in [30]. The main ideas presented there are very similar to ours: updated estimates are obtained from prior estimates using the Kaczmarz update with the equations that are available at the node, and distributed estimates are averaged together at a single node (which the authors refer to as a fusion center; for us, it is the root of the tree). In [30], the convergence analysis is limited to the case of consistent systems of equations, and inconsistent systems are handled by Tikhonov regularization [31,32]. Another distributed version was proposed in [33], which has a shared memory architecture. Finally, the Kaczmarz algorithm has been proposed for online processing of data in [34,35]. In these studies, the processing is online and so is neither distributed nor parallel.

The Kaczmarz algorithm, at its most basic, is an alternating projection method, consisting of iterations of (affine) projections. Our distributed Kaczmarz algorithm (whether randomized or not) consists of iterations of averages of these projections. When consistent, the iterations converge to an element of the common fixed point set of these operators. This is a special case of the common fixed point problem, and our algorithm is a special case of the string-averaging methods for finding a common fixed point set. The string-averaging method has been extensively studied, for example [36,37,38,39] in the cyclic control regime, and [40,41] in the random (dynamic) control regime. An application of string averaging methods to medical imaging is found in [42]. The recent study [43] provides an overview of the method and extensive bibliography. While our situation is a special case of these methods, our analysis of the algorithm provides stronger conclusions, since our main results (Theorems 2 and 3) provide explicit estimates on the convergence rates of our algorithm, rather than the qualitative convergence results found in the literature on string-averaging methods. In addition, Theorem 3 provides a convergence analysis even in the inconsistent case, which is typically not available for string-averaging methods, as the standard convergence analysis requires that the common fixed point set is nonempty (though ref. [44] proves that for certain inconsistent cases, convergence is still guaranteed).

1.4. Main Contributions

Our main contributions in this study concern quantitative convergence results of the distributed Kaczmarz algorithm for systems of linear equations that are distributed over a tree. Just as in the case of cyclic control of the classical Kaczmarz algorithm, in our distributed setting, we are able to prove these quantitative results by introducing randomness into the control law of the method. We prove that the random control as described in Algorithm 1 converges at a rate that depends on the parameters of the probability distribution as well as the spectral data of the coefficient matrix. This is in contrast to typical distributed estimation algorithms for which convergence is guaranteed but the convergence rate is unknown.

As a result of this quantitative convergence analysis, we are able to utilize Algorithm 1 to handle the context of (unknown) corrupted equations. Again, this is in contrast to distributed estimation methods or string-averaging methods, which are known to not converge when the system of equations is inconsistent. We note that Algorithm 1 also will not necessarily converge when the system is inconsistent. We suppose that the number of corrupted equations is small in comparison to the total number of equations, and the remaining equations are in fact consistent. If we have an estimate on the number of corrupted equations, by utilizing Algorithms 2 and 3, with high probability we can identify those equations and successfully remove them, thereby finding the solution to the remaining equations. Likewise, in contrast to the string averaging methods, we are are able to prove convergence rates when the solution set (i.e., the fixed point set in the literature on string-averaging methods) is nonempty, as well as handle the case of when the fixed point set is empty provided we have an estimate on the number of outliers (i.e., the number of equations that can be removed so that the solution set of the remaining equations is nonempty). Our Algorithms 2 and 3 are nearly verbatim those found in [45], as are the theorems (i.e., Theorems 4 and 5) supporting the efficacy of those algorithms. We prove a necessary result (Lemma 1), with the remaining analysis as in [45], which also has an extensive analysis of numerical experiments that we do not reproduce here.

Algorithm 1 Randomized Tree Kaczmarz (RTK) algorithm.

1: Input A, $\overrightarrow{b}$, ${\overrightarrow{x}}^{\left(0\right)}$, $\mathcal{D}$, K 2: for  $k\le K$do 3:    Draw sample $Z\sim \mathcal{D}$ 4:    if $r\in Z$ then 5:      ${\overrightarrow{x}}_r={\overrightarrow{x}}^{(k-1)}+{\displaystyle \frac{b_r-{\overrightarrow{a}}_r^{*}{\overrightarrow{x}}^{(k-1)}}{\parallel {\overrightarrow{a}}_r{\parallel }^2}}{\overrightarrow{a}}_r$ 6:    else 7:      ${\overrightarrow{x}}_r={\overrightarrow{x}}^{(k-1)}$ 8:    end if 9:    for $q=1,\dots ,Depth$ do 10:      for $v\mathrm{with}d(v,r)=q$ do 11:         if $v\in Z$ then 12:           ${\overrightarrow{x}}_v={\overrightarrow{x}}_{\mathcal{P}\left(v\right)}+{\displaystyle \frac{b_v-{\overrightarrow{a}}_v^{*}{\overrightarrow{x}}_{\mathcal{P}\left(v\right)}}{\parallel {\overrightarrow{a}}_v{\parallel }^2}}{\overrightarrow{a}}_v$ 13:         else 14:           ${\overrightarrow{x}}_v={\overrightarrow{x}}_{\mathcal{P}\left(v\right)}$ 15:         end if 16:      end for 17:    end for 18:    for $\ell \in \mathcal{L}$ do 19:      ${\overrightarrow{y}}_{\ell }={\overrightarrow{x}}_{\ell }$ 20:    end for 21:    for $q=Depth-1,\dots ,0$ do 22:      for $u\mathrm{with}d(u,r)=q$ do 23:         $T\left(u\right)=\{v\in \mathcal{C}\left(u\right):{\overrightarrow{y}}_v\ne {\overrightarrow{x}}_u\}$ 24:         if $T\left(u\right)\ne \varnothing$ then 25:           ${\overrightarrow{y}}_u={\displaystyle \frac{1}{\left|T\right(u\left)\right|}}{\sum }_{v\in T\left(u\right)}{\overrightarrow{y}}_v$ 26:         else 27:           ${\overrightarrow{y}}_u={\overrightarrow{x}}_u$ 28:         end if 29:      end for 30:    end for 31:    ${\overrightarrow{x}}^{\left(k\right)}={\overrightarrow{y}}_r$ 32: end for 33: return  ${\overrightarrow{x}}^{\left(K\right)}$

Algorithm 2 Multiple Round Randomized Tree Kaczmarz (MRRTK) algorithm.

1: Input A, $\overrightarrow{b}$, ${\overrightarrow{x}}^{\left(0\right)}$, $\mathcal{D}$, K, W, d 2: $S=\varnothing$ 3: for  $i\le W$do 4:    ${\overrightarrow{x}}^{(K,i)}=RTK(A,\overrightarrow{b},{\overrightarrow{x}}^0,\mathcal{D},K)$ 5:    $D=argma{x}_{D\subset \left[A\right],\left|D\right|=d}{\sum }_{j\in D}{|A{\overrightarrow{x}}^{(K,i)}-\overrightarrow{b}|}_j$ 6:    $S=S\cup D$ 7: end for 8: return $\overrightarrow{x}$, where $A_{S^C}\overrightarrow{x}={\overrightarrow{b}}_{S^C}$

Algorithm 3 Multiple Round Randomized Tree Kaczmarz (MRRTKUS) algorithm with Unique Selection.

1: Input A, $\overrightarrow{b}$, ${\overrightarrow{x}}^{\left(0\right)}$, $\mathcal{D}$, K, W, d 2: $S=\varnothing$ 3: for  $i\le W$do 4:    ${\overrightarrow{x}}^{(K,i)}=RTK(A,\overrightarrow{b},{\overrightarrow{x}}^0,\mathcal{D},K)$ 5:    $D=argma{x}_{D\subset \left[A\right]\backslash S,\left|D\right|=d}{\sum }_{j\in D}{|A{\overrightarrow{x}}^{(K,i)}-\overrightarrow{b}|}_j$ 6:    $S=S\cup D$ 7: end for 8: return $\overrightarrow{x}$, where $A_{S^C}\overrightarrow{x}={\overrightarrow{b}}_{S^C}$

2. Randomization of the Distributed Kaczmarz Algorithm

The Distributed Kaczmarz Algorithm (DKA) described in Section 1.2 was introduced in [5]. The main results there concern qualitative convergence guarantees of the DKA: Theorems 2 and 4 prove that the DKA converges to the solution (solution of minimal norm) when the system has a unique solution (is consistent, respectively). Theorem 14 proves that when the system of equations is inconsistent, the relaxed version of the DKA converges for every appropriate relaxation parameter, and the limits approximate a weighted least-squares solution. No quantitative estimates of the convergence rate are given in [5], and in fact it is observed in [46] that the convergence rate is dependent upon the topology of the tree as well as the distribution of the equations across the nodes.

2.1. Randomized Variants

In this subsection, we consider randomized variants of the protocol introduced in Section 1.2 (see Algorithm 1). This will allow us to provide quantitative estimates on the rate of convergence in terms of the spectral data of A. We will be using the analysis of the randomized Kaczmarz algorithm as presented in [8] and the analysis of the randomized block Kaczmarz algorithm as presented in [14].

We will have two randomized variants, but both can be thought of in a similar manner. During the dispersion stage of the iteration, one or more of the nodes will be active, meaning that the estimate they receive will be updated according to Equation (3) then passed on to its successor nodes (or held if the node is a leaf). The remaining nodes will be passive, meaning that the estimate they receive will be passed on to successive nodes without updating. In the first variant, exactly one node will be chosen randomly to be active for the current iteration, and the remaining nodes will be passive. In the second variant, several of the nodes will be chosen randomly to be active subject to the constraint that no two active nodes are in a predecessor-successor relationship. The pooling stage proceeds with the following variation. When a node receives estimates from its successors, it averages only those estimates that differ from its estimate during the dispersion stage. If a node receives estimates from all of its successors that are the same as its own estimate during the dispersion stage, it passes this estimate to its predecessor.

For these random choices, we will require that the root node know the full topology of the network. For each iteration, the root node will select the active nodes for that iteration according to some probability distribution; the nodes that are selected for activation will be notified by the root node during the iteration.

In both of our random variants, we make the assumption that the system of equations is consistent. This assumption is required for the results that we use from [8,14]. As such, no relaxation parameter is needed in our randomized variants, though in Section 2.3 we observe that convergence can be accelerated by over-relaxation. See [9,47] for results concerning the randomized Kaczmarz algorithm in the context of inconsistent systems of equations.

See Algorithm 1 for pseudocode description of the randomized variants; we refer to this algorithm as the Randomized Tree Kaczmarz (RTK) algorithm.

2.1.1. Single Active Nodes

Let Y denote a random variable whose values are in V. In our first randomized variant, the root node selects $v\in V$ according to the probability distribution

$$P(Y=v)={\displaystyle \frac{\parallel {\overrightarrow{a}}_v{\parallel }^2}{{\parallel A\parallel }_F^2}};$$

denote this distribution by ${\mathcal{D}}_0$. Note that this requires the root node to have access to the norms $\{\parallel {\overrightarrow{a}}_v{\parallel \}}_{v\in V}$. During the dispersion stage of iteration n, the node that is selected, denoted by $Y_n$, is notified by the root node as estimate ${\overrightarrow{x}}^{\left(n\right)}$ traverses the tree.

Proposition 1.

Suppose that the sequence of approximations ${\overrightarrow{x}}^{\left(n\right)}$ are obtained by Algorithm 1 with distribution ${\mathcal{D}}_0$. Then, the approximations have the form

$${\overrightarrow{x}}^{\left(n\right)}={\overrightarrow{x}}^{(n-1)}+{\displaystyle \frac{b_{Y_n}-{\overrightarrow{a}}_{Y_n}^{*}{\overrightarrow{x}}^{(n-1)}}{\parallel {\overrightarrow{a}}_{Y_n}{\parallel }^2}}{\overrightarrow{a}}_{Y_n}.$$

Proof. 

At the end of the dispersion stage of the iteration, we have that the leaves $\ell \prec Y_n$ possess an estimate that has been updated; all other leaves have estimates that are not updated. Thus, we have ${\overrightarrow{x}}_{\ell }^{(n-1)}={\overrightarrow{x}}_{Y_n}^{(n-1)}={\overrightarrow{x}}^{(n-1)}+{\displaystyle \frac{b_{Y_n}-{\overrightarrow{a}}_{Y_n}^{*}{\overrightarrow{x}}^{(n-1)}}{\parallel {\overrightarrow{a}}_{Y_n}{\parallel }^2}}{\overrightarrow{a}}_{Y_n}$ for those $\ell \prec Y_n$, and ${\overrightarrow{x}}_{\ell }^{(n-1)}={\overrightarrow{x}}^{(n-1)}$ otherwise.

Then, during the pooling stage, the only nodes that receive an estimate that is different from their estimate during the dispersion stage are $u\succ Y_n$, and those estimates are all ${\overrightarrow{x}}_{Y_n}^{(n-1)}$. Thus, for all such nodes, ${\overrightarrow{y}}_u={\overrightarrow{x}}_{Y_n}^{(n-1)}$. Every other node has ${\overrightarrow{y}}_u={\overrightarrow{x}}^{(n-1)}$. Since the root $r\succ Y_n$, we obtain that

$${\overrightarrow{x}}^{\left(n\right)}={\overrightarrow{y}}_r^{(n-1)}={\overrightarrow{x}}_{Y_n}^{(n-1)}={\overrightarrow{x}}^{(n-1)}+{\displaystyle \frac{b_{Y_n}-{\overrightarrow{a}}_{Y_n}^{*}{\overrightarrow{x}}^{(n-1)}}{\parallel {\overrightarrow{a}}_{Y_n}{\parallel }^2}}{\overrightarrow{a}}_{Y_n}.$$

□

Corollary 1.

Suppose the sequence of approximations ${\overrightarrow{x}}^{\left(n\right)}$ are obtained by Algorithm 1 with distribution ${\mathcal{D}}_0$. Then, the following linear convergence rate in expectation holds:

$$\mathbb{E}\parallel {\overrightarrow{x}}^{\left(n\right)}-\mathrm{\Pi }{\overrightarrow{x}}^{\left(n\right)}{\parallel }^2\le {\left(1-{\displaystyle \frac{{\lambda }_{min}^{nz}\left(A^{T}A\right)}{{\parallel A\parallel }_F^2}}\right)}^n{\parallel {\overrightarrow{x}}^{\left(0\right)}-\mathrm{\Pi }{\overrightarrow{x}}^{\left(0\right)}\parallel }^2.$$

(6)

Proof. 

When the blocks are singletons, by Proposition 1, the update is identical to the Randomized Kaczmarz algorithm of [8]. The estimate in Equation (6) is given in [14]. □

2.1.2. Multiple Active Nodes

We now consider blocks of nodes, meaning multiple nodes, that are active during each iteration. For our analysis, we require that the nodes that are active during any iteration are independent of each other in terms of the topology of the tree. Let $\mathbb{P}\left(V\right)$ denote the power set of the set of nodes V. Let Z be a random variable whose values are in $\mathbb{P}\left(V\right)$ with probability distribution $\mathcal{D}$.

Definition 1.

For $I\in \mathbb{P}\left(V\right)$, we say that I satisfies the incomparable condition whenever the following holds: for every distinct pair $u,v\in I$, neither $v\prec u$ nor $u\prec v$. We say that the probability distribution $\mathcal{D}$ satisfies the incomparable condition whenever the following implication holds: if $I\in \mathbb{P}\left(V\right)$ is such that $P(Z=I)>0$, then I satisfies the incomparable condition.

Following [14], we define the expectation for each node $v\in V$:

$$p_v=P(v\in Z).$$

We then define the matrix

$$W=\sum _{v\in V}{p}_v{\displaystyle \frac{a_v{a}_v^{*}}{\parallel a_v{\parallel }^2}}.$$

(7)

For $I\in \mathbb{P}\left(V\right)$ and $u\in V$, we define

$$T(u,I)=\{w\in \mathcal{C}(u\left)\right|\exists v\in Is.t.v⪯w\}$$

We then define for $v\in I$:

$$\gamma (v,I)=\prod _{u\succ v}{\displaystyle \frac{1}{\left|T\right(u,I\left)\right|}}.$$

(8)

These quantities reflect how estimates travel from the leaves of the tree back to the root. As multiple estimates are averaged at a node in the tree, the node needs to know how many of its descendants have estimates that have been updated, which (essentially) corresponds to how many descendants have been chosen to be active during that iteration. (Note that it is possible that a node could be active, but its estimate is NOT updated because it may be the case that the estimate that is passed to it is already a solution it its equation, but to simplify the analysis, we suppose that this does not occur). The weights $\gamma (v,I)$ are the final weights used in the update when the estimates ultimately return to the root. Note that these quantities depend on the choice of $I\in P\left(\mathbb{V}\right)$ as well as the topology of the tree itself.

Proposition 2.

Suppose that the sequence of approximations ${\overrightarrow{x}}^{\left(n\right)}$ are generated by Algorithm 1, where the probability distribution $\mathcal{D}$ satisfies the incomparable condition. Let $Z_n$ be the n-th sample of the random variable Z. Then, the approximations have the form

$${\overrightarrow{x}}^{\left(n\right)}={\overrightarrow{x}}^{(n-1)}+\sum _{v\in Z_n}\gamma (v,Z_n){\displaystyle \frac{b_v-{\overrightarrow{a}}_v^{*}{\overrightarrow{x}}^{(n-1)}}{\parallel {\overrightarrow{a}}_v{\parallel }^2}}{\overrightarrow{a}}_v.$$

(9)

Proof. 

For any node w such that there is no $v\in Z_n$ with $w\prec v$, then ${\overrightarrow{x}}_w^{(n-1)}={\overrightarrow{x}}_r^{(n-1)}={\overrightarrow{x}}^{(n-1)}$. However, if there is a $v\in Z_n$ with $w\prec v$, then by the incomparable condition,

$${\overrightarrow{x}}_w^{(n-1)}={\overrightarrow{x}}_v^{(n-1)}={\overrightarrow{x}}^{(n-1)}+{\displaystyle \frac{b_v-{\overrightarrow{a}}_v^{*}{\overrightarrow{x}}^{(n-1)}}{\parallel {\overrightarrow{a}}_v{\parallel }^2}}{\overrightarrow{a}}_v.$$

(10)

We have in the pooling stage, if $v\in Z_n$ then ${\overrightarrow{y}}_v={\overrightarrow{x}}_v$. Moreover, for $u=\mathcal{P}\left(v\right)$,

$${\overrightarrow{y}}_u^{(n-1)}={\displaystyle \frac{1}{\left|T\right(u,Z_n\left)\right|}}\sum _{w\in T(u,Z_n)}{\overrightarrow{y}}_w^{(n-1)}={\displaystyle \frac{1}{\left|T\right(u,Z_n\left)\right|}}\sum _{\begin{array}{c}w\in Z_n\\ w\prec u\end{array}}{\overrightarrow{y}}_w^{(n-1)}={\displaystyle \frac{1}{\left|T\right(u,Z_n\left)\right|}}\sum _{\begin{array}{c}w\in Z_n\\ w\prec u\end{array}}{\overrightarrow{x}}_w^{(n-1)}$$

where the second equation follows from the incomparable condition. It now follows by induction that

$${\overrightarrow{y}}_r^{(n-1)}=\sum _{w\in Z_n}\left(\prod _{w\prec u}{\displaystyle \frac{1}{\left|T\right(u,Z_n\left)\right|}}\right){\overrightarrow{x}}_w^{(n-1)}.$$

We now obtain Equation (9) from Equation (8). □

For $I\in \mathbb{P}\left(V\right)$ that satisfies the incomparable condition, we define

$$B_I=\sum _{v\in I}\gamma (v,I){\displaystyle \frac{a_v{a}_v^{*}}{\parallel a_v{\parallel }^2}}$$

(11)

where $\gamma (v,I)$ are as in Equation (8).

Let $\mathcal{D}$ be a probability distribution on $\mathbb{P}\left(V\right)$ that satisfies the incomparable condition, and let Z be a $\mathbb{P}\left(V\right)$-valued random variable with distribution $\mathcal{D}$. For each $I\in \mathbb{P}\left(V\right)$ such that $P(Z=I)>0$, let

$${\gamma }_{min}\left(I\right)=min\left\{\gamma (v,I)\right|v\in I\};{\gamma }_{max}\left(I\right)=max\left\{\gamma (v,I)\right|v\in I\};$$

where $\gamma (v,I)$ are as in Equation (8). Then, let

$$\mathrm{\Gamma }(A,\mathcal{D})=min\{2{\gamma }_{min}\left(I\right)-{\gamma }_{max}\left(I\right){\lambda }_{max}\left(B_I\right)|P(Z=I)>0\}.$$

(12)

For notational brevity, we define the quantity

$$\mathrm{\Sigma }(A,\mathcal{D}):=1-\mathrm{\Gamma }(A,\mathcal{D}){\lambda }_{min}^{nz}\left(W\right).$$

(13)

We note that a priori there is no reason that $\mathrm{\Sigma }(A,\mathcal{D})<1$. However, we will see in Section 2.2 examples for which $\mathrm{\Sigma }$ is less than 1 as well as conditions which guarantee this inequality.

We will use Theorem 4.1 in [14]. We alter the statement somewhat and include the proof for completeness.

Theorem 1.

Let $Z_1$ be a sample of the random variable Z with distribution $\mathcal{D}$. Let Π be the projection onto the space of solutions to the system of equations, and let ${\overrightarrow{x}}^{\left(0\right)}$ be an initial estimate of a solution that is in the range of $A^T$. Let

$${\overrightarrow{x}}^{\left(1\right)}={\overrightarrow{x}}^{\left(0\right)}+\left(\sum _{v\in Z_1}\gamma (v,Z_1){\displaystyle \frac{b_v-{\overrightarrow{a}}_v^{*}{\overrightarrow{x}}^{\left(0\right)}}{\parallel {\overrightarrow{a}}_v{\parallel }^2}}{\overrightarrow{a}}_v\right).$$

Then, the following estimate holds in expectation:

$$\mathbb{E}\parallel {\overrightarrow{x}}^{\left(1\right)}-\mathrm{\Pi }{\overrightarrow{x}}^{\left(1\right)}{\parallel }^2\le \mathrm{\Sigma }(A,\mathcal{D}){\parallel {\overrightarrow{x}}^{\left(0\right)}-\mathrm{\Pi }{\overrightarrow{x}}^{\left(0\right)}\parallel }^2.$$

(14)

Proof. 

As derived in Theorem 4.1 in [14], we have

$$\parallel {\overrightarrow{x}}^{\left(1\right)}-\mathrm{\Pi }{\overrightarrow{x}}^{\left(1\right)}{\parallel }^2\le {\left({\overrightarrow{x}}^{\left(0\right)}-\mathrm{\Pi }{\overrightarrow{x}}^{\left(0\right)}\right)}^{*}\left(I-2B_{Z_1}+B_{Z_1}^2\right)\left({\overrightarrow{x}}^{\left(0\right)}-\mathrm{\Pi }{\overrightarrow{x}}^{\left(0\right)}\right).$$

(15)

We make the following estimates:

$$B_{Z_1}⪰{\gamma }_{min}\left(Z_1\right)\left(\sum _{v\in Z_1}{\displaystyle \frac{{\overrightarrow{a}}_v{\overrightarrow{a}}_v^{*}}{\parallel {\overrightarrow{a}}_v{\parallel }^2}}\right),$$

and

$$\begin{array}{cc}\hfill B_{Z_1}^2& ⪯{\lambda }_{max}\left(B_{Z_1}\right)B_{Z_1}\hfill \\ \hfill & ⪯{\lambda }_{max}\left(B_{Z_1}\right){\gamma }_{max}\left(Z_1\right)\left(\sum _{v\in Z_1}{\displaystyle \frac{{\overrightarrow{a}}_v{\overrightarrow{a}}_v^{*}}{\parallel {\overrightarrow{a}}_v{\parallel }^2}}\right).\hfill \end{array}$$

We thus obtain the estimate

$$\begin{array}{cc}\hfill I-2B_{Z_1}+B_{Z_1}^2& ⪯I-2{\gamma }_{min}\left(Z_1\right)\left(\sum _{v\in Z_1}{\displaystyle \frac{{\overrightarrow{a}}_v{\overrightarrow{a}}_v^{*}}{\parallel {\overrightarrow{a}}_v{\parallel }^2}}\right)+{\gamma }_{max}\left(Z_1\right){\lambda }_{max}\left(B_{Z_1}\right)\left(\sum _{v\in Z_1}{\displaystyle \frac{{\overrightarrow{a}}_v{\overrightarrow{a}}_v^{*}}{\parallel {\overrightarrow{a}}_v{\parallel }^2}}\right)\hfill \\ \hfill & ⪯I-\mathrm{\Gamma }(A,\mathcal{D})\left(\sum _{v\in Z_1}{\displaystyle \frac{{\overrightarrow{a}}_v{\overrightarrow{a}}_v^{*}}{\parallel {\overrightarrow{a}}_v{\parallel }^2}}\right),\hfill \end{array}$$

from which Equation (15) becomes

$$\parallel {\overrightarrow{x}}^{\left(1\right)}-\mathrm{\Pi }{\overrightarrow{x}}^{\left(1\right)}{\parallel }^2\le {\left({\overrightarrow{x}}^{\left(0\right)}-\mathrm{\Pi }{\overrightarrow{x}}^{\left(0\right)}\right)}^{*}\left(I-\mathrm{\Gamma }(A,\mathcal{D})\left(\sum _{v\in Z_1}{\displaystyle \frac{{\overrightarrow{a}}_v{\overrightarrow{a}}_v^{*}}{\parallel {\overrightarrow{a}}_v{\parallel }^2}}\right)\right)\left({\overrightarrow{x}}^{\left(0\right)}-\mathrm{\Pi }{\overrightarrow{x}}^{\left(0\right)}\right).$$

(16)

Taking the expectation of the left side, we obtain

$$\begin{array}{cc}\hfill \mathbb{E}\parallel {\overrightarrow{x}}^{\left(1\right)}-\mathrm{\Pi }{\overrightarrow{x}}^{\left(1\right)}{\parallel }^2& \le {\left({\overrightarrow{x}}^{\left(0\right)}-\mathrm{\Pi }{\overrightarrow{x}}^{\left(0\right)}\right)}^{*}\left(I-\mathrm{\Gamma }(A,\mathcal{D})W\right)\left({\overrightarrow{x}}^{\left(0\right)}-\mathrm{\Pi }{\overrightarrow{x}}^{\left(0\right)}\right)\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill & \le \mathrm{\Sigma }(A,\mathcal{D})\parallel {\overrightarrow{x}}^{\left(0\right)}-\mathrm{\Pi }{\overrightarrow{x}}^{\left(0\right)}{\parallel }^2.\hfill \end{array}$$

(18)

The last inequality follows from the Courant–Fischer inequality applied to the matrix $D^{1/2}A$: for the matrix $W=A^{T}DA$, with $D=diag\left({\displaystyle \frac{p_v}{\parallel {\overrightarrow{a}}_v{\parallel }^2}};v\in V\right)$, we obtain

$${\left({\overrightarrow{x}}^{\left(0\right)}-\mathrm{\Pi }{\overrightarrow{x}}^{\left(0\right)}\right)}^{*}W\left({\overrightarrow{x}}^{\left(0\right)}-\mathrm{\Pi }{\overrightarrow{x}}^{\left(0\right)}\right)=\parallel D^{1/2}A\left({\overrightarrow{x}}^{\left(0\right)}-\mathrm{\Pi }{\overrightarrow{x}}^{\left(0\right)}\right){\parallel }^2\ge {\lambda }_{min}^{nz}\left(W\right){\parallel {\overrightarrow{x}}^{\left(0\right)}-\mathrm{\Pi }{\overrightarrow{x}}^{\left(0\right)}\parallel }^2.$$

□

Theorem 2.

Suppose the sequence of approximations ${\overrightarrow{x}}^{\left(n\right)}$ are obtained by Algorithm 1 with the distribution $\mathcal{D}$ satisfying the incomparable condition and initialized with ${\overrightarrow{x}}^{\left(0\right)}\in \mathcal{R}\left(A^T\right)$. Then, the following linear convergence rate in expectation holds:

$$\mathbb{E}\parallel {\overrightarrow{x}}^{\left(n\right)}-\mathrm{\Pi }{\overrightarrow{x}}^{\left(n\right)}{\parallel }^2\le {\left(\mathrm{\Sigma }(A,\mathcal{D})\right)}^n{\parallel {\overrightarrow{x}}^{\left(0\right)}-\mathrm{\Pi }{\overrightarrow{x}}^{\left(0\right)}\parallel }^2.$$

(19)

Proof. 

We take the expected value of $\parallel {\overrightarrow{x}}^{\left(n\right)}-\mathrm{\Pi }{\overrightarrow{x}}^{\left(n\right)}{\parallel }^2$ conditioned on the history $Z_1,\dots ,Z_{n-1}$. By Theorem 1, we have the estimate

$$\begin{array}{cc}\hfill \mathbb{E}& \left\{\parallel {\overrightarrow{x}}^{\left(n\right)}-\mathrm{\Pi }{\overrightarrow{x}}^{\left(n\right)}{\parallel }^2:Z_1,\dots ,Z_{n-1}\right\}\le \mathbb{E}\left\{\parallel {\overrightarrow{x}}^{\left(n\right)}-\mathrm{\Pi }{\overrightarrow{x}}^{(n-1)}{\parallel }^2:Z_1,\dots ,Z_{n-1}\right\}\hfill \\ \hfill & \le \mathbb{E}\left\{\mathrm{\Sigma }(A,\mathcal{D})\parallel {\overrightarrow{x}}^{(n-1)}-\mathrm{\Pi }{\overrightarrow{x}}^{(n-1)}{\parallel }^2:Z_1,\dots ,Z_{n-1}\right\}\hfill \\ \hfill & \le \mathrm{\Sigma }(A,\mathcal{D})\parallel {\overrightarrow{x}}^{(n-1)}-\mathrm{\Pi }{\overrightarrow{x}}^{(n-1)}{\parallel }^2.\hfill \end{array}$$

We now take the expectation over the entire history to obtain

$$\mathbb{E}\parallel {\overrightarrow{x}}^{\left(n\right)}-\mathrm{\Pi }{\overrightarrow{x}}^{\left(n\right)}{\parallel }^2\le \mathrm{\Sigma }(A,\mathcal{D})\mathbb{E}{\parallel {\overrightarrow{x}}^{(n-1)}-\mathrm{\Pi }{\overrightarrow{x}}^{(n-1)}\parallel }^2.$$

The result now follows by iterating. □

Remark 1.

We note here that Theorem 2 recovers Corollary 1 as follows: if $\mathcal{D}$ selects only singletons from $\mathbb{P}\left(V\right)$, and selects singleton $\left\{v\right\}$ with probability ${\displaystyle \frac{\parallel {\overrightarrow{a}}_v{\parallel }^2}{{\parallel A\parallel }_F^2}}$, then we have

$${\gamma }_{min}\left(\left\{v\right\}\right)={\gamma }_{max}\left(\left\{v\right\}\right)={\lambda }_{max}\left(B_{\left\{v\right\}}\right)=\mathrm{\Gamma }(A,\mathcal{D})=1$$

and $W={\displaystyle \frac{A^{T}A}{{\parallel A\parallel }_F^2}}$. Thus, $\mathrm{\Sigma }(A,\mathcal{D})=1-{\displaystyle \frac{{\lambda }_{min}^{nz}\left(A^{T}A\right)}{{\parallel A\parallel }_F^2}}$.

Remark 2.

A similar result to Theorem 2 is obtained in [15]. There, the authors make additional assumptions that we do not. First, in [15], each block that is selected always contains the same number of rows; our analysis works when the blocks have different sizes, which is necessary as we will consider in several of our sampling schemes different block sizes. Second, in [15], their analysis requires the assumption that the expectation $p_v$ and the weights $\gamma (v,Z)$ satisfy the following constraint: there exists a $\alpha >0$ such that for every v, $p_v\gamma (v,Z){\parallel {\overrightarrow{a}}_v\parallel }^{-2}=\alpha$. We do not make this assumption, and in fact this need not hold, since the weights $\gamma (v,Z)$ are determined both by Z and the tree structure. Thus, we do not have control over this quantity.

2.2. Sampling Schemes

We propose here several possible sampling schemes for Algorithm 1 and illustrate their asymptotics in the special case of a binary tree. Recall that m is the number of equations (and hence the number of nodes in the tree), and t is the number of leaves (nodes with no successors) in the tree. To simplify our analysis, we assume that each $\parallel {\overrightarrow{a}}_v\parallel =1$. We note that for any set $I\in \mathbb{P}\left(V\right)$, we have the estimate

$${\lambda }_{max}\left(B_I\right)\le 1$$

(20)

since ${\sum }_{v\in I}\gamma (v,I)=1$. In addition, if we assume that the distribution $\mathcal{D}$ satisfies the condition that the set $\mathcal{I}=\{I\in \mathbb{P}(V):P(Z=I)>0\}$ is a partition of V, then

$${\lambda }_{min}^{nz}\left(W\right)\le 1$$

(21)

since we have that ${\sum }_{v\in V}{p}_v=1$. As a consequence of these estimates, we obtain the following guarantee that $\mathrm{\Sigma }(A,\mathcal{D})<1$.

Proposition 3.

Suppose $\mathcal{D}$ satisfies the incomparable condition and that Equation (21) is satisfied. In addition, suppose that for every $I\in \mathcal{I}$ has the property that $2{\gamma }_{min}\left(I\right)-{\gamma }_{max}\left(I\right)>0$. Then, $\mathrm{\Sigma }(A,\mathcal{D})<1$.

Generations. We block the nodes by their distance from the root: $G_k=\{v:d(r,v)=k\}$. If the depth of the tree is K, then we draw from $\{G_0,\dots ,G_{K-1}\}$ uniformly. Here, the probabilities $p_v={\displaystyle \frac{1}{K}}$, so we have $W={\displaystyle \frac{1}{K}}{A}^{T}A$ since we are also assuming that $\parallel {\overrightarrow{a}}_v\parallel =1$. Thus, the spectral data ${\lambda }_{min}^{nz}\left(W\right)$ reduces to ${\displaystyle \frac{1}{K}}{\lambda }_{min}^{nz}\left(A^{T}A\right)$. Thus, our convergence rate is

$$\mathrm{\Sigma }(A,\mathcal{D})=1-\mathrm{\Gamma }(A,\mathcal{D}){\displaystyle \frac{{\lambda }_{min}^{nz}\left(A^{T}A\right)}{K}}.$$

For arbitrary trees, the quantities ${\gamma }_{min}\left(G_k\right)$ and ${\gamma }_{max}\left(G_k\right)$ depend on the topology, but for p-regular trees (meaning all nodes that are not leaves have p successors), we have

$${\gamma }_{min}\left(G_k\right)={\gamma }_{max}\left(G_k\right)={\displaystyle \frac{1}{p^k}}.$$

Thus, from Equation (20) we obtain the estimate

$$\mathrm{\Gamma }(A,\mathcal{D})\ge {\displaystyle \frac{1}{p^{K-1}}}$$

and our convergence rate is bounded by

$$1-\mathrm{\Gamma }(A,\mathcal{D}){\lambda }_{min}^{nz}\left(W\right)\le 1-{\displaystyle \frac{{\lambda }_{min}^{nz}\left(A^{T}A\right)}{K{p}^{K-1}}}.$$

For our regular p-tree, $K=O(logm)$ and $p^{K-1}=O\left(m\right)$, so asymptotically the convergence rate is at worst $1-O\left({(mlogm)}^{-1}\right){\lambda }_{min}^{nz}\left(A^{T}A\right)$.

Families. Here, blocks consist of all immediate successors (children) of a common node, i.e., $\mathcal{C}\left(u\right)$ for u not a leaf. The singleton $\left\{r\right\}$ also is a block. We select each block uniformly, so $p_v={\displaystyle \frac{1}{m-t}}$. In this case, for each family (block) F,

$${\gamma }_{min}\left(F\right)={\gamma }_{max}\left(F\right)=\frac{1}{\left|F\right|}.$$

Thus, we obtain the estimate

$$\mathrm{\Gamma }(A,\mathcal{D})\ge {\displaystyle \frac{1}{c}},$$

where c denotes the largest family. We obtain a convergence rate of

$$\mathrm{\Sigma }(A,\mathcal{D})=1-{\displaystyle \frac{{\lambda }_{min}^{nz}\left(A^{T}A\right)}{c(m-t)}}.$$

In the case of a binary tree, $c=2$, and $m-t=O\left(m\right)$, so asymptotically the convergence rate is at worst $1-O\left(m^{-1}\right){\lambda }_{min}^{nz}\left(A^{T}A\right)$.

2.3. Accelerating the Convergence via Over-Relaxation

We can accelerate the convergence, i.e., lower the convergence factor, by considering larger stepsizes. In the classical cyclic Kaczmarz algorithm, a relaxation parameter $\omega \in (0,2)$ is allowed, and the update is given by

$${\overrightarrow{x}}^{\left(n\right)}={\overrightarrow{x}}^{(n-1)}+\omega {\displaystyle \frac{b_n-{\overrightarrow{a}}_n^{*}{\overrightarrow{x}}^{(n-1)}}{\parallel {\overrightarrow{a}}_n{\parallel }^2}}{\overrightarrow{a}}_n.$$

Experimentally, convergence is faster with $\omega >1$ [4,14,46]. We consider here such a relaxation parameter in Algorithm 1. This alters the analysis of Theorem 1 only slightly. Indeed, the update in Proposition 2 becomes:

$${\overrightarrow{x}}^{\left(n\right)}={\overrightarrow{x}}^{(n-1)}+\omega \sum _{v\in Z_n}\gamma (v,Z_n){\displaystyle \frac{b_v-{\overrightarrow{a}}_v^{*}{\overrightarrow{x}}^{(n-1)}}{\parallel {\overrightarrow{a}}_v{\parallel }^2}}{\overrightarrow{a}}_v.$$

(22)

Thus, Equation (15) in the proof of Theorem 1 becomes:

$$\parallel {\overrightarrow{x}}^{\left(1\right)}-\mathrm{\Pi }{\overrightarrow{x}}^{\left(1\right)}{\parallel }^2\le {\left({\overrightarrow{x}}^{\left(0\right)}-\mathrm{\Pi }{\overrightarrow{x}}^{\left(0\right)}\right)}^{*}\left(I-\omega 2B_{Z_1}+{\omega }^2{B}_{Z_1}^2\right)\left({\overrightarrow{x}}^{\left(0\right)}-\mathrm{\Pi }{\overrightarrow{x}}^{\left(0\right)}\right).$$

(23)

The remainder of the calculation follows through, with the final estimate

$$\mathbb{E}\parallel {\overrightarrow{x}}^{\left(1\right)}-\mathrm{\Pi }{\overrightarrow{x}}^{\left(1\right)}{\parallel }^2\le \left(1-{\mathrm{\Gamma }}_{\omega }(A,\mathcal{D}){\lambda }_{min}^{nz}\left(W\right)\right){\parallel {\overrightarrow{x}}^{\left(0\right)}-\mathrm{\Pi }{\overrightarrow{x}}^{\left(0\right)}\parallel }^2,$$

(24)

where

$${\mathrm{\Gamma }}_{\omega }(A,\mathcal{D})=min\left\{2\omega {\gamma }_{min}\left(I\right)-{\omega }^2{\gamma }_{max}\left(I\right){\lambda }_{max}\left(B_I\right)|P(Z=I)>0\right\}.$$

If we assume that

$${\lambda }_{max}^{block}:=max\left\{{\lambda }_{max}\left(B_I\right)|P(Z=I)>0\right\}<1,$$

then we can maximize a lower bound on ${\mathrm{\Gamma }}_{\omega }(A,\mathcal{D})$ as a function of $\omega$. Indeed, if we assume that for each I, ${\gamma }_{min}\left(I\right)={\gamma }_{max}\left(I\right)=:\gamma$, then the maximum occurs at

$${\omega }_0={\displaystyle \frac{1}{{\lambda }_{max}^{block}}},$$

and we then obtain the estimate

$${\mathrm{\Gamma }}_{{\omega }_0}(A,\mathcal{D})\ge {\displaystyle \frac{\gamma }{{\lambda }_{max}^{block}}}$$

(25)

This suggests that the rate of convergence can be accelerated by choosing the stepsize ${\omega }_0$, since the estimate from Equation (25) is better than the estimate

$$\mathrm{\Gamma }(A,\mathcal{D})\ge 2(1-{\lambda }_{max}^{block}).$$

Our numerical experiments presented in Section 4 empirically support acceleration through over-relaxation and in fact suggest further improvement than what we prove here.

3. The RTK in the Presence of Noise

We now consider the performance of the Randomized Tree Kaczmarz algorithm in the presence of noise. That is to say, we consider the system of equations $A\overrightarrow{x}=\overrightarrow{b}+\overrightarrow{ϵ}$, where $\overrightarrow{ϵ}$ represents noise within the observed measurements. We assume that the noiseless matrix equation $A\overrightarrow{x}=\overrightarrow{b}$ is consistent, and its solution is the solution we want to estimate. We suppose that the equations ${\overrightarrow{a}}_v^{*}\overrightarrow{x}=b_v+{ϵ}_v$ are distributed across a network that is a tree, as before. We will consider two aspects of the noisy case: first, we establish the convergence rate of the RTK in the presence of noise and estimate the errors in the approximations due to the noise; second, we will consider methods for mitigating the noise, meaning that if the noise vector $\overrightarrow{ϵ}$ satisfies a certain sparsity constraint, then we can estimate which nodes are corrupted by noise (i.e., anomalous) and ignore them in the RTK.

3.1. Convergence Rate in the Presence of Noise

We now consider the convergence rate of Algorithm 1 in the presence of noise. The randomized Kaczmarz method in the presence of noise was investigated in [47]. The main result of that study is that when the measurement vector $\overrightarrow{b}$ is corrupted by noise (likely causing the system to be inconsistent), the randomized Kacmarz algorithm displays the same convergence rate as the randomized Kaczmarz algorithm does in the consistent case up to an error term that is proportional to the variance of the noise, and the constant of proportionality is given by spectral data of the coefficient matrix.

To formalize, we consider the case that the system of equations $A\overrightarrow{x}=\overrightarrow{b}$ is consistent but that the measurement vector $\overrightarrow{b}$ is corrupted by noise, yielding the observed system of equations $A\overrightarrow{x}=\overrightarrow{b}+\overrightarrow{ϵ}$. The update in Algorithm 1 then becomes:

$$\begin{array}{cc}\hfill {\overrightarrow{x}}^{\left(n\right)}& ={\overrightarrow{x}}^{(n-1)}+\sum _{v\in I}\gamma (v,I){\displaystyle \frac{b_v+{ϵ}_v-{\overrightarrow{a}}_v^{*}{\overrightarrow{x}}^{(n-1)}}{\parallel {\overrightarrow{a}}_v{\parallel }^2}}{\overrightarrow{a}}_v\hfill \\ \hfill & ={\overrightarrow{x}}^{(n-1)}+\sum _{v\in I}\gamma (v,I){\displaystyle \frac{b_v-{\overrightarrow{a}}_v^{*}{\overrightarrow{x}}^{(n-1)}}{\parallel {\overrightarrow{a}}_v{\parallel }^2}}{\overrightarrow{a}}_v+\sum _{v\in I}\gamma (v,I){\displaystyle \frac{{ϵ}_v}{\parallel {\overrightarrow{a}}_v{\parallel }^2}}{\overrightarrow{a}}_v.\hfill \end{array}$$

We denote the error in the update by

$${\mathcal{E}}_I=\sum _{v\in I}\gamma (v,I){\displaystyle \frac{{ϵ}_v}{\parallel {\overrightarrow{a}}_v{\parallel }^2}}{\overrightarrow{a}}_v.$$

Note that

$$\parallel {\mathcal{E}}_I\parallel \le \sum _{v\in I}\gamma (v,I){\displaystyle \frac{|{ϵ}_v|}{\parallel {\overrightarrow{a}}_v\parallel }}\le \underset{v\in V}{max}\left\{{\displaystyle \frac{|{ϵ}_v|}{\parallel {\overrightarrow{a}}_v\parallel }}\right\}.$$

(26)

For $d\times d$ matrices $A_1,\dots ,A_N$, we denote the product $A_N{A}_{N-1}\cdots A_1={\prod }_{n=1}^N{A}_n$, so that the product notation is indexed from right to left. For a product where the beginning index is greater than the ending index, e.g., ${\prod }_{n=k+1}^k{A}_n$, we define the product to be the identity I. As before, Z is a $\mathbb{P}\left(V\right)$ valued random variable with distribution $\mathcal{D}$, and $B_Z$ is as given in Equation (11).

Theorem 3.

Suppose the system of equations $A\overrightarrow{x}=\overrightarrow{b}$ is consistent, and let Π denote the projection onto the solution space. Let ${\overrightarrow{x}}^{\left(n\right)}$ be the n-th iterate of Algorithm 1 run with the noisy measurements $A\overrightarrow{x}=\overrightarrow{b}+\overrightarrow{ϵ}$, distribution $\mathcal{D}$, and initialization ${\overrightarrow{x}}^{\left(0\right)}\in \mathcal{R}\left(A^T\right)$. Then, the following estimate holds in expectation:

$$\mathbb{E}\parallel {\overrightarrow{x}}^{\left(n\right)}-\mathrm{\Pi }{\overrightarrow{x}}^{\left(n\right)}{\parallel \le \mathrm{\Sigma }(A,\mathcal{D})}^{n/2}\parallel {\overrightarrow{x}}^{\left(0\right)}-\mathrm{\Pi }{\overrightarrow{x}}^{\left(0\right)}\parallel +{\left[1-\mathrm{\Sigma }{(A,\mathcal{D})}^{1/2}\right]}^{-1}\underset{v\in V}{max}\left\{{\displaystyle \frac{|{ϵ}_v|}{\parallel {\overrightarrow{a}}_v\parallel }}\right\}$$

(27)

where $\mathrm{\Sigma }(A,\mathcal{D})$ is as given in Equation (13).

Proof. 

Let ${\overrightarrow{x}}^S$ be any solution to the system of equations $A\overrightarrow{x}=\overrightarrow{b}$. We have by induction that

$$\begin{array}{cc}\hfill {\overrightarrow{x}}^S-{\overrightarrow{x}}^{\left(n\right)}& =(I-B_{Z_n})({\overrightarrow{x}}^S-{\overrightarrow{x}}^{(n-1)})+{\mathcal{E}}_{Z_n}\hfill \\ \hfill & =(I-B_{Z_n})(I-B_{Z_{n-1}})({\overrightarrow{x}}^S-{\overrightarrow{x}}^{(n-2)})+(I-B_{Z_n})\left({\mathcal{E}}_{Z_{n-1}}\right)+{\mathcal{E}}_{Z_n}\hfill \\ \hfill & =\dots \hfill \\ \hfill & =\prod _{j=1}^n(I-B_{Z_j})({\overrightarrow{x}}^S-{\overrightarrow{x}}^{\left(0\right)})+\sum _{j=1}^n\prod _{k=j+1}^n(I-B_{Z_k}){\mathcal{E}}_{Z_j}.\hfill \end{array}$$

Note that the first term is precisely the estimates obtained from Algorithm 1 with $\overrightarrow{ϵ}=0$, so we can utilize Theorem 2 to obtain the following estimate

$$\begin{array}{cc}\hfill \mathbb{E}\parallel {\overrightarrow{x}}^S-{\overrightarrow{x}}^{\left(n\right)}\parallel & \le \mathbb{E}∥\prod _{j=1}^n(I-B_{Z_j})({\overrightarrow{x}}^S-{\overrightarrow{x}}^{\left(0\right)})∥+\mathbb{E}∥\sum _{j=1}^n\prod _{k=j+1}^n(I-B_{Z_k}){\mathcal{E}}_{Z_j}∥\hfill \\ \hfill & \le {\left(\mathrm{\Sigma }(A,\mathcal{D})\right)}^{n/2}\parallel {\overrightarrow{x}}^S-{\overrightarrow{x}}^{\left(0\right)}\parallel +\mathbb{E}\sum _{j=1}^n∥\prod _{k=j+1}^n(I-B_{Z_k}){\mathcal{E}}_{Z_j}∥.\hfill \end{array}$$

Thus, we need to estimate the terms in the sum.

As in the proof of Theorem 2, we can estimate the expectation conditioned on $Z_1,\dots ,$$Z_{n-1}$ as

$$\mathbb{E}\left\{∥\prod _{k=j+1}^n(I-B_{Z_k}){\mathcal{E}}_{Z_j}∥:Z_1,\dots ,Z_{n-1}\right\}\le {\left(\mathrm{\Sigma }(A,\mathcal{D})\right)}^{1/2}∥\prod _{k=j+1}^{n-1}(I-B_{Z_k}){\mathcal{E}}_{Z_j}∥.$$

Iterating this estimate $n-j$ times using the tower property of conditional expectation yields

$$\mathbb{E}\left\{∥\prod _{k=j+1}^n(I-B_{Z_k}){\mathcal{E}}_{Z_j}∥:Z_1,\dots ,Z_j\right\}\le {\left(\mathrm{\Sigma }(A,\mathcal{D})\right)}^{(n-j)/2}∥{\mathcal{E}}_{Z_j}∥.$$

We have by Equation (26) that

$$\mathbb{E}∥{\mathcal{E}}_{Z_j}∥\le \underset{v\in V}{max}\left\{{\displaystyle \frac{|{ϵ}_v|}{\parallel {\overrightarrow{a}}_v\parallel }}\right\}.$$

Thus, taking the full expectation over the entire history yields

$$\mathbb{E}∥\prod _{k=j+1}^n(I-B_{Z_k}){\mathcal{E}}_{Z_j}∥\le {\left(\mathrm{\Sigma }(A,\mathcal{D})\right)}^{(n-j)/2}\underset{v\in V}{max}\left\{{\displaystyle \frac{|{ϵ}_v|}{\parallel {\overrightarrow{a}}_v\parallel }}\right\}.$$

(28)

We thus obtain

$$\begin{array}{cc}\hfill \mathbb{E}\sum _{j=1}^n∥\prod _{k=j+1}^n(I-B_{Z_k}){\mathcal{E}}_{Z_j}∥& \le \sum _{j=1}^n{\left(\mathrm{\Sigma }(A,\mathcal{D})\right)}^{(n-j)/2}\underset{v\in V}{max}\left\{{\displaystyle \frac{|{ϵ}_v|}{\parallel {\overrightarrow{a}}_v\parallel }}\right\}\hfill \\ \hfill & \le \sum _{j=0}^{\infty }{\left(\mathrm{\Sigma }(A,\mathcal{D})\right)}^{j/2}\underset{v\in V}{max}\left\{{\displaystyle \frac{|{ϵ}_v|}{\parallel {\overrightarrow{a}}_v\parallel }}\right\}\hfill \end{array}$$

from which the estimate in Equation (27) now follows. □

Remark 3.

We note here that Theorem 3 recovers a similar, but coarser, estimate as the one obtained in Theorem 2.1 in [47]. Indeed, as in Remark 1, suppose that the distribution $\mathcal{D}$ only selects singletons from $\mathbb{P}\left(V\right)$, and each singleton $\left\{v\right\}$ is selected with probability ${\displaystyle \frac{\parallel a_v{\parallel }^2}{{\parallel A\parallel }_F^2}}$. Then, we have $\mathrm{\Sigma }(A,\mathcal{D})=1-{\displaystyle \frac{{\lambda }_{min}^{nz}\left(A^{T}A\right)}{{\parallel A\parallel }_F^2}}$, and so Theorem 3 becomes

$$\begin{array}{cc}\hfill \mathbb{E}\parallel {\overrightarrow{x}}^{\left(n\right)}-\mathrm{\Pi }{\overrightarrow{x}}^{\left(n\right)}\parallel & \le \mathrm{\Sigma }{(A,\mathcal{D})}^{n/2}\parallel {\overrightarrow{x}}^{\left(0\right)}-\mathrm{\Pi }{\overrightarrow{x}}^{\left(0\right)}\parallel +{\left[1-\mathrm{\Sigma }{(A,\mathcal{D})}^{1/2}\right]}^{-1}\underset{v\in V}{max}\left\{{\displaystyle \frac{|{ϵ}_v|}{\parallel {\overrightarrow{a}}_v\parallel }}\right\}\hfill \\ \hfill & ={\left(1-{\displaystyle \frac{1}{R}}\right)}^{n/2}\parallel {\overrightarrow{x}}^{\left(0\right)}-\mathrm{\Pi }{\overrightarrow{x}}^{\left(0\right)}\parallel +{\left(1-\sqrt{1-{\displaystyle \frac{1}{R}}}\right)}^{-1}\underset{v\in V}{max}\left\{{\displaystyle \frac{|{ϵ}_v|}{\parallel {\overrightarrow{a}}_v\parallel }}\right\}.\hfill \end{array}$$

Here, $R={\displaystyle \frac{{\parallel A\parallel }_F^2}{{\lambda }_{min}^{nz}\left(A^{T}A\right)}}$ in the notation of Theorem 2.1 in [47]. The estimate is similar for $R\approx 1$, but for $R>>1$, our estimate is worse. This is because the proof of Theorem 2.1 [47] utilizes orthogonality at a crucial step, which is not valid for our situation—the error ${\mathcal{E}}_I$ is not orthogonal to the solution space for the affected equations.

3.2. Anomaly Detection in Distributed Systems of Noisy Equations

We again consider the case of noisy measurements, again denoted by $A\overrightarrow{x}=\overrightarrow{b}+\overrightarrow{ϵ}$, where now the error vector $\overrightarrow{ϵ}$ is assumed to be sparse, and the nonzero entries are large. This situation is considered in [45]. In that study, the authors propose multiple methods of using the Randomized Kaczmarz algorithm to estimate which equations are corrupted by the noise, i.e., which equations correspond to the nonzero entries of $\overrightarrow{ϵ}$. Once those equations are detected, they are removed from the system. The assumption is that the subsystem of uncorrupted equations is consistent; thus, once the corrupted equations are removed, the Randomized Kaczmarz algorithm can be used to estimate a solution. Moreover, the Randomized Kaczmarz algorithm can be used on the full (corrupted) system of equations to obtain an estimate of the solution with positive probability. We demonstrate here that the methods proposed in [45] can be utilized in our context of distributed systems of equations to identify corrupted equations and estimate a solution to the uncorrupted equations.

Indeed, we utilize without any alteration the methods of [45] to detect corrupted equations; we provide the Algorithms 2 and 3 for completeness. To prove that the algorithms are effective in our distributed context, we follow the proofs in [45] with virtually no change. Once we establish an initial lemma, the proofs of the main results (Theorems 4 and 5) are identical. The lemma we require is an adaptation of Lemma 2 in [45] to our Distributed Randomized Kaczmarz algorithm. Our proof proceeds similarly to that in [45]; we include it here for completeness.

We establish some notation first. For an arbitrary $U\subset V$, we use $A_{V\backslash U}$ to denote the submatrix of A obtained by removing the rows indexed by U. Similarly, for the vector $\overrightarrow{b}$, ${\overrightarrow{b}}_{V\backslash U}$ consists of the components whose indices are in $V\backslash U$. For the probability distribution $\mathcal{D}$ and $U\subset V$, we denote by $\tilde{\mathcal{D}}$ the conditional probability distribution on $\mathbb{P}(V\backslash U)$ conditioned on $I\cap U=\varnothing$ for $I\subset V\backslash U$.

For the remainder of this subsection, let $U\subset V$ denote the support of the noise $\overrightarrow{ϵ}$, with $\left|U\right|=s$; let ${\epsilon }^{*}=min\left\{\right|{\overrightarrow{ϵ}}_j|:j\in U\}$. We assume that $A_{V\backslash U}\overrightarrow{x}={\overrightarrow{b}}_{V\backslash U}$ has a unique solution; let ${\overrightarrow{x}}^S$ be that solution to this restricted system. Let

$$\mathcal{P}(\mathcal{D},U)=\sum _{I\cap U=\varnothing }{P}_{\mathcal{D}}\left(I\right).$$

(29)

Recall that k is the number of variables in the system of equations.

Lemma 1.

Let $0<\delta <1$. Define

$$n^{*}=\max \left(0,⌈{\displaystyle \frac{log\left({\displaystyle \frac{\delta {\left({\epsilon }^{*}\right)}^2}{4\parallel {\overrightarrow{x}}^S{\parallel }^2}}\right)}{log\mathrm{\Sigma }(A_{V\backslash U},\tilde{\mathcal{D}})}}⌉\right)$$

(30)

Then, in round i of Algorithm 2 or Algorithm 3, the iterate ${\overrightarrow{x}}^{(n^{*},i)}$ produced by $n^{*}$ iterations of the RTK satisfies

$$P\left[\parallel {\overrightarrow{x}}^{(n^{*},i)}-{\overrightarrow{x}}^S\parallel \le {\displaystyle \frac{{\epsilon }^{*}}{2}}\right]\ge (1-\delta ){\left(\mathcal{P}(\mathcal{D},U)\right)}^{n^{*}}.$$

(31)

Proof. 

Let E be the event that the blocks $Z_1,\dots ,Z_{n^{*}}$ chosen according to distribution $\mathcal{D}$ are all uncorrupted, i.e., $Z_j\cap U=\varnothing$ for $j=1,2,\dots ,n^{*}$. This is equivalent to applying the RTK algorithm to the system $A_{V\backslash U}\overrightarrow{x}={\overrightarrow{b}}_{V\backslash U}$ with distribution $\tilde{\mathcal{D}}$. Thus, by Theorem 2, we have the conditional expectation:

$$\begin{array}{cc}\hfill \mathbb{E}\left[\parallel {\overrightarrow{x}}^{(n^{*},i)}-{\overrightarrow{x}}^S{\parallel }^2|E\right]& \le {\mathbb{E}}_{A_{V\backslash U},{\overrightarrow{b}}_{V\backslash U}}\left[\parallel {\overrightarrow{x}}^{(n^{*},i)}-{\overrightarrow{x}}^S{\parallel }^2|E\right]\hfill \\ \hfill & \le \mathrm{\Sigma }{(A_{V\backslash U},\tilde{\mathcal{D}})}^{n^{*}}{\parallel {\overrightarrow{x}}^S\parallel }^2.\hfill \end{array}$$

From Equation (30), we obtain

$$\mathbb{E}\left[\parallel {\overrightarrow{x}}^{(n^{*},i)}-{\overrightarrow{x}}^S{\parallel }^2|E\right]\le {\displaystyle \frac{\delta {\left({\epsilon }^{*}\right)}^2}{4}}.$$

Thus,

$$P\left[\parallel {\overrightarrow{x}}^{(n^{*},i)}-{\overrightarrow{x}}^S{\parallel }^2\ge {\displaystyle \frac{{\left({\epsilon }^{*}\right)}^2}{4}}\right]\le {\displaystyle \frac{\mathbb{E}\left[\parallel {\overrightarrow{x}}^{(n^{*},i)}-{\overrightarrow{x}}^S{\parallel }^2|E\right]}{{\displaystyle \frac{{\left({\epsilon }^{*}\right)}^2}{4}}}}\le \delta .$$

Hence,

$$P\left[\parallel {\overrightarrow{x}}^{(n^{*},i)}-{\overrightarrow{x}}^S{\parallel }^2\le {\displaystyle \frac{{\left({\epsilon }^{*}\right)}^2}{4}}|E\right]\ge 1-\delta$$

and

$$P\left[\parallel {\overrightarrow{x}}^{(n^{*},i)}-{\overrightarrow{x}}^S{\parallel }^2\le {\displaystyle \frac{{\left({\epsilon }^{*}\right)}^2}{4}}\right]\ge \left(1-\delta \right)P\left(E\right)\ge \left(1-\delta \right){\left(\mathcal{P}(\mathcal{D},U)\right)}^{n^{*}}.$$

□

The following are Theorems 2 and 3 in [45], respectively, restated to our situation; the proofs are identical using our Lemma 1 and are omitted.

Theorem 4.

Let $0<\delta <1$. Fix $d\ge s$, $W\le ⌊{\displaystyle \frac{\left|V\right|-k}{d}}⌋$, and let $n^{*}$ be as in Equation (30). Then, the MRRTK Algorithm (Algorithm 2) applied to $A,\overrightarrow{b}+\overrightarrow{e}$ will detect the corrupted equations with probability at least

$$1-{\left[1-(1-\delta ){\left(\mathcal{P}(\mathcal{D},U)\right)}^{n^{*}}\right]}^W.$$

Theorem 5.

Let $0<\delta <1$. Fix $d\ge 1$, $W\le ⌊{\displaystyle \frac{\left|V\right|-k}{d}}⌋$, and let $n^{*}$ be as in Equation (30). Then, the MRRTKUS Algorithm (Algorithm 3) applied to $A,\overrightarrow{b}+\overrightarrow{e}$ will detect the corrupted equations and the remaining equations will have solution ${\overrightarrow{x}}^S$ with probability at least

$$1-\sum _{j=0}^{\lceil s/d\rceil -1}\left(\begin{array}{c}W\\ j\end{array}\right)p^j{(1-p)}^{W-j}$$

where $p=(1-\delta ){\left(\mathcal{P}(\mathcal{D},U)\right)}^{n^{*}}.$

See [45] for an extensive analysis of numerical experiments of these algorithms, which we do not reproduce here.

4. Numerical Experiments

4.1. The Test Equations

We randomly generated several types of test equations, full and sparse, of various sizes. The results for different types of matrices were very similar, so we just present some results for full matrices with entries generated from a standard normal distribution.

We generated the matrices once, made sure they had full rank, and stored them. Thus, all algorithms are working on the same matrices. However, the sequence of equations used in the random algorithms is generated at runtime.

There are two types of problems we considered. In the underdetermined case, illustrated here with a $255\times 1023$ matrix, all algorithms converge to the solution of minimal norm. In the consistent overdetermined case, illustrated here with a $1023\times 255$ matrix, all algorithms converge to the standard solution. The matrix dimensions are of the form $2^d-1$, for easier experimentation with binary trees.

In the inconsistent overdetermined case, deterministic Kaczmarz algorithms will converge to a weighted least-squares solution, depending on the type of algorithm and on the relaxation parameter $\omega$. However, random Kaczmarz algorithms do not converge in this case but do accumulate around a weighted least-squares solution, e.g., Theorem 1 in [15], and Theorem 3.

4.2. The Algorithms

We included several types of deterministic Kaczmarz algorithms in the numerical experiments:

• Standard Kaczmarz.
• Sequential block Kaczmarz, with several different numbers of blocks. The equations are divided into a small number of blocks, and the updates are performed as an orthogonal projection onto the solution space of each block, rather than each individual equation.
• Distributed Kaczmarz based on a binary tree as in [5].
• Distributed block Kaczmarz. This is distributed Kaczmarz based on a tree of depth 2 with a small number of leaves, where each leaf contains a block of equations.

In sequential block Kaczmarz we work on each block in sequence. In distributed block Kaczmarz we work on each block in parallel and average the results.

The block Kaczmarz case, whether sequential or distributed, is not actually covered by our theory. However, we believe that our results could be extended to this case fairly easily, as long as the equations in each block are underdetermined and have full rank, following the approach in [4].

These deterministic algorithms are compared to corresponding types of random Kaczmarz algorithms:

• Random standard Kaczmarz; one equation at a time is randomly chosen.
• Random block Kaczmarz; one block at a time is randomly chosen. There is no difference between sequential and parallel random block Kaczmarz.
• Random distributed Kaczmarz based on a binary tree, for several kinds of random choices:

  -

  Generations, that is, we use all nodes at a randomly chosen distance from the root.

  -

  Families, that is, using the children of a randomly chosen node; for a binary tree, these are pairs.

  -

  Subtrees, that is, using the subtree rooted at a randomly chosen node. This is not an incomparable choice, so it is not covered by our theory.

For a matrix of size $m\times k$, in the deterministic cases one iteration consists of applying m updates, using each equation once. A block of size $n\times k$ counts as n updates. In the random cases, different random choices may involve different numbers of equations; we apply updates until the number of equations used reaches or slightly exceeds m.

After each iteration, we compute the 2-norm of the error. The convergence factor at each step is the factor by which the error has gone down at the last step. These factors often vary considerably in the first few steps and then settle down. The empirical convergence factors given in the tables below are calculated as the geometric average of the convergence factors over the second half of the iterations.

4.3. Numerical Results

The empirical convergence factors shown in Table 1 and Table 2 are based on 10 iterations. Each convergence factor is computed as the fifth root of the ratio of errors between iterations 5 and 10. For the random algorithms, each experiment (of 10 iterations) was run 20 times and the resulting convergence factors averaged.

Table 1. Convergence factors for various algorithms, for a random underdetermined equation of size $255\times 1023$. Numbers in parentheses represent the estimates from Equation (13).

	Relaxation Parameter $\mathit{\omega }$
	0.5	1	1.5	2	2.5	3	3.5
deterministic
standard	0.8138	0.5428	0.5579
sequential blocks
4 blocks	0.7963	0.4926	0.5227
16 blocks	0.8101	0.5362	0.5531
64 blocks	0.8135	0.5448	0.5628
parallel blocks
4 blocks	0.9346	0.8947	0.8604	0.8276	0.7948	0.7616	0.7273
16 blocks	0.9800	0.9636	0.9499	0.9379	0.9271	0.9173	0.9080
64 blocks	0.9947	0.9897	0.9849	0.9804	0.9761	0.9720	0.9681
255 blocks	0.9986	0.9973	0.9960	0.9947	0.9934	0.9922	0.9909
binary tree	0.9941	0.9903	0.9870	0.9841
random
standard	0.8440	0.7472	0.7039
blocks
4 blocks	0.8013	0.6736	0.6724
16 blocks	0.8146	0.7162	0.7001
64 blocks	0.8252	0.7393	0.7136
binary tree
family	0.9055	0.8510	0.8133	0.7742	0.7692	0.7528	0.8178
	(0.9099)	(0.8817)	(0.9099)
generation	0.9940	0.9903	0.9874	0.9849
	(0.9985)	(0.9980)	(0.9985)
subtree	0.9352	0.9017	0.8617	0.8735	0.9078

Table 2. Convergence factors for various algorithms, for a random overdetermined consistent equation of size $1023\times 255$. Numbers in parentheses represent the estimates from Equation (13).

	Relaxation Parameter $\mathit{\omega }$
	0.5	1	1.5	2	2.5	3	3.5
deterministic
standard	0.4923	0.2564	0.2424
sequential blocks
4 blocks	0.0625	0.0000	0.0625
16 blocks	0.4311	0.1863	0.1894
64 blocks	0.4759	0.2131	0.2263
255 blocks	0.4930	0.2588	0.2409
parallel blocks
4 blocks	0.5000	0.0000	0.5000
16 blocks	0.9125	0.8696	0.8303	0.7919	0.7550	0.7195	0.6795
64 blocks	0.9707	0.9483	0.9313	0.9178	0.9063	0.8958	0.8857
256 blocks	0.9920	0.9845	0.9775	0.9709	0.9647	0.9590	0.9536
1023 blocks	0.9980	0.9960	0.9940	0.9920	0.9901	0.9882	0.9864
binary tree	0.9889	0.9817	0.9758	0.9704
random
standard	0.5481	0.3421	0.2748
blocks
4 blocks	0.0625	0.0000	0.0625
16 blocks	0.4451	0.2464	0.2291
64 blocks	0.4690	0.2847	0.2579
256 blocks	0.4812	0.2874	0.2675
binary tree
family	0.7040	0.5401	0.4225	0.3356	0.2615	0.2769	0.4462
	(0.6879)	(0.6073)	(0.6879)
generation	0.9889	0.9809	0.9768	0.9709
	(0.9985)	(0.9980)	(0.9985)
subtree	0.8349	0.7474	0.6486	0.6408	0.7103

For binary trees, with a random choice of generations or families, we also calculated the estimated convergence factors described in Equation (13). These estimates are for one random step. For a binary tree of K levels, it takes on average K choices of generation to use the entire tree once. For families, it is $2^{K-1}$ choices of families (pairs, in this case). To estimate the convergence factor for one iteration, we took a corresponding power of the estimates.

Table 1 shows the convergence factors for the underdetermined case. An empty entry means that the algorithm did not converge for this value of $\omega$.

Here are some observations about Table 1:

• Sequential block Kaczmarz and random block Kaczmarz for 255 blocks are identical to their standard Kaczmarz counterparts and are not shown.
• Sequential methods, including standard Kacmarz and sequential block Kaczmarz, converge faster than parallel methods, such as binary trees or distributed block Kaczmarz. This is not surprising: in sequential methods, each step uses the results of the preceding step; in parallel methods, each step uses older data.
• The same reasoning explains why the Family selection is faster than Generations. Consider level 3, as an example. With Generations, we do 8 equations in parallel. With Families, we do four sets of 2 equations each, but each pair uses the result from the previous step.
• The block algorithm for a single block with $\omega =1$ converges in a single step, so the convergence factor is 0. At the other end of the spectrum, with 255 blocks of one equation each, the block algorithm becomes standard Kaczmarz. As the number of blocks increases, the convergence factor is observed to increase and approach the standard Kaczmarz value.
• Standard Kaczmarz, deterministic or random, converges precisely for $\omega \in (0,2)$. By the results in [4], this is also true for sequential block Kaczmarz.
  Distributed Kaczmarz methods are guaranteed to converge for the same range of $\omega$, but in practice they often converge for larger $\omega$ as well, sometimes up to $\omega$ near 4. Random distributed methods appear to have similar behavior.
• The observed convergence factors for random algorithms are comparable to those for their deterministic counterparts but slightly worse. We attribute this to the fact that in the underdetermined case, all equations are important; random algorithms on an $m\times k$ matrix do not usually include all equations in a set of m updates, while deterministic algorithms do.
  As pointed out in [8], there are types of equations where random algorithms are significantly faster than deterministic algorithms, but our sample equations are obviously not in that category.

Table 2 shows the convergence factors for the consistent overdetermined case.

Observations about Table 2:

• All algorithms converge faster in the overdetermined consistent case than in the underdetermined case. That is not surprising: since we have four times more equations than we actually need; one complete run through all equations is comparable to four complete run-throughs for the underdetermined case.
• For the same reason, the parallel block algorithm with four blocks (or fewer) for $\omega =1$ converges in a single step.
• We observe that random algorithms are still slower in the overdetermined case, even though the argument from the underdetermined case does not apply here.