A Peptides Prediction Methodology with Fragments and CNN for Tertiary Structure Based on GRSA2
Abstract
1. Introduction
2. Background
- To understand the physical code in which an amino acid sequence dictates its NS.
- Design an algorithm that quickly and efficiently finds the NS.
- To determine the NS using only amino acid sequence information.
- To determine the NS using protein structure information, such as the secondary structure (SS) or fragments of other known proteins.
2.1. Protein Structure Prediction
2.2. Deep Learning and CNN
2.3. HSA Algorithms
| Algorithm 1 GRSA2 algorithm Procedure |
| 1: Data: Tf, Tfp, Ti, E, S, α, KE |
| 2: α = 0.70 |
| 3: ϕ = 0.618 |
| 4: KE = 0 |
| 5: Tfp = Ti |
| 6: Tk = Ti |
| 7: Si = generateSolution() |
| 8: while Tk ≥ Tf do //Temperature cycle |
| 9: while Metropolis length do //Metropolis cycle |
| 10: Eold = E(Si) |
| 11: Sj = GRSA2pert(Si) |
| 12: EP = E(Sj) |
| 13: if (EP ≤ Eold + KE) then |
| 14: Si = Sj |
| 15: KE = ((Eold + KE) – EP) *random[0,1] |
| 16: end if |
| 17: end while //End Metropolis cycle |
| 18: GRSA_Cooling_Schema(Tfp) |
| 19: GRSA_Stop_Criterion() |
| 20: end while //End Temperature cycle |
| 21: end Procedure |
| Algorithm 2 GRSA2pert Function |
| 1: GRSA2pert(Si) |
| 2: moleColl, b |
| 3: if b > moleColl then |
| 4: Randomly select one particle Mω |
| 5: if Decompositioncriterionmet |
| 6: Sj = Decomposition(Si) |
| 7: else if |
| 8: Sj = SoftCollition(Si) |
| 9: end if |
| 10: end if |
| 11: return Sj |
| 12: end Function |
2.4. Performance Evaluation
2.4.1. TM-Score
2.4.2. GDT-TS
2.4.3. RMSD
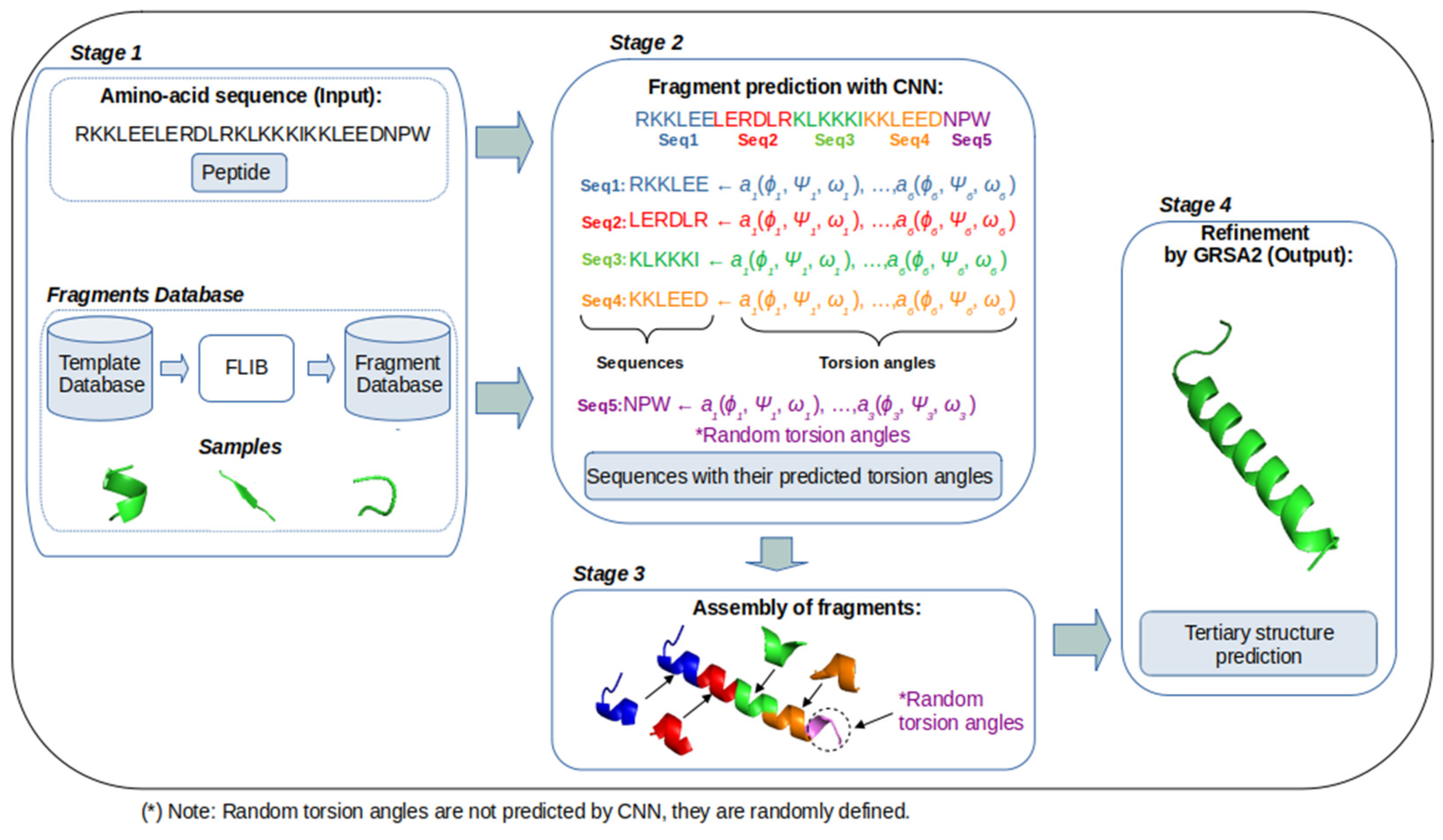
3. GRSA2-FCNN Methodology
- Amino acid sequence (Stage 1): The amino acid sequence of the target protein is the input for our method. In this stage, the fragments database contains a set of fragments that are classified according to their predominant alpha, beta, and loop secondary structures.
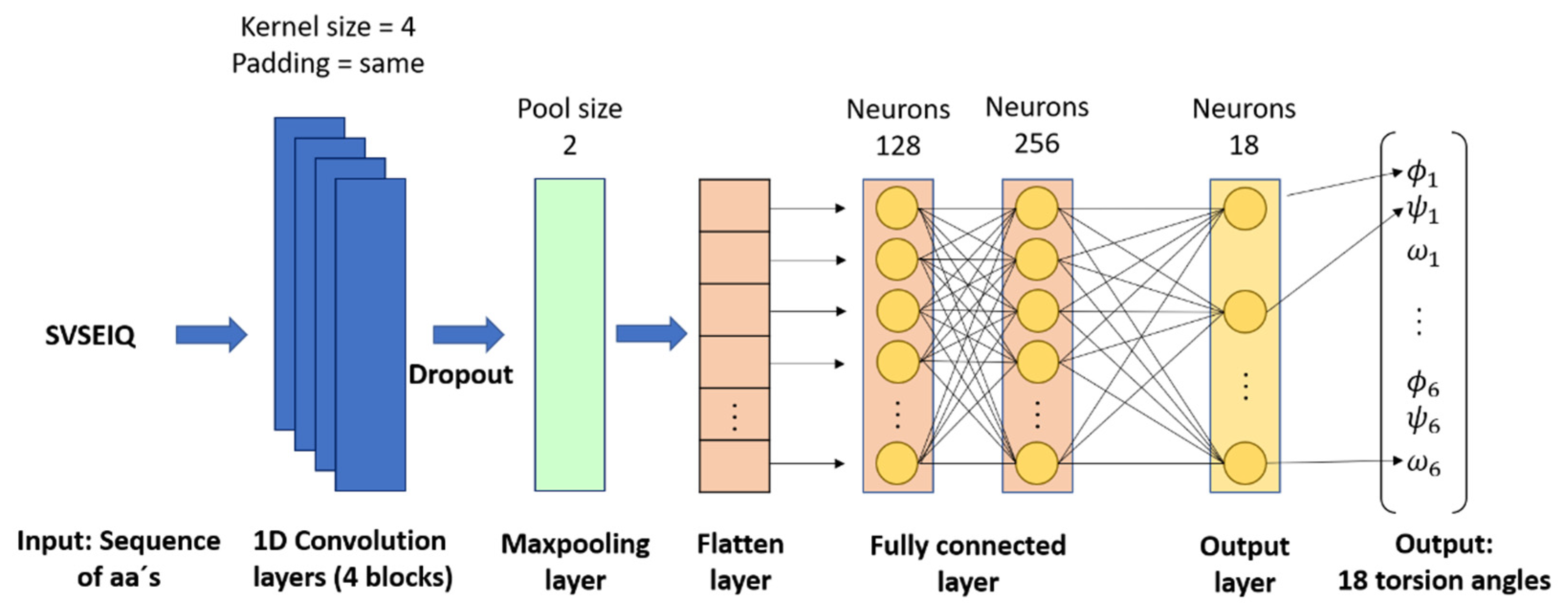
- Fragments prediction with CNN (Stage 2): The fragments database of stage 1 is used as the input for training a CNN, which performs the prediction of fragments (alpha, beta, and loop) and their torsion angles, which are the internal angles of the backbone of a protein (phi ϕ, psi ψ, and omega ω). A CNN is used to map aa sequences, described by their character-based representation, into their corresponding 3D configurations, which are described by the torsion angles ϕ, ψ, and ω of the bonds of their atoms. These inputs are short sequences of six amino acids only. We chose to work with sequences of this length to maintain low computational requirements. The notation used to represent the input and output of this stage is:where indicates the name of the n-th amino acid in the input sequence, and ϕ, ψ, and ω represent the n-th triplet of the torsion angles for .
- Assembly of fragments (Stage 3): The predicted fragments (vector of torsion angles) are concatenated to build a new model of the target sequence. This is to say, the preliminary predictions of the individual segments are concatenated one after the other to build a large vector of torsion angles that corresponds to the complete protein. In this process, the torsion angles of the fragments are assembled in cuts of six amino acids based on the sequence of the aa target. If eventually, the size of the target sequence is not proportional to the size of the fragments, some angles cannot be predicted. In this case, random values are used. This and other issues are solved in the next stage.
- Refinement by GRSA2 (Stage 4): The full preliminary model, formed by the concatenation of fragments from stage 3, is refined with the energy minimization algorithm GRSA2. The result of this stage is the final tertiary structure of the target protein.
3.1. Fragments Prediction with CNN (FCNN)
3.2. Assembly of Fragments
3.3. Refinement by GRSA2
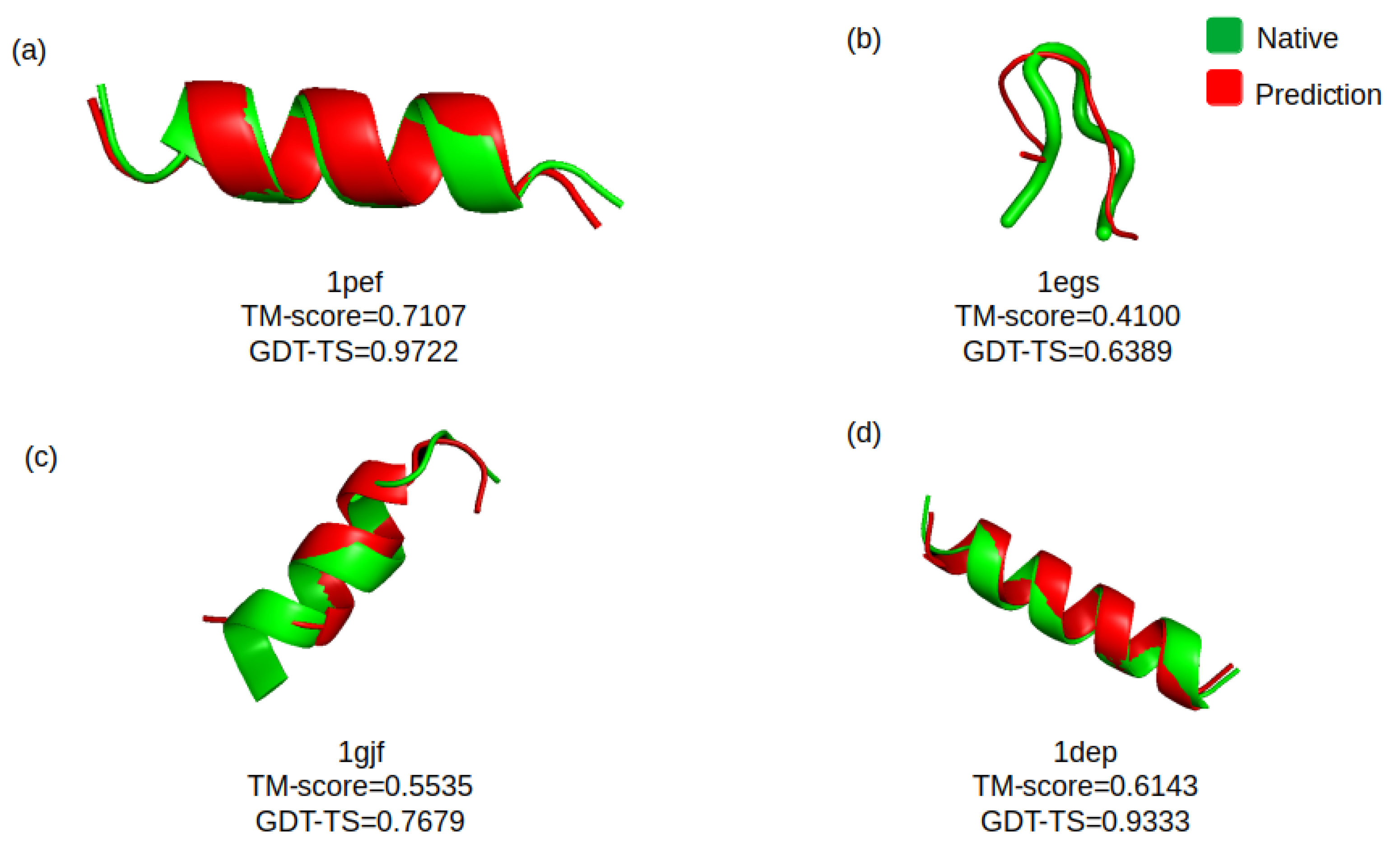
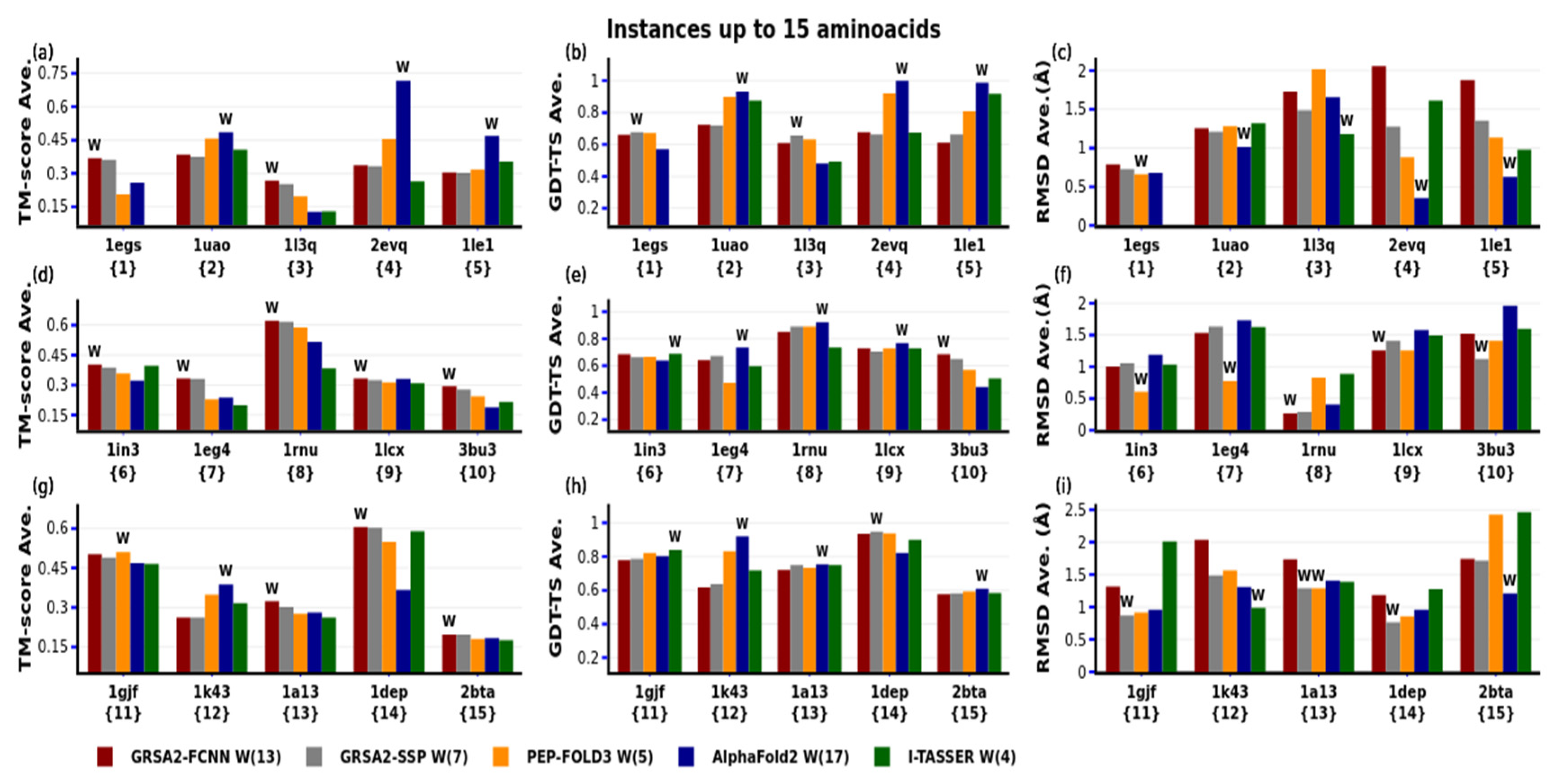
4. Results
4.1. First Evaluation
4.2. Second Evaluation
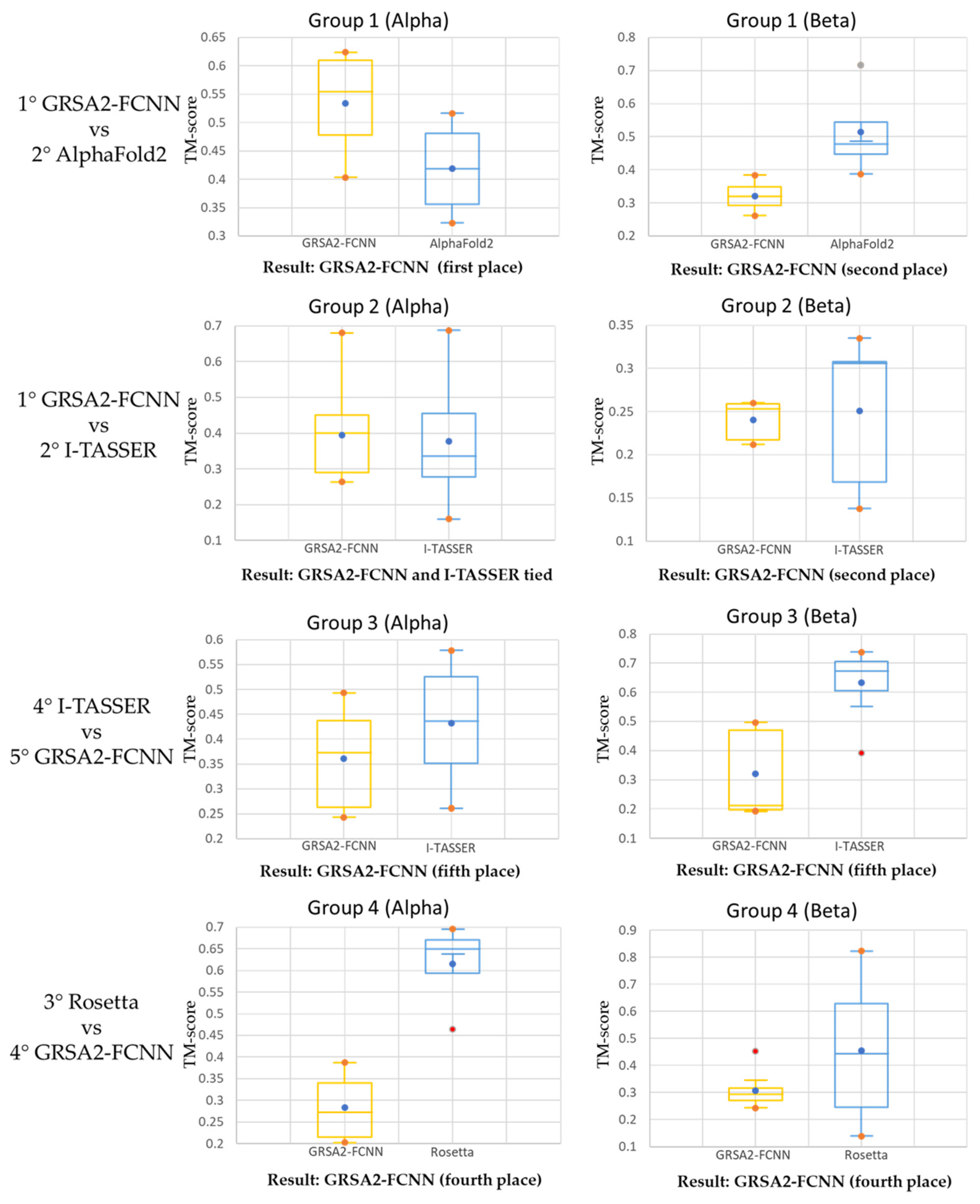
4.3. Third Evaluation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Anfinsen, C.; Haber, E.; Sela, M.; White, F.H.J. The kinetics of formation of native ribonuclease during oxidation of the reduced polypeptide chain. Proc. Natl. Acad. Sci. USA 1961, 47, 1309. [Google Scholar] [CrossRef] [PubMed]
- Patel, L.N.; Zaro, J.L.; Shen, W.-C. Cell Penetrating Peptides: Intracellular Pathways and Pharmaceutical Perspectives. Pharm. Res. 2007, 24, 1977–1992. [Google Scholar] [CrossRef] [PubMed]
- Agyei, D.; Danquah, M.K. Industrial-scale manufacturing of pharmaceutical-grade bioactive peptides. Biotechnol. Adv. 2011, 29, 272–277. [Google Scholar] [CrossRef] [PubMed]
- Uhlig, T.; Kyprianou, T.; Martinelli, F.G.; Oppici, C.A.; Heiligers, D.; Hills, D.; Verhaert, P. The Emergence of Peptides in the Pharmaceutical Business: From Exploration to Exploitation. EuPA Open Proteom. 2014, 4, 58–69. [Google Scholar] [CrossRef]
- Vetter, I.; Davis, J.L.; Rash, L.D.; Anangi, R.; Mobli, M.; Alewood, P.F.; King, G.F. Venomics: A new paradigm for natural products-based drug discovery. Amino Acids. 2010, 40, 15–28. [Google Scholar] [CrossRef]
- Craik, D.J.; Fairlie, D.P.; Liras, S.; Price, D. The future of peptide-based drugs. Chem. Biol. Drug Des. 2013, 81, 136–147. [Google Scholar] [CrossRef]
- Fosgerau, K.; Hoffmann, T. Peptide Therapeutics: Current Status and Future Directions. Drug Discov. Today 2015, 20, 122–128. [Google Scholar] [CrossRef]
- Wang, D.; Geng, L.; Zhao, Y.J.; Yang, Y.; Huang, Y.; Zhang, Y.; Shen, H.B. Artificial intelligence-based multi-objective optimization protocol for protein structure refinement. Bioinformatics 2020, 36, 437–448. [Google Scholar] [CrossRef]
- Hiranuma, N.; Park, H.; Baek, M.; Anishchenko, I.; Dauparas, J.; Baker, D. Improved protein structure refinement guided by deep learning based accuracy estimation. Nat. Commun. 2021, 12, 1–11. [Google Scholar] [CrossRef]
- Senior, A.W.; Evans, R.; Jumper, J.; Kirkpatrick, J.; Sifre, L.; Green, T.; Qin, C.; Žídek, A.; Nelson, A.W.R.; Bridgland, A.; et al. Protein structure prediction using multiple deep neural networks in the 13th Critical Assessment of Protein Structure Prediction (CASP13). Proteins Struct. Funct. Bioinform. 2019, 87, 1141–1148. [Google Scholar] [CrossRef]
- De Oliveira, S.; Law, E.C.; Shi, J.; Deane, C.M. Sequential search leads to faster, more efficient fragment-based de novo protein structure prediction. Bioinformatics 2017, 34, 1132–1140. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Scheraga, H.A. Monte Carlo-minimization Approach to the Multiple-minima Problem in Protein Folding. Proc. Natl. Acad. Sci. USA 1987, 84, 6611–6615. [Google Scholar] [CrossRef] [PubMed]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Xu, D.; Zhang, Y. Toward optimal fragment generations for ab initio protein structure assembly. Proteins 2013, 81, 229–239. [Google Scholar] [CrossRef]
- Lamiable, A.; Thévenet, P.; Rey, J.; Vavrusa, M.; Derreumaux, P.; Tufféry, P. PEP-FOLD3: Faster de Novo Structure Prediction for Linear Peptides in Solution and in Complex. Nucleic Acids Res. 2016, 44, W449–W454. [Google Scholar] [CrossRef]
- Frausto, J.; Sánchez, J.P.; Sánchez, M.; García, E.L. Golden Ratio Simulated Annealing for Protein Folding Problem. Int. J. Comput. Methods 2015, 12, 1550037. [Google Scholar] [CrossRef]
- Frausto, J.; Sánchez, J.P.; Maldonado, F.; González, J.J. GRSA Enhanced for Protein Folding Problem in the Case of Peptides. Axioms 2019, 8, 136. [Google Scholar] [CrossRef]
- Sánchez-Hernández, J.P.; Frausto-Solís, J.; González-Barbosa, J.J.; Soto-Monterrubio, D.A.; Maldonado-Nava, F.G.; Castilla-Valdez, G. A Peptides Prediction Methodology for Tertiary Structure Based on Simulated Annealing. Math. Comput. Appl. 2021, 26, 39. [Google Scholar] [CrossRef]
- Zhang, Y.; Skolnick, J. Scoring function for automated assessment of protein structure template quality. Proteins 2004, 57, 702–710. [Google Scholar] [CrossRef]
- Zemla, A.; Venclovas, C.; Moult, J.; Fidelis, K. Processing and analysis of casp3 protein structure predictions. Proteins Struct. Funct. Genet. 1999, 3, 22–29. [Google Scholar] [CrossRef]
- Dill, K.A.; MacCallum, J.L. The Protein-Folding Problem, 50 Years On. Science 2012, 338, 1042–1046. [Google Scholar] [CrossRef] [PubMed]
- Dorn, M.; e Silva, M.B.; Buriol, L.S.; Lamb, L.C. Three-dimensional protein structure prediction: Methods and computational strategies. Comput. Biol. Chem. 2014, 53, 251–276. [Google Scholar] [CrossRef] [PubMed]
- Levinthal, C. Are there pathways for protein folding? J. De Chim. Phys. 1968, 65, 44–45. [Google Scholar] [CrossRef]
- Zheng, W.; Zhang, C.; Bell, E.W.; Zhang, Y. I-TASSER gateway: A protein structure and function prediction server powered by XSEDE. Future Gener. Comput. Syst. 2019, 99, 73–85. [Google Scholar] [CrossRef]
- Mulnaes, D.; Porta, N.; Clemens, R.; Apanasenko, I.; Reiners, J.; Gremer, L.; Gohlke, H. TopModel: Template-based protein structure prediction at low sequence identity using top-down consensus and deep neural networks. J. Chem. Theory Comput. 2020, 16, 1953–1967. [Google Scholar] [CrossRef]
- Simons, K.T.; Kooperberg, C.; Huang, E.; Baker, D. Assembly of protein tertiary structures from fragments with similar local sequences using simulated annealing and bayesian scoring functions. J. Mol. Biol. 1997, 268, 209–225. [Google Scholar] [CrossRef]
- Senior, A.W.; Evans, R.; Jumper, J.; Kirkpatrick, J.; Sifre, L.; Green, T.; Hassabis, D. Improved protein structure prediction using potentials from deep learning. Nature 2020, 577, 706–710. [Google Scholar] [CrossRef]
- Conway, P.; Tyka, M.D.; DiMaio, F.; Konerding, D.E.; Baker, D. Relaxation of backbone bond geometry improves protein energy landscape modeling. Protein Sci. 2014, 23, 47–55. [Google Scholar] [CrossRef]
- Mirdita, M.; Schütze, K.; Moriwaki, Y.; Heo, L.; Ovchinnikov, S.; Steinegger, M. ColabFold: Making protein folding accessible to all. Nat. Methods 2022, 19, 679–682. [Google Scholar] [CrossRef]
- Mirdita, M.; Steinegger, M.; Söding, J. MMseqs2 desktop and local web server app for fast, interactive sequence searches. Bioinformatics 2019, 35, 2856–2858. [Google Scholar] [CrossRef]
- Muhammad, K.; Ahmad, J.; Lv, Z.; Bellavista, P.; Yang, P.; Baik, S.W. Efficient Deep CNN-Based Fire Detection and Localization in Video Surveillance Applications. IEEE Trans. Sys. Man Cybernetics Sys. 2019, 49, 1419–1434. [Google Scholar] [CrossRef]
- Dyrmann, M.; Karstoft, H.; Midtiby, H.S. Plant species classification using deep convolutional neural network. Biosyst. Eng. 2016, 151, 72–80. [Google Scholar] [CrossRef]
- Frausto-Solís, J.; Hernández-González, L.J.; González-Barbosa, J.J.; Sánchez-Hernández, J.P.; Román-Rangel, E.F. Convolutional Neural Network–Component Transformation (CNN–CT) for Confirmed COVID-19 Cases. Math. Comput. Appl. 2021, 26, 29. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A.; Bengio, Y. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Alzubaidi, L.; Zhang, J.; Humaidi, A.J.; Al-Dujaili, A.; Duan, Y.; Al-Shamma, O.; Farhan, L. Review of deep learning: Concepts, CNN architectures, challenges, applications, future directions. J. Big Data 2021, 8, 1–74. [Google Scholar] [CrossRef]
- Černý, V. Thermodynamical approach to the traveling salesman problem: An efficient simulation algorithm. J. Optim. Theory Appl. 1985, 45, 41–51. [Google Scholar] [CrossRef]
- Frausto, J.; Román, E.F.; Romero, D.; Soberon, X.; Liñán, E. Analytically Tuned Simulated Annealing Applied to the Protein Folding Problem. In Proceedings of the 7th International Conference on Computational Science, Beijing, China, 27–30 May 2007; pp. 370–377. [Google Scholar]
- Kufareva, I.; Abagyan, R. Methods of protein structure comparison. Methods Mol Biol. 2012, 857, 231–257. [Google Scholar] [CrossRef]
- De Oliveira, S.H.; Shi, J.; Deane, C.M. Building a better fragment library for de novo protein structure prediction. PLoS ONE 2015, 10, e0123998. [Google Scholar] [CrossRef]
- Bernstein, F.C.; Koetzle, T.F.; Williams, G.J.; Meyer Jr, E.E.; Brice, M.D.; Rodgers, J.R.; Kennard, O.; Shimanouchi, T.; Tasumi, M. The Protein Data Bank: A Computer-based Archival File For Macromolecular Structures. J. Mol. Biol. 1977, 112, 535. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference on Learning Representations, ICLR, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Maupetit, J.; Derreumaux, P.; Tuffery, P. PEP-FOLD: An online resource for de novo peptide structure prediction. Nucleic Acids Res. 2009, 37, W498–W503. [Google Scholar] [CrossRef]
- Shen, Y.; Maupetit, J.; Derreumaux, P.; Tufféry, P. Improved PEP-FOLD approach for peptide and miniprotein structure pre-diction. J. Chem. Theory Comput. 2014, 10, 4745–4758. [Google Scholar] [CrossRef]
- Eisenmenger, F.; Hansmann, U.H.; Hayryan, S.; Hu, C.-K. [SMMP] A modern package for simulation of proteins. Comput. Phys. Commun. 2001, 138, 192–212. [Google Scholar] [CrossRef]


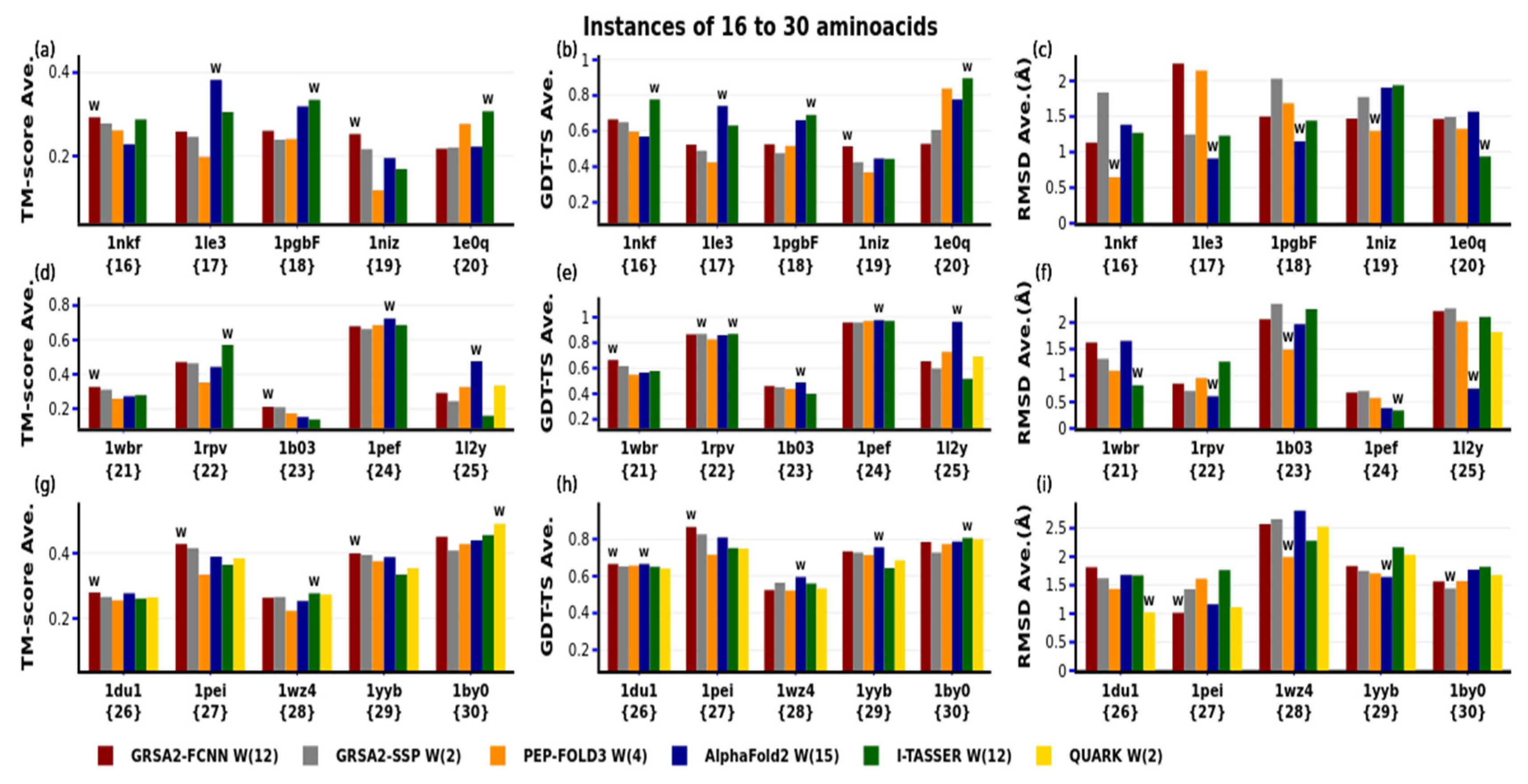

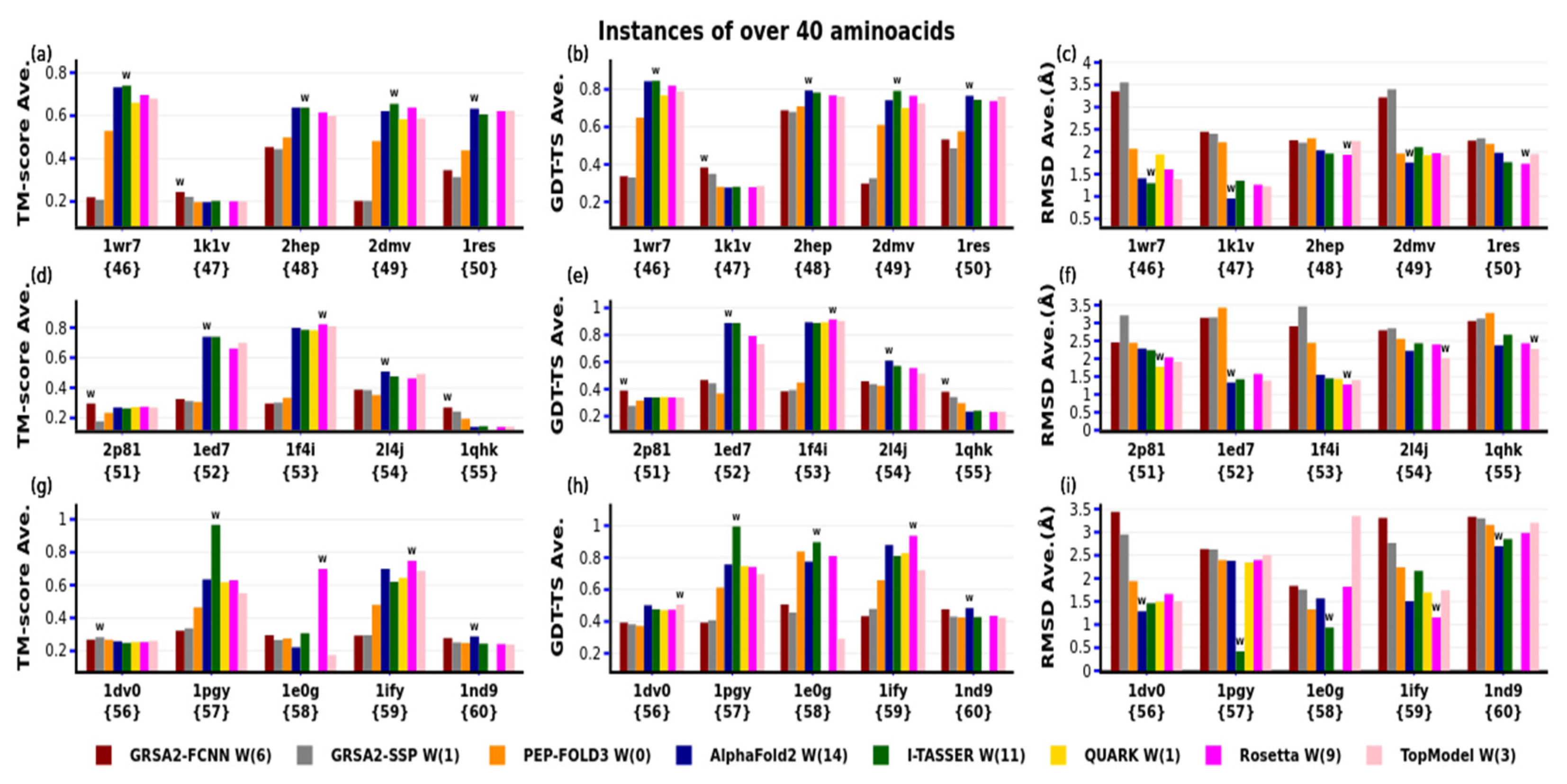

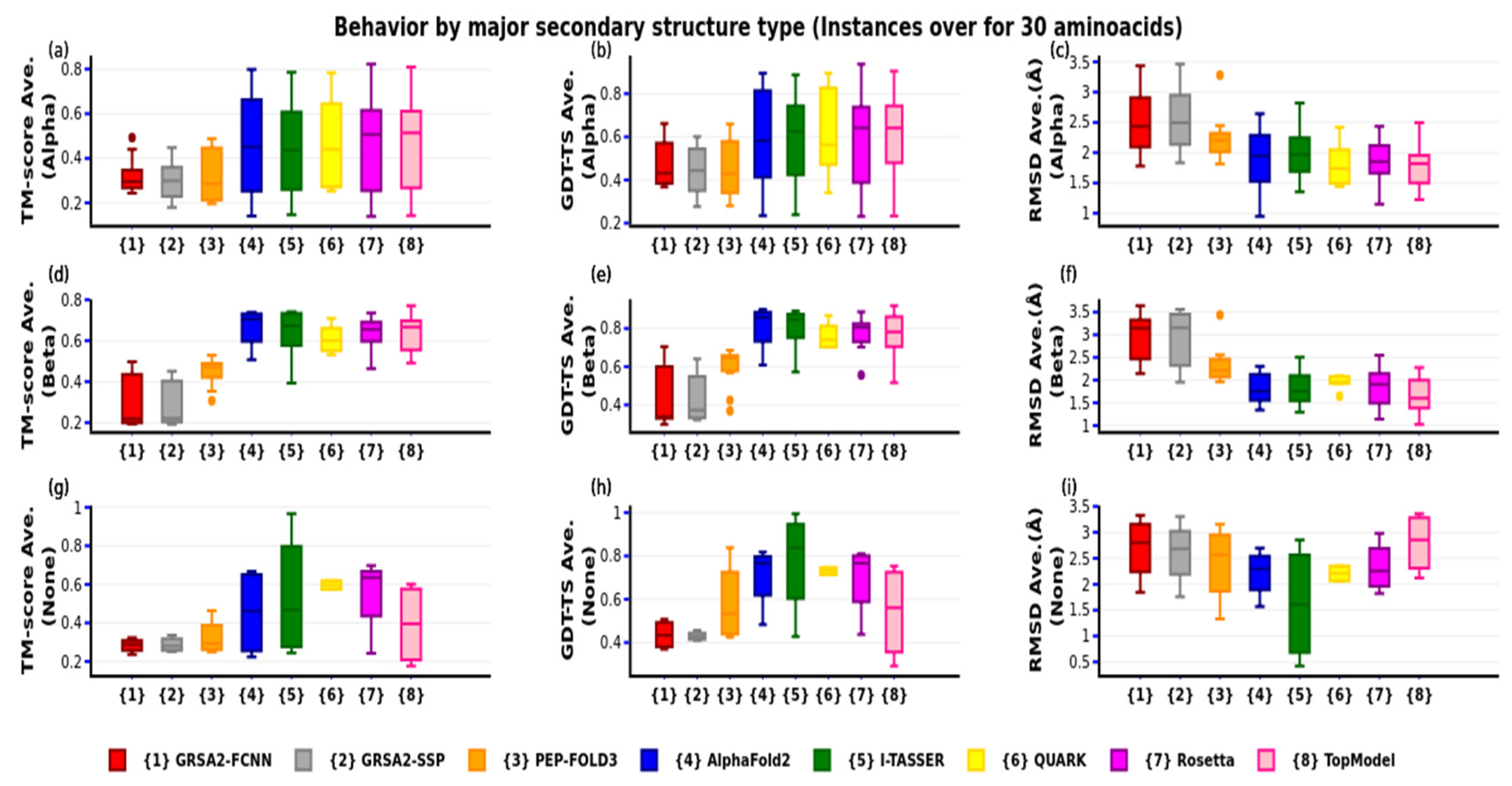

| N | PDB-Code | N° aa | Var. | Type SS | Exp | N | PDB-code | N° aa | Var. | Type SS | Exp |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1egs | 9 | 49 | none | NMR | 31 | 1t0c | 31 | 163 | none | NMR |
| 2 | 1uao | 10 | 47 | beta | NMR | 32 | 2gdl | 31 | 201 | alpha | NMR |
| 3 | 1l3q | 12 | 62 | none | NMR | 33 | 2l0g | 32 | 183 | alpha | NMR |
| 4 | 2evq | 12 | 66 | beta | NMR | 34 | 2bn6 | 33 | 200 | alpha | NMR |
| 5 | 1le1 | 12 | 69 | beta | NMR | 35 | 2kya | 34 | 210 | alpha | NMR |
| 6 | 1in3 | 12 | 74 | alpha | NMR | 36 | 1wr3 | 36 | 197 | beta | NMR |
| 7 | 1eg4 | 13 | 61 | none | X-ray | 37 | 1wr4 | 36 | 206 | beta | NMR |
| 8 | 1rnu | 13 | 81 | alpha | X-ray | 38 | 1e0m | 37 | 206 | beta | NMR |
| 9 | 1lcx | 13 | 81 | none | NMR | 39 | 1yiu | 37 | 212 | beta | NMR |
| 10 | 3bu3 | 14 | 74 | none | X-ray | 40 | 1e0l | 37 | 221 | beta | NMR |
| 11 | 1gjf | 14 | 79 | alpha | NMR | 41 | 1bhi | 38 | 216 | none | NMR |
| 12 | 1k43 | 14 | 84 | beta | NMR | 42 | 1jrj | 39 | 208 | beta | NMR |
| 13 | 1a13 | 14 | 85 | none | NMR | 43 | 1i6c | 39 | 218 | alpha | NMR |
| 14 | 1dep | 15 | 94 | alpha | NMR | 44 | 1bwx | 39 | 242 | alpha | NMR |
| 15 | 2bta | 15 | 100 | none | NMR | 45 | 2ysh | 40 | 213 | beta | NMR |
| 16 | 1nkf | 16 | 86 | alpha | NMR | 46 | 1wr7 | 41 | 222 | beta | NMR |
| 17 | 1le3 | 16 | 91 | beta | NMR | 47 | 1k1v | 41 | 279 | alpha | NMR |
| 18 | 1pgbF | 16 | 93 | beta | X-ray | 48 | 2hep | 42 | 268 | alpha | NMR |
| 19 | 1niz | 16 | 97 | beta | NMR | 49 | 2dmv | 43 | 229 | alpha | NMR |
| 20 | 1e0q | 17 | 109 | beta | NMR | 50 | 1res | 43 | 268 | beta | NMR |
| 21 | 1wbr | 17 | 120 | none | NMR | 51 | 2p81 | 44 | 295 | alpha | NMR |
| 22 | 1rpv | 17 | 124 | alpha | NMR | 52 | 1ed7 | 45 | 247 | beta | NMR |
| 23 | 1b03 | 18 | 109 | beta | NMR | 53 | 1f4i | 45 | 276 | alpha | NMR |
| 24 | 1pef | 18 | 124 | alpha | X-ray | 54 | 2l4j | 46 | 250 | beta | NMR |
| 25 | 1l2y | 20 | 100 | alpha | NMR | 55 | 1qhk | 47 | 272 | alpha | NMR |
| 26 | 1du1 | 20 | 134 | alpha | NMR | 56 | 1dv0 | 47 | 279 | alpha | NMR |
| 27 | 1pei | 22 | 143 | alpha | NMR | 57 | 1pgy | 47 | 304 | none | NMR |
| 28 | 1wz4 | 23 | 123 | alpha | NMR | 58 | 1e0g | 48 | 294 | none | NMR |
| 29 | 1yyb | 27 | 160 | alpha | NMR | 59 | 1ify | 49 | 290 | none | NMR |
| 30 | 1by0 | 27 | 193 | alpha | NMR | 60 | 1nd9 | 49 | 303 | alpha | NMR |
| Group 1 | Group 2 | Group 3 | Group 4 |
|---|---|---|---|
| 1° GRAS2-FCNN | 1°GRAS2-FCNN | 1° AlphaFold2 | 1° AlphaFold2 |
| 2° AlphaFold2 | 2° I-TASSER | 2° TopModel | 2° I-TASSER |
| 3° PEP-FOLD3 | 3° AlphaFold2 | 3° Rosetta | 3° Rosetta |
| 4° I-TASSER | 4° QUARK | 4° I-TASSER | 4° GRAS2-FCNN |
| 5° GRSA2-SSP | 5° PEP-FOLD3 | 5° GRAS2-FCNN | 5° GRAS2-SSP |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sánchez-Hernández, J.P.; Frausto-Solís, J.; Soto-Monterrubio, D.A.; González-Barbosa, J.J.; Roman-Rangel, E. A Peptides Prediction Methodology with Fragments and CNN for Tertiary Structure Based on GRSA2. Axioms 2022, 11, 729. https://doi.org/10.3390/axioms11120729
Sánchez-Hernández JP, Frausto-Solís J, Soto-Monterrubio DA, González-Barbosa JJ, Roman-Rangel E. A Peptides Prediction Methodology with Fragments and CNN for Tertiary Structure Based on GRSA2. Axioms. 2022; 11(12):729. https://doi.org/10.3390/axioms11120729
Chicago/Turabian StyleSánchez-Hernández, Juan P., Juan Frausto-Solís, Diego A. Soto-Monterrubio, Juan J. González-Barbosa, and Edgar Roman-Rangel. 2022. "A Peptides Prediction Methodology with Fragments and CNN for Tertiary Structure Based on GRSA2" Axioms 11, no. 12: 729. https://doi.org/10.3390/axioms11120729
APA StyleSánchez-Hernández, J. P., Frausto-Solís, J., Soto-Monterrubio, D. A., González-Barbosa, J. J., & Roman-Rangel, E. (2022). A Peptides Prediction Methodology with Fragments and CNN for Tertiary Structure Based on GRSA2. Axioms, 11(12), 729. https://doi.org/10.3390/axioms11120729









