A Fresh Approach to a Special Type of the Luria–Delbrück Distribution

Abstract

The mutant distribution that accommodates both fitness and plating efficiency is an important class of the Luria–Delbrück distribution. Practical algorithms for computing this distribution do not coincide with the theoretically most elegant ones, as existing generic methods often either produce unreliable results or freeze the computational process altogether when employed to solve real-world research problems. Exploiting properties of the hypergeometric function, this paper offers an algorithm that considerably expands the scope of application of this important class of the Luria–Delbrück distribution. An integration method is also devised to complement the novel algorithm. Asymptotic properties of the mutant probability are derived to help gauge the new algorithm. An illustrative example and simulation results provide further guidelines on the use of the new algorithm.

1. Introduction

The first distribution in the Luria–Delbrück (LD) distribution family was proposed by Delbrück [1] to provide a mathematical foundation for a trailblazing experimental protocol proposed by Luria. Their joint paper, now a classic in genetics research, ushered in an 80-year period of relentless progress in the experimental determination of microbial mutation rates. The experimental protocol is variously referred to as the fluctuation test, the fluctuation experiment, or the Luria–Delbrück experiment. The data generated by such an experiment are called fluctuation assay data, which is a sequence of nonnegative integers representing the numbers of mutants found by the experimentalist in a series of cultures. (For details about the experimental protocol, see Ref. [2].) Today, despite rapid advances in sequencing technology, the LD experimental protocol remains a widely favored tool for studying microbial mutation rates in the laboratory. While there has been little alteration to the experimental protocol, the LD distribution family has been augmented considerably.

The first addition to the LD distribution family was made by Lea and Coulson [3] to overcome an important drawback of the distribution proposed by Delbrück. Note that Delbrück used a continuous distribution to model the number of bacterial mutants observed in Luria’s experiments. However, the numbers of mutants in those experiments were small random numbers, and they rarely exceeded 1000. Seeing that a continuous distribution was not an efficient tool to model the number of mutants, Lea and Coulson employed a stochastic birth process to construct a new discrete distribution. The distribution constructed by Lea and Coulson is uniquely determined by a single parameter m, which is the expected number of mutations. Lea and Coulson defined their new distribution by giving the probability generating function of the form

$$e^{-m}exp\left\{m\left(\frac{z}{1\times 2}+\frac{z^2}{2\times 3}+\frac{z^3}{3\times 4}+\dots \right)\right\}$$

along with its more compact form ${(1-z)}^{m(1-z)/z}$ (see Equation (15) in Ref. [3]). This distribution is now widely referred to as the Luria–Delbrück distribution mainly due to historical reasons, as the original distribution proposed by Delbrück fell into disuse soon after the work of Lea and Coulson.

Further augmentation of the LD distribution family was effected by laboratory needs and theoretical considerations. Mandelbrot [4] and Koch [5] independently extended the Lea–Coulson distribution to accommodate distinctive cell growth rates between mutants and nonmutants. The resulting distribution has a fitness parameter w, which is the ratio of the mutant growth rate to the nonmutant growth rate. Another driving force in the augmentation of the LD distribution is the fact that the number of mutants in a culture is often too large to count. This laboratory difficulty clamors for the study of distributions having a plating efficiency parameter $ϵ$ that indicates how large a portion of each culture is actually plated to ease the counting burden. After a brief initial study of this kind of distribution by Armitage ([6], p. 14), several investigators explored these distributions more thoroughly in the 1990s [7,8,9,10,11]. More recently, further impetus for augmenting the LD distribution family comes from work on mathematical modeling of tumor progression. Antal and Krapivsky [12] studied the joint distribution of the numbers of both mutants and nonmutants. They allowed not only distinct cell growth rates between mutants and nonmutants, but also distinct cell death rates for both types of cells. In addition, Kessler and Levine [13] proposed a unified approach for computing mutant probabilities.

Efficient algorithms for computing various LD distributions are key to meaningful inference of microbial mutation rates. An algorithm must satisfy two practical requirements to be useful in the analysis of fluctuation assay data. First, it should remain operational for a wide range of key parameter values that an experimentalist might encounter in the laboratory. Among such parameters are $m,w$ and $ϵ$. Second, it should be capable of computing $p_k$ (the probability of k mutants) reasonably fast for $k\le K$ for some meaningful K (e.g., K = 2000). In the past 30 years, an idea introduced by Ma et al. [14] to compute the Lea–Coulson distribution has served as the backbone of several algorithms for computing a variety of extensions of the Lea–Coulson distribution. In 2013, Kessler and Levine [15] outlined a new, unified approach that relied on numerical integration to compute a much wider class of LD distributions. More details were given later by the same authors [13]. Mazoyer et al. [16] employed a possibly similar integration-based approach to compute a wide assortment of LD distributions in the R package flan. For the most part, the implementation in flan achieved impressive accuracy and computing speed. However, there are situations where this universal approach may not be optimal, convenient, or practical, as shown by the following example.

This example was inspired by an inquiry from a yeast microbiologist. Her group was planning fluctuation experiments to measure the rate of extra-chromosome loss in yeast cells. Due to the high rates of extra-chromosome loss seen in a pilot study, these investigators would like to plate a 0.5% portion of each culture. They also planned to measure cell growth rates to help enhance the accuracy of their rate estimates. Clearly, their data would require an LD distribution involving $m,w$ and $ϵ$. Because $ϵ=0.005$, it is sensible to set $m=100$ as a testing value to allow a manageable number of mutants to be observed in the plated portion of a culture. Next, a value for the fitness parameter w is needed. Meaningful values for w lie around $1.0$, and we here regard all real numbers on the interval $(0.1,2.0)$ as values for w that may be encountered in real-world research. To produce a complete testing example, we set $w=0.7$. With this testing example, the latest version of flan (v. 0.9) can compute $p_k$ easily for $k\le 205$. However, computing $p_k$ for any $k\ge 206$ would cause flan to stop responding. Perhaps such an annoying problem can be circumvented by tweaking the algorithm on a case-by-case basis. Still, it is worthwhile to seek alternative algorithms to compute this special type of three-parameter LD distributions. In this paper, we offer a more practical algorithm for the three-parameter LD distribution that is crucial to the yeast microbiologist’s investigation and to numerous other investigations. We begin by studying this distribution’s probability generating function.

2. The Probability Generating Function

As just mentioned, sometimes a culture may contain too many mutants for the experimentalist to count. A way of overcoming this difficulty is to count mutants in only a fraction of the whole culture, a practice called partial plating. If an $ϵ$ portion of the whole culture is taken (plated, in microbiology parlance) to count mutants, it is conceptually equivalent to subjecting all mutants in the whole culture to a binomial sampling process with the success probability being $ϵ$. (The parameter $ϵ$ is called the plating efficiency). Therefore, the distribution of the number of mutants observed by the experimentalist is related to the distribution of the number of mutants in the whole culture. Armitage ([6], Equation (50)) gave the relation in terms of the two distributions’ generating functions as follows.

$$G_Y\left(z\right)=G_X(1-ϵ+ϵz).$$

(1)

Here, $G_X$ and $G_Y$ are respectively the generating functions of the number of mutants in the whole culture and of the number of mutants in the plated culture, and $ϵ$ is the plating efficiency. A brief proof of Equation (1) may run as follows.

Let X be the number of mutants in the whole culture, and let Y be the number of mutants in the plated culture. From elementary theory of conditional probability it follows that

$$\begin{array}{cc}\hfill P(Y=k)& =\sum _{m=k}^{\infty }P(Y=k|x=m)P(X=m)\hfill \\ \hfill & =\sum _{m=k}^{\infty }\left(\genfrac{}{}{0pt}{}{m}{k}\right){ϵ}^k{(1-ϵ)}^{m-k}P(X=m).\hfill \end{array}$$

(2)

Therefore,

$$\begin{array}{cc}\hfill G_Y\left(z\right)& =\sum _{k=0}^{\infty }P(Y=k)z^k\hfill \\ \hfill & =\sum _{k=0}^{\infty }\sum _{m=k}^{\infty }\left[\left(\genfrac{}{}{0pt}{}{m}{k}\right){ϵ}^k{(1-ϵ)}^{m-k}P(X=m)\right]z^k\hfill \\ \hfill & =\sum _{m=0}^{\infty }\sum _{k=0}^m\left[\left(\genfrac{}{}{0pt}{}{m}{k}\right){\left(ϵz\right)}^k{(1-ϵ)}^{m-k}\right]P(X=m)\hfill \\ \hfill & =\sum _{m=0}^{\infty }\sum _{k=0}^m\left[\left(\genfrac{}{}{0pt}{}{m}{k}\right){\left(\frac{ϵz}{1-ϵ}\right)}^k\right]{(1-ϵ)}^{m}P(X=m)\hfill \\ \hfill & =\sum _{m=0}^{\infty }{(1-ϵ+ϵz)}^{m}P(X=m)=G_X(1-ϵ+ϵz).\hfill \end{array}$$

(3)

Now the distribution to be investigated can be assembled by using (1). The distribution of the number of mutants in the whole culture is the same distribution studied by Mandelbrot [4] and Koch [5]. This distribution is known [17] to have an approximate generating function of the form

$$g_0\left(z\right)=exp\left(-m+\frac{m}{w}\sum _{k=1}^{\infty }B\left(k,1+w^{-1}\right)z^k\right)$$

(4)

where $B(a,b)={\int }_0^1{t}^{a-1}{(1-t)}^{b-1}dt$ denotes the beta function. However, an equivalent expression due to Kessler and Levine [13] would facilitate subsequent development. Setting the two cell death rates to zero and adopting new notation, we reduce Equation (45) of Kessler and Levine [13] to

$$g_1\left(z\right)=exp\left\{-mF\left(1,\frac{1}{w},1+\frac{1}{w},\frac{z}{z-1}\right)\right\}.$$

(5)

Here, the symbol $F(a,b,c,z)$ is simplified notation for $F(a,b;c;z)$, which denotes the hypergeometric function as defined in Ref. [18], p. 238. Note that the generating function $g_1\left(z\right)$ in (5) is well-defined for $z\in (-\infty ,1)$. The adoption of the hypergeometric function to help manipulate the generating function in (4) has caused the generating function to lose its definition at $z=1$, as $g_1\left(z\right)$ is clearly undefined at $z=1$. However, this small price paid for mathematical convenience does not compromise the ensuing development. Combining (1) with (5) and simplifying, we obtain the desired generating function $G\left(z\right)=g_1(1-ϵ+ϵz)$ of the form

$$G\left(z\right)=exp\left\{-mF\left(1,\frac{1}{w},1+\frac{1}{w},\frac{z+\theta }{z-1}\right)\right\}$$

(6)

with

$$\theta =\frac{1-ϵ}{ϵ}.$$

(7)

3. An Integration-Based Method

Let $p_k$ be the probability of k mutants. That is, $p_k=\left[z^k\right]G\left(z\right)$. Here, we use the notation $\left[z^k\right]f\left(z\right)$ to denote the coefficient of $z^k$ in the Maclaurin series expansion of $f\left(z\right)$. The integration method is based on Cauchy’s integral formula for derivatives:

$$p_k=\frac{1}{2\pi i}{\int }_{\gamma }\frac{G\left(z\right)}{z^{k+1}}dz.$$

(8)

Note that $G\left(z\right)$ is the pgf in (6) and $\gamma$ is a circle around the origin with a radius smaller than one. By definition, for any given $r\in (0,1)$, the above integral can be computed by

$$p_k=\frac{1}{2\pi }{\int }_0^{2\pi }\frac{G\left(r{e}^{i\theta }\right)}{r^k{e}^{ik\theta }}d\theta ,$$

where $e^{i\theta }=cos\left(\theta \right)+isin\left(\theta \right)$. However, in practice, there are important drawbacks to this idea. First, the integrand is a complex-valued function, which makes implementation and computation needlessly complicated. Second, it is not clear how to choose an appropriate value of r for a given problem, as a poorly chosen value of r can lead to a nonsensical result. Kessler and Levine [13] proposed a clever way of deforming the integration contour $\gamma$ to overcome these difficulties. In this section, we adapt their strategy to devise an improved integration-based algorithm for computing $p_k$.

The basic idea of Kessler and Levine was to transform the complex integral in (8) to a real integral along the positive real axis. One way to accomplish this task is to deform the contour $\gamma$ into a new contour as depicted in Figure 1, which has previously been done in Ref. [19]. We first transform the integral in (8) to a real integral along the ray $[1,\infty ]$. To facilitate the transformation, we rewrite the hypergeometric function appearing in the pgf in (6). Applying the transform $z\to 1/z$ via Equation (9.5.9) in Ref. [18], we obtain

$$\begin{array}{cc}\hfill F\left(1,\frac{1}{w},1+\frac{1}{w},\frac{z+\theta }{z-1}\right)& =\frac{\mathsf{\Gamma }(\frac{1}{w}-1)}{w\mathsf{\Gamma }\left(\frac{1}{w}\right)}\frac{1-z}{\theta +z}F\left(1,1-\frac{1}{w},2-\frac{1}{w},\frac{z-1}{z+\theta }\right)\hfill \\ \hfill & +\frac{\pi }{wsin\left(\frac{\pi }{w}\right)}{\left(\frac{1-z}{\theta +z}\right)}^{1/w}F\left(\frac{1}{w},0,\frac{1}{w},\frac{z-1}{z+\theta }\right).\hfill \end{array}$$

(9)

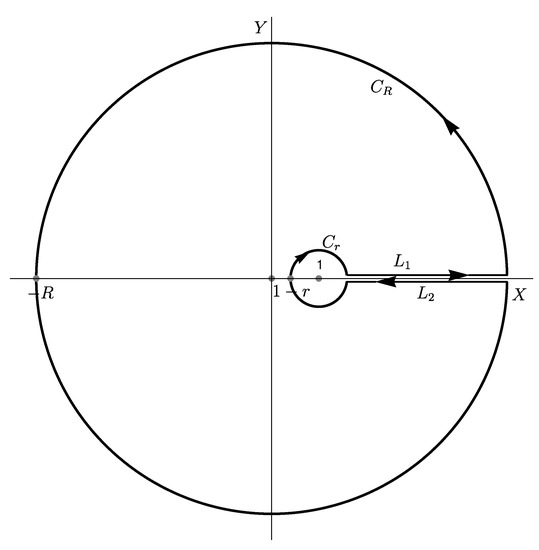
Figure 1. A contour used to derive the algorithm for computing $p_k$ given by (15).

Note that the hypergeometric function appearing in the first term on the right-hand side of (9) will invalidate this transform when $w=1/k$ for $k=2,3,\cdots$, because $F(\alpha ,\beta ,\gamma ,z)$ is undefined for $\gamma =0,-1,-2,\cdots$. This kind of drawback of the integration approach has been noticed in a previous study [19]. The practical implications of this drawback are worth noting. For example, when $w=0.5$, the integration-based algorithm fails altogether. Moreover, for values of w close to 0.5, the algorithm may produce unreliable results. Nevertheless, the transform in (9), introduced to the study of the Luria–Delbrück distribution by Kessler and Levine [13], simplifies the integral in (8) in two important ways. First, for $z\in [1,\infty )$, $(z-1)/(z+\theta )\in [0,1).$ Therefore, the hypergeometric function appearing in the first term on the right-hand side of (9) is a single-valued function of z for z on both edges of the ray $[1,\infty )$. Second, because $F(a,0,c,z)=1$ for all z, the second term on the right-hand side of (9) does not involve the hypergeometric function; but it can be a multivalued function, depending on whether z lies on the upper edge or lower edge of the ray. Therefore, we now focus on the second term on the right-hand side of (9) with the hypergeometric function removed.

For z on the upper and lower edges of the the ray $[1,\infty ]$, which are labeled $L_1$ and $L_2$, respectively, in Figure 1, we have

$$\begin{array}{cc}\hfill {\left(\frac{1-z}{\theta +z}\right)}^{1/w}& =exp\left\{\frac{1}{w}\left[log\frac{x-1}{x+\theta }\mp i\pi \right]\right\}\hfill \\ \hfill & ={\left(\frac{x-1}{x+\theta }\right)}^{1/w}exp\left(\mp i\frac{\pi }{w}\right)\hfill \\ \hfill & ={\left(\frac{x-1}{x+\theta }\right)}^{1/w}\left[cos\frac{\pi }{w}\mp isin\frac{\pi }{w}\right].\hfill \end{array}$$

(10)

Therefore, it follows that

$$\frac{-m\pi }{wsin\frac{\pi }{w}}{\left(\frac{1-z}{\theta +z}\right)}^{1/w}=\frac{-m\pi }{w}{\left(\frac{x-1}{x+\theta }\right)}^{1/w}\left[cot\frac{\pi }{w}\mp i\right].$$

(11)

Exponentiating (11) and then taking the imaginary part, we find that one factor of the integrand is

$$B\left(x\right):=exp\left[\frac{-m\pi }{wtan\left(\frac{\pi }{w}\right)}{\left(\frac{x-1}{x+\theta }\right)}^{1/w}\right]\times sin\left[\frac{m\pi }{w}{\left(\frac{x-1}{x+\theta }\right)}^{1/w}\right].$$

(12)

More precisely, $B\left(x\right)$ is the imaginary part of the quantity in (11) when z lives on the upper edge of the ray $[1,\infty$]. If z is on the lower edge of the ray, the imaginary part of (11) is $-B\left(x\right)$.

In light of (9), the other factor of the integrand is

$$A\left(x\right):=exp\left[\frac{m\mathsf{\Gamma }(\frac{1}{w}-1)}{w\mathsf{\Gamma }\left(\frac{1}{w}\right)}\frac{x-1}{\theta +x}F\left(1,1-\frac{1}{w},2-\frac{1}{w},\frac{x-1}{x+\theta }\right)\right].$$

(13)

It is now necessary to assume that the integral along the small circle $C_r$ and that long the large circle $C_R$ vanish as $r\to 0$ and $R\to \infty$. As shown in Ref. [19], this kind of claim requires excessive amounts of tedious mathematics to prove, and we do not attempt to prove the two claims here. Assuming the validity of these two claims, we add the integrals on $L_1$ and $L_2$ to obtain

$$p_k=\frac{1}{\pi }{\int }_1^{\infty }\frac{A\left(x\right)B\left(x\right)}{x^{k+1}}dx.$$

(14)

Following Kessler and Levine [13], we recast the above to an integral on the entire positive real axis:

$$p_k=\frac{1}{\pi }{\int }_0^{\infty }\frac{exp(A_1\left(t\right)+A_2\left(t\right)/tan(\pi /w))}{{(t+1)}^{k+1}}sin(-A_2\left(t\right))dt,$$

(15)

where

$$\begin{array}{cc}\hfill A_1\left(t\right):=& \frac{m\mathsf{\Gamma }(w^{-1}-1)}{w\mathsf{\Gamma }\left(w^{-1}\right)}\frac{t}{t+\theta +1}F\left(1,1-\frac{1}{w},2-\frac{1}{w},\frac{t}{t+\theta +1}\right),\hfill \\ \hfill A_2\left(t\right):=& \frac{-m\pi }{w}{\left(\frac{t}{t+\theta +1}\right)}^{1/w}.\hfill \end{array}$$

(16)

Note that the expressions for $p_0$ and $p_1$ are expressible as

$$p_0=exp\left\{-mF(1,1/w,1+1/w,-\theta )\right\}$$

and

$$p_1=\frac{m{p}_0}{ϵ(1+w)}F(2,1+1/w,2+1/w,-\theta ).$$

4. A More Practical Algorithm

Unlike the preceding strategy that extracts $p_k$ directly from the generating function $G\left(z\right)$, the strategy here focuses on the expansion of $H\left(z\right)$ after recasting the generating function as $G\left(z\right)=exp\left(\alpha H\right(z\left)\right)$. The success of this strategy relies on an obscure property of the exponential function. Let $g\left(z\right)$ and $G\left(z\right)$ be functions analytic inside the unit circle. Let $g\left(z\right)={\sum }_{k=0}^{\infty }{q}_k{z}^k$ and $G\left(z\right)={\sum }_{k=0}^{\infty }{p}_k{z}^k$. Assume further that $G\left(z\right)=exp\left(\alpha g\right(z\left)\right)$. Then the $p_k$ sequence can be determined by the $q_k$ sequence as follows.

$$\begin{array}{cc}\hfill p_0& =exp\left(\alpha q_0\right)\hfill \\ \hfill p_n& =\frac{\alpha }{n}\sum _{k=0}^{n-1}(n-k)q_{n-k}{p}_k=\frac{\alpha }{n}\sum _{k=1}^{n}k{q}_k{p}_{n-k}(n\ge 1).\hfill \end{array}$$

(17)

Equation (17) can be established by differentiating the identity $G\left(z\right)=exp\left(\alpha g\right(z\left)\right)$ and then equating the coefficients for each separate power of z. This helpful relation can be traced to a once-popular calculus textbook published in the 1950s ([20], p. 448). In 1992, Ma et al. [14] used it to compute the Lea–Coulson distribution.

It follows from (6) that the generating function can be viewed as $G\left(z\right)=exp(-mh(z\left)\right)$ with

$$h\left(z\right)=F\left(1,\frac{1}{w},1+\frac{1}{w},\frac{z+\theta }{z-1}\right).$$

A straightforward way to compute the $q_k$ sequence is to regard $h\left(z\right)$ as a composite function

$$h\left(z\right)=F\left(1,\frac{1}{w},1+\frac{1}{w},l\left(z\right)\right)$$

with

$$l\left(z\right)=(z+\theta )/(z-1).$$

The $q_k$ sequence can then be obtained by Faà di Bruno’s formula [21]. Theoretically, it seems an easy task. First, applying the Leibniz rule to the function $l\left(z\right)$ leads to

$$l^{\left(k\right)}\left(z\right)=\frac{{(-1)}^{k}k!(z+\theta )}{{(z-1)}^{k+1}}+\frac{{(-1)}^{k-1}k!}{{(z-1)}^k}.$$

(18)

Therefore,

$$l_k\equiv l^{\left(k\right)}\left(0\right)=-(1+\theta )k!.$$

(19)

Second, note that

$$\begin{array}{cc}\hfill & \frac{d^k}{d{z}^k}F\left(1,\frac{1}{w},1+\frac{1}{w},z\right)\hfill \\ \hfill =& \frac{{\left(1\right)}_k{(1/w)}_k}{{(1+1/w)}_k}F\left(k+1,k+\frac{1}{w},k+1+\frac{1}{w},z\right)\hfill \\ \hfill =& \frac{k!}{kw+1}F\left(k+1,k+\frac{1}{w},k+1+\frac{1}{w},z\right).\hfill \end{array}$$

(20)

Hence, $g_k\equiv F^{\left(k\right)}(1,1/w,1+1/w,l\left(0\right))$ can be computed by

$$g_k=\frac{k!}{kw+1}F\left(k+1,k+\frac{1}{w},k+1+\frac{1}{w},-\theta \right).$$

(21)

Third, the derivatives $h_k\equiv h^{\left(k\right)}\left(0\right)$ can be computed from the $l_k$ and $g_k$ sequences using Faà di Bruno’s formula (e.g., Equation (2.2) in Ref. [21]). Finally, note that $q_0=F(1,1/w,1+1/w,-\theta )$ and for $k\ge 1$ we have $q_k=h_k/k!$. Despite its obvious educational value, this method is of limited use in practice. According to the results of this author’s computational experiments, the computation of $q_k$ by this method is prohibitively expensive when $k>25$.

A more practical algorithm for computing $q_k$ can be devised by a novel route. Applying Pfaff’s formula (e.g., Equation (9.5.1) in Ref. [18]) yields

$$F\left(1,\frac{1}{w},1+\frac{1}{w},\frac{z+\theta }{z-1}\right)=\frac{1-z}{1+\theta }F\left(1,1,1+\frac{1}{w},\frac{z+\theta }{1+\theta }\right).$$

(22)

Therefore, we can rewrite the generating function in (6) as $G\left(z\right)=exp\left(H\right(z\left)\right)$ with

$$H\left(z\right)=\frac{m}{1+\theta }(z-1)F\left(1,1,1+\frac{1}{w},\frac{z+\theta }{1+\theta }\right).$$

(23)

Applying the differentiation formula for the hypergeometric function, e.g., Equation (9.2.3) in Ref. [18], we have for $k\ge 1$

$$\begin{array}{cc}\hfill f_k\equiv & \left[z^k\right]F\left(1,1,1+\frac{1}{w},\frac{z+\theta }{1+\theta }\right)\hfill \\ \hfill =& \frac{k!\mathsf{\Gamma }(1+1/w)}{\mathsf{\Gamma }(k+1+1/w)}{\left(\frac{1}{1+\theta }\right)}^{k}F\left(k+1,k+1,k+1+\frac{1}{w},\frac{\theta }{1+\theta }\right)\hfill \\ \hfill =& \frac{k!\mathsf{\Gamma }(1+1/w)}{\mathsf{\Gamma }(k+1+1/w)}{ϵ}^{k}F\left(k+1,k+1,k+1+\frac{1}{w},1-ϵ\right).\hfill \end{array}$$

(24)

Clearly,

$$f_0=F\left(1,1,1+\frac{1}{w},1-ϵ\right).$$

(25)

It follows from (23) that $q_k=\left[z^k\right]H\left(z\right)$ can be computed by

$$q_k=mϵ(f_{k-1}-f_k)(k\ge 1)$$

(26)

with

$$q_0=-mϵf_0.$$

(27)

The computation of the $q_k$ sequence can be improved by noting that for $k\ge 1$

$$f_{k-1}-f_k={\eta }_k\left[F_{k-1}-\frac{kϵ}{k+1/w}{F}_k\right],$$

where

$$F_k=F\left(k+1,k+1,k+1+\frac{1}{w},1-ϵ\right)(k\ge 0)$$

(28)

and

$${\eta }_k=\frac{(k-1)!\mathsf{\Gamma }(1+1/w)}{\mathsf{\Gamma }(k+1/w)}{ϵ}^{k-1}.$$

Furthermore, setting ${\eta }_1=1$, we can also compute the ${\eta }_k$ sequence recursively.

$${\eta }_{k+1}=\frac{kϵ}{k+1/w}{\eta }_k(k\ge 1).$$

(29)

It follows from (26) and (27) that

$$q_k=mϵ{\eta }_k\left[F_{k-1}-\frac{kϵ}{k+1/w}{F}_k\right]$$

(30)

with

$$q_0=-mϵF_0.$$

(31)

The forgoing development gives the following recipe for computing $p_i$ for $i=0,1,\dots ,n$.

• computing ${\eta }_i$ for $i=1,\dots ,n$ by (29).
• computing $F_i$ for $i=0,\dots ,n$ by (28).
• computing $q_i$ for $i=0,\dots ,n$ by (30) and (31).
• computing $p_i$ for $i=0,\dots ,n$ by (17).

5. Asymptotic Behavior of the Mutant Probability

Knowledge of the asymptotic behavior of $p_n$ is of theoretical interest in its own right. Moreover, it plays a helpful role in testing computer implementations of algorithms for computing $p_n$. A standard tool for fathoming the asymptotic behavior of $p_n$ is classical analysis that relies on so-called transfer theorems in the spirit of the Tauberian method. To seek an asymptotic expression for $p_n$ by this route, we first cite two existing results.

Proposition 1. 

Let $f\left(z\right)$ be a complex-valued function analytic in $\mathrm{\Delta }(\psi ,\eta )\setminus \left\{1\right\}$ for some $\eta >0$ and $\psi \in (0,\pi /2)$. Assume that as $z\to 1$ in $\mathrm{\Delta }(\psi ,\eta )$,

$$f\left(z\right)\sim K{(1-z)}^{\alpha }$$

for some constants K and α. If $\alpha \ne 0,1,\dots$, then

$$\left[z^n\right]f\left(z\right)\sim \frac{K}{\mathsf{\Gamma }(-\alpha )}{n}^{-\alpha -1}.$$

On the other hand, if α is a nonnegative integer, then

$$\left[z^n\right]f\left(z\right)\sim o\left(n^{-\alpha -1}\right).$$

Here, the symbol $\mathrm{\Delta }(\psi ,\eta )$ defines the close domain $\{z:|z|\le 1+\eta ,|arg(z-1)|\ge \psi \}$ with $\eta >0$ and $\psi \in (0,\pi /2)$. This result is due to Flajolet and Odlyzko ([22], Corollary 2).

The second result has appeared in the classic text of Titchmarsh ([23], p. 226) as an exercise for students.

Proposition 2. 

Assume that $a+b>c$. As $z\to 1$,

$$F(a,b,c,z)\sim \frac{\mathsf{\Gamma }\left(c\right)\mathsf{\Gamma }(a+b-c)}{\mathsf{\Gamma }\left(a\right)\mathsf{\Gamma }\left(b\right)}{(1-z)}^{c-a-b}.$$

(32)

In Proposition 2 as stated in Ref. [23], z approaches 1 only along the real axis within the unit circle. In the following informal process, we assume that (32) holds for $z\to 1$ inside some $\mathrm{\Delta }(\psi ,\eta )$. This assumption requires the symbol $F(a,b,c,z)$ in (32) to represent the analytic continuation of the hypergeometric function defined in the complex plane cut long the segment $[1,\infty ]$.

Now an intuitive derivation of the asymptotic behavior of $p_n$ can be executed. Begin with the function $H\left(z\right)$ defined in (23). Note that

$$\underset{z\to 1}{lim}\frac{z+\theta }{1+\theta }=1.$$

Therefore, in view of Proposion 2, as $z\to 1$, for $w>1$,

$$F\left(1,1,1+\frac{1}{w},\frac{z+\theta }{1+\theta }\right)\sim \mathsf{\Gamma }\left(1+\frac{1}{w}\right)\mathsf{\Gamma }\left(1-\frac{1}{w}\right){\left(\frac{1-z}{1+\theta }\right)}^{-1+1/w}.$$

(33)

Because (23) can be rewritten as

$$H\left(z\right)=\frac{-m(1-z)}{1+\theta }F\left(1,1,1+\frac{1}{w},\frac{z+\theta }{1+\theta }\right),$$

it follows from (33) that as $z\to 1$

$$H\left(z\right)\sim \mathsf{\Gamma }\left(1+\frac{1}{w}\right)\mathsf{\Gamma }\left(1-\frac{1}{w}\right)(-m){ϵ}^{1/w}{(1-z)}^{1/w}.$$

(34)

Observe that (34) is equivalent to

$$H\left(z\right)=\mathsf{\Gamma }\left(1+\frac{1}{w}\right)\mathsf{\Gamma }\left(1-\frac{1}{w}\right)(-m){ϵ}^{1/w}{(1-z)}^{1/w}+o\left({(1-z)}^{1/w}\right).$$

Hence it follows from the relation $G\left(z\right)=e^{H\left(z\right)}$ that

$$G\left(z\right)=1-m\mathsf{\Gamma }\left(1+\frac{1}{w}\right)\mathsf{\Gamma }\left(1-\frac{1}{w}\right){ϵ}^{1/w}{(1-z)}^{1/w}+o\left({(1-z)}^{1/w}\right).$$

(35)

Let $G^{*}\left(z\right)=G\left(z\right)-1$. Then $G^{*}\left(z\right)$ satisfies the condition $G^{*}\left(z\right)\sim K{(1-z)}^{1/w}$. Applying Proposition 1 to $G^{*}\left(z\right)$ and noting the identity $\mathsf{\Gamma }(1-1/w)=(-1/w)\mathsf{\Gamma }(-1/w)$, we obtain the relation

$$\left[z^n\right]G^{*}\left(z\right)\sim \frac{m}{w}\mathsf{\Gamma }\left(1+\frac{1}{w}\right){ϵ}^{1/w}{n}^{-1-1/w}.$$

As the constant 1 in (35) has no effect on the asymptotic behavior of $\left[z^n\right]G\left(z\right)$, we conclude that

$$p_n\sim \frac{m}{w}\mathsf{\Gamma }\left(1+\frac{1}{w}\right){ϵ}^{1/w}{n}^{-1-1/w}.$$

(36)

The foregoing argument ceases to work when $w\le 1$. However, the case $w=1$ has been tackled earlier by a slightly different approach [24], and the result is in agreement with (36):

$$p_n\sim \frac{ϵm}{n^2}.$$

It appears an elusive goal to translate the above intuitive argument into a formal mathematical proof of (36). A perspicacious reviewer has offered a refreshing, rigorous proof that makes ingenious use of elaborate probabilistic machinery. To help the reader focus on the essence of the probabilistic proof, we present separately two results that play an integral role in the proof but that may distract the reader from the main idea if not proved before the proof of (36). The first result is a special case of a theorem due to Borovkov ([25], p. 258).

Proposition 3. 

Let $h\left(z\right)$ be analytic in a region containing the unit disk. Then

$$\left[z^n\right]exp\left(h\left(z\right)\right)\sim exp\left(h\left(1\right)\right)\left[z^n\right]h\left(z\right).$$

If $g\left(z\right)=e^{h\left(z\right)}$ is a probability generating function, then $h\left(1\right)=0$ because $g\left(1\right)\equiv 1$. Therefore, $\left[z^n\right]g\left(z\right)\sim \left[z^n\right]h\left(z\right)$.

The next result is more elementary.

Proposition 4. 

Let $f_1$ and $f_2$ be nonnegative continuous functions on $(0,\infty )$. Let $Y_n$ be a sequence of nonnegative discrete random variables. Assume that

1. 

${\sum }_{k=1}^{\infty }{f}_i\left(k\right)<\infty$ for $i=1,2$;

2. 

$f_1\left(x\right)\sim f_2\left(x\right)$ as $x\to \infty$;

3. 

there exists a sequence $\{c_n;n\ge 1\}$ of positive constants such that $c_n\to \infty$ and $P\left({\displaystyle \bigcap _{n=1}^{\infty }}\{Y_n\ge c_n\}\right)=1.$

Then

$$E\left[f_1\left(Y_n\right)\right]\sim E\left[f_2\left(Y_n\right)\right].$$

Proof. 

Given $ϵ>0$, there exists $x_{ϵ}>0$ such that $x>x_{ϵ}$ implies

$$(1-ϵ)f_2\left(x\right)<f_1\left(x\right)<(1+ϵ)f_2\left(x\right).$$

On the other hand, due to assumption 3, there exists $n_{ϵ}>1$ such that

$$Y_n>x_{ϵ} \mathrm{for} \mathrm{all} n>n_{ϵ}$$

holds almost everywhere. Therefore, for $n>n_{ϵ}$,

$$(1-ϵ)f_2\left(Y_n\right)<f_1\left(Y_n\right)<(1+ϵ)f_2\left(Y_n\right)$$

holds almost everywhere. Note that assumption 1 guarantees the existence of $E\left[f_i\left(Y_n\right)\right]$ for $i=1,2$. Taking expectations leads to

$$(1-ϵ)E\left[f_2\left(Y_n\right)\right]\le E\left[f_1\left(Y_n\right)\right]\le (1+ϵ)E\left[f_2\left(Y_n\right)\right],$$

which is the desired conclusion. □

Now we proceed to present the probabilistic proof of (36). Consider the generating function $g_0$ in (4). Combining (1) and (4) leads to the generating function of interest

$$G_0\left(z\right)=exp\left(A\left(z\right)\right),$$

where

$$A\left(z\right)=-m+\frac{m}{w}\sum _{k=0}^{\infty }B(k,1+w^{-1}){(1-ϵ+ϵz)}^k.$$

Let $a_n=\left[z^n\right]A\left(z\right)$. Applying the usual binomial-expansion formula and collecting coefficients of $z^n$, we have

$$\begin{array}{cc}\hfill a_n& =\frac{m}{w}\sum _{k=n}^{\infty }B(k,1+w^{-1})\left(\genfrac{}{}{0pt}{}{k}{n}\right){ϵ}^k{(1-ϵ)}^{k-n}\hfill \\ \hfill & =\frac{m}{ϵw}\sum _{j=0}^{\infty }B(n+j,1+w^{-1})\left(\genfrac{}{}{0pt}{}{n+j}{j}\right){ϵ}^{n+1}{(1-ϵ)}^j.\hfill \end{array}$$

Now, consider two real-valued functions defined on $(0,\infty )$:

$$\varphi \left(x\right)=\frac{m}{ϵw}B(x,1+w^{-1})=\frac{m\mathsf{\Gamma }(1+w^{-1})}{ϵw}\frac{\mathsf{\Gamma }\left(x\right)}{\mathsf{\Gamma }(x+1+w^{-1})}$$

(37)

and

$$\psi \left(x\right)=\frac{m\mathsf{\Gamma }(1+w^{-1})}{ϵw}{\left(\frac{1}{x}\right)}^{1+1/w}.$$

(38)

Observe that $\varphi \left(x\right)\sim \psi \left(x\right)$ as $x\to \infty$ (see, e.g., p. 15 of Ref. [18]). Write

$$a_n=E\left[\varphi (n+{\nu }_n)\right],$$

(39)

where ${\nu }_n$ is a random variable following a negative binomial distribution with parameters $n+1$ and $ϵ$. Because ${\nu }_n$ can be viewed as the sum of $n+1$ independently and identically distributed random variables obeying the geometric distribution with parameter $ϵ$, it follows from the strong law of large numbers (see, e.g., p. 42 of Ref. [26]) that

$$\frac{{\nu }_n}{n+1}\stackrel{a.e.}{⟶}\frac{1-ϵ}{ϵ}.$$

Here, the symbol $\stackrel{a.e.}{⟶}$ signifies convergence almost everywhere. Therefore,

$$1+\frac{{\nu }_n}{n}\stackrel{a.e.}{⟶}1+\frac{1-ϵ}{e}=\frac{1}{ϵ}.$$

(40)

For any $\alpha >0$, the random variable $1+{\nu }_n/n$ satisfies

$$0<{\left(1+\frac{{\nu }_n}{n}\right)}^{-\alpha }={\left(\frac{n}{n+{\nu }_n}\right)}^{\alpha }\le 1.$$

Hence it follows from the dominated convergence theorem (see, e.g., p. 42 of Ref. [26]) and (40) that

$$\underset{n\to \infty }{lim}E\left[{\left(1+\frac{{\nu }_n}{n}\right)}^{-\alpha }\right]={ϵ}^{\alpha }.$$

(41)

Clearly, $\psi \left(x\right)$ satisfies assumption 1 in Proposition 4. Because $\mathsf{\Gamma }\left(x\right)/\mathsf{\Gamma }(x+a)\sim x^{-a}$, it follows that $\varphi \left(x\right)$ also satisfies assumption 1. Moreover, the random variable sequence $Y_n:=n+{\nu }_n$ satisfies assumption 3 in Proposition 4 with $c_n=n$. In view of Proposition 4 and (41), (39) leads to

$$\begin{array}{cc}\hfill a_n& =E\left[\varphi (n+{\nu }_n)\right]\sim E\left[\psi (n+{\nu }_n)\right]\hfill \\ \hfill & =E\left[\psi \left(n(1+{\nu }_n/n)\right)\right]=\frac{m\mathsf{\Gamma }(1+1/w)}{ϵw}{\left(\frac{1}{n}\right)}^{1+1/w}E\left[{\left(1+\frac{{\nu }_n}{n}\right)}^{-(1+1/w)}\right]\hfill \\ \hfill & \sim \frac{m\mathsf{\Gamma }(1+1/w)}{ϵw}{\left(\frac{1}{n}\right)}^{1+1/w}{ϵ}^{1+1/w}=\frac{m\mathsf{\Gamma }(1+1/w)}{w}\frac{{ϵ}^{1/w}}{n^{1+1/w}}.\hfill \end{array}$$

This is equivalent to (36) due to Proposition 3.

To show the usefulness of formula (36), we here employ it as a check on the recursive algorithm given in the preceding section. Consider cases where $m=58.7$ and $ϵ=0.005$. For $w=1.4,1.0,0.7$ and selected values of n, Table 1, Table 2 and Table 3 list exact values of $p_n$ computed by the recursive algorithm and their corresponding asymptotic values ${\tilde{p}}_n$ computed by formula (36). The relative errors, defined by $|p_n-{\tilde{p}}_n|÷p_n$, are shown in the last column.

Table 1. Comparison of exact and asymptotic $p_k$. $m=58.7,ϵ=0.005,w=1.4$.

k	Recursive	Asymptotic	Error
1000	6.3946195 × 10${}^{-6}$	6.2485639 × 10${}^{-6}$	2.28%
1200	4.6651675 × 10${}^{-6}$	4.5713128 × 10${}^{-6}$	2.01%
1400	3.5743179 × 10${}^{-6}$	3.5097405 × 10${}^{-6}$	1.81%
1600	2.8383575 × 10${}^{-6}$	2.7916453 × 10${}^{-6}$	1.65%
1800	2.3163411 × 10${}^{-6}$	2.2812359 × 10${}^{-6}$	1.52%
2000	1.9314605 × 10${}^{-6}$	1.9042712 × 10${}^{-6}$	1.41%
2500	1.3147908 × 10${}^{-6}$	1.2989647 × 10${}^{-6}$	1.20%
3000	9.6046479 × 10${}^{-7}$	9.5029417 × 10${}^{-7}$	1.06%
3500	7.3661056 × 10${}^{-7}$	7.2961229 × 10${}^{-7}$	0.95%
4000	5.8539548 × 10${}^{-7}$	5.8033314 × 10${}^{-7}$	0.86%
4500	4.7803264 × 10${}^{-7}$	4.7422815 × 10${}^{-7}$	0.80%
5000	3.9881054 × 10${}^{-7}$	3.9586392 × 10${}^{-7}$	0.74%
5500	3.3853023 × 10${}^{-7}$	3.3619173 × 10${}^{-7}$	0.69%
6000	2.9149900 × 10${}^{-7}$	2.8960539 × 10${}^{-7}$	0.65%
7500	1.9865134 × 10${}^{-7}$	1.9754916 × 10${}^{-7}$	0.55%
8000	1.7780098 × 10${}^{-7}$	1.7685851 × 10${}^{-7}$	0.53%
8500	1.6021445 × 10${}^{-7}$	1.5940085 × 10${}^{-7}$	0.51%
9000	1.4523093 × 10${}^{-7}$	1.4452265 × 10${}^{-7}$	0.49%
9500	1.3235060 × 10${}^{-7}$	1.3172937 × 10${}^{-7}$	0.47%
10,000	1.2118944 × 10${}^{-7}$	1.2064088 × 10${}^{-7}$	0.45%
10,500	1.1144824 × 10${}^{-7}$	1.1096090 × 10${}^{-7}$	0.44%
11,000	1.0289091 × 10${}^{-7}$	1.0245558 × 10${}^{-7}$	0.42%

Table 2. Comparison of exact and asymptotic $p_k$. $m=58.7,ϵ=0.005,w=1.0$.

k	Recursive	Asymptotic	Error
1000	2.9574909 × 10${}^{-7}$	2.9350000 × 10${}^{-7}$	0.76%
1200	2.0513796 × 10${}^{-7}$	2.0381944 × 10${}^{-7}$	0.64%
1400	1.5058433 × 10${}^{-7}$	1.4974490 × 10${}^{-7}$	0.56%
1600	1.1521612 × 10${}^{-7}$	1.1464844 × 10${}^{-7}$	0.49%
1800	9.0988439 × 10${}^{-8}$	9.0586420 × 10${}^{-8}$	0.44%
2000	7.3670246 × 10${}^{-8}$	7.3375000 × 10${}^{-8}$	0.40%
2500	4.7113536 × 10${}^{-8}$	4.6960000 × 10${}^{-8}$	0.33%
3000	3.2701091 × 10${}^{-8}$	3.2611111 × 10${}^{-8}$	0.28%
3500	2.4016450 × 10${}^{-8}$	2.3959184 × 10${}^{-8}$	0.24%
4000	1.8382465 × 10${}^{-8}$	1.8343750 × 10${}^{-8}$	0.21%
4500	1.4521236 × 10${}^{-8}$	1.4493827 × 10${}^{-8}$	0.19%
5000	1.1760123 × 10${}^{-8}$	1.1740000 × 10${}^{-8}$	0.17%
5500	9.7176953 × 10${}^{-9}$	9.7024793 × 10${}^{-9}$	0.16%
6000	8.1645662 × 10${}^{-9}$	8.1527778 × 10${}^{-9}$	0.14%
7500	5.2239033 × 10${}^{-9}$	5.2177778 × 10${}^{-9}$	0.12%
8000	4.5910062 × 10${}^{-9}$	4.5859375 × 10${}^{-9}$	0.11%
8500	4.0665264 × 10${}^{-9}$	4.0622837 × 10${}^{-9}$	0.10%
9000	3.6270442 × 10${}^{-9}$	3.6234568 × 10${}^{-9}$	0.10%
9500	3.2551386 × 10${}^{-9}$	3.2520776 × 10${}^{-9}$	0.09%
10,000	2.9376332 × 10${}^{-9}$	2.9350000 × 10${}^{-9}$	0.09%
10,500	2.6644134 × 10${}^{-9}$	2.6621315 × 10${}^{-9}$	0.09%
11,000	2.4276104 × 10${}^{-9}$	2.4256198 × 10${}^{-9}$	0.08%

Table 3. Comparison of exact and asymptotic $p_k$. $m=58.7,ϵ=0.005,w=0.7$.

k	Recursive	Asymptotic	Error
1000	2.8496504 × 10${}^{-9}$	2.8380054 × 10${}^{-9}$	0.41%
1200	1.8289321 × 10${}^{-9}$	1.8227030 × 10${}^{-9}$	0.34%
1400	1.2571893 × 10${}^{-9}$	1.2535188 × 10${}^{-9}$	0.29%
1600	9.0866594 × 10${}^{-10}$	9.0634442 × 10${}^{-10}$	0.26%
1800	6.8242226 × 10${}^{-10}$	6.8087237 × 10${}^{-10}$	0.23%
2000	5.2823729 × 10${}^{-10}$	5.2715748 × 10${}^{-10}$	0.20%
2500	3.0711312 × 10${}^{-10}$	3.0661083 × 10${}^{-10}$	0.16%
3000	1.9718894 × 10${}^{-10}$	1.9692016 × 10${}^{-10}$	0.14%
3500	1.3558537 × 10${}^{-10}$	1.3542696 × 10${}^{-10}$	0.12%
4000	9.8019343 × 10${}^{-11}$	9.7919126 × 10${}^{-11}$	0.10%
4500	7.3626620 × 10${}^{-11}$	7.3559704 × 10${}^{-11}$	0.09%
5000	5.6999368 × 10${}^{-11}$	5.6952742 × 10${}^{-11}$	0.08%
5500	4.5218134 × 10${}^{-11}$	4.5184507 × 10${}^{-11}$	0.07%
6000	3.6602731 × 10${}^{-11}$	3.6577779 × 10${}^{-11}$	0.07%
7500	2.1286359 × 10${}^{-11}$	2.1274749 × 10${}^{-11}$	0.05%
8000	1.8197713 × 10${}^{-11}$	1.8188408 × 10${}^{-11}$	0.05%
8500	1.5705871 × 10${}^{-11}$	1.5698313 × 10${}^{-11}$	0.05%
9000	1.3669876 × 10${}^{-11}$	1.3663663 × 10${}^{-11}$	0.05%
9500	1.1987501 × 10${}^{-11}$	1.1982339 × 10${}^{-11}$	0.04%
10,000	1.0583261 × 10${}^{-11}$	1.0578931 × 10${}^{-11}$	0.04%
10,500	9.4005077 × 10${}^{-12}$	9.3968451 × 10${}^{-12}$	0.04%
11,000	8.3961125 × 10${}^{-12}$	8.3929899 × 10${}^{-12}$	0.04%

6. Examples and Simulation Results

As alluded to earlier, the foregoing algorithms were motivated by an investigation on chromosome loss in yeast cells. The experimental context of this investigation is similar to that described in a previous study in Refs. [27,28]. In this experimental context, the colonies are the equivalent of the parallel cultures in a classic fluctuation experiment [28]. Table 4 and Table 5 give two fictitious data sets that mimic the real-world data to highlight several important features of such data. First, as reported by Wu et al. [28], there is high variation in $N_t$, the final total number of viable cells in a culture. Second, there is also high variation in the plating efficiency $ϵ$. Due to these two challenging features, the mutation rate $\mu$ should be estimated directly, not via the estimation of m as is commonly practiced [2,29]. Therefore, the log likelihood function is

$$l\left(\mu \right)=\sum _{i=1}^{n}logp(y_i;\mu N_{t,i},{ϵ}_i,w).$$

(42)

Table 4. Fictitious data set A ($w=1.5$).

${\mathit{N}}_{\mathit{t}}$	$\mathit{ϵ}\times 100\%$	Mutant
881,200	0.12	2
1,147,200	0.11	1
529,800	0.22	19
1,215,300	0.14	42
230,000	0.2	10
748,400	0.04	0
296,500	0.4	6
378,800	0.87	8
1,318,500	0.63	32
1,328,000	0.27	10
999,400	0.28	3
1,567,500	0.5	11

Table 5. Fictitious data set B ($w=0.8$).

${\mathit{N}}_{\mathit{t}}$	$\mathit{ϵ}\times 100\%$	Mutant
432,900	0.86	213
54,300	5.61	31
145,600	2.40	481
103,700	4.70	79
138,600	3.69	151
115,000	5.25	161
100,100	3.57	833
51,400	8.14	895
364,100	1.46	1262
118,800	3.93	899

Here, $y_i$ is the number of mutants in the ith culture; $N_{t,i}$ and ${ϵ}_i$ are respectively $N_t$ and $ϵ$ for the ith culture. The experiment consists of n cultures and w is the fitness that is assumed to be constant cross all cultures (or colonies in the present context). The maximum likelihood (ML) estimator of $\mu$, denoted by $\widehat{\mu }$, is defined by

$$\widehat{\mu }=\underset{\mu }{argmax}l\left(\mu \right).$$

(43)

Many optimization algorithms can be employed to compute $\widehat{\mu }$. The golden section search method ([30], p. 293) is one of the simplest methods for that purpose. The experimentalist starts the computational process by first bracketing the mutation rate via trial and error or by using prior knowledge. Furthermore, the log likelihood function in (42) can also be used to compute confidence intervals (CIs) for the mutation rates. Specifically, to compute the two boundary points of a $(1-\alpha )100\%$ CI for the mutation rate, we solve numerically the following equation:

$$l\left(\mu \right)=l\left(\widehat{\mu }\right)-0.5{\chi }_{\alpha ,1}^2.$$

(44)

Here, ${\chi }_{\alpha }^2$ denotes the $(1-\alpha )$th quantile of the ${\chi }^2$ distribution with one degree of freedom. The bisection method ([30], p. 261) can be used to solve (44). The foregoing work extends previous research [31].

Assume that the unknown mutation rates in both fictitious experiments lie in the interval $[1\times {10}^{-6},1\times {10}^{-2}]$. Applying the above ideas to the first experiment yields a mutation rate estimate $\widehat{\mu }=5.91\times {10}^{-4}$ and a 95% likelihood ratio confidence interval $[4.16\times {10}^{-4},7.86\times {10}^{-4}]$. For the second experiment, the same method yields $\widehat{\mu }=0.00126$ and a 95% likelihood ratio confidence interval $[0.000833,0.00172]$.

Another essential task in microbial mutation research is the comparison of mutation rates under different conditions or between different strains. Let $y_{i,j}$$j=1,2$ and $i=1,\dots ,n_j$ be mutant data generated by two fluctuation experiments. In particular, the sample sizes are $n_1$ and $n_2$ respectively. Let the symbol $N_{t,i,j},{ϵ}_{i,j}$ and $w_j$ be corresponding values of the parameters $N_t,ϵ$ and w associated with the mutant count data $y_{i,j}$. Let the two mutation rates be ${\mu }_1$ and ${\mu }_2$, respectively. Here, $w_j$ is assumed to be constant for all cultures in experiment $j(j=1,2)$, but this assumption can be relaxed without affecting the ensuing discussion.

The preferred method for comparing mutation rates in two independent fluctuation experiments is the likelihood ratio (LR) test [32]. To perform an LR test, we first compute ML estimates ${\widehat{\mu }}_1$ and ${\widehat{\mu }}_2$ separately using log likelihood functions $l_1$ and $l_2$ similarly defined as in (42). We next construct a combined log likelihood function

$$l_c\left(\mu \right)=\sum _{i=1}^{n_1}p(y_{i,1};\mu N_{t,i,1},{ϵ}_{i,1},w_1)+\sum _{i=1}^{n_2}p(y_{i,2};\mu N_{t,i,2},{ϵ}_{i,2},w_2),$$

(45)

from which we compute a combined mutation rate estimate ${\widehat{\mu }}_c$ according to the definition

$${\widehat{\mu }}_c=\underset{\mu }{argmax}{l}_c\left(\mu \right).$$

(46)

Finally, we compute an LR statistic $\mathsf{\Lambda }$ using the definition

$$\mathsf{\Lambda }=2(l_1\left({\widehat{\mu }}_1\right)+l_2\left({\widehat{\mu }}_2\right)-l_c\left({\widehat{\mu }}_c\right)).$$

(47)

The test statistic $\mathsf{\Lambda }$ asymptotically obeys a chi-squared distribution with one degree of freedom. Applying the LR test to the mutation rates in the two fictitious experiments, we obtain $\mathsf{\Lambda }=8.026$ and $p=4.61\times {10}^{-3}$.

In addition, two groups of experiments were simulated to help assess the performance of the new algorithm. Each group comprises 10,000 experiments with a common mutation rate $5\times {10}^{-6}$, and each experiment comprises 20 cultures. In the first group, the other parameter values were $w=1.2,N_t=2\times {10}^8$ and $ϵ=0.002$; in the second group, $w=0.7,N_t=9\times {10}^7$ and $ϵ=0.06$. The above inference methods were applied to the two groups of simulated experiments to gauge the new algorithm for computing mutant distributions. The means and medians of the ML estimates and the coverage rates of the attendant 95% CIs are summarized in Table 6. The overall distributional patterns of the ML estimates are displayed in Figure 2. Moreover, experiments in the two groups were paired by their indices and then the LR test was performed on each of the 10,000 pairs of experiments. The sorted p-values produced by the tests exhibited an expected linear pattern as shown in Figure 3. Among the p-values, 545 of them were below 0.05. These results indicate that the new algorithm performed satisfactorily in this simulation study.

Table 6. Summary of algorithm performance.

Group	Mean of $\widehat{\mathit{\mu }}$	Median of $\widehat{\mathit{\mu }}$	95% CI Coverage
A	5.071 × 10${}^{-6}$	5.029 × 10${}^{-6}$	94.75%
B	5.010 × 10${}^{-6}$	5.001 × 10${}^{-6}$	95.30%

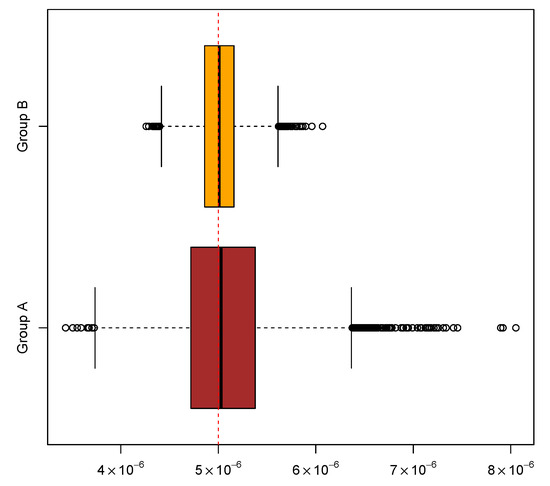
Figure 2. Distributional patterns of maximum likelihood estimates of mutation rates based on two groups of simulated experiments. Each group comprises 10,000 experiments simulated by assuming a common mutation rate of $5\times {10}^{-6}$.

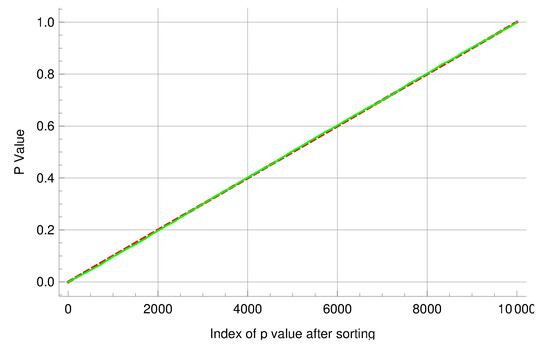
Figure 3. The p-values generated by performing likelihood ratio tests on 10,000 pairs of simulated fluctuation experiments. Because the two mutation rates were equal, the sorted p-values exhibited an expected linear pattern. The solid line represents the observed p-values, and the dashed line represents the theoretical reference lines with slope ${10}^{-4}$ and y-intercept 0.

7. Concluding Remarks

This paper raises an oft-overlooked issue in research on the Luria–Delbrück distribution. Pure mathematical elegance is sometimes incongruous with real-world problems. A practical solution to a complex problem may occasionally appear inelegant and cumbersome at first sight. A large proportion of fluctuation experiments will produce data that are more amenable to the seemingly complicated and inefficient recursive algorithm presented here than to the integration or other existing algorithms. Admittedly, no algorithm is infallible under all circumstances. Combinations of values of $m,ϵ,w$ and k can be found that allow certain $p(k;m,ϵ,w)$ to baffle the new algorithm as well as the existing algorithms for the Luria–Delbrück distribution. Thus, caution is advisable in practice. Furthermore, a unified algorithm does not seem to be recommendable. If either $w=1$ or $ϵ=1$ holds, practitioners should use the simpler, more efficient existing algorithms [17]. The present investigation may herald a new paradigm for the estimation of microbial mutation rates using the Luria–Delbrück protocol. The examples based on fictitious data show how variations in $N_t$ and $ϵ$ can be accounted for simultaneously using the new algorithm. The new algorithm may catalyze the exploration of untrodden territories in microbial mutation research.