A Two-Stage Model Based on EFQM, FBWM, and FMOORA for Business Excellence Evaluation in the Process of Manufacturing
Abstract
1. Introduction
2. Literature Review
2.1. European Foundation for Quality Management Model
2.2. Fuzzy Best-Worst Method
2.3. Fuzzy Multi-Objective Optimization by Ratio Analysis
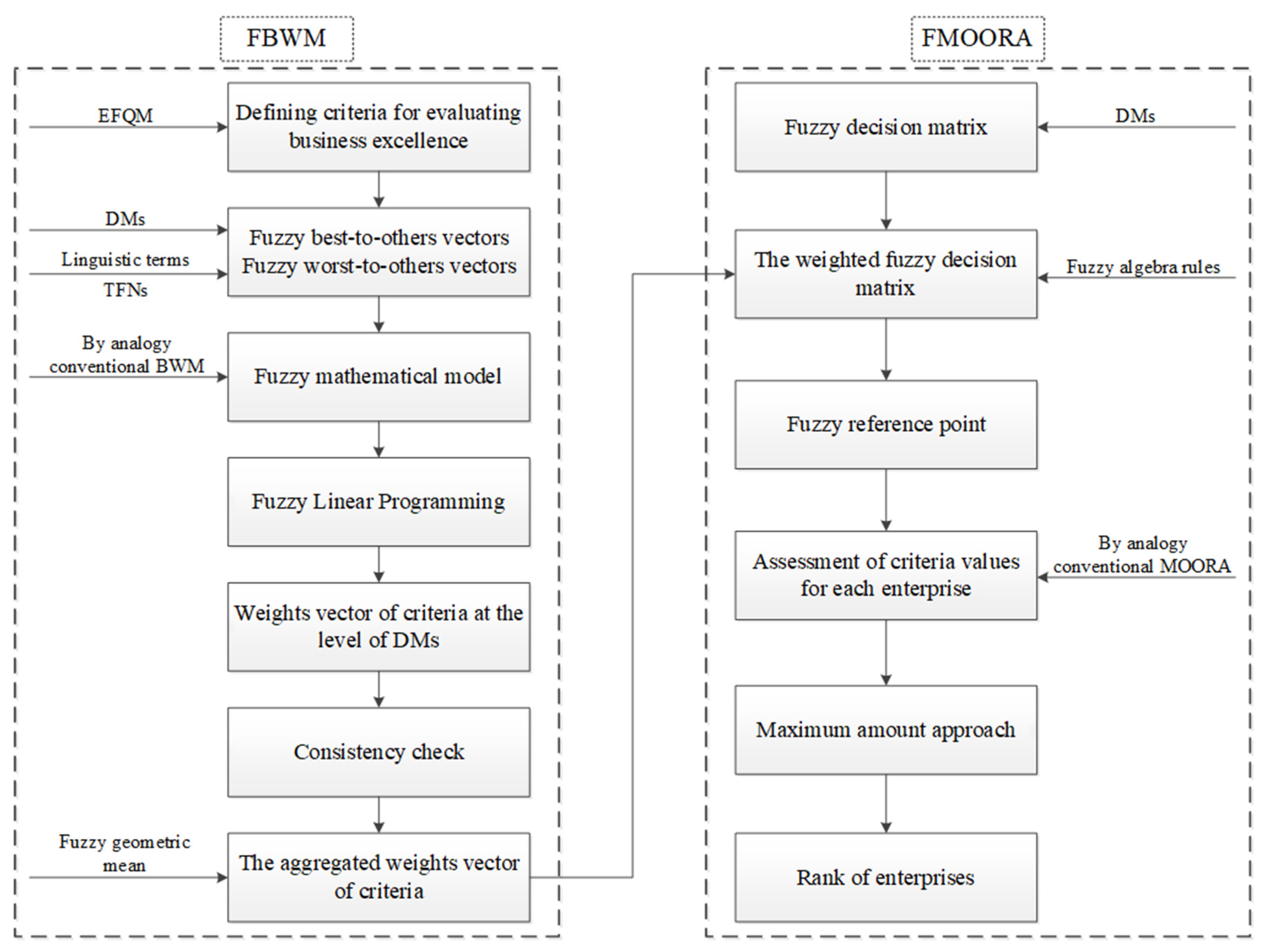
3. The Methodology
3.1. Definition of a Finite Set of Criteria
3.2. Definition of a Finite Set of Enterprises
3.3. Definition of Set of Decision Makers
3.4. Modeling of the Existing Uncertainties
- equally important (E1):
- slightly more important (E2):
- medium more important (E3):
- much more important (E4):
- extremely more important (E5):
- very low value (V1):
- low value (V2):
- fairly low value (V3):
- medium value (V4):
- fairly high value (V5):
- high value (V6):
- very high value (V7):
3.5. The Proposed Fuzzy Best-Worst Method
- is TFN that corresponds to the relative importance of the best criterion over the rest criteria
- is TFN that corresponds to the relative importance of the worst criterion over the rest criteria
- is TFN that corresponds to the weight of the best criterion
- is TFN that corresponds to the weight of the worst criterion
- is TFN that corresponds to the weight of the criterion .
3.6. The Proposed Fuzzy Multi-Objective Optimization by Ratio Analysis
4. Case Study
4.1. An application of the proposed Fuzzy Best-Worst Method for Determining the Criteria Weights
4.2. An Application of the Proposed Fuzzy Multi-Objective Optimization by Ratio Analysis
5. Conclusions
- (1)
- Modeling of existing uncertainties based on TFNs,
- (2)
- The relative importance of the EFQM criteria is set as a fuzzy group decision-making problem;
- (3)
- The weight vector of EFQM criteria at the level of each DM is determined by FBWM; from the aspect of practical application, applying FBWM has certain advantages related to the AHP framework;
- (4)
- The aggregated weighted vector of EFQM criteria is given by using a fuzzy geometric mean. The authors believe that the aggregation procedure applied in this research has significantly better characteristics in relation to the aggregation of estimates of DMs because, due to the occurrence of inconsistency in the estimates of DMs, it can be easily determined and the error can be eliminated more quickly;
- (5)
- The SMEs are ranked by using the proposed FMOORA based on the fuzzy reference point; compared to other similar MADMs extended with fuzzy sets theory the proposed FMOORA requires less complex calculation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AHP | Analytic Hierarchy Process |
| BE | Business Excellence |
| BEM | Business Excellence Model |
| BWM | Best Worst Method |
| DM | Decision Makers |
| EFQM | European Foundation for Quality Management model |
| ELECTRE | Elimination and Choice Translating Reality |
| FBO | Fuzzy Best-Ordered Matrix |
| FBWM | Fuzzy Best-Worst Method |
| FLP | Fuzzy Linear Programming |
| FMEA | Failure Mode and Effect Analysis |
| FMOORA | Fuzzy Multi-Objective Optimization by Ratio Analysis |
| FOW | fuzzy Other-to-Worst Vector |
| FWO | Fuzzy Worst Ordered Matrix |
| GRIM | Graded Mean Integration Representation |
| MADM | Multi-Attribute Decision-Making |
| MBNQA | Malcolm Baldrige National Quality Award |
| MCDM | Multi-Criteria Decision-Making |
| MCOA | Modified Center of Area |
| MOORA | Multi-Objective Optimization by Ratio Analysis |
| PROMETHEE | The Preference Ranking Organization Method for Enrichment of Evaluations |
| TFN | Triangular Fuzzy Number |
| TOPSIS | Technique for Order of Preference by Similarity to Ideal Solution |
References
- Sulistyo, B.; Amani, H.; Widaningrum, S.; Mohammad, M.; Ibrahim, R. Comparative Study of Business Excellence Frameworks and Awards in Southeast Asian Countries. Int. J. Bus. Soc. 2021, 22, 1123–1142. [Google Scholar] [CrossRef]
- Jankalová, M.; Jankal, R. Sustainability assessment according to the selected business excellence models. Sustainability 2018, 10, 3784. [Google Scholar] [CrossRef]
- Calvo-Mora, A.; Picón, A.; Ruiz, C.; Cauzo, L. The relationships between soft-hard TQM factors and key business results. Int. J. Oper. Prod. Manag. 2014, 34, 115–143. [Google Scholar] [CrossRef]
- Tickle, M.; Mann, R.; Adebanjo, D. Deploying business excellence—Success factors for high performance. Int. J. Qual. Reliab. Manag. 2016, 33, 197–230. [Google Scholar] [CrossRef]
- Suárez, E.; Calvo-Mora, A.; Roldán, J.L.; Periánez-Cristóbal, R. Quantitative research on the EFQM excellence model: A systematic literature review (1991–2015). Eur. Res. Manag. Bus. Econ. 2017, 23, 147–156. [Google Scholar] [CrossRef]
- Rahman, M.; Islam, R.; Husain, W.R.W.; Ahmad, K. Developing a hierarchical model to enhance business excellence in hotel industry of Bangladesh. Int. J. Contemp. Hosp. Manag. 2019, 31, 1836–1856. [Google Scholar] [CrossRef]
- Amponsah, C.T.; Ahmed, G. New global dimensions of business excellence. Int. J. Bus. Excell. 2017, 13, 60–78. [Google Scholar] [CrossRef]
- Bakır, M.; Atalık, Ö. Application of fuzzy AHP and fuzzy MARCOS approach for the evaluation of e-service quality in the airline industry. Decis. Mak. Appl. Manag. Eng. 2021, 4, 127–152. [Google Scholar] [CrossRef]
- Khorshidi, M.; Erkayman, B.; Albayrak, Ö.; Kılıç, R.; Demir, H.İ. Solar power plant location selection using integrated fuzzy DEMATEL and fuzzy MOORA method. Int. J. Ambient Energy 2022, 43, 7400–7409. [Google Scholar] [CrossRef]
- Mahmood, T.; Ullah, K.; Khan, Q.; Jan, N. An approach toward decision-making and medical diagnosis problems using the concept of spherical fuzzy sets. Neural Comput. Appl. 2019, 31, 7041–7053. [Google Scholar] [CrossRef]
- Liu, P.; Munir, M.; Mahmood, T.; Ullah, K. Some similarity measures for interval-valued picture fuzzy sets and their applications in decision making. Information 2019, 10, 369. [Google Scholar] [CrossRef]
- Ullah, K. Picture fuzzy maclaurin symmetric mean operators and their applications in solving multiattribute decision-making problems. Math. Probl. Eng. 2021, 2021, 1098631. [Google Scholar] [CrossRef]
- Khan, Q.; Mahmood, T.; Ullah, K. Applications of improved spherical fuzzy Dombi aggregation operators in decision support system. Soft Comput. 2021, 25, 9097–9119. [Google Scholar] [CrossRef]
- Nestic, S.; Gojkovic, R.; Petrovic, T.; Tadic, D.; Mimovic, P. Quality Performance Indicators Evaluation and Ranking by Using TOPSIS with the Interval-Intuitionistic Fuzzy Sets in Project-Oriented Manufacturing Companies. Mathematics 2022, 10, 4174. [Google Scholar] [CrossRef]
- Brauers, W.K.M.; Zavadskas, E.K. Robustness of MULTIMOORA: A method for multi-objective optimization. Informatica 2012, 23, 1–25. [Google Scholar] [CrossRef]
- Mavi, R.K.; Goh, M.; Zarbakhshnia, N. Sustainable third-party reverse logistic provider selection with fuzzy SWARA and fuzzy MOORA in plastic industry. Int. J. Adv. Manuf. Technol. 2017, 91, 2401–2418. [Google Scholar] [CrossRef]
- Ersöz, F.; Kinci, C.H.; Ersöz, T. A model proposal for course selection with the fuzzy MOORA approach. Avrupa Bilim. Teknol. Derg. 2018, 14, 369–377. [Google Scholar]
- Arabsheybani, A.; Paydar, M.M.; Safaei, A.S. An integrated fuzzy MOORA method and FMEA technique for sustainable supplier selection considering quantity discounts and supplier’s risk. J. Clean. Prod. 2018, 190, 577–591. [Google Scholar] [CrossRef]
- Emovon, I.; Okpako, O.S.; Edjokpa, E. Application of fuzzy MOORA method in the design and fabrication of an automated hammering machine. World J. Eng. 2020, 18, 37–49. [Google Scholar] [CrossRef]
- Arslankaya, S.; Çelik, M.T. Green supplier selection in steel door industry using fuzzy AHP and fuzzy Moora methods. Emerg. Mater. Res. 2021, 10, 357–369. [Google Scholar] [CrossRef]
- Aydin, S.; Kahraman, C.; Kaya, İ. A new fuzzy multicriteria decision making approach: An application for European Quality Award assessment. Knowl.-Based Syst. 2012, 32, 37–46. [Google Scholar] [CrossRef]
- Liu, Y.L.; Ko, P.F. A modified EFQM Excellence Model for effective evaluation in the hotel industry. Total Qual. Manag. Bus. Excell. 2018, 29, 1580–1593. [Google Scholar] [CrossRef]
- Metaxas, I.N.; Koulouriotis, D.E.; Spartalis, S.H. A multicriteria model on calculating the Sustainable Business Excellence Index of a firm with fuzzy AHP and TOPSIS. Benchmarking Int. J. 2016, 23, 1522–1557. [Google Scholar] [CrossRef]
- Fonseca, L. The EFQM 2020 model. A theoretical and critical review. Total Qual. Manag. Bus. Excell. 2022, 33, 1011–1038. [Google Scholar] [CrossRef]
- EFQM. EFQM 2020 Model—EFQM. 2020. Available online: https://www.efqm.org/index.php/efqm-model/download-your-free-short-copy-of-the-efqm-model/ (accessed on 20 May 2021).
- Rezaei, J. Best-worst multi-criteria decision-making method: Some properties and a linear model. Omega 2016, 64, 126–130. [Google Scholar] [CrossRef]
- Kar, B.; Mohapatra, B.; Kar, S.; Tripathy, S. Small and Medium Enterprise Debt Decision: A Best-Worst Method Framework. Oper. Res. Eng. Sci. Theory Appl. 2022. [Google Scholar] [CrossRef]
- Hafezalkotob, A.; Hafezalkotob, A. A novel approach for combination of individual and group decisions based on fuzzy best-worst method. Appl. Soft Comput. 2017, 59, 316–325. [Google Scholar] [CrossRef]
- Guo, S.; Zhao, H. Fuzzy best-worst multi-criteria decision-making method and its applications. Knowl.-Based Syst. 2017, 121, 23–31. [Google Scholar] [CrossRef]
- Omrani, H.; Alizadeh, A.; Emrouznejad, A. Finding the optimal combination of power plants alternatives: A multi response Taguchi-neural network using TOPSIS and fuzzy best-worst method. J. Clean. Prod. 2018, 203, 210–223. [Google Scholar] [CrossRef]
- Karimi, H.; Sadeghi-Dastaki, M.; Javan, M. A fully fuzzy best–worst multi attribute decision making method with triangular fuzzy number: A case study of maintenance assessment in the hospitals. Appl. Soft Comput. 2020, 86, 105882. [Google Scholar] [CrossRef]
- Allahviranloo, T.; Lotfi, F.H.; Kiasary, M.K.; Kiani, N.A.; Alizadeh, L. Solving fully fuzzy linear programming problem by the ranking function. Appl. Math. Sci. 2008, 2, 19–32. [Google Scholar]
- Kurniawan, V.R.B.; Puspitasari, F.H. A Fuzzy BWM Method for Evaluating Supplier Selection Factors in a SME Paper Manufacturer. In IOP Conference Series: Materials Science and Engineering, Proceedings of the International Conference on Advanced Science and Technology (ICAST 2020), Jakarta, Indonesia, 28 November 2020; IOP Publishing: Bristol, UK, 2021; Volume 1071, p. 012004. [Google Scholar] [CrossRef]
- Ecer, F.; Pamucar, D. Sustainable supplier selection: A novel integrated fuzzy best worst method (F-BWM) and fuzzy CoCoSo with Bonferroni (CoCoSo’B) multi-criteria model. J. Clean. Prod. 2020, 266, 121981. [Google Scholar] [CrossRef]
- Gul, M.; Ak, M.F. Assessment of occupational risks from human health and environmental perspectives: A new integrated approach and its application using fuzzy BWM and fuzzy MAIRCA. Stoch. Environ. Res. Risk Assess. 2020, 34, 1231–1262. [Google Scholar] [CrossRef]
- Guo, S.; Qi, Z. A Fuzzy Best-Worst Multi-Criteria Group Decision-Making Method. IEEE Access 2021, 9, 118941–118952. [Google Scholar] [CrossRef]
- Liang, F.; Brunelli, M.; Rezaei, J. Consistency issues in the best worst method: Measurements and thresholds. Omega 2020, 96, 102175. [Google Scholar] [CrossRef]
- Moslem, S.; Gul, M.; Farooq, D.; Celik, E.; Ghorbanzadeh, O.; Blaschke, T. An integrated approach of best-worst method (bwm) and triangular fuzzy sets for evaluating driver behavior factors related to road safety. Mathematics 2020, 8, 414. [Google Scholar] [CrossRef]
- Roy, P.K.; Shaw, K. Developing a multi-criteria sustainable credit score system using fuzzy BWM and fuzzy TOPSIS. Environ. Dev. Sustain. 2022, 24, 5368–5399. [Google Scholar] [CrossRef]
- Dong, J.; Wan, S.; Chen, S.M. Fuzzy best-worst method based on triangular fuzzy numbers for multi-criteria decision-making. Inf. Sci. 2021, 547, 1080–1104. [Google Scholar] [CrossRef]
- Soner, O.; Celik, E.; Akyuz, E. A fuzzy best–worst method (BWM) to assess the potential environmental impacts of the process of ship recycling. Marit. Policy Manag. 2022, 49, 396–409. [Google Scholar] [CrossRef]
- Liang, X.; Chen, T.; Ye, M.; Lin, H.; Li, Z. A hybrid fuzzy BWM-VIKOR MCDM to evaluate the service level of bike-sharing companies: A case study from Chengdu, China. J. Clean. Prod. 2021, 298, 126759. [Google Scholar] [CrossRef]
- Sagnak, M.; Berberoglu, Y.; Memis, İ.; Yazgan, O. Sustainable collection center location selection in emerging economy for electronic waste with fuzzy Best-Worst and fuzzy TOPSIS. Waste Manag. 2021, 127, 37–47. [Google Scholar] [CrossRef]
- Saaty, T.L. The modern science of multicriteria decision making and its practical applications: The AHP/ANP approach. Oper. Res. 2013, 61, 1101–1118. [Google Scholar] [CrossRef]
- Şişman, B. Bulanık MOORA yöntemi kullanılarak yeşil tedarikçi geliştirme programlarının seçimi ve değerlendirilmesi. Yaşar Üniversitesi E-Derg. 2016, 11, 302–315. [Google Scholar] [CrossRef]
- Stanujkic, D.; Magdalinovic, N.; Jovanovic, R.; Stojanovic, S. An objective multi-criteria approach to optimization using MOORA method and interval grey numbers. Technol. Econ. Dev. Econ. 2012, 18, 331–363. [Google Scholar] [CrossRef]
- Karabašević, D.; Stanujkić, D.; Urošević, S. The MCDM Model for Personnel Selection Based on SWARA and ARAS Methods. Management 2015, 20, 43–52. [Google Scholar]
- Brauers, W.K.; Zavadskas, E.K. Robustness of the multi-objective MOORA method with a test for the facilities sector. Technol. Econ. Dev. Econ. 2009, 15, 352–375. [Google Scholar] [CrossRef]
- Karande, P.; Chakraborty, S. Application of multi-objective optimization on the basis of ratio analysis (MOORA) method for materials selection. Mater. Des. 2012, 37, 317–324. [Google Scholar] [CrossRef]
- Park, J.H.; Lim, K.M.; Park, J.S.; Kwun, Y.C. Distances between interval-valued intuitionistic fuzzy sets. J. Phys. Conf. Ser. 2008, 96, 012089. [Google Scholar] [CrossRef]
- Tzeng, G.H.; Teng, J.Y. Transportation investment project selection with fuzzy multiobjectives. Transp. Plan. Technol. 1993, 17, 91–112. [Google Scholar] [CrossRef]
- Durmić, E.; Stević, Ž.; Chatterjee, P.; Vasiljević, M.; Tomašević, M. Sustainable supplier selection using combined FUCOM–Rough SAW model. Rep. Mech. Eng. 2020, 1, 34–43. [Google Scholar] [CrossRef]
- Zimmermann, H.J. Fuzzy set theory. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 317–332. [Google Scholar] [CrossRef]
- Liu, H.C.; Fan, X.J.; Li, P.; Chen, Y.Z. Evaluating the risk of failure modes with extended MULTIMOORA method under fuzzy environment. Eng. Appl. Artif. Intell. 2014, 34, 168–177. [Google Scholar] [CrossRef]
| MADM | Computational Time | Simplicity | Mathematical Computational | Stability | Information Type |
|---|---|---|---|---|---|
| MOORA | Very less | Very simple | minimum | good | quantitative |
| TOPSIS | Very high | Very critical | maximum | poor | mixed |
| AHP | moderate | Moderate critical | moderate | medium | quantitative |
| VIKOR | less | simple | moderate | medium | quantitative |
| ELECTRE | high | Moderate critical | moderate | medium | mixed |
| PROMETHEE | high | Moderate critical | moderate | medium | mixed |
| Authors | Number, Type and Domains of Linguistic Terms | Group Decision-Making/Aggregation Method | Criteria Weights/Aggregated Criteria Weights | Consistency Check | Application Domain |
|---|---|---|---|---|---|
| [28] | 6/TFNs/ [1–9] | - | The proposed procedure for solving FLP [28]/TFNs | Procedure based on self-reliance coefficient and possibility level | Illustrative example |
| [29] | 5/TFNs/ [1–4.5] | - | Procedure proposed by [28]/TFNs | Fuzzy Consistency Index [29] | Illustrative example |
| [30] | 5/TFNs/ [1–4.5] | - | Procedure proposed by [28]/TFNs | Fuzzy Consistency Index [29] | Weighing sub-indicators for finding power plant prob-lems |
| [31] | 6/TFNs/ [1–9] | - | method to fully solve FLP with TFNs [32] | Conventional BWM [26] | Maintenance assessment in the hospitals |
| [33] | 5/TFNs/ [1–4.5] | - | Procedure proposed by [28]/TFNs | Fuzzy Consistency Index [29] | Supplier selection |
| [34] | 5/TFNs/ [1–4.5] | Yes/- | Procedure proposed by [28]/TFNs | Fuzzy Consistency Index [29] | Determination criteria weights for sustainable supplier selection problems |
| [35] | 5/TFNs/ [1–4.5] | - | Procedure proposed by [28] | Fuzzy Consistency Index [29] | Determine the importance and weight of Fine–Kinney parameters prior to be used in ranking hazards |
| [36] | 5,7,9/TFNs/ [1–9] | Yes/- | Procedure proposed by the [28]/mean method, the max-min method, and the method based on consensus degree | Fuzzy Consistency Index [37] | Illustrative example |
| [38] | 5/TFNs/ [1–4.5] | - | Procedure proposed by [28]/TFNs | Fuzzy Consistency Index [29] | Evaluating Driver Behavior Factors Related to Road Safety |
| [39] | 5/TFNs/ [1–4.5] | - | mixed approach by [40]/TFNs/crisp | Procedure by [40] | Criteria weights for evaluation of a sustainable credit score system |
| [41] | 5/TFNs/ [1–4.5] | Yes/- | Procedure proposed by [28]/precise numbers by GMIR/ averaging method | Fuzzy Consistency Index [29] | Assess the potential environmental impacts of the process of ship recycling |
| [42] | 6/TFNs/ [1–5.5] | Yes/- | Procedure proposed by [28]/precise numbers by GMIR/ averaging method | Fuzzy Consistency Index [29] | Determination of criteria weights in the problem evaluate the service level of bike-sharing enterprises |
| [43] | -/TFNs/ [0–1] | - | Procedure proposed by [28]/TFNs | Fuzzy Consistency Index [29] | Determination weights of criteria and sub-criteria in the problem selection of locations in the emerging economy for electronic waste |
| The proposed model | 9/TFNs/ [1–9] | Yes/- | Procedure proposed by [28]/fuzzy geometric mean/TFNs | Fuzzy Consistency Index [29] | Determination criteria weights for the problem of assessing the quality of the enterprise’s operations |
| Authors | Number, Type and Domains of Linguistic Terms | Group Decision Making/ Aggregation Method | The Normalized Fuzzy Decision Matrix Procedure | The Fuzzy Ratio Method | Fuzzy Reference Point | Fuzzy Multiplicative Form | Application Domain |
|---|---|---|---|---|---|---|---|
| [16] | 5/TFNs/ [0.22–1] | +/fuzzy arithmetic mean | The vector normalization procedure [49] | Defuzzification by MCOA | - | - | Sustainable reverse logistic provider |
| [17] | 5/TFNs/ [1–9] | +/fuzzy arithmetic mean | The vector normalization procedure [49] | By applying Euclidean distance | - | - | Course selection |
| [18] | 5/TFNs/ [1–9] | - | - | Defuzzification by MCOA | - | - | sustainable supplier selection |
| [19] | 5/TFNs/ [1–9] | +/fuzzy arithmetic mean | The vector normalization procedure [49] | Defuzzification by MCOA | - | - | design and fabrication of an automated hammering machine |
| [20] | 7/TFNs/ [0–10] | - | The vector normalization procedure [49] | By applying Euclidean distance | - | - | Green supplier selection |
| [9] | 7/TFNs/ [0–1] | - | The vector normalization procedure [49] | Defuzzification by MCOA | Defuzzification by MCOA | Defuzzification by center of area | Selection of solar power plant location |
| The proposed model | 7/TFNs/ [1–9] | - | - | - | Extended Grzegorzewski’s method [50] | - | Ranking production enterprises |
| V5 | V5 | V4 | V6 | V5 | V5 | V4 | |
| V5 | V5 | V5 | V5 | V5 | V5 | V6 | |
| V6 | V6 | V4 | V5 | V4 | V6 | V5 | |
| V7 | V6 | V6 | V7 | V7 | V5 | V7 | |
| V5 | V6 | V4 | V5 | V4 | V4 | V5 | |
| V6 | V6 | V6 | V4 | V6 | V4 | V6 | |
| V4 | V4 | V4 | V4 | V3 | V5 | V5 | |
| V5 | V4 | V4 | V5 | V3 | V4 | V7 | |
| V6 | V4 | V4 | V3 | V3 | V5 | V5 | |
| V6 | V7 | V6 | V6 | V7 | V6 | V7 | |
| V7 | V6 | V5 | V5 | V3 | V6 | V7 | |
| V5 | V5 | V5 | V6 | V6 | V4 | V5 | |
| V6 | V5 | V4 | V5 | V3 | V5 | V4 | |
| V6 | V5 | V6 | V6 | V7 | V6 | V7 | |
| V4 | V5 | V4 | V5 | V6 | V6 | V7 | |
| V6 | V4 | V4 | V5 | V5 | V5 | V4 | |
| V6 | V6 | V5 | V5 | V7 | V6 | V7 | |
| V6 | V5 | V4 | V5 | V6 | V6 | V6 | |
| V6 | V5 | V5 | V6 | V5 | V4 | V7 | |
| V6 | V5 | V5 | V6 | V5 | V5 | V6 |
| i = 1 | |||||||
| i = 2 | |||||||
| i = 3 | |||||||
| i = 4 | |||||||
| i = 5 | |||||||
| i = 6 | |||||||
| i = 7 | |||||||
| i = 8 | |||||||
| i = 9 | |||||||
| i = 10 | |||||||
| i = 11 | |||||||
| i = 12 | |||||||
| i = 13 | |||||||
| i = 14 | |||||||
| i = 15 | |||||||
| i = 16 | |||||||
| i = 17 | |||||||
| i = 18 | |||||||
| i = 19 | |||||||
| i = 20 | |||||||
| Rank | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.0114 | 0.0171 | 0.0479 | 0.0450 | 0.0200 | 0.0082 | 0.1050 | 0.1050 | 15–19 | |
| 0.0114 | 0.0171 | 0.0139 | 0.0600 | 0.0200 | 0.0082 | 0.0450 | 0.0600 | 6–14 | |
| 0.0086 | 0.0129 | 0.0479 | 0.0600 | 0.0350 | 0 | 0.0600 | 0.0600 | 6–14 | |
| 0 | 0.0129 | 0 | 0 | 0 | 0.0082 | 0 | 0.0129 | 1 | |
| 0.0114 | 0.0129 | 0.0479 | 0.0450 | 0.0350 | 0.0279 | 0.0600 | 0.0600 | 6–14 | |
| 0.0086 | 0.0129 | 0 | 0.1050 | 0.0150 | 0.0279 | 0.0450 | 0.1050 | 15–19 | |
| 0.0214 | 0.0300 | 0.0479 | 0.1050 | 0.0525 | 0.0082 | 0.0600 | 0.1050 | 15–19 | |
| 0.0114 | 0.0300 | 0.0479 | 0.0600 | 0.0525 | 0.0279 | 0 | 0.0600 | 6–14 | |
| 0.0086 | 0.0300 | 0.0479 | 0.1575 | 0.0525 | 0.0082 | 0.0600 | 0.1575 | 20 | |
| 0.0086 | 0 | 0 | 0.0450 | 0 | 0 | 0 | 0.0450 | 2–5 | |
| 0 | 0.0129 | 0.0139 | 0.0600 | 0.0525 | 0 | 0 | 0.0600 | 6–14 | |
| 0.0114 | 0.0171 | 0.0139 | 0.0450 | 0.0150 | 0.0279 | 0.0600 | 0.0600 | 6–14 | |
| 0.0086 | 0.0171 | 0.0479 | 0.0600 | 0.0350 | 0.0082 | 0.1050 | 0.1050 | 15–19 | |
| 0.0086 | 0.0171 | 0 | 0.0450 | 0 | 0 | 0 | 0.0450 | 2–5 | |
| 0.0214 | 0.0171 | 0.0479 | 0.0600 | 0.0150 | 0 | 0 | 0.0600 | 6–14 | |
| 0.0086 | 0.0300 | 0.0479 | 0.0600 | 0.0200 | 0.0082 | 0.1050 | 0.1050 | 15–19 | |
| 0.0086 | 0.0129 | 0.0139 | 0.0600 | 0 | 0 | 0 | 0.0600 | 6–14 | |
| 0.0086 | 0.0171 | 0.0479 | 0.0600 | 0.0150 | 0 | 0.0450 | 0.0600 | 6–14 | |
| 0.0086 | 0.0129 | 0.0139 | 0.0450 | 0.0200 | 0.0279 | 0 | 0.0450 | 2–5 | |
| 0.0086 | 0.0171 | 0.0139 | 0.0450 | 0.0200 | 0.0082 | 0.0450 | 0.0450 | 2–5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Petrović, T.; Vesić Vasović, J.; Komatina, N.; Tadić, D.; Klipa, Đ.; Đurić, G. A Two-Stage Model Based on EFQM, FBWM, and FMOORA for Business Excellence Evaluation in the Process of Manufacturing. Axioms 2022, 11, 704. https://doi.org/10.3390/axioms11120704
Petrović T, Vesić Vasović J, Komatina N, Tadić D, Klipa Đ, Đurić G. A Two-Stage Model Based on EFQM, FBWM, and FMOORA for Business Excellence Evaluation in the Process of Manufacturing. Axioms. 2022; 11(12):704. https://doi.org/10.3390/axioms11120704
Chicago/Turabian StylePetrović, Tijana, Jasmina Vesić Vasović, Nikola Komatina, Danijela Tadić, Đuro Klipa, and Goran Đurić. 2022. "A Two-Stage Model Based on EFQM, FBWM, and FMOORA for Business Excellence Evaluation in the Process of Manufacturing" Axioms 11, no. 12: 704. https://doi.org/10.3390/axioms11120704
APA StylePetrović, T., Vesić Vasović, J., Komatina, N., Tadić, D., Klipa, Đ., & Đurić, G. (2022). A Two-Stage Model Based on EFQM, FBWM, and FMOORA for Business Excellence Evaluation in the Process of Manufacturing. Axioms, 11(12), 704. https://doi.org/10.3390/axioms11120704







