Forecasting High-Dimensional Covariance Matrices Using High-Dimensional Principal Component Analysis
Abstract
1. Introduction
2. Factor Model and PCA
2.1. Factor Structure
2.2. Sparsity
2.2.1. Thresholding Method
2.2.2. The Number of Factors
2.3. PCA for High-Frequency Data
2.3.1. POET Method
2.3.2. Shrinkage POET Method
3. Forecasting Models
3.1. EWMA Model
3.2. VAR Model
3.3. V-HAR Model
4. Simulation Study
4.1. Simulation Design
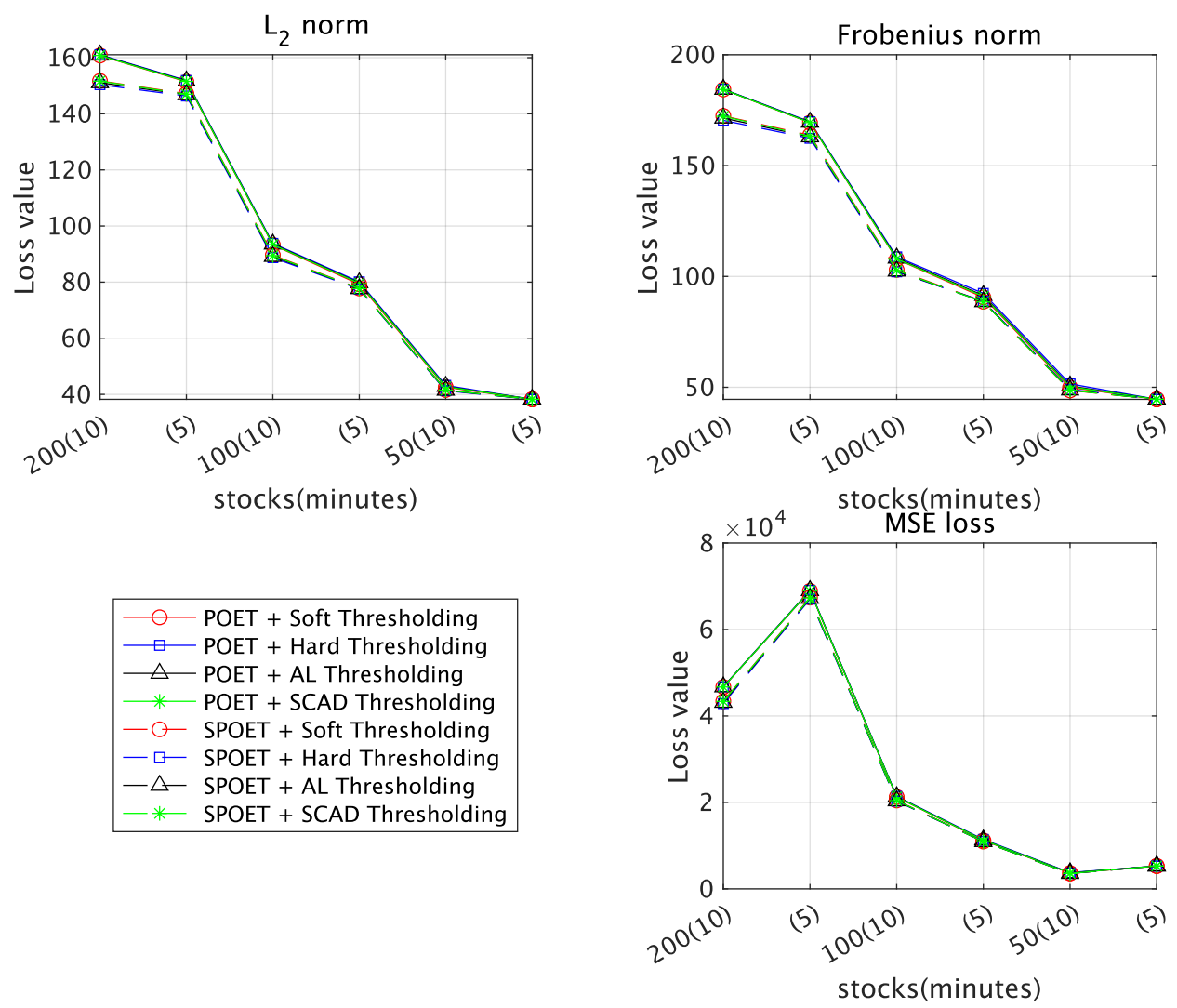
4.2. Simulation Result
5. Empirical Analysis
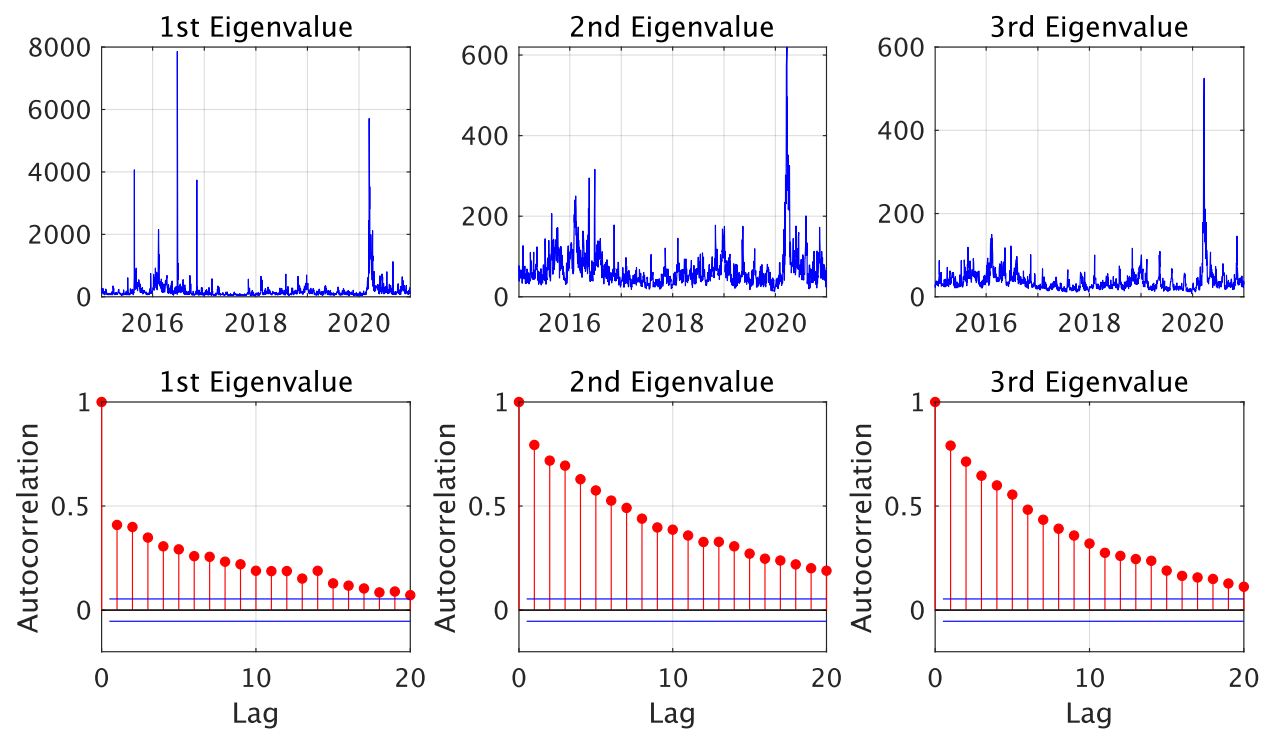
5.1. Data
5.2. Out-of-Sample
5.2.1. Loss Functions and MCS
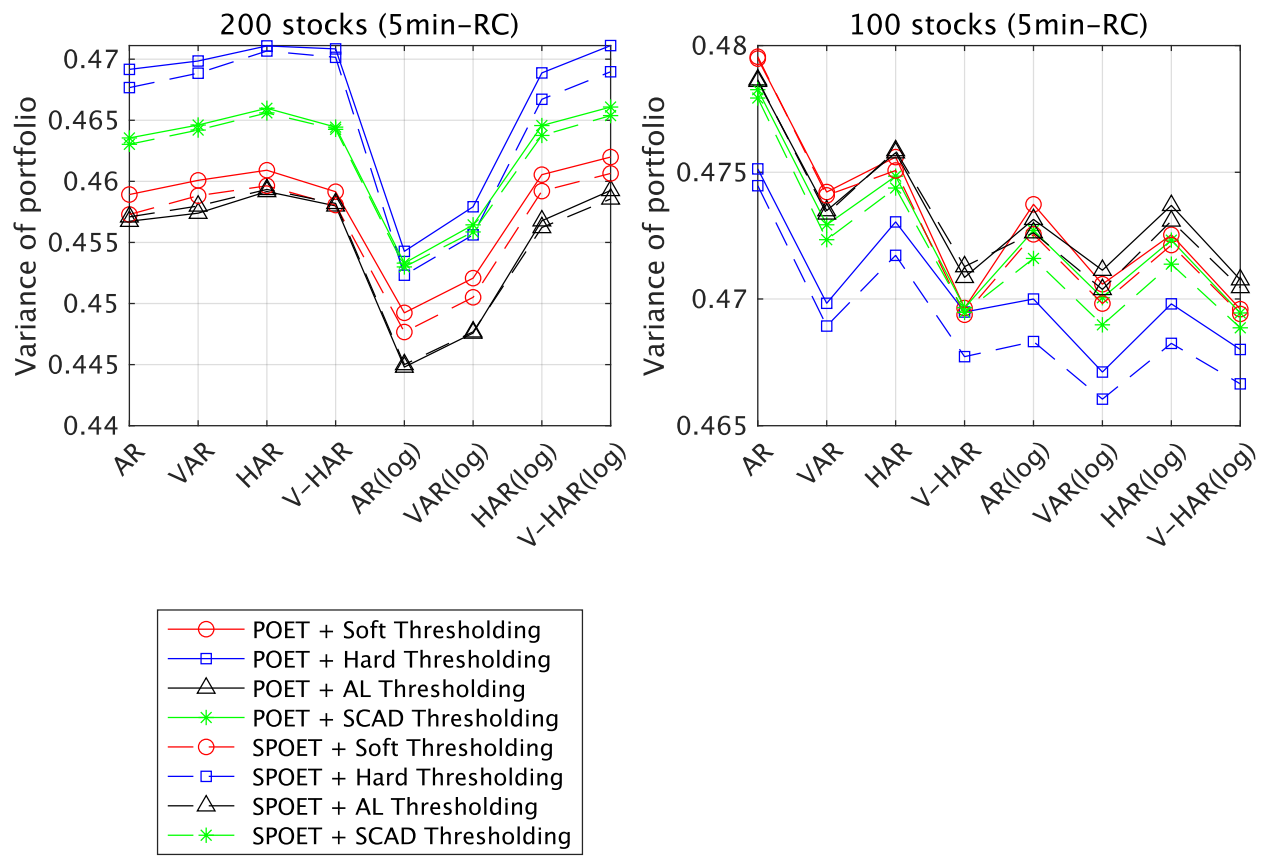
5.2.2. Portfolio Performance
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bauwens, L.; Laurent, S.; Rombouts, J. Multivariate GARCH models: A survey. J. Appl. Econom. 2006, 21, 79–109. [Google Scholar] [CrossRef]
- Engle, R.; Kroner, K. Multivariate simultaneous generalized arch. Econom. Theory 1995, 11, 122–150. [Google Scholar] [CrossRef]
- Tse, Y.; Tsui, A. A multivariate generalized autoregressive conditional heteroscedasticity model with time-varying correlations. J. Bus. Econ. Stat. 2002, 20, 351–362. [Google Scholar] [CrossRef]
- Engle, R. Dynamic conditional correlation: A simple class of multivariate generalized autoregressive conditional heteroskedasticity models. J. Bus. Econ. Stat. 2002, 20, 339–350. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, O.; Shephard, N. Econometric analysis of realized covariation: High frequency based covariance, regression, and correlation in financial economics. Econometrica 2004, 72, 885–925. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, O.; Hansen, P.; Lunde, A.; Shephard, N. Multivariate realised kernels: Consistent positive semi-definite estimators of the covariation of equity prices with noise and non-synchronous trading. J. Econom. 2011, 162, 149–169. [Google Scholar] [CrossRef]
- Bubák, V.; Kočenda, E.; Žikeš, F. Volatility transmission in emerging European foreign exchange markets. J. Bank. Financ. 2011, 35, 2829–2841. [Google Scholar] [CrossRef]
- Golosnoy, V.; Gribisch, B.; Liesenfeld, R. The conditional autoregressive Wishart model for multivariate stock market volatility. J. Econom. 2012, 167, 211–223. [Google Scholar] [CrossRef]
- Bauwens, L.; Storti, G.; Violante, F. Dynamic conditional correlation models for realized covariance matrices. CORE DP 2012, 60, 104–108. [Google Scholar]
- Engle, R.; Ledoit, O.; Wolf, M. Large dynamic covariance matrices. J. Bus. Econ. Stat. 2019, 37, 363–375. [Google Scholar] [CrossRef]
- Nakagawa, K.; Imamura, M.; Yoshida, K. Risk-based portfolios with large dynamic covariance matrices. Int. J. Financ. Stud. 2018, 6, 52. [Google Scholar] [CrossRef]
- Moura, G.; Santos, A.; Ruiz, E. Comparing high-dimensional conditional covariance matrices: Implications for portfolio selection. J. Bank. Financ. 2020, 118, 105882. [Google Scholar] [CrossRef]
- De Nard, G.; Engle, R.; Ledoit, O.; Wolf, M. Large dynamic covariance matrices: Enhancements based on intraday data. J. Bank. Financ.. 2022, 138, 106426. [Google Scholar] [CrossRef]
- Trucíos, C.; Mazzeu, J.; Hallin, M.; Hotta, L.; Valls Pereira, P.L.; Zevallos, M. Forecasting conditional covariance matrices in high-dimensional time series: A general dynamic factor approach. J. Bus. Econ. Stat. 2021, 1–13. [Google Scholar] [CrossRef]
- Wang, Y.; Zou, J. Vast volatility matrix estimation for high-frequency financial data. Ann. Stat. 2010, 38, 943–978. [Google Scholar] [CrossRef]
- Tao, M.; Wang, Y.; Yao, Q.; Zou, J. Large volatility matrix inference via combining low-frequency and high-frequency approaches. J. Am. Stat. Assoc. 2011, 106, 1025–1040. [Google Scholar] [CrossRef]
- Kim, D.; Wang, Y.; Zou, J. Asymptotic theory for large volatility matrix estimation based on high-frequency financial data. Stoch. Process. Their Appl. 2016, 126, 3527–3577. [Google Scholar] [CrossRef]
- Shen, K.; Yao, J.; Li, W. Forecasting high-dimensional realized volatility matrices using a factor model. Quant. Financ. 2020, 20, 1879–1887. [Google Scholar] [CrossRef]
- Fan, J.; Liao, Y.; Mincheva, M. Large covariance estimation by thresholding principal orthogonal complements. J. R. Stat. Soc. Ser. B Stat. Methodol. 2013, 75, 603–680. [Google Scholar] [CrossRef]
- Fan, J.; Furger, A.; Xiu, D. Incorporating global industrial classification standard into portfolio allocation: A simple factor-based large covariance matrix estimator with high-frequency data. J. Bus. Econ. Stat. 2016, 34, 489–503. [Google Scholar] [CrossRef]
- Brownlees, C.; Nualart, E.; Sun, Y. Realized networks. J. Appl. Econom. 2018, 33, 986–1006. [Google Scholar] [CrossRef]
- Koike, Y. De-biased graphical lasso for high-frequency data. Entropy 2020, 22, 456. [Google Scholar] [CrossRef]
- Fan, J.; Fan, Y.; Lv, J. High dimensional covariance matrix estimation using a factor model. J. Econom. 2008, 147, 186–197. [Google Scholar] [CrossRef]
- Aït-Sahalia, Y.; Xiu, D. Using principal component analysis to estimate a high dimensional factor model with high-frequency data. J. Econom. 2017, 201, 384–399. [Google Scholar] [CrossRef]
- Dai, C.; Lu, K.; Xiu, D. Knowing factors or factor loadings, or neither? Evaluating estimators of large covariance matrices with noisy and asynchronous data. J. Econom. 2019, 208, 43–79. [Google Scholar] [CrossRef]
- Zou, H. The adaptive lasso and its oracle properties. J. Am. Stat. Assoc. 2006, 101, 1418–1429. [Google Scholar] [CrossRef]
- Fan, J.; Li, R. Variable selection via nonconcave penalized. J. Am. Stat. Assoc. 2001, 96, 1348–1360. [Google Scholar] [CrossRef]
- Cai, T.; Liu, W. Adaptive thresholding for sparse covariance matrix estimation. J. Am. Stat. Assoc. 2011, 106, 672–684. [Google Scholar] [CrossRef]
- Jian, Z.; Deng, P.; Zhu, Z. High-dimensional covariance forecasting based on principal component analysis of high-frequency data. Econ. Model. 2018, 75, 422–431. [Google Scholar] [CrossRef]
- Yata, K.; Aoshima, M. Effective PCA for high-dimension, low-sample-size data with noise reduction via geometric representations. J. Multivar. Anal. 2012, 105, 193–215. [Google Scholar] [CrossRef]
- Wang, W.; Fan, J. Asymptotics of empirical eigenstructure for high dimensional spiked covariance. Ann. Stat. 2017, 45, 1342–1374. [Google Scholar] [CrossRef] [PubMed]
- Rothman, A.; Levina, E.; Zhu, J. Generalized thresholding of large covariance matrices. J. Am. Stat. Assoc. 2009, 104, 177–186. [Google Scholar] [CrossRef]
- J.P. Morgan/Reuters. Risk Metrics. Thechnical Document, 4th ed.; J.P. Morgan/Reuters: New York, NY, USA, 1996. [Google Scholar]
- Andersen, T.; Bollerslev, T.; Diebold, F. Roughing it up: Including jump components in the measurement, modeling, and forecasting of return volatility. Rev. Econ. Stat. 2007, 89, 701–720. [Google Scholar] [CrossRef]
- Corsi, F. A simple approximate long-memory model of realized volatility. J. Financ. Econom. 2009, 7, 174–196. [Google Scholar] [CrossRef]
- Andersen, T.; Dobrev, D.; Schaumburg, E. Jump-robust volatility estimation using nearest neighbor truncation. J. Econom. 2012, 169, 75–93. [Google Scholar] [CrossRef]
- Bollerslev, T.; Patton, A.; Quaedvlieg, R. Modeling and forecasting (un)reliable realized covariances for more reliable financial decisions. J. Econom. 2018, 207, 71–91. [Google Scholar] [CrossRef]
- Diebold, F.; Mariano, R. Comparing predictive accuracy. J. Bus. Econ. Stat. 1995, 13, 253–265. [Google Scholar]
- Hansen, P.R.; Lunde, A.; Nason, J.M. The Model Confidence Set. Econometrica 2011, 79, 453–497. [Google Scholar] [CrossRef]
- Laurent, S.; Rombouts, J.; Violante, F. On loss functions and ranking forecasting performances of multivariate volatility models. J. Econom. 2013, 173, 1–10. [Google Scholar] [CrossRef]

| 10-min | 5-min | ||||||
|---|---|---|---|---|---|---|---|
| Stocks | Mean | ||||||
| TRUE | 194.543 | 62.640 | 33.081 | 194.543 | 62.640 | 33.081 | |
| 200 | POET | 325.517 | 109.111 | 58.144 | 328.368 | 105.507 | 56.128 |
| SPOET | 313.308 | 96.902 | 45.935 | 322.158 | 99.297 | 49.918 | |
| TRUE | 104.448 | 35.652 | 20.452 | 104.448 | 35.652 | 20.452 | |
| 100 | POET | 181.294 | 63.451 | 36.127 | 174.270 | 60.168 | 35.083 |
| SPOET | 175.185 | 57.342 | 30.018 | 171.146 | 57.044 | 31.959 | |
| TRUE | 49.150 | 18.694 | 11.180 | 49.150 | 18.694 | 11.180 | |
| 50 | POET | 83.807 | 31.995 | 19.540 | 83.246 | 31.389 | 18.679 |
| SPOET | 81.243 | 29.431 | 16.977 | 81.916 | 30.059 | 17.349 | |
| Max | |||||||
| TRUE | 7843.507 | 581.130 | 487.202 | 7843.507 | 581.130 | 487.202 | |
| 200 | POET | 10,095.698 | 1050.907 | 806.341 | 15,710.724 | 985.235 | 727.615 |
| SPOET | 10,059.541 | 941.379 | 681.527 | 15,692.497 | 927.323 | 669.703 | |
| TRUE | 3811.211 | 271.343 | 192.545 | 3811.211 | 271.343 | 192.545 | |
| 100 | POET | 6609.435 | 608.361 | 299.445 | 4421.615 | 524.372 | 335.179 |
| SPOET | 6579.344 | 554.550 | 245.634 | 4412.434 | 506.948 | 310.397 | |
| TRUE | 1662.291 | 209.630 | 117.863 | 1662.291 | 209.630 | 117.863 | |
| 50 | POET | 2477.492 | 448.610 | 230.080 | 3922.754 | 382.988 | 169.577 |
| SPOET | 2469.275 | 420.733 | 202.203 | 3918.187 | 369.209 | 155.799 | |
| Min | |||||||
| TRUE | 29.612 | 10.916 | 6.306 | 29.612 | 10.916 | 6.306 | |
| 200 | POET | 47.262 | 18.211 | 13.739 | 38.446 | 14.410 | 10.803 |
| SPOET | 40.198 | 14.555 | 9.429 | 36.110 | 12.581 | 8.916 | |
| TRUE | 13.115 | 6.480 | 4.319 | 13.115 | 6.480 | 4.319 | |
| 100 | POET | 22.374 | 10.855 | 8.103 | 23.954 | 9.939 | 7.046 |
| SPOET | 19.595 | 8.971 | 6.208 | 22.705 | 8.972 | 6.046 | |
| TRUE | 6.555 | 2.437 | 1.915 | 6.555 | 2.437 | 1.915 | |
| 50 | POET | 11.404 | 5.572 | 3.550 | 12.459 | 4.673 | 3.687 |
| SPOET | 10.144 | 4.857 | 2.835 | 12.025 | 4.301 | 3.315 | |
| 10-min | 5-min | |||||
|---|---|---|---|---|---|---|
| Mean | ||||||
| POET | 199.61 | 67.38 | 37.20 | 175.16 | 56.31 | 35.14 |
| SPOET | 191.78 | 59.55 | 29.37 | 170.06 | 51.21 | 30.04 |
| Max | ||||||
| POET | 7859.83 | 619.82 | 524.94 | 4930.99 | 1379.47 | 331.24 |
| SPOET | 7835.62 | 546.92 | 452.04 | 4909.13 | 1361.80 | 288.60 |
| Min | ||||||
| POET | 31.52 | 12.46 | 7.69 | 22.70 | 14.25 | 7.54 |
| SPOET | 28.49 | 10.13 | 5.36 | 20.65 | 12.24 | 5.90 |
| 10 min | 200 Stocks | 100 Stocks | 50 Stocks | |||
|---|---|---|---|---|---|---|
| Observations | 30 | |||||
| Factors | 3 | 4 | 6 | |||
| Frobenius | POET | SPOET | POET | SPOET | POET | SPOET |
| AR | 219.06 | 210.41 *** | 117.65 | 114.12 *** | 54.99 | 54.47 *** |
| VAR | 202.31 | 195.70 *** | 108.42 | 105.75 *** | 50.79 | 50.65 ** |
| HAR | 204.99 | 196.76 *** | 111.17 | 107.84 *** | 52.45 | 52.01 *** |
| V-HAR | 199.47 | 192.11 *** | 108.09 | 105.41 *** | 50.67 | 50.24 *** |
| AR(log) | 192.98 | 184.47 *** | 105.79 | 102.33 *** | 49.61 | 49.14 *** |
| VAR(log) | 189.82 | 181.66 *** | 103.50 | 100.30 *** | 48.62 | 48.26 |
| HAR(log) | 188.63 | 180.09 *** | 103.21 | 99.75 *** | 48.52 | 48.06 *** |
| V-HAR(log) | 188.57 | 179.98 *** | 102.81 | 99.41 *** | 48.39 | 47.96 |
| EWMA | 212.02 | 203.34 *** | 115.63 | 112.10 *** | 54.73 | 54.18 *** |
| MSE | ||||||
| AR | 5.1307 | 4.8785 | 1.4675 | 1.4156 | 0.3484 | 0.3446 * |
| VAR | 4.8692 | 4.6519 | 1.3938 | 1.3534 | 0.3273 | 0.3262 |
| HAR | 4.5806 | 4.3417 * | 1.3232 | 1.2742 * | 0.3220 | 0.3185 * |
| V-HAR | 4.3779 | 4.1552** | 1.2834 | 1.2416 ** | 0.3061 | 0.3028 |
| AR(log) | 5.3709 | 5.1806 | 1.5393 | 1.4987 | 0.3652 | 0.3629 |
| VAR(log) | 5.2869 | 5.1063 | 1.5049 | 1.4711 | 0.3629 | 0.3624 |
| HAR(log) | 4.8197 | 4.6170 | 1.3723 | 1.3304 | 0.3308 | 0.3284 |
| V-HAR(log) | 4.8930 | 4.6684 * | 1.3854 | 1.3413 | 0.3391 | 0.3368 |
| EWMA | 6.0374 | 5.7767 | 1.6822 | 1.6272 | 0.4088 | 0.4034 * |
| 5 min | 200 Stocks | 100 Stocks | ||
|---|---|---|---|---|
| Observations | 60 | |||
| Factors | 3 | 4 | ||
| Frobenius | POET | SPOET | POET | SPOET |
| AR | 170.86 | 165.89 *** | 94.80 | 93.33 *** |
| VAR | 157.61 | 153.61 *** | 87.50 | 86.38 |
| HAR | 158.93 | 154.26 *** | 88.93 | 87.58 *** |
| V-HAR | 156.93 | 152.52 *** | 88.05 | 86.72 *** |
| AR(log) | 153.33 | 148.61 *** | 86.49 | 85.11 |
| VAR(log) | 150.30 | 145.84 *** | 84.16 ** | 82.94 |
| HAR(log) | 149.11 | 144.33 *** | 84.01 | 82.62 |
| V-HAR(log) | 148.74 | 143.98 *** | 83.56 | 82.12 |
| EWMA | 171.51 | 166.62 *** | 95.52 | 94.05 *** |
| MSE | ||||
| AR | 3.2853 | 3.1792 | 1.0234 | 1.0062 |
| VAR | 3.0918 | 3.0000 | 0.9562 | 0.9441 |
| HAR | 2.9739 | 2.8748 | 0.9212 | 0.9056 |
| V-HAR | 2.8736 | 2.7764 * | 0.8970 | 0.8818 ** |
| AR(log) | 3.7911 | 3.7246 | 1.1351 | 1.1243 |
| VAR(log) | 3.7055 | 3.6469 | 1.0873 | 1.0823 |
| HAR(log) | 3.3425 | 3.2647 | 1.0035 | 0.9913 |
| V-HAR(log) | 3.3448 | 3.2621 | 0.9946 | 0.9816 |
| EWMA | 4.5155 | 4.3992 | 1.2842 | 1.2645 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shigemoto, H.; Morimoto, T. Forecasting High-Dimensional Covariance Matrices Using High-Dimensional Principal Component Analysis. Axioms 2022, 11, 692. https://doi.org/10.3390/axioms11120692
Shigemoto H, Morimoto T. Forecasting High-Dimensional Covariance Matrices Using High-Dimensional Principal Component Analysis. Axioms. 2022; 11(12):692. https://doi.org/10.3390/axioms11120692
Chicago/Turabian StyleShigemoto, Hideto, and Takayuki Morimoto. 2022. "Forecasting High-Dimensional Covariance Matrices Using High-Dimensional Principal Component Analysis" Axioms 11, no. 12: 692. https://doi.org/10.3390/axioms11120692
APA StyleShigemoto, H., & Morimoto, T. (2022). Forecasting High-Dimensional Covariance Matrices Using High-Dimensional Principal Component Analysis. Axioms, 11(12), 692. https://doi.org/10.3390/axioms11120692





