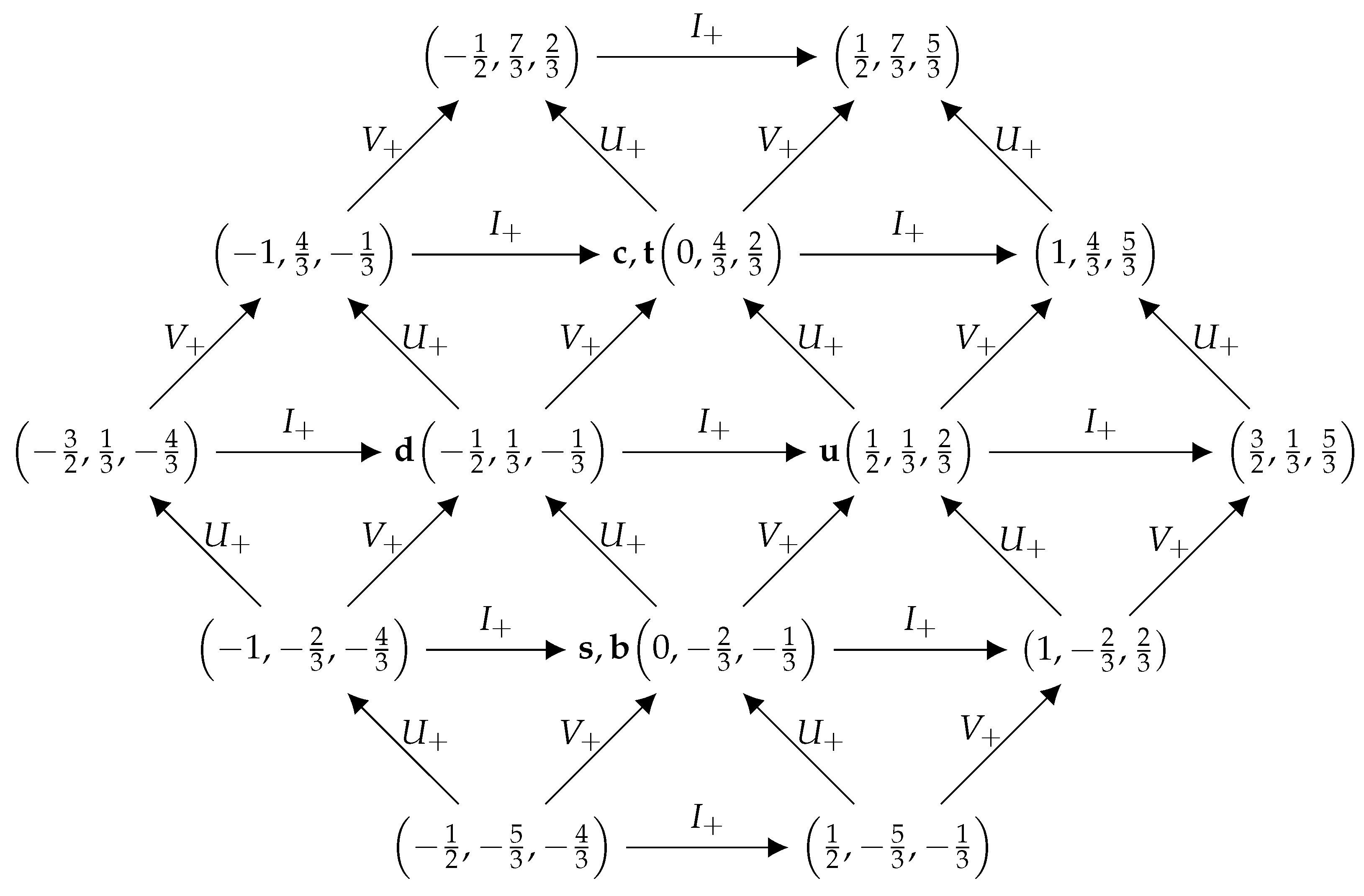1. Introduction
In the theory of grand unification based on the structural group
, the mathematical number of space dimensions is equal to 11. In this case, four dimensions refer to real physical space–time, whereas the remaining seven correspond to some abstract space [
1], within the framework of which one can introduce such quantum characteristics of elementary particles as isospin, hypercharge, colour, flavour, etc. The number of dimensions of that additional abstract space may increase as ever new conserved quantum characteristics of elementary particles are discovered. This scheme of development of the theory is rather simple; however, one cannot get reed of the feeling that it is ad hoc and strained.
There were several attempts to introduce additional dimensions: supermembranes [
2,
3], extending M-theory [
4], F-theory [
5,
6], strings [
7], 12D super Yang–Mills and supergravity theories for constant lightlike vectors [
8,
9]. An elaborate theory is proposed in [
10] and then developed in respect to elementary particles in [
11] and gravity [
12]. The efforts of introducing additional dimensions in various ways were presented in the review [
13].
From the literature, one can see that the standard theory itself, as well as most of alternative ways introduce many additional dimensions to form a mathematical structure, which is able to support necessary quantum characteristics. Even if the increase in dimensions is moderate as in [
10], the proposed modifications seem arbitrary from the mathematical point of view and look more like a fitting to explain certain features.
Our key idea here is to recall the basic principle of relativity theory: the fundamental equality in treatment of space and time, which is reflected in the formula of the invariant interval:
in the system where
. So far,
t was perceived as a single-dimensional time and
x was a three-dimensional space, giving
Despite the declared principle, time and space are no longer handled equally in (
2). We propose to establish the equality truly, to obtain a really symmetric scheme, where each spatial dimension has its temporal counterpart:
It turns out that
is sufficient to construct a space, the symmetry groups of which describe known quantum characteristics.
In [
14], the six-dimensional manifold of symmetric signature
and the special metric is proposed to build a unified theory of gravity and electromagnetism. Here, we consider its typical tangential layer, which is pseudo-Euclidean space
, as being the real physical space–time in the microcosm.
The article has the following structure. At first,
is considered as an image of spinor space, and its hidden groups of proper motions are examined. It is shown that these motions constitute the
group. Taking this, the conserved quantum characteristics generated by
are derived in a standard way. The simplest non-trivial representation of
is built as an example. It is shown that starting from
, one can obtain known conserved quantum characteristics and quarks in a mathematically rigorous way. Then, the representations of
through hyperbolic numbers are considered. The properties of the metric in this space allow predicting the number of quarks equal to 18. The appropriate scheme is presented. Finally, the question of a reduction from
space to our usual
space is examined. It is assumed that the world time flows along a certain axis in the three-dimensional temporal subspace of the six-dimensional space. For physical processes in very small time intervals, the temporal subspace is isotropic with fair accuracy. However, for a larger time duration, the presence of a certain time axis leads to the violation of spherical symmetry. Some symmetries are lost, which leads to the violation of conservation laws for a bigger time scale. This behaviour can be an explanation of the violation of some laws in weak interactions (weak decay time is above
s [
15]; typical weak interaction time is
s [
16]), while these laws hold in strong interactions (strong decay time is around
s [
15]).
2. Pseudo-Euclidean Space as an Image of the Spinor Space
Consider the pseudo-Euclidean space
, and let
designate the metric there, i.e.,
The squared interval in
is given by
where
is a vector in
, and summation is meant by the same upper and lower indices. The group of proper motions of metric (
5) in
is given by a group of proper pseudo-Euclidean rotations
.
Let us now introduce the four-dimensional complex space
, whose elements are the four-component complex vectors, called spinors
, and the space
itself is referred to as spinor space [
17]. Now, denote
,
,
.
For any vector
, one can find such a spinor
such that the following will hold:
where
is the complex conjugate to the
spinor component and
i is the imaginary unit. Formula (
6) may be rewritten in a more elegant form. To do so, consider the complex matrix algebra
in spinor space
. In this algebra, let us choose the matrices
where
are Pauli matrices. The matrices (
7) form the six-dimensional basis in the subalgebra
L of the algebra
. The following commutation relationships take place:
where
,
is the completely antisymmetric tensor, product
is zero if indices of the pair belong to different triplets (
;
), and
where
is the two-dimensional orthogonal projector in the spinor space
. At that, if
, then
; if
then
,
,
.
According to the relationships (
8), (
9), and (
10), the Lie algebra (
7) is reducible. To each pair
there is a corresponding
m-th coordinate of the vector
according to the formula:
where
is the scalar product in
, given by
.
One can readily notice that the representations (
6) and (
11) are equivalent. Thus, the material coordinates of the vectors of pseudo-Euclidean space
can be represented as the average values of the Hermitian operators of the form (
7) upon spinors in
space.
3. Hidden Groups of Proper Motions of the Metric
From Formula (
11), it follows that, if an arbitrary vector
with coordinates
is set, then in the general case, there exists a pair
, determinable to within the unitary equivalence with respect to the group
, and the relation (
11) holds. This means that the pseudo-Euclidean metric (
5) in spinor space
is invariant relative to the action of the group
, which may be regarded as the hidden proper motions of this metric. Before studying the relation of the group
with the conserved quantum characteristics of elementary particles, we consider simpler groups, leading us to conservation laws of such characteristics as spin, “weak” isospin, electric charge, and “weak” hypercharge.
Consider the two-parameter group of unitary transformations
, which is represented in
as unitary matrices of the following kind:
and which operates in
. The transformations of the group
leave the right-hand sides of the relations (
6) invariant, i.e., the coordinates of the vectors in
remain unchanged under such transformations. Therefore, the metric (
5) itself of the space
remains invariant. We will say that the transformations of the kind (
12) of the group
represent hidden motions of the metric (
5). Group
generates two conservation laws. The first law generated by the operator
will be interpreted as the law of conservation of “weak” hypercharge. The second law, induced by the generator of the group
will be interpreted as the law of conservation of the electric charge. The appearance of the “weak” hypercharge conservation law is related to the hidden symmetries in the three-dimensional temporal subspace, which for the sake of brevity will be referred to as isospace.
Let us now proceed to the consideration of the more complicated unitary group. The representation of the unitary group with the Lie algebra, which is determined by the generators (
7) and which operates in the space
, is quite reducible and may be expressed in the form of the direct sum of irreducible representations
. Each of the irreducible representations corresponds to the group
of unitary unimodular matrices
U of dimension two, i.e.,
,
. In the case of the first irreducible representation, such matrices may be represented in the form
,
, where
are the Hermitian Pauli matrices and
are arbitrary real numbers. These matrices implement the identical representation of dimension two in the two-dimensional isospin space
with elements
put over the two basis spinors
and
. In the case of the second irreducible representation, we will obtain the similar group of unitary unimodular matrices
,
, where the same Pauli matrices
appear as generators according to the relation (
7). These matrices realize a group of dimension two in the two-dimensional spinor space
with elements
put over two basis spinors. Thus, the isospace is the spin space related to the three-dimensional temporal subspace. Therefore, such an important characteristic of elementary particles as weak isospin has a pure geometric nature, and its conservation law is related to the invariance of the metric of the six-dimensional space
with respect to the group of rotations in the three-dimensional temporal subspace.
4. Group and the Conserved Quantum Characteristics It Generates
It has been shown above that the group
leaves the metric of space
invariant. Let us now proceed to study in more detail the properties of the group
and its Lie algebra for the necessity of giving their physical interpretations. The generators
,
of the Lie algebra may be represented as 15 traceless Hermitian four-dimensional matrices:
We note that the Lie algebra for the group
contains the Gell-Mann subalgebra for the group
, assigned by the generators
, as well as the Pauli subalgebra for the group
, assigned by generators
. Let us introduce the following designations:
where
are the raising and lowering operators for isospin projection,
Y is the Hermitian hypercharge operator, and
B is the Hermitian baryon charge operator. Among the operators given by (
13), there is not one for the electrical charge
Q. It can be assigned by the following Hermitian traceless matrix:
Then, the relation:
takes place, which was discovered phenomenologically by Gell-Mann [
18] and Nishijima [
19].
Hermitian operators
,
Y,
Q, and
B satisfy the following commutation relations:
i.e., all four operators commutate. This means that the physical characteristics of elementary particles given by the eigenvalues of these operators are simultaneously observable. Let us now find the expressions to describe the relationship of the commutating Hermitian operators. We write out the commutators for the operators of creation and annihilation given by (
14):
Operator
Q may be used also, for instance
.
Let us tabulate the commutators, which are useful for constructing finite-dimensional representations of
group. The first component is given by the row, and the second is assigned as the column. The commutators of
,
Y,
Q, and
B with the rest are presented in the
Table 1.
From the commutation relations given above, it follows that operators , , , , and are raising and , , , , and lowering the eigenvalues of . Operators , , , , and are raising and , , , , and are lowering the eigenvalues of Y. Operators , , , , and are raising and , , , , and are lowering the eigenvalues of Q. Operators , , and are raising, , , and are lowering, and , , and keep unchanged the eigenvalues of B.
Commutators of the rest of operators are given in
Table 2.
It is worth noting here that the studied quantum characteristics
,
Q,
Y, and
B or the notion of quarks are not derived or dependent on the standard theory. For instance, isospin was introduced in 1932 by Heisenberg to explain symmetries of the then newly discovered neutron [
20]. They were introduced before, and the standard theory presents some scheme of them. Here, we propose an alternative description based on the six-dimensional
space.
5. Simplest Irreducible Representation of
Using the commutation relations from
Table 1 and
Table 2, we will construct, as an example, the simplest irreducible finite-dimensional representation for the
group. The states that are contained in the representations are characterized by a set of values of the quantum characteristics
. Transitions between various states are introduced with the aid of the raising and lowering operators given above.
Let us introduce four orthogonal vectors:
in the four-dimensional space induced by the set of quantum characteristics
. These vectors are the eigenvectors of the Hermitian operators
,
Y,
Q, and
B, given by the matrices of the type of (
14) and with the following eigenvalues:
:
,
Y:
,
Q:
,
B:
. Let the state
be set. It is determined as a representation vector, which satisfies the following relations:
This state is an eigenvector of operators
,
Y,
Q, and
B and corresponds to the
u quark. Subjecting this state to the operator
, we obtain new state
, which corresponds to the
s quark:
This can be written briefly as
The state with the same set of characteristics corresponds to the
b quark. It may be obtained by applying
operators subsequently to
:
Next, applying the
operator to the
state and using the commutators from
Table 2, one can obtain a state
, corresponding to the
d quark:
From the
state using the
operator, one may transfer to the
state, or with the help of the
operator, a state
may be obtained, which corresponds to the anti-baryon with the characteristics of
,
,
, and
:
Four states
,
,
, and
establish a space of the simplest irreducible finite-dimensional representation of the
group. In this space, a state
also exists. It corresponds to the
c quark and can be reached from
by the
operator or from
with the help of the
operator:
The state with the same set of characteristics
, which is related to the
t quark, can be obtained from
and
as
These results can be illustrated in the form of the transition diagram (
Figure 1).
Figure 1 shows the simplest irreducible non-trivial representation of the
group, containing four quarks in three states and one anti-baryon with the proper state
. This figure can be thought of as a tetrahedron in some abstract 3D space. The triangle containing the quarks forms a plane with baryon charge
. The operators
,
, and
are moving between states in this plane. The other three operator pairs (
,
,
) are changing the baryon charge.
7. Hyperbolic Groups of Unitary Symmetry and Their Representations
The metric of the six-dimensional pseudo-Euclidean space
is invariant relative to a number of hidden symmetry groups, which emerge as a result of representing the pseudo-Euclidean metric with the aid of hyperbolic complex numbers in the
space according to (
30). Consider the unitary hyperbolic group
, which operates in the
space. It is a three-parameter group of
H-unitary matrices:
which leave the bilinear form (
30) invariant. The Hermitian-conjugated matrix
is inverse of
U, and
. The Lie algebra of this group is commutative, and its basis is formed as
The identical representation (
32) of the group
is reducible as a direct sum of irreducible representations, which operate in invariant single-dimension subspaces
:
The generators of this group induce three conservation laws. Running a little bit ahead, we note that these conservation laws are associated with the three colour quantum characteristics of quarks. A more detailed discussion can be found in [
21]. The unitary transformations of the group
in the
space correspond to the Lorenz transformations in the pseudo-Euclidean space
.
Consider now the hyperbolic group of unitary matrices
, which operates in the three-dimensional hyperbolic space
. This group
consists of hyperbolic matrices
U with dimension four, which are unitary unimodular, i.e., they satisfy the conditions
,
. Such a matrix may be represented as
,
, where
are Hermitian traceless matrices, having the form of
where
are arbitrary real numbers.
The matrices (
36) form a three-dimensional basis in the Lie algebra of the
group and differ from the Pauli matrices only by replacing the imaginary unit
i with the hyperbolic imaginary unit
j. The basis elements (
36) of the Lie algebra satisfy the following commutation relations:
where
is a third-rank tensor with values
,
,
,
,
,
.
The structural constants of the Lie algebra of the group coincide with that of the group to within a sign.
From the components of the six-dimensional vector , one can choose three so as to avoid all three being of the same type, i.e., triplets and are excluded. There are eighteen such triplets. They can be joined in pairs so as to have all six components in a pair. For instance, for the triplet , its pair will be . Thus, there are nine pairs.
For each triplet of type
, which contains two spatial coordinates, we assign a matrix:
and to its pair
,
,
,
, we assign a matrix:
The following relation takes place:
For any hyperbolic unitary matrices
, the independent unitary transformations:
leave the bilinear square form in the right side of (
40) invariant, by the equality:
Thus, the unitary transformations over the pairs of matrices Y and from the group correspond to the pseudo-orthogonal transformations in the space , leaving the pseudo-Euclidean metric invariant.
There are altogether nine groups of this kind, where each representation of such groups expands into the direct sum of two irreducible conjugated representations, which operate in the three-dimensional subspaces of the six-dimensional space–time. To these eighteen representations of the hyperbolic unitary symmetry groups there should correspond eighteen conservation laws. Running ahead, we note that the conserved quantum characteristics may be interpreted as quark flavours. The fact that eighteen representations are paired means that quark flavours appear in pairs , , , etc.
Now, consider the plane
in
Figure 1 and the operators
,
, and
. It is easy to see that applying them as in (
24), (
22), and (
25) repeatedly and in various sequences, one can construct an infinite hexagonal grid in the plane
. Let us select four grid nodes where six known quarks (
u,
d,
s,
b,
and
t) reside and the grid nodes immediately adjacent to those; see
Figure 2.
There are 14 nodes involved. Taking into account that the states in the internal nodes are multiplied [
22], there appear to be in total 18 states described by this grid. The internal nodes contain known quarks. Node
corresponds to quarks
c and
t, and node
represents quarks
s and
b. However, internal nodes
obtain only one
d quark, and the node
obtains a single
u. One can suppose that other quarks compose particles with very short decay periods and very big masses. Thus, they have not been discovered yet. We may call the proposed quark, which shares a node with
u as
h (hazy) and the one paired with
d as
v (vague). Presumably,
h and
v quarks form the most long-living particles among others currently undiscovered. Each of the outer nodes of the diagram contain a single quark.
The Klein–Fock–Gordon equation:
in the space
can be written as
and treated as an eigenvalue problem. The spectrum of the operator contains particle masses. The masses of the
quark triplet, forming long-living particles, were estimated in [
23]. Other components of spectrum might be found further.
8. Reduction to Unisotropic Space
So far, in this paper, we have discussed the fully symmetric space or the isomorphic one, i.e., the space with signature . However, the commonly known space where we live has a signature of . The question arises about how we come from six to four dimensions and what are the related effects. Here, we present three of them: weak interaction asymmetry, treatment of electric charge, and decreasing the number of quarks.
Within the common formalism, there is no explanation of the causes of the violation of the conservation laws for hypercharge and isospin in weak interactions. In the proposed approach, this phenomenon has a rather simple explanation. According to the above, the laws of conservation of isospin and hypercharge appear due to the presence of spherical symmetry in the three-dimensional temporal subspace. If that space would always remain isotropic, these laws would be rigorous. However, if a preferable direction appears in the three-dimensional temporal subspace, then the spherical symmetry is broken and the laws are violated. Strong interactions run over a time of order s. One can propose that, as this scale, the temporal subspace remains spherically symmetric, and hence, the conservation laws of hypercharge and isospin stay valid. Weak interactions run much slower with typical intervals of s, and the existence of the preferable time axis cannot be neglected. This breaks the spherical symmetry, and the conservation laws associated with it are violated. Only laws based on axial symmetry remain.
Two temporal dimensions may be compactified according to the following model introduced by the authors in an application to electromagnetism [
14]. At a small time scale, all directions in the temporal subspace (
are equal, and the subspace has spherical symmetry. For a bigger scale, one direction is selected, and let it be the axis
. The plane
then has a one-parametric group of rotations, where the parameter can be an angle of rotation around the origin. Selecting the parameter as
, one can write the following compactification rule:
Integral curves
,
compose a vector field, which in the plane
is
. In the plane of the tangent splitting, there is a circulation of this field along the circle of constant radius
:
.
Traditionally, Maxwell’s equations of electromagnetism include electric charge and currents as ontology phenomena without a clear mathematical definition. The proposed approach gives a more rigorous and consistent understanding of electromagnetism equations linking the different components of the electromagnetic tensor in six-dimensional space. Within the framework of this model, a purely geometrical interpretation of the concept of the electromagnetic field and point electric charge can be derived. The appearance of the point electric charge is associated with the circulation of the vector potential around a dedicated time axis in the three-dimensional temporal subspace. This is given in more detail in [
14].
The number of quarks was derived as the number of combinations of coordinate axes, which satisfy the condition (
42). One can note that the obtained result rests on the assumption that the temporal subspace is isotropic, i.e., there is no preferable time axis. However, if this is not so and such a preferable time direction exists, let it be
, then the spherical symmetry in the temporal subspace is violated and only axial symmetry remains. In this case, only three pairs are left:
To each pair there corresponds a pair of conjugated matrices (
38) and (
39), inducing six conservation laws for quark flavours. Therefore, only six quarks are possible in a space with signature
.