1. Introduction
Infectious diseases spread among humans, and individuals become worried and work diligently to cure diseases. They are trying to find a way to treat the infection and are looking for help from doctors. Infections produced by bacteria, viruses, fungi, or parasitic animals are instances of contagious diseases. A wide range of organisms live in human organs. They are normally harmless or useful, yet some organisms may transmit disease under certain conditions. “Leptospirosis” is one of the most contagious diseases. Leptospirosis is a disorder originating from a specific type of bacteria known as “Leptospira”. Both humans and livestock are commonly affected by the disease [
1,
2,
3]. Humans become ill after entering the water where a dead rat is located, and animals that drink this water become infected. Because the Leptospirosis infection germs were released via the urine, the individual whose urine was used by other animals and cattle became severely ill. This disease is frequently transmitted by those who walk through polluted water. In 1886, Weil recognized Leptospirosis as a distinct chronic disease, three decades before Inada and his colleagues discovered the individual’s etiology. High body temperature, headache, chills, muscle pain, conjunctivitis (red eyes), diarrhea, vomiting, kidney or liver issues, anemia, and rash are also all signs of Leptospirosis infection. The indications might persist anywhere from a few days to a few months. This disease can cause death, although it is uncommon. In some situations, illnesses are minor and have no visible symptoms [
4,
5,
6,
7,
8]. The majority of frameworks have indeed been presented to capture mammalian, and vector evolutionary processes [
9,
10,
11]. Pongsuumpun et al. [
12] used computational models to analyze Leptospirosis epidemic behavior. These show the pace of change in both the rat and human populations. Adolescents and mature phases are the two main categories within global occupants. Triampo et al. [
13] proposed a mathematical framework for Leptospirosis affliction dissemination. The investigators looked at various Leptospirosis illnesses in Thailand and demonstrated mathematical visualizations. Zaman et al. [
14] studied the vigorous deportment and function of optimal control theory using actual information from [
13]. Zaman et al. [
15] describe the sequential interconnection between a Leptospirosis-contaminated vector and a global community, including local and global resilience. Their paper also depicted bifurcation analyses and gave numerical computations for various infectious rates. A.A. Lashari et al. introduced an endemic prototype of malaria in [
16] and reached their best solutions by employing three control factors. For additional information, check [
16,
17,
18,
19]. Salmonellosis causes typhoid bugs and bacterial contamination. Typically, this infection is characterized by the consumption of food or beverages contaminated with feces or urine of infected people. However, typhoid infection has spread from person to person, which airborne organisms might have helped. High body temperature, headaches, and coughing are common side effects; however, some people are asymptomatic shippers and can still be infected. The most well-known case is a teenage chef who had been held responsible for infecting at least 53 people with typhoid, three of whom died [
20]. Another infection with similar characteristics is cholera. Cholera is another illness with comparable features. The far more important and prevalent dissemination routes are contaminated food and water, although human-to-human dissemination is indeed conceivable [
21]. This suggests that certain bug families should be required to represent both direct and environmentally friendly mediation. Sick people seek adequate medication when they become well-known, but the therapy is often inadequate, and the medicated people remain virulent. According to the CDC, over 5% of persons who are hospitalized for typhoid continue to spread the disease after treatment [
22]. Nearly every year, millions of people die from different infectious diseases. These expansions played a vital role in the spread of HIV in the 1980s.
The World Health Organization (WHO) estimates that 32.6 million people are infected with Aids currently [
23]. The global population benefits from awareness of the prevalence and severity of pandemic illnesses to avoid significant damage. Mathematical modeling of infectious diseases was first introduced in 1760 by the general practitioner and mathematician Daniel Bernoulli, son of John Bernoulli and nephew of Bernoulli. His energy was about illustrating the advantages of vaccination of less poisonous smallpox to stop the bug, weighing the threats. The mathematical models become usable tools to predict future phenomena [
24,
25]. From then on, physicians started using mathematical models to illuminate the important tools that influence transmitting transmissible diseases. One of the vital presentations of mathematical models is to help and recognize control approaches to remove a disease or reduce its endemicity [
25,
26,
27,
28,
29,
30,
31,
32]. In current centuries, numerous attempts have been made to examine the spread-changing aspects of infectious bugs. Moreover, the asymptotic deeds of these epidemic models are studied in [
33,
34,
35,
36]. Vaccination and antiviral remedies are the most effective way to change a contagious disease. Real antiviral treatment may not be available in sufficient amounts. For example, Bird flu bugs H5N1 and H7N9, having periodically infested souls, become dexterous of tainting cells and take a stride towards revolving into a pandemic causing pressure [
37,
38].
Many simple models have generated beneficial intuitions into the disease transmission dynamics. For example, in the regular SIR compartment model for infectious diseases, the population is divided into three compartments: Susceptible
, Infected
, and Recovered
. Based on the theory of epidemics in [
39], the blowout of transferable bugs is termed compartmental simulations such as SIR or SIRS models that mention every alphabet to a compartment in which the individual could exist. Lastly, vaccination is added to decrease the effect of diseases. SIS, SIRS, and SEIR models have also been used to study various biological questions related to different bugs. Certain contagious diseases are passed from person to person, while others are spread via bug or animal stings. Others are generated as a result of ingestion of degraded food, drinking polluted water, or being subjected to environmental organisms. Each communicable disease has unique symptoms, although fever, coughing, and exhaustion are common. Vaccination helps intercept several communicable diseases, such as measles and chickenpox. Hands that are cleaned regularly and thoroughly help protect us from most viral infectious diseases. In the beginning, treatment of any infectious disease is very rare and costly, and people try to control it in such a way that is low in cost, reliable, and efficient. It is especially of great interest when living standards are not up to the mark. Different types of experiments were performed for the treatment, such as vaccinations, antibiotics, and awareness. The progress in the development of sanitation, antibiotics, and well-organized vaccination policies brought forth a situation in the last half of the previous century that viral diseases would be abolished. Due to this reason, the treatment of the diseases like Cancer and HIV has been made possible by doctors. However, the viral disease vectors took up a new form, and in resultant new ailments came into being, and preexisted epidemics adopted new forms. Precautionary measures, except these approaches, are of special importance. In developed countries, noncommunicable diseases (NCDs) are replaced by communicable viral diseases (CVDs) [
40,
41,
42,
43,
44]. The leading epidemic in the tropical and subtropical regions is Dengue, which inflicts economic, health, and social issues [
45]. According to the World Health Organization (WHO), 50 to 100 million Dengue illnesses are recorded each year, with 500,000 cases of Dengue Hemorrhagic Fever (DHF) involving twenty-two thousand deaths, the overwhelming of which are adolescents [
46]. The Mediterranean is at high risk for this vector-borne disease [
47]. Elbasha et al. [
48] explored the design of vaccination strategies to overcome various types of Human Population virus (HPV). The vector of dengue fever is a female mosquito known as
Aedes. No vaccine is available to eradicate Dengue, but prevention is the best possible way to cure it. Dengue has mainly affected the warm parts of the world, such as India, Sri Lanka, Central Asia, China, Central America, and Pakistan. The breeding of
Aedes in urban areas is not the same as in rural areas. Dengue has become endemic in over a hundred countries, among different parts of the globe, in the last two decades [
49].
Aedes prefer to live in human habitation regions.
Aedes bites at dusk and dawn. Breeding of
Aedes in urban areas is at a high rate in discarded tires, broken bottles, flower vases, and water containers. The poor environmental conditions and poor sanitation encourage the spread of disease [
50]. Mathematical models provide a powerful way that leads to investigate infections. Anderson et al. [
51] studied infectious diseases using mathematical models. Kermack et al. [
52] introduced the susceptible, infected, and recovered (SIR) model for a fixed population. The host population is divided into compartments, each containing individuals who are the same with respect to the disease. Different numerical techniques are used in every era to find the solution to the epidemic model. Attaullah et al. [
53] discussed the computational analysis of the HIV model and the immune system interaction using the Galerkin scheme. Amin et al. [
54] used the Haar wavelet approach to estimate the solution of the mathematical model of HIV infection CD4 + T-Cells. Laarabi et al. [
55] considered the SIRS model with vaccination and treatment control. AIDS is an infectious disease that HIV causes. It is a viral infection that can be transferred through blood, or during pregnancy from mother to child, by sharing needles or by blood transfusions [
56]. Zhao et al. [
57] discussed the behavior of an SVIR epidemic model with stochastic perturbation. Zhao et al. [
58] presented a qualitative evaluation of a two-group SVIR epidemic model with random effect. Djilali et al. [
59] investigated the global dynamics of an SVIR epidemic model with distributed delay and an imperfect vaccine. Wang et al. [
60] explored the global stability of a multigroup SVIR model with vaccination age. Xing et al. [
61] explained the periodic solutions for a relapse-based SVIR epidemic model.
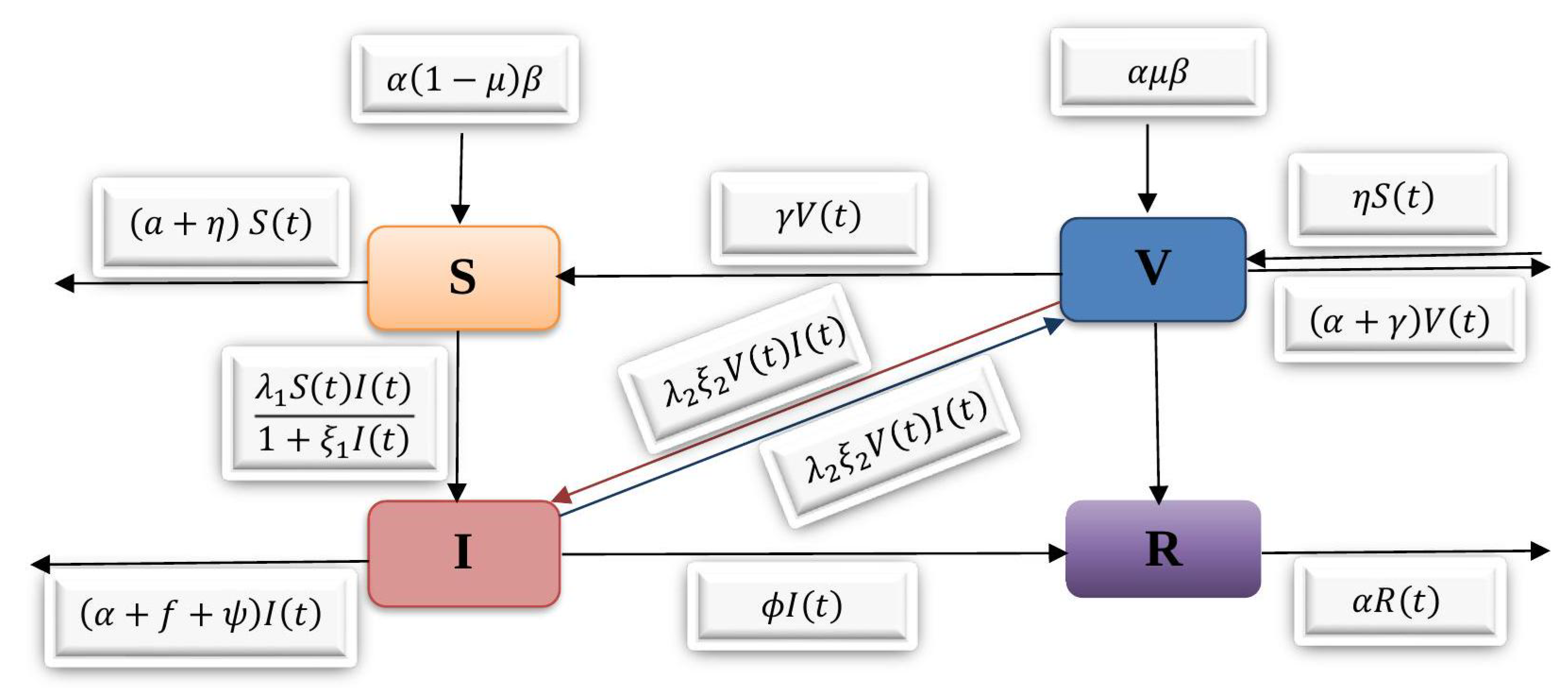
The fundamental aim of the present paper is to examine the SVIR based on four coupled non-linear ordinary differential equations. We discuss a detailed explanation of the model equilibrium, its basic reproduction number
local stability, and global stability. It is observed that the disease-free equilibrium is stable if
, while the endemic equilibrium exists and the disease exists permanently in the population if
. The mentioned model is solved by applying the well-known Runge–Kutta scheme. This method has superiority to some extent over the other traditional techniques [
62,
63]. Furthermore, adjusting the values of various medical predictors in the prototype allows for observation of variance. To illustrate the reliability of the suggested scheme, the model is solved using Euler and Euler modified methods, and the findings are compared with those obtained using the RK4 technique. All the findings are visualized through different graphs. The detailed analysis of the aforementioned model demonstrates that the RK4 scheme is more authentic and accurate than the previous approaches employed for the model.
The following is how the article’s content is organized:
Section 2 introduces the fundamental concepts—the formulation of the SVIR model. The disease-free equilibrium of the proposed model was introduced in
Section 3.
Section 4 represents the basic reproduction number of the model. The local stability of the model was shown in
Section 5 and followed by the global stability in
Section 6.
Section 7 provides the well-known Runge–Kutta method implemented for the model. The numerical results, the behaviors of different parameters, and comparison of the solutions of the RK4 method with other classical techniques applied to the model are discussed in
Section 8. Finally,
Section 9 gives the conclusion of the article. A computer code written in MATLAB is used to perform the computations.
8. Numerical Results
The numerical solution of the SVIR model is described using the Runge–Kutta technique of order four (RK4 method) in this section. We alternate the values of certain specified parameters while keeping all other parameters constant to determine the behavior of distinct parameters in the recommended model. The model’s geometrical representation shows the behavior of different parameters. From the figures, it might be clear that the dynamic behavior of
, and
shows different results by changing the values of the parameters. This study deals with how the approval of an equilibrium solution changes with deviating parameters. We intended only for the case where only one parameter is assorted. We numerically examined the model based on the previous results and textured the classic’s properties by changing the parameters’ values by keeping fixed variables and using the different initial conditions. We dispute the dynamics of
(the disease included death rate) in susceptible, vaccinated, infected, and recovered individuals, respectively, that are shown in
Figure 2a–d. In
Figure 2a, by increasing the value of
, a decrease occurs in susceptible individuals over time.
Figure 2b analyses the effects of different values of
on vaccinated individuals. By increasing the value of
, the strength of the vaccinated individuals increased and gradually decreased after some time. Moreover, in
Figure 2c, the concentration of infected individuals increased by increasing the value of the disease-included death rate, i.e.,
. In
Figure 2d, by increasing the value of the disease-included death rate, the recovered individuals’ population increased, decreased, and became stout after approximately ten weeks. In
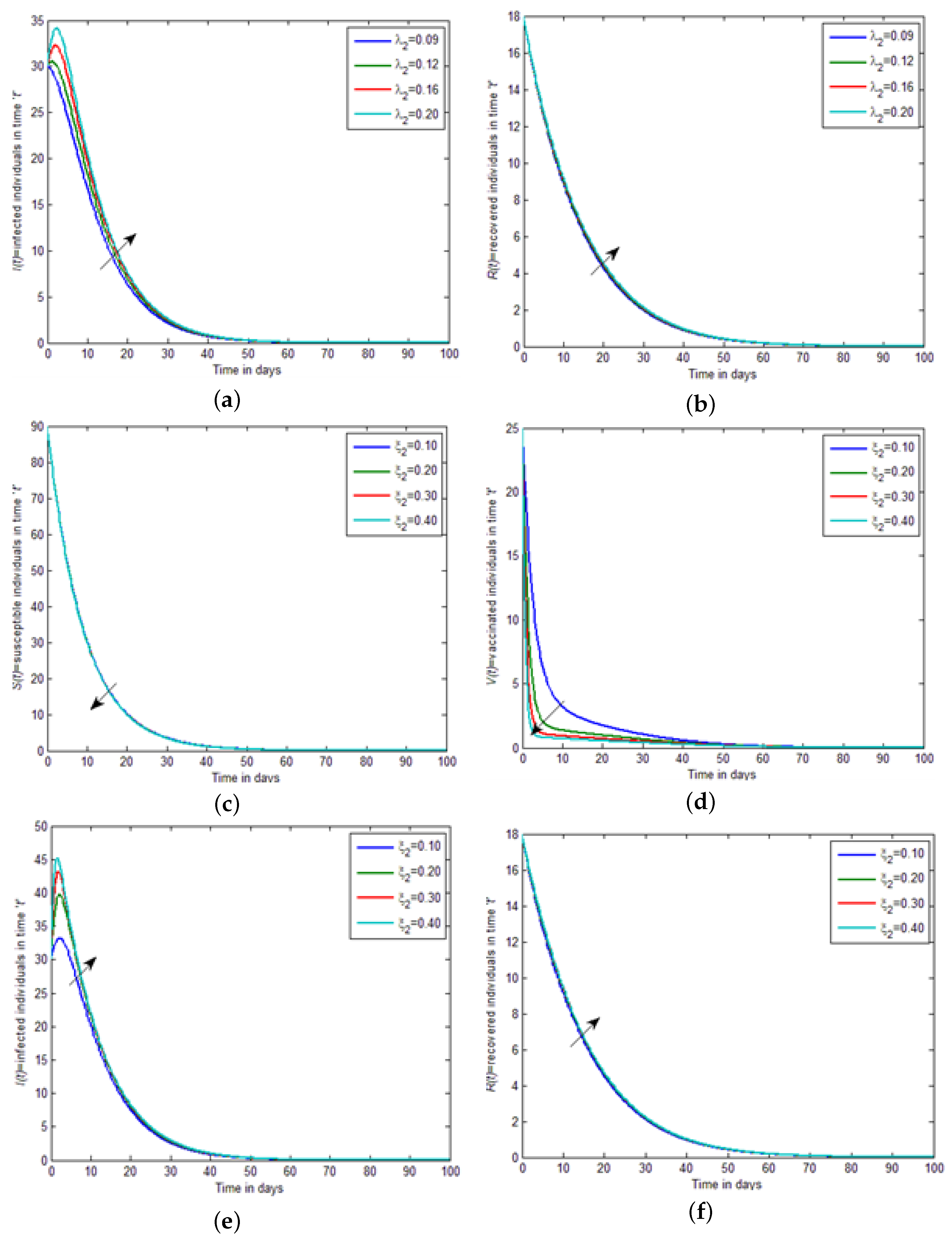
Figure 2a–f, by increasing the value of the interaction between vaccinated and infected individuals, i.e.,
, the strength of susceptible individuals and vaccinated individuals become equal, and then slightly decreases in
Figure 3a,b, by increasing the value of the interaction between vaccinated and infected, i.e.,
, the strength of infected individuals and recovered individuals become equal, and then slightly increases. In
Figure 3c,d, by increasing the value of the saturation constant, i.e.,
, the strength of susceptible individuals and vaccinated individuals decreases. While in
Figure 3e,f, by increasing the value of the saturation constant, i.e.,
, the strength of infected individuals and recovered individuals increases. In
Figure 4a–d, by decreasing the initial conditions, the concentration of susceptible, vaccinated, infected, and recovered individuals decrease in the results of infected individuals.
Figure 4e describes the population dynamics of all four individuals, i.e., susceptible, vaccinated, infected, and recovered. Finally, in
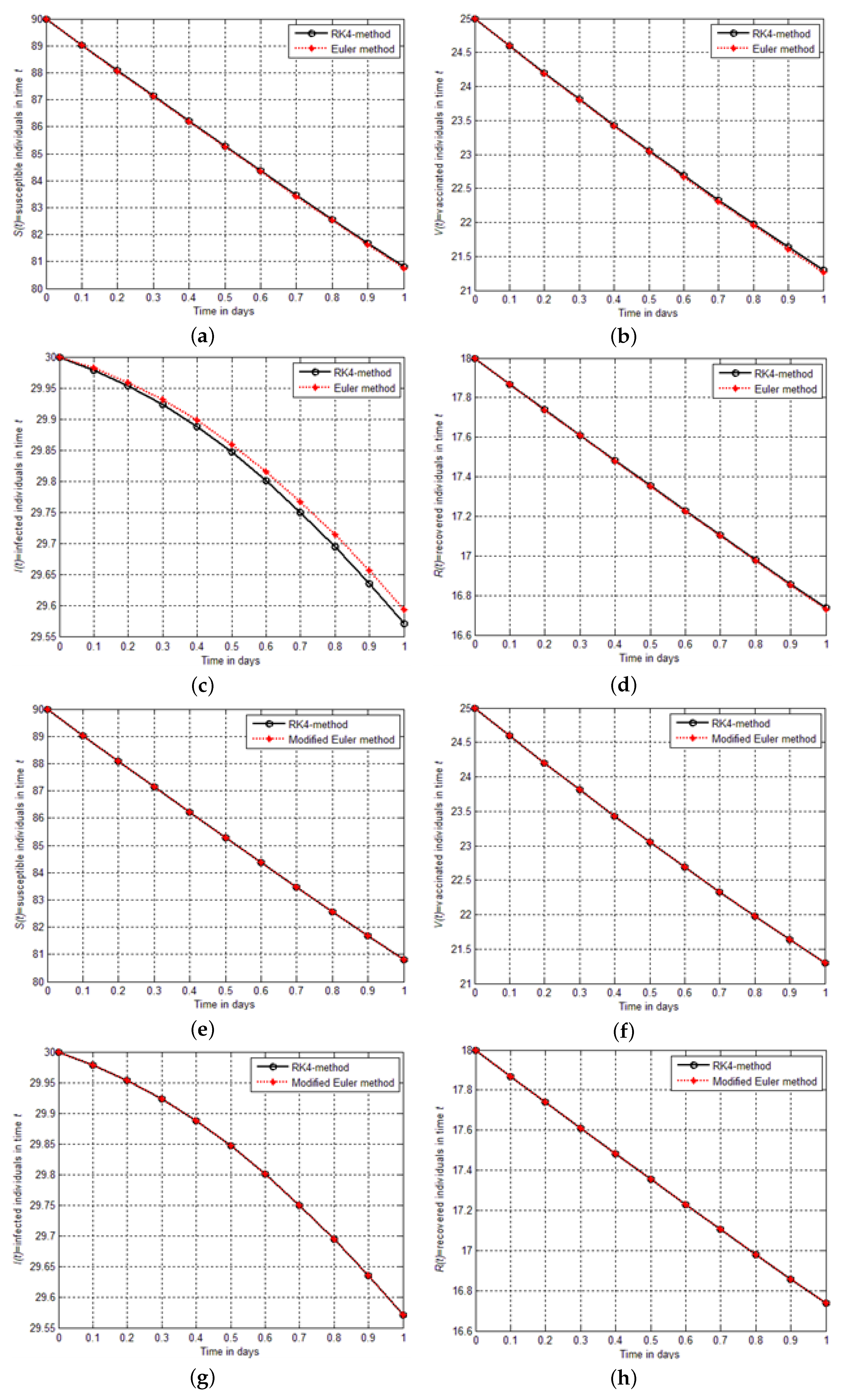
Figure 5a–h are shown the graphical comparison between the aforementioned schemes implemented for the model
, and
. From the figure, it could be seen that the Euler modified finding is closer to the results of RK4 than the findings of Euler solutions.
8.1. The Euler’s Method
Although Euler’s method is rarely used in practice, the simplicity of its derivation can be used to illustrate the techniques involved in the construction of some of the more advanced techniques without the cumbersome algebra that accompany these constructions. Euler’s method aims to obtain an approximation to the well-posed initial value problem.
In actuality, a continuous approximation to the solution
will not be obtained; instead, approximations to
y will be generated at various values, called mesh points, in the interval
. This condition is ensured by choosing a positive integer
N and selecting the mesh points.
The common distance between the points
is called the step size. We will use Taylor’s Theorem to derive Euler’s method. Suppose that
, the unique solution to Equation (
12), has two continuous derivatives on
, so that for each
,
for some number
in
. Since
, we have
and, since
satisfies the differential Equation (
12),
Euler’s method constructs
, for each
, by deleting the remainder term. Thus, Euler’s method is as follows:
8.2. The Modified Euler Method
The modified Euler method is used to numerically solve first-order initial-value problems. Let
is the initial value problem with the initial condition
, let
be an integer and we set
is the step size. Partition the whole interval into the
N subinterval with mesh points
, for
. Then the Modified Euler method can be described as:
8.3. Comparison between the Results of Euler, Modified Euler, and RK4 Method
In this section, we solve the model for SVIR infection using Euler and modified Euler methods and compare the results graphically and numerically with those obtained from the RK4 method. We illustrate the precision and effectiveness of the RK4 method. In
Table 2,
Table 3,
Table 4 and
Table 5, the comparison between the results of the Euler method and the Rk4 method for
, and
are shown.
Table 6,
Table 7,
Table 8 and
Table 9 show that the modified Euler method solutions are much closer to the RK4 method solutions than the solutions of the Euler method. Finally, absolute errors are computed between the results of RK4, Euler, and modified Euler schemes. The comparison shows that the RK4 technique is effective and reliable in obtaining an approximate solution to real-world initial value problems.