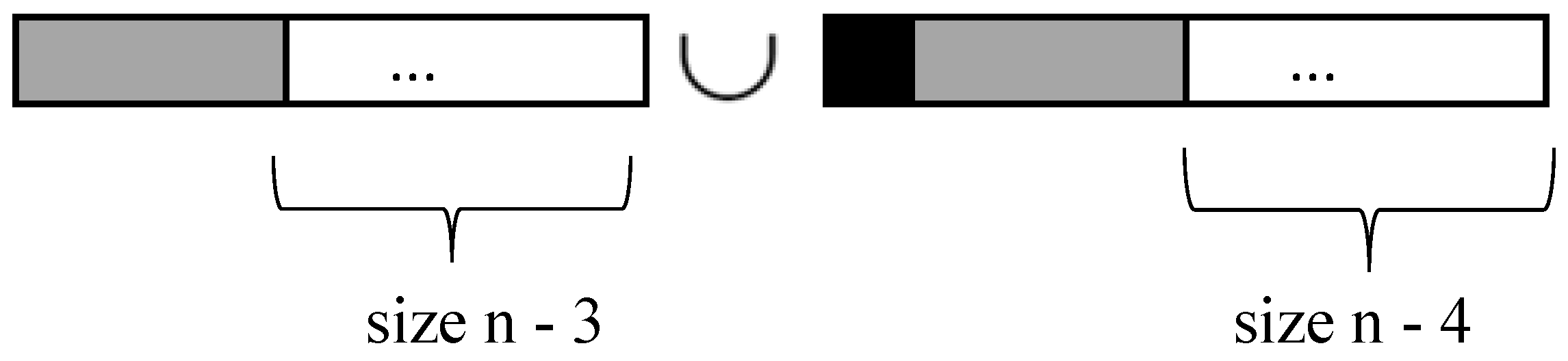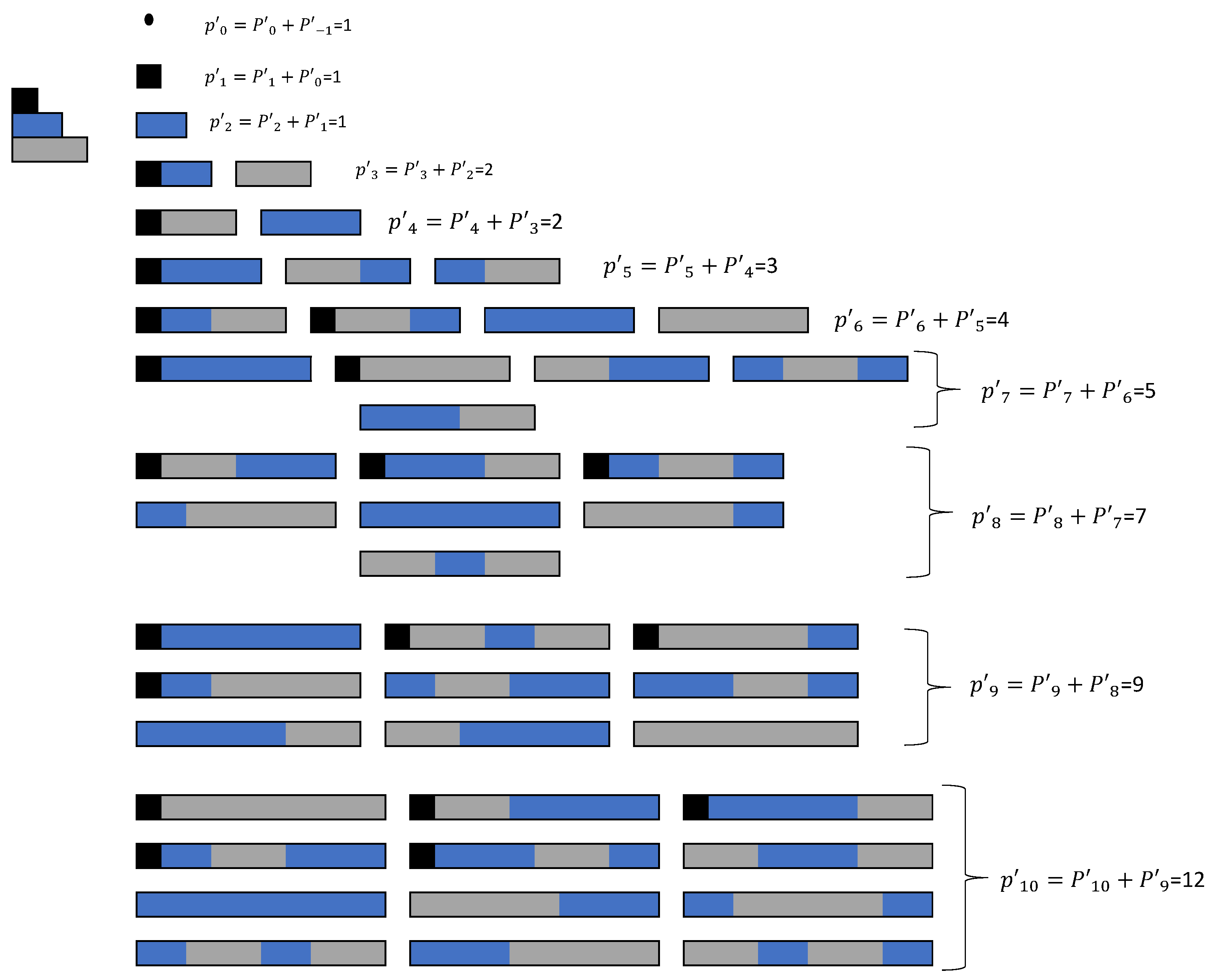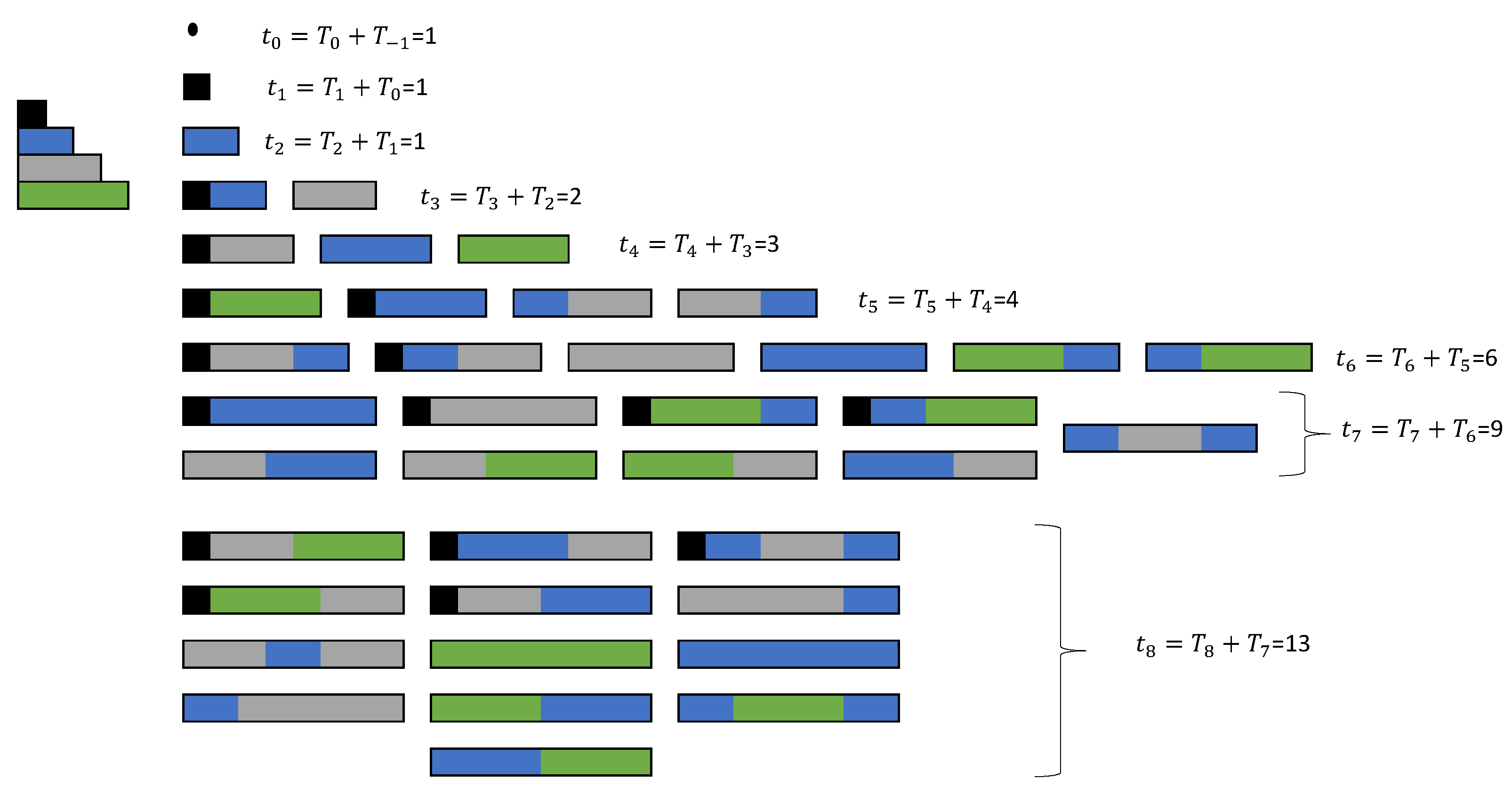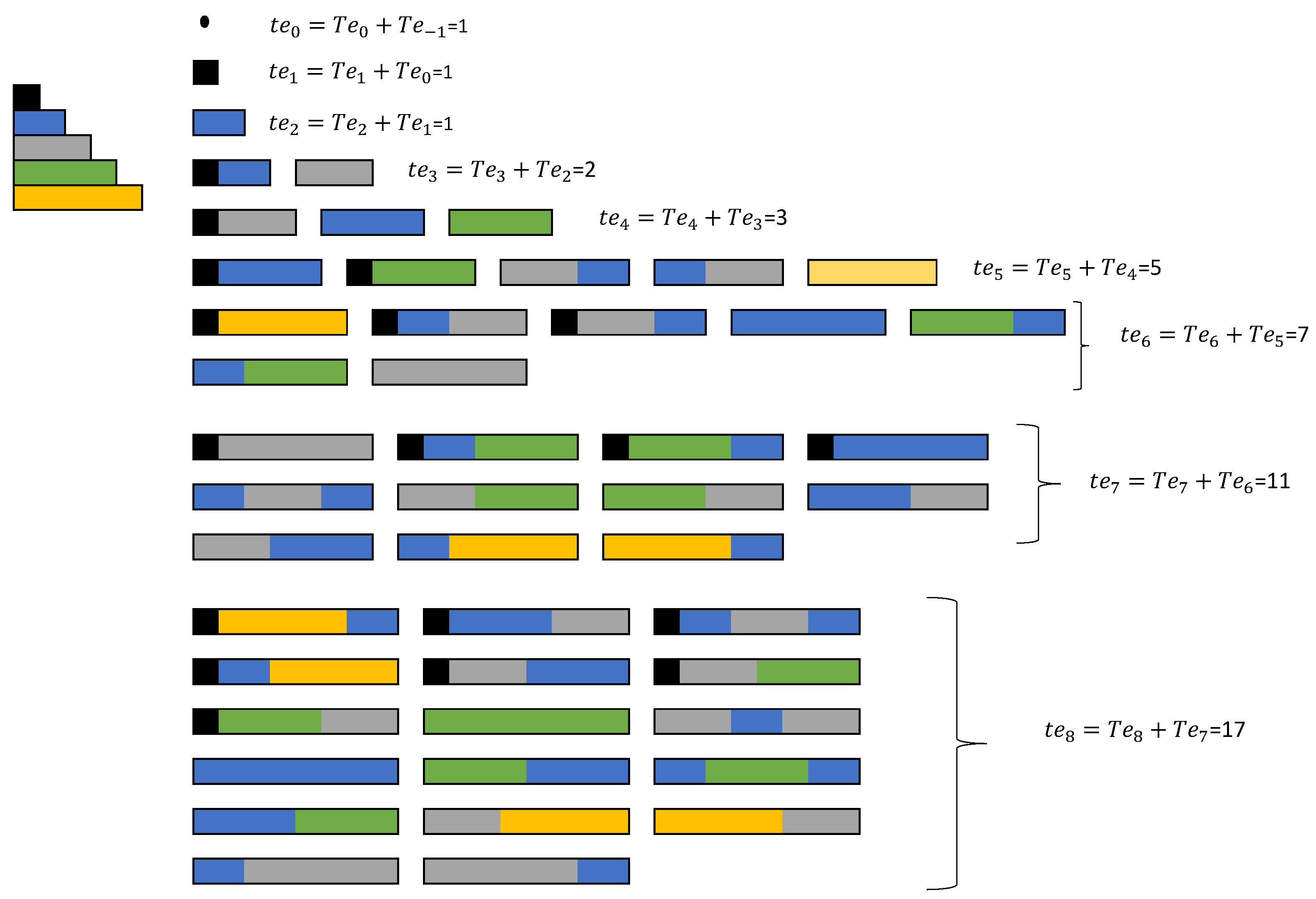Combinatorial Interpretation of Numbers in the Generalized Padovan Sequence and Some of Its Extensions

Abstract

There is ongoing research into combinatorial methods and approaches for linear and recurrent sequences. Using the notion of a board defined for the Fibonacci sequence, this work introduces the Padovan sequence combinatorial approach. Thus, mathematical theorems are introduced that refer to the study of the Padovan combinatorial model and some of its extensions, namely Tridovan, Tetradovan and its generalization (Z-dovan). Finally, we obtained a generalization of the Padovan combinatorial model, which was the main result of this research.

1. Introduction

Research involving the combinatorial study of the Fibonacci sequence was carried out within the scope of the mathematical literature. The Fibonacci sequence is related to other sequences, for example, the Padovan sequence, which is sometimes considered to be a cousin of the Fibonacci sequence. The present paper is concerned with the Padovan sequence and provides a combinatorial interpretation of this sequence by utilizing an approach that, in general, presents an alternative for visualizing the sequence via combinatorial boards.

The results presented in this research are relevant to the area of liner and recurrent sequences, introducing a context for combinatorial sequence interpretation. It is noteworthy that there have not yet been any studies on the combinatorial model of the Padovan sequence.

Let us explain the content of this paper in more detail, featuring a part of the Padovan sequence. The Padovan sequence was created by the Italian architect Richard Padovan. It is a third-order linear recurrent sequence, where its recurrence relation is given by $P_n=P_{n-2}+P_{n-3}, n⩾3$ with the respective initial values of $P_0=P_1=P_2=1$. Several studies have referred to this sequence as a cousin of the Fibonacci sequence [1,2,3,4]. Some works have discussed the modified Padovan sequence, with the respective initial values of $P_0=1, P_1=0, P_2=1$. We call this modified version the shifted Padovan sequence as it shows a delay in two terms compared to the original Padovan sequence [5].

It is possible to verify that the study of recurring numerical sequences and their generalizations has usually been neglected in contemporary books on the history of mathematics [6,7,8]. An interesting approach to studying recurrent numeric sequences is the combinatorial interpretation of the Fibonacci sequence via tiling, based on the recurrence of the Fibonacci sequence. The Fibonacci sequence is given by $F_n=F_{n-1}+F_{n-2}, n⩾2$, with the respective initial values of $F_0=F_1=1$. For the tiling definition, we used a 1 × n board with two types of tiles: 1 × 1 white tiles and 1 × 2 blue tiles (dominoes). This n-one-dimensional board is shown in Figure 1.

Definition 1.

A board is formed of squares called houses, cells or positions, which are enumerated according to their positions. A given board of length n is called n-board [9].

The theorem that was studied in the work of Spivey states that $f_n$ is the number of configurations of tiles in a board of length n (squares and dominoes) [10]. This theorem provides a combinatorial interpretation of the Fibonacci numbers on a board.

The present paper is based on the works of Benjamin and Quinn [11,12], Spreafico [9,13], who described the notion of an n-board for the Fibonacci sequence. The definitions of terms and methods therein were used in a similar manner in this research, in which the combinatorial properties presented by Benjamin and Quinn were applied to the Padovan sequence and its extensions. In particular, we transferred the combinatorial properties of the Fibonacci sequence stated in [11,12] to the case of the Padovan sequence and its generalizations. The works of [14] and Vieira et al. [15] presented extensions of the Padovan sequence and, by gathering the results of the aforementioned works, the mathematical theorem referring to the boards for the Padovan sequence extensions was introduced.

2. Combinatorial Interpretation of the Generalized Padovan Sequence

In this section, the main results of our research are introduced. In particular, we define Padovan, Tridovan, Tetradovan and Z-dovan boards. Our study of the extensions and generalization of the Padovan sequence was based on the work of Vieira and Alves [14] and Vieira et al. [15].

2.1. A Combinatorial Model for the Padovan Sequence

Koshy [13] and Benjamin and Quinn [12] analyzed the combinatorial behavior of the Fibonacci sequence via tiling. By applying the same idea, we obtained the rules for the construction of a board for the Padovan sequence.

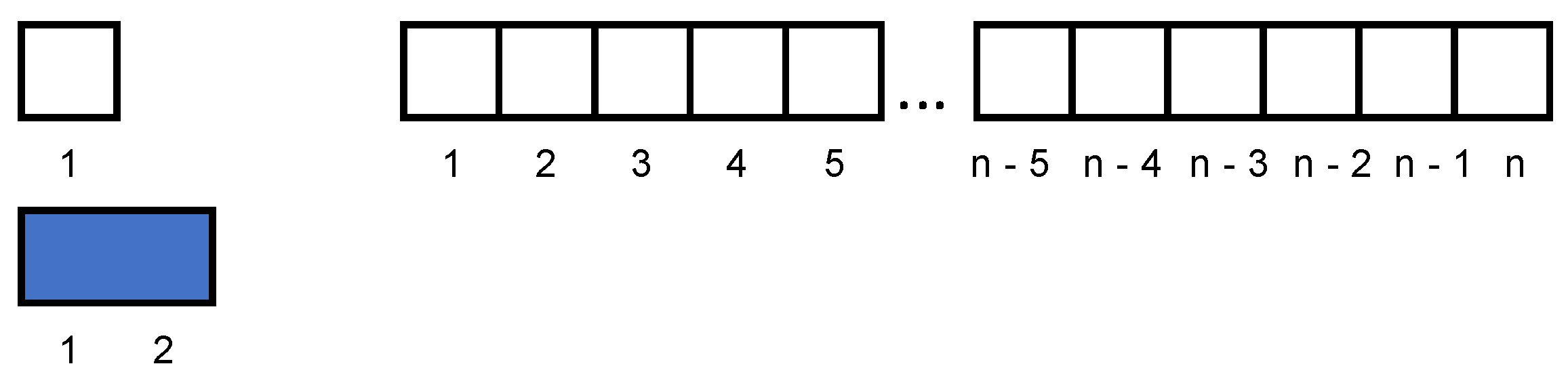
Definition 2.

Considering extended domino tiles (defined as rectangles of size 1 × 3: a 1 × 1 black square and a 1 × 2 domino), any board for the Padovan sequence is formed by arranging these defined shapes. The black square is intended to complement the unfilled tiles, subject to the rule of only being inserted at the beginning and only once in each tile. These particular aforementioned rules are defined for the theorem referring to Padovan tiling.

Thus, an n-board is filled using the following tile shapes: 1 × 1 black squares, 1 × 2 blue dominoes and extended 1 × 3 gray dominoes, all with a weight of 1. In Figure 2, it is possible to notice that the term $p_n$ refers to the number of tile shapes in the n-board; thus, we can determine that $p_n=P_n, n⩾0$. We can consider $p_0=P_0=1$ to be fixed since there is no board of size 1 × 0 and $p_1=P_1=1$ when there is only one black square. Therefore, there is an exception to the rules above since, in this case, the black square is the only shape that is simultaneously at the beginning and at the end.

The number of tiles that start with black squares corresponds to a number in the Padovan sequence, which is given by $p_{n-3}$. The number of tiles that do not start with black squares is given by $p_{n-2}$ (Figure 2).

The discussion above gives rise to the following theorem, which relates the elements of the Padovan sequence to the numbers $P_n$. This theorem was the basis for further combinatorial investigations regarding the Padovan sequence in our study.

Theorem 1.

For $n⩾0$, the possible tiling of a 1 × n board with black square, blue domino and extended gray domino tiles is given by:

$$p_n=P_n,$$

where $p_n$ is the number of ways to fill in the 1 × n board and $P_n$ is the n-th term of the Padovan sequence.

Proof of Theorem 1.

Let $p_n$ denote the number of tiles in a given board, where $p_0=1=P_0$ and $p_1=1=P_1$.

Considering an arbitrary set of tiles of size n (Figure 1), where $n⩾0$, it can be noticed that the board is formed by the union of two large subsets that are formed of two smaller subsets. These subsets are presented below:

Case 1: Let the two subsets be tiles starting with black squares and the other tiles in a $n-2$-board, where the tiles are of size $n-2$. Consider a new set of tiles starting with blue dominoes of size 1 × 2, juxtaposed with tiles of size $n-2$ that do not start with black squares in union with the set of tiles of size 1 × 1 that start with black squares by inserting blue dominoes of size 1 × 2 right after these squares. This union results in a tiling board of size n (Figure 3).

Thus, the number of tiles starting with blue dominoes is given by $p_{n-4}$, while the number of tiles starting with black squares followed by blue dominoes is given by $p_{n-5}$. The sum of such tiles is $p_{n-2}$.

Case 2: Let the two subsets be tiles that start with extended dominoes (i.e., tiles that do not start with black squares) and tiles that start with black squares followed by extended dominoes in an $n-3$-board, where the tiles are of size $n-3$. Consider a new set of tiles starting with extended gray dominoes of size 1 × 3 juxtaposed with tiles of size $n-3$ that do not start with black squares in union with the subset of tiles of size 1 × 1 that start with black squares by inserting gray extended dominoes of size 1 × 3 just after these squares. This union results in a tiling board of size n (Figure 4).

Thus, the number of tiles starting with extended gray dominoes is given by $p_{n-5}$, whereas the number of tiles starting with black squares followed by extended gray dominoes is given by $p_{n-6}$. The sum of such tiles is $p_{n-3}$.

Therefore, $p_n=p_{n-2}+p_{n-3}$, according to the addition principle of the independent analyzed cases, which satisfies the Padovan recurrence ($P_n=P_{n-2}+P_{n-3}$), with the initial conditions of $p_0=P_0$ and $p_1=P_1$. Thus, $p_n=P_n$. □

Some Padovan identities are associated with the notion of breaking cells, which was initially introduced by Benjamin and Quinn [12]. Thus, we have that a tile of size n is breakable in cell k if it is possible to decompose the tile into two: One part covering cells 1 to k and the other covering cells $k+1$ to n. On the other hand, the board in cell k is unbreakable if dominoes occupy cells k and $k+1$ or if extended dominoes occupy cells $k-1$, k and $k+1$ or $k, k+1$ and $k+2$.

2.2. The Combinatorial Models of Tridovan, Tetradovan and Z-Dovan Sequences

The Padovan sequence was studied by Seenukul et al. [16], who presented the following initial values: $P_0^{\prime }=1, P_1^{\prime }=0, P_2^{\prime }=1$. It can be noted that the aforementioned work presented a shifted variation of the Padovan sequence, which was primarily introduced by Richard Padovan. Likewise, this work defined a shifted Padovan sequence: $P_n^{\prime }$. The first terms of this shifted sequence are described in

Table 1. A description of some early terms in our shifted Padovan sequence.

${\mathit{P}}_0^{\prime }$	${\mathit{P}}_1^{\prime }$	${\mathit{P}}_2^{\prime }$	${\mathit{P}}_3^{\prime }$	${\mathit{P}}_4^{\prime }$	${\mathit{P}}_5^{\prime }$	${\mathit{P}}_6^{\prime }$	${\mathit{P}}_7^{\prime }$	${\mathit{P}}_8^{\prime }$	${\mathit{P}}_9^{\prime }$
1	0	1	1	1	2	2	3	4	5

.

Thus, an n-board was considered with the following tile shapes: 1 × 1 black squares, 1 × 2 blue dominoes and extended 1 × 3 gray dominoes, all with a weight of 1. We emphasize that this rule is introduced and presented in this article for the first time (Section 2.1). In Figure 5, it can be seen the term $p_n^{\prime }$ denotes the number of tile shapes in the n-board; thus, by following the above rules, it can be determined that $p_n^{\prime }=P_n^{\prime }+P_{n-1}^{\prime }, n⩾0$.

Theorem 2.

For $n⩾0$, the possible tiling of a 1 × n board with black square, blue domino and extended gray domino tiles is given by:

$$p_n^{\prime }=P_n^{\prime }+P_{n-1}^{\prime },$$

where $p_n^{\prime }$ is the number of ways to fill in the 1 × n board and $P_n^{\prime }$ is the n-th term of the shifted Padovan sequence.

Proof of Theorem 2.

This theorem can be validated in a similar way to the proof of Theorem 1. □

Next, we explore some of the extensions of the Padovan sequence based on the work of Vieira and Alves [14] and Vieira et al. [15], which addressed the definitions of the Tridovan and Tetradovan sequences.

The Tridovan sequence ($T_n$) is an extension of the Padovan sequence that is a fourth-order sequence and has a recurrence relation given by $T_n=T_{n-2}+T_{n-3}+T_{n-4}, n⩾4$, with the respective initial values of $T_0=1, T_1=0, T_2=1, T_3=1$. The first terms in the Tridovan sequence are shown in

Table 2. A description of some of the initial terms in the Tridovan sequence.

${\mathit{T}}_0$	${\mathit{T}}_1$	${\mathit{T}}_2$	${\mathit{T}}_3$	${\mathit{T}}_4$	${\mathit{T}}_5$	${\mathit{T}}_6$	${\mathit{T}}_7$	${\mathit{T}}_8$	${\mathit{T}}_9$
1	0	1	1	2	2	4	5	8	11

.

Therefore, following the indications provided by Mehdaoui (2021) [17], a one-dimensional n-board was considered and the following tile shapes were considered: 1 × 1 black squares, 1 × 2 blue dominoes, extended 1 × 3 gray dominoes and double 1 × 4 green dominoes, all with a weight of 1. In Figure 6, it is possible to note that the term $t_n$ is the number of tile shapes in the n-board; thus, by following the aforementioned rules, it can be determined that $t_n=T_n+T_{n-1}, n⩾0$. Accordingly, we obtained the following theorem.

Theorem 3.

For $n⩾0$, the possible tiling of a 1 × n board with black square, blue domino, extended gray domino and double green domino tiles is given by:

$$t_n=T_n+T_{n-1},$$

where $t_n$ is the number of ways to fill in the 1 × n board and $T_n$ is the n-th term of the Tridovan sequence.

Proof of Theorem 3.

This theorem can be verified in a similar way to the proof of Theorem 1. We leave the details to the reader. □

In

Table 3. A description of some of the initial terms in the Tetradovan sequence.

${\mathit{T}\mathit{e}}_0$	${\mathit{T}\mathit{e}}_1$	${\mathit{T}\mathit{e}}_2$	${\mathit{T}\mathit{e}}_3$	${\mathit{T}\mathit{e}}_4$	${\mathit{T}\mathit{e}}_5$	${\mathit{T}\mathit{e}}_6$	${\mathit{T}\mathit{e}}_7$	${\mathit{T}\mathit{e}}_8$	${\mathit{T}\mathit{e}}_9$
1	0	1	1	2	3	4	7	10	16

, we consider the recurrent Tetradovan sequence, as defined in the work of Vieira and Alves [14] and Vieira et al. [15], given by $T{e}_n=T{e}_{n-2}+T{e}_{n-3}+T{e}_{n-4}+T{e}_{n-5}, n⩾5$, with the respective initial values of $T{e}_0=1, T{e}_1=0, T{e}_2=1, T{e}_3=1, T{e}_4=2$.

We considered a one-dimensional n-board and the following tile shapes: 1 × 1 black squares, 1 × 2 blue dominoes, extended 1 × 3 gray dominoes, double 1 × 4 green dominoes and extended double 1 × 5 yellow dominoes, all with a weight of 1. In Figure 7, it is possible to note that the term $t{e}_n$ is the number of tile shapes in the n-board; thus, by following the rules presented in Section 2.1, we can determine that $t{e}_n=T{e}_n+T{e}_{n-1}, n⩾2$. Accordingly, we obtained the following theorem.

Theorem 4.

For $n⩾0$, the possible tiling of a 1 × n board with black square, blue domino, extended gray domino, double green domino and extended double yellow domino tiles is given by:

$$t{e}_n=T{e}_n+T{e}_{n-1},$$

where $t{e}_n$ is the number of ways to fill in the 1 × n board and $T{e}_n$ is the n-th term of the Tetradovan sequence.

Proof of Theorem 4.

This theorem can be verified in a similar way to the proof of Theorem 1. We leave the details to the reader. □

The generalization of the Padovan sequence, called Z-dovan, was studied by Vieira [5], in which the generalized recurrent sequence was defined as ${\displaystyle Z_{n+z}=\sum _{i=0}^{z-2}{Z}_{n+i}}$, where $n⩾z$, $n\in \mathbb{N}$, $Z=z-1$ and Z represents the n-th term of the Z-dovan sequence.

Thus, a one-dimensional n-board and the following tile shapes were considered: 1 × 1 black squares, 1 × 2 blue dominoes, extended 1 × 3 gray dominoes, double 1 × 4 green dominoes, extended double 1 × 5 yellow dominoes and 1 × z orange square, all with a weight of 1. In Figure 8, it is possible to note that the term $z_n$ is the number of tile shapes in the n-board; thus, by following the rules presented in Section 2.1, we can determine that $z_n=Z_n+Z_{n-1}, n⩾0$. It is noteworthy that the generalized Z-dovan tiling originated from the modified Padovan sequence or considering the original Padovan sequence, the generalization originated from the Tridovan sequence.

Corollary 1.

For $n⩾0$, the possible tiling of a 1 × n board with 1 × 1 black square, 1 × 2 blue domino, extended 1 × 3 gray domino, double 1 × 4 green domino, extended double 1 × 5 yellow dominoes and 1 × z orange square tiles is given by:

$$z_n=Z_n+Z_{n-1},$$

where $z_n$ is the number of ways to fill in the 1 × n board and $Z_n$ is the n-th term of the Z-dovan sequence.

3. Conclusions

Due to the broad range of scenarios and the interest in research involving all forms of the generalization of linear and recurrent sequences, extensions of the Padovan sequence are fundamental contributions to this research. On the other hand, the combinatorial approach has been presented as an important factor regarding advances in research into recurrent sequences. Thus, the combinatorial study of the Padovan sequence was introduced by defining boards.

Correlated with the Fibonacci sequence, the initial terms of the Padovan sequence that resulted from the combinatorial study of Tridovan, Tetradovan and Z-dovan sequences were presented in this work via our Padovan combinatorial tiling model. We presented a combinatorial approach to the study of the Padovan sequence and its extensions as the main result of this work, which enables the generalization of this sequence.