Hyperbolic B-Spline Function-Based Differential Quadrature Method for the Approximation of 3D Wave Equations
Abstract
1. Introduction
2. The Hyperbolic B-Spline Differential Quadrature Method
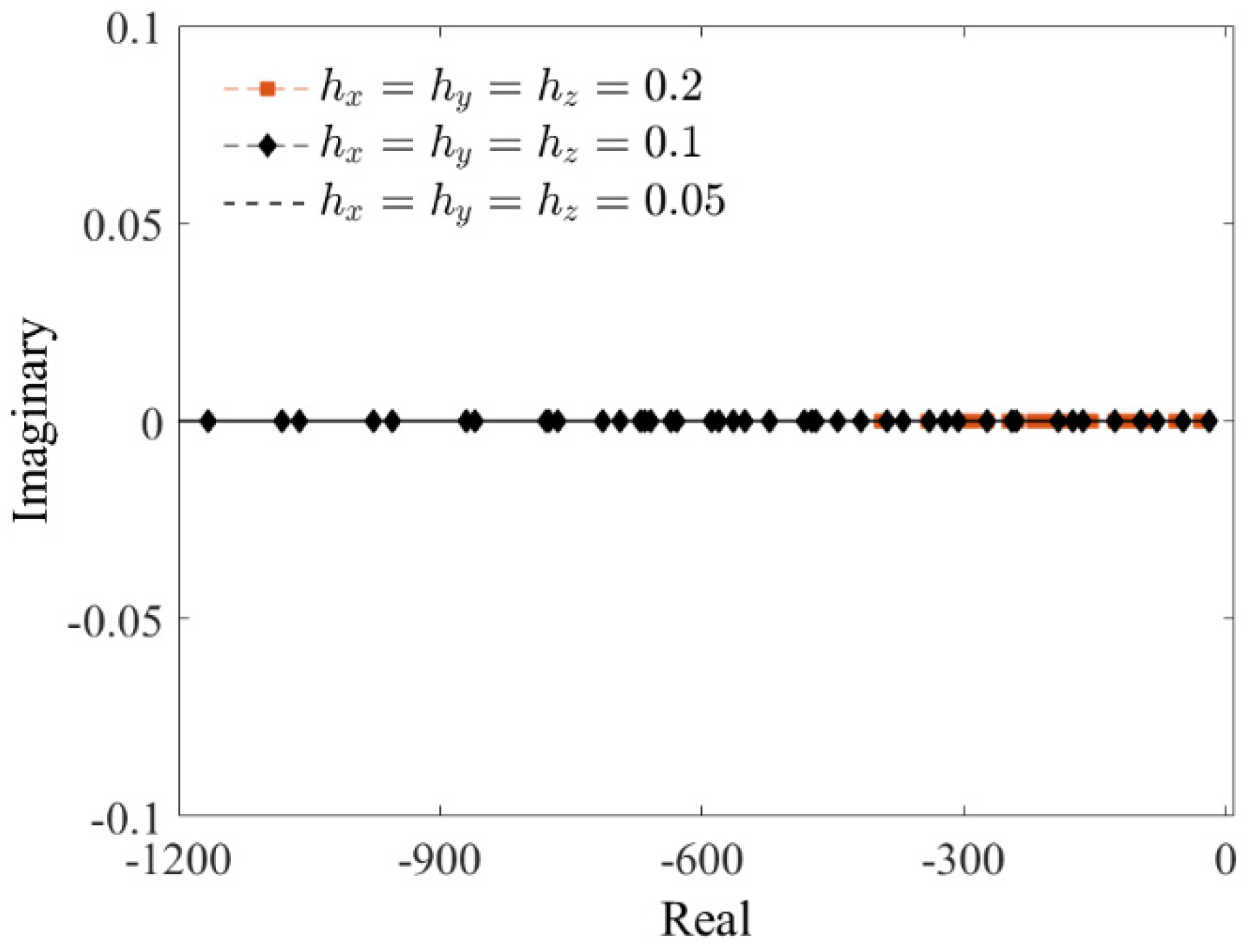
3. Stability Analysis
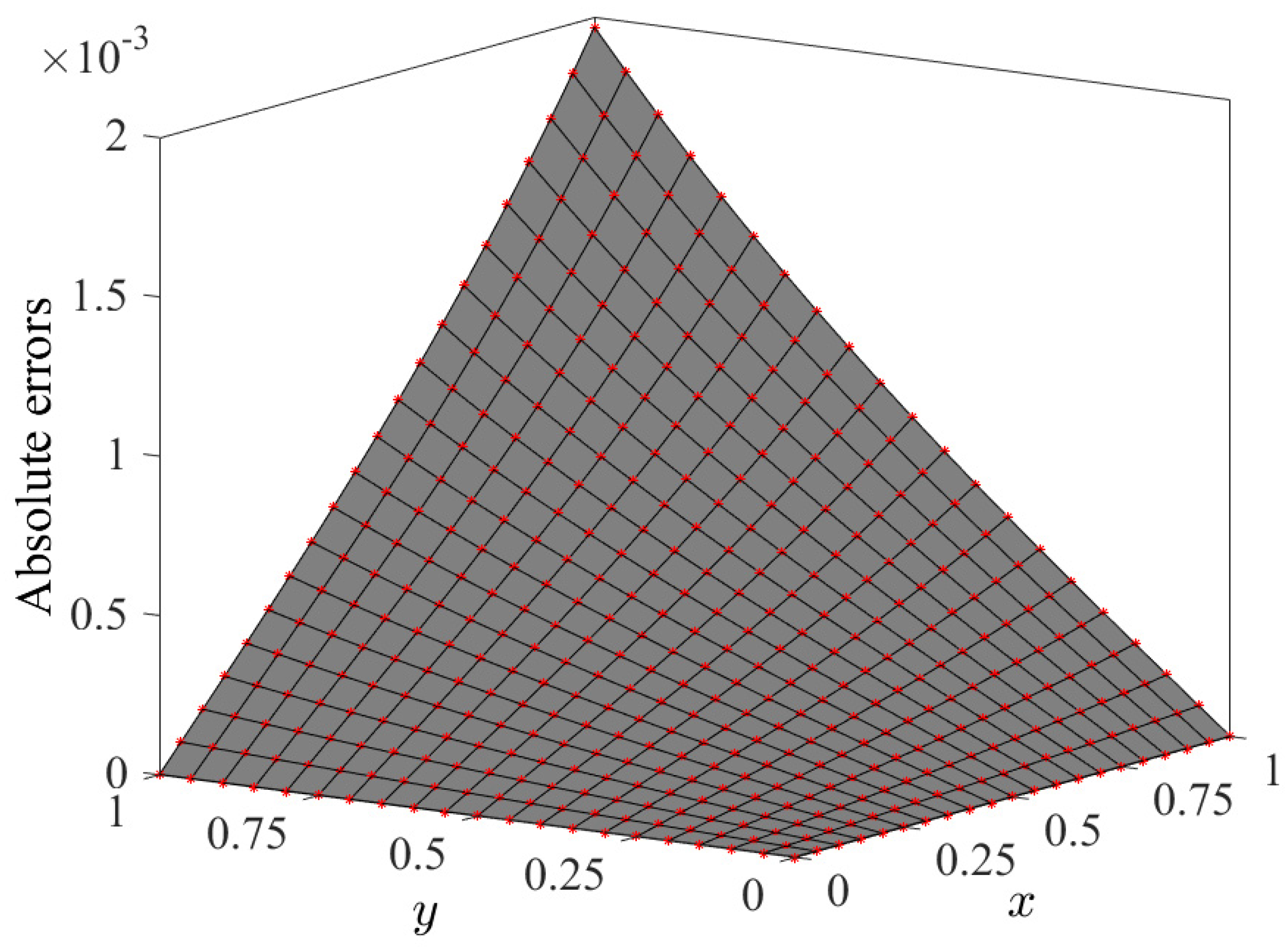
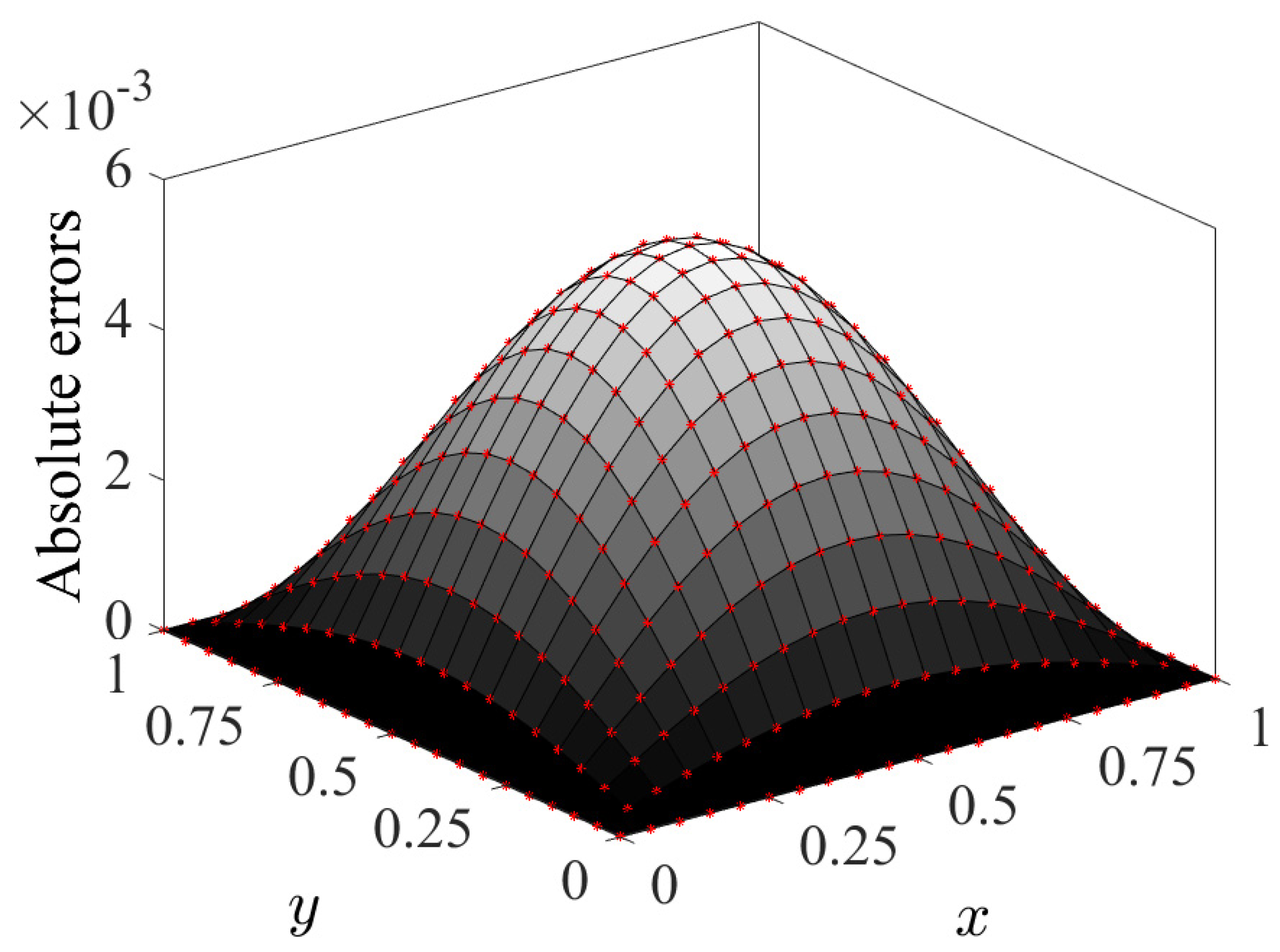
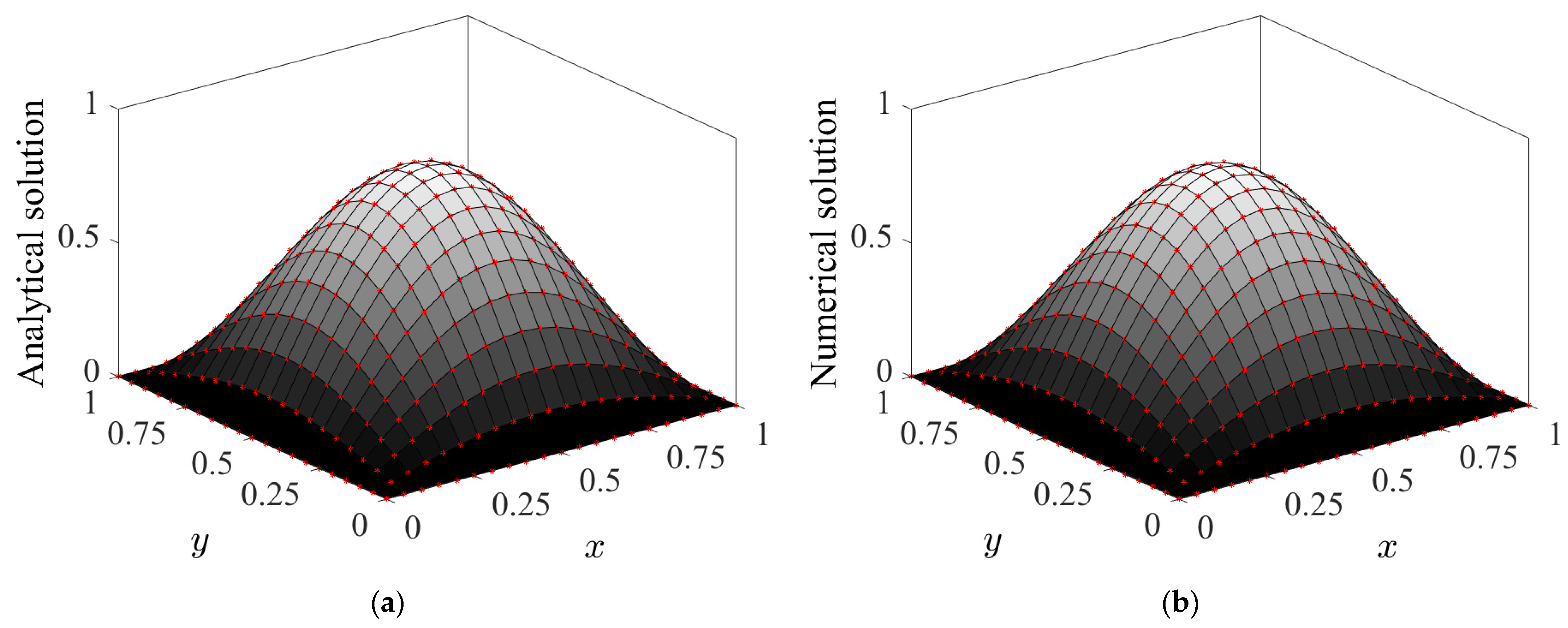
4. Computational Results
Computational Complexity
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, H.; Zhou, H.; Jiang, S.; Rao, Y. Fractional Laplacian viscoacoustic wave equation low-rank temporal extrapolation. IEEE Access 2019, 99, 1–11. [Google Scholar] [CrossRef]
- Li, P.-W.; Fan, C.-M. Generalized finite difference method for two-dimensional shallow water equations. Eng. Anal. Bound. Elem. 2017, 80, 58–71. [Google Scholar] [CrossRef]
- Baccouch, M.; Temimi, H. A high-order space-time ultra-weak discontinuous Galerkin method for the second-order wave equation in one space dimension. J. Comput. Appl. Math. 2021, 389, 113331. [Google Scholar] [CrossRef]
- Yang, S.P.; Liu, F.W.; Feng, L.B.; Turner, I. A novel finite volume method for the nonlinear two-sided space distributed-order diffusion equation with variable coefficients. J. Comput. Appl. Math. 2021, 388, 113337. [Google Scholar] [CrossRef]
- Xie, X.; Liu, Y.J. An adaptive model order reduction method for boundary element-based multi-frequency acoustic wave problems. Comput. Meth. Appl. Mech. Engin. 2021, 373, 113532. [Google Scholar] [CrossRef]
- Takekawa, J.; Mikada, H. A mesh-free finite-difference method for elastic wave propagation in the frequency-domain. Comput. Geosci. 2018, 118, 65–78. [Google Scholar] [CrossRef]
- Gao, L.F.; Keyes, D. Combining finite element and finite difference methods for isotropic elastic wave simulations in an energy-conserving manner. J. Comput. Phys. 2019, 378, 665–685. [Google Scholar] [CrossRef]
- Ranocha, H.; Mitsotakis, D.; Ketcheson, D.I. A broad class of conservative numerical methods for dispersive wave equations. Commun. Comput. Phys. 2021, 29, 979–1029. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, J.; Ahmad, I.; Farooq, A.; Ahmad, H. A novel meshfree strategy for a viscous wave equation with variable coefficients. Front. Phys. 2021, 9, 359. [Google Scholar]
- Bakushinsky, A.B.; Leonov, A.S. Numerical solution of a three-dimensional coefficient inverse problem for the wave equation with integral data in a cylindrical domain. Numer. Analys. Appl. 2019, 12, 311–325. [Google Scholar] [CrossRef]
- Dehghan, M. On the solution of an initial-boundary value problem that combines Neumann and integral condition for the wave equation. Numer. Meth. Part. Diff. Eq. 2005, 21, 24–40. [Google Scholar] [CrossRef]
- Dehghan, M. Finite difference procedures for solving a problem arising in modeling and design of certain optoelectronic devices. Math. Comput. Simul. 2006, 71, 16–30. [Google Scholar] [CrossRef]
- Mohanty, R.K.; Gopal, V. A new off-step high order approximation for the solution of three-space dimensional nonlinear wave equations. Appl. Math. Model. 2013, 37, 2802–2815. [Google Scholar] [CrossRef]
- Titarev, V.A.; Toro, E.F. ADER schemes for three-dimensional non-linear hyperbolic systems. J. Comput. Phys. 2005, 204, 715–736. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, D.; Cheng, Y.; Liew, K. The improved element-free Galerkin method for three-dimensional wave equation. Acta Mech. Sin. 2012, 28, 808–818. [Google Scholar] [CrossRef]
- Shivanian, E. Meshless local Petrov-Galerkin (MLPG) method for three-dimensional nonlinear wave equations via moving least squares approximation. Eng. Anal. Bound. Elem. 2015, 50, 249–257. [Google Scholar] [CrossRef]
- Shukla, H.S.; Tamsir, M.; Jiwari, R.; Srivastava, V.K. A numerical algorithm for computation modelling of 3D nonlinear wave equations based on exponential modified cubic B-spline differential quadrature method. Int. J. Comput. Math. 2018, 95, 752–766. [Google Scholar] [CrossRef]
- Bellman, R.; Kashef, B.G.; Casti, J. Differential quadrature: A technique for the rapid solution of nonlinear differential equations. J. Comput. Phy. 1972, 10, 40–52. [Google Scholar] [CrossRef]
- Korkmaz, A.; Dag, I. Shock wave simulations using sinc differential quadrature method. Eng. Comput. 2011, 28, 654–674. [Google Scholar] [CrossRef]
- Shu, C.; Chew, Y.T. Fourier expansion-based differential quadrature and its application to Helmholtz eigenvalue problems. Commun. Numer. Methods Eng. 1997, 13, 643–653. [Google Scholar] [CrossRef]
- Shu, C.; Xue, H. Explicit computation of weighting coefficients in the harmonic differential quadrature. J. Sound Vib. 1997, 204, 549–555. [Google Scholar] [CrossRef]
- Bashan, A.; Karakoc, S.B.G.; Geyikli, T. Approximation of the KdVB equation by the quintic B-spline differential quadrature method. Kuwait J. Sci. 2015, 42, 67–92. [Google Scholar]
- Korkmaz, A.; Dag, I. Cubic B-spline differential quadrature methods and stability for Burgers equation. Eng. Comput. 2013, 30, 320–344. [Google Scholar] [CrossRef]
- Shukla, H.S.; Tamsir, M.; Srivastava, V.K.; Kumar, J. Numerical solution of two dimensional coupled viscous Burger equation using modified cubic B-spline differential quadrature method. AIP Adv. 2014, 4, 117134. [Google Scholar] [CrossRef]
- Shukla, H.S.; Tamsir, M.; Srivastava, V.K. Numerical simulation of two dimensional sine-Gordon solitons using modified cubic B-spline differential quadrature method. AIP Adv. 2015, 5, 017121. [Google Scholar] [CrossRef]
- Korkmaz, A.; Dag, I. Cubic B-spline differential quadrature methods for the advection-diffusion equation. Int. J. Numer. Meth. Heat Fluid Flow 2012, 22, 1021–1036. [Google Scholar] [CrossRef]
- Tamsir, M.; Srivastava, V.K.; Jiwari, R. An algorithm based on exponential modified cubic B-spline differential quadrature method for nonlinear Burgers’ equation. Appl. Math. Comput. 2016, 290, 111–124. [Google Scholar] [CrossRef]
- Jiwari, R.; Pandit, S.; Mittal, R.C. Numerical simulation of two-dimensional sine-Gordon solitons by differential quadrature method. Comput. Phys. Commun. 2012, 183, 600–616. [Google Scholar] [CrossRef]
- Korkmaz, A.; Dag, I. Numerical simulations of boundary-forced RLW equation with cubic B-spline-based differential quadrature methods. Arab. J. Sci. Eng. 2013, 38, 1151–1160. [Google Scholar] [CrossRef]
- Korkmaz, A.; Dag, I. Quartic and quintic B-spline methods for advection diffusion equation. Appl. Math. Comput. 2016, 274, 208–219. [Google Scholar] [CrossRef]
- Jiwari, R. Lagrange interpolation and modified cubic B-spline differential quadrature methods for solving hyperbolic partial differential equations with Dirichlet and Neumann boundary conditions. Comput. Phys. Commun. 2015, 193, 55–65. [Google Scholar] [CrossRef]
- Lin, J.; Reutskiy, S. A cubic B-spline semi-analytical algorithm for simulation of 3D steady-state convection-diffusion-reaction problems. Appl. Math. Comput. 2020, 371, 124944. [Google Scholar] [CrossRef]
- Ali, I.; Seadawy, A.R.; Rizvi, S.T.R.; Younis, M.; Ali, K. Conserved quantities along with Painlevé analysis and optical solitons for the nonlinear dynamics of Heisenberg ferromagnetic spin chains model. Int. J. Mod. Phys. B 2020, 34, 2050283. [Google Scholar] [CrossRef]
- Lu, D.; Seadwy, A.R.; Iqbal, M. Mathematical methods via construction of traveling and solitary wave solutions of three coupled system of nonlinear partial differential equations and their applications. Res. Phys. 2018, 11, 1161–1171. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Khalid, K.A.; Nuruddeen, R.I. A variety of soliton solutions for the fractional Wazwaz-Benjamin-Bona-Mahony equations. Res. Phys. 2019, 12, 2234–2241. [Google Scholar]
- Akram, U.; Seadawy, A.R.; Rizvi, S.T.R.; Younis, M.; Althobaiti, S.; Sayed, S. Traveling wave solutions for the fractional Wazwaz–Benjamin–Bona–Mahony model in arising shallow water waves. Res. Phys. 2021, 20, 103725. [Google Scholar] [CrossRef]
- Ahlberg, J.H.; Nilson, E.N.; Walsh, J.L. The Theory of Splines and Their Applications; Academic Press: New York, NY, USA, 1967. [Google Scholar]
- Lu, C. Error analysis for interpolating complex cubic splines with deficiency 2. J. Approx. Theory 1982, 36, 183–196. [Google Scholar] [CrossRef][Green Version]
- Kapoor, M.; Joshi, V. Numerical approximation of 1D and 2D non-linear Schrödinger equations by implementing modified cubic Hyperbolic B-spline based DQM. Part. Diff. Eq. Appl. Math. 2021, 4, 100076. [Google Scholar] [CrossRef]
- Shu, C. Differential Quadrature and its Application in Engineering, 1st ed.; Athenaeum Press Ltd.: Newcastle Upon Tyne, UK, 2000. [Google Scholar]
- Gottlieb, S.; Ketcheson, D.I.; Shu, C.W. High order strong stability preserving time discretizations. J. Sci. Comput. 2009, 38, 251–289. [Google Scholar] [CrossRef]



| 0 | 0 | ||||
| 0 | 0 | 0 |
| Present Method | EFG Method [16] | MLPG Method [16] | Expo-MCBDQM [17] | |
|---|---|---|---|---|
| 0.1 | 9.131 × 10−7 | 1.361376 × 10−1 | 6.389040 × 10−4 | 1.013 × 10−6 |
| 0.2 | 9.126 × 10−7 | 1.108673 × 10−1 | 1.621007 × 10−3 | 1.666 × 10−6 |
| 0.3 | 9.751 × 10−7 | 9.031794 × 10−2 | 2.069397 × 10−3 | 1.725 × 10−6 |
| 0.4 | 9.357 × 10−7 | 7.555177 × 10−2 | 1.851491 × 10−3 | 1.498 × 10−6 |
| 0.5 | 9.263 × 10−7 | 6.113317 × 10−2 | 1.406413 × 10−3 | 1.196 × 10−6 |
| 0.6 | 8.105 × 10−7 | 5.076050 × 10−2 | 1.120239 × 10−3 | 9.059 × 10−7 |
| 0.7 | 6.102 × 10−7 | 4.276296 × 10−2 | 8.762877 × 10−4 | 7.061 × 10−7 |
| 0.8 | 4.458 × 10−7 | 3.416178 × 10−2 | 5.762842 × 10−4 | 5.566 × 10−7 |
| 0.9 | 3.614 × 10−7 | 3.072394 × 10−2 | 7.778958 × 10−4 | 4.758 × 10−7 |
| 1.0 | 3.326 × 10−7 | 2.562088 × 10−2 | 8.638225 × 10−4 | 4.417 × 10−7 |
| Present Method | EFG Method [16] | MLPG Method [17] | Expo-MCBDQM [17] | |
|---|---|---|---|---|
| 0.1 | 4.472 × 10−6 | 1.653265 × 100 | 2.777931 × 10−3 | 5.667 × 10−6 |
| 0.2 | 8.511 × 10−6 | 1.005632 × 100 | 8.477482 × 10−3 | 9.701 × 10−6 |
| 0.3 | 2.23 × 10−6 | 9.786343 × 10−1 | 1.352534 × 10−2 | 1.231 × 10−5 |
| 0.4 | 5.02 × 10−6 | 7.456237 × 10−1 | 1.583307 × 10−2 | 1.512 × 10−5 |
| 0.5 | 1.143 × 10−5 | 6.213675 × 10−1 | 1.550351 × 10−2 | 1.824 × 10−5 |
| 0.6 | 1.062 × 10−5 | 4.354421 × 10−1 | 1.367202 × 10−2 | 2.222 × 10−5 |
| 0.7 | 1.231 × 10−5 | 1.345213 × 10−1 | 1.052578 × 10−2 | 2.570 × 10−5 |
| 0.8 | 1.324 × 10−5 | 9.973233 × 10−2 | 6.216680 × 10−3 | 2.866 × 10−5 |
| 0.9 | 2.014 × 10−5 | 7.132423 × 10−2 | 5.280951 × 10−3 | 3.117 × 10−5 |
| 1.0 | 2.1025 × 10−5 | 6.124572 × 10−2 | 2.276681 × 10−3 | 3.329 × 10−5 |
| Present Method | EFG Method [16] | MLPG Method [16] | Expo-MCBDQM [17] | |
|---|---|---|---|---|
| 0.1 | 1.673 × 10−7 | 1.435666 × 10−3 | 8.903029 × 10−5 | 2.887 × 10−7 |
| 0.2 | 2.481 × 10−7 | 3.867576 × 10−3 | 9.910264 × 10−5 | 1.257 × 10−6 |
| 0.3 | 1.522 × 10−6 | 5.033494 × 10−3 | 1.590358 × 10−4 | 2.944 × 10−6 |
| 0.4 | 4.137 × 10−6 | 7.655177 × 10−3 | 3.776687 × 10−4 | 5.348 × 10−6 |
| 0.5 | 7.465 × 10−6 | 9.119769 × 10−3 | 4.781290 × 10−4 | 8.787 × 10−6 |
| 0.6 | 3.304 × 10−6 | 1.034540 × 10−2 | 6.416380 × 10−4 | 1.361 × 10−5 |
| 0.7 | 1.007 × 10−5 | 3.279875 × 10−2 | 8.809498 × 10−4 | 2.029 × 10−5 |
| 0.8 | 1.716 × 10−5 | 5.233178 × 10−2 | 9.279331 × 10−4 | 2.918 × 10−5 |
| 0.9 | 3.014 × 10−5 | 6.072234 × 10−2 | 1.059260 × 10−4 | 4.049 × 10−5 |
| 1.0 | 4.221 × 10−5 | 7.545088 × 10−2 | 1.529316 × 10−3 | 5.432 × 10−5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tamsir, M.; Meetei, M.Z.; Msmali, A.H. Hyperbolic B-Spline Function-Based Differential Quadrature Method for the Approximation of 3D Wave Equations. Axioms 2022, 11, 597. https://doi.org/10.3390/axioms11110597
Tamsir M, Meetei MZ, Msmali AH. Hyperbolic B-Spline Function-Based Differential Quadrature Method for the Approximation of 3D Wave Equations. Axioms. 2022; 11(11):597. https://doi.org/10.3390/axioms11110597
Chicago/Turabian StyleTamsir, Mohammad, Mutum Zico Meetei, and Ahmed H. Msmali. 2022. "Hyperbolic B-Spline Function-Based Differential Quadrature Method for the Approximation of 3D Wave Equations" Axioms 11, no. 11: 597. https://doi.org/10.3390/axioms11110597
APA StyleTamsir, M., Meetei, M. Z., & Msmali, A. H. (2022). Hyperbolic B-Spline Function-Based Differential Quadrature Method for the Approximation of 3D Wave Equations. Axioms, 11(11), 597. https://doi.org/10.3390/axioms11110597






