A Reliable Technique for Solving Fractional Partial Differential Equation
Abstract
1. Introduction
2. Preliminaries
- 1.
- 2.
- 3.
3. General Methodology of LRPSM
- and for each .
- We will now solve the system below recursively in order to define the coefficient functions .
4. Numerical Examples
4.1. Problem
4.2. Problem
4.3. Problem
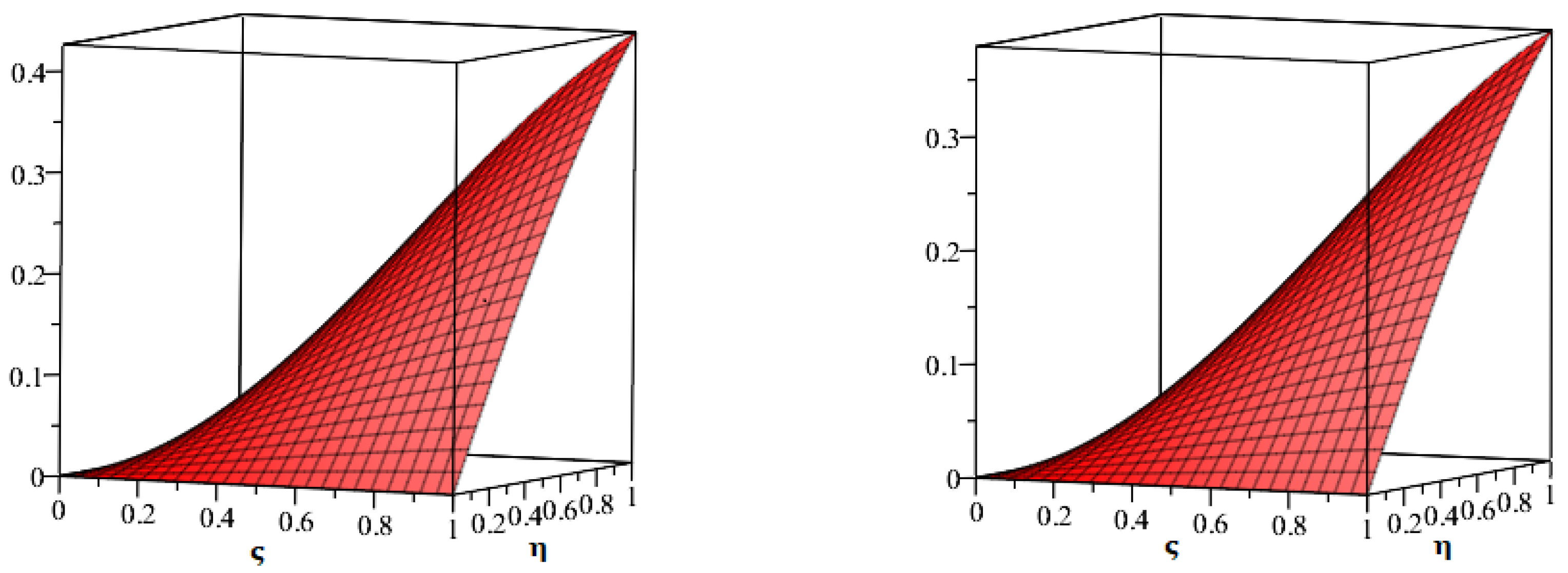
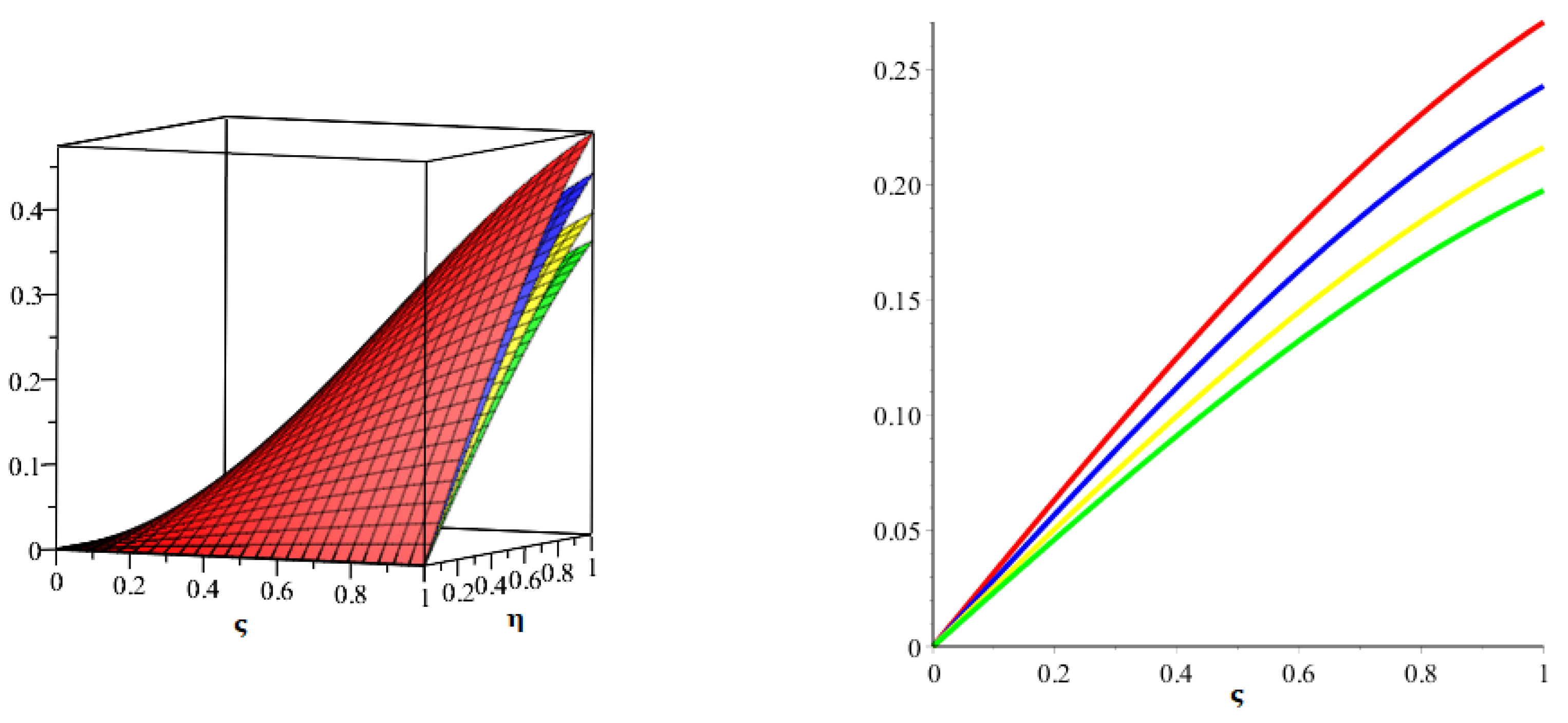
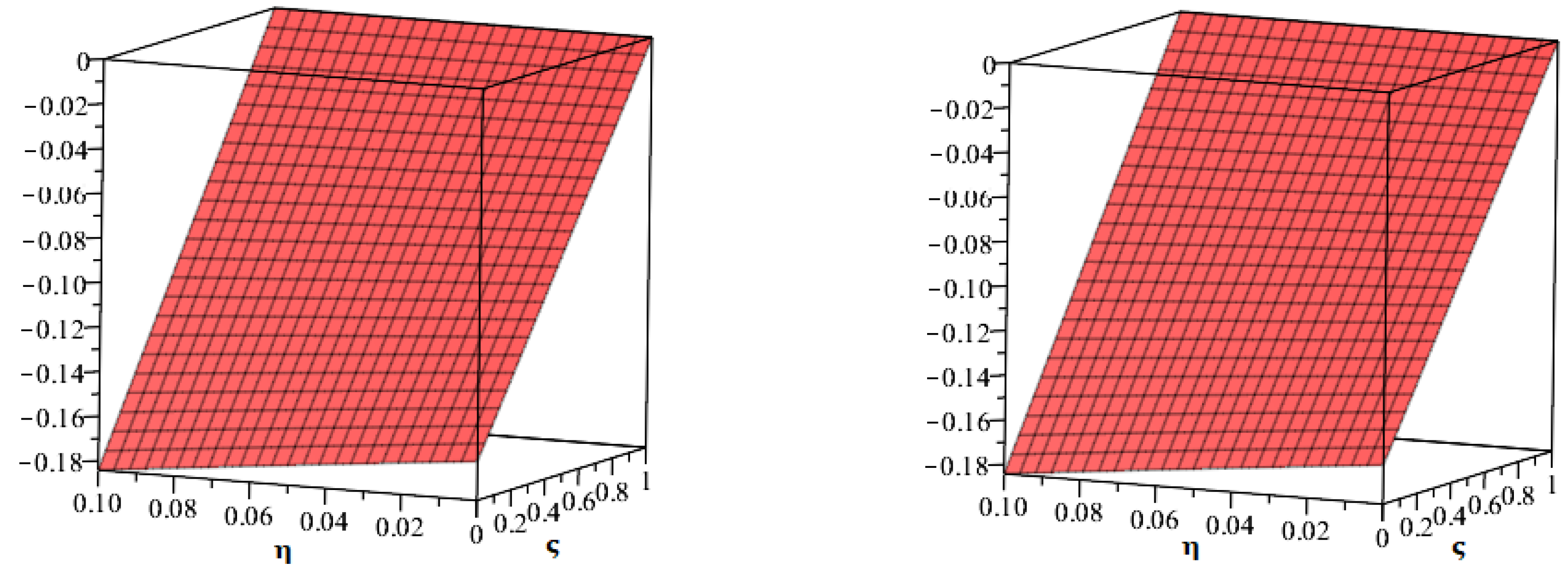
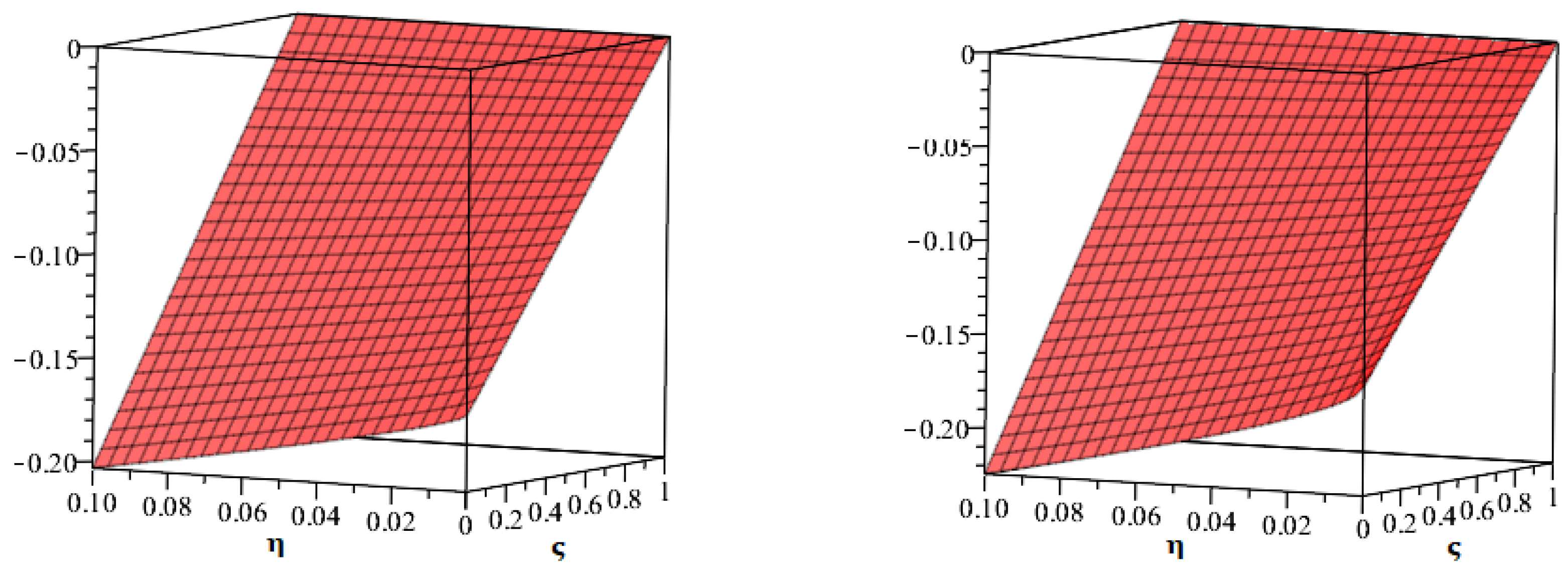
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; North-Holland Mathematics Studies; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Ablowitz, M.J.; Clarkson, P.A. Solitons, Nonlinear Evolution Equations and Inverse Scattering; Cambridge University Press: New York, NY, USA, 1991. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach: Yverdon, Switzerland, 1993. [Google Scholar]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent-II. Geophys. J. Int. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Debnath, L. Recent applications of fractional calculus to science and engineering. Int. J. Math. Math. Sci. 2003, 2003, 3413–3442. [Google Scholar] [CrossRef]
- Jafari, H.; Seifi, S. Solving a system of nonlinear fractional partial differential equations using homotopy analysis method. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 1962–1969. [Google Scholar] [CrossRef]
- Kemple, S.; Beyer, H. Global and Causal Solutions of Fractional Differential Equations. In Proceedings of the 2nd International Workshop on Transform Methods and Special Functions (SCTP), Varna, Bulgaria, 23–30 August 1996; p. 210. [Google Scholar]
- Oldham, K.B.; Spanier, J. The fractional calculus, academic press, new york. In The Fractional Calculus; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Momani, S.; Shawagfeh, N. Decomposition method for solving fractional Riccati differential equations. Appl. Math. Comput. 2006, 182, 1083–1092. [Google Scholar] [CrossRef]
- Zhang, L.; Rahman, M.U.; Ahmad, S.; Riaz, M.B.; Jarad, F. Dynamics of fractional order delay model of coronavirus disease. AIMS Math. 2022, 7, 4211–4232. [Google Scholar] [CrossRef]
- Shen, W.Y.; Chu, Y.M.; ur Rahman, M.; Mahariq, I.; Zeb, A. Mathematical analysis of HBV and HCV co-infection model under nonsingular fractional order derivative. Results Phys. 2021, 28, 104582. [Google Scholar] [CrossRef]
- Zhang, L.; ur Rahman, M.; Arfan, M.; Ali, A. Investigation of mathematical model of transmission co-infection TB in HIV community with a non-singular kernel. Results Phys. 2021, 28, 104559. [Google Scholar] [CrossRef]
- Rahman, M.U.; Ahmad, S.; Arfan, M.; Akgül, A.; Jarad, F. Fractional Order Mathematical Model of Serial Killing with Different Choices of Control Strategy. Fractal Fract. 2022, 6, 162. [Google Scholar] [CrossRef]
- Xu, C.; ur Rahman, M.; Baleanu, D. On fractional-order symmetric oscillator with offset-boosting control. Nonlinear Anal. Model. Control 2022, 27, 994–1008. [Google Scholar] [CrossRef]
- Baleanu, D.; Wu, G.-C.; Zeng, S.-D. Chaos analysis and asymptotic stability of generalized Caputo fractional differential equations. Chaos Solitons Fractals 2017, 102, 99–105. [Google Scholar] [CrossRef]
- Sweilam, N.H.; Hasan, M.M.A.; Baleanu, D. New studies for general fractional financial models of awareness and trial advertising decisions. Chaos Solitons Fractals 2017, 104, 772–784. [Google Scholar] [CrossRef]
- Liu, D.Y.; Gibaru, O.; Perruquetti, W.; Laleg-Kirati, T.M. Fractional order differentiation by integration and error analysis in noisy environment. IEEE Trans. Autom. Control 2015, 60, 2945–2960. [Google Scholar] [CrossRef]
- Esen, A.; Sulaiman, T.A.; Bulut, H.; Baskonus, H.M. Optical solitons to the space-time fractional (1+1)-dimensional coupled nonlinear Schrödinger equation. Optik 2018, 167, 150–156. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.G.; Baskonus, H.M. New numerical surfaces to the mathematical model of cancer chemotherapy effect in Caputo fractional derivatives. Chaos 2019, 29, 013119. [Google Scholar] [CrossRef]
- Shah, N.A.; Agarwal, P.; Chung, J.D.; El-Zahar, E.R.; Hamed, Y.S. Analysis of optical solitons for nonlinear Schrodinger equation with detuning term by iterative transform method. Symmetry 2020, 12, 1850. [Google Scholar] [CrossRef]
- Prakash, A.; Veeresha, P.; Prakasha, D.G.; Goyal, M. A homotopy technique for fractional order multi-dimensional telegraph equation via Laplace transform. Eur. Phys. J. Plus 2019, 134, 1–18. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.G.; Baskonus, H.M. Novel simulations to the time-fractional Fisher’s equation. Math. Sci. 2019, 13, 33–42. [Google Scholar] [CrossRef]
- Almutlak, S.A.; Weera, W.; El-Tantawy, S.A.; El-Sherif, L.S. Fractional View Analysis of Swift-Hohenberg Equations by an Analytical Method and Some Physical Applications. Fractal Fract. 2022, 6, 524. [Google Scholar] [CrossRef]
- Alshehry, A.S.; Imran, M.; Khan, A.; Weera, W. Fractional View Analysis of Kuramoto-Sivashinsky Equations with Non-Singular Kernel Operators. Symmetry 2022, 14, 1463. [Google Scholar] [CrossRef]
- Shah, N.A.; Hamed, Y.S.; Abualnaja, K.M.; Chung, J.D.; Shah, R.; Khan, A. A comparative analysis of fractional-order kaup-kupershmidt equation within different operators. Symmetry 2022, 14, 986. [Google Scholar] [CrossRef]
- Shah, N.A.; Alyousef, H.A.; El-Tantawy, S.A.; Shah, R.; Chung, J.D. Analytical Investigation of Fractional-Order Korteweg-De-Vries-Type Equations under Atangana-Baleanu-Caputo Operator: Modeling Nonlinear Waves in a Plasma and Fluid. Symmetry 2022, 14, 739. [Google Scholar] [CrossRef]
- Çenesiz, Y.; Baleanu, D.; Kurt, A.; Tasbozan, O. New exact solutions of Burgers’ type equations with conformable derivative. Waves Random Complex Media 2017, 27, 103–116. [Google Scholar] [CrossRef]
- Nonlaopon, K.; Alsharif, A.M.; Zidan, A.M.; Khan, A.; Hamed, Y.S.; Shah, R. Numerical investigation of fractional-order Swift-Hohenberg equations via a Novel transform. Symmetry 2021, 13, 1263. [Google Scholar] [CrossRef]
- Shah, N.A.; El-Zahar, E.R.; Akgül, A.; Khan, A.; Kafle, J. Analysis of Fractional-Order Regularized Long-Wave Models via a Novel Transform. J. Funct. Spaces 2022, 2022, 2754507. [Google Scholar] [CrossRef]
- Özkan, O.; Kurt, A. On conformable double Laplace transform. Opt. Quantum Electron. 2018, 50, 103. [Google Scholar] [CrossRef]
- Sunthrayuth, P.; Alyousef, H.A.; El-Tantawy, S.A.; Khan, A.; Wyal, N. Solving Fractional-Order Diffusion Equations in a Plasma and Fluids via a Novel Transform. J. Funct. Spaces 2022, 2022, 1899130. [Google Scholar] [CrossRef]
- Qin, Y.; Khan, A.; Ali, I.; Al Qurashi, M.; Khan, H.; Shah, R.; Baleanu, D. An efficient analytical approach for the solution of certain fractional-order dynamical systems. Energies 2020, 13, 2725. [Google Scholar] [CrossRef]
- Hashemi, M.S. Invariant subspaces admitted by fractional differential equations with conformable derivatives. Chaos Solitons Fractals 2018, 107, 161–169. [Google Scholar] [CrossRef]
- Zidan, A.M.; Khan, A.; Shah, R.; Alaoui, M.K.; Weera, W. Evaluation of time-fractional Fisher’s equations with the help of analytical methods. AIMS Math. 2022, 7, 18746–18766. [Google Scholar] [CrossRef]
- Alaoui, M.K.; Fayyaz, R.; Khan, A.; Shah, R.; Abdo, M.S. Analytical investigation of Noyes-Field model for time-fractional Belousov-Zhabotinsky reaction. Complexity 2021, 2021, 3248376. [Google Scholar] [CrossRef]
- Liu, J.; Hou, G. Numerical solutions of the space-and time-fractional coupled Burgers equations by generalized differential transform method. Appl. Math. Comput. 2011, 217, 7001–7008. [Google Scholar] [CrossRef]
- Sejdić, E.; Djurovixcx, I.; Stankovixcx, L. Fractional Fourier transform as a signal processing tool: An overview of recent developments. Signal Process. 2011, 91, 1351–1369. [Google Scholar] [CrossRef]
- Yusufoglu, E.; Bekir, A. Numerical simulations of the Boussinesq equation by He’s variational iteration method. Int. J. Comput. Math. 2009, 86, 676–683. [Google Scholar] [CrossRef]
- Özkan, O. Approximate analytical solutions of systems of fractional partial differential equations. Karaelmas Sci. Eng. J. 2017, 7, 63–67. [Google Scholar]
- Alderremy, A.A.; Aly, S.; Fayyaz, R.; Khan, A.; Shah, R.; Wyal, N. The Analysis of Fractional-Order Nonlinear Systems of Third Order KdV and Burgers Equations via a Novel Transform. Complexity 2022, 2022, 4935809. [Google Scholar] [CrossRef]
- Ahmad, E.-A. Adapting the Laplace transform to create solitary solutions for the nonlinear time-fractional dispersive PDEs via a new approach. Eur. Phys. J. Plus 2021, 136, 1–22. [Google Scholar]
- Areshi, M.; Khan, A.; Nonlaopon, K. Analytical investigation of fractional-order Newell-Whitehead-Segel equations via a novel transform. AIMS Math. 2022, 7, 6936–6958. [Google Scholar] [CrossRef]
- Arqub, O.A.; El-Ajou, A.; Momani, S. Construct and predicts solitary pattern solutions for nonlinear time-fractional dispersive partial differential equations. J. Comput. Phys. 2015, 293, 385–399. [Google Scholar] [CrossRef]
- Alquran, M.; Ali, M.; Alsukhour, M.; Jaradat, I. Promoted residual power series technique with Laplace transform to solve some time-fractional problems arising in physics. Results Phys. 2020, 19, 103667. [Google Scholar] [CrossRef]
- Maitama, S.; Abdullahi, I. A new analytical method for solving linear and nonlinear fractional partial differential equations. Progr. Fract. Differ. Appl. 2016, 2, 247–256. [Google Scholar] [CrossRef]

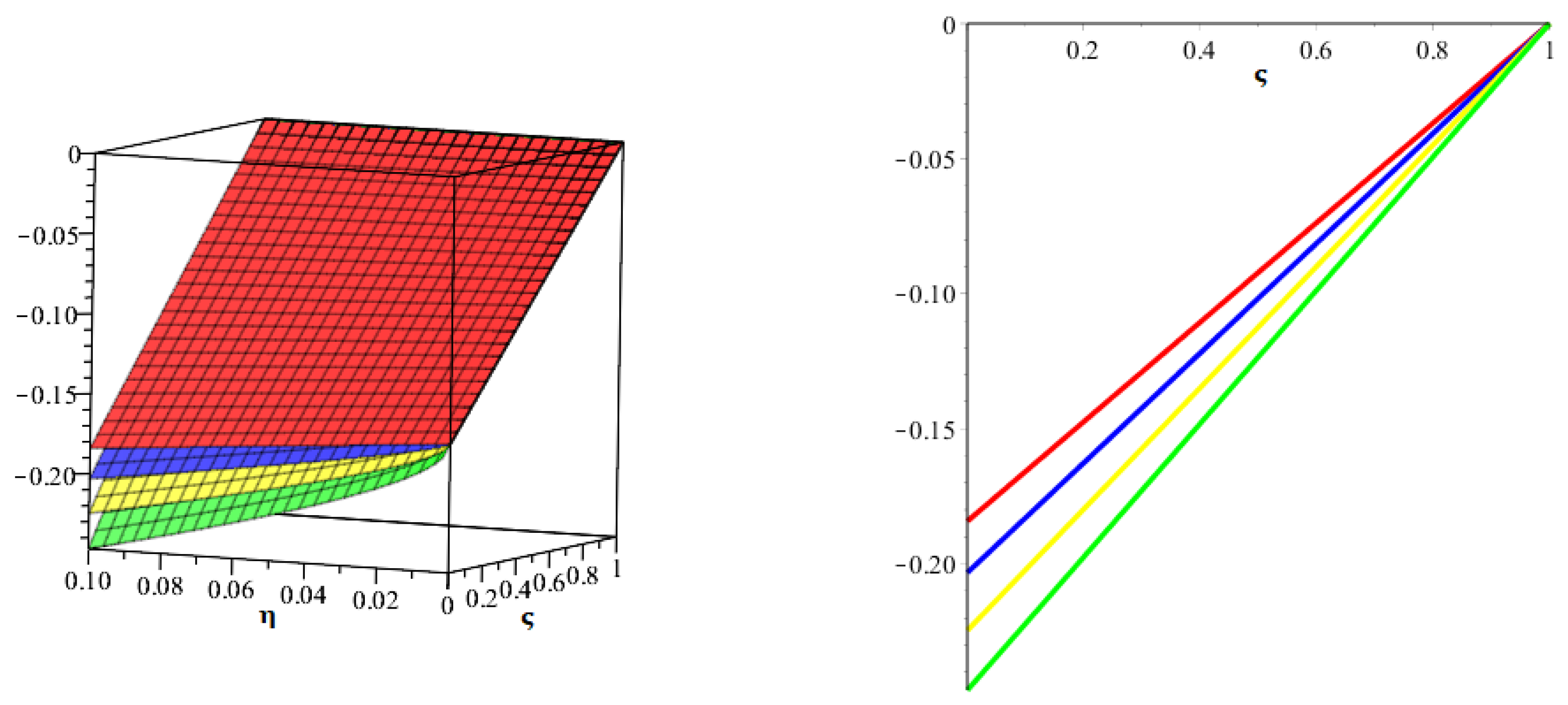

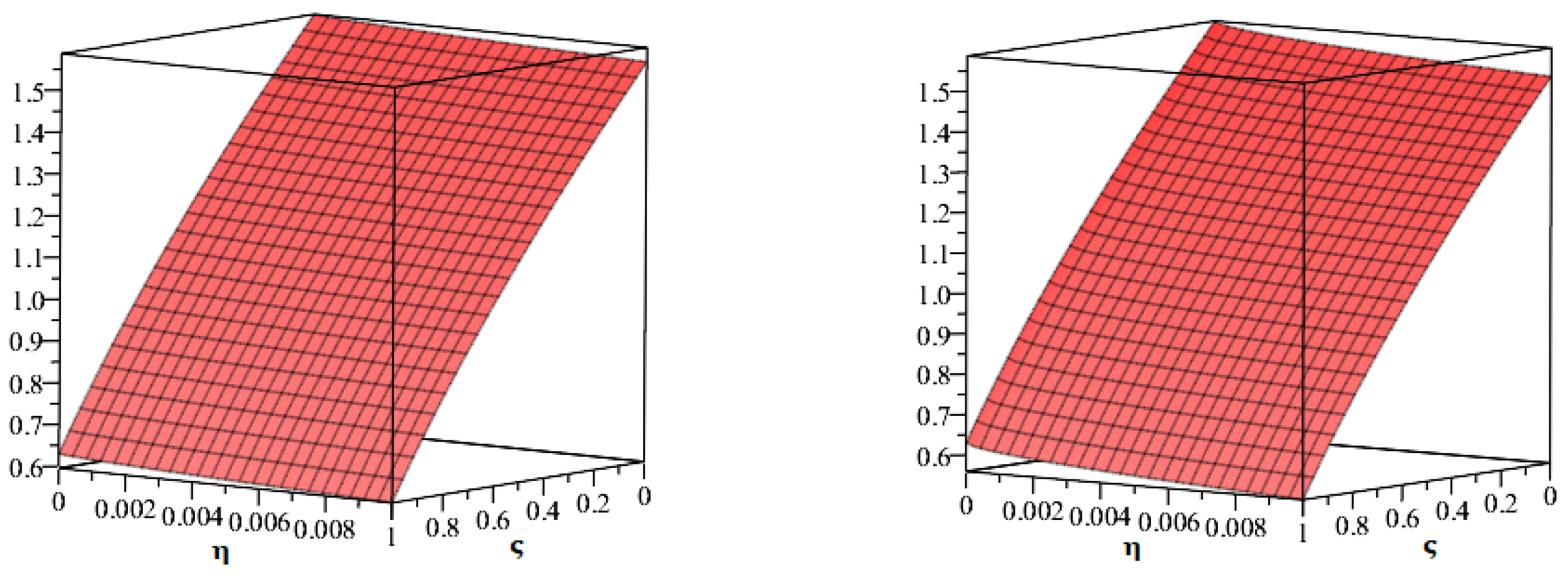
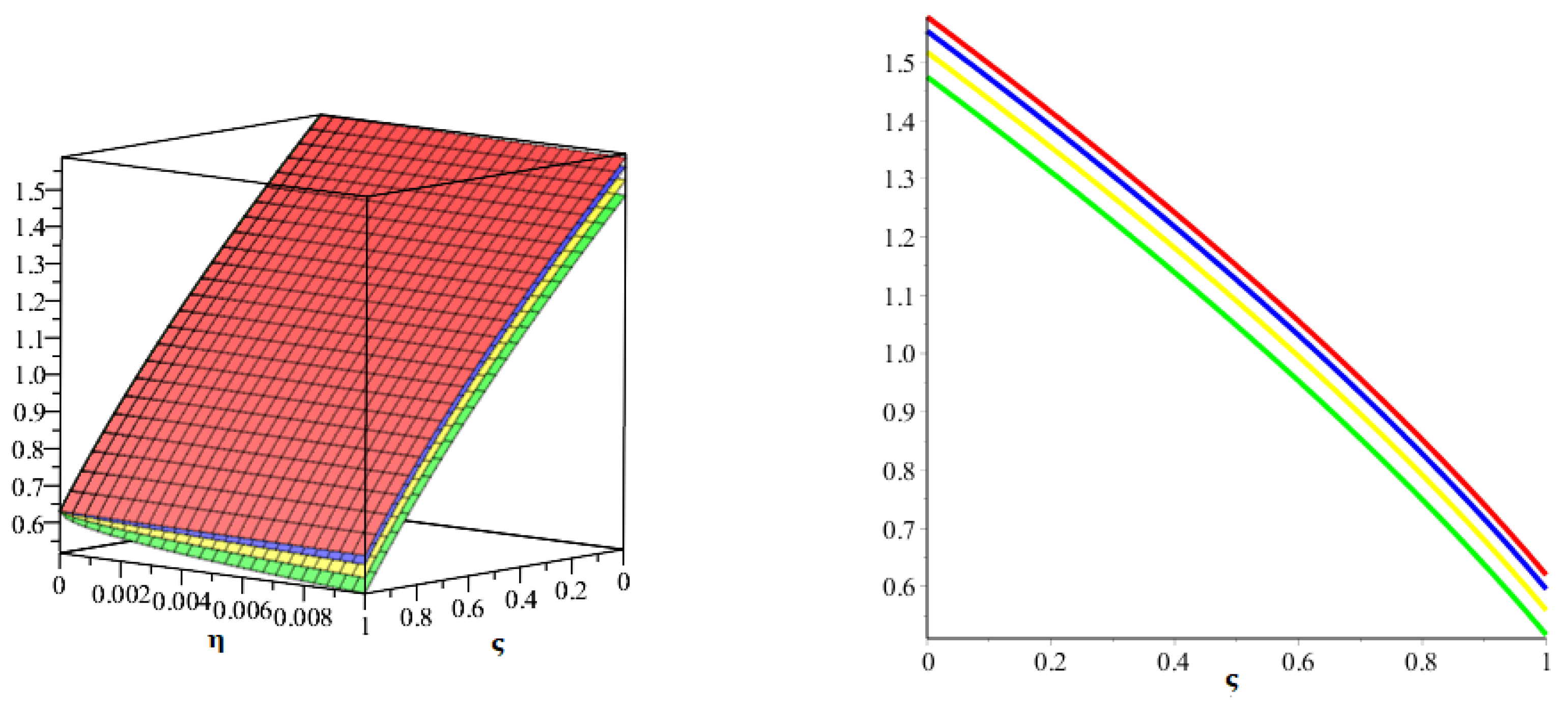
| [47] | |||||||
|---|---|---|---|---|---|---|---|
| 0.2 | 0.0914144 | 0.0915022 | 0.0915102 | 0.0915124 | 0.0915123 | 0.0915124 | |
| 0.4 | 0.1792532 | 0.1793622 | 0.1793743 | 0.1793766 | 0.1793765 | 0.1793766 | |
| 0.01 | 0.6 | 0.2600133 | 0.2600643 | 0.2600832 | 0.2600895 | 0.2600894 | 0.2600895 |
| 0.8 | 0.3303134 | 0.3304152 | 0.3304302 | 0.3304335 | 0.3304334 | 0.3304335 | |
| 1 | 0.3875321 | 0.3875931 | 0.3876011 | 0.3876042 | 0.3876041 | 0.3876042 | |
| 0.2 | 0.0878231 | 0.0879102 | 0.0879211 | 0.0879242 | 0.0879241 | 0.0879242 | |
| 0.4 | 0.1722330 | 0.1723331 | 0.1723412 | 0.1723431 | 0.1723430 | 0.1723431 | |
| 0.02 | 0.6 | 0.2497621 | 0.2498821 | 0.2498901 | 0.2498913 | 0.2498911 | 0.2498913 |
| 0.8 | 0.3173292 | 0.3174609 | 0.3174721 | 0.3174770 | 0.3174769 | 0.3174770 | |
| 1 | 0.3723141 | 0.3723920 | 0.3724021 | 0.3724060 | 0.3724060 | 0.3724060 | |
| 0.2 | 0.0843204 | 0.0844602 | 0.0844720 | 0.0844766 | 0.0844765 | 0.0844766 | |
| 0.4 | 0.1654231 | 0.1655713 | 0.1655831 | 0.1655854 | 0.1655853 | 0.1655854 | |
| 0.03 | 0.6 | 0.2400015 | 0.2400820 | 0.2400912 | 0.2400929 | 0.2400928 | 0.2400929 |
| 0.8 | 0.3050004 | 0.3050121 | 0.3050242 | 0.3050286 | 0.3050285 | 0.3050286 | |
| 1 | 0.3577116 | 0.3577930 | 0.3578010 | 0.3578038 | 0.3578037 | 0.3578038 | |
| 0.2 | 0.0810192 | 0.0811513 | 0.0811614 | 0.0811642 | 0.0811641 | 0.0811642 | |
| 0.4 | 0.1590002 | 0.1590105 | 0.1590903 | 0.1590927 | 0.1590926 | 0.1590927 | |
| 0.04 | 0.6 | 0.2305280 | 0.2306696 | 0.2306754 | 0.2306787 | 0.2306786 | 0.2306787 |
| 0.8 | 0.2930001 | 0.2930530 | 0.2930632 | 0.2930682 | 0.2930681 | 0.2930682 | |
| 1 | 0.3436561 | 0.3437631 | 0.3437709 | 0.3437741 | 0.3437740 | 0.3437741 | |
| 0.2 | 0.0778561 | 0.0779702 | 0.0779800 | 0.0779817 | 0.0779816 | 0.0779817 | |
| 0.4 | 0.1527245 | 0.1528461 | 0.1528502 | 0.1528546 | 0.1528545 | 0.1528546 | |
| 0.05 | 0.6 | 0.2215890 | 0.2216241 | 0.2216312 | 0.2216337 | 0.2216336 | 0.2216337 |
| 0.8 | 0.2814600 | 0.2815653 | 0.2815731 | 0.2815769 | 0.2815768 | 0.2815769 | |
| 1 | 0.3301343 | 0.3302863 | 0.3302916 | 0.3302945 | 0.3302944 | 0.3302945 |
| [47] | |||||||
|---|---|---|---|---|---|---|---|
| 0.2 | −0.1334995 | −0.1334877 | −0.1334768 | −0.1334668 | −0.1334669 | −0.1334668 | |
| 0.4 | −0.1001246 | −0.1001158 | −0.1001076 | −0.1001001 | −0.1001002 | −0.1001001 | |
| 0.01 | 0.6 | −0.0667497 | −0.0667438 | −0.0667384 | −0.0667334 | −0.0667335 | −0.0667334 |
| 0.8 | −0.0333748 | −0.0333719 | −0.0333692 | −0.0333667 | −0.0333668 | −0.0333667 | |
| 1 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 | |
| 0.2 | −0.1336590 | −0.1336381 | −0.1336185 | −0.1336005 | −0.1336006 | −0.1336005 | |
| 0.4 | −0.1002443 | −0.1002286 | −0.1002139 | −0.1002004 | −0.1002005 | −0.1002004 | |
| 0.02 | 0.6 | −0.0668295 | −0.0668190 | −0.0668092 | −0.0668002 | −0.0668001 | −0.0668002 |
| 0.8 | −0.0334147 | −0.0334095 | −0.0334046 | −0.0334001 | −0.0334002 | −0.0334001 | |
| 1 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 | |
| 0.2 | −0.1338163 | −0.1337871 | −0.1337597 | −0.1337345 | −0.1337346 | −0.1337345 | |
| 0.4 | −0.1003622 | −0.1003403 | −0.1003197 | −0.1003009 | −0.1003009 | −0.1003009 | |
| 0.03 | 0.6 | −0.0669081 | −0.0668935 | −0.0668798 | −0.0668672 | −0.0668673 | −0.0668672 |
| 0.8 | −0.0334540 | −0.0334467 | −0.0334399 | −0.0334336 | −0.0334337 | −0.0334336 | |
| 1 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 | |
| 0.2 | −0.1339721 | −0.1339352 | −0.1339005 | −0.1338688 | −0.1338689 | −0.1338688 | |
| 0.4 | −0.1004791 | −0.1004514 | −0.1004253 | −0.1004016 | −0.1004017 | −0.1004016 | |
| 0.04 | 0.6 | −0.0669860 | −0.0669676 | −0.0669502 | −0.0669344 | −0.0669345 | −0.0669344 |
| 0.8 | −0.0334930 | −0.0334838 | −0.0334751 | −0.0334672 | −0.0334673 | −0.0334672 | |
| 1 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 | |
| 0.2 | −0.1341270 | −0.1340828 | −0.1340411 | −0.1340033 | −0.1340034 | −0.1340033 | |
| 0.4 | −0.1005952 | −0.1005621 | −0.1005308 | −0.1005025 | −0.1005026 | −0.1005025 | |
| 0.05 | 0.6 | −0.0670635 | −0.0670414 | −0.0670205 | −0.0670016 | −0.0670017 | −0.0670016 |
| 0.8 | −0.0335317 | −0.0335207 | −0.0335102 | −0.0335008 | −0.0335009 | −0.0335008 | |
| 1 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 |
| [47] | |||||||
|---|---|---|---|---|---|---|---|
| 0.2 | 2.3919191 | 2.3920191 | 2.3921191 | 2.3922195 | 2.3922194 | 2.3922195 | |
| 0.4 | 2.2607964 | 2.2608964 | 2.2609964 | 2.2610967 | 2.2610966 | 2.2610967 | |
| 0.01 | 0.6 | 2.1257538 | 2.1258538 | 2.1259538 | 2.1260541 | 2.1260540 | 2.1260541 |
| 0.8 | 1.9862757 | 1.9863757 | 1.9864757 | 1.9865760 | 1.9865759 | 1.9865760 | |
| 1 | 1.8417147 | 1.8418147 | 1.8419147 | 1.8420150 | 1.8420150 | 1.8420150 | |
| 0.2 | 2.3919181 | 2.3920181 | 2.3921181 | 2.3922188 | 2.3922187 | 2.3922188 | |
| 0.4 | 2.2607954 | 2.2608954 | 2.2609954 | 2.2610961 | 2.2610960 | 2.2610961 | |
| 0.02 | 0.6 | 2.1257528 | 2.1258528 | 2.1259528 | 2.1260534 | 2.1260533 | 2.1260534 |
| 0.8 | 1.9862747 | 1.9863747 | 1.9864747 | 1.9865753 | 1.9865752 | 1.9865753 | |
| 1 | 1.8417137 | 1.8418137 | 1.8419137 | 1.8420142 | 1.8420141 | 1.8420142 | |
| 0.2 | 2.3919171 | 2.3920171 | 2.3921171 | 2.3922182 | 2.3922181 | 2.3922182 | |
| 0.4 | 2.2607944 | 2.2608944 | 2.2609944 | 2.2610954 | 2.2610953 | 2.2610954 | |
| 0.03 | 0.6 | 2.1257518 | 2.1258518 | 2.1259518 | 2.1260527 | 2.1260526 | 2.1260527 |
| 0.8 | 1.9862737 | 1.9863737 | 1.9864737 | 1.9865746 | 1.9865745 | 1.9865746 | |
| 1 | 1.8417127 | 1.8418127 | 1.8419127 | 1.8420135 | 1.8420134 | 1.8420135 | |
| 0.2 | 2.3919161 | 2.3920161 | 2.3921161 | 2.3922175 | 2.3922174 | 2.3922175 | |
| 0.4 | 2.2607934 | 2.2608934 | 2.2609934 | 2.2610947 | 2.2610946 | 2.2610947 | |
| 0.04 | 0.6 | 2.1257508 | 2.1258508 | 2.1259508 | 2.1260520 | 2.1260519 | 2.1260520 |
| 0.8 | 1.9862727 | 1.9863727 | 1.9864727 | 1.9865739 | 1.9865738 | 1.9865739 | |
| 1 | 1.8417117 | 1.8418117 | 1.8419117 | 1.8420128 | 1.8420127 | 1.8420128 | |
| 0.2 | 2.3919151 | 2.3920151 | 2.3921151 | 2.3922169 | 2.3922168 | 2.3922169 | |
| 0.4 | 2.2607924 | 2.2608924 | 2.2609924 | 2.2610941 | 2.2610940 | 2.2610941 | |
| 0.05 | 0.6 | 2.1257498 | 2.1258498 | 2.1259498 | 2.1260514 | 2.1260513 | 2.1260514 |
| 0.8 | 1.9862717 | 1.9863717 | 1.9864717 | 1.9865732 | 1.9865731 | 1.9865732 | |
| 1 | 1.8417107 | 1.8418107 | 1.8419107 | 1.8420120 | 1.8420120 | 1.8420120 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alshehry, A.S.; Shah, R.; Shah, N.A.; Dassios, I. A Reliable Technique for Solving Fractional Partial Differential Equation. Axioms 2022, 11, 574. https://doi.org/10.3390/axioms11100574
Alshehry AS, Shah R, Shah NA, Dassios I. A Reliable Technique for Solving Fractional Partial Differential Equation. Axioms. 2022; 11(10):574. https://doi.org/10.3390/axioms11100574
Chicago/Turabian StyleAlshehry, Azzh Saad, Rasool Shah, Nehad Ali Shah, and Ioannis Dassios. 2022. "A Reliable Technique for Solving Fractional Partial Differential Equation" Axioms 11, no. 10: 574. https://doi.org/10.3390/axioms11100574
APA StyleAlshehry, A. S., Shah, R., Shah, N. A., & Dassios, I. (2022). A Reliable Technique for Solving Fractional Partial Differential Equation. Axioms, 11(10), 574. https://doi.org/10.3390/axioms11100574








