A Demand Side Management Control Strategy Using RUNge Kutta Optimizer (RUN)
Abstract
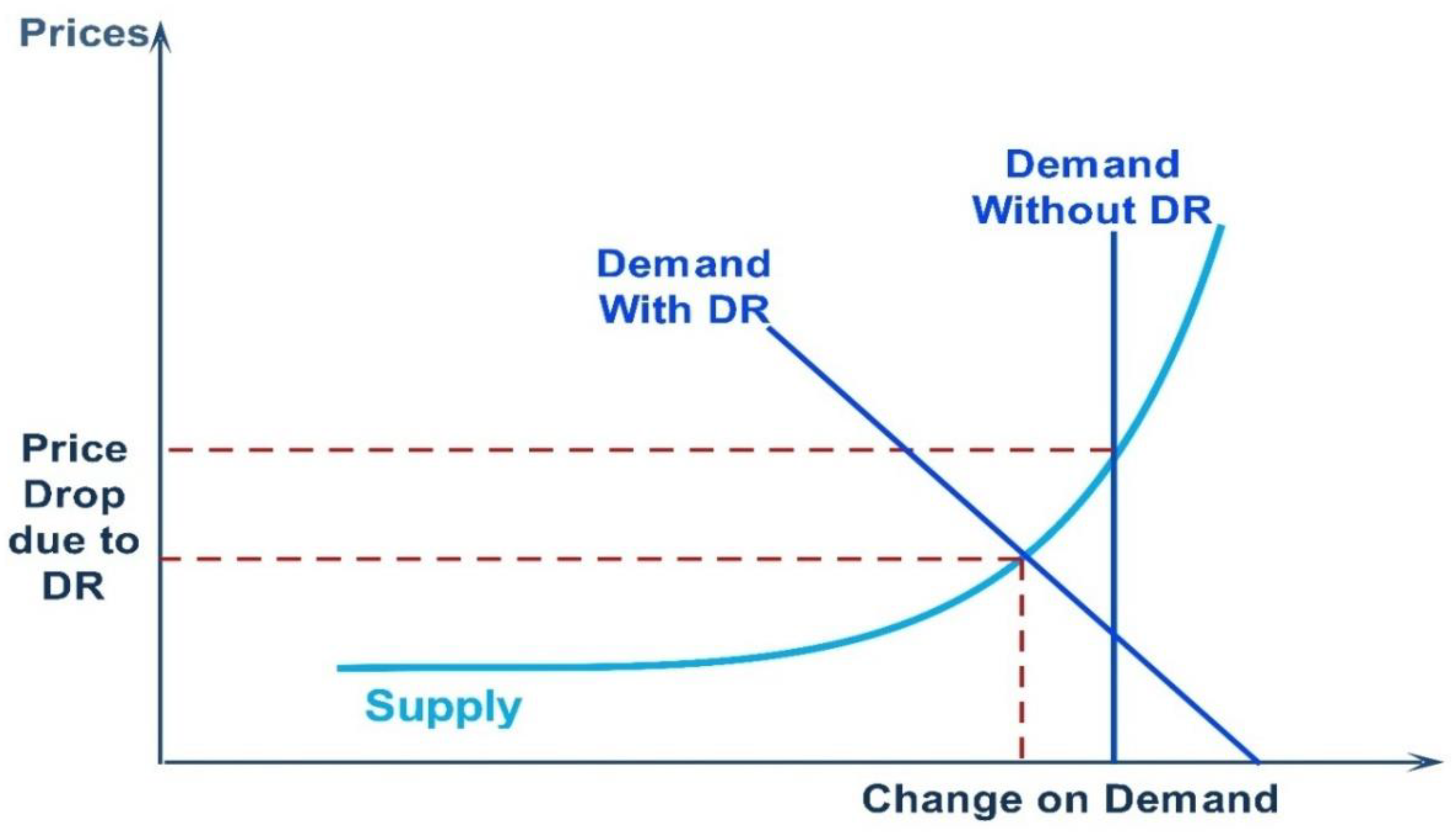
1. Introduction
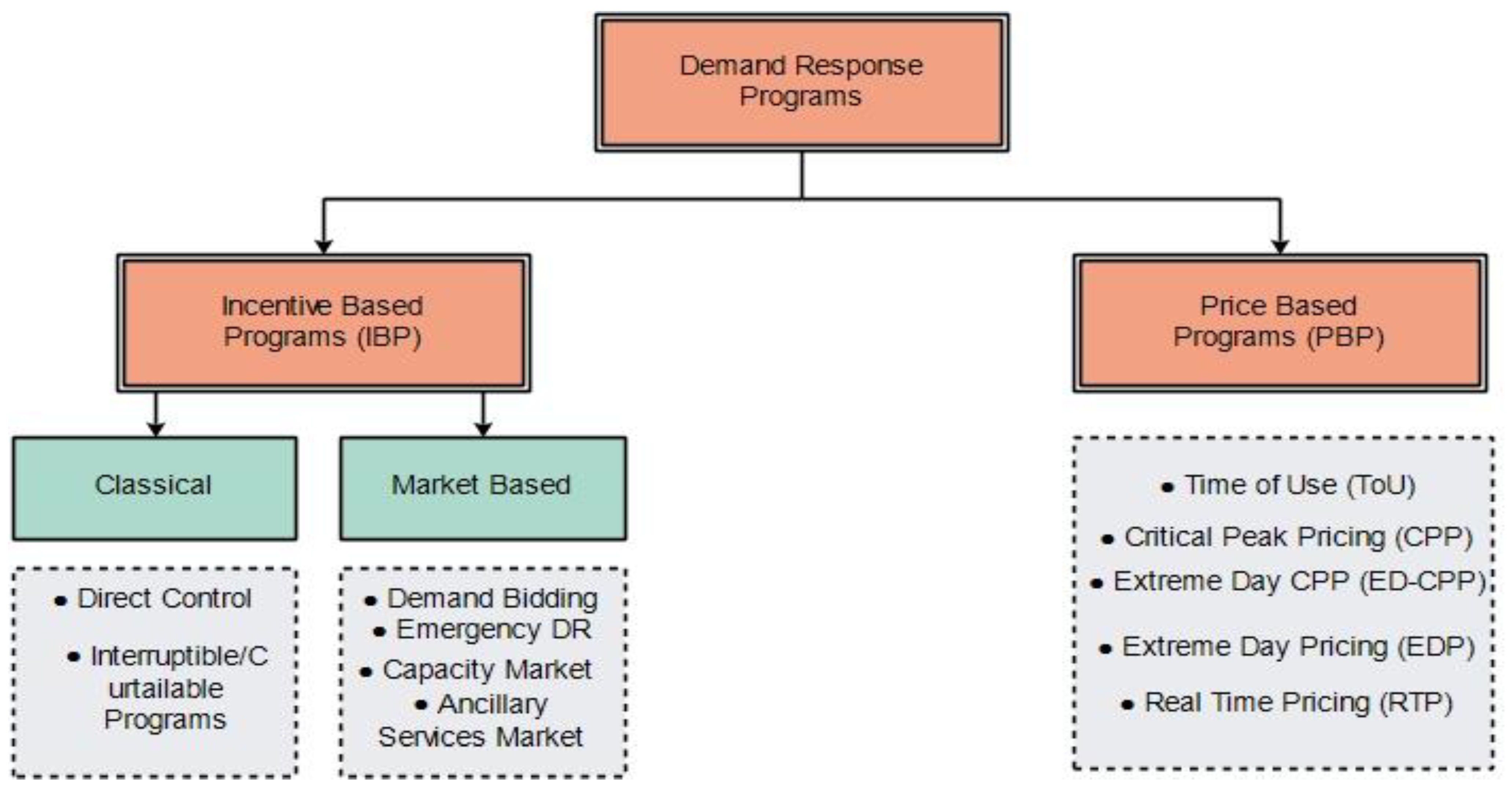
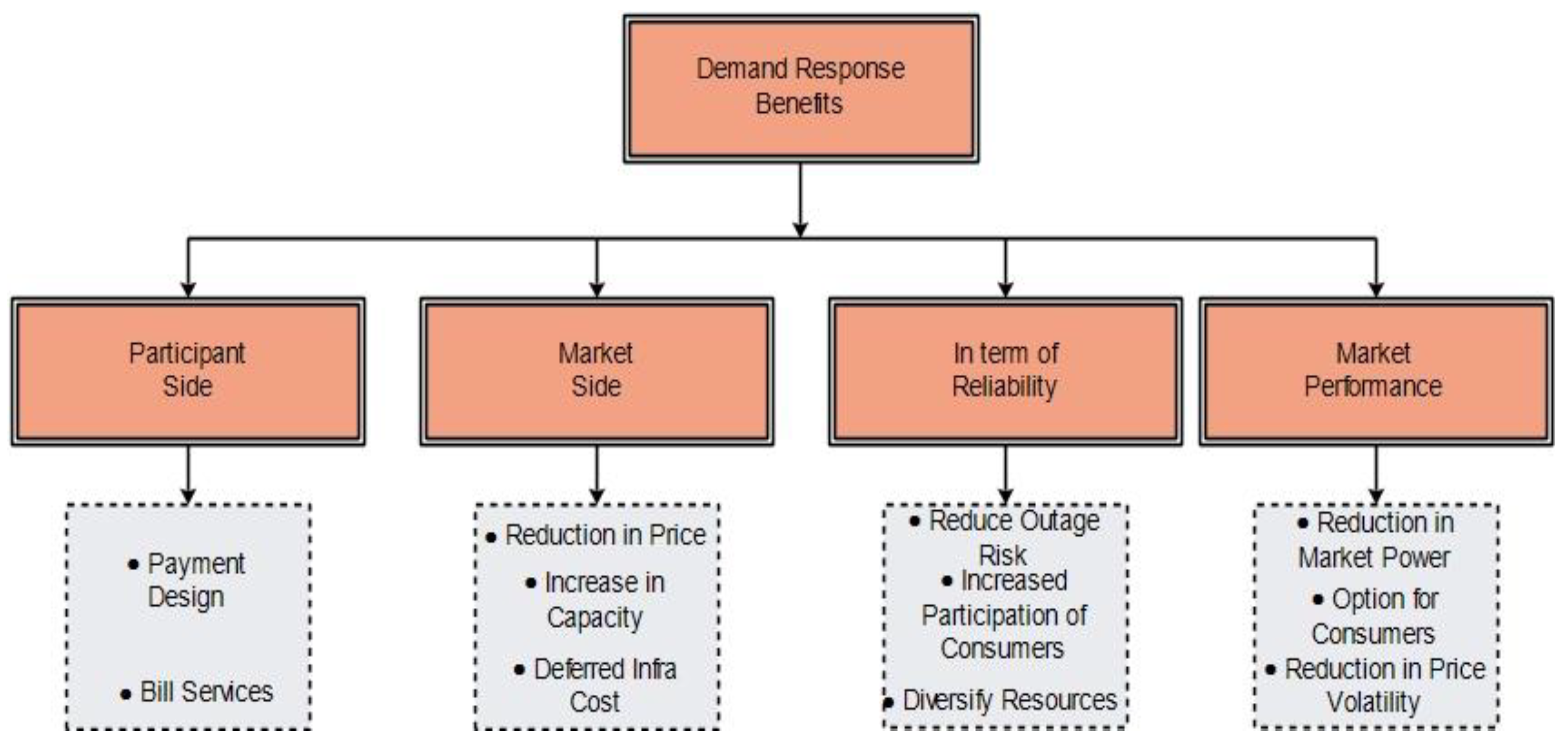
Classifications and Benefits of Demand Response Program
- Using a unique population-based meta-heuristic optimization technique known as the RUNge Kutta optimizer (RUN), the control of the switching of multiple devices of different classes in each test smart grid has been achieved.
- Calculated the decrease in operational costs and peak demand and contrasted the output from the RUNge Kutta optimizer (RUN) with the whale optimization algorithm (WOA), slime mould algorithm (SMA), Sine Cosine Algorithm (SCA), and moth–flame optimization (MFO).
- Proved the efficacy of RUN over WOA, SMA, SCA, and MFO.
2. Techniques in Demand Response
3. Used Demand Response Technique
3.1. DSM Problem Formulation
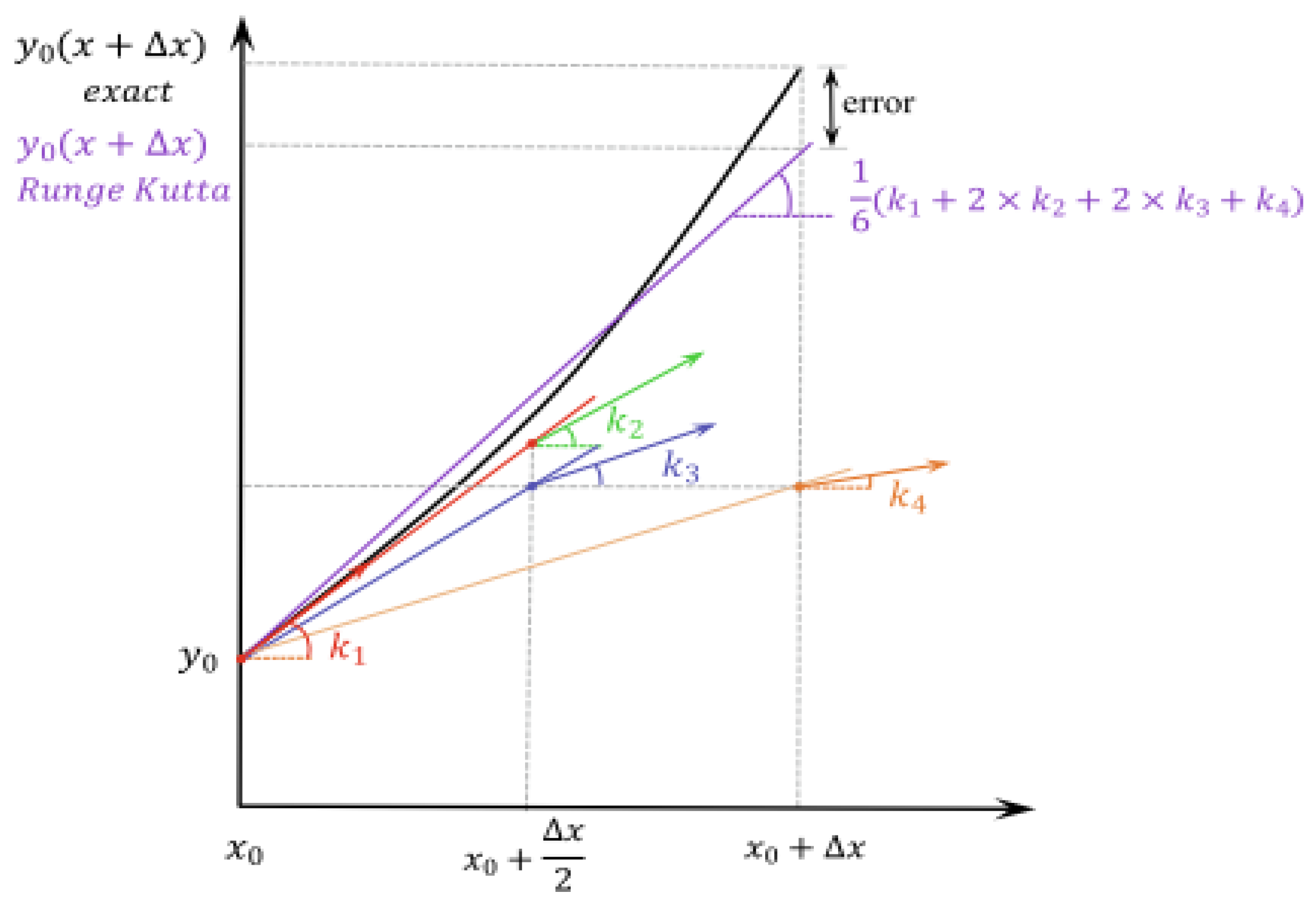
3.2. Overview of RUNge Kutta Method
3.3. Introducing the RUNge Kutta Optimizer (RUN)
- MAs are algorithms that use natural laws to solve challenging real-world issues. They are inspired by nature.
- MAs acquire a stochastic nature when random components are added.
- Because the algorithm does not use derivatives, it takes less time.
- With the help of many control parameters, MAs are customised to the nature of the issue.
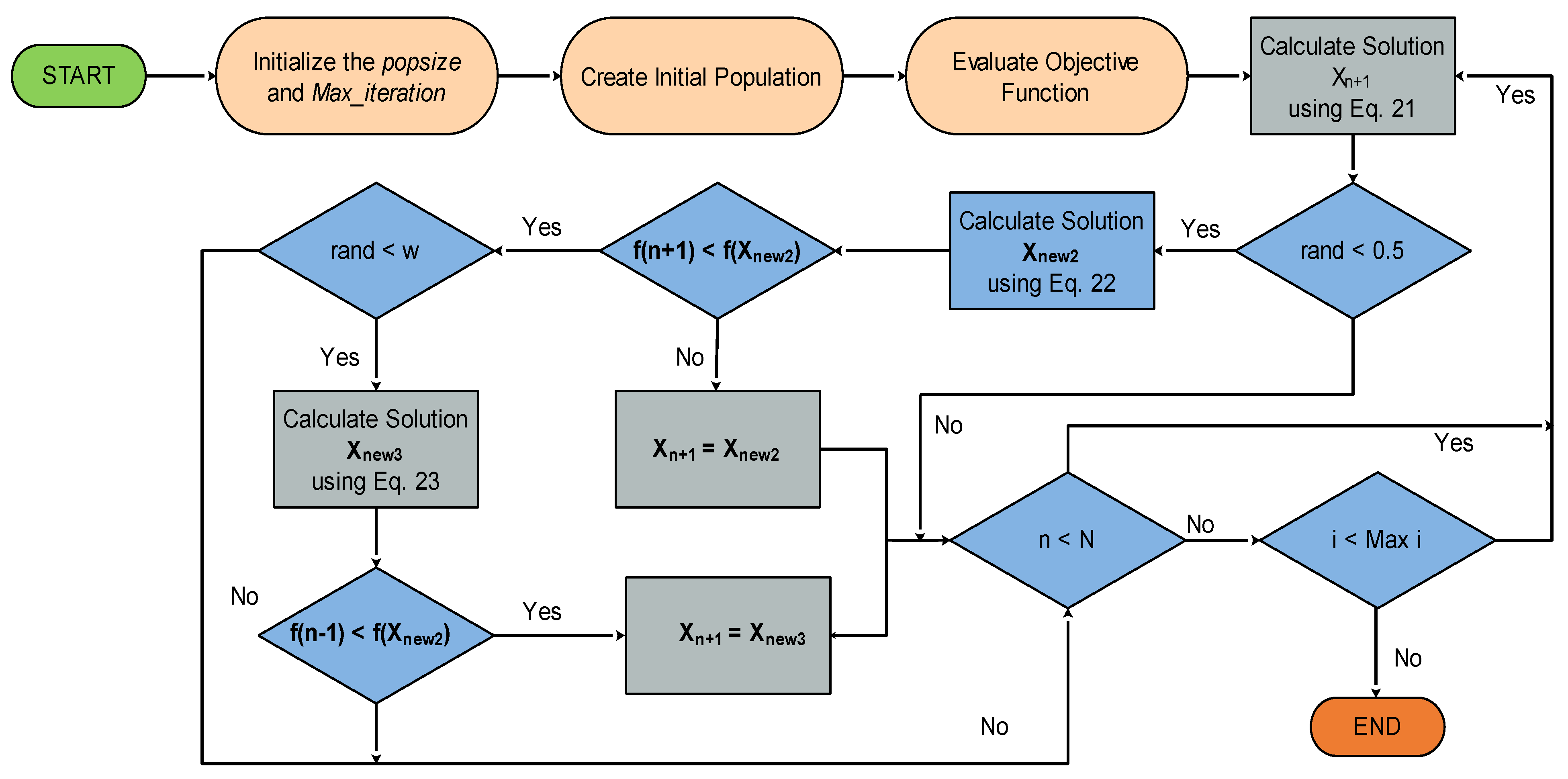
3.3.1. Initialization Step
3.3.2. Root of Search Mechanism
3.3.3. Updating Solutions
3.3.4. Enhanced Solution Quality
| Algorithm 1. The pseudo-code of RUN [46] |
| Stage 1. Initialization |
| Initialize a and b |
| (n = 1,2, …, N) |
| Determine each population member’s objective function. |
| Stage 2. RUN operators |
| Updating solutions |
| using Equation (18) |
| End for |
| Enhance the solution quality |
| using Equation (19) |
| using Equation (20) |
| End |
| End |
| End |
| End for |
| End |
| Stage 3. Return |
- The randomised adaption feature of the scale factor (SF) helps RUN further enhance the exploration and exploitation phases. This setting guarantees a seamless changeover from exploration to exploitation.
- In the initial iterations, RUNs propensity for exploration can be encouraged by using the average position of solutions.
- To improve both exploration and exploitation capabilities, RUN uses a search mechanism based on the RK approach.
- The RUN algorithm’s improved solution quality (ESQ) feature makes use of the best solution found so far to increase the solution quality and accelerate convergence.
- If the new solution in the RUN algorithm does not place the current solution in a better position, it may be able to identify a new position within the search space to place the current solution in a better position. This method can raise the standard of the solutions and raise the convergence rate.
- To highlight the significance of the best solution and progress toward the global best solution, which may successfully balance the exploration and exploitation processes, the search mechanism and ESQ use two randomised variables.
4. A Brief Introduction about Test Smart Grid
4.1. A Residential Area
4.2. A Commercial Area
5. Results and Discussion
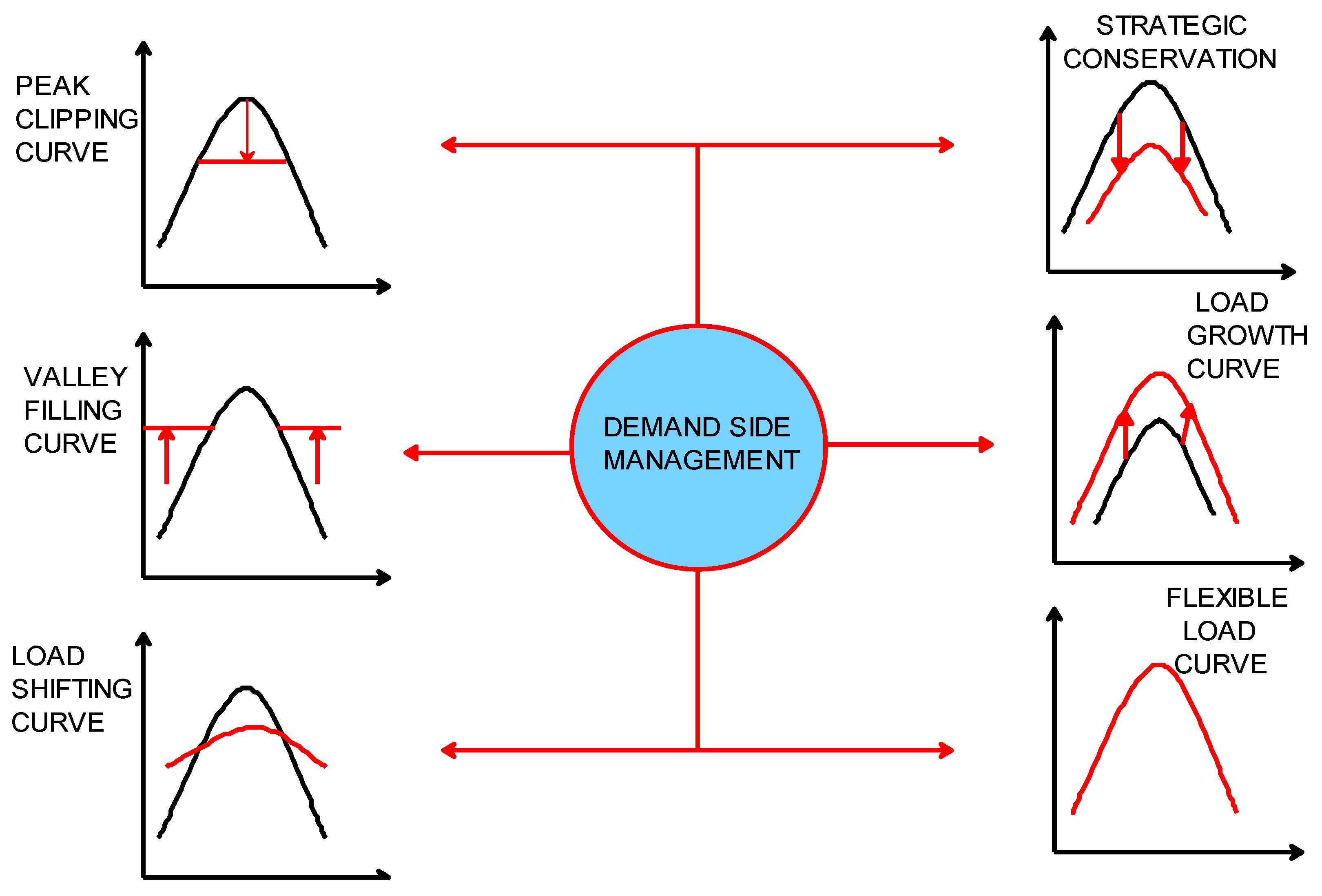
- Test Boat 1: Strategic Conservation.
- Test Boat 2: Load Shifting.
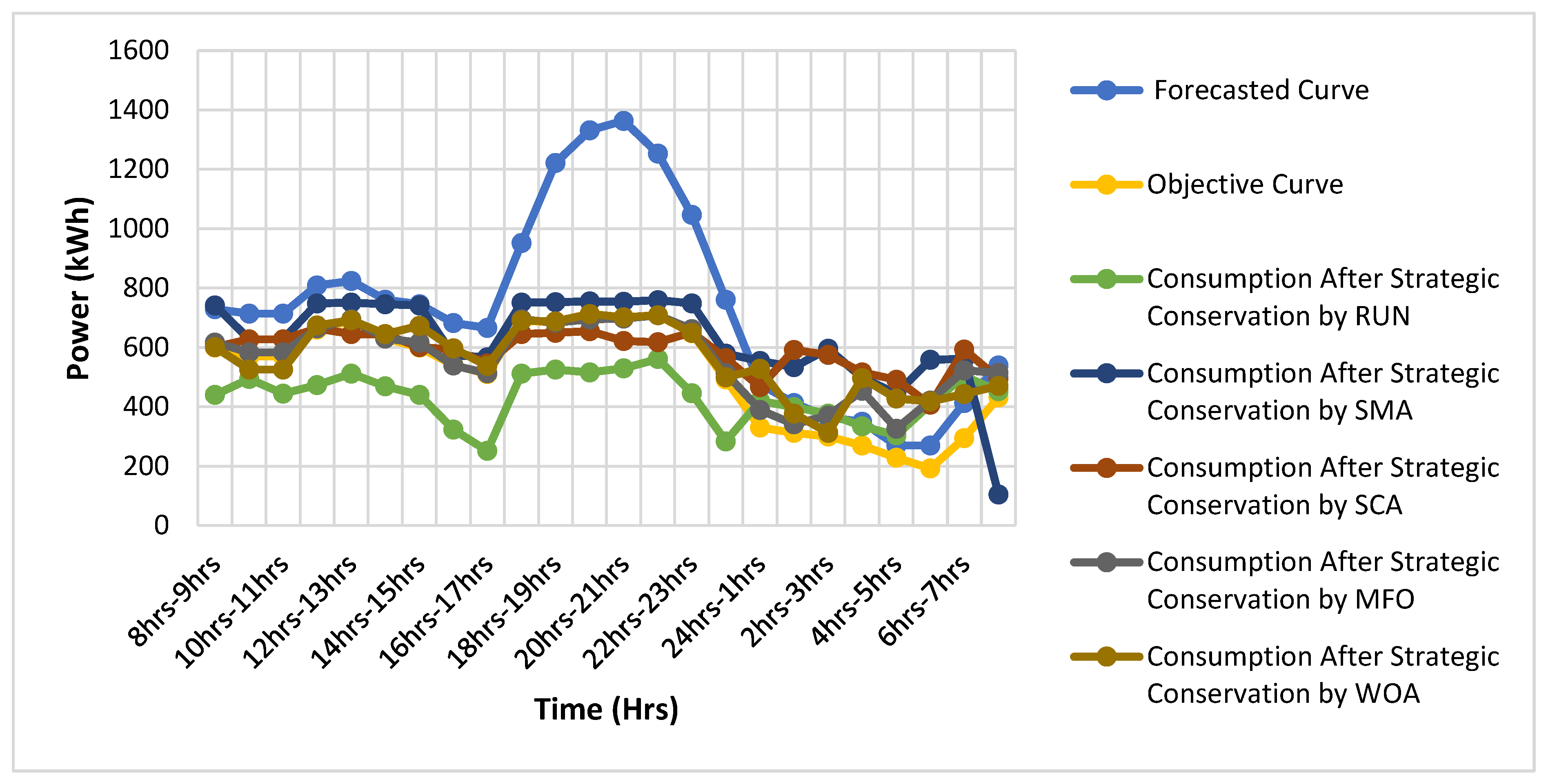
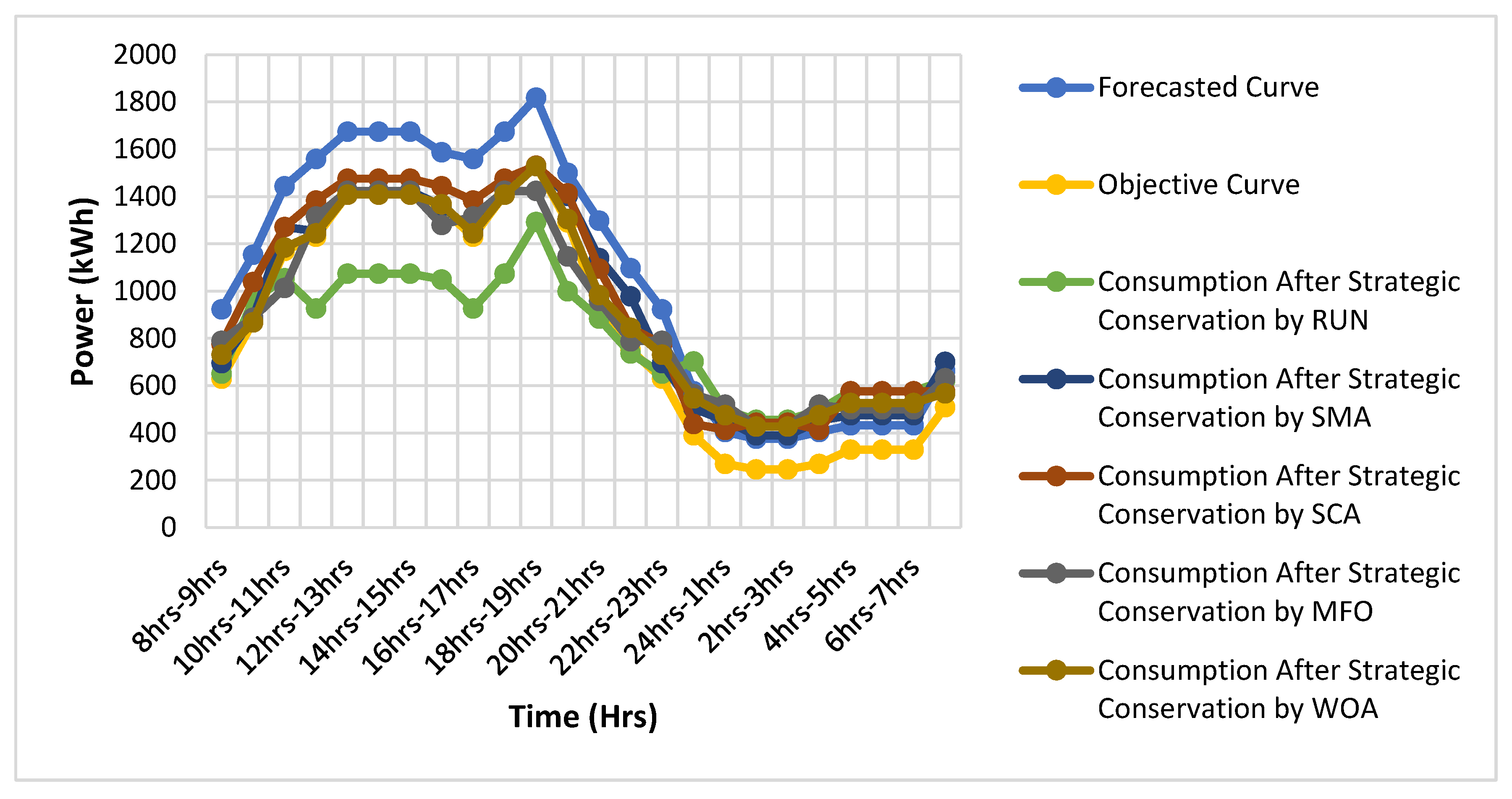
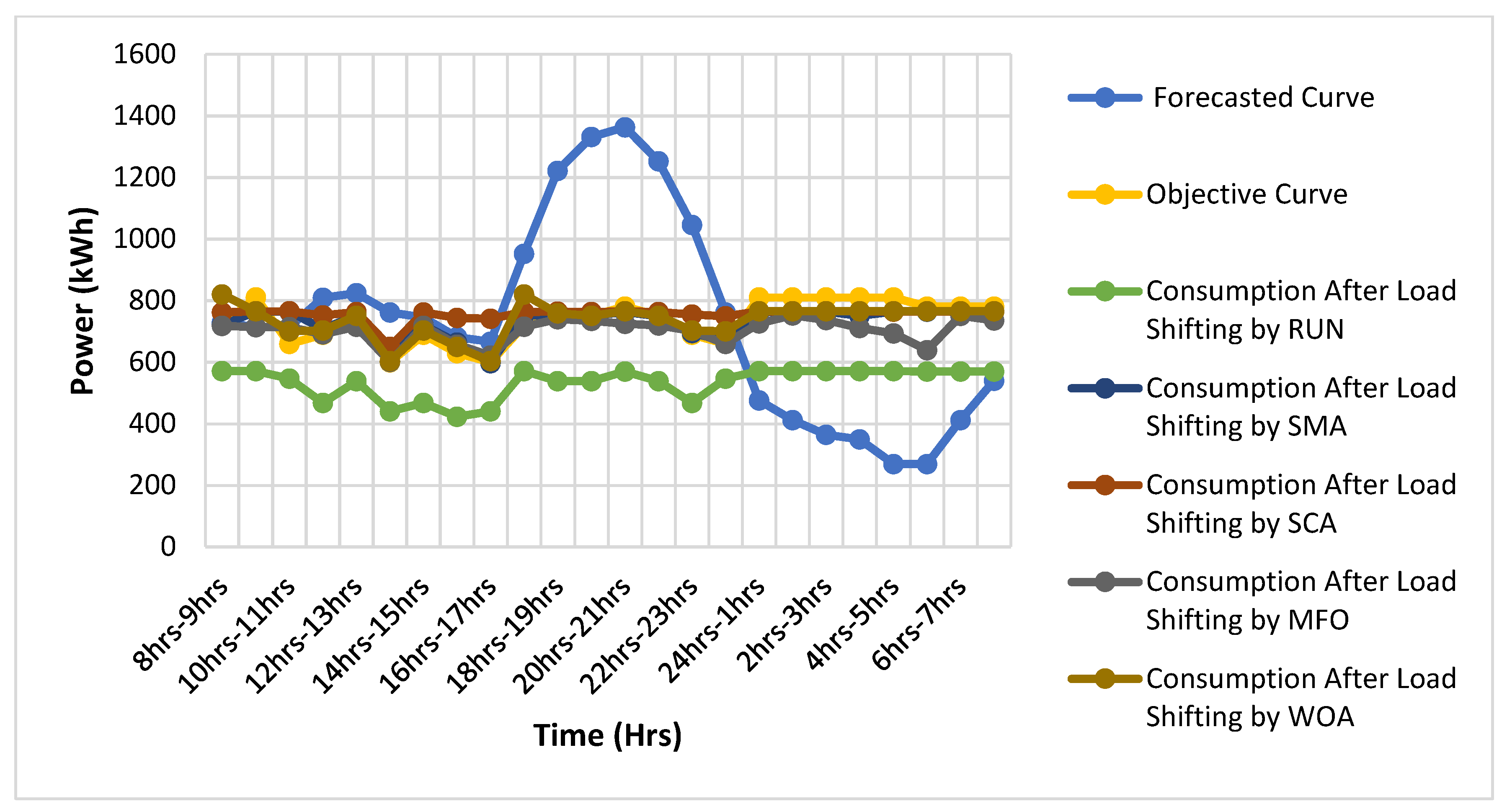
5.1. Test Boat 1: Strategic Conservation
5.2. Test Boat 2: Load Shifting:
6. Conclusions
- The energy demand curves provide a wealth of actual information regarding the amount of electricity consumed and the cost of energy.
- Additionally, a comparison of the RUNs performance in terms of delivering demand-side management techniques for the area’s residential and commercial consumers, such as strategic conversion and load shifting tactics, has been done.
- After comparing the findings, we see that there are favourable implications, such as a decrease in cost and peak demand. When compared to contemporary optimization algorithms, the RUN offers the best performance.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, Q.; Zhou, M. The future-oriented grid-smart grid. J. Comput. 2011, 6, 98–105. [Google Scholar] [CrossRef]
- Agrawal, P. Overview of DOE microgrid activities. In Proceedings of the Symposium on Microgrid, Montreal, QC, Canada, 23 June 2006; Volume 23. [Google Scholar]
- Albadi, M.; El-Saadany, E. A summary of demand response in electricity markets. Electr. Power Syst. Res. 2008, 78, 1989–1996. [Google Scholar] [CrossRef]
- Herter, K.; McAuliffe, P.; Rosenfeld, A. An exploratory analysis of California residential customer response to critical peak pricing of electricity. Energy 2007, 32, 25–34. [Google Scholar] [CrossRef]
- Piette, M.A.; Sezgen, O.; Watson, D.S.; Motegi, N.; Shockman, C.; Ten Hope, L. Development and Evaluation of Fully Automated Demand Response in Large Facilities; CEC-500-2005-013, LBNL-55085; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2005. [Google Scholar]
- Valero, S.; Ortiz, M.; Senabre, C.; Alvarez, C.; Franco, F.J.G.; Gabaldon, A. Methods for customer and demand response policies selection in new electricity markets. IET Gener. Transm. Distrib. 2007, 1, 104–110. [Google Scholar] [CrossRef]
- Sezgen, O.; Goldman, C.; Krishnarao, P. Option value of electricity demand response. Energy 2007, 32, 108–119. [Google Scholar] [CrossRef]
- Albadi, M.H.; El-Saadany, E.F. Demand response in electricity markets: An overview. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–5. [Google Scholar]
- Goel, L.; Wu, Q.; Wang, P. Reliability enhancement of a deregulated power system considering demand response. In Proceedings of the 2006 IEEE Power Engineering Society General Meeting, Montreal, QC, Canada, 18–22 June 2006; p. 6. [Google Scholar]
- Spees, K.; Lave, L.B. Demand response and electricity market efficiency. Electr. J. 2007, 20, 69–85. [Google Scholar] [CrossRef]
- Barbose, G.; Goldman, C.; Neenan, B. A Survey of Utility Experience with Real Time Pricing; LBNL-54238; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2004. [Google Scholar]
- Caves, D.; Eakin, K.; Faruqui, A. Mitigating price spikes in wholesale markets through market-based pricing in retail markets. Electr. J. 2000, 13, 13–23. [Google Scholar] [CrossRef]
- Lai, C.-M.; Teh, J. Comprehensive review of the dynamic thermal rating system for sustainable electrical power systems. Energy Rep. 2022, 8, 3263–3288. [Google Scholar] [CrossRef]
- Metwaly, M.K.; Teh, J. Probabilistic peak demand matching by battery energy storage alongside dynamic thermal ratings and demand response for enhanced network reliability. IEEE Access 2020, 8, 181547–181559. [Google Scholar] [CrossRef]
- Khoo, W.C.; Teh, J.; Lai, C.-M. Demand response and dynamic line ratings for optimum power network reliability and ageing. IEEE Access 2020, 8, 175319–175328. [Google Scholar] [CrossRef]
- Khoo, W.C.; Teh, J.; Lai, C.-M. Integration of wind and demand response for optimum generation reliability, cost and carbon emission. IEEE Access 2020, 8, 183606–183618. [Google Scholar] [CrossRef]
- Lai, C.-M.; Teh, J. Network topology optimisation based on dynamic thermal rating and battery storage systems for improved wind penetration and reliability. Appl. Energy 2022, 305, 117837. [Google Scholar] [CrossRef]
- DeMeo, E.A.; Grant, W.; Milligan, M.R.; Schuerger, M.J. Wind plant integration [wind power plants]. IEEE Power Energy Mag. 2005, 3, 38–46. [Google Scholar] [CrossRef]
- Smith, J.C.; Milligan, M.R.; DeMeo, E.A.; Parsons, B. Utility wind integration and operating impact state of the art. IEEE Trans. Power Syst. 2007, 22, 900–908. [Google Scholar] [CrossRef]
- DeMeo, E.A.; Jordan, G.A.; Kalich, C.; King, J.; Milligan, M.R.; Murley, C.; Oakleaf, B.; Schuerger, M.J. Accommodating wind’s natural behavior. IEEE Power Energy Mag. 2007, 5, 59–67. [Google Scholar] [CrossRef]
- Papavasiliou, A.; Oren, S.S. Coupling wind generators with deferrable loads. In Proceedings of the 2008 IEEE Energy 2030 Conference, Atlanta, GA, USA, 17–18 November 2008; pp. 1–7. [Google Scholar]
- Sioshansi, R. Evaluating the impacts of real-time pricing on the cost and value of wind generation. IEEE Trans. Power Syst. 2009, 25, 741–748. [Google Scholar] [CrossRef]
- Dietrich, K.; Latorre, J.M.; Olmos, L.; Ramos, A. Demand response in an isolated system with high wind integration. IEEE Trans. Power Syst. 2011, 27, 20–29. [Google Scholar] [CrossRef]
- Cheng, Y.; Dong, N.; Ren, Y. Investigation on electric load peak and valley characters and demand response evaluation based on spectral analysis. In Proceedings of the 2011 International Conference on Advanced Power System Automation and Protection, Beijing, China, 16–20 October 2011; Volume 2, pp. 1258–1262. [Google Scholar]
- Wu, J.; Ai, X.; Zhao, Y.; Wu, D. Research on modeling and appliance of a new price mechanism demand response. In Proceedings of the 2013 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Hong Kong, China, 8–11 December 2013; pp. 1–5. [Google Scholar]
- Abdullah, M.M.; Dwolatzky, B. Demand-side energy management performed using direct feedback via mobile systems: Enables utilities to deploy consumer based demand response programs. In Proceedings of the 2010 IEEE International Energy Conference, Manama, Bahrain, 18–22 December 2010; pp. 172–177. [Google Scholar]
- Mathieu, J.L.; Callaway, D.S.; Kiliccote, S. Examining uncertainty in demand response baseline models and variability in automated responses to dynamic pricing. In Proceedings of the 2011 50th IEEE Conference on Decision and Control and European Control Conference, Orlando, FL, USA, 12–15 December 2011; pp. 4332–4339. [Google Scholar]
- Panapakidis, I.; Frantza, S.; Papagiannis, G. Implementation of price-based demand response programs through a load pattern clustering process. In Proceedings of the MedPower 2014, Athens, Greece, 2–5 November 2014; pp. 1–8. [Google Scholar]
- Andreou, G.T.; Symeonidis, A.; Diou, C.; Mitkas, P.A.; Labridis, D.P. A framework for the implementation of large scale Demand Response. In Proceedings of the 2012 International Conference on Smart Grid Technology, Economics and Policies (SG-TEP), Nuremberg, Germany, 3–4 December 2012; pp. 1–4. [Google Scholar]
- Shipman, R.; Gillott, M.; Naghiyev, E. SWITCH: Case studies in the demand side management of washing appliances. Energy Procedia 2013, 42, 153–162. [Google Scholar] [CrossRef]
- Khomami, H.P.; Javidi, M.H. An efficient home energy management system for automated residential demand response. In Proceedings of the 2013 13th international conference on environment and electrical engineering (EEEIC), Wroclaw, Poland, 1–3 November 2013; pp. 307–312. [Google Scholar]
- Liu, B.; Wei, Q. Home energy control algorithm research based on demand response programs and user comfort. In Proceedings of the 2013 2nd International Conference on Measurement, Information and Control, Harbin, China, 16–18 August 2013; Volume 2, pp. 995–999. [Google Scholar]
- Shen, S.; Zhao, Y.; Pang, J.; Yu, W.; Wu, K. Exploring the use value of air conditioners in residential peak demand response. In Proceedings of the 2012 China International Conference on Electricity Distribution, Shanghai, China, 10–14 September 2012; pp. 1–5. [Google Scholar]
- Wu, Z.; Xia, X. A Portfolio Approach of Demand Side Management. IFAC-PapersOnLine 2017, 50, 171–176. [Google Scholar] [CrossRef]
- Meyabadi, A.F.; Deihimi, M.H. A review of demand-side management: Reconsidering theoretical framework. Renew. Sustain. Energy Rev. 2017, 80, 367–379. [Google Scholar] [CrossRef]
- Attia, H.A. Mathematical formulation of the demand side management (DSM) problem and its optimal solution. In Proceedings of the 14th International Middle East Power Systems Conference (MEPCON’10), Cairo, Egypt, 19–21 December 2010. [Google Scholar]
- Logenthiran, T.; Srinivasan, D.; Shun, T.Z. Demand side management in smart grid using heuristic optimization. IEEE Trans. Smart Grid 2012, 3, 1244–1252. [Google Scholar] [CrossRef]
- Bansal, J.C.; Sharma, H.; Jadon, S.S.; Clerc, M. Spider monkey optimization algorithm for numerical optimization. Memetic Comput. 2014, 6, 31–47. [Google Scholar] [CrossRef]
- Simon, D. Biogeography-based optimization. IEEE Trans. Evol. Comput. 2008, 12, 702–713. [Google Scholar] [CrossRef]
- Kutta, W. Beitrag zur naherungsweisen integration totaler differentialgleichungen. Z. Math. Phys. 1901, 46, 435–453. [Google Scholar]
- Runge, C. Über die numerische Auflösung von Differentialgleichungen. Math. Ann. 1895, 46, 167–178. [Google Scholar] [CrossRef]
- Zheng, L.; Zhang, X. Modeling and Analysis of Modern Fluid Problems; Academic Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Patil, P.; Verma, U. Numerical Computational Methods; Alpha Science International Ltd.: Oxford, UK, 2006. [Google Scholar]
- England, R. Error estimates for Runge-Kutta type solutions to systems of ordinary differential equations. Comput. J. 1969, 12, 166–170. [Google Scholar] [CrossRef]
- Hu, J.; Chen, H.; Heidari, A.A.; Wang, M.; Zhang, X.; Chen, Y.; Pan, Z. Orthogonal learning covariance matrix for defects of grey wolf optimizer: Insights, balance, diversity, and feature selection. Knowl.-Based Syst. 2021, 213, 106684. [Google Scholar] [CrossRef]
- El-Dabah, M.A.; El-Sehiemy, R.A.; Ebrahim, M.A.; Alaas, Z.; Ramadan, M.M. Identification study of solar cell/module using recent optimization techniques. Int. J. Electr. Comput. Eng. (IJECE) 2022, 12, 1189–1198. [Google Scholar] [CrossRef]
- Sharma, A.K.; Saxena, A.; Palwalia, D.K.; Soni, B.P. An optimal demand response strategy using gray wolf optimization. In Applications of Artificial Intelligence in Engineering; Springer: Singapore, 2021; pp. 893–908. [Google Scholar]

| Time | Electricity Price (Cent/kWh) | Forecasted Load (kW) | |
|---|---|---|---|
| Residential Microgrid | Commercial Microgrid | ||
| 8 h–9 h | 12 | 12.2 | 15.4 |
| 9 h–10 h | 9.19 | 11.9 | 19.2 |
| 10 h–11 h | 12.3 | 11.9 | 24.1 |
| 11 h–12 h | 20.7 | 13.5 | 26 |
| 12 h–13 h | 26.8 | 13.7 | 27.9 |
| 13 h–14 h | 27.4 | 12.7 | 27.9 |
| 14 h–15 h | 13.8 | 12.4 | 27.9 |
| 15 h–16 h | 17.3 | 11.4 | 26.5 |
| 16 h–17 h | 16.4 | 11.1 | 26 |
| 17 h–18 h | 9.83 | 15.9 | 27.9 |
| 18 h–19 h | 8.63 | 20.3 | 30.3 |
| 19 h–20 h | 8.87 | 22.2 | 25 |
| 20 h–21 h | 8.35 | 22.7 | 21.6 |
| 21 h–22 h | 16.4 | 20.9 | 18.3 |
| 22 h–23 h | 16.2 | 17.4 | 15.4 |
| 23 h–24 h | 8.87 | 12.7 | 9.62 |
| 24 h–1 h | 8.65 | 7.93 | 6.73 |
| 1 h–2 h | 8.11 | 6.87 | 6.25 |
| 2 h–3 h | 8.25 | 6.08 | 6.25 |
| 3 h–4 h | 8.1 | 5.81 | 6.73 |
| 4 h–5 h | 8.14 | 4.49 | 7.22 |
| 5 h–6 h | 8.13 | 4.49 | 7.22 |
| 6 h–7 h | 8.34 | 6.87 | 7.22 |
| 7 h–8 h | 9.35 | 8.99 | 11.1 |
| Device Type | Hourly Load of Device (kW) | Number of Devices | ||
|---|---|---|---|---|
| I Hr | II Hr | III Hr | ||
| Cloth Dryer | 1.2 | 189 | ||
| Dish Washer | 0.7 | 288 | ||
| Washing Machine | 0.5 | 0.4 | 268 | |
| Oven | 1.3 | 279 | ||
| Iron | 1 | 340 | ||
| Vacuum Cleaner | 0.4 | 158 | ||
| Fan | 0.2 | 0.2 | 0.2 | 288 |
| Kettle | 2 | 406 | ||
| Toaster | 0.9 | 48 | ||
| Rice Cooker | 0.85 | 59 | ||
| Hair Dryer | 1.5 | 58 | ||
| Blender | 0.3 | 66 | ||
| Frying Pen | 1.1 | 101 | ||
| Coffee Maker | 0.8 | 56 | ||
| Total | 2604 | |||
| Type of Device | Hourly Load of Device (kW) | Number of Devices | ||
|---|---|---|---|---|
| I Hr | II Hr | III Hr | ||
| Water Dispenser | 2.5 | 156 | ||
| Dryer | 3.5 | 117 | ||
| Kettle | 3 | 2.5 | 123 | |
| Oven | 5 | 77 | ||
| Coffee Maker | 2 | 2 | 99 | |
| Fan | 3.5 | 3 | 93 | |
| Air Conditioner | 4 | 3.5 | 3 | 56 |
| Lights | 2 | 1.75 | 1.5 | 87 |
| Total | 808 | |||
| Operational Cost Reduction | ||||
|---|---|---|---|---|
| Area | Algorithm | Operational Cost without DSM in USD | Operational Cost with DSM in USD | Reduction in Percentage |
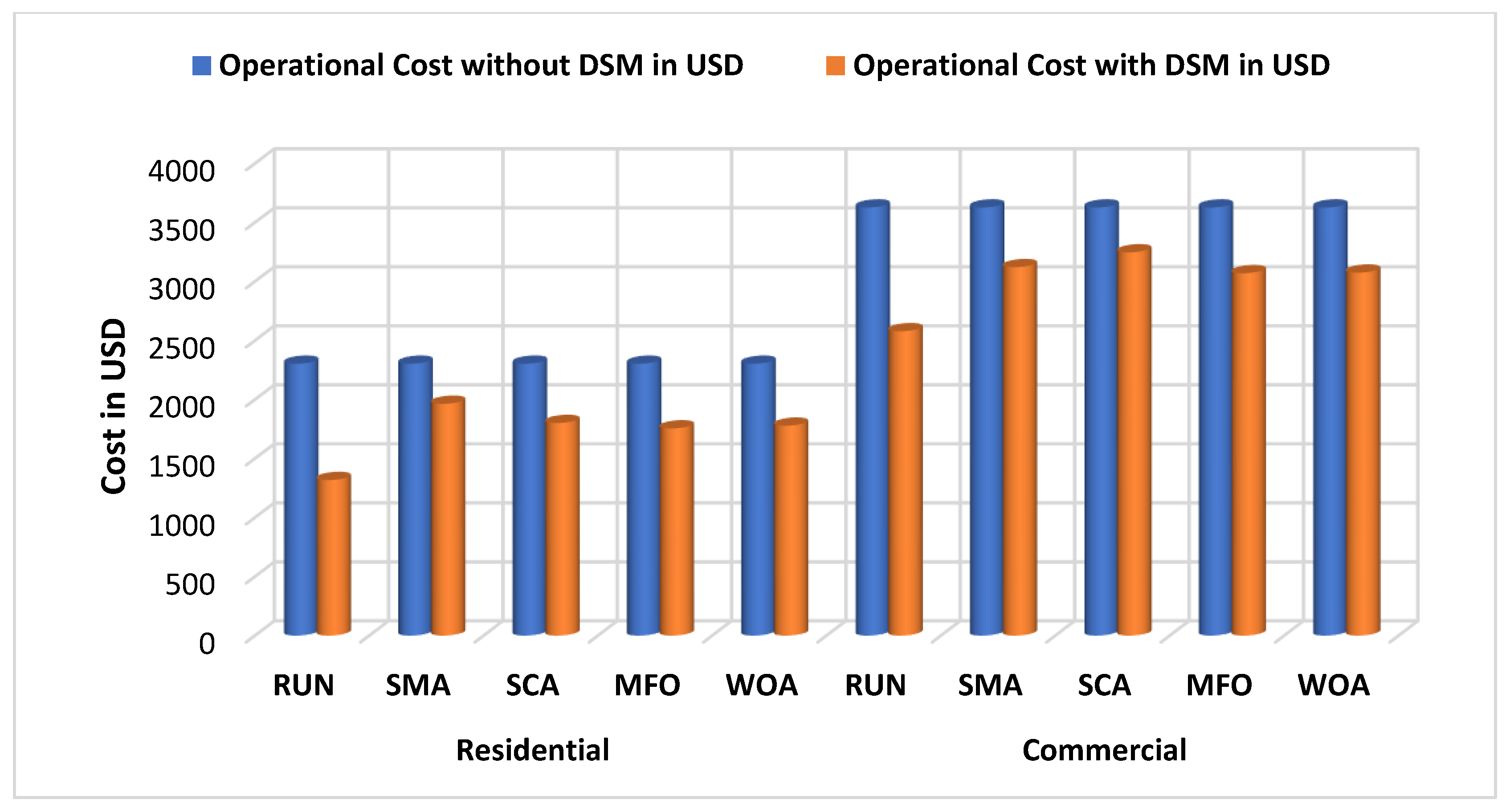
| Residential | RUN | 2302.87928 | 1317.85 | 42.77 |
| SMA | 2302.87928 | 1963.54 | 14.73 | |
| SCA | 2302.87928 | 1801.08 | 21.79 | |
| MFO | 2302.87928 | 1755.39 | 23.77 | |
| WOA | 2302.87928 | 1778.13 | 22.78 | |
| Commercial | RUN | 3626.6396 | 2578.48 | 28.90 |
| SMA | 3626.6396 | 3120.97 | 13.94 | |
| SCA | 3626.6396 | 3246.64 | 10.47 | |
| MFO | 3626.6396 | 3069.87 | 15.35 | |
| WOA | 3626.6396 | 3075.12 | 15.20 | |
| Peak Demand Reduction | ||||
| Area | Algorithm | Peak Reduction without DSM (kWh) | Peak Reduction with DSM (kWh) | Reduction in Percentage |
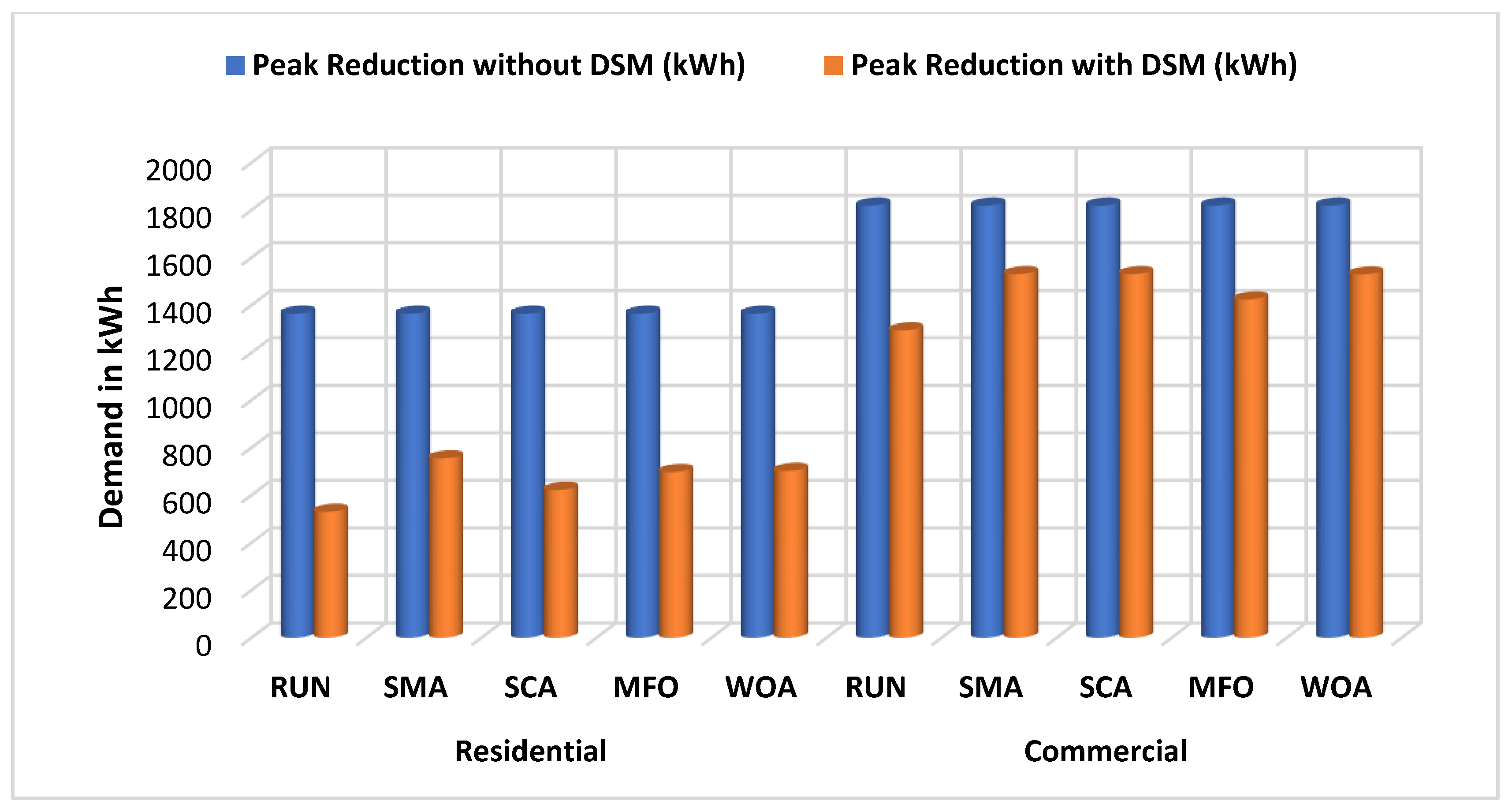
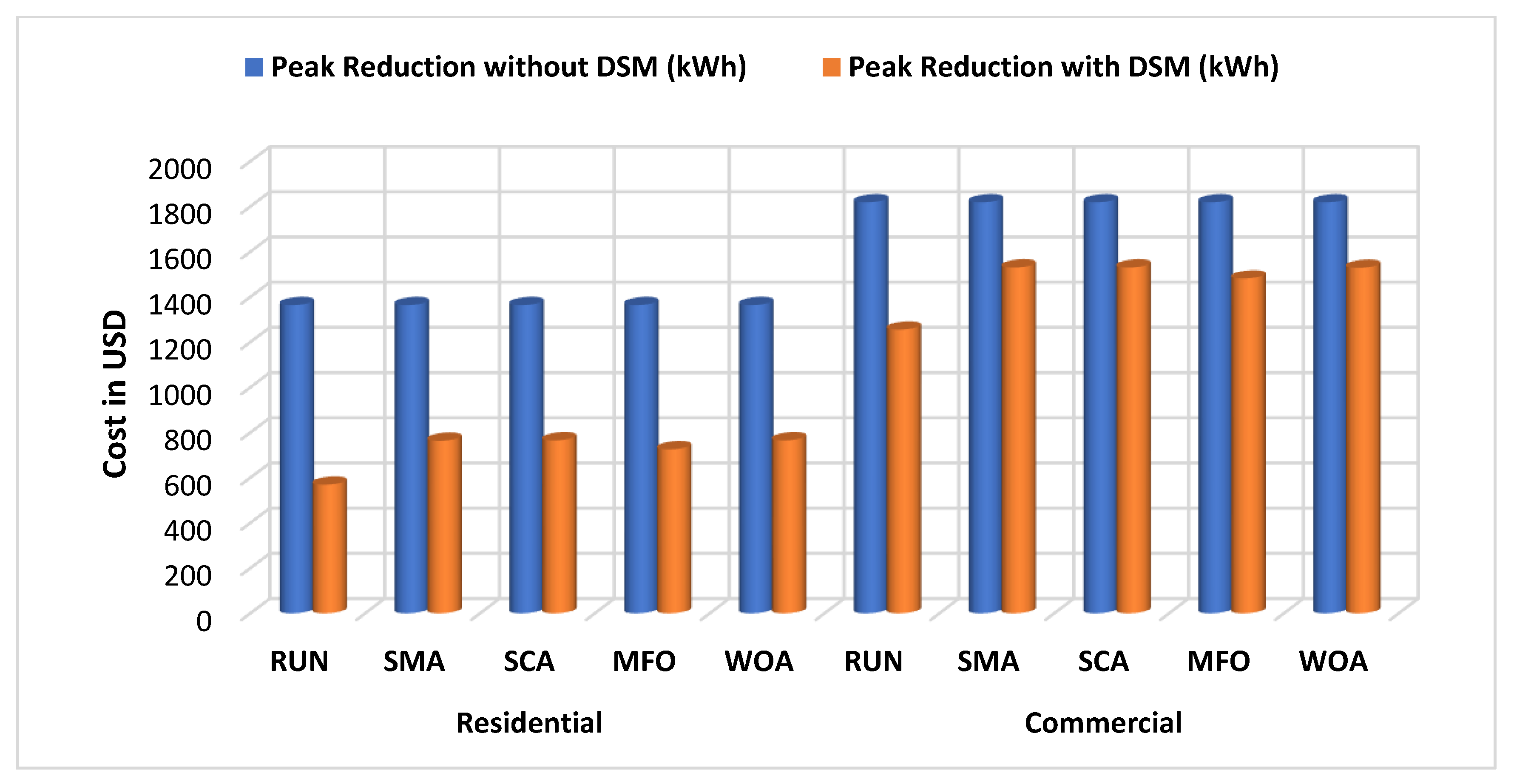
| Residential | RUN | 1363.6 | 529.60 | 61.16 |
| SMA | 1363.6 | 754.38 | 44.67 | |
| SCA | 1363.6 | 621.42 | 54.42 | |
| MFO | 1363.6 | 697.08 | 48.87 | |
| WOA | 1363.6 | 701.82 | 48.53 | |
| Commercial | RUN | 1818.2 | 1293.20 | 28.87 |
| SMA | 1818.2 | 1529.99 | 15.85 | |
| SCA | 1818.2 | 1529.99 | 15.85 | |
| MFO | 1818.2 | 1423.30 | 21.71 | |
| WOA | 1818.2 | 1528.62 | 15.92 | |
| Operational Cost Reduction | ||||
|---|---|---|---|---|
| Area | Algorithm | Operational Cost without DSM in USD | Operational Cost with DSM in USD | Reduction in Percentage |
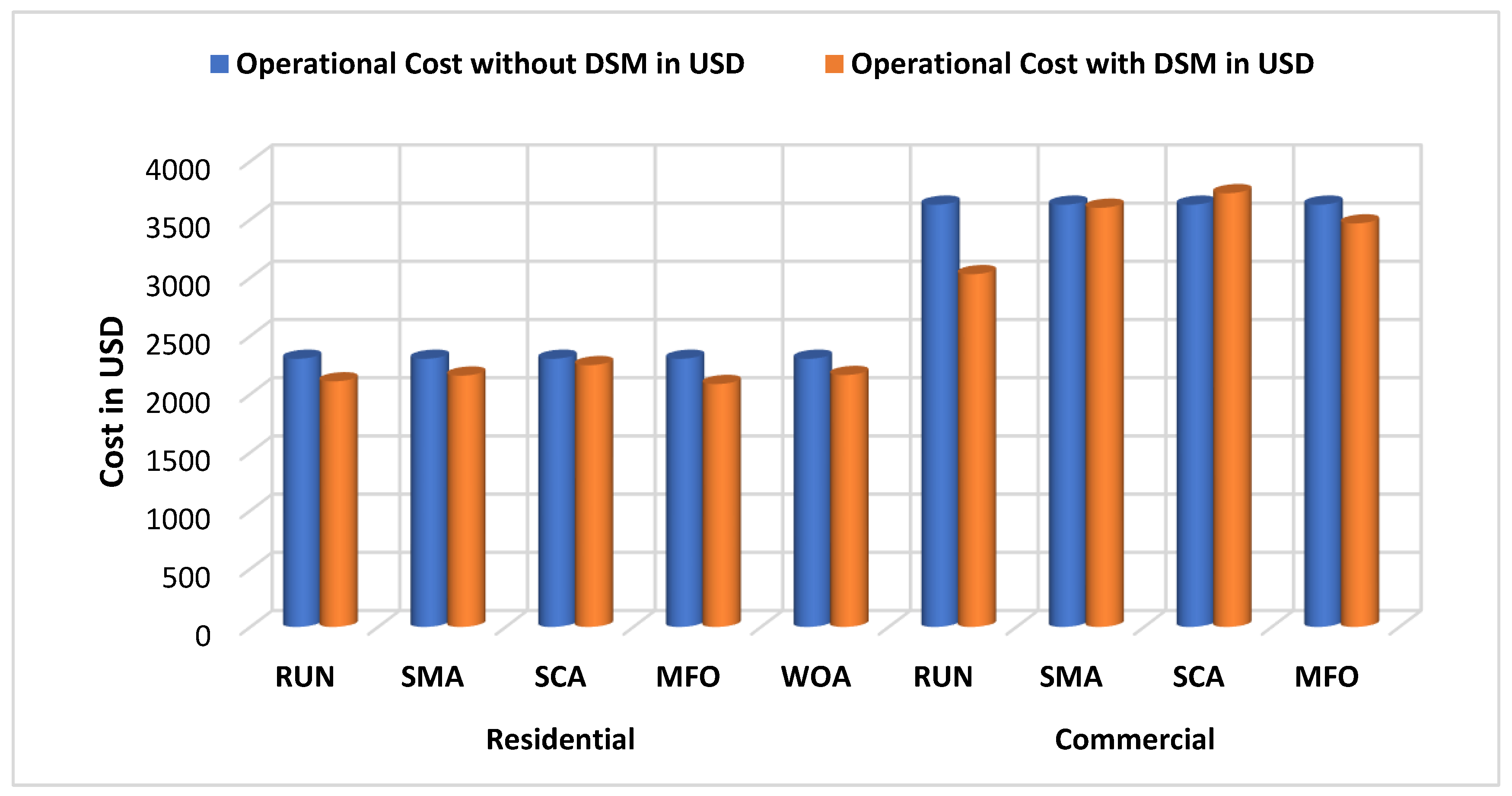
| Residential | RUN | 2302.87928 | 2109.10 | 8.41 |
| SMA | 2302.87928 | 2158.53 | 6.26 | |
| SCA | 2302.87928 | 2248.47 | 2.36 | |
| MFO | 2302.87928 | 2086.24 | 9.40 | |
| WOA | 2302.87928 | 2163.48 | 6.05 | |
| Commercial | RUN | 3626.6396 | 3029.83 | 16.45 |
| SMA | 3626.6396 | 3600.41 | 0.72 | |
| SCA | 3626.6396 | 3725.54 | -2.72 | |
| MFO | 3626.6396 | 3465.72 | 4.43 | |
| WOA | 3626.6396 | 3381.39 | 6.76 | |
| Peak Demand Reduction | ||||
| Area | Algorithm | Peak Reduction without DSM (kWh) | Peak Reduction with DSM (kWh) | Reduction in Percentage |
| Residential | RUN | 1363.6 | 569.12 | 58.26 |
| SMA | 1363.6 | 763.21 | 44.02 | |
| SCA | 1363.6 | 764.99 | 43.89 | |
| MFO | 1363.6 | 725.48 | 46.79 | |
| WOA | 1363.6 | 764.99 | 43.89 | |
| Commercial | RUN | 1818.2 | 1255.06 | 30.97 |
| SMA | 1818.2 | 1529.99 | 15.85 | |
| SCA | 1818.2 | 1529.99 | 15.85 | |
| MFO | 1818.2 | 1481.12 | 18.53 | |
| WOA | 1818.2 | 1528.62 | 15.92 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharma, A.K.; Alshamrani, A.M.; Alnowibet, K.A.; Alrasheedi, A.F.; Saxena, A.; Mohamed, A.W. A Demand Side Management Control Strategy Using RUNge Kutta Optimizer (RUN). Axioms 2022, 11, 538. https://doi.org/10.3390/axioms11100538
Sharma AK, Alshamrani AM, Alnowibet KA, Alrasheedi AF, Saxena A, Mohamed AW. A Demand Side Management Control Strategy Using RUNge Kutta Optimizer (RUN). Axioms. 2022; 11(10):538. https://doi.org/10.3390/axioms11100538
Chicago/Turabian StyleSharma, Ankit Kumar, Ahmad M. Alshamrani, Khalid A. Alnowibet, Adel F. Alrasheedi, Akash Saxena, and Ali Wagdy Mohamed. 2022. "A Demand Side Management Control Strategy Using RUNge Kutta Optimizer (RUN)" Axioms 11, no. 10: 538. https://doi.org/10.3390/axioms11100538
APA StyleSharma, A. K., Alshamrani, A. M., Alnowibet, K. A., Alrasheedi, A. F., Saxena, A., & Mohamed, A. W. (2022). A Demand Side Management Control Strategy Using RUNge Kutta Optimizer (RUN). Axioms, 11(10), 538. https://doi.org/10.3390/axioms11100538









