Application of Orthogonal Polynomial in Orthogonal Projection of Algebraic Surface

Abstract

Point orthogonal projection onto an algebraic surface is a very important topic in computer-aided geometric design and other fields. However, implementing this method is currently extremely challenging and difficult because it is difficult to achieve to desired degree of robustness. Therefore, we construct an orthogonal polynomial, which is the ninth formula, after the inner product of the eighth formula itself. Additionally, we use the Newton iterative method for the iteration. In order to ensure maximum convergence, two techniques are used before the Newton iteration: (1) Newton’s gradient descent method, which is used to make the initial iteration point fall on the algebraic surface, and (2) computation of the foot-point and moving the iterative point to the close position of the orthogonal projection point of the algebraic surface. Theoretical analysis and experimental results show that the proposed algorithm can accurately, efficiently, and robustly converge to the orthogonal projection point for test points in different spatial positions.

1. Introduction

Orthogonal projection is an important topic in geometric modeling and computer-aided geometric design, etc. The concept of orthogonal projection and how to orthogonally project a spatial parametric curve onto a parametric surface and algebraic surface was first proposed by Pegna et al. [1]. The orthogonal projection involves finding a point on the curve or surface such that the line segment connected by this objective point and the given point is perpendicular to the tangent line or the tangent plane of the curve or the surface at this objective point. Since the distance projection is the extended form of the orthogonal projection, the study of this problem will greatly promote the study of orthogonal projections [1]. The study in [1] also presented many applications of orthogonal projections. In design, for the cutting, patching, and welding of free-form shell structures, such as in naval and aeronautical architecture, or in car body design, surfaces have to be cut along pre-defined trimming lines before their assembly. Such a trimming line is usually defined in parametric space for parametric surfaces and in three-dimensional space for implicit surfaces.

The orthogonal projection problem has been widely studied by many experts. A first-order tangent line perpendicular method for a point orthogonal projection onto a parametric curve and surface was proposed by Hartmann [2]. For the supplementation and the improvement of the first-order tangent line perpendicular method [2], Liang et al. [3] and Li et al. [4] proposed two hybrid second-order methods for the two same topics, respectively. Hu et al. [5] proposed a second-order geometric curvature information mode for approximating the orthogonal projection problem of parametric curves and surfaces. Based on their work [5], Li et al. [6] proposed an improved method for orthogonal projection onto a general parametric surface, such that the efficiency in [6] was improved, compared with the existing methods. Ma et al. [7] proposed the topic for point orthogonal projection onto NURBS curves and surfaces, including a four-step technique: subdividing the curve or surface into curve segments or surface patches, finding out the corresponding control polygon of the curve segments or surface patches, identifying the candidate curve segment or surface patch, and confirming some candidate projection points by comparison, with the final projective point being obtained by comparing the distance between the test point and these candidate projection points. Due to the minimum distance between two geometry objects being generated between a pair of special points, researchers [8,9,10] have studied the minimum distance problem between some specific geometric objects using the specific geometric property, and reached some satisfactory results.

Since the algebraic curve and algebraic surface do not have any parameter control form, finding out the orthogonal projection point on the algebraic curve and surface is very difficult. However, there are many fields such as geometric modeling, computer graphics, computer-aided geometric design, etc., that need to be addressed with point orthogonal projection onto algebraic curves and surfaces problems, which makes this a particularly important topic.

Presently, the research into point orthogonal projections onto algebraic curves and surfaces mainly involves point orthogonal projections onto planar algebraic curves. However, there is little research on point orthogonal projection onto an algebraic surface. There are more than 10 papers on point orthogonal projections onto planar algebraic curves, and they are divided into three types: local method, global method, and compromise method between the two methods. It can be seen from the basic geometric characteristic that the problem of point orthogonal projections onto planar algebraic curves can be transformed into solving the equation where the cross product of gradient $\nabla f_0\left(\mathbf{X}\right)$ of the planar algebraic curve $f_0\left(\mathbf{X}\right)$ and the vector $\overrightarrow{\mathbf{PX}}$ is zero at point $\mathbf{X}$. The specific equation can be expressed in the following form:

$$\nabla f_0\left(\mathbf{X}\right)\times (\mathbf{P}-\mathbf{X})=0$$

(1)

The corresponding Newton’s gradient descent iterative formula of Equation (1) can be expressed as the formula (2),

$${\mathbf{X}}_{n+1}={\mathbf{X}}_n-(f_0\left({\mathbf{X}}_n\right)/〈\nabla f_0\left({\mathbf{X}}_n\right),\nabla f_0\left({\mathbf{X}}_n\right)〉)\nabla f_0\left({\mathbf{X}}_n\right).$$

(2)

The second local iteration method is combined with the Lagrange multiplier and Newton’s gradient descent method for computing the orthogonal projection point on the planar algebraic curve, as in William et al. [11]. Of course, the combined method [11] is fast but local, and dependent on the initial point.

As for the Newton’s gradient descent method (2) for solving Equation (1) with an orthogonal projection problem of the planar algebraic curve, the first global approach for solving the system of nonlinear equations is the homotopy continuous method [12,13]. The most classical homotopy transformation technique adopted for solving the orthogonal projection problems of planar algebraic curves is the following:

$$\mathbf{H}(\mathbf{X},t)=(1-t)\mathbf{P}\left(\mathbf{X}\right)+t\mathbf{Q}\left(\mathbf{X}\right),t\in [0,1],$$

(3)

where t is a continuous parameter from 0 to 1, and $\mathbf{P}\left(\mathbf{X}\right)=0$ and $\mathbf{Q}\left(\mathbf{X}\right)=0$ are the original function to be solved and the objective solution function, respectively. All isolated solutions of the original function system $\mathbf{P}\left(\mathbf{X}\right)=0$ can be obtained using the global homotopy method [12,13], where all the isolated solutions of $\mathbf{P}\left(\mathbf{X}\right)=0$ are exactly the same as the objective solution function $\mathbf{Q}\left(\mathbf{X}\right)=0$. The robustness of the global continuous homotopy methods [12,13] with convergence is confirmed by [14], and their low efficiency is shown in [15]. The greatest difficulty of the homotopy method is in seeking out a very satisfactory and correct objective function $\mathbf{Q}\left(\mathbf{X}\right)=0$.

The second global method for point orthogonal projection onto a planar algebraic curve problem is the global resultants method [16,17,18,19], which transformed the projection problem into a results system. By using the elimination theory, a nonlinear system of equations with two variables can be turned into a resultant polynomial with one variable, where the characteristic of the solutions is equivalent to the original function system with two equations. The most important and classical resultant methods [16,17,18,19] are Sylvester’s resultant and Cayley’s resultant formed by Bézout’s method. The advantage of the global resultant methods [16,17,18,19] is that the degree of the planar algebraic curve must be less than 5. Therefore, all the roots of the univariate nonlinear polynomial equation yielded using the resultant methods can be completely solved. However, the resultant methods [16,17,18,19] fail to solve all roots of the nonlinear polynomial equation with a degree of 5 or more.

The third global technique is the Bézier clipping method [20,21,22]. Turning Equation (1) into the Bézier form with a convex hull property is the first step of the Bézier clipping technique. The remaining processing steps are completely equivalent to those of Ma et al. [7], the detailed description of which is omitted here. The advantage of the global Bézier clipping method is that all roots can be obtained, or all orthogonal projection points can be yielded using this technique. There are two disadvantages of the global clipping method: the first is that it takes a lot of time to subdivide, to seek, to judge, and to compare; the second is that transforming Equation (1) into the Bernstein–Bézier form for a small part of the planar algebraic curves is very difficult or even impossible.

The fourth global technique is to solve all the roots of the equations and systems of equations [23,24,25,26]. That is to say, the point orthogonal projection algebraic surface problem can be transformed into solving all the roots of the equations and systems of equations [23,24,25,26]. Bartoň M. [23] proposed two blending scheme solvers for the problem of finding all the roots. As a system of nonlinear equations, a simple linear combination of functions is realized for eliminating the no-root domain, and then all control points for its Bernstein–Bézier basis can be determined, having the same sign, which must be in accord with the seeking function. Then, through the continuous subdivision process, these types of functions are obtained to eliminate the no-root domains. Therefore, two blending schemes in [23] can efficiently reduce the number of subdivisions. van Sosin B. and Elber G. [24] constructed a variety of complex piecewise polynomial systems with zero or inequality constraints in zero-dimensional or one-dimensional solution spaces. To overcome the time cost of subdivision, Park, C.H. et al. [25] presented a hybrid parallel algorithm for solving systems of multivariate constraints by exploiting both the CPU and the GPU multicore architectures. This was achieved by decomposing the constraint solving technique into two different components, hierarchy traversal and polynomial subdivision, each of which is more suitable to CPUs and GPUs, respectively, whose solver can fully exploit the availability of the hybrid, multicore architectures of CPUs and GPUs. The proposed parallel method improved the performance compared to the state-of-the-art subdivision-based CPU solver. To further facilitate solving for all of the roots, Bartoň M. et al. [26] proposed a subdivision model of topological guarantee, whose core technique is to project the unknown multivariable region of the high-dimensional space to the two-dimensional plane according to the known region of all bounds of the univariate. The advantage of these four classical methods [23,24,25,26] is that the robustness of solving all the roots is very good, but the time consumption is relatively large.

In addition to the local and global methods, the third type of approach is the compromise method. The first compromise method was proposed by Hartmann [2,27] and it includes the geometric tangent perpendicular property for solving the orthogonal projection problem. The iterative formula (2) is repeatedly run until the iterative point iterates to the planar algebra curve. The iterative point on the planar algebraic curve is used as the initial point, and the foot-point is once again calculated using Equation (4),

$$\mathbf{Q}=\mathbf{P}-(〈\mathbf{P}-{\mathbf{Y}}_n,\nabla f_0\left({\mathbf{Y}}_n\right)〉/〈\nabla f_0\left({\mathbf{Y}}_n\right),\nabla f_0\left({\mathbf{Y}}_n\right)〉)\nabla f_0\left({\mathbf{Y}}_n\right).$$

(4)

The foot-point $\mathbf{Q}$ is used again as the initial iteration point of Equation (2), and the above two iterative formulas are repeatedly run until the foot-point $\mathbf{Q}$ completely collides with the orthogonal projection point. Unfortunately, if the test point is far away from a plane algebraic curve or algebraic surface, the foot-point $\mathbf{Q}$ being the next iterative point will cause more errors, and finally lead to non-convergence for a small part of the planar algebraic curves.

Redding [28] presented the second compromise method, which adopted the osculating circle technique for computing the orthogonal projection point of the planar algebraic curve. The osculating circle technique mainly consists of three important steps: (1) Computing the curvature and the corresponding radius and center of the curvature circle of the planar algebraic curve at the point. (2) Computing the line segment determined by the test point and the center of the curvature circle, and identifying the foot-point $\mathbf{Q}$ intersected with the line segment and the curvature circle. (3) Approximately taking the foot-point $\mathbf{Q}$ as the point being on the planar algebraic curve. The above three steps are run repeatedly until the foot-point $\mathbf{Q}$ is the same as the orthogonal projection point ${\mathbf{P}}_{\Gamma }$. Since the perpendicular foot-point regarded as the point on the planar algebraic curve will result in more errors and deviations in the third step of the osculating circle technique, and it is not representative of the original parameter, the convergence robustness of the osculating circle technique is sometimes not guaranteed.

The third compromise method is the circle shrinking technique [29]. Equation (2) is run repeatedly such that the iterative point ${\mathbf{P}}_{\mathtt{I}}$ can iterate to the planar algebraic curve maximally. Construct a circle whose the center and radius are the test point $\mathbf{P}$ and $∥\mathbf{P}-{\mathbf{P}}_{\mathtt{I}}∥$, respectively. Mark a point ${\mathbf{P}}^{+}$ on the circle by using the mean value theorem, and find out the intersection point between the line segment $\overline{{\mathbf{PP}}^{+}}$ and the circle. We name this intersection point the current iterative point ${\mathbf{P}}_{\mathtt{I}}$. Repeatedly iterate the above behavior until the current point ${\mathbf{P}}_{\mathtt{I}}$ and the previous point ${\mathbf{P}}_{\mathtt{I}}$ are completely overlapping. It takes more time to find point ${\mathbf{P}}^{+}$ each time for the circle shrinking technique [29]. At the same time, and if the degree of the planar algebraic curve is more than 5, it is not easy to directly solve the intersection ${\mathbf{P}}_{\mathtt{I}}$ of line segment $\overline{{\mathbf{PP}}^{+}}$ and the planar algebraic curve using the circle shrinking technique [29].

The fourth compromise method is associated with the circle double-and-bisect algorithm presented by Hu et al. [30]. Draw an initial small circle with the test point $\mathbf{P}$ as the center, and an arbitrarily small length as the radius $r_1$. A new circle with the same center $\mathbf{P}$ and radius $r_2=2r_1$(after that, the center of all circles is the test point $\mathbf{P}$) is drawn once again. If the second new circle and the planar algebraic curve do not intersect, redraw a new circle, such that the radius of the new circle is twice that of $r_2$. Repeat the above behavior until the latest circle and the planar algebraic curve are intersected. The previous circle and the latest circle are named as the interior circle and the exterior circle, respectively. Once the latest circle intersects with the planar algebraic curve, the remaining processing technique adopts the bisecting technology. A new circle with new radius $r=(r_1+r_2)/2$ is continuously drawn. If the current circle with radius r and the planar algebraic curve intersect, substitute r for $r_2$, or else, for $r_1$. Repeatedly run the above action until the interior circle and the exterior circle are completely coincident. However, it is difficult to determine using this method whether the exterior circle intersects with the curve or not [30], if the degree of the planar algebraic curve is more than 5. Additionally, it takes more time to find the intersection between the exterior circle and the planar algebraic curve in the double-and-bisect algorithm [30]. In addition, in the third compromise method [29] and the fourth compromise method [30], they have a common processing technology that needs to judge the sign of the function $f_0\left(\mathbf{Q}\right)$. If the topological structure of the planar algebraic curve is complex, or if there are many branches in the planar algebraic curve, it is not easy for the two compromise methods [29,30] to implement this technical link.

The fifth compromise method was proposed by Cheng T. et al. [31], and it is a point orthogonal projection onto a spatial algebraic curve. Its shortcoming is that the effect of the correction method of the third algorithm is not ideal, which leads to a reduction in efficiency.

Orthogonal polynomials not only play an important role in point orthogonal projection onto an algebraic surface, but they also have many important theoretical and application values in other aspects. Cesarano C. [32] proved the existence and uniqueness of the extremal node in the polynomial system for any fixed system of multiplicities. From the standard definitions of the incomplete two-variable Hermite polynomials, Cesarano C. et al. [33] proposed a non-trivial generalization polynomial with the Bessel-type functions as the Humbert functions and a non-trivial generalization Lagrange polynomial. Dattoli G. et al. [34] discussed the theory of Lagrange polynomials associated with generalized forms. They adopted two different approaches based on the integral transform method and the Umbral Calculus.

In a word, from the above literature description and analysis, the robustness of the point orthogonal projection onto an algebraic surface is still a very difficult issue to overcome. In order to improve the robustness and efficiency, we construct an orthogonal polynomial (Equation (9)) and use the Newton iterative method for iteration.

The proposed algorithm mainly contains three sub-algorithms: Algorithms 1–3. Equation (11) causes the initial point to be on the algebraic surface as much as possible, according to Newton’s gradient descent property. Then, the iteration point falls on the algebraic surface completely. After Step 2 and Step 3 of Algorithm 2 are jointly implemented five times, the first iteration point falling on the algebraic surface is gradually moved very close to the position of the orthogonal projection point. Additionally, the final iteration point conforms to Newton’s local iterative convergence condition of the two sub-equations of Equation (15). In this way, after repeatedly running Equation (15) of Algorithm 3, the iterative point converges to the objective point (the orthogonal projection point) quickly and robustly. The proposed algorithm mainly captures three important geometric features. First, it maximizes the effect of Newton’s gradient descent method; that is, when each sub-algorithm is implemented, the iteration point can always fall on the algebraic surface, which is a particularly important action for improving the robustness. Second, Algorithm 2 ensures that on the basis of the iteration point on the algebraic surface, the iteration point moves very close to the position of the orthogonal projection point. Third, the final iteration point of Algorithm 2 satisfies Newton’s local convergence condition of Algorithm 3. Algorithm 3 can quickly iterate the iteration point to the algebraic surface, and also speed up the orthogonalization (the final iteration point coincides with the orthogonal projection point).   

Algorithm 1: Newton’s gradient descent method.

Input: The test point P and the algebraic surface $f\left(\mathbf{X}\right)$ Output: The iterative point ${\mathbf{P}}_{\mathtt{I}}$ on the algebraic surface $f\left(\mathbf{X}\right)$ Description: Step 1:            ${\mathbf{X}}_{n+1}=\mathbf{P}-(0.1,0.1,0.1)$;            Do {                    ${\mathbf{X}}_n={\mathbf{X}}_{n+1}$;                    Update ${\mathbf{X}}_{n+1}$ according to Equation (11);            }while ($\left|f\left({\mathbf{X}}_{n+1}\right)\right|>\epsilon \&\&∥{\mathbf{X}}_{n+1}-{\mathbf{X}}_n∥>\epsilon )$; Step 2:            ${\mathbf{P}}_{\mathtt{I}}={\mathbf{X}}_{n+1}$;            Return ${\mathbf{P}}_{\mathtt{I}}$;

Algorithm 2: Computing the foot-point $\mathbf{Q}$ and moving the iterative point ${\mathbf{P}}_{\mathtt{I}}$ to the close position of the orthogonal projection point ${\mathbf{P}}_{\Gamma }$.

Input: The test point $\mathbf{P}$, the algebraic surface $\mathbf{S}$, and the iterative point ${\mathbf{P}}_{\mathtt{I}}$. Output: The current iterative point ${\mathbf{P}}_{\mathtt{I}}$ to the close position of the orthogonal projection point ${\mathbf{P}}_{\Gamma }$. Description: Step 1: With the neighbor point of the test point $\mathbf{P}$ as the initial point, obtain the iterative point          ${\mathbf{P}}_{\mathtt{I}}$ on the algebraic surface $\mathbf{S}$ via Algorithm 1. for(i = 0; i<5; i++) {       Step 2: Obtain the foot-point $\mathbf{Q}$ via Equation (14).       Step 3: With the foot-point $\mathbf{Q}$ as the initial point of Equation (11), compute the iterative                point ${\mathbf{P}}_{\mathtt{I}}$ on the algebraic surface $\mathbf{S}$ via Algorithm 1.     } Step 4: Return ${\mathbf{P}}_{\mathtt{I}}$;

Algorithm 3: Hybrid geometric accelerated orthogonal method.

Input: The current iterative point ${\mathbf{P}}_{\mathtt{I}}$ on the algebraic surface $f\left(\mathbf{X}\right)$ and the algebraic surface $f\left(\mathbf{X}\right)$. Output: The corresponding orthogonal projection point ${\mathbf{P}}_{\Gamma }$ of the test point $\mathbf{P}$. Description: Step 1:            ${\mathbf{X}}_{n+1}={\mathbf{P}}_{\mathtt{I}}$;            Do {                    ${\mathbf{X}}_n={\mathbf{X}}_{n+1}$;                    Compute ${\mathbf{X}}_{n+1}$ by using the iterative formula (15);            }while (${∥{\mathbf{X}}_{n+1}-{\mathbf{X}}_n∥}^2>\epsilon$&&$\left|f\left({\mathbf{X}}_{n+1}\right)\right|>\epsilon )$ Step 2:            ${\mathbf{P}}_{\Gamma }={\mathbf{X}}_{n+1}$;            Return ${\mathbf{P}}_{\Gamma }$;

2. Implementation of the Hybrid Geometry Strategy Algorithm

Let us elaborate on the general idea. There is an algebraic surface $\mathbf{S}$, where the equation of the algebraic surface is,

$$f\left(\mathbf{X}\right)=0,$$

(5)

where $\mathbf{X}=(x,y,z)$. Our aim is to find a point ${\mathbf{P}}_{\Gamma }$ on the algebraic surface $\mathbf{S}$ via a spatial test point $\mathbf{P}$, such that the relationship could be satisfied (see Figure 1),

$$∥\mathbf{P}-{\mathbf{P}}_{\Gamma }∥=\underset{\mathbf{X}\in \Gamma }{min}∥\mathbf{P}-\mathbf{X}∥.$$

(6)

The above problem can be written as

$$\left\{\begin{array}{c}f\left({\mathbf{P}}_{\Gamma }\right)=0,\hfill \\ ∥\mathbf{P}-{\mathbf{P}}_{\Gamma }∥=\underset{\mathbf{X}\in \Gamma }{min}∥\mathbf{P}-\mathbf{X}∥,\hfill \end{array}\right.$$

(7)

where the symbol $∥·∥$ is norm. Formula (7), related to the orthogonal projection point ${\mathbf{P}}_{\Gamma }$, provides two important criteria where the orthogonal projection point ${\mathbf{P}}_{\Gamma }$ should fall on the algebraic surface $\mathbf{S}$, and the distance $∥\mathbf{P}-{\mathbf{P}}_{\Gamma }∥$ is the shortest between the test point $\mathbf{P}$ and point $\mathbf{X}$ on the algebraic surface $\mathbf{S}$. From the second formula of Formula (7), the third important implied and potential geometric meaning that can also be indicated is that the vector $\overrightarrow{\mathbf{P}{\mathbf{P}}_{\Gamma }}$  is perpendicular to the tangent plane vector of the algebraic surface $\mathbf{S}$ at the orthogonal projection point ${\mathbf{P}}_{\Gamma }$, or that the cross product of the vector $\overrightarrow{{\mathbf{PP}}_{\Gamma }}$ and the gradient vector $\nabla f\left({\mathbf{P}}_{\Gamma }\right)$ is zero. Namely, we seek that the orthogonal projection point ${\mathbf{P}}_{\Gamma }$ (the objective point) should be satisfied with the relationship where the cross product of the vector $\overrightarrow{\mathbf{PX}}$ and the gradient vector $\nabla f\left(\mathbf{X}\right)$ is zero,

$$F_0\left(\mathbf{X}\right)=\nabla f\left(\mathbf{X}\right)\times (\mathbf{P}-\mathbf{X})=0,$$

(8)

where ${\displaystyle \nabla f=\left[\frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z}\right]}$ and symbol × are the Hamiltonian operator and the cross product, respectively. Since Equation (8) is a vector equation, not a scalar equation, it is not easy to solve Equation (8). Taking the inner product of the vector itself $\nabla f\left(\mathbf{X}\right)\times (\mathbf{P}-\mathbf{X})$ of Equation (8), it is transformed into the following corresponding equation, which is easy to solve,

$$F\left(\mathbf{X}\right)=〈\nabla f\left(\mathbf{X}\right)\times (\mathbf{P}-\mathbf{X}),\nabla f\left(\mathbf{X}\right)\times (\mathbf{P}-\mathbf{X})〉=0,$$

(9)

where the symbol $〈·,·〉$ is the inner product. The orthogonal projection ${\mathbf{P}}_{\Gamma }$ of the test point $\mathbf{P}$ orthogonally projecting onto the algebraic surface $\mathbf{S}$ should have three important geometric properties: (1) The orthogonal projection point ${\mathbf{P}}_{\Gamma }$ should fall onto the algebraic surface $\mathbf{S}$; (2) the distance $∥\mathbf{P}-{\mathbf{P}}_{\Gamma }∥$ is the shortest between the test point $\mathbf{P}$ and point $\mathbf{X}$ on the algebraic surface S; (3) the inner product of the vector $\overrightarrow{{\mathbf{PP}}_{\Gamma }}$ and the tangent plane vector of the algebraic surface $\mathbf{S}$ at the orthogonal projection point ${\mathbf{P}}_{\Gamma }$ is zero, or the cross product of the vector $\overrightarrow{{\mathbf{PP}}_{\Gamma }}$ and the gradient vector $\nabla f\left({\mathbf{P}}_{\Gamma }\right)$ is zero. These three important geometric properties can be expressed specifically as,

$$\left\{\begin{array}{c}f\left({\mathbf{P}}_{\Gamma }\right)=0,\hfill \\ F\left({\mathbf{P}}_{\Gamma }\right)=〈\nabla f\left({\mathbf{P}}_{\Gamma }\right)\times (\mathbf{P}-{\mathbf{P}}_{\Gamma }),\nabla f\left({\mathbf{P}}_{\Gamma }\right)\times (\mathbf{P}-{\mathbf{P}}_{\Gamma })〉=0,\hfill \\ ∥\mathbf{P}-{\mathbf{P}}_{\Gamma }∥=\underset{\mathbf{X}\in \Gamma }{min}∥\mathbf{P}-\mathbf{X}∥,\hfill \end{array}\right.$$

(10)

where $F\left(\mathbf{X}\right)=〈\nabla f\left(\mathbf{X}\right)\times (\mathbf{P}-\mathbf{X}),\nabla f\left(\mathbf{X}\right)\times (\mathbf{P}-\mathbf{X})〉$.

2.1. Newton’s Gradient Descent Method

The corresponding Newton’s gradient descent iterative formula related to Equation (5) is as follows,

$${\mathbf{X}}_{n+1}={\mathbf{X}}_n-(f\left({\mathbf{X}}_n\right)/〈\nabla f\left({\mathbf{X}}_n\right),\nabla f\left({\mathbf{X}}_n\right)〉)\nabla f\left({\mathbf{X}}_n\right).$$

(11)

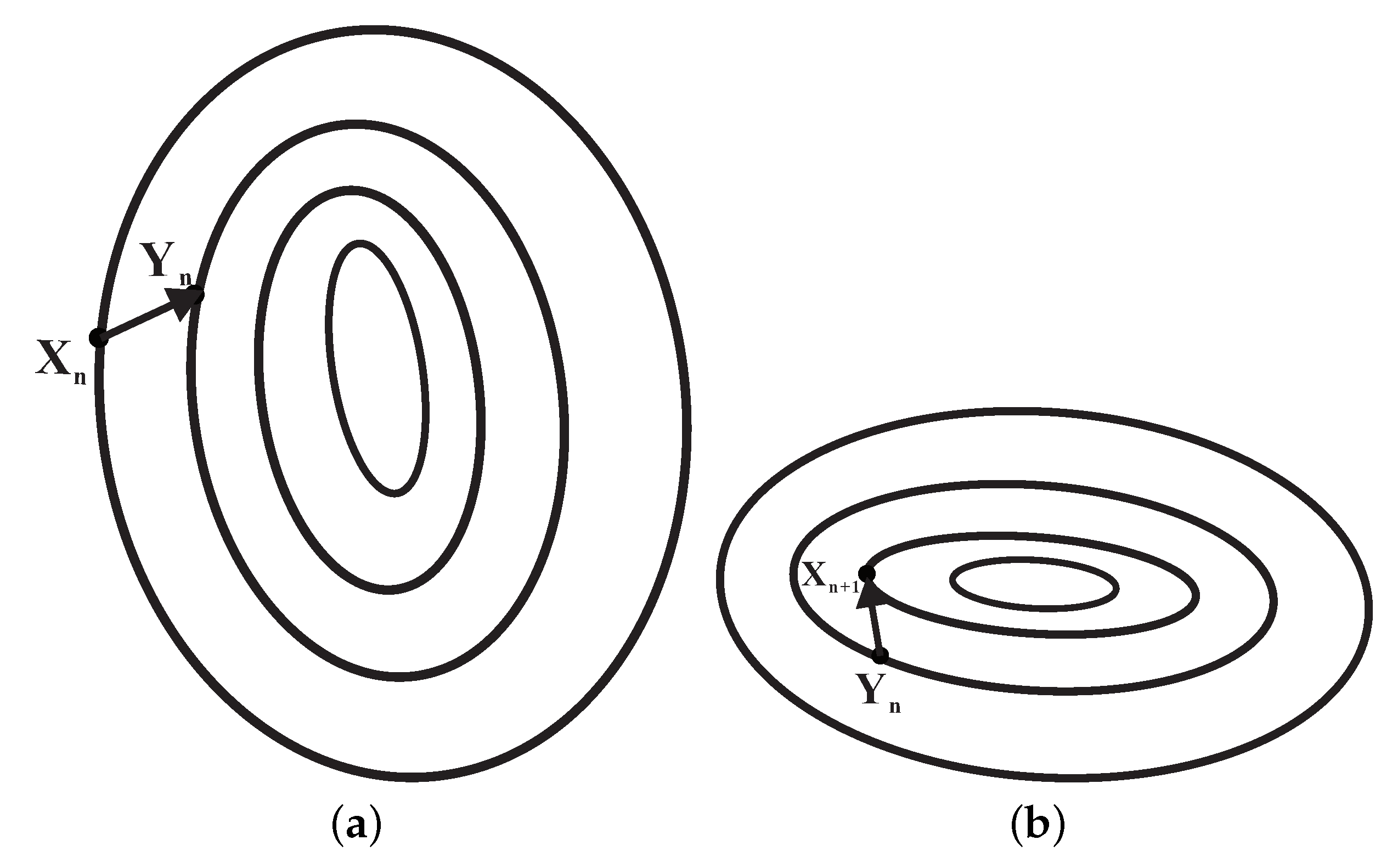
The purpose of this iterative Formula (11) is to prompt the iterative point to iterate to the algebraic surface according to the Newton’s gradient descent property. A detailed description of the idea can be concretely expressed as Algorithm 1 (see Figure 2).

Remark 1.

We present a geometric interpretation for Algorithm 1. In Figure 2, each closed loop is actually represented as a contour surface. The outermost layer of the contour surface is called the first contour surface, the second layer of the contour surface is called the second contour surface, followed by the third contour surface, the fourth contour surface, and so on. The initial iteration point of Equation (11) ${\mathbf{X}}_0$ upon the first contour surface has Newton’s gradient descent property. Using the first iteration of Equation (11), the first iteration point ${\mathbf{X}}_1$ falls on the second contour surface, and the vector $\overrightarrow{{\mathbf{X}}_0{\mathbf{X}}_1}$ is determined by the gradient vector $\nabla f\left({\mathbf{X}}_0\right)$, which is tangential to the second contour surface. Immediately, after the second iteration of Equation (11), ${\mathbf{X}}_1$ is an initial iterative point, and the gradient vector $\nabla f\left({\mathbf{X}}_1\right)$ is perpendicular to the gradient vector $\nabla f\left({\mathbf{X}}_0\right)$. The second iteration point ${\mathbf{X}}_2$ is fallen onto the third contour surface, and the vector $\overrightarrow{{\mathbf{X}}_1{\mathbf{X}}_2}$ is determined using the gradient vector $\nabla f\left({\mathbf{X}}_1\right)$, which is tangential to the third contour surface. Equation (11) is iterated repeatedly in this way; the iteration point ${\mathbf{X}}_{n+1}$ finally falls on the innermost contour surface. Of course, the innermost contour surface almost becomes a point that has fallen on the algebraic surface $\mathbf{S}$. The first property of Newton’s gradient descent indicates that the absolute value $\left|f\right(\mathbf{X}\left)\right|$ of the algebraic surface $f\left(\mathbf{X}\right)$ decreases fastest along the opposite direction to the gradient vector $\nabla f\left(\mathbf{X}\right)$. That is, for every iteration, the absolute value of the algebraic surface is rapidly smaller than the absolute value before the iteration ($\left|f\left({\mathbf{X}}_{k+1}\right)\right|<\left|f\left({\mathbf{X}}_k\right)\right|$), until the absolute value of the algebraic surface is almost zero $\left(\right|f\left(\mathbf{X}\right)|\approx 0)$, and the iteration is terminated. The second property of Newton’s gradient descent method is to select a direction with the largest slope from the current position to perform the next step. In the current position, the third property of Newton’s gradient descent method is to fit the algebraic surface $\mathbf{S}$ using the quadric as the local surface. Then, the path chosen by the Newton’s gradient descent method will be more consistent with the real optimal descent path. Therefore, Equation (11) causes the initial point ${\mathbf{X}}_0$ to be on the algebraic surface as much as possible according to the Newton’s gradient descent property. Finally, the iteration point falls on the algebraic surface completely.

2.2. Moving the Iterative Point ${\mathbf{P}}_{\mathtt{I}}$ to the Close Position of the Orthogonal Projection Point ${\mathbf{P}}_{\Gamma }$

From Algorithm 1, Equation (11) of Algorithm 1, characterized by the Newton’s gradient descent property, is to prompt the initialization point ${\mathbf{X}}_0$ to fall on the algebraic surface $\mathbf{S}$ maximally. The iterative point on the algebraic surface is named as the point ${\mathbf{P}}_{\mathtt{I}}$. After many tests, we find that the point ${\mathbf{P}}_{\mathtt{I}}$ is not far from the orthogonal projection point ${\mathbf{P}}_{\Gamma }$, but there is still a certain distance. Our idea is to make the iterative point ${\mathbf{P}}_{\mathtt{I}}$ as close to the orthogonal projection point ${\mathbf{P}}_{\Gamma }$ as much as possible. That is, to let the point ${\mathbf{P}}_{\mathtt{I}}$ gradually move to the position near the orthogonal projection point ${\mathbf{P}}_{\Gamma }$. This serves to lay a good foundation for the subsequent orthogonalization. In order to bring the iteration point ${\mathbf{P}}_{\mathtt{I}}$ closer to the orthogonal projection point ${\mathbf{P}}_{\Gamma }$, we adopt the tangent plane vertical foot technique to achieve this goal. The basic goal of this technique can be brought about by the following mode. We draw a vertical foot-point ${\mathbf{Q}}_0$ of the tangent plane derived from the iterative point ${\mathbf{P}}_{\mathtt{I}}$ via the test point $\mathbf{P}$. Its expression is the following,

$${\mathbf{Q}}_0=\mathbf{P}-(〈\mathbf{P}-{\mathbf{P}}_{\mathtt{I}},\nabla f\left({\mathbf{P}}_{\mathtt{I}}\right)〉/〈\nabla f\left({\mathbf{P}}_{\mathtt{I}}\right),\nabla f\left({\mathbf{P}}_{\mathtt{I}}\right)〉)\nabla f\left({\mathbf{P}}_{\mathtt{I}}\right).$$

(12)

At this moment, taking the foot-point ${\mathbf{Q}}_0$ as the initial point of Algorithm 1, we obtain the new iterative point ${\mathbf{P}}_{\mathtt{I}}$ on the algebraic surface $\mathbf{S}$, where the new iterative point ${\mathbf{P}}_{\mathtt{I}}$ is named as the current iterative point ${\mathbf{P}}_{\mathtt{I}}$. Based on our understanding and basic geometry properties, let us take the point closer to the algebraic surface as the foot-point. In order to make the foot-point $\mathbf{Q}$ close to the algebraic surface and the orthogonal projection point ${\mathbf{P}}_{\Gamma }$ at the same time, combining with geometric intuition, we select a foot-point $\mathbf{Q}$ on the line segment $\overline{{\mathbf{PQ}}_0}$ to satisfy the relationship

$$\frac{\overrightarrow{{\mathbf{Q}}_0\mathbf{Q}}}{\overrightarrow{{\mathbf{Q}}_0\mathbf{P}}}=d,$$

(13)

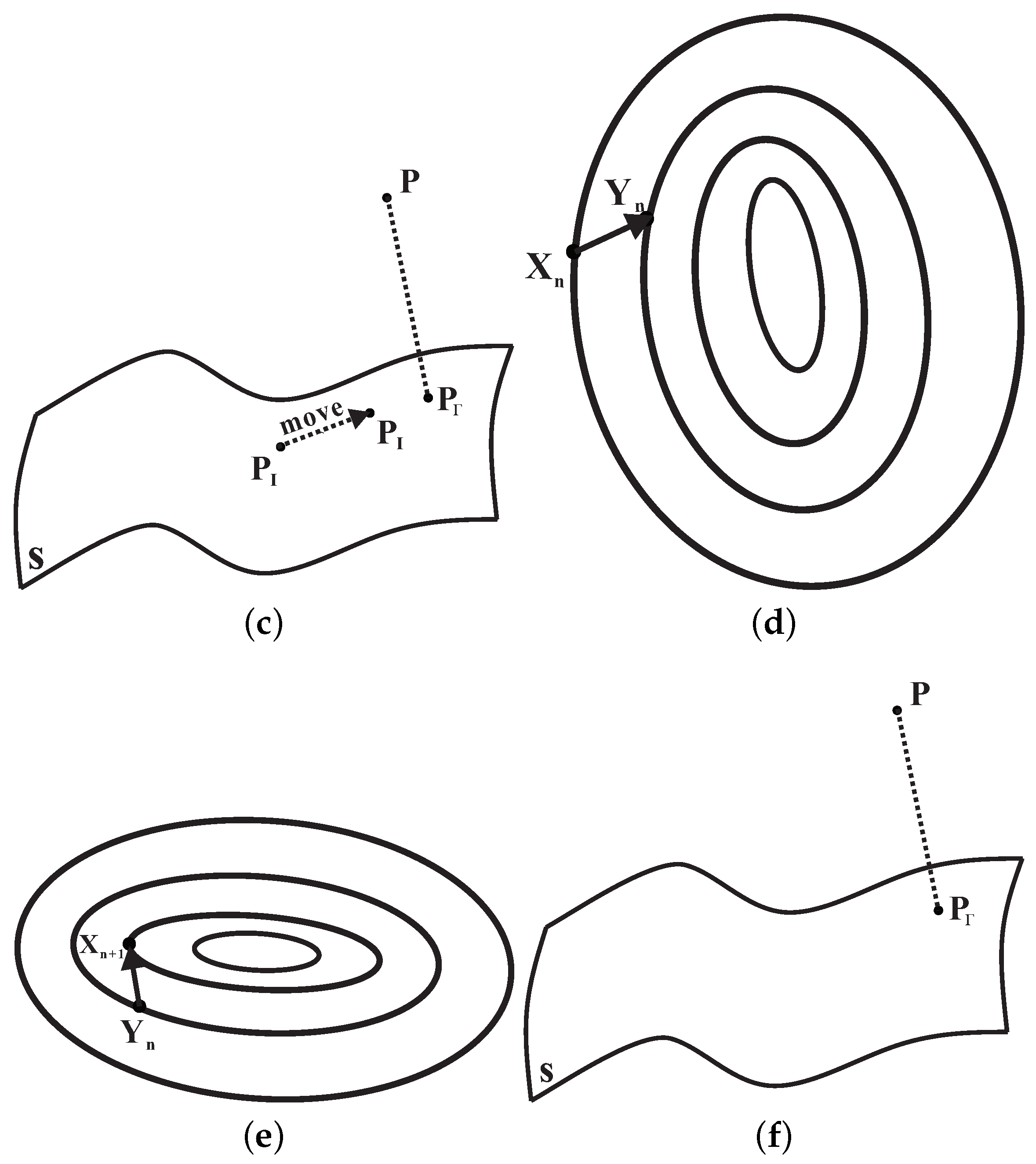
where ${\displaystyle d=\frac{d_1}{d_2}}$, $d_1=0.5·∥\overrightarrow{{\mathbf{P}}_{\mathtt{I}}{\mathbf{Q}}_0}∥$, $d_2=∥\overrightarrow{{\mathbf{Q}}_0\mathbf{P}}∥$. According to Equation (13), it is easy to obtain the following foot-point form $\mathbf{Q}$ (see Figure 3a),

$$\mathbf{Q}=d·(\mathbf{P}-{\mathbf{Q}}_0)+{\mathbf{Q}}_0.$$

(14)

Now, running Equation (14) and Algorithm 1 repeatedly, the iterative point ${\mathbf{P}}_{\mathtt{I}}$ can converge and move to the close position of the orthogonal projection point ${\mathbf{P}}_{\Gamma }$. The detailed description can be expressed as Algorithm 2 (see Figure 3b).

Remark 2.

We present a geometric interpretation for Algorithm 2. From Remark 1, the purpose of Algorithm 1 is to let the initial iteration point be on the algebraic surface maximally. Starting from the iterative point ${\mathbf{P}}_{\mathtt{I}}$, the foot-point $\mathbf{Q}$ is derived by Formula (14). According to our geometric intuition, the vertical point ${\mathbf{Q}}_0$ is located between the iterative point ${\mathbf{P}}_{\mathtt{I}}$ and the orthogonal projection point ${\mathbf{P}}_{\Gamma }$. There are four advantages to choosing point $\mathbf{Q}$ instead of point ${\mathbf{Q}}_0$ as the foot-point. Not only is the foot-point $\mathbf{Q}$ located between the iterative point ${\mathbf{P}}_{\mathtt{I}}$ and the orthogonal projection point ${\mathbf{P}}_{\Gamma }$, but the distance between the foot-point $\mathbf{Q}$ and the algebraic surface $\mathbf{S}$ is also shorter that the distance between the vertical point ${\mathbf{Q}}_0$ and the algebraic surface $\mathbf{S}$. Consequently, the iteration time with Algorithm 1 from the foot-point $\mathbf{Q}$ being used as the initialization point to iterate to the algebraic surface is less than that from the perpendicular point ${\mathbf{Q}}_0$ being used as the initialization point to iterate to the algebraic surface. The fourth advantage is that the closer the foot-point $\mathbf{Q}$ is to the algebraic surface, the higher the stability of the iterative point ${\mathbf{P}}_{\mathtt{I}}$ obtained through Algorithm 1. This means that the distance between the iterative point ${\mathbf{P}}_{\mathtt{I}}$ fallen on the algebraic surface $\mathbf{S}$ caused by Algorithm 1 with the foot-point $\mathbf{Q}$ as the initial iterative point and the orthogonal projection point ${\mathbf{P}}_{\Gamma }$ is not much longer than the distance between the iterative point ${\mathbf{P}}_{\mathtt{I}}$ fallen on the algebraic surface $\mathbf{S}$ caused by Algorithm 1 with the perpendicular point ${\mathbf{Q}}_0$ as the initial iterative point and the orthogonal projection point ${\mathbf{P}}_{\Gamma }$. After Step 2 and Step 3 are jointly implemented five times, the first iteration point ${\mathbf{P}}_{\mathtt{I}}$ fallen on the algebraic surface $\mathbf{S}$ is gradually moved very close to the position of the orthogonal projection point ${\mathbf{P}}_{\Gamma }$.

2.3. Hybrid Geometric Accelerating Orthogonal Method

From Section 2.2, it is not difficult to know that the current iterative point ${\mathbf{P}}_{\mathtt{I}}$ is not only fallen on the algebraic surface, but is also very close to the orthogonal projection point ${\mathbf{P}}_{\Gamma }$. If we convert the $\mathbf{for}$ loop body in Algorithm 2 into the $\mathbf{do}$…$\mathbf{while}$ loop body and the termination criteria are that the distance between the previous iterative point ${\mathbf{P}}_{\mathtt{I}}$ and the current iterative point ${\mathbf{P}}_{\mathtt{I}}$ is zero and the absolute value of the function $f\left({\mathbf{P}}_{\mathtt{I}}\right)$ is almost zero, the slightly improved version of Algorithm 2 is intrinsically and completely equivalent to the foot-point algorithm for an implicit surface in [27]. The slightly improved version of Algorithm 2 is robust and efficient for less partial algebraic surfaces; however, it cannot ensure convergence for total algebraic surfaces. Even if the slightly improved version of Algorithm 2 converges, the moving speed of the iteration point ${\mathbf{P}}_{\mathtt{I}}$ to the orthogonal projection point ${\mathbf{P}}_{\Gamma }$ is occurring very slowly, and the speed of the cross product being zero is determined by the vector $\overrightarrow{{\mathbf{PP}}_{\mathtt{I}}}$, and the vector $\nabla f\left({\mathbf{P}}_{\mathtt{I}}\right)$ is also very slow.

In order to improve the convergence rate, and to accelerate the satisfaction of the first two formulas in Equation (10),

$$\left\{\begin{array}{c}{\mathbf{Y}}_n={\mathbf{X}}_n-(〈f\left({\mathbf{X}}_n\right)〉/〈\nabla f\left({\mathbf{X}}_n\right),\nabla f\left({\mathbf{X}}_n\right)〉)\nabla f\left({\mathbf{X}}_n\right),\hfill \\ {\mathbf{X}}_{n+1}={\mathbf{Y}}_n-(〈F\left({\mathbf{Y}}_n\right)〉/〈\nabla F\left({\mathbf{Y}}_n\right),\nabla F\left({\mathbf{Y}}_n\right)〉)\nabla F\left({\mathbf{Y}}_n\right),\hfill \end{array}\right.$$

(15)

where $\nabla f=[\frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z}]\left|{}_{{\mathbf{X}}_n}\right.$, $\nabla F=[\frac{\partial F}{\partial x},\frac{\partial F}{\partial y},\frac{\partial F}{\partial z}]\left|{}_{{\mathbf{Y}}_n}\right.$. The algorithm formed by this iteration (15) for accelerating orthogonality and falling on the algebraic surface can be described by Algorithm 3 (see Figure 4).

Remark 3.

We present a geometric description for Algorithm 3. After performing Algorithm 2, the current iterative point ${\mathbf{P}}_{\mathtt{I}}$ is not only fallen on the algebraic surface, but the distance between the current iteration point ${\mathbf{P}}_{\mathtt{I}}$ and the orthogonal projection point ${\mathbf{P}}_{\Gamma }$ is also significantly smaller than the distance between the previous iteration point ${\mathbf{P}}_{\mathtt{I}}$ and the orthogonal projection point ${\mathbf{P}}_{\Gamma }$. That is, the current iteration point ${\mathbf{P}}_{\mathtt{I}}$ is closer to the orthogonal projection point ${\mathbf{P}}_{\Gamma }$, and after several iterations, the distance between the current iteration point ${\mathbf{P}}_{\mathtt{I}}$ and the orthogonal projection point ${\mathbf{P}}_{\Gamma }$ is very small. In this case, the current iteration point ${\mathbf{P}}_{\mathtt{I}}$ accords with the local convergence condition of the Newtonian type of Equation (15), which ensures the successful iterative convergence of Equation (15).

The purpose of the first formula of Equation (15) is to ensure that the iterative point can iterate to the algebraic surface maximally, according to the geometrical property of Newton’s gradient descent method. The prototype formula of the second formula of Equation (15) is Formula (9), the geometric essence of which is to seek out a point $\mathbf{X}$ on the algebraic surface. Therefore, we make the vector $\overrightarrow{\mathbf{PX}}$ be perpendicular to the tangent plane of the algebraic surface at the point $\mathbf{X}$. That is to say, we use Formula (9), where we seek the point $\mathbf{X}$ on the algebraic surface, as it plays an important role in accelerating orthogonalization. Namely, every iteration of the second formula of the iterative Formula (15) corresponding to Formula (9) is to ensure that the absolute value of Equation (9) with the expression $F\left({\mathbf{Y}}_n\right)$ becomes smaller or even zero under the condition that the initial iterative point falls on the algebraic surface. Although the second iterative formula of Equation (15) is a locally convergent Newton-type iterative formula, it can be seen from the final iteration point ${\mathbf{P}}_{\mathtt{I}}$ of Algorithm 2 that the final iteration point ${\mathbf{P}}_{\mathtt{I}}$ conforms to the Newton’s local iterative convergence condition of the two sub-equations of Equation (15), so that the iteration of Equation (15) can converge successfully. In this way, we repeatedly run Equation (15), and the iterative point converges to the objective point (the orthogonal projection point ${\mathbf{P}}_{\Gamma }$) quickly and robustly.

Through the above comprehensive analysis, we obtain Algorithm 4, which is the complete algorithm on the point orthogonal projection onto the algebraic surface (see Figure 5).  

Algorithm 4: The complete hybrid geometry strategy algorithm for point orthogonal projection onto an algebraic surface.

Input: Test point $\mathbf{P}$ and the algebraic surface $f\left(\mathbf{X}\right)=0$. Output: Final orthogonal projection point ${\mathbf{P}}_{\Gamma }$ of the test point $\mathbf{P}$. Description: Step 1: Starting from the adjacent point of test point $\mathbf{P}$, calculate the iterative point ${\mathbf{P}}_{\mathtt{I}}$ of the          algebraic surface via Algorithm 1. Step 2: Starting from the iteration point ${\mathbf{P}}_{\mathtt{I}}$, the new iteration point ${\mathbf{P}}_{\mathtt{I}}$ fallen on the algebraic         surface $f\left(\mathbf{X}\right)=0$ close to the orthogonal projection ${\mathbf{P}}_{\Gamma }$ is calculated using Algorithm 2. Step 3: Compute the orthogonal projection point ${\mathbf{P}}_{\Gamma }$ via Algorithm 3.            Return ${\mathbf{P}}_{\Gamma }$;

Remark 4.

In the actual programming implementation of Algorithm 4, we adopt three optimized techniques. Firstly, if the test point $\mathbf{P}$ is a long distance from its orthogonal projection on the algebraic surface, the initialization point ${\mathbf{X}}_0$ of Algorithm 1 is changed to a very small percentage of the test point. However, the initial iterative point ${\mathbf{X}}_0$ of Algorithm 1 in Step 3 of Algorithm 2 is still the foot-point $\mathbf{Q}$ computed using Step 2 of Algorithm 2. Secondly, in order to avoid degenerative situations (the denominators of the iterative Formulas (8), (9), (11), (12), and (15) are 0), we add up a very small perturbation positive number ε to the denominator of each iterative formula, such that Algorithm 4 and other algorithms can run and iterate normally. Thirdly, we have a wonderful discovery. In Algorithm 5, if the test point $\mathbf{P}$ is relatively close to the algebraic surface, or if the iteration point fallen on the algebraic surface of the test point $\mathbf{P}$ and the orthogonal projection point are close to each other, this indicates that the iterative point results of Algorithm 1 with Newton’s local convergence condition of Algorithm 3 have been satisfied. Algorithm 2 with for loop body can be omitted; Algorithm 4 only includes Algorithms 1 and 3. Therefore, the simplified Algorithm 4 can run more efficiently. However, if the test point $\mathbf{P}$ is far away from the algebraic surface, all steps of Algorithm 4 must be fully run, such that Algorithm 4 is very robust.

The simplified and efficient version of Algorithm 4 is represented as Algorithm 5 (see Figure 6).  

Algorithm 5: The simplified version hybrid geometry strategy algorithm for point orthogonal projection onto an algebraic surface.

Input: Test point $\mathbf{P}$ and the algebraic surface $f\left(\mathbf{X}\right)$. Output: Final orthogonal projection point ${\mathbf{P}}_{\Gamma }$ of the test point $\mathbf{P}$. Description: Step 1: Calculate the iterative point ${\mathbf{P}}_{\mathtt{I}}$ fallen on the $f\left(\mathbf{X}\right)$ via Algorithm 1. Step 2: Compute the orthogonal projection point ${\mathbf{P}}_{\Gamma }$ via Algorithm 3.            Return ${\mathbf{P}}_{\Gamma }$;

2.4. Treatment of Multiple Solutions

In practical computer graphics and computer-aided geometric design and other applications, we are going to calculate not just the single orthogonal projector, but sometimes even all the orthogonal projectors. If the topological structure of the algebraic surface is simple, where its genus is zero, and if the algebraic surface is smooth, we present a simple solving method. For a given test point $\mathbf{P}=(p_1,p_2,p_3)$, we assign seven other coordinate symbols to the test point $\mathbf{P}$, respectively. In this way, the changed coordinate symbols of the test point are $(p_1,p_2,-p_3)$, $(p_1,-p_2,p_3)$, $(p_1,-p_2,-p_3)$, $(-p_1,p_2,p_3)$, $(-p_1,p_2,-p_3)$, $(-p_1,-p_2,p_3)$, and $(-p_1,-p_2,-p_3)$, respectively. For each of the eight points, we present a certain percentage reduction, such as one-hundredth of every point, etc. Of course, if the distance between the test point and the corresponding orthogonal projection point of the algebraic surface is very large, one-hundredth of the proportion can be reduced to less. The eight points after scaling down are the initialization point of Algorithm 1, correspondingly. In this way, we want to move the initialization point of each quadrant of the 3D coordinates closer to the algebraic surface. Thus, in each quadrant of 3D coordinates, the corresponding orthogonal projection point can be obtained by using Algorithm 4 as much as possible.

If the topological structure of the algebraic surface is not simple, with its genus not being less than 1, or if the algebraic surface contains multiple branches, the simple method of solving is not fit for dealing with a complicated algebraic surface. Our preliminary idea is to outline the algebraic surface. For this reason, we try to identify a second method for computing several 3D bounding boxes within the prescribed region of the algebraic surface, where every algebraic surface patch is enclosed within one 3D bounding box. We randomly choose a point in each 3D bounding box as the initial point of Algorithm 4, and a corresponding orthogonal projection point is generated. Then, by calculating the distance between the test point $\mathbf{P}$ and each orthogonal projection point, and by finding out the minimum distance for all distances, the orthogonal projection point of the corresponding shortest distance can be found. According to the elementary knowledge of differential geometry, seeking out an orthogonal projection point is to seek out a point $\mathbf{X}$ on the algebraic surface where the cross product between the vector $\overrightarrow{\mathbf{PX}}$ and the normal vector $\mathbf{N}$($\mathbf{N}=\nabla f\left(\mathbf{X}\right))$ is zero. Namely, the vector $\overrightarrow{\mathbf{PX}}$ is orthogonal to the tangent plane of the algebraic surface at the point $\mathbf{X}$, where the corresponding expression determined by the geometric property is Equation (8). Since Equation (8) is a vector equation and not a scalar equation, it is not easy to solve. Taking the inner product of the vector itself $\nabla f\left(\mathbf{X}\right)\times (\mathbf{P}-\mathbf{X})$ of Equation (8), it naturally becomes the scalar equation with Equation (9). Of course, in essence, the geometry of Equation (9) is an algebraic surface, since the algebraic surface with Equation (9) can better embody the essential geometric property of an orthogonal projection than the algebraic surface with Equation (5). Therefore, in the actual selection of algebraic surface patches, we use an algebraic surface with Equation (9) to concretely realize the search for all orthogonal projection points.

Let us assume that the region $\Omega$ of the algebraic surface with Equation (9) is $\Omega =\left[a_1,a_2\right]\times \left[b_1,b_2\right]\times \left[c_1,c_2\right]$. We employ the adaptive affine arithmetic method [35,36,37] to mark a series of 3D bounding boxes where every algebraic surface patch is enclosed in every 3D bounding box. The algebraic surface $F\left(\mathbf{X}\right)=0$ is orthogonally projected onto the $y-z$ plane, the $x-z$ plane, and the $x-y$ plane at the point $(x_0,y_0,z_0)$, respectively. Thus, we obtain three planar algebraic curves $F(x_0,y,z)=0$, $F(x,y_0,z)=0$, and $F(x,y,z0)=0$ on three planes that are perpendicular to each other. To simplify the following expression, the planar algebraic curves $F(x_0,y,z)=0$, $F(x,y_0,z)=0$, and $F(x,y,z0)=0$ can be expressed as $F_1(y,z)=0$, $F_2(x,z)=0$, and $F_3(x,y)=0$, respectively. We construct an important judging function with the planar algebraic curve $F_1(y,z)=0$,

$${\Psi }_{yz}=\frac{2\left|F_{1yz}\right|}{\sqrt{{\left(\frac{F_{1y}}{y_2}\right)}^2+{\left(\frac{F_{1z}}{z_3}\right)}^2}}.$$

(16)

Analogously, we also construct an important judging function with the planar algebraic curve $F_2(x,z)=0$ and the planar algebraic curve $F_3(x,y)=0$,

$${\Psi }_{xz}=\frac{2\left|F_{2xz}\right|}{\sqrt{{\left(\frac{F_{2x}}{x_1}\right)}^2+{\left(\frac{F_{2z}}{z_3}\right)}^2}},$$

(17)

and

$${\Psi }_{xy}=\frac{2\left|F_{3xy}\right|}{\sqrt{{\left(\frac{F_{3x}}{x_1}\right)}^2+{\left(\frac{F_{3y}}{y_2}\right)}^2}},$$

(18)

where $F_{1y}=\frac{\partial F_1(y,z)}{\partial y}$, $F_{1z}=\frac{\partial F_1(y,z)}{\partial z}$, $F_{2x}=\frac{\partial F_2(x,z)}{\partial x}$, $F_{2z}=\frac{\partial F_2(x,z)}{\partial z}$, $F_{3x}=\frac{\partial F_3(x,y)}{\partial x}$, $F_{3y}=\frac{\partial F_3(x,y)}{\partial y}$, $F_{1yz}=\frac{{\partial }^2{F}_1(y,z)}{\partial y\partial z}$, $F_{2xz}=\frac{{\partial }^2{F}_2(x,z)}{\partial x\partial z}$, $F_{3xy}=\frac{{\partial }^2{F}_3(x,y)}{\partial x\partial y}$, $x_0=\frac{a_1+a_2}{2}$, $x_1=\frac{a_2-a_1}{2}$, $y_0=\frac{b_1+b_2}{2}$, $y_2=\frac{b_2-b_1}{2}$, $z_0=\frac{c_1+c_2}{2}$, and $z_3=\frac{c_2-c_1}{2}$. The unknown variable $\mathbf{X}$ in each of the nine partial derivative functions $F_{1y}$, $F_{1z}$, $F_{2x}$, $F_{2z}$, $F_{3x}$, $F_{3y}$, $F_{1yz}$, $F_{2xz}$, $F_{3xy}$ is replaced by a point value $(x_0,y_0,z_0)$, and afterwards, this point is named $(x_0,y_0,z_0)$ as the center point of the 3D bounding box. By combining three Formulas (16)–(18), we obtain the crucial judging function $\Psi$ with Equation (19),

$$\Psi =Max\{{\Psi }_{xy},{\Psi }_{yz},{\Psi }_{xz}\}.$$

(19)

We assign a critical value for the crucial judging function $\Psi$ with Equation (19). The adaptive approach method [38,39] of solving a series of 2D bounding boxes of the planar algebraic curve is adopted to solve a series of 3D bounding boxes of the algebraic surface. The exact interpretation of Equation (19) is completely the same as the interpretation in [38]. On an affine arithmetic, we mainly assimilate the idea of the work in [38]. However, we have to assimilate the idea of the paper [39] to investigate a series of 3D bounding boxes with the more complicated topological structure of the algebraic surface. The detailed description for solving a series of 3D bounding boxes of the algebraic surface can be described as Algorithm 6.  

Algorithm 6: To seek out a series of 3D bounding boxes of the algebraic surface $F\left(\mathbf{X}\right)=0$.

Input: The algebraic surface $F\left(\mathbf{X}\right)=0$ and the initial 3D bounding box including or intersecting with the algebraic surface $F\left(\mathbf{X}\right)=0$. Output: A number of 3D bounding boxes satisfied with certain conditions. Description: Step 1: Subdivide this 3D bounding box into 8 3D sub-bounding boxes by dividing by 2 on each axis. Step 2: Compute the critical value $\Psi$ of each 3D sub-bounding box through Equation (19). Step 3: if ($\Psi$$<=$ the critical value and recursion times $<10$){                  Execute Algorithm 6 with the 3D sub-bounding box.               }               if ($\Psi$$<=$ critical value and recursion times $==$ 10){                  Store all 3D bounding sub-boxes in one set.               } End Algorithm.

In short, three important techniques and schemes are adopted in the process of realizing a point orthogonal projection onto an algebraic surface. In the first step, the Newton gradient descent method of Algorithm 1 is used to ensure that the initial iteration can iterate and fall on the algebraic surface. In the second step, Algorithm 2 is used to gradually move the iterative point fallen on the algebraic surface to the orthogonal projection point at a very close position, such that the local convergence condition of the last step is satisfied. In the third step, Algorithm 3 is adopted to accelerate the iteration of the iteration point to the algebraic surface and orthogonalization by using the Newton gradient descent method and the second-order Newton iteration method under the condition of local convergence condition. Thus, Algorithm 4 is guaranteed to be robust and efficient. In the latter part of Section 2, a simplified state and a multi-solution state are also discussed and analyzed.

3. Convergence Analysis

Lemma 1.

Suppose that $F\in C^2\left(D\right)$, where this function F is Equation (9). Assume that the function $F:D\subseteq R\to R$ has a simple root ${\mathbf{X}}^{*}\in D$, where D is an open interval. If the initial iterative point ${\mathbf{X}}_0$ is sufficiently close to ${\mathbf{X}}^{*}$, then the method defined by the second step of Equation (15) has second-order convergence.

Proof. 

This lemma is completely similar to the fundamental local convergence theorem of Newton’s iterative method. We are not going to prove it. □

Theorem 1.

Algorithm 4 is able to converge successfully, and the order of convergence of Algorithm 4 is no more than 2.

Proof. Part One: 

Algorithm 4 is able to converge successfully.

Algorithm 4 mainly contains three important components: Algorithm 1 (Newton’s gradient descent method), Algorithm 2 (computing the foot-point $\mathbf{Q}$ and moving the iterative point ${\mathbf{P}}_{\mathtt{I}}$ to the close position of the orthogonal projection point ${\mathbf{P}}_{\Gamma }$), and Algorithm 3 (the hybrid geometric accelerated orthogonal method).

From Remark 1, the function of Equation (11) is to cause the initial point ${\mathbf{X}}_0$ to be on the algebraic surface as much as possible, according to the Newton’s gradient descent property. Consequently, the initial point ${\mathbf{X}}_0$ can be realized to be fallen on the algebraic surface.

From Remark 2, the essential geometric feature of Algorithm 2 is to make the iteration point ${\mathbf{P}}_{\mathtt{I}}$ of the first fallen on the algebraic surface realized by Algorithm 1 move five times, and to let the iteration point ${\mathbf{P}}_{\mathtt{I}}$ be gradually moved to the position that is particularly close to the orthogonal projection point ${\mathbf{P}}_{\Gamma }$. Thus, the final iteration point ${\mathbf{P}}_{\mathtt{I}}$ of Algorithm 2 satisfies the Newtonian’s local convergence condition of Algorithm 3.

From Remark 3, the geometric essence of Algorithm 3 is a Newton-type iteration. The final iteration point of Algorithm 2 as the initial iteration point of Algorithm 3 can satisfy the local convergence condition of Algorithm 3, or the initial iteration point of Algorithm 3 satisfies the convergence condition of iteration Formula (15); Algorithm 3 can converge quickly and successfully.

In short, from the above analysis, we can show that Algorithm 4 can be convergent.

Part Two: 

The order of convergence of Algorithm 4 is no more than 2.

In this part, a numerical analysis method is used to prove the order of convergence of Algorithm 4. Algorithm 4 mainly includes three sub-algorithms: Algorithm 1 that adopts Formula (11), Algorithm 2 that adopts Formula (14), and Algorithm 3 that adopts Formula (15).

Firstly, the order of convergence of the iterative formula (11) is proven to be 2. Without a loss of generality, it is assumed that the algebraic surface $f\left(\mathbf{X}\right)=0$ can be expressed in parameterized form, where the parameter $\mathbf{\alpha }={({\alpha }_1,{\alpha }_2)}^T$ is the corresponding parameter of the orthogonal projection point ${\mathbf{P}}_{\Gamma }$ of the test point $\mathbf{P}$ on the algebraic surface after parameterization. It is not difficult to tell that the corresponding parameterized Newton’s iteration of iteration (11) can be expressed as

$${\mathbf{U}}_{n+1}={\mathbf{U}}_n-G_1\left({\mathbf{U}}_n\right)F_1\left({\mathbf{U}}_n\right),$$

(20)

where $G_1\left(\mathbf{U}\right)=F_1^{\prime -1}\left(\mathbf{U}\right)$ is inverse matrix of the Jacobian matrix of the equation $F_1\left(\mathbf{U}\right)=0$. Taylor’s expansion is performed near the parameter root $\mathbf{\alpha }={({\alpha }_1,{\alpha }_2)}^T$ of the equation $F_1\left(\mathbf{U}\right)=0$, then we have

$$F_1\left({\mathbf{U}}_n\right)=C_0+C_1{\mathbf{e}}_n+C_2{\mathbf{e}}_n^2+o\left({\mathbf{e}}_n^3\right),$$

(21)

where ${\mathbf{e}}_n={\mathbf{U}}_n-\mathbf{\alpha },C_i=(1/i!)\left(F_1^{\left(j\right)}\left(\mathbf{\alpha }\right)\right),i=0,1,2$. From Equation (21), we can easily obtain the following two formulas,

$$F_1^{\prime }\left({\mathbf{U}}_n\right)=C_1+2C_2{\mathbf{e}}_n+o\left({\mathbf{e}}_n^2\right)$$

(22)

and

$$F_1^{\prime \prime }\left({\mathbf{U}}_n\right)=2C_2+o\left({\mathbf{e}}_n\right)$$

(23)

Thus, according to Equations (21)–(23), it can be concluded that the iterative error of Equation (20) is

$${\mathbf{e}}_{n+1}=C_1^{-1}{C}_2{\mathbf{e}}_n^2+o\left({\mathbf{e}}_n^3\right)$$

(24)

Equation (24) shows that iterative Equation (11) converges to order 2.

Secondly, it is deduced that the order of foot-point $\mathbf{Q}$ in Equation (14) is no more than 2. Since ${\mathbf{Q}}_0$ is the vertical foot derived from the tangent plane, it is clear that the order of foot-point $\mathbf{Q}$ in Equation (14) is 1. Therefore, the order of convergence of the foot-point $\mathbf{Q}$ is 1.

Thirdly, from Lemma 1, the order of convergence of the second equation of Equation (15) is 2, and the order of convergence of the first equation of Equation (15) is also 2. Then, the order of convergence of Equation (15) is 2.

Based on the above three parts, it can be seen that the order of convergence of Algorithm 4 is no more than 2. □

4. Experimental Results

Example 1.

Suppose that an algebraic surface $f(x,y,z)=\frac{x^2}{4}+xy+\frac{y^2}{13}+z-1=0$ (see Figure 7), in the region [−200, 200] × [−200, 200] × [−200, 200]. All the computations were performed using the mathematics and engineering computing software Maple 18, with $\epsilon ={10}^{-20}$ via Algorithm 4. In

Table 1. The obtained running results of Algorithm 4 through Example 1.

P	(320, 490, 730)	(376, 949, 738)	(276, 806, −528)
${\mathbf{P}}_{\Gamma }$	(0.6548, 0.1105, 0.8194)	(1.3100, −0.1467, 0.7615)	(−1.5632, 0.2567, 0.7853)
$\left|f\left({\mathbf{P}}_{\Gamma }\right)\right|$	$1.0\times {10}^{-20}$	$5.0\times {10}^{-20}$	$2.0\times {10}^{-20}$
$F\left({\mathbf{P}}_{\Gamma }\right)$	$3.1\times {10}^{-21}$	$1.3\times {10}^{-21}$	$3.3\times {10}^{-22}$
$\mathbf{P}$	(476, −606, 238)	(882, −206, 215)	(582, −406, −715)
${\mathbf{P}}_{\Gamma }$	(−3.2380, 3.7149, 9.3464)	(−1.8122, 5.1651, 7.4873)	(0.74713, −1.1846, 1.6375)
$\left|f\left({\mathbf{P}}_{\Gamma }\right)\right|$	$2.0\times {10}^{-19}$	$2.0\times {10}^{-20}$	0.0
$F\left({\mathbf{P}}_{\Gamma }\right)$	$6.5\times {10}^{-12}$	$9.0\times {10}^{-21}$	$4.9\times {10}^{-22}$
$\mathbf{P}$	(−622, 316, 213)	(−307, 416, 213)	(−207, 273, −376)
${\mathbf{P}}_{\Gamma }$	(2.1944, −4.1355, 7.5558)	(2.4351, −2.7091, 5.5502)	(−0.8714, 0.9816, 1.5914)
$\left|f\left({\mathbf{P}}_{\Gamma }\right)\right|$	$1.0\times {10}^{-19}$	$5.9\times {10}^{-18}$	$4.0\times {10}^{-20}$
$F\left({\mathbf{P}}_{\Gamma }\right)$	$2.5\times {10}^{-14}$	$1.5\times {10}^{-13}$	$5.6\times {10}^{-22}$
$\mathbf{P}$	(−359, −233, 246)	(−259, −333, 246)	(−249, −233, −556)
${\mathbf{P}}_{\Gamma }$	(−0.7784, −1.0665, −0.0692)	(−1.2903, −0.4026, 0.0517)	(0.3791, 0.2582, 0.8610)
$\left|f\left({\mathbf{P}}_{\Gamma }\right)\right|$	$1.0\times {10}^{-20}$	$3.0\times {10}^{-20}$	$1.0\times {10}^{-20}$
$F\left({\mathbf{P}}_{\Gamma }\right)$	$4.3\times {10}^{-17}$	$3.1\times {10}^{-22}$	$1.0\times {10}^{-18}$
$\mathbf{P}$	(476, 616, −5238)	(522, −606, −215)	(−237, 393, −256)
${\mathbf{P}}_{\Gamma }$	(−0.1122, −0.0347, 0.9928)	(3.2821, −3.9458, 10.060)	(−1.7864, 1.8008, 3.1697)
$\left|f\left({\mathbf{P}}_{\Gamma }\right)\right|$	$2.1\times {10}^{-18}$	$3.8\times {10}^{-19}$	$2.0\times {10}^{-19}$
$F\left({\mathbf{P}}_{\Gamma }\right)$	$8.9\times {10}^{-22}$	$9.8\times {10}^{-14}$	$1.9\times {10}^{-14}$
$\mathbf{P}$	(−249, −633, −256)
${\mathbf{P}}_{\Gamma }$	(2.5127, −0.2743, 0.1050)
$\left|f\left({\mathbf{P}}_{\Gamma }\right)\right|$	0.0
$F\left({\mathbf{P}}_{\Gamma }\right)$	$6.7\times {10}^{-17}$

, the four symbols $\mathbf{P}$, ${\mathbf{P}}_{\Gamma }$, $\left|f\left({\mathbf{P}}_{\Gamma }\right)\right|$, and $F\left({\mathbf{P}}_{\Gamma }\right)$ are the test point, the orthogonal projection point of the test point, the deviation degree of the orthogonal projection point on the algebraic surface, and the expression $〈\nabla f\left({\mathbf{P}}_{\Gamma }\right)\times (\mathbf{P}-{\mathbf{P}}_{\Gamma }),\nabla f\left({\mathbf{P}}_{\Gamma }\right)\times (\mathbf{P}-{\mathbf{P}}_{\Gamma })〉$ for the second formula of Equation (10), respectively. In the specified region, we randomly select a mass of 3D points as test points. The probability of non-convergence using Algorithm 4 with these test points is extremely low, which is detected to have very high robustness and efficiency. Furthermore, in each quadrant of eight quadrants, we arbitrarily choose two different test points. The corresponding orthogonal projection point for each test point is computed using Algorithm 4. The concrete computed values are displayed in Table 1, where the digital values of the orthogonal projective point we present are abbreviated. For example, if test point $\mathbf{P}$ is (320,490,730), the actual values ${\mathbf{P}}_{\Gamma }$, $\left|f\left({\mathbf{P}}_{\Gamma }\right)\right|$ and $F\left({\mathbf{P}}_{\Gamma }\right)$ are (0.65483015050952098661, 0.11053569270327875241, 0.819477407332403977390), 1.0 × 10${}^{-20}$, and 3.0900825879965 × 10${}^{-21}$, respectively. In Table 1, the corresponding values of the other test points are completely the same. Limited by Table 1, we only present four digits after the decimal point.

Example 2.

Suppose an algebraic surface $f(x,y,z)=x^3+y^3+z^3+1-{(x+y+z+1)}^4=0$ (see Figure 8), in the region [−200, 200] × [−200, 200] × [−200, 200]. All computations were performed using the Maple 18 environment with $\epsilon ={10}^{-20}$ via Algorithm 4. In

Table 2. The obtained running results of Algorithm 4 through Example 2.

P	(320, 490, 530)	(326, 449, 278)
${\mathbf{P}}_{\Gamma }$	(0.8978283018, −0.4745725889, −0.3003785997)	(0.5805473488, 0.0686066996, −0.6802898709)
$\left|f\left({\mathbf{P}}_{\Gamma }\right)\right|$	$9.4\times {10}^{-10}$	$6.1\times {10}^{-10}$
$F\left({\mathbf{P}}_{\Gamma }\right)$	$1.6\times {10}^{-12}$	$5.4\times {10}^{-13}$
$\mathbf{P}$	(276, 306, −328)	(376, 316, −238)
${\mathbf{P}}_{\Gamma }$	(0.3499239738, 0.2912835991, −0.9361716812)	(0.2734464553, 0.3875179615, −0.9183591981)
$\left|f\left({\mathbf{P}}_{\Gamma }\right)\right|$	$2.6\times {10}^{-10}$	$3.7\times {10}^{-10}$
$F\left({\mathbf{P}}_{\Gamma }\right)$	$1.8\times {10}^{-11}$	$4.0\times {10}^{-11}$
$\mathbf{P}$	(276, −309, 238)	(382, −206, 215)
${\mathbf{P}}_{\Gamma }$	(0.2785766037, −0.9391397370, 0.3606532988)	(0.1720828409, −0.9348105519, 0.5199384062)
$\left|f\left({\mathbf{P}}_{\Gamma }\right)\right|$	$5.2\times {10}^{-10}$	$6.7\times {10}^{-10}$
$F\left({\mathbf{P}}_{\Gamma }\right)$	$2.6\times {10}^{-11}$	$2.0\times {10}^{-11}$
$\mathbf{P}$	(382, −287, −409)	(422, −306, −217)
${\mathbf{P}}_{\Gamma }$	(0.2468466777, −0.3925225425, −0.4136091918)	(0.23453300365, −0.4031775077, −0.3865167494)
$\left|f\left({\mathbf{P}}_{\Gamma }\right)\right|$	$8.4\times {10}^{-10}$	$8.5\times {10}^{-10}$
$F\left({\mathbf{P}}_{\Gamma }\right)$	$1.3\times {10}^{-11}$	$1.1\times {10}^{-11}$
$\mathbf{P}$	(−422, 316, 213)	(−307, 216, 293)
${\mathbf{P}}_{\Gamma }$	(−0.2590172850, −0.1971877899, −0.2069292587)	(−0.2565723559, −0.2062237616, −0.1977314391)
$\left|f\left({\mathbf{P}}_{\Gamma }\right)\right|$	$9.5\times {10}^{-10}$	$7.8\times {10}^{-10}$
$F\left({\mathbf{P}}_{\Gamma }\right)$	$5.8\times {10}^{-11}$	$8.8\times {10}^{-11}$
$\mathbf{P}$	(−207, 273, −376)	(−237, 393, −256)
${\mathbf{P}}_{\Gamma }$	(−0.3472321429, 0.1281172458, −0.3965695863)	(−0.3615862188, 0.1322536132, −0.36628133060)
$\left|f\left({\mathbf{P}}_{\Gamma }\right)\right|$	$8.7\times {10}^{-10}$	$7.7\times {10}^{-10}$
$F\left({\mathbf{P}}_{\Gamma }\right)$	$4.0\times {10}^{-12}$	$2.3\times {10}^{-12}$
$\mathbf{P}$	(−359, −233, 246)	(−259,−333, 246)
${\mathbf{P}}_{\Gamma }$	(−0.3904801634, −0.3514720192, 0.1165325261)	(−0.3594935775, −0.3823713615, 0.1161247111)
$\left|f\left({\mathbf{P}}_{\Gamma }\right)\right|$	$8.3\times {10}^{-10}$	$7.2\times {10}^{-10}$
$F\left({\mathbf{P}}_{\Gamma }\right)$	$2.4\times {10}^{-12}$	$4.7\times {10}^{-11}$
$\mathbf{P}$	(−249, −233, −556)	(−249, −633, −256)
${\mathbf{P}}_{\Gamma }$	(0.6777775475, −0.6538305244, −1.0105058748)	(0.62667855421, −0.9971463160, −0.6338419899)
$\left|f\left({\mathbf{P}}_{\Gamma }\right)\right|$	$2.8\times {10}^{-10}$	$2.0\times {10}^{-10}$
$F\left({\mathbf{P}}_{\Gamma }\right)$	$3.1\times {10}^{-11}$	$2.2\times {10}^{-11}$

, the four symbols $\mathbf{P}$, ${\mathbf{P}}_{\Gamma }$, $\left|f\left({\mathbf{P}}_{\Gamma }\right)\right|$, and $F\left({\mathbf{P}}_{\Gamma }\right)$ are the test point, the orthogonal projection point of the test point, the deviation degree of the orthogonal projection point on the algebraic surface, and the expression $〈\nabla f\left({\mathbf{P}}_{\Gamma }\right)\times (\mathbf{P}-{\mathbf{P}}_{\Gamma }),\nabla f\left({\mathbf{P}}_{\Gamma }\right)\times (\mathbf{P}-{\mathbf{P}}_{\Gamma })〉$ for the second formula of Equation (10), respectively. In the specified region, we randomly select a mass of 3D points as test points; the probability of non-convergence using Algorithm 4 with these test points is extremely low, and it is detected with very high robustness and efficiency. Furthermore, in each quadrant of eight quadrants, we arbitrarily choose two different test points. The corresponding orthogonal projection point for each test point is computed using Algorithm 4. The concrete computed values are displayed in Table 2, where the digital values of the orthogonal projective point we present are abbreviated. For example, if test point $\mathbf{P}$ is (320,490,530), the actual values ${\mathbf{P}}_{\Gamma }$, $\left|f\left({\mathbf{P}}_{\Gamma }\right)\right|$ and $F\left({\mathbf{P}}_{\Gamma }\right)$ are (0.89782830182962418807, −0.47457258895408409955, −0.30037859976898496332), $9.418433921\times {10}^{-10}$, and $1.6452196947017076704\times {10}^{-12}$, respectively. In Table 2, the corresponding values of the other test points are completely the same. Limited by Table 2, we only present 10 digits after the decimal point.

Example 3.

Now, we consider a self-intersecting quasi-algebraic surface $f(x,y,z)=x^2-y^2+z^3=2$, where $y=exp(-xz)$ (see Figure 9). Since the surface is not a complete algebraic surface in the true sense, some parts of the surface are singular regions, which may not converge for Algorithm 4, but for non-singular regions, Algorithm 4 can still converge. In the specified region, we arbitrarily choose two different 3D test points. The implementation requirements and environment are exactly the same as those of Examples 1 and 2. The corresponding orthogonal projection point for each test point was computed using Algorithm 4. The concrete computed values are displayed in

Table 3. The obtained running results of Algorithm 4 through Example 3.

P	(6, 7, 8)	(8, 6, 5)
${\mathbf{P}}_{\Gamma }$	(0.9064333791, 6.9928001253, 1.1419222319)	(1.2015703426, 5.9813549954, 0.8314404941)
$\left|f\left({\mathbf{P}}_{\Gamma }\right)\right|$	$5.5\times {10}^{-7}$	$5.3\times {10}^{-6}$
$F\left({\mathbf{P}}_{\Gamma }\right)$	$4.6\times {10}^{-5}$	$6.0\times {10}^{-4}$
$\mathbf{P}$	(6, −6, 6)	(7, −6, 8)
${\mathbf{P}}_{\Gamma }$	(1.0295698711, −6.0000061990, 1.0295698711)	(0.9723667468, −6.0029643353, 1.0843126066)
$\left|f\left({\mathbf{P}}_{\Gamma }\right)\right|$	$3.0\times {10}^{-10}$	$1.6\times {10}^{-5}$
$F\left({\mathbf{P}}_{\Gamma }\right)$	$1.0\times {10}^{-9}$	$9.1\times {10}^{-6}$
$\mathbf{P}$	(−4, 4, −5)	(−4, 5, −6)
${\mathbf{P}}_{\Gamma }$	(−0.9304838087, 3.9918808576, −1.1213468254)	(−0.8542470910, 4.9870922392, −1.1851067449)
$\left|f\left({\mathbf{P}}_{\Gamma }\right)\right|$	$8.6\times {10}^{-5}$	$2.1\times {10}^{-5}$
$F\left({\mathbf{P}}_{\Gamma }\right)$	$9.4\times {10}^{-5}$	$5.9\times {10}^{-5}$
$\mathbf{P}$	(−7, −6, −8)	(−6, −8, −9)
${\mathbf{P}}_{\Gamma }$	(−0.9724553347, −6.0060342760, −1.0842198022023942600)	(−0.8575669009, −8.0072947909, −1.1814724407)
$\left|f\left({\mathbf{P}}_{\Gamma }\right)\right|$	$1.9\times {10}^{-5}$	$5.1\times {10}^{-5}$
$F\left({\mathbf{P}}_{\Gamma }\right)$	$2.9\times {10}^{-5}$	$4.5\times {10}^{-5}$

, and the digital values of the orthogonal projective point we present are abbreviated. From Table 3, the probability of convergence using Algorithm 4 with these test points is high, which is detected to be a sign of robustness and efficiency.

Remark 5.

In this remark, outside the regions [−200, 200] × [−200, 200] × [−200, 200] specified in Examples 1 and 2, we randomly selected two different test points in each quadrant that were far from the algebraic surface. Through Algorithm 4, each test point can be orthogonally projected onto the corresponding orthogonal projection point. The existing algorithms cannot converge to the corresponding orthogonal projection points because the test points are far from the algebraic surface, or the initialization points are not properly selected, etc.

Table 4. Comparison of convergence results of various algorithms and their reason analysis with Examples 1 and 2.

Algorithms	Convergence or Not	Reasons
Our Algorithm 4	Being convergent	Being independent of the initial point.
Newton’s method	Being divergent	Being dependent on the initial point.
Algorithm [1]	Being divergent	Being dependent on the initial point.
Homotopy method [12,13]	Being divergent	Difficulty in finding an objective solving system of nonlinear equations of homotopy method.
Resultant method [16,17,18,19]	Being divergent	Difficulty in directly solving all solutions of nonlinear polynomial system with the resultant method, due to the degree of the algebraic surface being more than 4.
Bézier clipping technique [20,21,22]	Being divergent	Equation (9) being difficult or even impossible to transform into Bernstein–Bézier form for a fraction of the algebraic surfaces.
Algorithm [27]	Being divergent	The vertical foot-point being regarded as the next iteration point resulting from the test point being far from the algebraic surface.

shows whether the various algorithms converge and the reasons for their convergence. Once again, it shows that Algorithm 4 can converge to the corresponding orthogonal projection point quickly, accurately, and efficiently.

5. Conclusions and Future Work

In this paper, we discuss and analyze a topic associated with point orthogonal projection onto the algebraic surface. The presented key and core algorithm is involved in constructing an orthogonal polynomial and using the Newton iterative method for iteration. In order to ensure maximum robustness, two techniques were adopted before the Newton iteration: (1) Newton’s gradient descent method, which is used to make the initial iteration point fall onto the algebraic surface; and (2) computing the foot-point and moving the iterative point to the close position of the orthogonal projection point. Theoretical analysis and experiences show that the proposed algorithm could accurately and efficiently converge to the orthogonal projection point for test points in different spatial positions.

In the future, we will try to study and explore some more efficient and robust algorithms for calculating the minimum distance between a point and an algebraic surface, or the shortest distance between two algebraic surfaces. For any unrestricted initial iteration point and test point for any position in three-dimensional space, or for an irregular algebraic surface, future work will involve constructing a brand new algorithm to satisfy the following conditions: the convergence of a new algorithm should be robust and efficient, and the convergent orthogonal projection point should simultaneously fit for three relationships of Equation (9). It will undoubtedly be a huge future challenge to develop and explore such satisfactory algorithms.