Approximating a Common Solution of Monotone Inclusion Problems and Fixed Point of Quasi-Pseudocontractive Mappings in CAT(0) Spaces

Abstract

In this paper, we aimed to introduce a new viscosity-type approximation method for finding the common fixed point of a class of quasi-pseudocontractive mapping and a system of monotone inclusion problems in CAT(0) spaces. We proved some fixed-point properties concerning the class of quasi-pseudocontractive mapping in CAT(0) spaces, which is more general than many other mappings such as nonexpansive, quasi-nonexpansive, pseudocontractive and demicontractive mappings which have been studied by other authors. A strong convergence result is proved under some mild conditions on the control sequences and some numerical examples were presented to illustrate the performance and efficiency of the proposed method.

1. Introduction

Recently, the monotone inclusion problem (shortly, MIP) has played a crucial role in the study of various optimization problems such as variational inequality problems, equilibrium problems, convex minimization problems, convex feasibility problems, saddle point problems, etc. Mathematically, this can be defined as

$$\mathrm{find}x\in D\left(A\right)\mathrm{such}\mathrm{that}0\in A\left(x\right),$$

(1)

where $A:X\to 2^{X^{\ast }}$ is a set-valued monotone operator, $D\left(A\right):=\{x\in X:\mathrm{dom}(A)\ne \varnothing \}$ is the effective domain of A and X is a topological space with dual $X^{\ast }.$ We denote the solution set of (1) by $A^{-1}\left(0\right)$. This problem is better studied using the idea of monotonicity along with sub-differentiability which is also a monotone operator (see [1]). Various iterative methods have been proposed to solve the MIP and other related optimization problems. One of the popular methods for finding a solution to the MIP is the proximal point algorithm (PPA) which was first introduced by Martinet [2] in Hilbert space and was later developed by Rockefeller [3] who proved that the PPA weakly converges to a zero of a monotone operator. As a result, many authors have modified the PPA to acquire strong convergence results in Banach and Hilbert space (see, e.g., [4,5] and references therein). Hadamard spaces are considered to be the most suitable framework for studying optimization problems and other related mathematical problems, since many applicable problems can be formulated in Hadamard spaces than in Hilbert and Banach spaces. For instance, the minimizer of an energy functional (which is an example of a convex and lower semicontinuous functional in Hadamard space) called harmonic mappings, are useful in geometry and analysis [6]; the proximal point algorithm for optimization problems in Hadamard spaces has been successfully applied for computing medians and means in computational phylogenetics, diffusion tensor, imaging, consensus algorithms and the modeling of airway systems in human lungs and blood vessels [7,8]; and many non-convex problems in linear settings can be viewed as convex problems in Hadamard space [9].

In 2016, Khatibzadeh and Ranjbar [10] generalized and studied the monotone operators in the framework of CAT(0) spaces. They established some fundamental properties of the resolvent of a monotone operator and studied the following PPA to approximate the solution of (1) in CAT(0) spaces: given $x_0\in X$ and $\lambda >0,$ compute

$$x_{n+1}=\left[\frac{1}{\lambda }\overrightarrow{x_n{x}_{n-1}}\right]\in A\left(x_n\right).$$

(2)

It was proven that (2) $\Delta$-converges towards a zero of the monotone operator in a complete CAT(0) space which is called a Hadamard space. The authors also proposed the following Mann-type and Halpern-type algorithms for approximating a solution of MIP: Given $u,x_0\in X,$$\lambda >0,$ $\left\{{\alpha }_n\right\}\subset (0,1),$ compute

$$x_{n+1}={\alpha }_n{x}_n\oplus (1-{\alpha }_n)J_{\lambda }^A{x}_n,$$

(3)

and

$$x_{n+1}={\alpha }_{n}u\oplus (1-{\alpha }_n)J_{\lambda }^A{x}_n,$$

(4)

where $J_{\lambda }^A:X\to 2^X$ is the resolvent of the monotone operator A defined by

$$J_{\lambda }^A\left(x\right):=\left\{z\in X:\left[\frac{1}{\lambda }\overrightarrow{zx}\right]\in Az\right\}.$$

The authors proved that the sequences $\left\{x_n\right\}$ generated by (3) and (4) converge weakly and strongly to a solution of MIP, respectively.

On the other hand, Moudafi [11] introduced the viscosity iterative scheme for approximating the fixed point of nonexpansive mappings in real Hilbert spaces as follows:

$$\left\{\begin{array}{c}{x}_0\in X,\hfill \\ x_{n+1}={\alpha }_{n}f\left(x_n\right)+(1-{\alpha }_n)T{x}_n,n\ge 1,\hfill \end{array}\right.$$

(5)

where $\left\{{\alpha }_n\right\}\subset [0,1],$$f:X\to X$ is a contraction mapping and T is a nonexpansive mapping on X. The viscosity approximation method is known to yield strong convergence sequences and most importantly, it performs better numerically than many other iterative methods such as the Mann, Ishikawa, Hybrid and Halpern iterative schemes for approximating the fixed point of nonlinear mappings. More so, the viscosity approximation method was incorporated for solving many optimization problems; see, e.g., [12,13,14,15,16]. Recently, the viscosity method was extended to CAT(0) spaces for approximating the fixed point of other nonlinear mappings such as strictly nonexpansive, pseudocontractive, nonspreading, and demicontractive mappings; see [12,13,14,15,16,17]. In particular, Aremu et al. [16] introduced a viscosity method for approximating a common solution of variational inequality problems and a fixed point of Lipschitz demicontractive mappings in CAT(0) spaces as follows:

$$\left\{\begin{array}{c}{w}_n={\gamma }_{n}f\left(x_n\right)\oplus (1-{\gamma }_n)x_n,\hfill \\ y_n={\beta }_{n,0}{w}_n\oplus {\displaystyle \sum _{i=1}^N}\oplus {\beta }_{n,i}{T}_{{\lambda }_{n,i}}{w}_n,\hfill \\ x_{n+1}={\alpha }_{n,0}{y}_n\oplus {\displaystyle \sum _{i=1}^N}\oplus {\alpha }_{n,i}{S}_i{y}_n,n\ge 1,\hfill \end{array}\right.$$

(6)

where $S_i:D\to D$ is a finite family of $L_i$-Lipschitz $k_i$-demicontractive mappings, $T_i:D\to X$ is a finite family of ${\alpha }_i$-inverse strongly monotone mappings, $f:D\to D$ is a contractive mapping, $P_D$ is the projection from X onto D and D is a nonempty, closed convex subset of the complete CAT(0) space X. The authors proved that the sequence $\left\{x_n\right\}$ generated by (6) converges strongly towards a common solution of the problem. Furthermore, Izuchukwu et al. [18] proposed the following viscosity approximation method for approximating a common solution of monotone inclusion problem and a fixed point of nonexpansive mapping:

$$\left\{\begin{array}{c}{y}_n={\beta }_0{x}_n\oplus {\beta }_1{J}_{{\mu }_n}^{A_1}{x}_n\oplus \cdots \oplus {\beta }_N{J}_{{\mu }_n}^{A_N}{x}_n,\hfill \\ x_{n+1}={\alpha }_{n}f\left(x_n\right)\oplus (1-\alpha )T{y}_n,n\ge 1,\hfill \end{array}\right.$$

(7)

where $\left\{{\alpha }_n\right\}\subset [0,1],$$\left\{{\mu }_n\right\}\subset (0,\infty ),$ $A_i:X\to 2^{X^{\ast }}$ is a finite family of monotone operators, $T:X\to X$ is a nonexpansive mapping and $f:X\to X$ is a contraction mapping.

Motivated by the results of Aremu et al. [16] and Izuchukwu et al. [18], we introduced a new viscosity-type approximation method which is comprised of the resolvent of a finite family of multivalued monotone operators and a finite family of quasi-pseudocontractive mappings in CAT(0) spaces. First, we prove some fixed point results for the class of quasi-pseudocontractive mappings in CAT(0) spaces. We also prove a strong convergence result for a common solution of monotone inclusion problem and fixed point of quasi-pseudocontractive mappings. Furthermore, we apply our results to approximate a common solution of other optimization problems in CAT(0) spaces. Finally, we give some numerical examples to illustrate the performance of the proposed method. Our results improve and extend the results of Izuchukwu et al. [18], Aremu et al. [16] and other important results in this direction in the literature.

2. Preliminaries

In this section, we present some basic concepts, definitions and preliminary results which are important to establish our results. We represent the strong convergence of the sequence $\left\{x_n\right\}\subset X$ to a point $\overline{x}\in X$ by $x_n\to \overline{x}$ and the weak convergence of $\left\{x_n\right\}$ to $\overline{x}$ by $x_n\rightharpoonup \overline{x}.$

Let $(X,d)$ be a metric space. A geodesic path connecting p to q (where $p,q\in X$) is a map $c:[0,l]\to X$ such that $c\left(0\right)=p$, $c\left(l\right)=q$ and $d(c\left(t\right),c\left(t^{\prime }\right))=|t-t^{\prime }|$ for all $t,t^{\prime }\in [0,l]$, where c is an isometry and $d(p,q)=l$. The image of a geodesic path is called the geodesic segment. The space $(X,d)$ is said to be a geodesic space if every two points $p,q\in X$ are connected by a geodesic segment. A space $(X,d)$ is said to be uniquely geodesic if every two points are connected by exactly one geodesic segment. A geodesic triangle $\Delta (p_1,p_2,p_3)$ in a geodesic metric space $(X,d)$ contains three points $p_1,p_2,p_3\in X$ (vertices of $\Delta$) and a geodesic segment between each pair of vertices (edges of the $\Delta$). A comparison triangle for the geodesic triangle $\Delta (p_1,p_2,p_3)$ in $(X,d)$ is a triangle $\overline{\Delta }(p_1,p_2,p_3)$=$\Delta (\overline{p_1},\overline{p_2},\overline{p_3})$ in the Euclidean plane ${\mathbb{R}}^2$ such that $d_{{\mathbb{R}}^2}(\overline{p_i},\overline{p_j})\le d(p_i,p_j)$ for all $i,j\in \{1,2,3\}$. A geodesic space is said to be a CAT(0) space if for each geodesic triangle $\Delta (p_1,p_2,p_3)$ in X and its comparison $\overline{\Delta }=\Delta (\overline{p_1},\overline{p_2},\overline{p_3})$ in ${\mathbb{R}}^2$, the CAT(0) inequality, i.e.,

$$d(p,q)\le d_{{\mathbb{R}}^2}(\overline{p},\overline{q})$$

is satisfied for all $p,q\in \Delta$ and comparison points $\overline{p},\overline{q}\in \overline{\Delta }$. Let $p,q_1,q_2$ be points in CAT(0) space and if $q_0$ is the midpoint of the segment $[q_1,q_2],$ then the CAT(0) inequality implies

$$d^2(p,q_0)\le \frac{1}{2}{d}^2(p,q_1)+\frac{1}{2}{d}^2(p,q_2)-\frac{1}{4}{d}^2(q_1,q_2).$$

(8)

The Equation (8) is called the (CN)-inequality of Bruhat and Tits [19]. Examples of CAT(0) spaces include pre-Hilbert spaces, R-trees [20], Euclidean buildings (see [21]), and the complex Hilbert ball with a hyperbolic metric (see [22]).

Furthermore, Berg and Nizolaev [23] initiated the idea of the quasilinearization as follows: denote a pair $(a,b)\in X\times X$ by $\overrightarrow{ab}$, then, the quasilinearization is defined as a map $⟨·,·⟩:(X\times X)(X\times X)\to \mathbb{R}$ defined by

$$⟨\overrightarrow{ab},\overrightarrow{cd}⟩=\frac{1}{2}(d^2(a,d)+d^2(b,c)-d^2(a,c)-d^2(b,d)),a,b,c,d\in X.$$

(9)

It can be seen that $⟨\overrightarrow{ab},\overrightarrow{cd}⟩=⟨\overrightarrow{cd},\overrightarrow{ad}⟩;⟨\overrightarrow{ab},\overrightarrow{cd}⟩=-⟨\overrightarrow{ba},\overrightarrow{cd}⟩$ and $⟨\overrightarrow{ax},\overrightarrow{cd}⟩+⟨\overrightarrow{xb},\overrightarrow{cd}⟩=⟨\overrightarrow{ab},\overrightarrow{cd}⟩$ for all $a,b,c,d,x\in X$. Furthermore, when X is a CAT(0) space, we say that X satisfies the Cauchy–Schwartz inequality if

$$⟨\overrightarrow{ab},\overrightarrow{cd}⟩\le d(a,b)d(c,d),\forall a,b,c,d\in X.$$

It is known that a geodesically connected metric space is a CAT(0) if and only if it satisfies the Cauchy–Schwartz inequality (see, e.g., ([23], Corollary 3)).

Let $(X,d)$ be a Hadamard space and C be a nonempty convex subset of X that is closed. Then, for each $x\in X$, there exists a unique point of C, denoted by $P_{C}x$, such that

$$d(x,P_{C}x)=\underset{y\in C}{inf}d(x,y),$$

(see [24]). A mapping $P_C:X\to C$ is called a metric projection. Let $\left\{x_n\right\}$ be a sequence that is bounded in a closed convex subset of C of a CAT(0) space X. For any $x\in X$, we define

$$r(x,\left\{x_n\right\})=\underset{n\to \infty }{lim\; sup}d(x,x_n).$$

The asymptotic radius $r\left(\left\{x_n\right\}\right)$ of $\left\{x_n\right\}$ is defined by

$$r\left(\left\{x_n\right\}\right)=inf\{r(x,\left\{x_n\right\}):x\in X\},$$

and the asymptotic center $A\left(\left\{x_n\right\}\right)$ of $\left\{x_n\right\}$ is the set

$$A\left(\left\{x_n\right\}\right)=\{x\in X:r\left(\left\{x_n\right\}\right)=r(x,\left\{x_n\right\})\}.$$

In CAT(0) spaces, it is known that the asymptotic center $A\left(\left\{x_n\right\}\right)$ consists of exactly one point [25].

Lemma 1

([26]). Let (X,d) be a complete CAT(0) space, $\left\{x_n\right\}$ be a sequence in X and $x\in X,$ then $\left\{x_n\right\}$Δ-converges to x if and only if

$$\underset{n\to \infty }{lim}⟨\overrightarrow{x{x}_n},\overrightarrow{xy}⟩\le 0\forall y\in X.$$

Lemma 2.

Let X be CAT(0) space and $\theta \in [0,1]$. Then, the following inequality holds for all $w,x,y,z\in X$:

(i) 

$d^2(\theta x\oplus (1-\theta )y,z)\le {\theta }^2{d}^2(x,z)+{(1-\theta )}^2{d}^2(y,z)+2\theta (1-\theta )⟨\overrightarrow{xz},\overrightarrow{yz}⟩$ [24],

(ii) 

$d(\theta w\oplus (1-\theta )x,\theta y\oplus (1-\theta \left)z\right)\le \theta d(w,y)+(1-\theta )d(x,z)$ [19],

(iii) 

$d\left(\right(1-\theta )x\oplus \theta y,z)\le (1-\theta )d(x,z)+\theta d(y,z)$ [19],

(iv) 

$d^2(\theta x\oplus (1-\theta )y,z)\le \theta d^2(x,z)+(1-\theta )d^2(y,z)-\theta (1-\theta )d^2(x,y)$ [19].

Lemma 3

([27,28]). Let $\left\{a_n\right\}$ be a sequence of non-negative real numbers satisfying $a_{n+1}\le (1-{\gamma }_n)a_n+{\sigma }_n,n\ge 0$ where $\left\{{\gamma }_n\right\}$ and $\left\{{\sigma }_n\right\}$ satisfy the following conditions:

(i) 

$\left\{a_n\right\}\subset [0,1],{\sum }_{n=0}^{\infty }{\gamma }_n=\infty$;

(ii) 

$\underset{n\to \infty }{lim\; sup}\frac{{\sigma }_n}{{\gamma }_n}\le 0$ or ${\displaystyle \sum _{n=1}^{\infty }}\left|{\sigma }_n\right|\le \infty .$

Then $\underset{n\to \infty }{lim}{a}_n=0.$

Lemma 4

([29]). Let $\left\{a_n\right\}$ be a sequence of real numbers such that there exists a subsequence $\left\{a_{n_i}\right\}$ of $\left\{a_n\right\}$ with $a_{n_i}<a_{n_i+1}$ for all $i\in \mathbb{N}$. Consider the integer $\left\{m_k\right\}$ defined by

$$\begin{array}{c}\hfill m_k=max\{j\le k:a_j<a_{j+1}\}.\end{array}$$

Then, $\left\{m_k\right\}$ is a non-decreasing sequence verifying ${lim}_{k\to \infty }{m}_k=\infty ,$ and for all $k\in \mathbb{N},$ the following estimate holds:

$$\begin{array}{c}\hfill a_{m_k}\le a_{m_k+1},\mathrm{and}{a}_k\le a_{m_k+1}.\end{array}$$

Definition 1.

Let X be a Hadamard space and C be a nonempty closed and convex subset of X. A mapping $T:C\to C$ is said to be

1. 

A contraction, if there exists $\alpha \in (0,1)$, such that

$$d(Tx,Ty)\le \alpha d(x,y),\forall x,y\in C,$$

when $\alpha =1$, then T is said to be nonexpansive;

2. 

Firmly nonexpansive if

$$d^2(Tx,Ty)\le ⟨\overrightarrow{TxTy},\overrightarrow{xy}⟩,$$

3. 

Quasi-nonexpansive, if $F\left(T\right)\ne \varnothing$ and

$$d(p,Tx)\le d(p,x),\forall p\in F\left(T\right),x\in C,\forall x,y\in C,$$

4. 

k-strictly pseudocontractive, if there exists $k\in [0,1]$ such that

$$d^2(Tx,Ty)\le d^2(x,y)+k{(d(x,Tx)+d(x,Ty))}^2,\forall x,y\in C,$$

5. 

k-demicontractive [30], if $F\left(T\right)\ne \varnothing$ and there exists $k\in [0,1)$ such that

$$d^2(Tx,p)\le d^2(x,p)+k{d}^2(Tx,x),\forall x\in C,p\in F\left(T\right),$$

6. 

Quasi-pseudocontractive if $F\left(T\right)\ne \varnothing$ and

$$d^2(Tx,p)\le d^2(x,p)+d^2(x,Tx),\forall x\in C,p\in F\left(T\right).$$

Remark 1.

From the definition above, it is easy to see that the following implication holds:

(1) ⇒(2) ⇒(3)⇒ (4)⇒ (5) ⇒ (6), however, the reverse is generally not true. This implies that the set of quasi-pseudocontractive is more general than the set of nonexpansive, firmly nonexpansive mappings, quasi-nonexpansive, k-strictly pseudocontractive and k-demicontactive.

Definition 2.

Let X be an Hadamard space and $X^{\ast }$ be its dual space. A multi-valued operator $A:X\to 2^{X^{\ast }}$ with domain $D\left(A\right)=\{x\in X:Ax=\varnothing \}$ is monotone, if for all $x,y\in D\left(A\right)$ with $x\ne y,$ we have

$$⟨x^{\ast }-y^{\ast },\overrightarrow{yx}⟩\le 0,\forall x^{\ast }\in Ax,y^{\ast }\in Ay.$$

Definition 3

([25]). Let $(X,d)$ be an Hadamard space. A mapping $T:X\to X$ is said to be Δ-demiclosed, if for any bounded sequence $\left\{x_n\right\}$ in X such that $\Delta -{lim}_{n\to \infty }{x}_n=p$ and ${lim}_{n\to \infty }d(x_n,T{x}_n)=0$, then $Tp=p.$

Definition 4

([31]). Let X be a complete CAT(0) space and $X^{\ast }$ be its dual space. The resolvent of an operator A of $\lambda >0$ is the multivalued mapping $J_{\lambda }^A\to 2^X$ defined by

$$\begin{array}{c}\hfill J_{\lambda }^A\left(x\right)=\left\{z\in X:\left[\frac{1}{\lambda }\overrightarrow{zx}\right]\in Az\right\}.\end{array}$$

(10)

The multivalued operator A is said to satisfy the range condition if $\mathbb{D}\left(J_{\lambda }\right)=X,$ for every $\lambda >0.$

Definition 5

([21]). Let X be a complete CAT(0) space and $X^{\ast }$ be its dual space. The Yosida approximation of A is the multivalued mapping $A_{\lambda }:X\to 2^{X^{\ast }}$ of an operator A of $\lambda >0$ which is defined by

$$\begin{array}{c}\hfill A_{\lambda }\left(x\right)=\left\{\left[\frac{1}{\lambda }\overrightarrow{yx}\right]:y\in J_{\lambda }^A\right\}.\end{array}$$

(11)

The following is due to [21] and it gives the connection between the monotone operator, their resolvents and Yosida approximation, in the framework of CAT(0) spaces.

Theorem 1

([10]). Let X be a CAT(0) space and $J_{\lambda }^A$ be the resolvent of a multivalued mapping A of order λ. Then:

(i) 

For $\lambda >0,R\left(J_{\lambda }^A\right)\subset D\left(A\right)$ and $F\left(J_{\lambda }^A\right)=A^{-1}\left(0\right),$ where $R\left(J_{\lambda }^A\right)$ is the range of $J_{\lambda }^A$,

(ii) 

If A is monotone then $J_{\lambda }^A$ is a single valued and firmly nonexpansive mapping,

(iii) 

If A is monotone and $0<\lambda \le \mu ,$ then $d^2(J_{\lambda }^{A}x,J_{\mu }^A)\le \frac{\mu -\lambda }{\mu +\lambda }{d}^2(x,J_{\lambda }^{A}x).$

3. Main Results

In this section, we present our main iterative scheme and prove its convergence analysis for approximating a common solution of finite families of monotone inclusion problems and the fixed point of quasi-pseudocontraction mappings. We first prove the following lemma, which is helpful in proving our result.

Lemma 5.

Let X be a complete CAT(0) space and $T:X\to X$ be L-Lipschitzian mappings with $L\ge 1.$ Set

$$T_{\xi }=\xi I\oplus (1-\xi )T(\beta I\oplus (1-\beta )T),$$

where $0\le \frac{1+L^2-\sqrt{1+L^2}}{L^2}<\beta <\xi <1,$ then the following holds:

$\left(i\right)$

$F\left(T\right)=F(\beta I+(1-\beta T))=F\left(T_{\xi }\right);$

$\left(ii\right)$

T is demiclosed at $0,$ if and only if $T(\beta I\oplus (1-\beta \left)T\right)$ is demiclosed at 0;

$\left(iii\right)$

In addition, if T is quasi-pseudocontractive, then $T_{\xi }$ is quasi-nonexpansive.

Proof. 

(i) Let $x^{\ast }\in F\left(T\right),$ then $T(\beta I\oplus (1-\beta )T)x^{\ast }=x^{\ast }$. This implies that $F\left(T\right)\subseteq F\left(T\right(\beta I\oplus (1-\beta )T\left)\right).$ Moreover, if $x^{\ast }\in F\left(T(\beta I\oplus (1-\beta )T)\right),$ then we have

$$\begin{array}{ccc}\hfill d(T{x}^{\ast },x^{\ast })& =& d(T{x}^{\ast },T(\beta I\oplus (1-\beta )T)x^{\ast })\hfill \\ & \le & Ld(x^{\ast },\beta x^{\ast }\oplus (1-\beta )T{x}^{\ast })\hfill \\ & \le & L[\beta d(x^{\ast },x^{\ast })+(1-\beta )d(T{x}^{\ast },x^{\ast })]\hfill \\ & =& L(1-\beta )d(T{x}^{\ast },x^{\ast }).\hfill \end{array}$$

Hence

$$(1-L(1-\beta ))d(T{x}^{\ast },x^{\ast })\le 0.$$

Thus, we have $d(T{x}^{\ast },x^{\ast })\le 0.$ Hence, $x^{\ast }\in F\left(T\right).$ This implies that $F\left(T\right(\beta I\oplus (1-\beta )T\left)\right)\subseteq F\left(T\right).$ Now, from the fact that $F\left(T\right)\subseteq F\left(T\right(\beta I\oplus (1-\beta )T\left)\right)$ and $F\left(T\right(\beta I\oplus (1-\beta )T\left)\right)\subseteq F\left(T\right),$ we thus obtain that

$$F\left(T\right)=F\left(T\right(\beta I\oplus (1-\beta )T\left)\right).$$

Furthermore, let $x^{\ast }\in F\left(T(\beta I\oplus (1-\beta )T)\right),$ then

$$\begin{array}{ccc}\hfill T_{\xi }{x}^{\ast }& =& (\xi I\oplus (1-\xi )T(\beta I\oplus (1-\beta )))x^{\ast }\hfill \\ & =& \xi x^{\ast }\oplus (1-\xi )x^{\ast }\hfill \\ & =& x^{\ast }.\hfill \end{array}$$

(12)

This implies that $x^{\ast }\in F\left(T_{\xi }\right)$, thus $F\left(T(\beta I\oplus (1-\beta )T)\right)\subseteq F\left(T_{\xi }\right).$

On the other hand, let $x^{\ast }\in F\left(T_{\xi }\right)$, then

$$\begin{array}{ccc}d(x^{\ast },T(\beta I\oplus (1-\beta )T)x^{\ast })\hfill & =\hfill & d(T_{\xi }{x}^{\ast },T(\beta I\oplus (1-\beta )T)x^{\ast })\hfill \\ \hfill & =\hfill & d(\xi x^{\ast }\oplus (1-\xi )T(\beta I\oplus (1-\beta )T)x^{\ast },T(\beta I\oplus (1-\beta )T)x^{\ast })\hfill \\ \hfill & \le \hfill & \xi d(x^{\ast },T(\beta I\oplus (1-\beta )T)x^{\ast })\hfill \\ \hfill & +\hfill & (1-\xi )d(T(\beta I\oplus (1-\beta )T)x^{\ast },T(\beta I\oplus (1-\beta )T{x}^{\ast })\hfill \\ \hfill & =\hfill & \xi d(x^{\ast },T(\beta I\oplus (1-\beta )T)x^{\ast }).\hfill \end{array}$$

(13)

Then, $(1-\xi )d(x^{\ast },T(\beta I\oplus (1-\beta )T)x^{\ast })\le 0.$ Thus, we have $d(x^{\ast },T(\beta I\oplus (1-\beta )T)x^{\ast })=0$ which implies that $T(\beta I\oplus (1-\beta )T)x^{\ast }=x^{\ast }.$ Then, $F\left(T_{\xi }\right)\subseteq F(\beta I\oplus (1-\beta )T).$ It follows that $F\left(T\right)=F(\beta I\oplus (1-\beta )T)=F\left(T_{\xi }\right).$

(ii) Let $\left\{x_n\right\}\subseteq X$ be such $x_n\rightharpoonup x^{\ast }$ as $n\to \infty .$ We have

$$\begin{array}{ccc}\hfill d(x_n,T{x}_n)& \le & d(x_n,T(\beta x_n\oplus (1-\beta )T{x}_n))+d(T(\beta x_n\oplus (1-\beta )T{x}_n,T{x}_n)\hfill \\ & \le & d(x_n,T(\beta x_n\oplus (1-\beta )T{x}_n))+L[\beta d(x_n,x_n)\oplus (1-\beta )d(T{x}_n,x_n)]\hfill \\ & =& d(x_n,T(\beta x_n\oplus (1-\beta )T{x}_n)+(1-\beta )Ld(T{x}_n,x_n).\hfill \end{array}$$

This implies that

$$(1-(1-\beta )L)d(x_n,T{x}_n)\le d(x_n,T(\beta x_n\oplus (1-\beta )T{x}_n)).$$

(14)

Similarly

$$\begin{array}{ccc}d(x_n,T(\beta I\oplus (1-\beta )T)x_n)\hfill & \le \hfill & d(x_n,T{x}_n)+d(T{x}_n,T(\beta I\oplus (1-\beta )T)x_n)\hfill \\ \hfill & \le \hfill & d(x_n,T{x}_n)+Ld(x_n,\beta x_n\oplus (1-\beta )T{x}_n)\hfill \\ \hfill & \le \hfill & d(x_n,T{x}_n)+L[\beta d(x_n,x_n)+(1-\beta )d(x_n,T{x}_n)]\hfill \\ \hfill & =\hfill & (1+(1-\beta )L)d\left(d(x_n,T{x}_n)\right).\hfill \end{array}$$

(15)

Combining (14) and (15), we obtain

$$(1-(1-\beta )L)d(x_n,T{x}_n)\le d(x_n,T(\beta x_n\oplus (1-\beta )T{x}_n))\le (1+(1-\beta )L)d\left(d(x_n,T{x}_n)\right).$$

Therefore, ${lim}_{n\to \infty }d(x_n,T{x}_n)=0\iff {lim}_{n\to \infty }d(x_n,T(\beta x_n\oplus (1-\beta )T{x}_n))=0$ and therefore $x^{\ast }\in F\left(T\right)\iff x^{\ast }\in F\left(T(\beta I\oplus (1-\beta ))T\right).$

(iii) Let $x^{\ast }\in F\left(T\right)$, from Lemma 2(ii) and from the fact that T is quasi-pseudocontractive, we have that

$$\begin{array}{ccc}{d}^2(\beta x\oplus (1-\beta )Tx,x^{\ast })\hfill & \le \hfill & \beta d^2(x,x^{\ast })+(1-\beta )d^2(Tx,x^{\ast })-\beta (1-\beta )d^2(Tx,x)\hfill \\ \hfill & \le \hfill & \beta d^2(x,x^{\ast })+(1-\beta )[d^2(x,x^{\ast })+d^2(Tx,x^{\ast })]-\beta (1-\beta )d(Tx,x)\hfill \\ \hfill & =\hfill & d^2(x,x^{\ast })+[(1-\beta )-\beta (1-\beta )]d(Tx,x)\hfill \\ \hfill & =\hfill & d^2(x,x^{\ast })+[1-2\beta +{\beta }^2]d^2(Tx,x).\hfill \end{array}$$

(16)

Furthermore, using Lemma 2 and the fact that T is Lipschitzian, we obtain

$$\begin{array}{ccc}{d}^2(T(\beta x\oplus (1-\beta )Tx),\beta x\oplus (1-\beta )Tx)\hfill & \le \hfill & \beta d^2(T(\beta x\oplus (1-\beta )Tx,x)\hfill \\ & +\hfill & (1-\beta )d^2(T(\beta x\oplus (1-\beta )Tx),Tx)\hfill \\ \hfill & -\hfill & \beta (1-\beta )d^2(Tx,x)\hfill \\ \hfill & \le \hfill & \beta d^2(T(\beta x\oplus (1-\beta )Tx,x)\hfill \\ & +\hfill & (1-\beta )L^2{d}^2(\beta x\oplus (1-\beta )Tx,x)-\beta (1-\beta )d^2(Tx,x)\hfill \\ \hfill & \le \hfill & \beta d^2(T(\beta x\oplus (1-\beta )Tx,x)+(1-\beta )L^2[\beta d^2(x,x)\hfill \\ \hfill & +\hfill & (1-\beta )d^2(Tx,x)]-\beta (1-\beta )d^2(Tx,x)\hfill \\ \hfill & =\hfill & \beta d^2\left(T(\beta x\oplus (1-\beta )Tx,x)\right)+L^2[(1-\beta )d^2(Tx,x)\hfill \\ \hfill & -\hfill & \beta (1-\beta )d^2(Tx,x)]\hfill \\ \hfill & =\hfill & \beta d^2(T(\beta x\oplus (1-\beta )Tx,x)\hfill \\ \hfill & +\hfill & {(1-\beta )}^2{L}^2{d}^2(Tx,x)-\beta (1-\beta )L^2{d}^2(Tx,x).\hfill \end{array}$$

(17)

Moreover, from (16), (17) and the fact that T is quasi pseudo-contractive, we obtain that

$$\begin{array}{ccc}{d}^2(T(\beta x\oplus (1-\beta )Tx),x^{\ast })\hfill & \le \hfill & d^2(\beta x\oplus (1-\beta )Tx,x^{\ast })+d^2(T(\beta x\oplus (1-\beta )Tx,\beta x\oplus (1-\beta )Tx)\hfill \\ \hfill & \le \hfill & d^2(x,x^{\ast })+[1-2\beta +{\beta }^2]d^2(Tx,x)+{(1-\beta )}^2{L}^2{d}^2(Tx,x)]\hfill \\ & -\hfill & \beta (1-\beta )d^2(Tx,x)+\beta d\left(T(\beta x\oplus (1-\beta )Tx,x)\right)\hfill \\ \hfill & =\hfill & d^2(x,x^{\ast })+[{(1-\beta )}^2+{(1-\beta )}^2{L}^2-\beta (1-\beta )]d^2(Tx,x)\hfill \\ & +\hfill & \beta d\left(T\right(kx\oplus (1-\beta )Tx),x)\hfill \\ \hfill & =\hfill & d^2(x,x^{\ast })+[1-2\beta +{\beta }^2-\beta +{\beta }^2+{(1-\beta )}^2{L}^2]d^2(Tx,x)\hfill \\ \hfill & =\hfill & d^2(x,x^{\ast })+[1-3\beta +2{\beta }^2+{(1-\beta )}^2{L}^2]d(Tx,x)\hfill \\ & +\hfill & \beta d\left(T\right(\beta x\oplus (1-\beta )Tx),x)\hfill \\ \hfill & =\hfill & d^2(x,x^{\ast })-(1-\beta )\left[(2\beta -1-(1-\beta )L^2)\right]d^2(Tx,x)\hfill \\ & +\hfill & \beta d^2(T(\beta x\oplus (1-\beta )Tx),x)\hfill \\ \hfill & \le \hfill & d^2(x,x^{\ast })+\beta d^2(T(\beta x\oplus (1-\beta )Tx),x).\hfill \end{array}$$

(18)

From Lemma 2 and (22), we obtain

$$\begin{array}{ccc}d(T_{\xi }x,x^{\ast })\hfill & =\hfill & d^2(\xi x\oplus (1-\xi )T(\beta x\oplus (1-\beta )Tx),x^{\ast })\hfill \\ \hfill & \le \hfill & \xi d^2(x,x^{\ast })+(1-\xi )d^2(T(\beta x\oplus (1-\beta )Tx),x^{\ast })-\xi (1-\xi )d^2(T(\beta x\oplus (1-\beta )Tx),x)\hfill \\ \hfill & \le \hfill & \xi d^2(x,x^{\ast })+(1-\xi )[d^2(x,x^{\ast })+\beta d^2(T(\beta x\oplus (1-\beta )Tx),x)]\hfill \\ & -\hfill & \xi (1-\xi )d^2(T(\beta x\oplus (1-\beta )Tx),x)\hfill \\ \hfill & \le \hfill & d^2(x,x^{\ast })+(1-\xi )\beta d^2\left(T(\beta x\oplus (1-\beta )Tx,x)\right)-\xi (1-\xi )d^2(T(\beta x\oplus (1-\beta )Tx),x)\hfill \\ \hfill & =\hfill & d^2(x,x^{\ast })+[(\beta -\beta \xi )-\xi +{\xi }^2]d^2(T(kx\oplus (1-\beta )Tx),x)\hfill \\ \hfill & =\hfill & d^2(x,x^{\ast })-(\xi -\beta )(1-\xi )d^2(T(\beta x\oplus (1-\beta )Tx),x).\hfill \end{array}$$

(19)

Since $\xi >\beta$, we thus have $d^2(T_{\xi }x,x^{\ast })\le d^2(x,x^{\ast })$ which implies that $T_{\xi }$ is quasi-nonexpansive.  □

We now present our iterative scheme and its convergence analysis. In what follows, we give a precise statement for our method as follows:

Let X be a complete CAT(0) space and $X^{\ast }$ be its dual space. For $i=1,2,\dots ,k$ let $A_i:X\to 2^{X^{\ast }}$ be multivalued monotone operators satisfying the range condition. Let $T_j,(j=1,2,\dots ,m)$ be a finite family of $L_i$-Lipschitzian quasi-pseudo-contractive mappings and $h:X\to X$ be a contraction mapping with the contractive coefficient $v\in (0,1).$ Assume that the solution set $\Gamma ={\cap }_{i=1}^k{A}_i^{-1}\left(0\right)\cap {\cap }_{j=1}^{m}F\left(T_j\right)\ne \varnothing$ for an arbitrary $x_0\in (0,1)$, ${\mu }_n>0$, $\left\{{\alpha }_n\right\}\subset [0,1],$${\left\{{\xi }_n^i\right\}}_{i=0}\subset (0,1)$ such that ${\sum }_{i=0}^m{\xi }_n^i=1,$ the sequence $\left\{x_n\right\}$ is generated by the following iterative scheme:

$$\left\{\begin{array}{c}{u}_n=J_{{\mu }_n}^{A_k}\circ J_{{\mu }_n}^{A_{k-1}}\circ \cdots \circ J_{{\mu }_n}^{A_1}{x}_n\hfill \\ y_n={\xi }_n^0{u}_n\oplus {\displaystyle \sum _{i=1}^m}\oplus {\xi }_n^i{T}_i({\beta }_n{u}_n\oplus (1-{\beta }_n)T_i{u}_n)\hfill \\ x_{n+1}={\alpha }_{n}h\left(x_n\right)\oplus (1-{\alpha }_n)y_n.\hfill \end{array}\right.$$

(20)

In addition, we assume that the control sequences satisfy the following condition:

(C1)

$\underset{n\to \infty }{lim}{\alpha }_n=0$ and ${\sum }_{n=0}^{\infty }{\alpha }_n=\infty ,$

(C2)

$\underset{n\to \infty }{lim\; inf}{\mu }_n>0$,

(C3)

$0\le \frac{1+L^2-\sqrt{1+L^2}}{L^2}<\underset{n\to \infty }{lim\; inf}{\beta }_n<\underset{n\to \infty }{lim\; inf}{\xi }_n^0<1.$

Now, we show that the sequence generated by Algorithm (20) is bounded.

Lemma 6.

Let $\left\{x_n\right\}$ be a sequence generated by Algorithm (20), then, $\left\{x_n\right\}$ is bounded. Consequently, $\left\{u_n\right\}$ and $\left\{y_n\right\}$ are bounded too.

Proof. 

Let $x^{\ast }\in \Gamma$, then $0\in A_i{x}^{\ast }$ for $i\in \{1,2,\dots ,k\}$ and $T_j{x}^{\ast }=x^{\ast }$ for $j=\{1,2,\dots ,m\}.$ Furthermore, let ${\psi }_n^i=J_{{\mu }_n}^{A_i}{\psi }_n^{i-1},$ for all $n\in \mathbb{N},$ where ${\psi }_n^0=x_n.$ Then, ${\psi }_n^k=u_n$ for all $n\ge 1.$ We obtain from (10) that $\left[\frac{1}{{\mu }_n}\overrightarrow{{\psi }_n^i{\psi }_n^{i-1}}\right]\in A_i\left({\psi }_n^i\right),$ for $i\in \{1,2,\dots ,k\}$ thus, by monotonicity of $A_i,$ we have

$$0\le ⟨\left[\frac{1}{{\mu }_n}\overrightarrow{{\psi }_n^i{\psi }_n^{i-1}}\right]-0,\overrightarrow{x^{\ast }{\psi }_n^i}⟩.$$

Hence, by the quasilinearization, we obtain that

$$0\le d^2({\psi }_n^{i-1},x^{\ast })-d^2({\psi }_n^i,x^{\ast })-d^2({\psi }_n^i,{\psi }_n^{i-1}).$$

(21)

Adding up the inequality in (21) from $i=1$ to k, we obtain

$$\begin{array}{ccc}0\hfill & \le \hfill & d^2(x_n,x^{\ast })+d({\psi }_n^1,x^{\ast })+\cdots +d^2({\psi }_n^{k-1},x^{\ast })\hfill \\ \hfill & -\hfill & [d^2({\psi }_n,x^{\ast })+d^2({\psi }_n^2,x^{\ast })]+,\cdots d^2({\psi }^k,x^{\ast })\hfill \\ \hfill & -\hfill & [d^2({\psi }_n^1,{\psi }_n^0)+d({\psi }_n^2,{\psi }_n^1)+d^2({\psi }_n^3,{\psi }_n^2)\hfill \\ \hfill & +\hfill & \cdots +d^2({\psi }_n^k,{\psi }_n^{k-1})]\hfill \\ \hfill & =\hfill & d^2({\psi }_n^0,x^{\ast })-d^2({\psi }_n^k,x^{\ast })-\sum _{i=1}^k{d}^2({\psi }_n^i,{\psi }_n^{i-1}).\hfill \end{array}$$

(22)

Thus, we obtain

$$d^2(u_n,x^{\ast })\le d^2(x_n,x^{\ast }).$$

Since $T_i$ is a quasi-pseudo-contractive for each i and Lemma 2, we have the following.

$$\begin{array}{ccc}{d}^2(T_i({\beta }_n{u}_n\oplus (1-{\beta }_n)T_i{u}_n),x^{\ast })\hfill & \le \hfill & d^2({\beta }_n{u}_n\oplus (1-{\beta }_n)T{u}_n,x^{\ast })\hfill \\ \hfill & +\hfill & d^2(T_i({\beta }_n{u}_n\oplus (1-{\beta }_n)T_i{u}_n),{\beta }_n{u}_n\oplus (1-{\beta }_n),T_i{u}_n).\hfill \end{array}$$

(23)

Moreover,

$$\begin{array}{ccc}{d}^2({\beta }_n{u}_n\oplus (1-{\beta }_n)T_i{u}_n,x^{\ast })\hfill & \le \hfill & {\beta }_n{d}^2(u_n,x^{\ast })+(1-{\beta }_n)d^2(T_i{u}_n,x^{\ast })\hfill \\ \hfill & -\hfill & {\beta }_n(1-{\beta }_n)d^2(T_i{u}_n,u_n)\hfill \\ \hfill & \le \hfill & {\beta }_n{d}^2(u_n,x^{\ast })+(1-{\beta }_n)[d^2(u_n,x^{\ast })\hfill \\ \hfill & +\hfill & d^2(T_i{u}_n,u_n)]-{\beta }_n(1-{\beta }_n)d^2(T_i{u}_n,u_n)\hfill \\ \hfill & \le \hfill & d^2(u_n,x^{\ast })+{(1-{\beta }_n)}^2{d}^2(T_i{u}_n,x^{\ast }).\hfill \end{array}$$

(24)

On the other hand, we have

$$\begin{array}{ccc}{d}^2({\beta }_n{u}_n\oplus (1-{\beta }_n)T_i{u}_n,T_i({\beta }_n{u}_n\oplus (1-{\beta }_n)T_i{u}_n))\hfill & \le \hfill & {\beta }_n{d}^2(u_n,T_i({\beta }_n{u}_n\oplus (1-{\beta }_n)T_i{u}_n))\hfill \\ \hfill & +\hfill & (1-{\beta }_n)d^2(T_i{u}_n,T_i({\beta }_n{u}_n\oplus (1-{\beta }_n)T_i{u}_n))\hfill \\ \hfill & \le \hfill & {\beta }_n{d}^2(u_n,T_i({\beta }_n{u}_n\oplus (1-{\beta }_n)T_i{u}_n)\hfill \\ \hfill & +\hfill & (1-{\beta }_n)L^2{d}^2(u_n,{\beta }_n{u}_n\oplus (1-{\beta }_n)T_i{u}_n)\hfill \\ \hfill & -\hfill & {\beta }_n(1-{\beta }_n)d^2(T_i{u}_n,u_n)\hfill \\ \hfill & \le \hfill & {\beta }_n{d}^2(u_n,T_i({\beta }_n{u}_n\oplus (1-{\beta }_n{u}_n)T_i{u}_n)\hfill \\ \hfill & +\hfill & (1-{\beta }_n)L_i^2[{\beta }_n{d}^2(u_n,u_n)+(1-{\beta }_n)d^2(u_n,T_i{u}_n)]\hfill \\ \hfill & -\hfill & {\beta }_n(1-{\beta }_n)d^2(T_i{u}_n,u_n)\hfill \\ \hfill & =\hfill & {\beta }_n{d}^2(u_n,T_i({\beta }_n{u}_n\oplus (1-{\beta }_n)T_i{u}_n))\hfill \\ \hfill & +\hfill & L_i^2{(1-{\beta }_n)}^2{d}^2(T_i{u}_n,u_n)\hfill \\ \hfill & -\hfill & {\beta }_n(1-{\beta }_n)d^2(T_i{u}_n,u_n).\hfill \end{array}$$

(25)

Substituting (24) and (25) in (23) we obtain

$$\begin{array}{ccc}{d}^2(T_i{({\beta }_n{u}_n\oplus (1-{\beta }_n)T_{i}u)}_n,x^{\ast })\hfill & \le \hfill & d^2(u_n,x^{\ast })+{(1-{\beta }_n)}^{2}d(T_i{u}_n,u_n)\hfill \\ \hfill & +\hfill & {\beta }_n{d}^2(u_n,T_i({\beta }_n{u}_n\oplus (1-{\beta }_n)T_i{u}_i))\hfill \\ \hfill & +\hfill & {(1-{\beta }_n)}^2{L}_i^2{d}^2(T_i{u}_n,u_n)-{\beta }_n(1-{\beta }_n)d^2(T_i{u}_n,u_n)\hfill \\ \hfill & =\hfill & d^2(u_n,x^{\ast })+{\beta }_n{d}^2(u_n,T_i({\beta }_n{u}_n\oplus (1-{\beta }_n)T_i{u}_n))\hfill \\ \hfill & +\hfill & {(1-{\beta }_n)}^2{L}_i^{2}d(T_i{u}_n,u_n)-(2{\beta }_n-1)(1-{\beta }_n)d^2(T_i{u}_n,u_n)\hfill \\ \hfill & =\hfill & d^2(u_n,x^{\ast })+{\beta }_n{d}^2(u_n,T_i({\beta }_n{u}_n\oplus (1-{\beta }_n)T_i{u}_n)\hfill \\ \hfill & -\hfill & (1-{\beta }_n)[2{\beta }_n-1-(1-{\beta }_n)L_i^2)]d^2(T_i{u}_n,u_n)\hfill \\ \hfill & \le \hfill & d^2(u_n,x^{\ast })+{\beta }_n{d}^2(u_n,T_i({\beta }_n{u}_n\oplus (1-{\beta }_n)T_i{u}_n)).\hfill \end{array}$$

(26)

From (26) and Lemma 2 (iv), and the fact that ${\displaystyle \sum _{i=0}^m}{\xi }_n^i=1,$ we then have that

$$\begin{array}{ccc}{d}^2(y_n,x^{\ast })\hfill & =\hfill & d^2({\xi }_n^0{u}_n\oplus {\displaystyle \sum _{i=1}^m}\oplus {\xi }_n^i{T}_i({\beta }_n{u}_n\oplus (1-{\beta }_n)T_i{u}_n),x^{\ast })\hfill \\ \hfill & =\hfill & d^2({\xi }_n^0{u}_n\oplus (1-{\xi }_n^0)T_i({\beta }_n{u}_n\oplus (1-{\beta }_n)T_i{u}_n,x^{\ast }))\hfill \\ \hfill & \le \hfill & {\xi }_n^0{d}^2(u_n,x^{\ast })+(1-{\xi }_n^0)d^2(T_i({\beta }_n{u}_n\oplus (1-{\beta }_n)T_i{u}_n),x^{\ast })\hfill \\ \hfill & -\hfill & {\xi }_n^0(1-{\xi }_n^0)d^2(u_n,T_i({\beta }_n\oplus (1-{\beta }_n)T_i{u}_n))\hfill \\ \hfill & \le \hfill & {\xi }_n^0{d}^2(u_n,x^{\ast })+(1-{\xi }_n^0)[d^2(u_n,x^{\ast })\hfill \\ \hfill & +\hfill & {\beta }_n{d}^2(u_n,T_i({\beta }_n{u}_n\oplus (1-{\beta }_n)T_i{u}_n))]\hfill \\ \hfill & -\hfill & {\xi }_n^0(1-{\xi }_n^0)d^2(u_n,T_i({\beta }_n\oplus (1-{\beta }_n)T_i{u}_n))\hfill \\ \hfill & =\hfill & d^2(u_n,x^{\ast })-(1-{\xi }_n^0)({\xi }_n^0-{\beta }_n)d^2(T_i({\beta }_n{u}_n\oplus (1-{\beta }_n)T_i{u}_n),u_n)\hfill \\ \hfill & \le \hfill & d^2(u_n,x^{\ast }).\hfill \end{array}$$

(27)

Therefore

$$\begin{array}{ccc}\hfill d^2(y_n,x^{\ast })& =& d^2({\xi }_n^0{u}_n\oplus \sum _{i=1}^m\oplus {\xi }_n^i{T}_i({\beta }_n{u}_n\oplus (1-{\beta }_n)T_i{u}_n),x^{\ast })\hfill \\ & \le & d^2(u_n,x^{\ast })\hfill \\ & \le & d^2(x_n,x^{\ast }).\hfill \end{array}$$

Thus

$$\begin{array}{ccc}\hfill d(x_{n+1},x^{\ast })& =& d({\alpha }_{n}h\left(x_n\right)\oplus (1-{\alpha }_n)y_n,x^{\ast })\hfill \\ & =& {\alpha }_{n}d(h\left(x_n\right),x^{\ast })+(1-{\alpha }_n)d(y_n,x^{\ast })\hfill \\ & \le & {\alpha }_n[d(h\left(x_n\right),h\left(x^{\ast }\right)+d(h\left(x^{\ast }\right),x^{\ast })]\hfill \\ & +& (1-{\alpha }_n)d(y_n,x^{\ast })\hfill \\ & \le & {\alpha }_n[vd(x_n,x^{\ast })+d(h\left(x^{\ast }\right),x^{\ast })]+(1-{\alpha }_n)d(x_n,x^{\ast })\hfill \\ & =& (1-{\alpha }_n(1-v))d(x_n,x^{\ast })+{\alpha }_{n}d(h\left(x^{\ast }\right),x^{\ast })\hfill \\ & =& (1-{\alpha }_n(1-v))d(x_n,x^{\ast })\hfill \\ & +& {\alpha }_n(1-v)\frac{d(h\left(x^{\ast }\right),x^{\ast })}{1-v}\hfill \\ & \le & max\left\{d(x_n,x^{\ast }),\frac{d(h\left(x^{\ast }\right),x^{\ast })}{1-v}\right\}\hfill \\ & ⋮& \hfill \\ & \le & max\left\{d(x_0,x^{\ast }),\frac{d(h\left(x^{\ast }\right),x^{\ast })}{1-v}\right\}.\hfill \end{array}$$

Therefore, $\left\{d(x_n,x^{\ast })\right\}$ is bounded, which implies that the sequence $\left\{x_n\right\}$ is also bounded. Moreover, $\left\{u_n\right\},\left\{y_n\right\}$ and $\left\{h\left(x_n\right)\right\}$ are bounded. □

Lemma 7.

Let $\left\{x_n\right\}$ be the sequence generated by Algorithm 20 and suppose that $d^2(x_n,x^{\ast })-d^2(x_{n+1},x^{\ast })\to 0$ as $n\to \infty .$ Then, the following conclusions hold:

(i) 

$\underset{n\to \infty }{lim}d(u_n,x_n)=0,$

(ii) 

$\underset{n\to \infty }{lim}d(u_n,T_i{u}_n)=0,$$i=1,\cdots ,m,$

(iii) 

$\underset{n\to \infty }{lim}d(u_n,y_n)=0,$

(iv) 

$\underset{n\to \infty }{lim}d(x_{n+1},x_n)=0.$

Proof. 

(i) First, from (22), we obtain that

$$\begin{array}{ccc}\sum _{i=1}^k{d}^2({\psi }_n^i,{\psi }_n^{i-1})\hfill & \le \hfill & d^2(x_n,x^{\ast })-d^2(u_n,x^{\ast })\hfill \\ \hfill & =\hfill & d^2(x_n,x^{\ast })-d^2(x_{n+1},x^{\ast })+d^2(x_{n+1},x^{\ast })-d^2(u_n,x^{\ast })\hfill \\ \hfill & =\hfill & d^2(x_n,x^{\ast })-d^2(x_{n+1},x^{\ast })\hfill \\ \hfill & +\hfill & {\alpha }_n{d}^2(h\left(x_n\right),x^{\ast })+(1-{\alpha }_n)d(u_n,x^{\ast })\hfill \\ \hfill & +\hfill & 2{\alpha }_n(1-{\alpha }_n)⟨\overrightarrow{h\left(x_n\right)x^{\ast }},\overrightarrow{x_{n+1}{x}^{\ast }}⟩-d^2(u_n,x^{\ast }).\hfill \end{array}$$

(28)

Therefore

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\sum _{i=1}^k{d}^2({\psi }_n^i,{\psi }_n^{i-1})=0.\end{array}$$

(29)

It follows that

$$\underset{n\to \infty }{lim}d({\psi }_n^i,{\psi }_n^{i-1})=0,i=1,\dots ,k.$$

By applying triangle inequality, we obtain

$$\begin{array}{c}\hfill d(u_n,x_n)=d(u_n,{\psi }_n^{k-1})+d({\psi }_n^{k-1},{\psi }_n^{k-2})+\cdots +d({\psi }_n^1,x_n).\end{array}$$

Thus

$$\underset{n\to \infty }{lim}{d}^2(x_n,u_n)=0.$$

(ii) From (27), we have

$$\begin{array}{ccc}\hfill (1-{\xi }_n^0)({\beta }_n-{\xi }_n^0)d^2\left(T_i({\beta }_n{u}_n\oplus (1-{\beta }_n)T_i{u}_n,u_n)\right)& \le & d^2(u_n,x^{\ast })-d^2(y_n,x^{\ast })\hfill \\ & \le & d^2(x_n,x^{\ast })-d^2(y_n,x^{\ast })\hfill \\ & =& d^2(x_n,x^{\ast })-d^2(x_{n+1},x^{\ast })+d^2(x_{n+1},x^{\ast })-d^2(y_n,x^{\ast })\hfill \\ & \le & d^2(x_{n+1},x^{\ast })-d^2(x_{n+1},x^{\ast })+{\alpha }_n{d}^2(h\left(x_n\right),x^{\ast })\hfill \\ & +& (1-{\alpha }_n)d^2(y_n,x^{\ast })+2{\alpha }_n(1-{\alpha }_n)⟨\overrightarrow{h\left(x_n\right)x^{\ast }},\overrightarrow{y_n{x}^{\ast }}⟩\hfill \\ & -& d^2(y_n,x^{\ast }).\hfill \end{array}$$

Hence

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}{d}^2(T_i({\beta }_n{u}_n\oplus (1-{\beta }_n)T_i{u}_n),u_n)=0.\end{array}$$

(30)

Furthermore

$$\begin{array}{ccc}\hfill d(T_i({\beta }_n{u}_n\oplus (1-\beta u_n)T_i{u}_n),u_n)& \le & d(T_i({\beta }_n\oplus (1-{\beta }_n)T_i{u}_n),T_i{u}_n)+d(T_i{u}_n,u_n)\hfill \\ & \le & Ld({\beta }_n{u}_n\oplus (1-{\beta }_n)T_i{u}_n,u_n)+d(T_i{u}_n,u_n)\hfill \\ & \le & L[{\beta }_{n}d(u_n,u_n)+(1-{\beta }_n)d(T{u}_n,u_n)]+d(T_i{u}_n,u_n)\hfill \\ & =& [1+L(1-{\beta }_n)]d(T_i{u}_n,u_n).\hfill \end{array}$$

Hence, using (30), we obtain

$$\underset{n\to \infty }{lim}{d}^2(u_n,T_i{u}_n)=0.$$

(iii) Furthermore, from (30) and Lemma 2 (iv), we have

$$\begin{array}{ccc}{d}^2(y_n,u_n)\hfill & =\hfill & d^2({\xi }_n^0{u}_n\oplus \sum _{i=1}^m\oplus {\xi }_n^i{T}_i({\beta }_n{u}_n\oplus (1-{\beta }_n)T_i{u}_n,u_n)\hfill \\ \hfill & =\hfill & d^2({\xi }_n^0{u}_n\oplus (1-{\xi }_n^0)T_i({\beta }_n{u}_n\oplus (1-{\beta }_n)T_i{u}_n),u_n)\hfill \\ \hfill & \le \hfill & {\xi }_n^0{d}^2(u_n,u_n)+(1-{\xi }_n^0)d^2(T_i{u}_n,{\beta }_n{u}_n\oplus (1-{\beta }_n)T_i{u}_n,u_n)\hfill \\ \hfill & =\hfill & (1-{\xi }_n^0)d^2(T_i({\beta }_n{u}_n\oplus (1-{\beta }_n)T_i{u}_n),u_n).\hfill \end{array}$$

(31)

Thus,

$$\underset{n\to \infty }{lim}{d}^2(y_n,u_n)=0.$$

(iv) Moreover, it is clear that

$$\begin{array}{ccc}{d}^2(x_{n+1},x_n)\hfill & =\hfill & d^2({\alpha }_{n}h\left(x_n\right)\oplus (1-{\alpha }_n)y_n,x_n)\hfill \\ \hfill & \le \hfill & {\alpha }_n{d}^2(h\left(x_n\right),x_n)+(1-{\alpha }_n)d^2(y_n,x_n)\hfill \\ \hfill & -\hfill & {\alpha }_n(1-{\alpha }_n)d^2(h\left(x_n\right),y_n).\hfill \end{array}$$

(32)

Since

$$\underset{n\to \infty }{lim}{\alpha }_n=0\mathrm{and}\underset{n\to \infty }{lim}d(x_n,y_n)=\underset{n\to \infty }{lim}(d(u_n,x_n)+d(u_n,y_n))=0,$$

thus we have

$$\underset{n\to \infty }{lim}d(x_{n+1},x_n)=0.$$

 □

Now, we provide our main theorem and its convergence analysis.

Theorem 2.

Let $\left\{x_n\right\}$ be the sequence generated by Algorithm 20. Then, $\left\{x_n\right\}$ converges strongly towards an element $x^{\ast }\in \Gamma .$

Proof. 

First, we showed that every weak subsequential limit of $\left\{x_n\right\}$ belongs to $\Gamma .$ Since $\left\{x_n\right\}$ is bounded, there exists a subsequence $\left\{x_{n_k}\right\}$ of $\left\{x_n\right\}$ such that $x_{n_k}\rightharpoonup q.$ By (11), the Yosadi approximation of $A_i$ for each $i\in \{1,2\dots k\},$ we have

$$A_{i{\mu }_{n_k}}{\psi }_{n_k}^{i-1}=\left[\frac{1}{{\mu }_{n_k}}\overrightarrow{{\psi }_{n_k}^i{\psi }_{n_k}^{i-1}}\right].$$

Since $\underset{k\to \infty }{lim}inf{\mu }_{n_k}>0$, from (29), we obtain the following

$$\underset{k\to \infty }{lim}{A}_{i,{\mu }_{n_k}}{\psi }_{n_k}^{i-1}=0.$$

Let $(p_1,p_2)\in G\left(A_i\right)$ for each $i\in 1,2\dots k,$ by the maximal monotonicity of $A_i,$ we have

$$\begin{array}{c}\hfill ⟨p_2-A_{i,\mu }{\psi }^{i-1},\overrightarrow{{\psi }_{n_k}^i{p}_1}⟩\ge 0.\end{array}$$

(33)

When we replace n by $n_k$ in (33) and taking the limit as $k\to \infty$, we obtain

$$⟨p_2,\overrightarrow{q{p}_1}⟩\ge 0.$$

Thus, by the maximal monotonicity of $A_i,$ we obtain $q\in A_i^{-1}\left(0\right)$ for each $i\in \{1,2,\dots ,k\},$ which implies that $q\in {\bigcap }_{i=1}^k{A}_i^{-1}\left(0\right).$

Moreover, since $d(u_{n_k},T_i\left(u_{n_k}\right))\to 0$ as $k\to \infty ,$ then, $q\in F\left(T_i\right)$ which implies that $q\in \Gamma .$

Now, we prove that the sequence $\left\{x_n\right\}$ converges strongly to $x^{\ast }$. Note from Lemma 1, we obtain

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim\; sup}⟨\overrightarrow{h\left(x_n\right)x^{\ast }},\overrightarrow{x_n{x}^{\ast }}⟩=\underset{k\to \infty }{lim}⟨\overrightarrow{h\left(x_n\right)x^{\ast }},\overrightarrow{x_{n_k}{x}^{\ast }}⟩=⟨\overrightarrow{h\left(x_n\right)x^{\ast }},\overrightarrow{q{x}^{\ast }}⟩\le 0.\end{array}$$

(34)

From Lemma 2 and quasilinearization properties, we obtain that

$$\begin{array}{ccc}\hfill d^2(x_{n+1},x^{\ast })& =& d^2({\alpha }_{n}h\left(x_n\right)\oplus (1-{\alpha }_n)y_n,x^{\ast })\hfill \\ & \le & {\alpha }_n^2{d}^2(h\left(x_n\right),x^{\ast })+{(1-{\alpha }_n)}^2{d}^2(y_n,x^{\ast })+2{\alpha }_n(1-{\alpha }_n)⟨\overrightarrow{h\left(x_n\right)x^{\ast }},\overrightarrow{y_n{x}^{\ast }}⟩\hfill \\ & \le & {\alpha }_n^2{d}^2(h\left(x_n\right),x^{\ast })+{(1-{\alpha }_n)}^2{d}^2(y_n,x^{\ast })+2{\alpha }_n(1-{\alpha }_n)[⟨\overrightarrow{h\left(x_n\right)h\left(x^{\ast }\right)},\overrightarrow{y_n{x}^{\ast }}⟩+⟨\overrightarrow{h\left(x^{\ast }\right)x^{\ast }},\overrightarrow{y_n{x}^{\ast }}⟩]\hfill \\ & \le & {\alpha }_n^2{d}^2(h\left(x_n\right),x^{\ast })+{(1-{\alpha }_n)}^2{d}^2(x_n,x^{\ast })+2{\alpha }_n(1-{\alpha }_n)[vd(x_n,x^{\ast })+⟨\overrightarrow{h\left(x^{\ast }\right)x^{\ast }},\overrightarrow{y_n{x}^{\ast }}⟩]\hfill \\ & \le & (1-2{\alpha }_n+2{\alpha }_{n}v)d^2(y_n,x^{\ast })+2{\alpha }_n(1-{\alpha }_n)⟨\overrightarrow{h\left(x^{\ast }\right)x^{\ast }},\overrightarrow{y_n{x}^{\ast }}⟩+{\alpha }_n^2(d^2(h\left(x_n\right),x^{\ast })+d^2(x_n,x^{\ast }))\hfill \\ & =& (1-2{\alpha }_n(1-v))d^2(x_n,x^{\ast })+2{\alpha }_n(1-v)[\frac{1-{\alpha }_n}{1-v}⟨\overrightarrow{h\left(x^{\ast }\right)x^{\ast }},\overrightarrow{x_n{x}^{\ast }}⟩\hfill \\ & +& \frac{{\alpha }_n}{2(1-v)}(d^2(h\left(x_n\right),x^{\ast })+d^2(x_n,x^{\ast }))].\hfill \end{array}$$

That is

$$\begin{array}{ccc}\hfill d^2(x_{n+1},x^{\ast })& \le & (1-2{\alpha }_n(1-v))d^2(x_n,x^{\ast })+2{\alpha }_n(1-v)H_n,\hfill \end{array}$$

(35)

where

$$H_n=\frac{1-{\alpha }_n}{1-v}⟨\overrightarrow{h\left(x^{\ast }\right)x^{\ast }},\overrightarrow{y_n{x}^{\ast }}⟩+\frac{{\alpha }_n}{2(1-v)}(d^2(h\left(x_n\right),x^{\ast })+d^2(x_n,x^{\ast })).$$

Thus, from (35), (34) and Lemma 3, we conclude that $\left\{x_n\right\}$ converges strongly to $x^{\ast }=P_{Sol}\left(h\left(x^{\ast }\right)\right).$

In order to finalize the proof, we also consider the case when $\left\{d(x_n,x^{\ast })\right\}$ is not monotonically decreasing, i.e., suppose there exists a subsequence $\left\{x_{n_t}\right\}$ of $x_n$ such that $d^2(x_{n_t},x^{\ast })\le d^2(x_{n_t+1},x^{\ast })$ for all $t\in \mathbb{N}$. Then, by Lemma 4, there exists a nondecreasing sequence $m_t\subset \mathbb{N}$ such that $m_t\to \infty$.

$$\begin{array}{c}\hfill d(x_{m_t},x^{\ast })<d(x_{m_t+1},x^{\ast })\mathrm{and}d(x_t,x^{\ast })<d(x_{m_t+1},x^{\ast })\forall t\in \mathbb{N}.\end{array}$$

(36)

Therefore

$$\begin{array}{ccc}0\hfill & \le \hfill & \underset{t\to \infty }{lim}d(x_{m_t+1},x^{\ast })\hfill \\ \hfill & \le \hfill & \underset{t\to \infty }{lim}sup(d(x_{m_t+1},x^{\ast })-d(x_{m_t},x^{\ast }))\hfill \\ \hfill & \le \hfill & \underset{t\to \infty }{lim}sup({\alpha }_{m_t}d(h\left(x_{m_t}\right),x^{\ast })+(1-{\alpha }_{m_t})d(x_{m_t},x^{\ast })-d\left(x_n{m}_t{x}^{\ast }\right))\hfill \\ \hfill & =\hfill & \underset{t\to \infty }{lim}{\alpha }_{m_t}d(h\left(x_{m_t}\right),x^{\ast }-d(x_{m_t},x^{\ast }))\hfill \\ \hfill & =\hfill & 0.\hfill \end{array}$$

(37)

This implies that

$$\begin{array}{c}\hfill \underset{t\to \infty }{lim}(d(x_{m_{t+1}},x^{\ast })-d(x_{m_t},x^{\ast }))=0.\end{array}$$

(38)

Following the argument as in (34), we obtain

$$\begin{array}{c}\hfill \underset{t\to \infty }{lim}⟨\overline{h\left(x_t\right)x^{\ast }},\overline{x_{m_t}{x}^{\ast }}⟩\le 0.\end{array}$$

(39)

Furthermore, from (35), we obtain that

$$d(x_{m_t+1},x^{\ast })\le (1-2{\alpha }_{m_t}(1-v))d^2(x_{m_t},x^{\ast })+2{\alpha }_{m_t}(1-v)H_{m_t},$$

where $H_{m_t}=\frac{1-{\alpha }_{m_t}}{1-v}⟨\overrightarrow{h\left(x^{\ast }\right)x^{\ast }},\overrightarrow{y_{m_t}{x}^{\ast }}⟩+\frac{{\alpha }_{m_t}}{2(1-v)}(d^2(h\left(x_{m_t}\right),x^{\ast })+d^2(x_{m_t},x^{\ast })).$

On the other hand, from (36), we have that

$$d^2(x_{m_t},x^{\ast })\le H_{n_t}$$

which implies that

$$\underset{t\to \infty }{lim}{d}^2(x_t,x^{\ast })=0.$$

As a consequence, we obtain that for all $n\ge m_l,$

$$0\le d^2(x_n,x^{\ast })\le max\{d^2(x_{m_t},x^{\ast }),d^2(x_{m_t+1},x^{\ast })\}=d^2(x_{m_t+1},x^{\ast }).$$

Hence, ${lim}_{n\to \infty }d(x_n,x^{\ast })=0.$ This implies that $\left\{x_n\right\}$ converges strongly towards $x^{\ast }\in \Gamma .$ This completes the proof.  □

The following results can be obtained as consequences of our main result.

(i) Setting $T_i$ to be quasi-nonexpansive mappings in Theorem 2, we obtain the following result:

Corollary 1.

Let X be complete CAT(0) space and $X^{\ast }$ be its dual space. For $i=1,2,\dots ,k,$ let $A:X\to 2^{X^{\ast }}$ be a multivalued monotone operator satisfying the range condition. Let T be finite family of quasi-nonexpansive mappings such that $I-T_j$ are demiclosed at zero and $h:X\to X$ be a contraction mapping with a contractive coefficient $v\in (0,1).$ Suppose that the solution set $Sol={\cap }_{i=1}^k{A}_i^{-1}\left(0\right)\cap {\cap }_{j=1}^{m}F\left(T_j\right)$ is nonempty. Let $\left\{x_n\right\}$ be generated by the following iterative scheme:

$$\left\{\begin{array}{c}{u}_n=J_{{\mu }_n}^{A_k}\circ J_{{\mu }_n}^{A_{k-1}}\circ \cdots \circ J_{{\mu }_n}^{A_1}{x}_n\hfill \\ x_{n+1}={\alpha }_{n}h\left(x_n\right)\oplus (1-{\alpha }_n)\underset{j=0}{\overset{m}{⨁}}{\xi }_n^j{T}_j{u}_n,n\ge 1,\hfill \end{array}\right.$$

(40)

where $x_0\in X,$$\left\{{\alpha }_n\right\},{\left\{{\xi }_n^j\right\}}_{j=1}^m\subset (0,1),$ such that ${\sum }_{j=0}^m{\xi }_n^j=1,$ and $\left\{{\mu }_n\right\}\subset (0,\infty )$ satisfy the following condition:

(i) 

${lim}_{n\to \infty }{\alpha }_n=0$ and ${\sum }_{n=0}^{\infty }{\alpha }_n=\infty ,$

(ii) 

$0<\mu \le {\mu }_n$ and ${lim}_{n\to \infty }{\mu }_n=\mu ,\forall n\ge 1,$

(iii) 

$0<{lim\; sup}_{n\to \infty }{\xi }_n^j<1.$

Then, the sequence $\left\{x_n\right\}$ converges strongly towards an element $x^{\ast }\in Sol$ where $x^{\ast }$ is the unique solution of the variational inequalities

$$⟨\overrightarrow{x^{\ast }h\left(x^{\ast }\right)},\overrightarrow{u{x}^{\ast }}⟩\ge 0,\forall u\in Sol.$$

(ii) Setting $m=k=1$ in Theorem 2, we also have the following result:

Corollary 2.

Let X be complete the CAT(0) space and $X^{\ast }$ be its dual space. Let $A:X\to 2^{X^{\ast }}$ be a multivalued monotone operator satisfying the range condition. Let $T:X\to X$ be a L-Lipschitzian quasi-pseudo-contractive mapping and $h:X\to X$ be a contraction mapping with contractive coefficient $v\in (0,1).$ Suppose that the solution set $Sol=A^{-1}\left(0\right)\cap F\left(T\right)$ is nonempty. Let $\left\{x_n\right\}$ be generated by the following iterative scheme:

$$\left\{\begin{array}{c}{u}_n=J_{{\mu }_n}^A{x}_n\hfill \\ y_n={\xi }_n{u}_n\oplus (1-{\xi }_n)T({\beta }_n{u}_n\oplus (1-{\beta }_n)T{u}_n)\hfill \\ x_{n+1}={\alpha }_{n}h\left(x_n\right)\oplus (1-{\alpha }_n)y_n,\forall n\ge 1,\hfill \end{array}\right.$$

(41)

where $x_0\in X,$$\left\{{\alpha }_n\right\},\left\{{\beta }_n\right\},\left\{{\xi }_n\right\}\subset (0,1)$ and $\left\{{\mu }_n\right\}\subset (0,\infty )$ satisfy the following condition:

(i) 

${lim}_{n\to \infty }{\alpha }_n=0$ and ${\sum }_{n=0}^{\infty }{\alpha }_n=\infty ,$

(ii) 

$0<\mu \le {\mu }_n$ and ${lim}_{n\to \infty }{\mu }_n=\mu ,\forall n\ge 1,$

(iii) 

$0<\frac{1+L^2-\sqrt{1+L^2}}{L^2}<{lim\; sup}_{n\to \infty }{\beta }_n<{lim\; sup}_{n\to \infty }{\xi }_n<1.$

Then, the sequence $\left\{x_n\right\}$ converges strongly towards an element $x^{\ast }\in Sol$ where $x^{\ast }$ is the unique solution of the variational inequalities

$$⟨\overrightarrow{x^{\ast }h\left(x^{\ast }\right)},\overrightarrow{u{x}^{\ast }}⟩\ge 0,\forall u\in Sol.$$

4. Applications

In this section, we apply our results to solve some nonlinear optimization problems. We note that similar applications have been given in ([18], Section 4), however, we include it here for completion purposes. Moreover, in [18], the authors only considered the approximation of the nonlinear optimization problems while in this section, we solve a common solution of the nonlinear optimizations and a fixed point of quasi-pseudocontractive mappings.

4.1. Application to Minimization Problem

Let X be a Hadamard space with dual $X^{\ast }.$ Let C be a nonempty, closed and convex subset of X and $\phi :X\to (-\infty ,\infty ]$ be a proper, convex and lower semicontinuous function. Consider the following minimization problem (MP):

$$\phi \left(x\right)=\underset{y\in X}{min}\phi \left(y\right).$$

(42)

We denote the solution set of MP (42) by $\Phi =\mathrm{argmin}\phi .$ It is well known that $\phi$ attains its minimum at $x\in X$ if and only if $0\in \partial \phi \left(x\right)$ (see, e.g., [32]), where $\partial \phi$ is the subdifferential of $\phi$ defined by

$$\partial \phi \left(x\right)=\left\{\begin{array}{cc}\{x^{\ast }\in X^{\ast }:\phi \left(x\right)-\phi \left(y\right)\ge ⟨x^{\ast },\overrightarrow{yx}⟩,\forall y\in X\},\hfill & \mathrm{if}x\in D\left(f\right),\hfill \\ \varnothing ,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

Moreover $\partial \phi$ is monotone and satisfies the range condition, i.e., $D\left(J_{\lambda }^{\partial \phi }\right)=X$ for all $\lambda >0.$ Thus, the MP (42) can be formulated as finding $x\in X$ such that

$$0\in \partial \phi \left(x\right).$$

Setting $A\equiv \partial \phi$ in Theorem 2, we have the following result for finding the common solution of a finite family of MP and the fixed-point of quasi-pesudocontractive mappings.

Theorem 3.

Let X be a complete CAT(0) space and $X^{\ast }$ be its dual space. For $i=1,2,\cdots ,k,$ let ${\phi }_i:X\to (-\infty ,\infty ]$ be finite family of proper, convex and lower semicontinuous function. Let $T_j,(j=1,2,\dots ,m)$ be a finite family of $L_i$-Lipschitz quasi-pseudo-contractive mappings and $h:X\to X$ be a contraction mapping with contractive coefficient $v\in (0,1).$ Suppose that the solution set $Sol={\cap }_{i=1}^k{\Phi }_i\cap {\cap }_{j=1}^{m}F\left(T_j\right)$ is nonempty. Let $\left\{x_n\right\}$ be generated by the following iterative scheme

$$\left\{\begin{array}{c}{u}_n=J_{{\mu }_n}^{\partial {\phi }_k}\circ J_{{\mu }_n}^{\partial {\phi }_{k-1}}\circ \cdots \circ J_{{\mu }_n}^{{\phi }_1}{x}_n\hfill \\ y_n={\xi }_n^0{u}_n\oplus \underset{j=1}{\overset{m}{⨁}}{\xi }_n^j{T}_j({\beta }_n{u}_n\oplus (1-{\beta }_n)T_j{u}_n)\hfill \\ x_{n+1}={\alpha }_{n}h\left(x_n\right)\oplus (1-{\alpha }_n)y_n.\hfill \end{array}\right.$$

(43)

where $x_0\in X,$$\left\{{\alpha }_n\right\},\left\{{\beta }_n\right\},{\left\{{\xi }_n^j\right\}}_{j=0}^m\subset (0,1)$ such that ${\sum }_{j=0}^m{\xi }_n^j=1,$ and $\left\{{\mu }_n\right\}\subset (0,\infty )$ satisfy the following conditions:

(A1) 

${lim}_{n\to \infty }{\alpha }_n=0$ and ${\sum }_{n=0}^{\infty }{\alpha }_n=\infty ,$

(A2) 

$0<\mu \le {\mu }_n$ and ${lim}_{n\to \infty }{\mu }_n=\mu ,\forall n\ge 1,$

(A3) 

$0<\frac{1+L^2-\sqrt{1+L^2}}{L^2}<{lim\; sup}_{n\to \infty }{\beta }_n<{lim\; sup}_{n\to \infty }{\xi }_n^j<1,$ where $L=\underset{1\le j\le m}{max}\left\{L_i\right\}.$

Then, the sequence $\left\{x_n\right\}$ generated by (43) converges strongly to an element $x^{\ast }\in Sol$ where $x^{\ast }$ is the unique solution of the variational inequalities

$$⟨\overrightarrow{x^{\ast }h\left(x^{\ast }\right)},\overrightarrow{u{x}^{\ast }}⟩\ge 0,\forall u\in Sol.$$

4.2. Application to Variational Inequality Problem

The variational inequality problem (VIP) was first introduced in the 1950s by [33,34] and recently extended into Hadamard spaces by Khatibzadeh and Ranjbar [35]. The VIP is defined by

$$\mathrm{find}x\in C\mathrm{such}\mathrm{that}⟨\overrightarrow{Txx},\overrightarrow{xy}⟩\ge 0,\forall y\in C,$$

(44)

where $T:C\to X^{\ast }$ is a nonexpansive mapping. The set of the solution of VIP (44) is denoted by $VIP(T,C).$ Recall that the metric projection $P_C:X\to C$ is defined for $x\in X$ by $d(x,P_C\left(x\right)):{\displaystyle =\underset{y\in C}{inf}}d(x,y)$ and characterized by

$$z=P_C\left(x\right)\mathrm{if}\mathrm{and}\mathrm{only}\mathrm{if}⟨\overrightarrow{zx},\overrightarrow{zy}⟩\le 0,\forall y\in C.$$

(45)

Now, using the characterization of $P_C$, we obtain

$$x=P_C\left(Tx\right)\iff ⟨\overrightarrow{Txx},\overrightarrow{xy}⟩\ge 0,\forall y\in C.$$

(46)

Therefore, $x\in F(P_C\circ T)$ if and only if x solves (44). The indicator function $i_C:X\to \mathbb{R}$ is defined by

$$i_C\left(x\right)=\left\{\begin{array}{cc}0,\hfill & \mathrm{if}x\in C,\hfill \\ +\infty ,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

The subdifferential of $i_C,$

$$\partial i_C\left(x\right)=\left\{\begin{array}{cc}\{x^{\ast }\in X^{\ast }:⟨x^{\ast },\overrightarrow{xy}⟩\le 0,\forall y\in C\},\hfill & \mathrm{if}x\in C,\hfill \\ \varnothing \hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

is a monotone operator and satisfies the range condition. Furthermore, by (10) and (46), we obtain

$$z=J_{\lambda }^{\partial i_C}\left(x\right)\iff \left[\frac{1}{\lambda }\overrightarrow{zx}\right]\in \partial i_C\iff ⟨\overrightarrow{zx},\overrightarrow{zy}⟩\le 0\forall y\in C\iff z=P_C\left(x\right).$$

Thus, setting $A\equiv \partial i_C$ in Theorem 2, we have the following result for solving the finite family of VIP and the fixed point of quasi-pseudocontractive mapping.

Theorem 4.

Let X be complete CAT(0) space and $X^{\ast }$ be its dual space and C be a nonempty, closed and convex subset of $X.$ For $i=1,2,\dots ,k,$ let $S_i:C\to X^{\ast }$ be finite family of nonexpansive mappings. Let $T_j,(j=1,2,\dots ,m)$ be a finite family of $L_i$-Lipschitz quasi-pseudo-contractive mappings and $h:X\to X$ be a contraction mapping with contractive coefficient $v\in (0,1).$ Suppose that the solution set $Sol={\cap }_{i=1}^{k}VIP(S_i,C)\cap {\cap }_{j=1}^{m}F\left(T_j\right)$ is nonempty. Let $\left\{x_n\right\}$ be generated by the following iterative scheme

$$\left\{\begin{array}{c}{u}_n=(S_k\circ J_{{\mu }_n}^{\partial i_C})\circ (S_{k-1}\circ J_{{\mu }_n}^{\partial i_C})\circ \cdots \circ (S_1\circ J_{{\mu }_n}^{i_C})x_n\hfill \\ y_n={\xi }_n^0{u}_n\oplus \underset{j=1}{\overset{m}{⨁}}{\xi }_n^j{T}_j({\beta }_n{u}_n\oplus (1-{\beta }_n)T_j{u}_n)\hfill \\ x_{n+1}={\alpha }_{n}h\left(x_n\right)\oplus (1-{\alpha }_n)y_n.\hfill \end{array}\right.$$

(47)

where $x_0\in X,$$\left\{{\alpha }_n\right\},\left\{{\beta }_n\right\},{\left\{{\xi }_n^j\right\}}_{j=0}^m\subset (0,1)$ such that ${\sum }_{j=0}^m{\xi }_n^j=1,$ and $\left\{{\mu }_n\right\}\subset (0,\infty )$ satisfy the following conditions:

(A1) 

${lim}_{n\to \infty }{\alpha }_n=0$ and ${\sum }_{n=0}^{\infty }{\alpha }_n=\infty ,$

(A2) 

$0<\mu \le {\mu }_n$ and ${lim}_{n\to \infty }{\mu }_n=\mu ,\forall n\ge 1,$

(A3) 

$0<\frac{1+L^2-\sqrt{1+L^2}}{L^2}<{lim\; sup}_{n\to \infty }{\beta }_n<{lim\; sup}_{n\to \infty }{\xi }_n^j<1,$ where $L={\displaystyle \underset{1\le j\le m}{max}}\left\{L_i\right\}.$

Then, the sequence $\left\{x_n\right\}$ generated by (47) strongly converges to an element $x^{\ast }\in Sol$ where $x^{\ast }$ is the unique solution of the variational inequalities

$$⟨\overrightarrow{x^{\ast }h\left(x^{\ast }\right)},\overrightarrow{u{x}^{\ast }}⟩\ge 0,\forall u\in Sol.$$

5. Numerical Examples

In this section, we present some numerical examples to illustrate the performance of our iterative scheme and compare with other methods.

We choose the following parameters: ${\alpha }_n=\frac{1}{n+3},$ ${\mu }_n=\frac{3n+1}{2n+1},$ ${\beta }_n=\frac{4n}{5n+4},$ ${\xi }_n^i=\frac{1}{m+1}$ and let $h:X\to X$ be defined by $h\left(x\right)=\frac{5}{8}x.$ Using the aforementioned parameters, the conditions $\left(i\right)$–$\left(iii\right)$ on (20) are satisfied. Thus, for $x_0\in X,$ our algorithm (20) becomes

$$\left\{\begin{array}{c}{u}_n=J_{{\mu }_n}^{A_k}\circ J_{{\mu }_n}^{A_{k-1}}\circ \cdots \circ J_{{\mu }_n}^{A_1}{x}_n\hfill \\ y_n=\frac{1}{m+1}{u}_n+\sum _{i=1}^m\frac{1}{m+1}{T}_i\left(\frac{4n}{5n+4}{u}_n+\frac{n+4}{5n+4}{T}_i{u}_n\right)\hfill \\ x_{n+1}=\frac{5}{8(n+3)}{x}_n+\frac{n+2}{n+3}{y}_n,n\le 1.\hfill \end{array}\right.$$

(48)

Example 1.

Now, we provide example in ${\mathbb{R}}^2$ and define $A_i:{\mathbb{R}}^2\to {\mathbb{R}}^2$ by

$$A_i\left(x\right)=(i(x_1+x_2),x_2-x_1).$$

Thus, $A_i$ is a monotone operator. Now, for $x\in {\mathbb{R}}^2$

$$\begin{array}{ccc}\hfill J_{{\mu }_n}^{A_i}\left(x\right)=z& \iff & \frac{1}{{\mu }_n}(x-z)A_{i}z\hfill \\ & \iff & x=(I+{\mu }_n{A}_i)z\hfill \\ & \iff & z={(I+{\mu }_n{A}_i)}^{-1}x.\hfill \end{array}$$

Thus the resolvent of $A_i$ is computed as follows

$$\begin{array}{cc}{J}_{{\mu }_n}^{A_i}\left(x\right)\hfill & ={\left(\left[\begin{array}{ccc}1+{\mu }_{n}i& {\mu }_{n}i& \\ -{\mu }_n& 1+{\mu }_n\end{array}\right]\right)}^{-1}\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]\hfill \\ \hfill & =\frac{1}{(1+{\mu }_n)+({\mu }_n+2{\mu }_n^2)i}\left[\begin{array}{cc}1+{\mu }_n& -{\mu }_{n}i\\ {\mu }_n& 1+{\mu }_{n}i\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]\hfill \\ \hfill & =\left[\begin{array}{cc}\frac{1+{\mu }_n}{(1+{\mu }_n)+({\mu }_n+2{\mu }_n^2)i}& \frac{-{\mu }_{n}i}{(1+{\mu }_n)+({\mu }_n+{\mu }_n^2)i}\\ \frac{{\mu }_n}{(1+{\mu }_n)+({\mu }_n+2{\mu }_n^2)i}& \frac{1+{\mu }_{n}i}{(1+{\mu }_n)+({\mu }_n+2{\mu }_n^2)i}\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]\hfill \\ \hfill & =\left[\begin{array}{cc}\frac{x_1(1+{\mu }_n)-{\mu }_{n}i{x}_2}{(1+{\mu }_n)+({\mu }_n+2{\mu }_n^2)i}& \\ \frac{{\mu }_n{x}_1+x_2(1+{\mu }_{n}i)}{(1+{\mu }_n)+({\mu }_n+2{\mu }_n^2)i}\end{array}\right].\hfill \end{array}$$

(49)

Let $X={\mathbb{R}}^2$ with a Euclidean metric. Let $T:X\to 2^X,$ where T is defined by

$$Tx=\left\{\begin{array}{c}(\frac{1}{2},\frac{1}{2}),x_2\in [0,\frac{1}{2}]\hfill \\ (0,0),\mathit{otherwise}.\hfill \end{array}\right.$$

It is clear that $F\left(T\right)=p$ where $p=(\frac{1}{2},\frac{1}{2}).$ Furthermore, if $x_2\in [0,\frac{1}{2}],$ and let $\overline{x}=(x_1,x_2)$, thus we have

$$d^2(T\overline{x},p)=0<d^2(\overline{x},p)+d^2(\overline{x},T\overline{x}).$$

On the other hand, we have

$$d^2(T\overline{x},p)={(0-\frac{1}{2})}^2+{(0-\frac{1}{2})}^2=\frac{1}{2}.$$

Additionally,

$$\begin{array}{ccc}\hfill d^2(\overline{x},p)& =& {(x_1-\frac{1}{2})}^2+{(x_2-\frac{1}{2})}^2\hfill \\ & =& x_1^2+x_2^2-(x_1+x_2)+\frac{1}{2},\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill d^2(\overline{x},T\overline{x})& =& {(x_1-0)}^2+{(x_2-0)}^2\hfill \\ & =& x_1^2+x_2^2.\hfill \end{array}$$

Thus

$$\begin{array}{ccc}\hfill d^2(\overline{x},T\overline{x})+d^2(\overline{x},p)& =& 2x_1^2+2x_2^2-(x_1+x_2)+\frac{1}{2},\hfill \end{array}$$

which implies that

$$d^2(T\overline{x},p)\le d^2(\overline{x},p)+d^2(\overline{x},T\overline{x}).$$

Now, we show that T is not demicontractive, i.e., there does not exists $\beta \in [0,1)$ such that $d^2(T\overline{x},p)\le d^2(\overline{x},p)+\beta d^2(x,T\overline{x})$ for all $x\in H.$ Suppose, on the contrary, that there exists $\beta \in [0,1)$, then $\frac{1}{2}\le \frac{1}{\beta +1}\le 1$ for $p=(\frac{1}{2},\frac{1}{2})$ and choose $\overline{x}=(x_1,x_2)$ such that $\frac{1}{2}\le x_2\le \frac{1}{\beta +1}$ which implies that $\beta \le \frac{1-x_2}{x_2}$ and so

$$\begin{array}{ccc}\hfill d^2(\overline{x},p)+\beta d^2(\overline{x},T\overline{x})& <& x_1^2+x_2^2-(x_1+x_2)+\frac{1}{2}+\frac{1-x_2}{x_2}(x_1^2+x_2^2)\hfill \\ & =& x_1^2-x_1+\left(\frac{1-x_2}{x_2}\right)x_1+\frac{1}{2}.\hfill \end{array}$$

In particular, consider $\overline{x}=(0,x_2)$, then we obtain

$$d^2(\overline{x},p)+\beta d(\overline{x},T\overline{x})<\frac{1}{2}=d^2(T\overline{x},p),$$

which implies that T is not demicontractive. Now, we can implement our algorithm using Theorem 2. In this case, $m=1$ and ${\xi }_n^i=\frac{1}{2}$. Choosing $x_0=(2,2)$ as the starting point, we test the algorithms for the following cases:

Case I: $N=5$;

Case II: $N=20;$

Case III: $N=50;$

Case IV: $N=100.$

We compare the performance of our algorithm with Aremu et al. [16], Ogwo et al. [17] and Izuchuwku et al. [18]. We used $\parallel x_{n+1}-x_n\parallel <{10}^{-4}$ as the stopping criterion. The numerical results are shown in Table 1 and Figure 1.

Table 1. Computation result for Example 1.

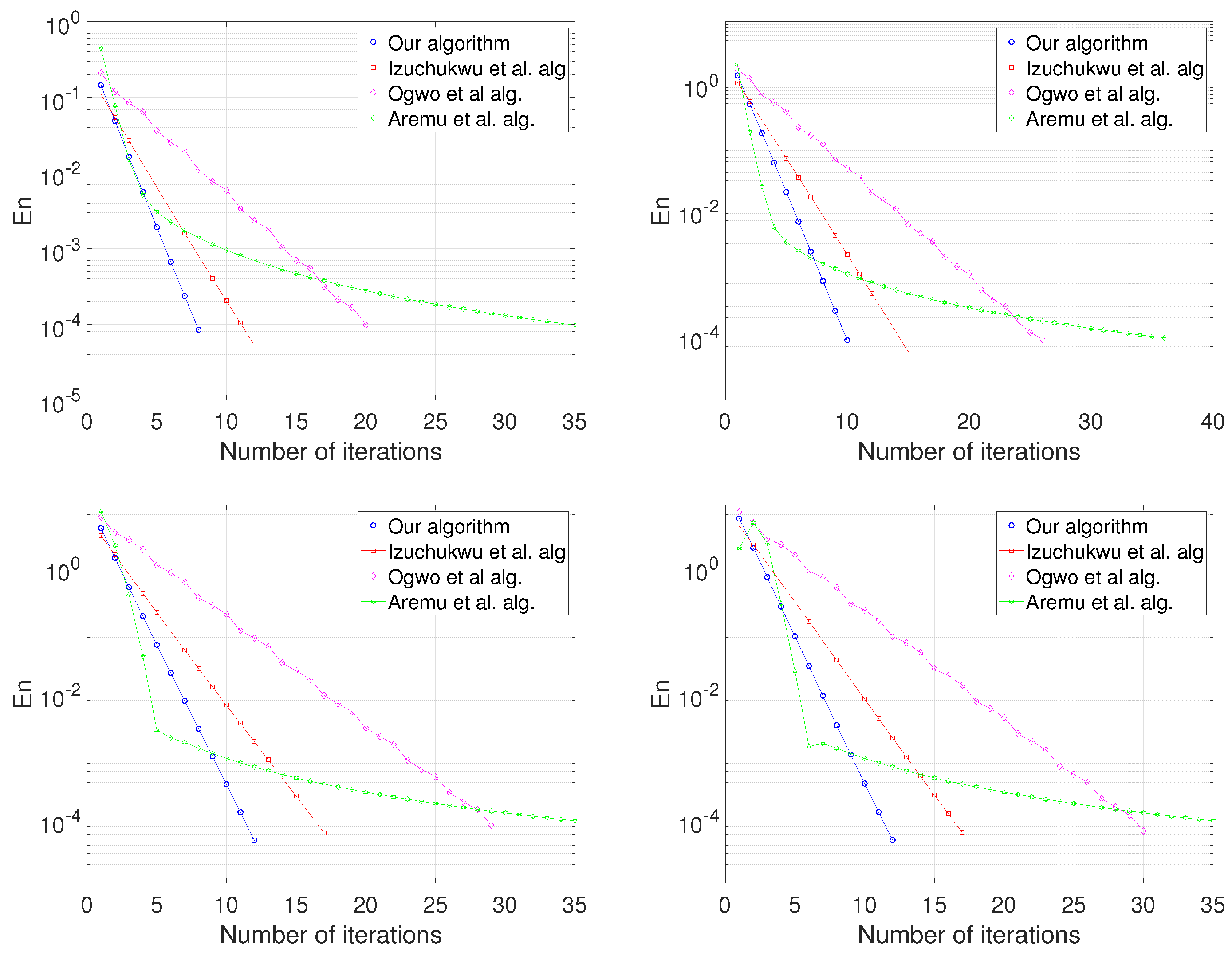
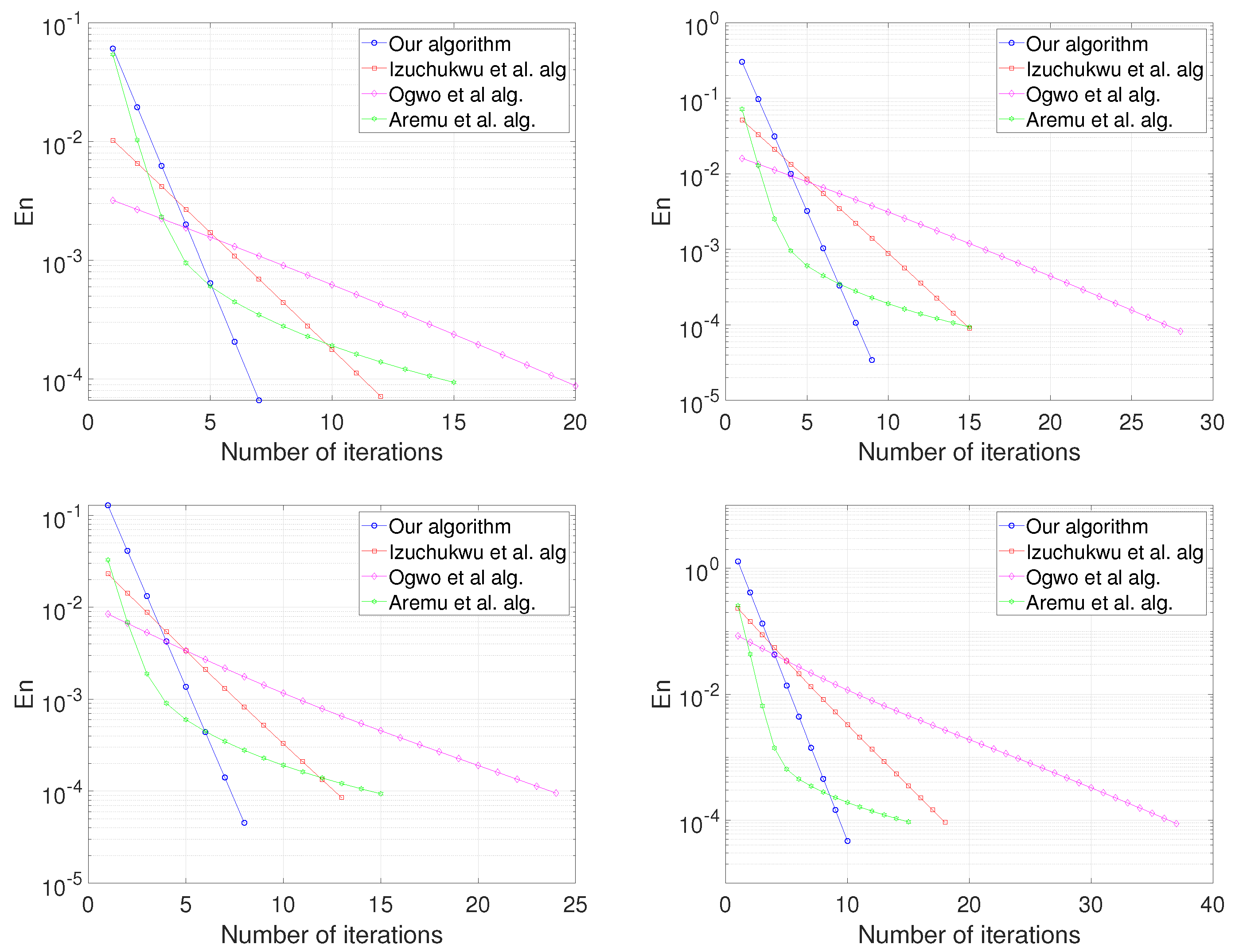
		Algorithm (48)	Izu et al. Alg. [18]	Ogwo et al. Alg [17]	Aremu et al. Alg. [16]
Case I	No of Iter.	8	12	20	35
	CPU time (s)	0.0034	0.0048	0.0122	0.0169
Case II	No of Iter.	10	15	26	36
	CPU time (s)	0.0046	0.0066	0.00197	0.0173
Case III	No of Iter.	12	17	29	35
	CPU time (s)	0.0095	0.0101	0.0150	0.0433
Case IV	No of Iter.	12	17	30	35
	CPU time (s)	0.0155	0.0170	0.0248	0.0481

Figure 1. Example 1, (Top Left): Case I; (Top Right): Case II; (Bottom Left): Case III; (Bottom Right): Case IV.

Example 2.

Take $N=m=2$ and let $X=L_2\left([0,1]\right)$ with norm ${\left|\right|x\left|\right|}_2={\left(|{\int }_0^1{x\left(t\right)|}^{2}dt\right)}^{\frac{1}{2}}.$ We define the sets

$$C=\{x\in X:|\left|x\right|{|}^2\le 1\}$$

and

$$Q=\{x\in X:x\left(t\right),3t^2=0\}.$$

It is known that the indicator function on C and Q, i.e., $i_C$ and $i_Q$ are proper convex and lower semi-continuous. Moreover, the sub-differentials $\partial i_C$ and $\partial i_Q$ are maximal monotone. The resolvent operator of $\partial i_C$ and $\partial i_Q$ are the metric projection which is defined by

$$P_C\left(x\left(t\right)\right)=\left\{\begin{array}{c}\frac{x\left(t\right)}{{\left|\right|x\left(t\right)\left|\right|}^2}{,if\left|\right|x\left(t\right)\left|\right|}^2>1\hfill \\ {x\left(t\right),if\left|\right|x\left(t\right)\left|\right|}^2\le 1\hfill \end{array}\right.$$

(50)

and

$$P_Q\left(x\left(t\right)\right)=\left\{\begin{array}{c}x\left(t\right)-\frac{⟨x\left(t\right),3t^2⟩3t^2}{\left|\right|3t^2{\left|\right|}^2},if⟨x\left(t\right),3t^2⟩\ne 0\hfill \\ x\left(t\right),if⟨x\left(t\right),3t^2⟩=0.\hfill \end{array}\right.$$

(51)

Let $T:X\to X$ be defined by $T_i\left(x\left(t\right)\right)=\frac{x\left(t\right)}{2i}$ for all $x\left(t\right)\in X.$ Then, $T_i$ is a quasi-pseudocontraction mapping. Using similar parameters as in Example 1, we compare the performance of our algorithm with Aremu et al. alg. [16], Ogwo et al. [17] and Izuchukwu et al. alg. [18]. We test the algorithms using the following initial point:

Choice (i): $x_0=sin\left(3t\right)$

Choice (ii): $x_0=\frac{exp\left(5t\right)}{7}$

Choice (iii): $x_0=t^3+2t-1$

Choice (iv): $x_0=t^{2}cos\left(3t\right).$

We used $\parallel x_{n+1}-x_n\parallel <{10}^{-4}$ as stopping criterion. The numerical results are shown in Table 2 and Figure 2.

Table 2. Computation results for Example 2.

		Algorithm (48)	Izu et al. Alg. [18]	Ogwo et al. Alg. [17]	Aremu et al. Alg. [16]
Choice (i)	No of Iter.	7	12	20	15
	CPU time (s)	0.0064	0.0096	0.0117	0.0075
Choice (ii)	No of Iter.	9	15	28	15
	CPU time (s)	0.0065	0.0099	0.0130	0.0076
Choice (iii)	No of Iter.	8	13	25	15
	CPU time (s)	0.0055	0.0077	0.0106	0.0089
Choice (iv)	No of Iter.	10	18	37	15
	CPU time (s)	0.0140	0.0356	0.0697	0.0378

Figure 2. Example 1, (Top Left): Choice (i); (Top Right): Choice (ii); (Bottom Left): Choice (iii); (Bottom Right): Choice (iv).

6. Conclusions

In this paper, we introduced a viscosity-type algorithm to approximate the common solution of monotone inclusion problem and the fixed point of quasi pseudo-contractive mappings in CAT(0) spaces. First, we provided some fixed point properties for the class of quasi pseudo-contractive mapping in CAT(0) spaces. We also showed that the class of quasi pseudocontractive mapping is more general than the class of demicontractive mapping. A strong convergence theorem was proven under certain mild conditions on the control sequence. We also presented some numerical examples to illustrate the performance and efficiency of the proposed method.