Abstract
The swarm-based Artificial Bee Colony (ABC) algorithm has a significant range of applications and is competent, compared to other algorithms, regarding many optimization problems. However, the ABC’s performance in higher-dimension situations towards global optima is not on par with other models due to its deficiency in balancing intensification and diversification. In this research, two different strategies are applied for the improvement of the search capability of the ABC in a multimodal search space. In the ABC, the first strategy, Patron–Prophet, is assessed in the scout bee phase to incorporate a cooperative nature. This strategy works based on the donor–acceptor concept. In addition, a self-adaptability approach is included to balance intensification and diversification. This balancing helps the ABC to search for optimal solutions without premature convergence. The first strategy explores unexplored regions with better insight, and more profound intensification occurs in the discovered areas. The second strategy controls the trap of being in local optima and diversification without the pulse of intensification. The proposed model, named the PP-ABC, was evaluated with mathematical benchmark functions to prove its efficiency in comparison with other existing models. Additionally, the standard and statistical analyses show a better outcome of the proposed algorithm over the compared techniques. The proposed model was applied to a three-bar truss engineering design problem to validate the model’s efficacy, and the results were recorded.
Keywords:
Patron–Prophet; self-adaptability; artificial bee colony; mathematical benchmark functions; swarm intelligence MSC:
68U01; 68U35; 90C26; 90C27
1. Introduction
In recent years, numerical optimization has received a tremendous response among researchers in science and engineering fields. Numerical problems also achieve greater complexity due to their non-convex, non-linearity, discontinuous, and non-differentiable natures [1]. In traditional optimization models such as Gradient Descent, Golden Search cannot address these complex problems due to its stringent conditions and convergence towards local optima. On the other hand, the optimization domain has reached yet another milestone in solving problems more effectively with the help of nature-inspired meta-heuristic optimization algorithms. Mathematical models of natural evolution include biological and physical development. Researchers from various domains have developed and utilized methods to address domain optimization issues. The Genetic Algorithm (GA) [2,3], Ant Colony Optimization (ACO) [4], Particle Swarm Optimization (PSO) [5,6,7], and Artificial Bee Colony (ABC) [8] are a few of the widely utilized methods. These models are significant in achieving globally optimum solutions for numerical optimization problems [9,10,11].
The ABC algorithm is inspired by the food foraging behaviour of honeybees [12]. Honeybees find their food source (i.e., honey) using three types of bees: employer, onlooker, and scout bees. By comparing the searching model of the ABC algorithm with other bio-inspired algorithms, it can be seen that the ABC possesses an effective searching model for optimal solutions with fewer computational expenses due to its fewer parameter considerations and strong searchability. This advantage boosted the usage of the ABC in solving a wide range of applications, such as mathematical benchmark functions [13,14,15], engineering design problems [16,17,18], and nurse scheduling problems [19,20]. In recent decades, it has been shown that ABC provides better outcomes than GA and PSO in several complex problems. However, its weak intensification capability diminishes ABC’s searching capability when applied to various issues [21]. A cooperative searching and balancing model toward diversification and intensification in the existing methods will effectively enrich ABC’s pursuit strategy.
The contributions of this research are described below:
- The concept of donor–acceptor, termed Patron–Prophet, is introduced to the ABC using the scout bee strategy.
- A self-adaptive model is proposed to adapt the coefficient values based on the balance between intensification and diversification.
- The introduced model is evaluated with different mathematical benchmark problems and associated with other techniques to prove its significance.
- Along with standard performance metrics and statistical performance indicators, the Wilcoxon Signed Rank test is utilized to evaluate the significance.
In this research, the ABC algorithm was equipped with the Patron–Prophet concept to solve continuous optimization problems. The motivational factor in proposing our algorithm to solve persistent optimization problems was that a wide range of applications exists under this category. In addition, a no-free lunch theorem exists [22], stating that one single algorithm that solves all existing problems does not exist. Continuous optimization problems tend to access parameter values (i.e., the variables to be optimized) within bounds that are restricted by constraints [23]. The choice of parameter values that are to be optimized has a high impact on objective functions. Additionally, the process of parameter optimization in continuous optimization problems can be easily adapted to the evolution of nature towards “survival of the fittest”, as both are ongoing processes, except for a few algorithms, such as Ant Colony Optimization and the Intelligent Water Drops algorithm.
The rest of the paper is structured as follows. Related works that enhance ABC and other approaches to improve the efficiency of optimization models are presented in Section 2. Section 3 discusses the proposed Patron–Prophet ABC and the standard ABC algorithm and its drawbacks. Section 4 presents the detailed evaluation process of the formulated technique with existing techniques. Finally, Section 5 discusses the proposed model’s outcome in the conclusion and future directions of work.
2. Related Works
Recently, many enhanced ABC techniques have been proposed to improve performance. These techniques can be classified into three types: (a) Finding newly emerged search equivalences. These equations are used in the ABC to determine adequate searching directions. They also produce new and appropriate solutions. The origin of these search equations improves the searching capability of ABCs. Based on a genetic algorithm, Zhu et al. (2010) presented a suitable directed system based on the ABC, coined the GABC [21]. The global guided search algorithm familiarizes the complete, most acceptable result into a search calculation of the bee algorithm. The novel search equation incorporates the exclusive data of the individual with the best fit. It progresses the intensification capability of ABCs, inspired by the transmutation operator. This operator was built with the help of DE, and the authors planned for three revised equations proposed by Gao et al. (2011) with the ABC [24]. The authors merged the benefits of the equations, which are wholly based on the adaptation of the mechanism, and they were retained to create the perfect equation. The proposed algorithm aims to represent an appropriate solution developed by Banharnsakun et al. (2011) [25]. This algorithm epitomized a best-so-far selection strategy and was deployed effectively by regulating the search radius. The method is constructed on the fair function values derived from PSO.
Xiang et al. (2014) planned a practical approach inspired by particle swarm and merged the core concept of multi-elitists [26]. It also includes ABC to improve effectiveness and is denoted as PS-MEABC. The goal of this algorithm is to extemporize the search equation. This searching feature helps to detect the best global solution (Gbest). Gao et al. (2014) anticipated an algorithm that can implement novel equations for searching purposes and is defined as EABC [27]. It provides perfect stability for intensification. The EABC algorithm helps to handle the stability problem by having proper diversification. Gao et al. (2013) designed an improved diversification equation comparable to the operator, and the operator belongs to GA, which emits crossover operations [28]. The direction search incorporates unbiased orthogonal Learning, which is referred to as CABC Karaboga (2014) and sets a platform for the onlooker bee phase by enhancing their searching abilities, which are denoted as a quick ABC (QABC) algorithm [29].
Wang et al. (2014) presented numerous equations into ABC for an effective solution [30]. It is mainly achieved to have a perfect steadiness for diversification, and the proposed strategy helps to achieve a stable intensification. The equations stage a comparative statement with other equations to obtain good candidate results with the help of the directional information; Kiran et al. (2015) planned an effective searching strategy with a bee algorithm referred to as dABC algorithm [31]. It produces offspring constructed on the preceding guiding information. Kiran et al. (2015) also projected an algorithm known as ABCVSS that comprises five search equations [32]. These equations show a diverse character yielded to form a flawless candidate result. Cui et al. (2017) anticipated a standing-based AABC algorithm in this algorithm [1]. The food sources of the parent are kept in the diversification calculation, and it is used for identifying the positions to carry the harvest process offspring.
Chu et al. (2020) proposed a variant on ABC, namely ABC, with various flexible competition for global optimization issues [33]. Complementary behaviour is implemented to improve the search capability of ABC. A practical technique is imposed to balance the intensification and diversification. In addition, it performs the search using competition among the individuals and migrant models. Yavuz et al. (2019) [34] proposed a self-adaptive search using the ABC algorithm model. This equation improves the intensification capability of ABC. Three different strategies, namely self-adaptive, local search improvisation, and total population, are imposed to improve the concept of ABC on mathematical benchmark procedures. The model is evaluated with competitor datasets, namely CEC’14 and 17. Song et al. (2019) [35] proposed an optimal model to study diversification and intensification in ABC. Based on the search capability, the selection model handpicks the results for the subsequent iterations based on the success rate. The algorithm’s results are successful in terms of accuracy and success rate while associating the acquired outcome with other models. Rong et al. [36] (2019) improved the execution time of ABC using an improved onlooker bee selection strategy. An operator called the Cauchy operator is used for balancing diversification and intensification. Different aspects of benchmark procedures are utilized to prove the significance of the introduced model.
In 2016, Gao et al. [37] introduced a hybrid ABC (DGABC) with DE to enhance the ABC technique’s search strategy. This model incorporated an oppositional-based population initialization to impose a diversified search capability. An effective learning strategy is also charged with learning from previous experiences. In examining the results of the proposed model, it performs on par with most of the existing algorithms. Cui et al. [38] proposed another variant of ABC with an adaptive population size (APABC) for improving the balance between diversification and intensification. This model presents a novel solution search calculation for the scout bee phase when the population space is about to reduce the solution count. The proposed model is more operative than the existing models in terms of convergence speed. Li et al. (2017) [39] proposed an effective foraging model in ABC. The proposed model is intended for the employee bees to search for high-quality solutions. A new Gene Recombination operator was presented to generate a better key from the highly qualified solution genes. A wide range of evaluations is carried over among different variants of ABC.
In 2018, Xue et al. [40] introduced a Self-Adaptive Artificial Bee Colony technique with Global Best (SABC-SG). An effective population initialization strategy and k-means clustering algorithm for maintaining the diversity in the population are imposed in SABC-SG. Different versions of the proposed model are evaluated, and the resultant convergence was better than the other existing models. Cui et al. (2018) [41] presented the Dual Population Framework (DPF) to enrich the convergence speed of ABC. In DPF, the population is divided into convergence and diverse population. The convergence population is responsible for intensification, and a diverse population will look after the diversification. For evaluation, the proposed DPF is embedded with different variants of ABC.
In 2019, Gao et al. [42] proposed a modified ABC that includes three different search strategies incorporated and evaluated using the Parzen window method. This Parzen window method reduces the computational cost of evaluating the solutions. In this model, two other techniques are used to maintain the diversity in the population. In 2020, Wang et al. [43] projected an improved version of ABC using a neighbourhood selection mechanism. In this model, solutions are selected after the neighbourhood similarity computation. It will reduce the selection of similar solutions for the next generation, improving the diversity in the population. In the same year, the authors [44] proposed a knowledge-based ABC algorithm (KFABC) for addressing different modal problems. This research defines three search strategies for managing two other models (Unimodal and Multimodal). An effective learning technique is also projected to find the appropriate search strategy for the respective modal problems. The results show significant results when compared with the existing models.
In 2021, Yang et al. [45] proposed ABC with Covariance Matrix (ACoM-ABC) to enhance the intensification of search. Eigen and natural coordinates are used over standard ABC to balance diversification and intensification. However, based on the computational cost in terms of time, the proposed model takes more time to converge towards optimal solutions. In the same year, Xu et al. [46] proposed a Multi-population ABC (MPABC), which comprises two different search strategies applied to the employee bee phase. A novel probability-based selection strategy is involved with these search strategies using the SoftMax function. These strategies improved the intensification capability of the standard ABC. In the same year, an effective ABC algorithm is used for scheduling digital microfluidic biochip operations [47]. Along with ABC, many algorithms in bio-inspired models solve various problems in many domains [48,49,50,51,52,53,54].
The recent applications of ABC in the engineering and non-engineering disciplines are listed as follows: In 2021, Xui et al. [55] used a discrete version of ABC for call centre scheduling and weekend-off fairness. In 2022, Yibing Cui et al. proposed a reinforced ABC for robot path planning that intelligently tunes the perturbation frequency [56]. In 2022, Xin et al. [57] proposed a self-adaptive ABC for decoding the resource-constrained and attains effective perturbation solutions. Yavuz et al. [58] proposed an enhanced ABC for constrained optimization. In this research work, the authors imposed the distance savant on employees and onlooker bees for better intensification. In 2022, Rafal et al. [59] utilized ABC for scheduling the palletizing task with the help of a robotic arm and ABC algorithm. This research used a multi-objective version of ABC to identify an optimal solution that satisfies four different objective functions.
The state-of-the-art algorithms discussed hold an effective search capability. However, the extraction of knowledge from the discarded solutions and an inbuilt balancing between diversification and intensification is missing in these models. To address the aforementioned issues, the authors of this paper propose a Patron–Prophet-based ABC.
3. Patron–Prophet Artificial Bee Colony Algorithm
This section presents the standard working model of ABC, its drawbacks in searching and the proposed Patron–Prophet Artificial Bee Colony algorithm (PP-ABC).
3.1. Standard ABC
ABC mimics the behaviour of food foraging of honeybees. This population-based model consists of three search bees: employee bees, onlooker bees, and scout bees. The total number of employees and onlooker bees are equal in each colony. Each solution in the population is mapped to an employee bee. The employee bees waggle and dance to tell onlooker bees where to obtain food. Onlooker bees hunt for higher-quality food sources based on probability calculations. Food sources with low superiority are excluded, and employee bees become scouts if the food source runs out. The modified scout bee must find nourishment. The in-depth details of the standard ABC algorithm can be found in [60].
3.1.1. Initialization
Food sources () for n-dimensional vectors are generated in the initialized population. denotes the solution population. Equation (1) creates population solutions as below
where represents a solution, denotes the dimension of solution. denotes Upper and Lower bound values in dimension . The food sources are provided to the employee bees at random. Accordingly, the fitness calculation for the solution is assessed.
3.1.2. Employee Bee Phase
In this phase, candidate solutions are generated, and food source positions will be scrutinized. The mathematical model of the candidate individual is formulated and shown in Equation (2)
where and and is the constriction factor that controls the influence of the difference between the current and neighbourhood solutions, and its value varies between [−1, 1]. A greedy method is used to choose between and based on the fitness estimate. The individual is changed to if has a better fitness value than .
3.1.3. Probability Calculation
After calculating their fitness, employee bees communicate the location of the food supply with onlooker bees. In addition, the evaluation of the employee search individual will be made with the aid of the likelihood value . The likelihood and appropriateness of an individual are calculated and presented in Algorithm 1. In Algorithm 1, represents the fitness value computed using the objective function of the problem.
| Algorithm 1: Computation of Probability Values for Every Solution. |
| Begin for = 1: perform end for End |
3.1.4. Onlooker Bee Phase
Each onlooker search individual picks the food source contingent on the likelihood value . Using Equation (2), it modifies throughout this bee phase. To choose the optimal solution from and a greedy strategy resembling the employee bee phase is used.
3.1.5. Scout Bee Phase
After the employee and onlooker search individual, the solution disappears when the evolved solution cannot achieve a new best and if the evolution period is exhausted for the predefined trial. Additionally, the corresponding employee bee acts as a scout search individual for searching for novel food bases using Equation (1).
3.2. Drawbacks of Standard ABC
There are two significant drawbacks to the existing standard ABC: non-cooperative behaviour and non-balanced diversification and intensification.
3.2.1. Non-Cooperative Behaviour in Scout Bee Phase
The cooperative behaviour of honeybees can be visible while sharing information on food sources between employees and onlookers. However, the solution is not improvised in a limited period, the individual is eliminated from the population, and the new solution will be replaced. At this level, the cooperative behaviour of bees while generating new solutions is not present.
3.2.2. Non-Balanced Diversification and Intensification
Balancing diversification and intensification is an essential part of any optimization algorithm. This balancing leads the algorithm to search towards global optima throughout the entire run in meta-heuristic optimization models. The diversification and intensification phases in ABC perform better when the problem dimensions are few. However, when the sizes increase in a problem, the effect of intensification is highly affected due to its less neighbourhood search strategy [21].
3.3. Proposed Patron–Prophet ABC
The proposed Patron–Prophet ABC consists of two incorporations to enhance standard ABC’s working model: the Patron–Prophet and Self-Adaptive strategies to improve the balance between diversification and intensification.
3.3.1. Patron–Prophet Strategy
The Patron–Prophet strategy follows the donor–acceptor concept. The Patron is responsible for donating the information regarding the deviation from the best solutions. The Prophet is the receiver, the newly generated individual who is groomed efficiently based on the Patron’s information. In ABC, the unimproved individual is eradicated at the scout bee phase, and a novel individual is generated and replaced. In this model, if the individual about to be discarded has provided the information of how it was deleted, it might be helpful for the newly generated solution to carry on the searching process in further iterations.
Thus, the solution is identified as unimproved throughout iterations and discarded. The information on how much it has deviated from the suitable solution can be derived using the proposed model in [61]. In addition, the systematic process of the Patron–Prophet strategy is presented in Figure 1. This extracted information can be supplementary to the newly generated solution to enrich the pursuit capability. The Patron–Prophet strategy can be mathematically formulated as
where , and .
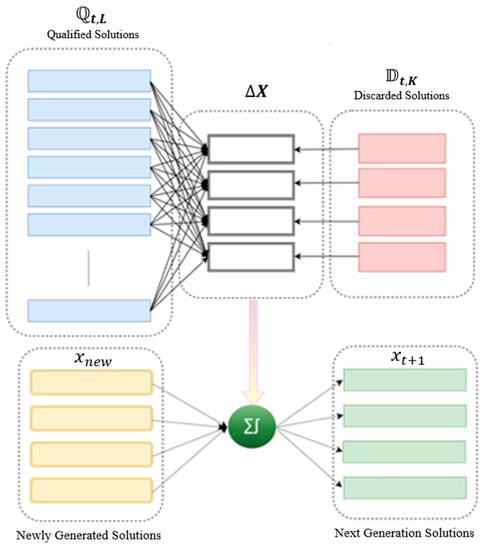
Figure 1.
Schematic view of the Patron–Prophet concept of ABC.
The new solution is generated using the extracted information from abandoned solutions, as follows:
where represents the generation number.
3.3.2. Self-Adaptability
The Self-Adaptability strategy is proposed for ABC for balancing diversification and intensification. Throughout the pursuit process of the onlooker individual strategy, a set of solutions undergo intensification to find an effective solution in the neighbourhood. However, when the dimension of the problem increases, the individual may not be capable of exploiting more dimensions when the tuning factor affects only one of the chosen dimensions. Hence, when self-adaptability is deployed in the onlooker bee phase, controlling the search space would be much more effective for balancing diversification and intensification. The self-adaptable strategy can be mathematically represented as
where specifies the best solution suitability value concerning the objective function (), denotes the iteration, and denotes the average in the fitness values of all solutions at iteration . and are the shrinking features that influence the value of .
The proposed PP-ABC is shown in Algorithm 2.
| Algorithm 2: PP-ABC. |
| Input: Lower and upper bound of every dimension, # of the individual in a population (), the total number of dimensions (S), Population Initialization For i = 1: , do |
| For j = 1: S, do |
| Create individual |
| End for End for |
| // Population fitness evaluation using Algorithm 1 |
| Repeat |
| { // Employee individual strategy For each , do |
| Select between and End For |
| // Onlooker individual strategy Set While () If(0,1) < with Algorithm 1, then Select between and r = r + 1 End if End while |
| // Scout individual strategy for where end |
| Remember the best individual position obtained so far |
| } |
| Until ( ) |
3.4. The Working Process of PP-ABC
In Algorithm 2, the initial phase starts with the population initialization as in Equation (1), and every solution is generated as feasible solutions within the lower and upper bound. After the population initialization phase, every individual is evaluated based on the fitness function. This fitness function is dependent on the problem’s nature. This fitness value of every solution quantifies individual superiority.
After the fitness evaluation, the generation evolution of solutions start in the first iteration. This generation is evaluated until the termination criteria are satisfied. The termination criteria can be any epoch value or the best fitness value. The first phase of the ABC algorithm comes with the employee bee phase. The employee bee phase generates a neighbourhood candidate solution for every individual solution in the population as its base. In the employee bee phase, the individual undergoes a slight change among the selected genes of the original candidate solution in the population. If the newly generated solution’s fitness value is better when compared to the base individual, then that solution is replaced by the newly developed solution; otherwise, the old one is retained.
After the employee bee phase, based on Algorithm 1, every solution has a probability value before it undergoes the evolution of the onlooker bee phase. If the probability value is greater than the arbitrary value, the current individual experiences the transition using onlooker bees. The random number imposes the uncertainty principle in ABC. In the onlooker bee phase, the surpassed solutions use the Self-Adaptive parameter ( to generate new solutions. This self-adaptive parameter develops new solutions concerning the current scenario of the swarm. If most of the individuals in the hive work towards the best solution, the value will be high in the range with the intensity to generate new individuals with more diversity. If the number of solutions near to best solution is lower, the next solution generation in the onlooker bee phase creates better solutions in intensification. After the solution generation, a greedy method will be pragmatic to retain the best solutions for the next generation population, similar to the employee bee phase.
Throughout the entire procedure, every individual solution keeps track of its betterment over iterations. If any individual is undeveloped after a certain number of trials, it will be eliminated by the scout bees, and new solutions will be obtained in place of abandoned solutions. During the scout bee phase, our proposed Patron–Prophet concept makes the abandoned solutions impose a procedure called cooperative behaviour. The qualified and abandoned solutions are identified and separated. Then, the amount of deviation from the suitable individuals for every abandoned solution is determined and kept as using Equation (4). This information is incorporated into the newly generated key using Equation (5). The entire process of PP-ABC is carried out until it reaches the maximum number of iterations (.
4. Experimental Procedure and Result Analysis
This section presents the experimental setup of the formulated system and other techniques. In addition, we compare the proposed outcome with other methods, and statistical measures are conducted to ensure the efficacy of the proposed work.
4.1. Experimental Setup
The PP-ABC algorithm’s evaluation purpose was applied to 15 benchmark functions [29,30]. These mathematical benchmark functions were chosen because these are widely used for the performance evaluations of metaheuristic algorithms in the literature. The classification of chosen benchmark functions is shown below:
Function F1–F4: Unimodal functions
Function F5–F11: Multimodal functions
Function F12, F13: Multimodal functions with penalized
Function F14, F15: Composite functions
Out of these 15 benchmark functions, function f3 holds the multimodality property if its dimensions are more than 3 (i.e., ). Other existing algorithms are compared with our proposed algorithm by the minimum global optimum value attained (), the mean of the population that achieved the minimum global optimum solution (mean), and the standard deviation of the entire population (). The performance of PP-ABC was measured and compared with the performance of other existing algorithms. In addition, we also included the standard ABC and six different recently proposed approaches, namely DGABC [37], KFABC [44] for testing the learning mechanism, SABC-SG [40] to test the self-adaptability, APABC [38], ACoM-ABC [45], and MPABC [46], for comparing the balanced diversification and intensification. The parameter backgrounds of the proposed system are presented in Table 1. In addition, the range of each function is shown in Table 2.

Table 1.
Parameter settings.

Table 2.
Range of each dimension for the benchmark functions.
The proposed technique was performed on MATLAB 12.0, and the processor used was an Intel core i7-2620M processor with 4 GB of RAM. Two different versions were prepared to examine the performance of the Self-Adaptability and Patron–Prophet strategies of ABC, one only with Patron–Prophet in ABC and another only with Self-Adaptability in ABC. The obtained results are presented in Table 3.

Table 3.
Comparison of the Patron–Prophet and Self-Adaptability modes.
The effect of the Patron–Prophet model and Self-Adaptability on an individual basis in the standard ABC technique is presented in Table 3. We interpreted the outcome in achieving the minimum as the objective of the six functions to perform its best in mutual between both the models. As a standalone process, the Patron–Prophet model attained a maximum of four parts, and the Self-Adaptability strategy achieved three other functions. The proposed method shows the capability of the Patron–Prophet on intensification towards optimal solutions. In addition, interpreting the standard deviation values of Self-Adaptability offers a diverse range of results at the end of the run, showing the search capability (diversification) of the Self-Adaptability model of ABC. Hence, combining these two models and incorporating them in ABC results in better mathematical benchmark functions in terms of intensification towards optimal solutions and diversification throughout the search space.
From the results shown in Table 4, which covers the 10-dimensional problem set of the provided functions, the outcome of the PP-ABC technique converges towards globally optimal solutions compared with other stated algorithm results. In unimodal functions (F1, F2), the multimodal function (F9, F11) results of the proposed algorithm achieve exact global optimum solutions in the entire algorithm population. In multimodal (F5, F7) and penalty functions (F12), some individuals of the proposed algorithm attain optimal solutions with some deviation compared to another individual in the entire population.

Table 4.
Simulation results of benchmark functions with ten dimensions.
Table 5 shows the results of the 30-dimensional problem set of the provided benchmark functions. Apart from functions F2, F3, F5, F6, and F10, the F13 PP-ABC achieves superior outcomes in all the other parts. The proposed algorithm attains a global solution of 0 in the entire population for the functions F1, F7, F8, F9, and F14. The proposed model shows the consistency of the proposed algorithm over other algorithms. The proposed algorithm is second best in achieving global minimum within the provided iterations on two benchmark functions, including F2 and F11. Figure 2 shows the convergence frequency of the proposed algorithm concerning generations for the benchmark functions of 30 dimensions.

Table 5.
Simulation results of benchmark functions with 30 dimensions.
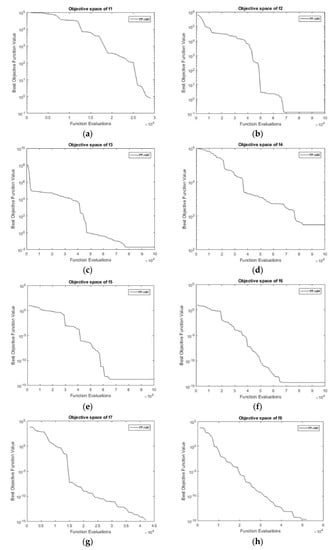
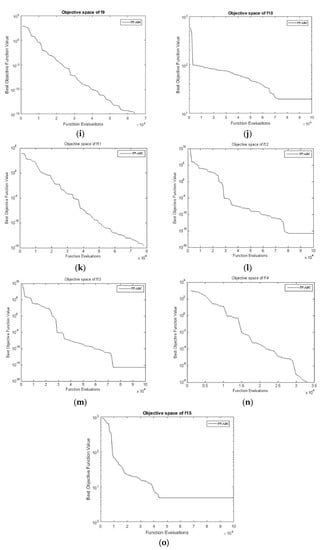
Figure 2.
Convergence rate of the (a) F1 and (b) F2 benchmark functions. Convergence rate of the (c) F3, (d) F4, (e) F5, (f) F6, (g) F7, and (h) F8 benchmark functions. Convergence rate of the (i) F9, (j) F10, (k) F11, (l) F12, (m) F13, and (n) F14 benchmark functions. Convergence rate of the (o) F15 benchmark function.
4.1.1. Analysis of the Intensification Capability of PP-ABC
Functions F1–F4 represent the unimodal benchmark functions since only one global optimal solution exists in the search space. Unimodal functions were evaluated in this paper to analyze the proposed algorithm’s intensification capability [61]. Table 4 and Table 5 show that the PP-ABC strategy performs significantly better in determining the optimal solution and is competitive in relation to other existing algorithms. In Table 4, the proposed PP-ABC provides the best result for F1–F3 functions and the best for the F4 unimodal function. In Table 5, for unimodal functions with 30 dimensions, the proposed PP-ABC delivers optimal results for functions F1 and F4, and at least second best for part F2 and third best for F3. Thus, it is apparent that the proposed algorithm holds significant intensification capability.
4.1.2. Analysis of Diversification Capability of PP-ABC
In contrast with unimodal functions, multimodal functions (F5–F11) comprise multiple local optima that induce high local optima concerning problem dimensions. Addressing these benchmark functions to evaluate an algorithm’s performance results in its diversification capability over the provided search space. Table 4 and Table 5 demonstrate the proposed algorithm’s performance in determining the optimal best-fit solution in the shared multimodal search space of 10 and 30-dimension mathematical benchmark functions. On multimodal functions (F5–F11) with ten dimensions, in Table 3, it is noticeable that the PP-ABC obtains optimal solutions on five different search spaces (F5, F7–F9, and F11) out of seven multimodal mathematical functions. For multimodal operations with 30 dimensions, the proposed PP-ABC outperforms other existing algorithms on functions F7–F9 and F11. Indeed, the proposed algorithm is better in terms of diversification over most test problems.
4.1.3. Analysis of Skipping Capability from Local Optima of PP-ABC
Achieving global optima in composite test functions is a challenging task where only the algorithm with a balanced diversification and intensification capability has the potential to accomplish it. From Table 4 and Table 5, it can be observed that the proposed PP-ABC outperforms and is better than the compared algorithms F14 and F15 of 10 and 30 dimensions, respectively. From the results of F14 and F15 in Table 4, we can observe that PP-ABC has better outcomes for the F15 composite function and second best for function F14. In Table 5, on composite parts with 30 dimensions, the proposed PP-ABC obtained an optimal solution for both hybrid procedures.
- A.
- Statistical analysis of the mathematical benchmark function results
A pairwise statistical test, namely Wilcoxon Signed Rank Test (WSRT), was utilized to associate the PP-ABC with the existing algorithms. The test results of each algorithm run were used for effective pairwise comparison with a significant value of 0.05. Table 6 and Table 7 show the statistical non-parametrical pairwise Wilcoxon Signed Rank test comparing PP-ABC with other existing algorithms on 10- and 30-dimensional benchmark functions to prove the significant difference. ‘+’ represents the outcome that shows Null Hypothesis is rejected, and the proposed PP-ABC shows a superior performance with the compared algorithm. ‘=’ refers to no statistical variations among the compared algorithms. ‘−’ refers to being rejected, and PP-ABC shows inferior performance than the proposed algorithm. At the end of each table, the total number of all cases of pairwise comparisons is provided. A p-value below 1.76 × 10-6 is rounded and represents 0.

Table 6.
WSRT for benchmark functions with 10 dimensions.

Table 7.
WSRT for benchmark functions with 30 dimensions.
Table 6 shows the pairwise comparison of the PP-ABC with the existing techniques. T− represents the cumulative rank the proposed PP-ABC obtained in 30 runs. T+ represents the cumulative rank accepted by the competitive algorithm when the minimum attained values are ranked. The attribute winner represents ‘+’ for the algorithm that attained maximum cumulative rank in minimization. ‘=‘ describes that neither algorithm obtained the winner status.
Additionally, ‘−’ represents our proposed algorithm’s loss in relation to the competitive algorithm. The last row of Table 5 illustrates the consolidated position of the pairwise comparison. On analyzing the statistical performance of PP-ABC on mathematical benchmark functions with ten dimensions, PP-ABC outperforms DGABC on 12 benchmark functions, is superior on 11 benchmark functions over APABC and ABC, is excellent on 10 dimensions on SABC-SG, KFABC, and MPABC, and has a particular minimum inference on 8 dimensions against ACoM-ABC.
Table 7 shows the pairwise comparison of proposed PP-ABC on benchmark functions with 30 dimensions with the existing algorithms. Comparing the results of PP-ABC with DGABC shows the former’s superior performance over 13 benchmark functions and on 12 procedures over KFABC and SABC-SG, respectively. Additionally, the proposed PP-ABC has equal competence with the algorithms ACoM-ABC and MPABC on six superior performances and equivalent competence on six functions with an inferior performance over three different tasks. Thus, this shows that PP-ABC has a better outcome on high-dimensional benchmark functions and is no less to the existing bio-inspired algorithms.
Table 8 and Table 9 show a category-based (UM, MM, PF, and CF) comparison for 10- and 30-dimensional functions. The values of Table 8 and Table 9 are counted from Table 6 and Table 7 according to the category stated, respectively. The consolidated tables in Table 8 and Table 9 show that the proposed PP-ABC leads to a significantly superior performance in most cases. In particular, from Table 8, it can be inferred that PP-ABC provides ideal solutions compared to the existing techniques in the MM function category, which is considered the core part of the algorithm in solving problems with multimodal search space. Additionally, in the function categories PF and CF, PP-ABC performs no worse than the existing techniques. From Table 9, it can be inferred that, on unimodal functions with high dimensions, PP-ABC outperforms the current algorithms with a high performance. Additionally, for the MM function category, PP-ABC defeats DGABC, APABC, ABC, SABC-SG, and KFABC and competes with ACoM-ABC and MPABC with its high diversification capability.

Table 8.
Category-based comparison for the proposed PP-ABC algorithm for benchmark functions with 10 dimensions.

Table 9.
Category-based comparison for the proposed PP-ABC algorithm for benchmark functions with 30 dimensions.
4.2. Time Complexity Analysis of Patron–Prophet ABC
The time complexity of the proposed ABC method lies on three major factors, namely the population size the dimension of a problem and the total number of iterations for a single run (.
- Initial phase: For population initialization, the time complexity is .
- Employee bee phase: In the employee bee phase, all the individuals take part in the computation of another individual and hence the time complexity of .
- Onlooker bee phase: Only in the onlooker bee phase, the selected individuals take part in the generation of solutions for the subsequent iterations, and hence the time complexity can be an average of based on asymptotic notations, and it is expressed as .
- Scout bee phase: Only in the scout bee phase, the unimproved solutions are subject to improvisation. Since the balancing factor between intensification and diversification is handled efficiently, on every iteration, the scout bee phase obtains its computation half the way lower than the previous iteration. However, during each computation, all abandoned solutions act as a source of information for every newly generated key. Since every time the quantity of solution obtains half, we can define as and the computation in every turn of the scout bee phase is ; the final statement is and for the scout bee phase is , which results in .
- Fitness computation: The computational complexity for the fitness calculation is .
On the entire process, the total computation of Patron–Prophet can be summarized as Based on asymptotic notations considering the upper bound time complexity, it can be represented as .
4.3. Three-Bar Truss Design Optimization Problem
The balance in load with a three-bar truss in terms of volume was mathematically modelled as an engineering design problem with different constraints, such as stress, deflection, and buckling. In this engineering design problem, there are two design variables that are to be optimized, namely and . The three-bar truss design model is depicted in Figure 3. The objective function for this model was mathematically formulated as follows:
where . This model is subject to three different constraints, and they are mathematically modelled as follows:
where and should be in the range [0, 1], , and .
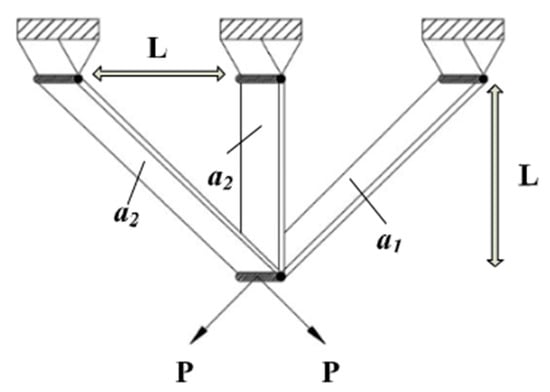
Figure 3.
Three-bar truss design model.
The proposed model wa compared with the existing algorithms in Table 10, and the current results were obtained from [62]. The proposed model was implemented in MATLAB version 2018a in the computational system discussed in Section 4.1. The number of iterations for every run was a maximum of 250, with 25 as the population size. The comparison of the performance of PP-ABC shows that it competes equally with the existing models in recent studies.

Table 10.
The comparison results of PP-ABC with the existing models on three-bar truss design.
5. Conclusions
This work proposed the Patron–Prophet ABC for effectively addressing numerical optimization problems. The proposed PP-ABC strategy consists of a Patron–Prophet mode and balanced diversification and intensification factors for handling high dimensional issues. The Patron–Prophet strategy is imposed to obtain knowledge regarding deviation from suitable to discarded solutions. Additionally, one other Self-Adaptability aspect, namely is to retain the balance of diversification and intensification. PP-ABC’s performance was measured and compared with the literature techniques for mathematical benchmark functions with different dimensions and categories. The performance was assessed in three various forms: conventional performance metrics (minimum, mean, and std.dev), statistical analysis, Wilcoxon Signed Rank Test, and performance evaluation in multimodality. Concerning standard and statistical outcome trials, the introduced PP-ABC provides a superior solution compared to other techniques on normal unimodal, multimodal, and hybrid benchmark functions. This research can be extended by solving different engineering applications that are in much need of optimized solutions.
Author Contributions
Conceptualization, K.T.; methodology, K.T. and R.R.; validation, S.S.A. and M.R.; formal analysis, D.M.; writing—original draft preparation, K.T.; writing—review and editing, R.R. and K.J.; supervision, R.R. and M.R.; funding acquisition, S.S.A. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by the Deanship of Scientific Research, Taif University Researchers Supporting Project number (TURSP-2020/215), Taif University, Taif, Saudi Arabia.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data in this research paper will be shared upon request to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cui, L.; Li, G.; Wang, X.; Lin, Q.; Chen, J.; Lu, N.; Lu, J. A ranking-based adaptive artificial bee colony algorithm for global numerical optimization. Inform. Sci. 2017, 417, 169–185. [Google Scholar] [CrossRef]
- Wang, W.J.; Yuan, S.Q.; Pei, J.; Zhang, J.F. Optimization of the diffuser in a centrifugal pump by combining response surface method with multi-island genetic algorithm. Proc. Inst. Mech. Eng. Part E J. Process. Mech. Eng. 2017, 231, 191–201. [Google Scholar] [CrossRef]
- Liu, H.; Shi, S.; Yang, P.; Yang, J. An Improved Genetic Algorithm Approach on Mechanism Kinematic Structure Enumeration with Intelligent Manufacturing. J. Intell. Robot. Syst. 2017, 89, 343–350. [Google Scholar] [CrossRef]
- Xiaowei, H.; Xiaobo, Z.; Jiewen, Z.; Jiyong, S.; Xiaolei, Z.; Holmes, M. Measurement of total anthocyanins content in flowering tea using near infrared spectroscopy combined with ant colony optimization models. Food Chem. 2014, 164, 536–543. [Google Scholar] [CrossRef]
- Chen, X.; Tianfield, H.; Mei, C.; Du, W.; Liu, G. Biogeography-based learning particle swarm optimization. Soft Comput. 2016, 21, 7519–7541. [Google Scholar] [CrossRef]
- Yang, X.; Chen, L.; Xu, X.; Wang, W.; Xu, Q.; Lin, Y.; Zhou, Z. Parameter identification of electrochemical model for vehicular lithium-ion battery based on particle swarm optimization. Energies 2017, 10, 1811. [Google Scholar] [CrossRef]
- Nagra, A.A.; Han, F.; Ling, Q.H.; Mehta, S. An improved hybrid method combining gravitational search algorithm with dynamic multi swarm particle swarm optimization. IEEE Access 2019, 7, 50388–50399. [Google Scholar] [CrossRef]
- Wang, B.; Yu, M.; Zhu, X.; Zhu, L.; Jiang, Z. A Robust Decoupling Control Method Based on Artificial Bee Colony-Multiple Least Squares Support Vector Machine Inversion for Marine Alkaline Protease MP Fermentation Process. IEEE Access 2019, 7, 32206–32216. [Google Scholar] [CrossRef]
- Li, K.; Pan, L.; Xue, W.; Jiang, H.; Mao, H. Multi-Objective Optimization for Energy Performance Improvement of Residential Buildings: A Comparative Study. Energies 2017, 10, 245. [Google Scholar] [CrossRef]
- Chen, X.; Cai, X.; Liang, J.; Liu, Q. Ensemble Learning Multiple LSSVR With Improved Harmony Search Algorithm for Short-Term Traffic Flow Forecasting. IEEE Access 2018, 6, 9347–9357. [Google Scholar] [CrossRef]
- Wang, S.; Yu, C.; Shi, D.; Sun, X. Research on speed optimization strategy of hybrid electric vehicle queue based on particle swarm optimization. Math. Probl. Eng. 2018, 2018, 1–15. [Google Scholar] [CrossRef]
- Karaboga, D. An idea based on Honey Bee Swarm for Numerical Optimization, Erciyes University, Engineering Faculty. Comput. Eng. Dep. 2005, 12, 1–10. [Google Scholar]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Shah, H.; Tairan, N.; Garg, H.; Ghazali, R.; Zhu, G.; Kwong, S. Global gbest guided-artificial bee colony algorithm for numerical function optimization. Computers 2018, 7, 69. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. Artificial bee colony (ABC) optimization algorithm for solving constrained optimization problems. In International Fuzzy Systems Association World Congress; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Akay, B.; Karaboga, D. Artificial bee colony algorithm for large-scale problems and engineering design optimization. J. Intell. Manuf. 2012, 23, 1001–1014. [Google Scholar] [CrossRef]
- Garg, H. Solving structural engineering design optimization problems using an artificial bee colony algorithm. J. Ind. Manag. Optim. 2014, 10, 777–794. [Google Scholar] [CrossRef]
- Yildiz, A.R. A new hybrid artificial bee colony algorithm for robust optimal design and manufacturing. Appl. Soft Comput. 2013, 13, 2906–2912. [Google Scholar] [CrossRef]
- Rajeswari, M.; Amudhavel, J.; Pothula, S.; Dhavachelvan, P. Directed Bee Colony Optimization Algorithm to Solve the Nurse Rostering Problem. Comput. Intell. Neurosci. 2017, 2017, 1–26. [Google Scholar] [CrossRef]
- Muniyan, R.; Ramalingam, R.; Alshamrani, S.S.; Gangodkar, D.; Dumka, A.; Singh, R.; Gehlot, A.; Rashid, M. Artificial Bee Colony Algorithm with Nelder–Mead Method to Solve Nurse Scheduling Problem. Mathematics 2022, 10, 2576. [Google Scholar] [CrossRef]
- Zhu, G.; Kwong, S. Gbest-guided artificial bee colony algorithm for numerical function optimization. Appl. Math. Comput. 2010, 217, 3166–3173. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No Free Lunch Theorems for Optimization. IEEE Trans. Evol. Comput. 1997, 1, 67. [Google Scholar] [CrossRef]
- Gould, N. An Introduction to Algorithms for Continuous Optimization; Computational Mathematics and Group: Didcot, UK, 2006. [Google Scholar]
- Gao, W.; Liu, S. Improved artificial bee colony algorithm for global optimization. Inf. Process. Lett. 2011, 111, 871–882. [Google Scholar] [CrossRef]
- Banharnsakun, A.; Achalakul, T.; Sirinaovakul, B. The best-so-far selection in Artificial Bee Colony algorithm. Appl. Soft Comput. 2011, 11, 2888–2901. [Google Scholar] [CrossRef]
- Xiang, Y.; Peng, Y.; Zhong, Y.; Chen, Z.; Lu, X.; Zhong, X. A particle swarm inspired multi-elitist artificial bee colony algorithm for real-parameteroptimization. Comput. Optim. Appl. 2014, 57, 493–516. [Google Scholar] [CrossRef]
- Gao, W.-F.; Liu, S.-Y.; Huang, L.-L. Enhancing artificial bee colony algorithm using more information-based search equations. Inf. Sci. 2014, 270, 112–133. [Google Scholar] [CrossRef]
- Gao, W.-F.; Liu, S.-Y.; Huang, L.-L. A Novel Artificial Bee Colony Algorithm Based on Modified Search Equation and Orthogonal Learning. IEEE Trans. Cybern. 2013, 43, 1011–1024. [Google Scholar]
- Karaboga, D.; Gorkemli, B. A quick artificial bee colony (qABC) algorithm and its performance on optimization problems. Appl. Soft Comput. 2014, 23, 227–238. [Google Scholar] [CrossRef]
- Wang, H.; Wu, Z.; Rahnamayan, S.; Sun, H.; Liu, Y.; Pan, J.-S. Multi-strategy ensemble artificial bee colony algorithm. Inf. Sci. 2014, 279, 587–603. [Google Scholar] [CrossRef]
- Kıran, M.S.; Fındık, O. A directed artificial bee colony algorithm. Appl. Soft Comput. 2015, 26, 454–462. [Google Scholar] [CrossRef]
- Kiran, M.S.; Hakli, H.; Gunduz, M.; Uguz, H. Artificial bee colony algorithm with variable search strategy for continuous optimization. Inform. Sci. 2015, 300, 140–157. [Google Scholar] [CrossRef]
- Chu, X.; Cai, F.; Gao, D.; Li, L.; Cui, J.; Xu, S.X.; Qin, Q. An artificial bee colony algorithm with adaptive heterogeneous competition for global optimization problems. Appl. Soft Comput. 2020, 93, 106391. [Google Scholar] [CrossRef]
- Yavuz, G.; Aydın, D. Improved Self-adaptive Search Equation-based Artificial Bee Colony Algorithm with competitive local search strategy. Swarm Evol. Comput. 2019, 51, 100582. [Google Scholar] [CrossRef]
- Song, X.; Zhao, M.; Yan, Q.; Xing, S. A high-efficiency adaptive artificial bee colony algorithm using two strategies for continuous optimization. Swarm Evol. Comput. 2019, 50, 100549. [Google Scholar] [CrossRef]
- Lu, R.; Hu, H.; Xi, M.; Gao, H.; Pun, C.-M. An improved artificial bee colony algorithm with fast strategy, and its application. Comput. Electr. Eng. 2019, 78, 79–88. [Google Scholar] [CrossRef]
- Gao, W.-F.; Huang, L.-L.; Wang, J.; Liu, S.-Y.; Qin, C.-D. Enhanced artificial bee colony algorithm through differential evolution. Appl. Soft Comput. 2016, 48, 137–150. [Google Scholar] [CrossRef]
- Cui, L.; Li, G.; Zhu, Z.; Lin, Q.; Wen, Z.; Lu, N.; Wong, K.-C.; Chen, J. A novel artificial bee colony algorithm with an adaptive population size for numerical function optimization. Inf. Sci. 2017, 414, 53–67. [Google Scholar] [CrossRef]
- Li, G.; Cui, L.; Fu, X.; Wen, Z.; Lu, N.; Lu, J. Artificial bee colony algorithm with gene recombination for numerical function optimization. Appl. Soft Comput. 2017, 52, 146–159. [Google Scholar] [CrossRef]
- Xue, Y.; Jiang, J.; Zhao, B.; Ma, T. A self-adaptive artificial bee colony algorithm based on global best for global optimization. Soft Comput. 2017, 22, 2935–2952. [Google Scholar] [CrossRef]
- Cui, L.; Li, G.; Luo, Y.; Chen, F.; Ming, Z.; Lu, N.; Lu, J. An enhanced artificial bee colony algorithm with dual-population framework. Swarm Evol. Comput. 2018, 43, 184–206. [Google Scholar] [CrossRef]
- Gao, W.; Wei, Z.; Luo, Y.; Cao, J. Artificial bee colony algorithm based on Parzen window method. Appl. Soft Comput. 2019, 74, 679–692. [Google Scholar] [CrossRef]
- Wang, H.; Wang, W.; Xiao, S.; Cui, Z.; Xu, M.; Zhou, X. Improving artificial Bee colony algorithm using a new neighborhood selection mechanism. Inf. Sci. 2020, 527, 227–240. [Google Scholar] [CrossRef]
- Wang, H.; Wang, W.; Zhou, X.; Zhao, J.; Wang, Y.; Xiao, S.; Xu, M. Artificial bee colony algorithm based on knowledge fusion. Complex Intell. Syst. 2020, 7, 1139–1152. [Google Scholar] [CrossRef]
- Yang, J.; Cui, J.; Zhang, Y.-D. Artificial bee colony algorithm with adaptive covariance matrix for hearing loss detection. Knowledge-Based Syst. 2021, 216, 106792. [Google Scholar] [CrossRef]
- Xu, M.; Wang, W.; Wang, H.; Xiao, S.; Huang, Z. Multipopulation artificial bee colony algorithm based on a modified probability selection model. Concurr. Comput. Pr. Exp. 2021, 33, e6216. [Google Scholar] [CrossRef]
- Rajesh, K.; Pyne, S. A hybrid artificial bee colony algorithm for scheduling of digital microfluidic biochip operations. Concurr. Comput. Pr. Exp. 2021, 33, e6223. [Google Scholar] [CrossRef]
- Anguraj, D.K.; Thirugnanasambandam, K. Enriched cluster head selection using augmented bifold cuckoo search algorithm for edge-based internet of medical things. Int. J. Commun. Syst. 2021, 34, e4817. [Google Scholar] [CrossRef]
- Thirugnanasambandam, K.; Sudha, S.; Saravanan, D.; Ravi, R.V.; Anguraj, D.K.; Raghav, R. Reinforced Cuckoo Search based fugitive landfill methane emission estimation. Environ. Technol. Innov. 2020, 21, 101207. [Google Scholar] [CrossRef]
- Rajeswari, M.; Thirugnanasambandam, K.; Raghav, R.S.; Prabu, U.; Saravanan, D.; Anguraj, D.K. Flower Pollination Algorithm with Powell’s Method for the Minimum Energy Broadcast Problem in Wireless Sensor Network. Wirel. Pers. Commun. 2021, 119, 1111–1135. [Google Scholar] [CrossRef]
- Thirugnanasambandam, K.; Anitha, R.; Enireddy, V.; Raghav, R.S.; Anguraj, D.K.; Arivunambi, A. Pattern mining technique derived ant colony optimization for document information retrieval. J. Ambient Intell. Humaniz. Comput. 2021, 12, 1–13. [Google Scholar] [CrossRef]
- Thirugnanasambandam, K.; Raghav, R.S.; Loganathan, J.; Dumka, A.; Dhilipkumar, V. Optimal path planning for intelligent automated wheelchair using DDSRPSO. Int. J. Pervasive Comput. Commun. 2020, 17, 109–120. [Google Scholar] [CrossRef]
- Koti, P.; Dhavachelvan, P.; Kalaipriyan, T.; Arjunan, S.; Uthayakumar, J.; Sujatha, P. An efficient healthcare framework for kidney disease using hybrid harmony search algorithm. Electron. Gov. Int. J. 2020, 16, 56–68. [Google Scholar] [CrossRef]
- Saravanan, D.; Janakiraman, S.; Chandraprabha, K.; Kalaipriyan, T.; Raghav, R.S.; Venkatesan, S. Augmented Powell-Based Krill Herd Optimization for Roadside Unit Deployment in Vehicular Ad Hoc Networks. J. Test. Eval. 2019, 47, 4108–4127. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, X. An artificial bee colony algorithm for scheduling call centres with weekend-off fairness. Appl. Soft Comput. 2021, 109, 107542. [Google Scholar] [CrossRef]
- Cui, Y.; Hu, W.; Rahmani, A. A reinforcement learning based artificial bee colony algorithm with application in robot path planning. Expert Syst. Appl. 2022, 203, 117389. [Google Scholar] [CrossRef]
- Tao, X.R.; Pan, Q.K.; Gao, L. An efficient self-adaptive artificial bee colony algorithm for the distributed resource-constrained hybrid flowshop problem. Comput. Ind. Eng. 2022, 169, 108200. [Google Scholar] [CrossRef]
- Yavuz, G.; Durmuş, B.; Aydın, D. Artificial Bee Colony Algorithm with Distant Savants for constrained optimization. Appl. Soft Comput. 2021, 116, 108343. [Google Scholar] [CrossRef]
- Szczepanski, R.; Erwinski, K.; Tejer, M.; Bereit, A.; Tarczewski, T. Optimal scheduling for palletizing task using robotic arm and artificial bee colony algorithm. Eng. Appl. Artif. Intell. 2022, 113, 104976. [Google Scholar] [CrossRef]
- Ghambari, S.; Rahati, A. An improved artificial bee colony algorithm and its application to reliability optimization problems. Appl. Soft Comput. 2018, 62, 736–767. [Google Scholar] [CrossRef]
- Thirugnanasambandam, K.; Prakash, S.; Subramanian, V.; Pothula, S.; Thirumal, V. Reinforced cuckoo search algorithm-based multimodal optimization. Appl. Intell. 2019, 49, 2059–2083. [Google Scholar] [CrossRef]
- Lin, X.; Yu, X.; Li, W. A heuristic whale optimization algorithm with niching strategy for global multi-dimensional engineering optimization. Comput. Ind. Eng. 2022, 171, 108361. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).