A New 3-Parameter Bounded Beta Distribution: Properties, Estimation, and Applications
Abstract
:1. Introduction
- Our model can be used to define well-known distributions with a variety of parameters and supports, some of which are listed in Table 1;
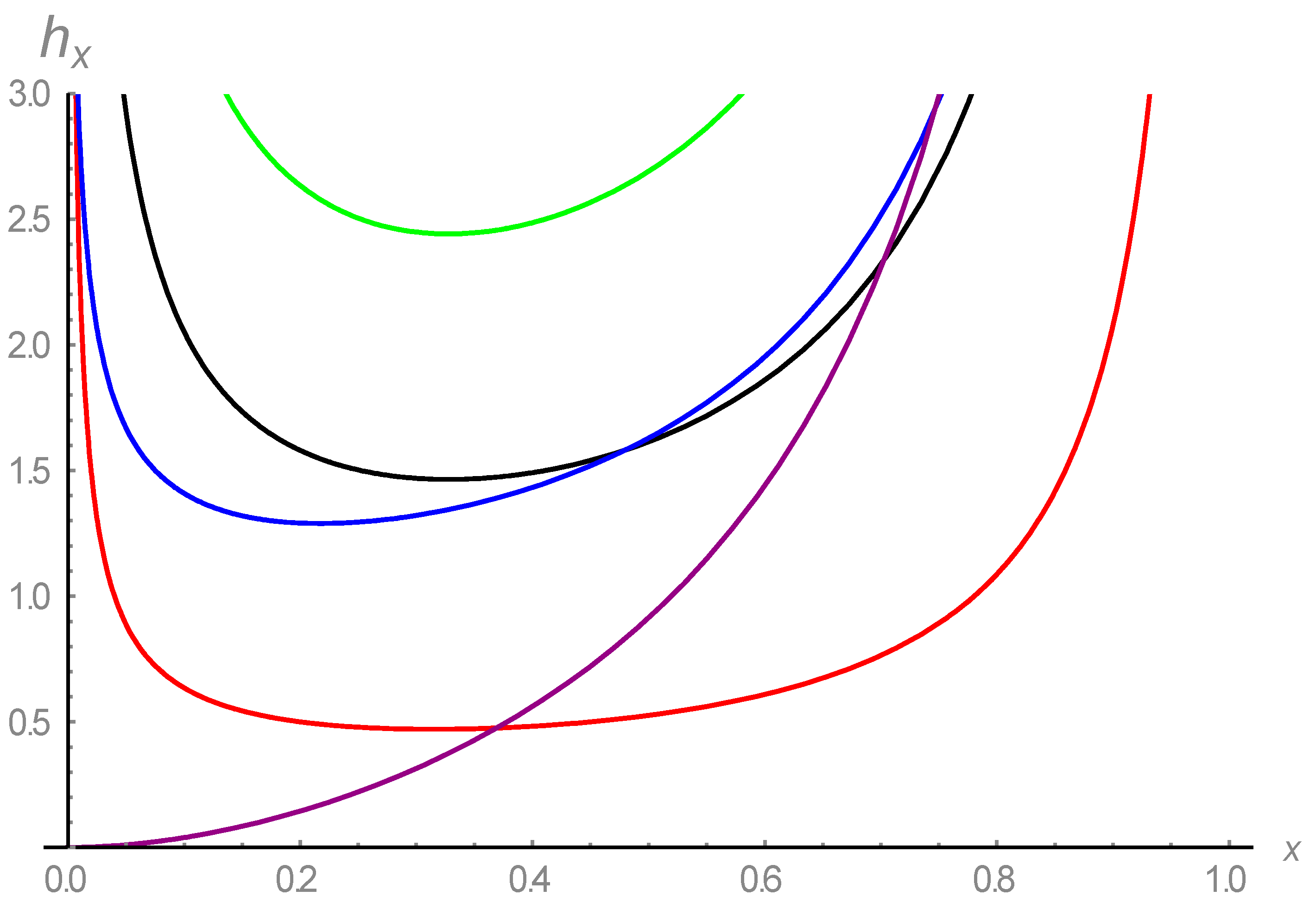
- In addition, our model’s hazard rate assumes several forms, including U, increasing, and the bathtub shapes. Consequently, it may be beneficial to also study mortality and biological data;
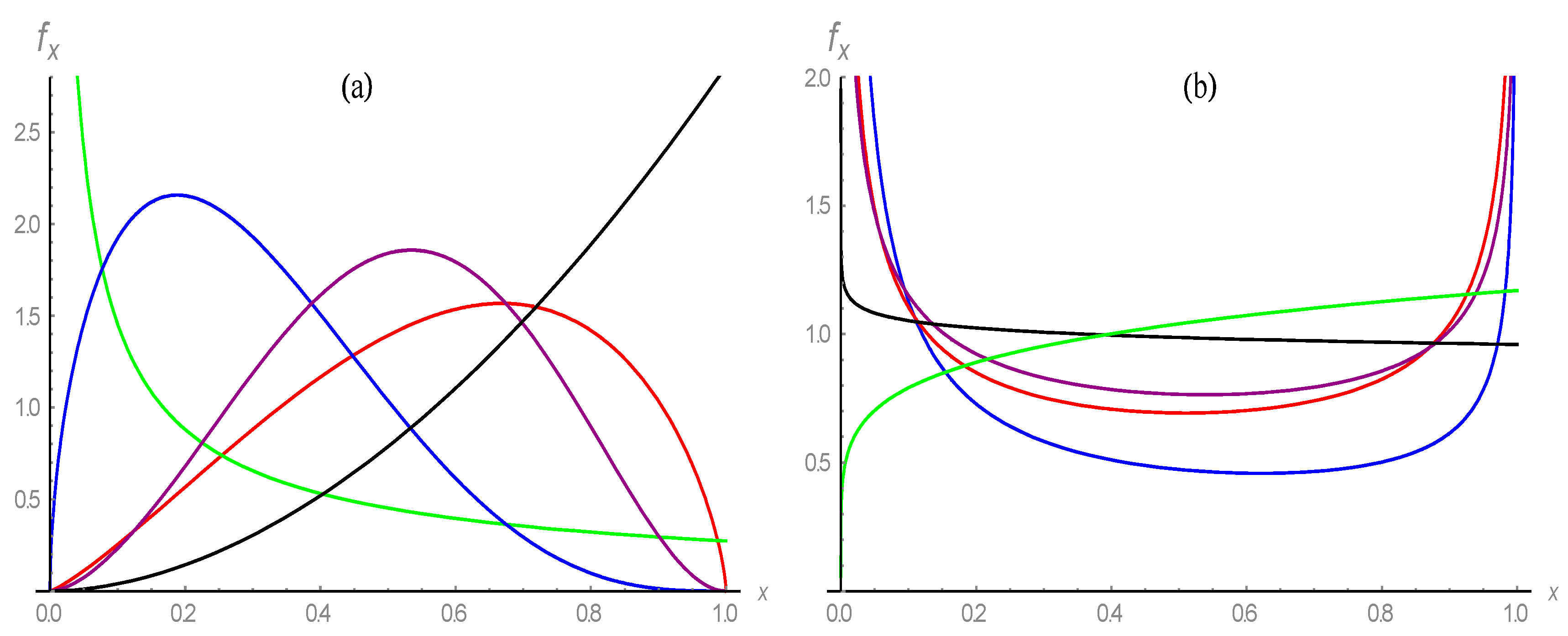
- The density function has increasing, decreasing, left-skewed, right-skewed, approximately symmetric, bathtub, and upside-down bathtub shapes, as shown in Figure 1. Our model’s advantageis thatit provides a wide range of shapes without requiring any additional parameters in its formulation;
- This model is more adaptable to real data than beta (B), log-Lindley, power log-Lindley, power logarithmic (PL), reduced Kies (RK), log-gamma (LG), log-weighted power (LWP), transmuted power (TP), and Kumaraswamy (K) distributions, as will be shown in Section 7.
2. The 3PB Distribution
3. Mathematical Properties of the 3PB Model
3.1. Moments
3.2. Conditional Moments
3.3. Mean Residual Life Function
3.4. Mean Deviations
3.5. Entropy
4. Classical Estimations
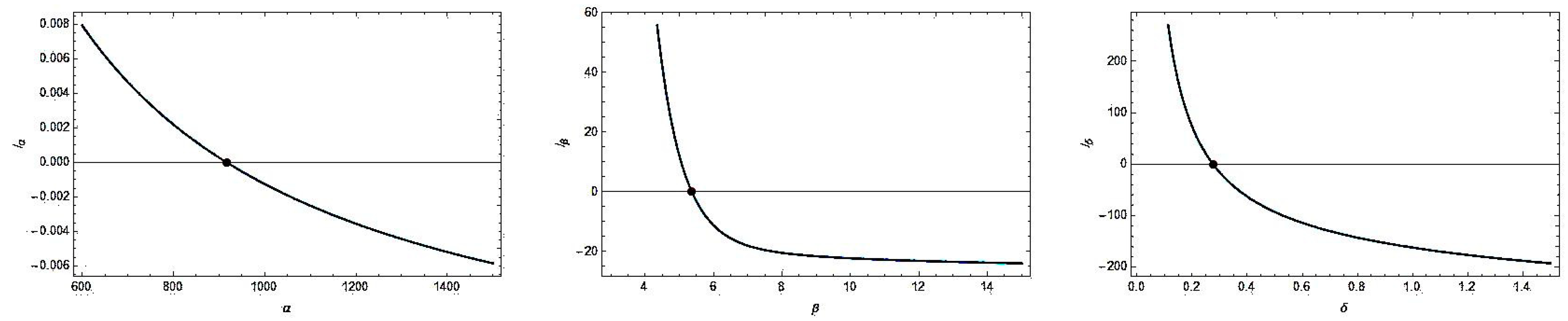
4.1. Maximum Likelihood Estimation
4.2. Asymptotic Confidence Intervals
5. Bayesian Estimation
MCMC Method
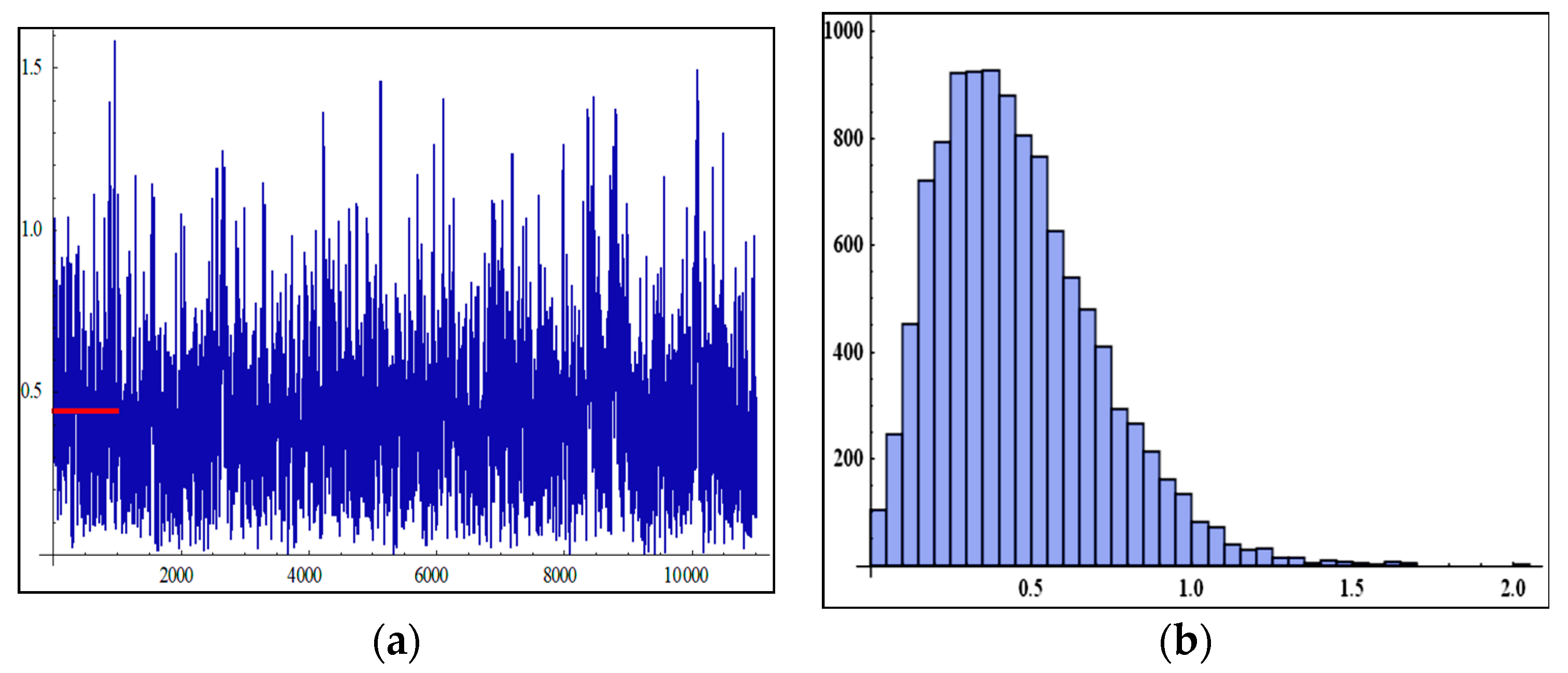
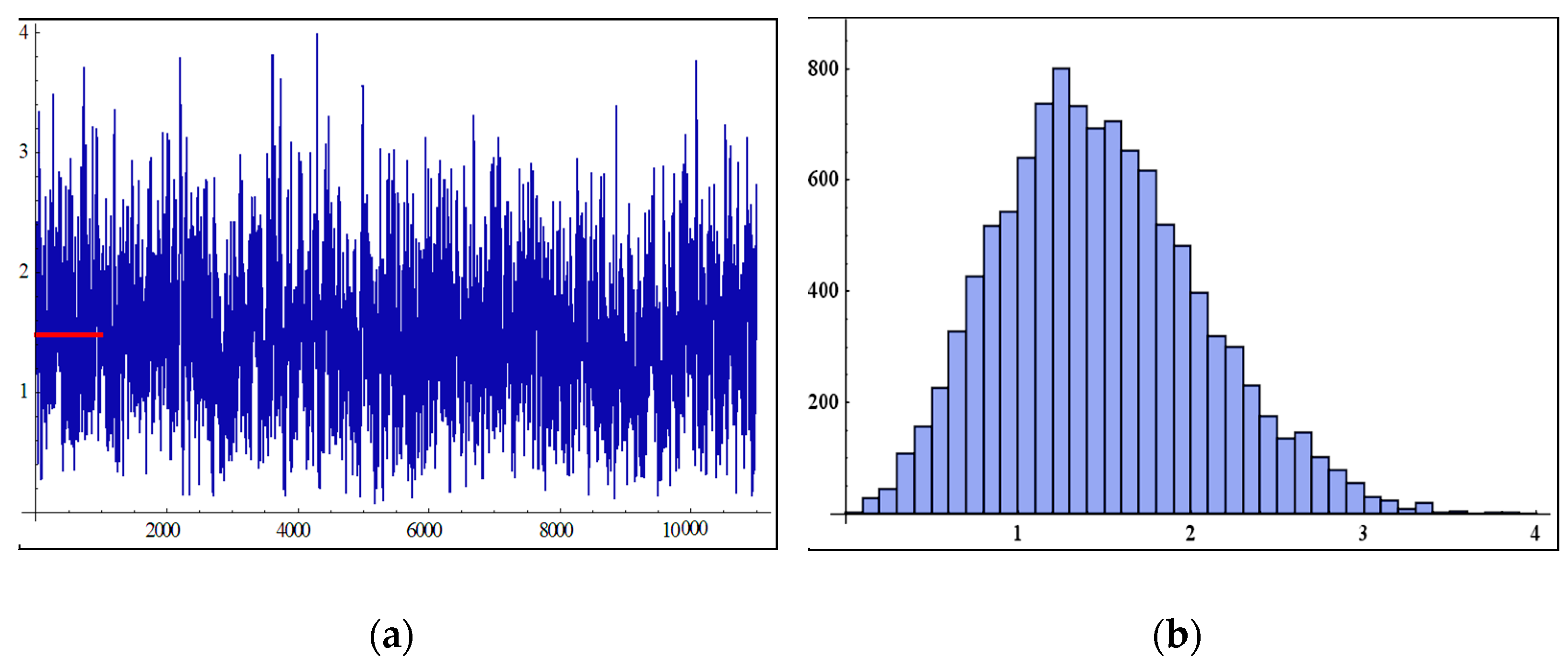
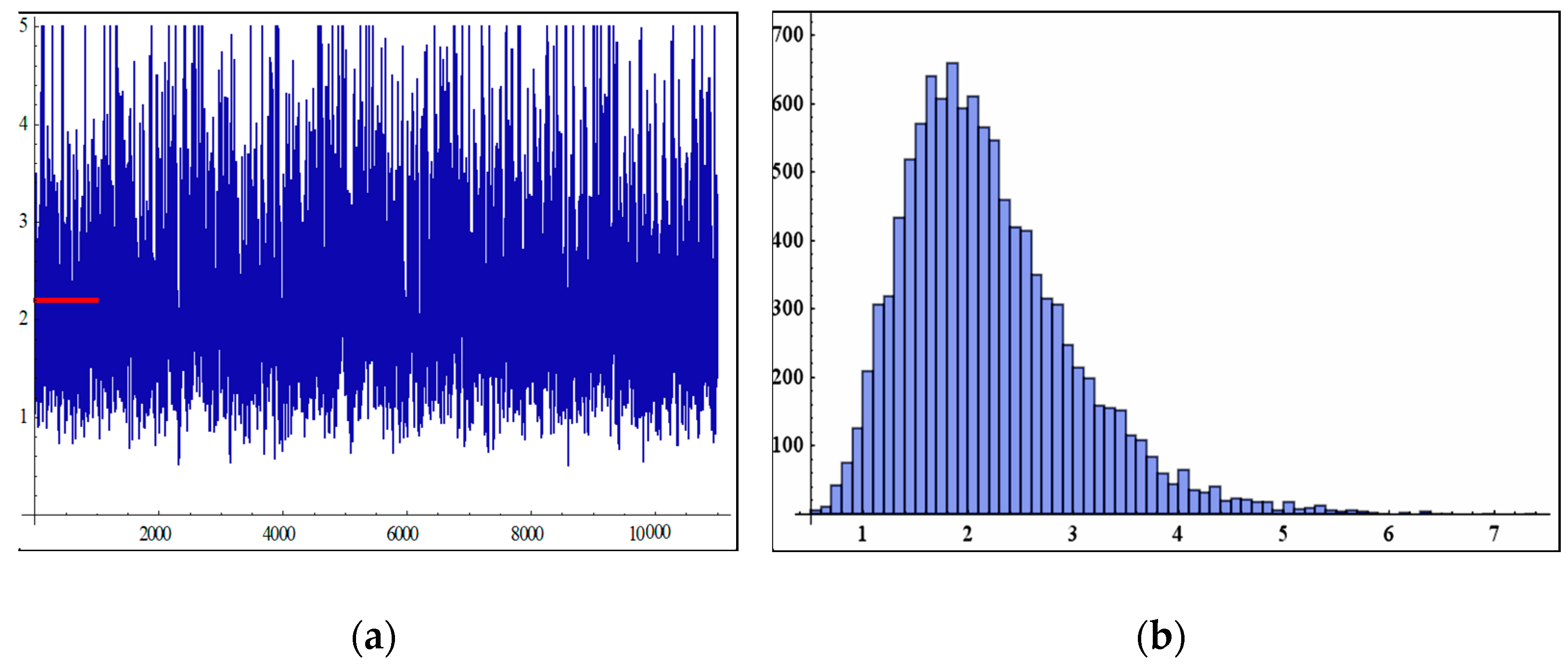
6. Simulation Study
| Algorithm 1 |
|
- In Table 2, when the sample size increases, the MSEs of MLEs and BEs decrease as the sample size increases, except for a few cases. This may be due to fluctuations in data.
- The BEs give more accurate results through the MSEs than the MLEs for all sample size n.
- The MSEs under LINEX loss function have the smallest as compared with estimates under MLEs and SE loss function.
- It was also observed for very large sample sizes that the BEs and the MLEs become closer in terms of MSEs. That is, for very large sample sizes, the performances are so far similar as expected.
- In Table 3, the length of credible Cis decreases as the sample size increases and the credible CIs give more accurate results than MLE CIs through the length and the CPs of CIs.
- It can be easily checked that the values of CPs are quite close to the nominal level 0.95 in many of the considered cases of credible CIs.
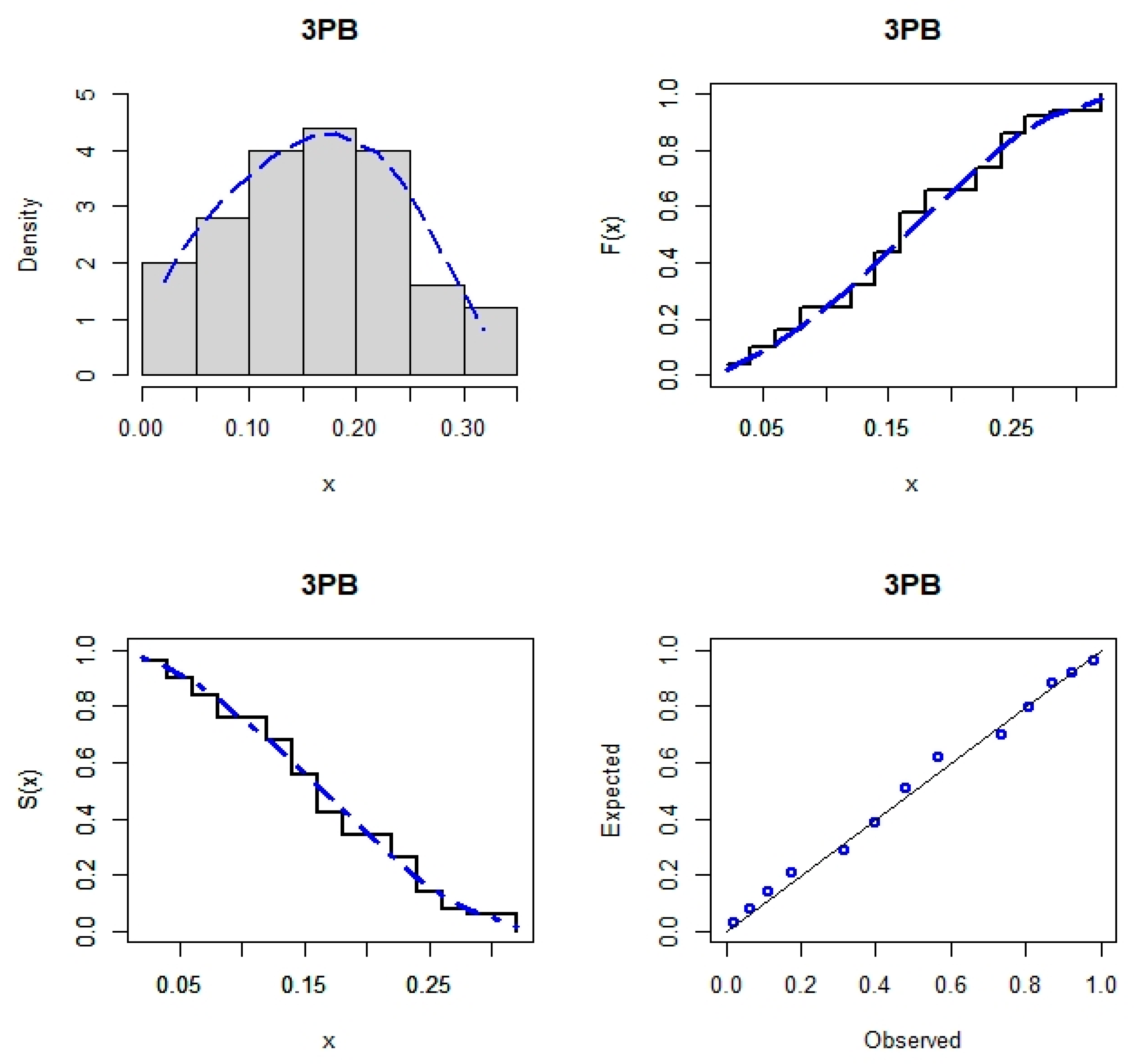
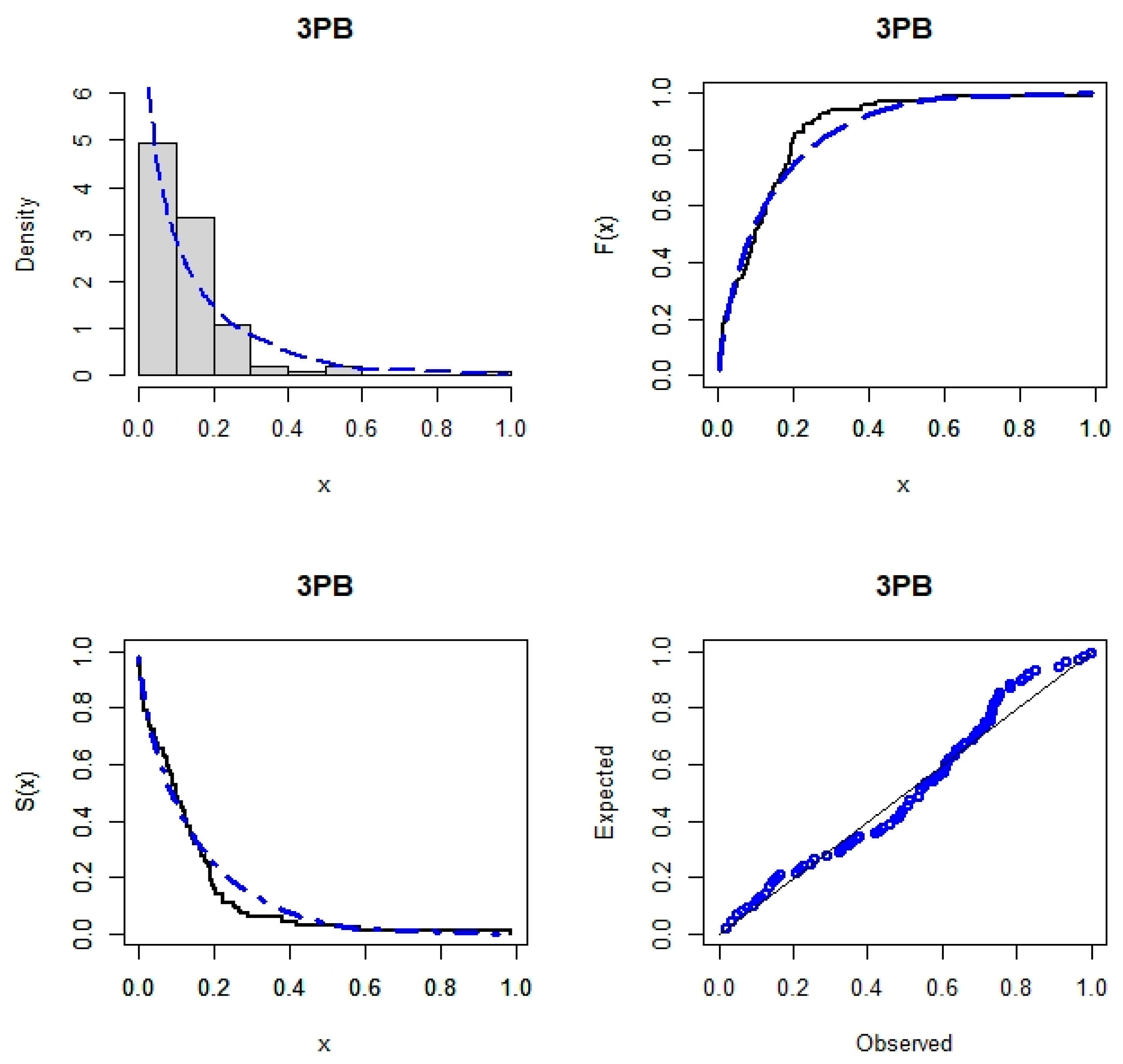
7. Real Data Analysis
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Johnson, N.L.; Kemp, A.W.; Balakrishnan, N. Continuous Univariate Distributions, 2nd ed.; Wiley: New York, NY, USA, 1995; Volume 1. [Google Scholar]
- Johnson, N.L.; Kotz, S.; Balakrisnan, N. Continuous Univariate Distributions, 2nd ed.; Wiley: New York, NY, USA, 1994; Volume 1. [Google Scholar]
- Chotikapanich, D.; Rao, D.S.P.; Tang, K.K. Estimating income inequality in China using grouped data and the generalized beta distribution. In Review of Income and Wealth; Wiley: Hoboken, NY, USA, 2007; Volume 53, pp. 127–147. ISSN 1475-4991. [Google Scholar]
- Ng, D.W.W.; Koh, S.K.; Sim, S.Z.; Lee, M.C. The study of properties in generalized beta distribution. IOP Conf. Series J. Phys. 2019. [Google Scholar] [CrossRef]
- Albassam, M.; Soliman, E.E.A.; Ali, S.S. Bayesian Estimation of Multivariate Pure Moving Average Processes. IEEE Access 2022, 10, 14225–14235. [Google Scholar] [CrossRef]
- Bertschinger, N.; Mozzhorin, I. Bayesian estimation and likelihood-based comparison of agent based volatility models. J. Econ. Interact. Coord. 2021, 16, 173–210. [Google Scholar] [CrossRef]
- Saboor, A.; Bakouch, H.S.; Khan, M.N. Beta Sarhan-Zaindin modified Weibull distribution. Appl. Math. Model. 2016, 40, 6604–6621. [Google Scholar] [CrossRef]
- Shannon, C.E. Prediction and entropy of printed English. Bell Syst. Tech. J. 1951, 30, 50–64. [Google Scholar] [CrossRef]
- Rényi, A. On measures of entropy and information. In Contributions to the Theory of Statistics, Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 20 June–30 July 1960; University of California Press: Berkeley, CA, USA, 1961; Volume 1, pp. 547–561. [Google Scholar]
- Kim, C.; Jung, J.; Chung, Y. Bayesian estimation for the generalized Weibull model under Type II progressive censoring. Stat. Pap. 2011, 52, 53–70. [Google Scholar] [CrossRef]
- Singh, S.K.; Singh, U.; Kumar, M.; Vishwakarma, P.K. Classical and Bayesian inference for an extension of the exponential distribution under progressive Type- II censored data with binomial removals. J. Stat. Appl. Prob. Lett. 2014, 1, 75–86. [Google Scholar] [CrossRef]
- Upadhyay, S.K.; Gupta, A. Bayes analysis of modified Weibull distribution via Markov chain Monte Carlo simulation. J. Stat. Compu. Simul. 2010, 80, 241–254. [Google Scholar] [CrossRef]
- Dasgupta, R. On the distribution of burr with applications. Sankhya B 2011, 73, 1–19. [Google Scholar] [CrossRef]
- Barlow, R.; Toland, R.; Freeman, T. A Bayesian analysis of stress-rupture life of kevlar/epoxy spherical pressure vessels. In Accelerated Life Testing and Experts Opinions in Reliability; Clarotti, C., Lindley, D., Eds.; Elsevier Science Ltd.: Amsterdam, The Netherlands, 1988; pp. 203–236. [Google Scholar]
- Gómez-Déniz, E.; Sordo, M.A.; Calderín-Ojedac, E. The log-Lindley distribution as an alternative to the beta regression model with applications in insurance. Insur. Math. Econ. 2014, 54, 49–57. [Google Scholar] [CrossRef]
- Abd El-Bar, A.M.T.; Da Silva, W.B.F.; Nascimento, A.D.C. An extended log-Lindley-G family: Properties and experiments in repairable data. Mathematics 2021, 9, 3108. [Google Scholar] [CrossRef]
- Abd El-Bar, A.M.T.; Lima, M.S.; Ahsanullah, M. Some inferences based on a mixture of power function and continuous logarithmic distribution. J. Taibah Univ. Sci. 2020, 14, 1116–1126. [Google Scholar] [CrossRef]
- Kumar, C.S.; Dharmaja, S.H.S. On reduced Kies distribution. In Collection of Recent Statistical Methods and Applications; Department of Statistics, University of Kerala Publishers: Trivandrum, India, 2013; pp. 111–123. [Google Scholar]
- Amini, M.; Mir Mostafaee, S.M.T.K.; Ahmadi, J. Log-gamma-generated families of distributions. Statistics 2014, 48, 913–932. [Google Scholar] [CrossRef]
- Chesneau, C. On a logarithmic weighted power distribution: Theory, modeling and applications. J. Math. Sci. Adv. Appl. 2021, 67, 1–59. [Google Scholar] [CrossRef]



| Parametric Values and Transformation in (3) | Models |
|---|---|
| Beta distribution | |
| Arcsine distribution | |
| Beta exponential distribution | |
| Exponential distribution | |
| Exponentiated exponential distribution | |
| Uniform distribution on (0, 1) | |
| Kumaraswamy distribution | |
| Generalized beta of the first kind model | |
| Beta power distribution |
| n | MLE | BE | ||
|---|---|---|---|---|
| SE | LINEXc = 1 | |||
| 10 | 0.247 (1.832) | 0.373 (0.942) | 0.391 (0.744) | |
| 1.214 (0.641) | 1.291 (0.321) | 1.332 (0.266) | ||
| 2.784 (0.814) | 2.541 (0.342) | 2.322 (0.388) | ||
| 20 | 0.251 (1.511) | 0.392 (0.795) | 0.399 (0.553) | |
| 1.143 (0.622) | 1.313 (0.314) | 1.343 (0.392) | ||
| 2.527 (0.702) | 2.392 (0.284) | 2.321 (0.251) | ||
| 30 | 0.291 (1.421) | 0.412 (0.484) | 0.432 (0.439) | |
| 1.209 (0.497) | 1.365 (0.278) | 1.382 (0.331) | ||
| 2,563 (0.773) | 2.313 (0.279) | 2.275 (0.215) | ||
| 40 | 0.301 (1.252) | 0.431 (0.421) | 0.439 (0.462) | |
| 1.292 (0.447) | 1.397 (0.185) | 1.413 (0.158) | ||
| 2.413 (0.559) | 2.293 (0.212) | 2.311 (0.198) | ||
| 50 | 0.347 (0.873) | 0.441 (0.218) | 0.452 (0.195) | |
| 1.256 (0.119) | 1.429 (0.094) | 1.463 (0.084) | ||
| 2.392 (0.235) | 2.143 (0.182) | 2.114 (0.089) | ||
| n | MLE | BE | |||
|---|---|---|---|---|---|
| Length | CP | Length | CP | ||
| 10 | α β δ | 1.437 | 0.793 | 0.543 | 0.864 |
| 4.542 | 0.772 | 1.394 | 0.852 | ||
| 2.482 | 0.902 | 0.934 | 0.934 | ||
| 20 | α β δ | 1.374 | 0.832 | 0.574 | 0.877 |
| 4.326 | 0.829 | 1.485 | 0.869 | ||
| 2.165 | 0.921 | 0.854 | 0.994 | ||
| 30 | α β δ | 1.394 | 0.805 | 0.395 | 0.896 |
| 3.925 | 0.793 | 1.293 | 0.875 | ||
| 1.947 | 0.911 | 0.795 | 1 | ||
| 40 | α β δ | 1.243 | 0.849 | 0.321 | 0.918 |
| 4.186 | 0.836 | 1.147 | 0.878 | ||
| 2.095 | 0.932 | 0.753 | 0.957 | ||
| 50 | α β δ | 0.983 | 0.873 | 0.201 | 0.929 |
| 3.744 | 0.884 | 1.082 | 0.914 | ||
| 1.782 | 0.939 | 0.593 | 0.971 | ||
| Model | −L | AIC | CAIC | HQIC | AD | CM | KS | KS p-Value | Est. Parameters (SEs) |
|---|---|---|---|---|---|---|---|---|---|
| 3PB | −57.513 | −109.027 | −108.506 | −106.843 | 0.43405 | 0.07304 | 0.09988 | 0.70076 | 916.89 (2899.91) 5.36001 (2.91255) 0.275398 (0.188897) |
| B | −54.606 | −105.213 | −104.958 | −103.757 | 0.91234 | 0.15390 | 0.14146 | 0.26969 | a = 2.68257 (0.507179) b = 13.8658 (2.82802) |
| LL | −31.826 | −59.653 | −59.3977 | −58.1968 | 6.56759 | 1.22677 | 0.31813 | 0.00008 | 1.00664 (0.0762406) 0.00001 (0.129734) |
| PLL | −31.826 | −57.653 | −57.1313 | −55.4687 | 6.56759 | 1.22677 | 0.31813 | 0.00008 | 1.89694 (0.645369) 0.530664 (0.151324) (1.23461) |
| PL | −31.8265 | −57.653 | −57.1313 | −55.4687 | 6.5676 | 1.22677 | 0.31813 | 0.00008 | 0.006640 (0.100664) 0.003714 (27.6384) 2.3294 (792681) |
| RK | −11.6763 | −21.3526 | −21.2692 | −20.6244 | 21.7194 | 4.86516 | 0.56334 | <0.0001 | a = 0.736768 (0.087676) |
| LG | −31.8265 | −61.653 | −61.5697 | −60.9249 | 6.56759 | 1.22677 | 0.31813 | 0.00008 | σ = 1.00664 (0.100664) |
| LWP | −31.8265 | −59.653 | −59.3977 | −58.1968 | 6.56759 | 1.22677 | 0.31813 | 0.00008 | 1.00664 (0.173704) 1.0 (0.511507) |
| TP | −30.3176 | −56.6353 | −56.3799 | −55.179 | 6.79842 | 1.26438 | 0.32094 | 0.00006 | 0.733619 (0.11218) 1.0 (0.631411) |
| K | −56.0687 | −108.137 | −107.882 | −106.681 | 0.67763 | 0.10421 | 0.11025 | 0.57766 | a = 2.0774 (0.25485) b = 33.1374 (13.9216) |
| Model | −L | AIC | CAIC | HQIC | AD | CM | KS | KS p-Value | Est. Parameters (SEs) |
|---|---|---|---|---|---|---|---|---|---|
| 3PB | −100.494 | −194.989 | −194.741 | −191.813 | 1.41392 | 0.21918 | 0.10707 | 0.19717 | 3.16676 (0.424279) 0.00849 (0.204003) 135.631 (3282.79) |
| B | −97.5517 | −191.103 | −190.981 | −188.986 | 1.73053 | 0.25368 | 0.12956 | 0.06733 | a = 0.66105 (0.079057) b = 3.84874 (0.607836) |
| LL | −95.7616 | −187.523 | −187.401 | −185.406 | 4.08476 | 0.68173 | 0.19114 | 0.00124 | 0.72667 (0.052133) 0.025905 (0.03995) |
| PLL | −95.7616 | −185.523 | −185.276 | −182.347 | 4.08476 | 0.68173 | 0.19114 | 0.00124 | α = 1.42502 (2995.65) 0.50994 (1071.99) 0.036915 (77.6033) |
| PL | −84.6077 | −163.215 | −162.968 | −160.039 | 18.0604 | 3.66177 | 0.33304 | <0.0001 | 4.88982 (0.070983) 0.00148 (0.238805) 0.248041 (3.97841) |
| RK | −52.5838 | −103.168 | −103.127 | −102.109 | 28.6785 | 6.41016 | 0.45906 | 0.0000 | a = 0.45559 (0.035412) |
| LG | −95.3337 | −188.667 | −188.627 | −187.609 | 3.94175 | 0.65339 | 0.18805 | 0.00157 | 0.73344 (0.051605) |
| LWP | −95.7616 | −187.523 | −187.401 | −185.406 | 4.08476 | 0.68173 | 0.19114 | 0.00124 | 0.72667 (0.052133) 0.98152 (0.027749) |
| TP | −93.9055 | −183.811 | −183.689 | −181.694 | 4.54964 | 0.76099 | 0.19844 | 0.00070 | 0.53593 (0.0402053) 0.97495 (0.038706) |
| K | −98.9507 | −193.901 | −193.779 | −191.784 | 1.55811 | 0.231637 | 0.11767 | 0.121948 | a = 0.70876 (0.068023) b = 3.45759 (0.554958) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Althubyani, F.A.; Abd El-Bar, A.M.T.; Fawzy, M.A.; Gemeay, A.M. A New 3-Parameter Bounded Beta Distribution: Properties, Estimation, and Applications. Axioms 2022, 11, 504. https://doi.org/10.3390/axioms11100504
Althubyani FA, Abd El-Bar AMT, Fawzy MA, Gemeay AM. A New 3-Parameter Bounded Beta Distribution: Properties, Estimation, and Applications. Axioms. 2022; 11(10):504. https://doi.org/10.3390/axioms11100504
Chicago/Turabian StyleAlthubyani, Faiza A., Ahmed M. T. Abd El-Bar, Mohamad A. Fawzy, and Ahmed M. Gemeay. 2022. "A New 3-Parameter Bounded Beta Distribution: Properties, Estimation, and Applications" Axioms 11, no. 10: 504. https://doi.org/10.3390/axioms11100504
APA StyleAlthubyani, F. A., Abd El-Bar, A. M. T., Fawzy, M. A., & Gemeay, A. M. (2022). A New 3-Parameter Bounded Beta Distribution: Properties, Estimation, and Applications. Axioms, 11(10), 504. https://doi.org/10.3390/axioms11100504





