1. Introduction
Directed graphs are everywhere. They are fundamental mathematical objects not only for mathematical interests but also for applications including electric circuits, neural networks, social relationships, etc. [
1,
2]. Naturally classifying directed graphs through algebraic invariants is an important problem, and there have been various attempts (see [
3] and references therein). Among them, a recent development of path-space homology and cohomology for directed graphs by Grigor’yan, Lin, Muranov, and Yau [
3,
4,
5] is of particular interest. Their constructions are not too trivial, not too hard to compute, can be non-trivial for degrees greater than one, and satisfy similar properties to those invariants in the continuous and smooth setup. It turns out that path-space homology satisfies discrete analogs of Eilenberg–Steenrod axioms [
6], i.e., the Künneth formula [
7]; it is generalized to multigraphs and quivers [
8] and has applications to discretizing Morse theory [
9].
An interesting result regarding the path space homology is that it satisfies homotopy invariance. The history of homotopy theory for directed graphs goes back to [
10,
11] and more recently to [
12]. In 2014, Grigor’yan, Lin, Muranov, and Yau [
13] considered digraph homotopy as a notion of a discrete analog of homotopy in topology and proved that their path-space homology is invariant under this version of homotopy. Indeed, their homotopy theory for directed graphs is a natural “discretization” that is leading to establishing a dictionary between homotopy theory of spaces and its discrete counterpart. For example, several theorems in classical homotopy theory, such as van Kampen theorem, Hurewicz theorem, and Brown representability theorem [
14,
15], are successfully discretized (see [
13,
16]), and model structures in the category of directed graphs and related questions are currently being investigated [
17].
From the perspective of homotopy theory and category theory, the homotopy theory for directed graphs is an interesting source to understand existing classical results. Any time a classical construction or theory fails to be discretized or satisfy expected properties, the failure itself or remedies to it reveal the essence of the classical theory. For example, the path-space homology satisfies all discrete analogs of Eilenberg–Steenrod axioms, but these axioms are not complete (see [
6]), and we note that the completeness of Eilenberg–Steenrod axioms has a topological nature in it. Another example is a failure of homotopy extension property for directed graphs [
16], which reveals that the Brown representability theorem for not-necessarily-finite CW complexes is likely to be a special feature of CW complexes rather than a consequence of generalities in category theory.
In [
16], the authors have proven Brown representability theorem for finite directed graphs by adopting the methodology of J. F. Adams [
18]. The gist of technical innovation was the use of digraph cofibers and mapping tubes (see [
16] (Definitions 2.21 and 2.25)). It means that a natural discretization of Adams’ proof itself does not yield Brown representability theorem, but by appropriately modifying category-theoretic and homotopy-theoretic constructions, one can obtain this result. Accordingly, searching for constructions in directed graphs that satisfy general homotopy-theoretic properties lies at the technical core of discretizing classical results.
This paper is a brief note on a possible construction of a cofiber of directed graph map satisfying the property that the image of the directed graph map can be homotoped to a point. A cofiber of continuous map in the category of spaces satisfies this property in an obvious manner. However, in the category of directed graphs, any time there is an edge from a vertex in the range of the directed graph map to a vertex outside, it prevents defining a directed graph homotopy. We have constructed a model of cofiber that is free from such issues.
This paper is organized as follows.
Section 2 collects preliminaries to work in the category of directed graphs.
Section 3 and
Section 4 review necessary operations in the category of directed graphs and homotopy theory for directed graphs. In
Section 5, we give a construction of a directed graph cofiber proposed above and prove that it satisfies the desired property.
2. The Category of Directed Graphs
In this section, we shall review basic definitions and notations comprising the category of directed graphs.
Definition 1 ([
13]).
A directed graph (or digraph for short) is a pair consisting of a set of vertices V and a set E of ordered pairs of distinct vertices in V called edges. Note that our digraphs do not allow loop-edges or multiple edges with the same source and target. A point is a digraph with V a singleton and E an empty set.
Definition 2. Let . Ann-step line digraphis a digraph consisting of vertices labeled by 0, 1, ⋯, n and exactly one edge at every two consecutive vertices, i.e., either or for all such that .
An n-step line digraph is also called a path digraph or a linear digraph. When , there are two possible line digraphs, and .
Notation 1. We will denote by an arbitrary n-step line digraph and by the totality of all possible n-step line digraphs. The set of all line digraphs of any length will be denoted by .
Definition 3. Adigraph map, , is a function from the vertex set of to the vertex set of such that whenever is an edge in either in or is an edge in .
Definition 4. Theimage digraph of a digraph map is a directed graph consisting of a vertex set and an edge set .
Definition 5. Thecategory of directed graphs is a category in which the objects are directed graphs, , and the morphisms are digraph maps, .
3. Operations in Directed Graphs
In this section, we review operations in directed graphs. The definition of an identification digraph is central in yielding homotopy-theoretic constructions in the category of directed graphs.
Definition 6. Asub-digraph of a digraph denoted is a digraph for which and .
Note that even if and , it is not necessarily the case that .
Definition 7. Aninduced sub-digraph of a digraph denoted is a sub-digraph in which whenever and , then as well.
Definition 8. Thevertex boundary of a sub-digraph is Definition 9. Theintersection of digraphs and , denoted by , is the digraph consisting of and .
Definition 10. Theunion of digraphs and , denoted by , is the digraph consisting of and .
Definition 11. Thedisjoint union of two digraphs and , denoted is given by the disjoint union of their respective vertex sets and edge sets, as sets.
Definition 12. Thegraph Cartesian product □ of two directed graphs and is a directed graph , where the vertices are all ordered pairs such that and , and is an edge in if either and in , or in and .
Remark 1. Given a fixed vertex , we will denote by the -slice of . It is the induced sub-digraph where the vertices are all ordered pairs such that and the edges are those resulting from the edges of .
Definition 13. Let and be digraphs and ∼ an equivalence relation on vertex sets of and such that whenever , , and , then either or . Theidentification digraph resulting from the relation ∼ is a digraph whose vertices are equivalence classes and whose edges are the edges between the representatives of the classes.
Definition 14. Aquotient digraph, for and not necessarily connected, is an identification digraph where for all .
4. Homotopy for Digraphs
In this section, we review the notion of homotopy a là Grigor’yan, Lin, Muranov, and Yau [
13].
Definition 15. Two digraph maps arehomotopic, denoted , if there exists an and a digraph map , for some line digraph (recall Notation 1), such that and .
Definition 16. Two digraphs are said to behomotopically equivalent (or to be of the same homotopy type) if there exist two digraph maps, and , such that and .
Example 1. Let be a digraph map. The mapping cylinder and the digraph are homotopically equivalent. This can be shown by taking a homotopy defined by , for all and for all .
Definition 17. A digraph is said to becontractible if there exists a homotopy between and a constant digraph map.
Definition 18. Thehomotopy category of directed graphs , denoted , is a category in which the objects are directed graphs and the morphisms are equivalence classes of digraph maps where whenever f and g are homotopic.
5. Main Construction
In this section, we give a construction of a digraph cofiber satisfying the property that the image of a digraph map is contractible in the digraph cofiber. To this end, we set up extensions of a mapping cylinder and a cone that enables lifting edges. The main outcome in this paper is Construction 1, from which Theorem 1 follows.
Definition 19. Themapping cylinder of a digraph map is given by
where
for all
.
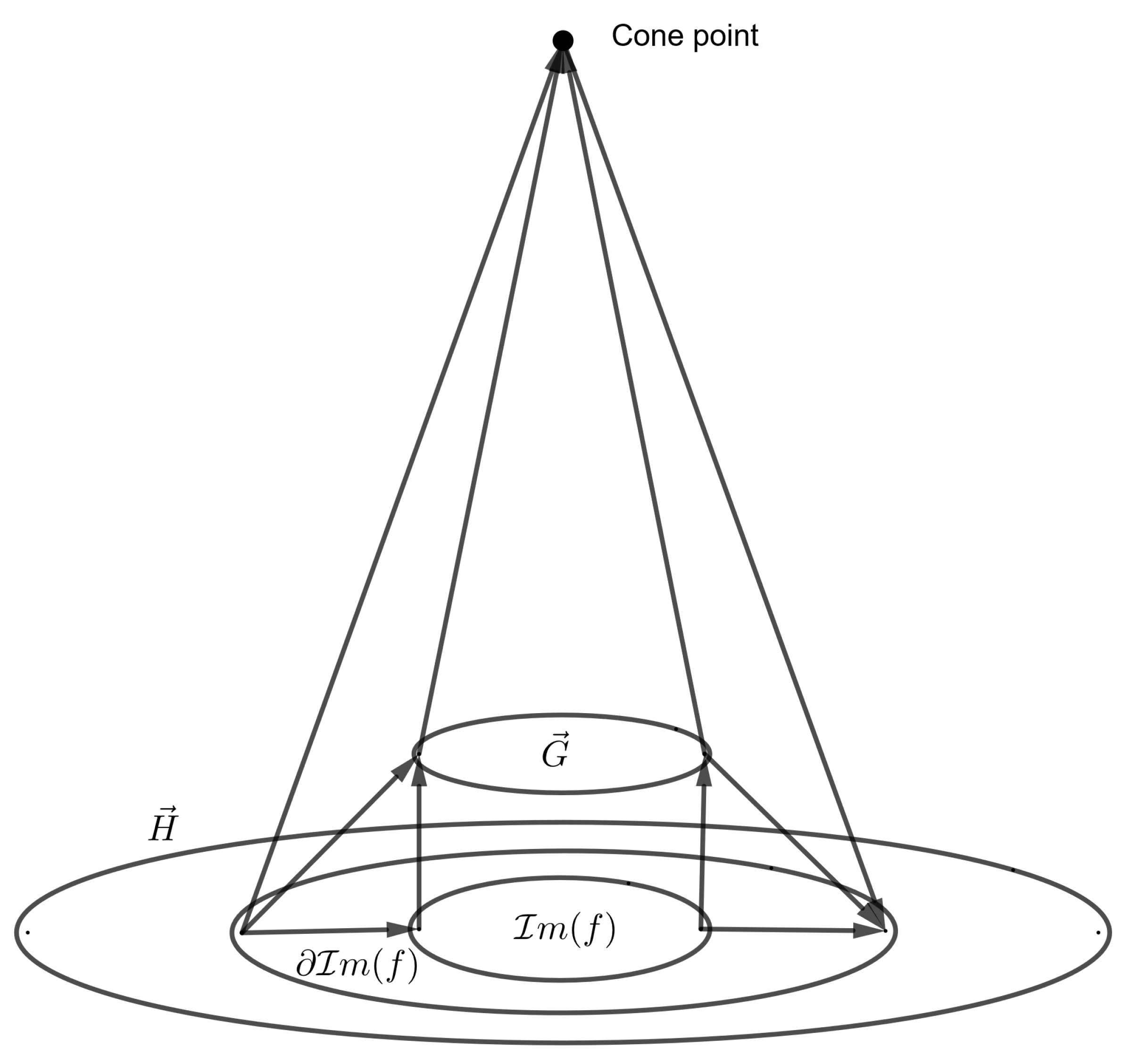
Definition 20. Anextension of a mapping cylinder for a digraph map is the digraph where,and is an edge in if for some and or in the opposite direction is an edge if for some and . Definition 21. Anextended mapping cylinder for a digraph map is given by the digraph .
Definition 22. Thecone over a digraph is the digraph ∼, where for all
Definition 23. Anextension of a cone over a sub-digraph is the digraph where , p is the cone point, and if and only if for some and or if and only if for some and .
Definition 24. Anextended cone over the sub-digraph in is .
Construction 1. Thedigraph cofiber for a map is an extension of a cone over (viewed as an induced subdigraph of ) unioned with the identification digraph where and the extension of this reversed mapping cylinder (See Figure 1). Remark 2. The resulting structure in the above definition is a “two-step extended cone” with a middle slice that preserves a copy of . It should be noted that is not a category-theoretic cofiber. However, from the perspective of homotopy theory for digraphs, category-theoretic cofibers do not carry much meaning. Specifically, for a digraph map , note that its category-theoretic cofiber is a pushout of the following diagram in the category .
where • is a point, the inclusion, and the constant map. Not only does the pushout not have a slice of in it, and as mentioned in Section 1, but one cannot homotope to the vertex of the cone. To further develop homotopy theory for digraphs, we have to construct a cofiber that retains essential properties of a cofiber of continuous map, and from the construction above, one can see that our construction retains a copy of the domain digraph . We claim that can be homotoped to the cone vertex as stated below.
Theorem 1. Suppose is a map of digraphs. Consider the sequence where the map i is the inclusion. Then the composition is homotopically trivial.
Proof. We have to prove that the subdigraph is contractible in . By construction of , we define a homotopy that takes every for to in the -slice in ∼ and then that takes this slice to the cone vertex. The existence of digraph maps and is guaranteed by Definition 23. □