Multi-Layered Blockchain Governance Game
Abstract
:1. Introduction
- Mathematically analyzing a complex network management;
- An analytical solution that can support optimal values of configuring parameters for network securities;
- A complicated decentralized network can be securely designed and managed by using this innovative theoretical framework.
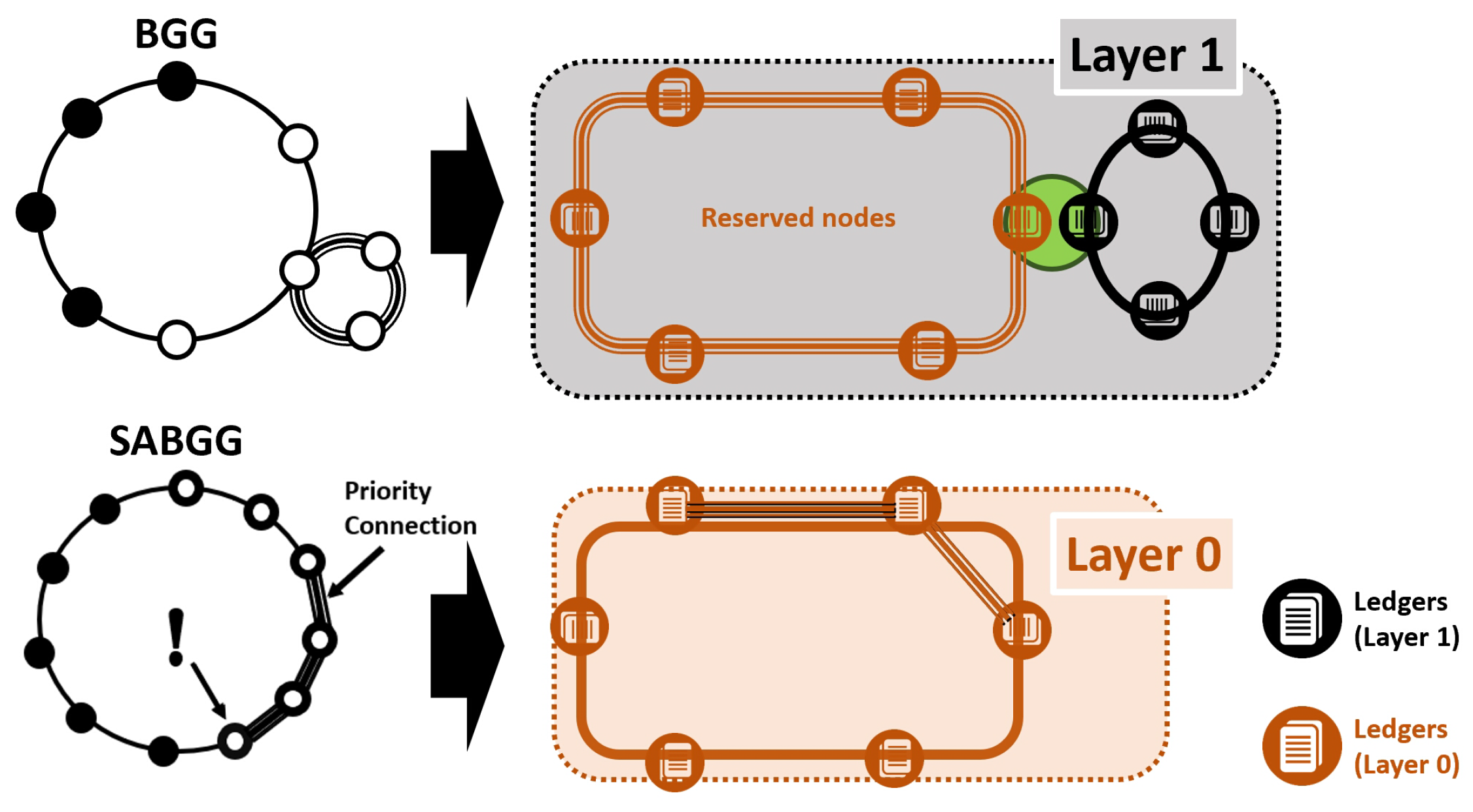
2. Multi-Layered Blockchain Governance Game
2.1. Layer 1: BGG Stochastic Modelling
2.2. Layer 0: SABGG Stochastic Modelling
3. Multiple Layered IoT-Server Network Design
3.1. Multiple Layered IoT-Server Network Architecture
3.2. Stochastic Optimization
4. Model Simulations
4.1. Preliminaries
- Two cases (one is with the BGG, the other is without the BGG) per each layer are simulated;
- Simulating the 51 percent attack to evaluate whether the nodes in the network are protected by the BGG or not;
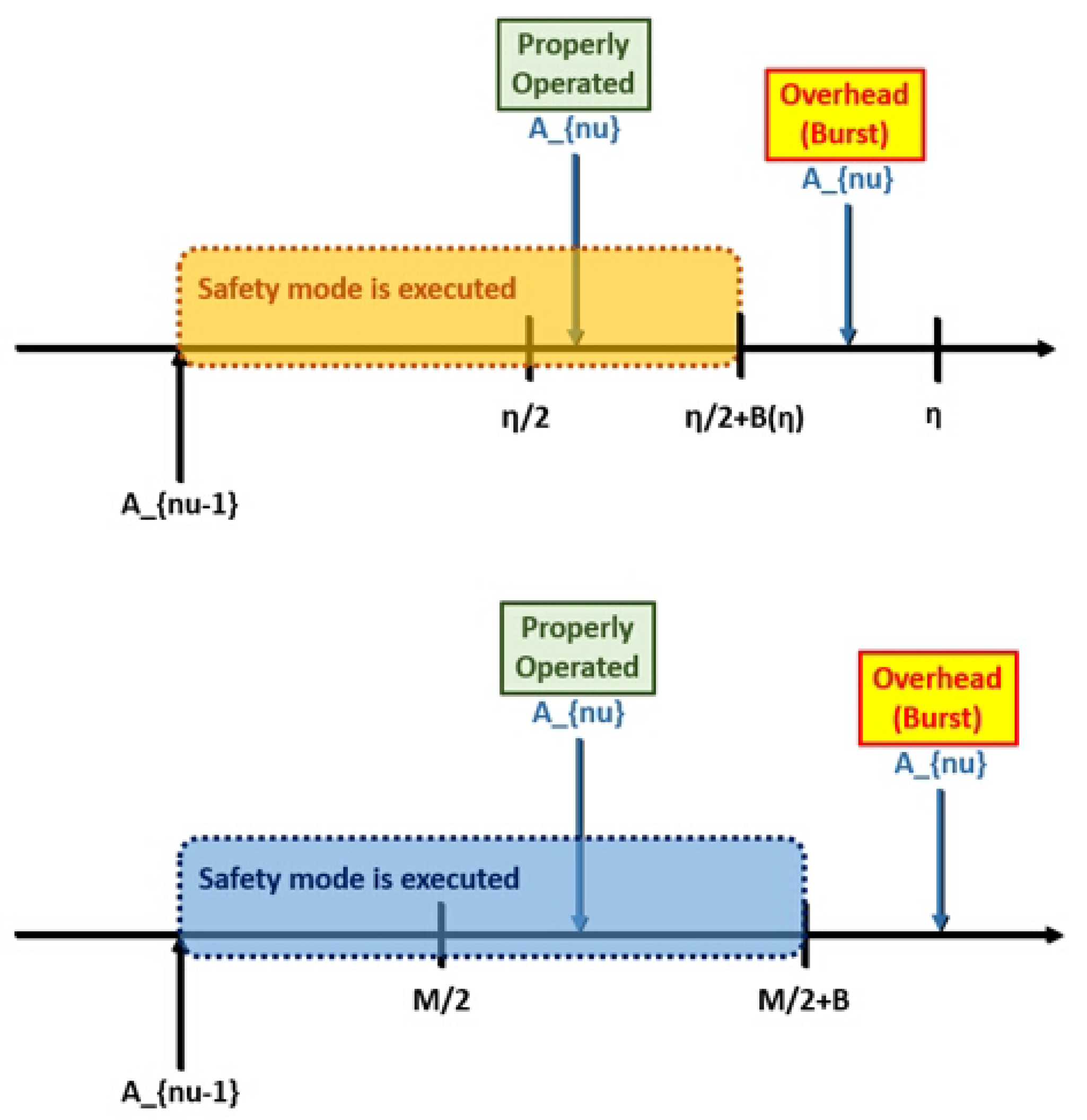
- If the number of nodes governed by the attack is more than half at (i.e., ), the networks in layer 1 are burst;
- If the number of nodes governed by the attack is more than half at (i.e., ), the network of layer 0 is burst;
- The safety modes for each layer are randomly executed based on the Binomial random variables;
- The observation (i.e., the duration of the proof-of-work) are the same within the same layer.
4.2. Optimizing Backup Nodes for the Layer 1
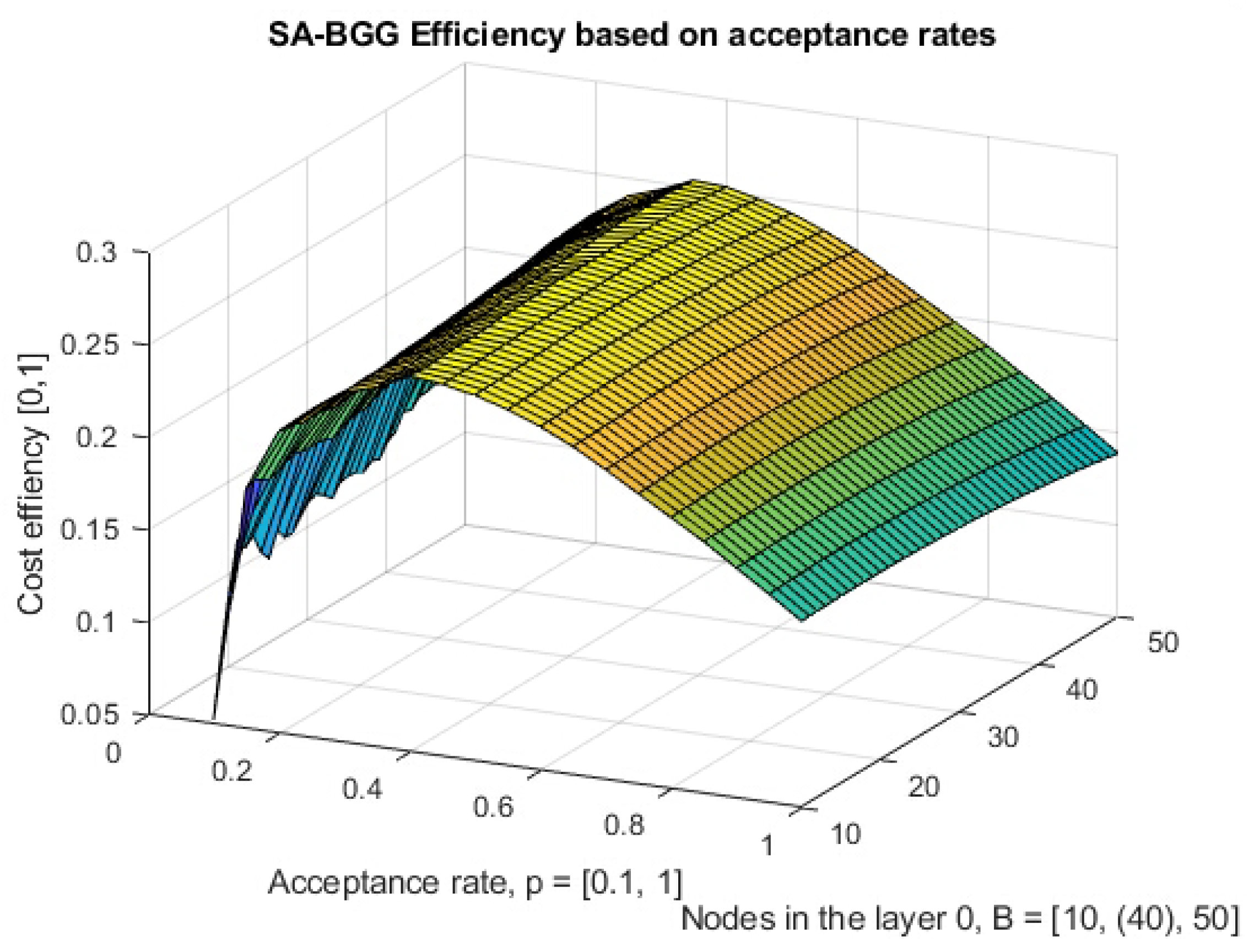
4.3. Acceptance Rate of Strategic Alliance in the Layer 0
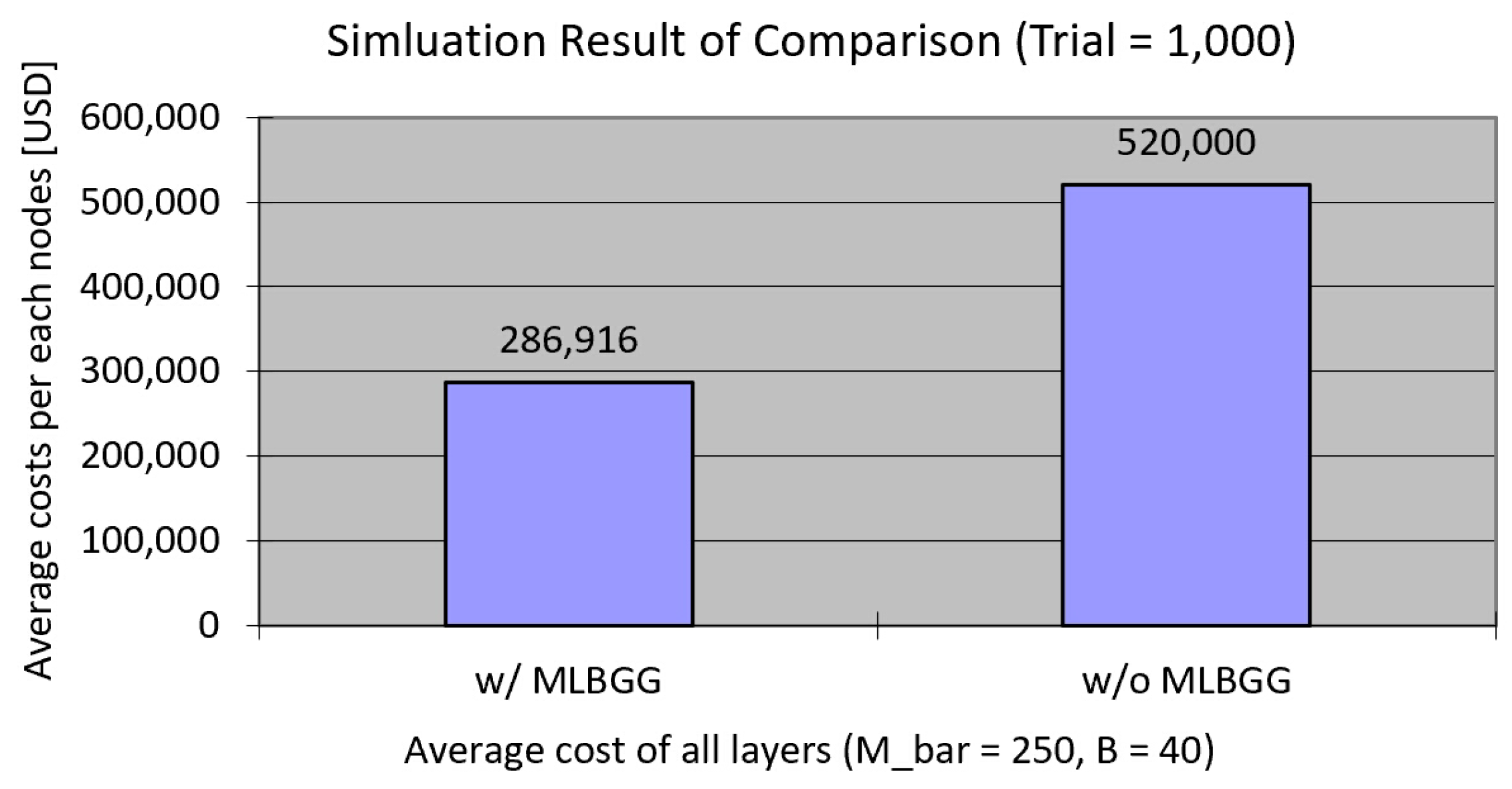
4.4. Overall Performance Discussion of a Multi-Layered BGG
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. 2009. Available online: http://www.bitcoin.org (accessed on 10 November 2021).
- Beikverdi, A.; Song, J. Trend of centralization in Bitcoin’s distributed network. In Proceedings of the 2015 IEEE/ACIS 16th International Conference on Software Engineering, Artificial Intelligence, Networking and Parallel/Distributed Computing (SNPD), Takamatsu, Japan, 1–3 June 2015; pp. 1–6. [Google Scholar]
- Yli-Huumo, I.; Ko, D.; Choi, S.; Park, S.; Smolander, K. Where Is Current Research on Blockchain Technology? A Systematic Review. PLoS ONE 2016, 11, e0163477. [Google Scholar] [CrossRef] [PubMed]
- Decker, C.; Wattenhofer, R. Information propagation in the Bitcoin network. In Proceedings of the IEEE P2P 2013 Proceedings, Trento, Italy, 9–11 September 2013; pp. 1–10. [Google Scholar]
- Kim, W. Bitcoin, Blockchain Mechanism and Its Evolution. 2018. Available online: http://www.itfind.or.kr/publication/ (accessed on 10 November 2021). (In Korean).
- Narayanan, A.; Clar, J. Bitcoin’s Academic Pedigree. Mag. Commun. ACM 2017, 60, 36–45. [Google Scholar] [CrossRef]
- Weiss, M.; Corsi, E. Bitfury: Blockchain for Government. HBP Case 2018, 12, 818-031. [Google Scholar]
- Armknecht, F.; Karame, G.O.; Mandal, A.; Youssef, F.; Zenner, E. Ripple: Overview and Outlook. In Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2015; Volume 9229, pp. 163–180. [Google Scholar]
- Micali, S.; Rabin, M.O.; Vadhan, S.P. Verifiable random functions. In Proceedings of the 40th IEEE Symposium on Foundations of Computer Science, New York, NY, USA, 17–18 October 1999; pp. 120–130. [Google Scholar]
- Goldberg, S.; Reyzin, L.; Papadopoulos, D.; Vcelak, J. Verifiable Random Functions. IETF. 2021. Available online: https://datatracker.ietf.org/doc/draft-irtf-cfrg-vrf/09/ (accessed on 10 November 2021).
- Restuccia, F.; D’Oro, S.; Kanhere, S.S.; Melodia, T.; Das, S.K. Blockchain for the Internet of Things: Present and Future. 2018. Available online: https://arxiv.org/abs/1903.07448 (accessed on 1 May 2019).
- Bolton, T.; Dargahi, T.; Belguith, S.; Al-Rakhami, M.S.; Sodhro, A.H. On the Security and Privacy Challenges of Virtual Assistants. Sensors 2021, 21, 2312. [Google Scholar] [CrossRef] [PubMed]
- Rouse, M. Internet of Vehicles. 2018. Available online: https://whatis.techtarget.com/definition/Internet-of-Vehicles (accessed on 1 May 2019).
- Dandala, T.T.; Krishnamurthy, V.; Alwan, R. Internet of Vehicles (IoV) for traffic management. In Proceedings of the 2017 International Conference on Computer, Communication and Signal Processing (ICCCSP), Chennai, India, 10–11 January 2017; pp. 1–4. [Google Scholar]
- Conoscenti, M.; Vetro, A.; De Martin, J.C. Blockchain for the Internet of Things: A systematic literature review. In Proceedings of the 13th IEEE/ACS International Conference of Computer Systems and Applications (AICCSA 2016), Agadir, Morocco, 29 November–2 December 2016. [Google Scholar]
- Haig, S. Ford to Use Cryptocurrency for Inter-Vehicle Communication System. 2017. Available online: https://news.bitcoin.com/ford-cryptocurrency-inter-vehicle-communication-system/ (accessed on 1 May 2019).
- Hamid, U.Z.A.; Zamzuri, H.; Limbu, D.K. Internet of Vehicle (IoV) Applications in Expediting the Implementation of Smart Highway of Autonomous Vehicle: A Survey. In Performability in Internet of Things; Springer: Cham, Switzerland, 2018; pp. 137–157. [Google Scholar]
- Dorri, A.; Steger, M.; Kanhere, S.S.; Jurdak, R. BlockChain: A Distributed Solution to Automotive Security and Privacy. IEEE Commun. Mag. 2017, 55, 119–125. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.-K. Enhanced IoV Security Network by Using Blockchain Governance Game. Mathematics 2021, 9, 109. [Google Scholar] [CrossRef]
- Baker, J. Edge Computing—The New Frontier of the Web. 2017. Available online: https://hackernoon.com/edge-computing-a-beginners-guide-8976b6886481 (accessed on 10 November 2021).
- ERPINNEW. Fog Computing vs. Edge Computing. 2017. Available online: https://erpinnews.com/fog-computing-vs-edge-computing (accessed on 1 May 2019).
- Cisco Networking Academy. Connecting Networks Companion Guide; Cisco Press: Indianapolis, IN, USA, 2014. [Google Scholar]
- Eyal, I.; Sirer, E. Majority Is Not Enough: Bitcoin Mining Is Vulnerable. In Lecture Notes in Computer Science; Springer: Berlin, Germany, 2014; Volume 8437, pp. 436–454. [Google Scholar]
- Abdalzaher, M.S.; Seddik, K.; Elsabrouty, M.; Muta, O.; Furukawa, H.; Abdel-Rahman, A. Game Theory Meets Wireless Sensor Networks Security Requirements and Threats Mitigation: A Survey. Sensors 2016, 16, 1003. [Google Scholar] [CrossRef] [Green Version]
- Hu, J.; Reed, M.; Thomos, N.; AI-Naday, M.F.; Yang, K. Securing SDN-Controlled IoT Networks Through Edge Blockchain. IEEE Internet Things 2021, 8, 2102–2115. [Google Scholar] [CrossRef]
- Wang, T.; Bai, X.; Wang, H.; Liew, S.C.; Zhang, S. Game-Theoretical Analysis of Mining Strategy for Bitcoin-NG Blockchain Protocol. IEEE Syst. 2021, 15, 2708–2719. [Google Scholar] [CrossRef]
- Abdalzaher, M.S.; Muta, O. A Game-Theoretic Approach for Enhancing Security and Data Trustworthiness in IoT Applications. IEEE Internet Things 2020, 7, 11250–11261. [Google Scholar] [CrossRef]
- Abdalzaher, M.S.; Seddik, K.; Muta, O. An effective Stackelberg game for high-assurance of data trustworthiness in WSNs. In Proceedings of the 2017 IEEE Symposium on Computers and Communications (ISCC), Heraklion, Greece, 3–6 July 2017; pp. 1257–1262. [Google Scholar]
- Liu, Z.; Luong, N.C.; Wang, W.; Niyato, D.; Wang, P.; Liang, Y.C.; Kim, D.I. A Survey on Applications of Game Theory in Blockchain. arXiv 2019, arXiv:1902.10865. [Google Scholar]
- Kim, S.-K. Blockchain Governance Game. Comput. Ind. Eng. 2019, 136, 373–380. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.-K. Strategic Alliance for Blockchain Governance Game. Probab. Eng. Inf. Sci. 2021, 1–17. [Google Scholar] [CrossRef]
- Dshalalow, J.H.; Ke, H.-J. Layers of noncooperative games. Nonlinear Anal. 2009, 71, 283–291. [Google Scholar] [CrossRef]
- Dshalalow, J.H. First Excess Level Process, Advances in Queueing; CRC Press: Boca Raton, FL, USA, 1995; pp. 244–261. [Google Scholar]
- Kim, S.-K. Design of stochastic hitless-prediction router by using the first exceed level theory. Math. Methods Appl. Sci. 2003, 28, 1481–1490. [Google Scholar] [CrossRef]



| Name | Value | Description |
|---|---|---|
| 250 | Average number of nodes of each network in layer 1 | |
| 10,000 [USD] | Average value of each network in layer 1 | |
| − | The cost for reserving nodes to avoid attacks in layer 1 | |
| − | The rate of attacking in layer 1 | |
| B | − | The number of backup nodes supported from layer 0 () |
| Name | Value | Description |
|---|---|---|
| (or p) | − | Acceptance rate for strategic alliance in layer 0 |
| 120,000 [USD] | Total value of the layer 0 network | |
| − | The cost for reserving nodes to avoid attacks in layer 0 | |
| − | The rate of governing nodes by attackers in layer 0 | |
| N | 41 [Nodes] | Total number of nodes in layer 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.-K. Multi-Layered Blockchain Governance Game. Axioms 2022, 11, 27. https://doi.org/10.3390/axioms11010027
Kim S-K. Multi-Layered Blockchain Governance Game. Axioms. 2022; 11(1):27. https://doi.org/10.3390/axioms11010027
Chicago/Turabian StyleKim, Song-Kyoo (Amang). 2022. "Multi-Layered Blockchain Governance Game" Axioms 11, no. 1: 27. https://doi.org/10.3390/axioms11010027
APA StyleKim, S.-K. (2022). Multi-Layered Blockchain Governance Game. Axioms, 11(1), 27. https://doi.org/10.3390/axioms11010027






