(ζ^−m, ζ^m)-Type Algebraic Minimal Surfaces in Three-Dimensional Euclidean Space

Abstract

We introduce the real minimal surfaces family by using the Weierstrass data $({\zeta }^{-m},{\zeta }^m)$ for $\zeta \in \mathbb{C}$, $m\in {\mathbb{Z}}_{\ge 2},$ then compute the irreducible algebraic surfaces of the surfaces family in three-dimensional Euclidean space ${\mathbb{E}}^3$. In addition, we propose that family has a degree number (resp., class number) $2m(m+1)$ in the cartesian coordinates $x,y,z$ (resp., in the inhomogeneous tangential coordinates $a,b,c$).

1. Introduction

A minimal surface is a kind of vanishing mean curvature surface in the three-dimensional Euclidean space ${\mathbb{E}}^3$. There are many classical and modern minimal surfaces in the literature. See [1,2,3,4,5,6,7,8,9] for some books, [10,11,12,13,14] for some papers related to minimal surfaces in ${\mathbb{E}}^3,$ and also [15] for those in ${\mathbb{E}}^4.$

Lie [10] studied algebraic minimal surfaces and gave a table for these kinds of surfaces. See also [6,16,17,18,19,20,21,22,23,24] for details.

In this paper, we consider the minimal surfaces family by using the Weierstrass data $({\zeta }^{-m},{\zeta }^m)$ for $\zeta \in \mathbb{C}$, and some integers $m\ge 2$, and then show that these kinds of surfaces are algebraic in ${\mathbb{E}}^3$.

In Section 2, we give the real minimal surfaces family in the $\left(r,\theta \right)$ and $(u,v)$ coordinates by using the Weierstrass representation in ${\mathbb{E}}^3$. In Section 3, we find irreducible algebraic equations by defining surfaces ${\mathfrak{S}}_m(u,v)$ in terms of running the coordinates $x,y,z,$ and $a,b,c$, and we also compute degrees and classes of ${\mathfrak{S}}_m(u,v)$. Finally, we present a conclusion with all findings in Table 1 and Table 2, with a conjecture in the last section.

Table 1. Some results of irreducible algebraic surfaces $Q_m(x,y,z)=0$.

Algebraic Surface	Degree of Surface	Number of Terms	Gröbner Time (s)	FGb Time (s)
Q${}_2$	12	19	0.406	0.025
Q${}_3$	24	51	25.247	0.070
Q${}_4$	40	111	*	4.118
Q${}_5$	60	202	*	68.367
Q${}_6$	84	337	*	1352.439
Q${}_7$	112	517	*	6535.346
Q${}_8$	*	*	*	*
⋮	⋮	⋮	⋮	⋮
Q${}_m$	$2m(m+1)$	*	*	*

Table 2. Some results of irreducible algebraic surfaces ${\widehat{Q}}_m(a,b,c)=0$.

Algebraic Surface	Class of Surface	Number of Terms	Gröbner Time (s)	FGb Time (s)
${\widehat{Q}}_2$	12	46	0.375	0.025
${\widehat{Q}}_3$	24	234	16.813	0.207
${\widehat{Q}}_4$	40	730	*	1.726
${\widehat{Q}}_5$	60	1996	*	311.201
${\widehat{Q}}_6$	84	4395	*	626.654
${\widehat{Q}}_7$	*	*	*	*
⋮	⋮	⋮	⋮	⋮
${\widehat{Q}}_m$	$2m(m+1)$	*	*	*

Here, “*” means “out of memory”. See the last section for details.

2. $\left({\mathit{\zeta }}^{-\mathit{m}},{\mathit{\zeta }}^{\mathit{m}}\right)-$Type Minimal Surfaces

With the natural metric ${⟨.,.⟩}_{\mathbb{R}}=d{x}^2+d{y}^2+d{z}^2$, let ${\mathbb{E}}^3$ be a three-dimensional Euclidean space. We will refer to $\overrightarrow{x}$ and $\overrightarrow{x^t}$ from here on without further comment.

Let $\mathcal{U}$ be an open subset of $\mathbb{C}$. A minimal (or lenghtless) curve is an analytic function $\vartheta :\mathcal{U}\to {\mathbb{C}}^n$ such that ${⟨{\vartheta }^{\prime }\left(\zeta \right),{\vartheta }^{\prime }\left(\zeta \right)⟩}_{\mathbb{C}}=0,$ where $\zeta \in \mathcal{U}$ and ${\vartheta }^{\prime }:=\frac{\partial \vartheta }{\partial \zeta }.$ In addition, if ${⟨{\vartheta }^{\prime }\left(\zeta \right),\overline{{\vartheta }^{\prime }}\left(\zeta \right)⟩}_{\mathbb{C}}={\left|{\vartheta }^{\prime }\right|}^2\ne 0,$ then $\vartheta$ is a regular minimal curve. We then have the minimal surfaces in the associated family of a minimal curve, such as that given by the following Weierstrass representation theorem for minimal surfaces (see [13] for details).

Theorem 1.

Let $g\left(\omega \right)$ be a meromorphic function, and let $f\left(\omega \right)$ be a holomorphic function, $f{g}^2$ is analytic, defined on a simply connected open subset $U\subset \mathbb{C}$ such that $f\left(\omega \right)$ does not vanish on U except at the poles of $g\left(\omega \right)$. Then, the following

$$\mathbf{x}(u,v)=Re{\int }^{\zeta }\left(\begin{array}{c}f\left(1-g^2\right)\\ if\left(1+g^2\right)\\ 2fg\end{array}\right)d\omega \left(\zeta =u+iv\right)$$

(1)

is a conformal immersion with a mean curvature identically 0 (i.e., conformal minimal surface). Conversely, any conformal minimal surface can be described in this manner.

Next, we present some findings on the Weierstrass data and the minimal curve to constuct the minimal surfaces used in the whole paper.

Definition 1.

A pair of the meromorphic function g and the holomorphic function $f,$$(f,g)$ is called the Weierstrass data for a minimal surface.

Lemma 1.

The curve

$${\mathfrak{s}}_m\left(\zeta \right)=\left(\frac{{\zeta }^{1-m}}{1-m}-\frac{{\zeta }^{m+1}}{m+1},i\left(\frac{{\zeta }^{1-m}}{1-m}+\frac{{\zeta }^{m+1}}{m+1}\right),2\zeta \right)$$

(2)

is a minimal curve, $\zeta \in \mathbb{C}-\left\{0\right\}$, $i=\sqrt{-1}$.

We then have $⟨{\mathfrak{s}}_m^{\prime },{\mathfrak{s}}_m^{\prime }⟩=0$ by using (2). Hence, in ${\mathbb{E}}^3$, our minimal surface is given by the following equation:

$${\mathfrak{S}}_m\left(u,v\right)=Re\int {\mathfrak{s}}_m^{\prime }\left(\zeta \right)d\zeta ,$$

(3)

where $\zeta =u+iv.$ Therefore, $Im\int {\mathfrak{s}}_m^{\prime }\left(\zeta \right)d\zeta$ gives the adjoint minimal surface ${\mathfrak{S}}_m^{adj}\left(u,v\right)$ of the surface ${\mathfrak{S}}_m\left(u,v\right)$ in (3).

Then, we get the following

Corollary 1.

The Weierstrass data

$$\left({\zeta }^{-m},{\zeta }^m\right)$$

is a representation of minimal surface (3).

Taking into account the findings above with $\zeta =r{e}^{i\theta }$, we obtain the following minimal surfaces family

$${\mathfrak{S}}_m\left(r,\theta \right)=\left(\begin{array}{c}\frac{r^{1-m}}{1-m}cos\left[\left(1-m\right)\theta \right]-\frac{r^{m+1}}{m+1}cos\left[\left(m+1\right)\theta \right]\\ -\frac{r^{1-m}}{1-m}sin\left[\left(1-m\right)\theta \right]-\frac{r^{m+1}}{m+1}sin\left[\left(m+1\right)\theta \right]\\ 2rcos\theta \end{array}\right)$$

(4)

where $m\ne -1,1.$ See Figure 1 for the surfaces ${\mathfrak{S}}_2,{\mathfrak{S}}_3,{\mathfrak{S}}_4$ in the $\left(r,\theta \right)$ coordinates.

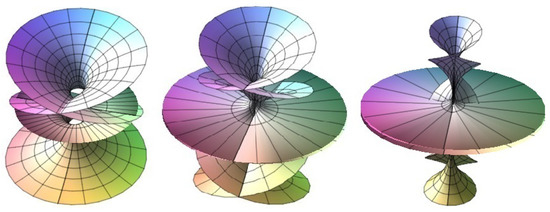
Figure 1. Minimal surfaces (Left) ${\mathfrak{S}}_2\left(r,\theta \right)$, (Middle) ${\mathfrak{S}}_3\left(r,\theta \right)$, (Right) ${\mathfrak{S}}_4\left(r,\theta \right)$.

Hence, with the use of the binomial formula, we obtain a clearer representation of the ${\mathfrak{S}}_m\left(u,v\right)$ in (3):

$$\begin{array}{ccc}x\left(u,v\right)\hfill & =\hfill & Re\left\{\frac{1}{1-m}{\displaystyle \sum _{k=0}^{1-m}}\left(\begin{array}{c}1-m\\ k\end{array}\right)u^{1-m-k}{\left(iv\right)}^k-\frac{1}{m+1}{\displaystyle \sum _{k=0}^{m+1}}\left(\begin{array}{c}m+1\\ k\end{array}\right)u^{m+1-k}{\left(iv\right)}^k\right\},\hfill \\ \hfill & \hfill & \\ y\left(u,v\right)\hfill & =\hfill & Re\left\{\frac{i}{1-m}{\displaystyle \sum _{k=0}^{1-m}}\left(\begin{array}{c}1-m\\ k\end{array}\right)u^{m-1-k}{\left(iv\right)}^k+\frac{i}{m+1}{\displaystyle \sum _{k=0}^{m+1}}\left(\begin{array}{c}m+1\\ k\end{array}\right)u^{m+1-k}{\left(iv\right)}^k\right\},\hfill \\ \hfill & \hfill & \\ z\left(u,v\right)\hfill & =\hfill & Re\left\{2\left(u+iv\right)\right\}.\hfill \end{array}$$

(5)

We study the surface ${\mathfrak{S}}_m\left(u,v\right)$ in the $(u,v)$ coordinates for $m=2,3,\dots ,7$ (we have similar results for the surface ${\mathfrak{S}}_m\left(u,v\right)$ for $m=-2,-3,\dots ,-7),$ taking $\zeta =u+iv$ at the cartesian coordinates $x,y,z$, and also in the inhomogeneous tangential coordinates $a,b,c,$ by using the Weierstrass representation equation.

Remark 1.

The surface

$${\mathfrak{S}}_2\left(u,v\right)=\left(\begin{array}{c}-\frac{u\left(u^4-2u^2{v}^2-3v^4+3\right)}{3\left(u^2+v^2\right)}\\ -\frac{v\left(3u^4+2u^2{v}^2-v^4+3\right)}{3\left(u^2+v^2\right)}\\ 2u\end{array}\right)=\left(\begin{array}{c}x(u,v)\\ y(u,v)\\ z(u,v)\end{array}\right)$$

(6)

which has the Weierstrass data $\left({\zeta }^{-2},{\zeta }^2\right)$, is known as the Richmond’s minimal surface [24].

We compute the following Gauss map (see Figure 3, Left) of the surface ${\mathfrak{S}}_2$

$$e_2=\left(\frac{2\left(u^2-v^2\right)}{{\lambda }^2+1},\frac{4uv}{{\lambda }^2+1},\frac{{\lambda }^2-1}{{\lambda }^2+1}\right),$$

(7)

where $\lambda =u^2+v^2.$

Next, we give a theorem about the minimality of surface ${\mathfrak{S}}_m\left(u,v\right)$ for the integer $m=3$.

Theorem 2.

The surface

$${\mathfrak{S}}_3\left(u,v\right)=\left(\begin{array}{c}-\frac{u^8-4u^6{v}^2-10u^4{v}^4-4u^2{v}^6+v^8+2u^2-2v^2}{4{\left(u^2+v^2\right)}^3}\\ -\frac{uv\left(u^6+4u^4{v}^2-u^2{v}^4-v^6+1\right)}{{\left(u^2+v^2\right)}^3}\\ 2u\end{array}\right)=\left(\begin{array}{c}x(u,v)\\ y(u,v)\\ z(u,v)\end{array}\right)$$

(8)

is a minimal surface in ${\mathbb{E}}^3$.

Proof. 

The coefficients of the first fundamental form of the surface ${\mathfrak{S}}_3\left(u,v\right)$ (${\mathfrak{S}}_3$, for short) are given by the following

$$E={\lambda }^{-3}{\left({\lambda }^3+1\right)}^2=G\mathrm{and}F=0,$$

where $\lambda =u^2+v^2.$ That is, conformality holds. Then, the Gauss map (see Figure 3, Middle) of the surface ${\mathfrak{S}}_3$ is given by the equation below

$$e_3=\left(\frac{2u\left(u^2-3v^2\right)}{{\lambda }^3+1},\frac{2v\left(3u^2-v^2\right)}{{\lambda }^3+1},\frac{{\lambda }^3-1}{{\lambda }^3+1}\right).$$

(9)

The coefficients of the second fundamental form of ${\mathfrak{S}}_3$ are as follows

$$L=-6u{\lambda }^{-1}=-N\mathrm{and}M=-6v{\lambda }^{-1}.$$

We obtain the mean curvature and the Gaussian curvature of ${\mathfrak{S}}_3$, respectively, as follows

$$H=0\mathrm{and}K=-\frac{36{\lambda }^7}{{\left(\lambda +1\right)}^4{\left({\left(\lambda +1\right)}^2-4u^2\right)}^2{\left({\left(\lambda +1\right)}^2-4v^2\right)}^2}.$$

Hence, the surface is minimal and has a negative Gaussian curvature. □

3. Degree and Class of Minimal Surfaces ${\mathfrak{S}}_m\left(u,v\right)$

In this section, with the use of the elimination techniques, we compute the irreducible algebraic surface equations, the degrees, and the classes of the minimal surfaces family ${\mathfrak{S}}_m\left(u,v\right)$ for the integers $2\le m\le 7.$

Next, we look at some definitions on the topic.

Definition 2.

An algebraic function is a function $z=f(x,y)$ which satisfies $Q(x,y,f(x,y\left)\right)=0$, where $Q(x,y,z)$ is a polynomial in $x,y$, and z with integer coefficients. Briefly, an algebraic function is a function that can be defined as the root of a polynomial equation.

Definition 3.

A polynomial is said to be irreducible if it cannot be factored into nontrivial polynomials over the same field.

By eliminating u and v of $\mathbf{s}\left(u,v\right)=(x(u,v),y(u,v),z(u,v)),$ we can see an irreducible algebraic equation $Q(x,y,z)=0$ in the cartesian coordinates. See [25] for the elimination theory.

Definition 4.

The set of roots of a polynomial $Q(x,y,z)=0$ gives the algebraic surface equation. An algebraic surface $\mathbf{s}$ is said to be of degree $\mathbf{d}$, when $\mathbf{d}=deg\left(\mathbf{s}\right).$

Definition 5.

At a point $(u,v)$ on a surface $\mathbf{s}\left(u,v\right)=(x(u,v),y(u,v),z(u,v)),$ the tangent plane is given by the following equation

$$Xx+Yy+Zz+P=0,$$

(10)

where $e=\left(X\right(u,v),Y(u,v),Z(u,v\left)\right)$ is the Gauss map, and $P=P(u,v).$ Then, we have the surface $\widehat{\mathbf{s}}\left(u,v\right)$ in the inhomogeneous tangential coordinates $a,b,c,$ as follows

$$\widehat{\mathbf{s}}\left(u,v\right)=\left(a(u,v),b(u,v),c(u,v)\right)=\left(X/P,Y/P,Z/P\right).$$

(11)

Finally, by eliminating u and v, we can obtain an irreducible algebraic equation $\widehat{Q}(a,b,c)=0$ of $\widehat{\mathbf{s}}\left(u,v\right)$ in the inhomogeneous tangential coordinates.

Definition 6.

The maximum degree of the equation $\widehat{Q}(a,b,c)=0$ gives the $class$ of $\widehat{\mathbf{s}}\left(u,v\right).$

See [6] for details.

In 1901, Richmond [23] proposed the following:

Proposition 1.

There exists a real minimal surface of order 12 whose class number is 12. There are no other real minimal surfaces of order 12.

See also [11,24] for details. Next, we will obtain irreducible algebraic surfaces. Let us see our findings for the degrees and classes.

3.1. Degree

We compute the irreducible algebraic surface equation $Q_2(x,y,z)=0$ (see Figure 2, Left) of the Richmond’s minimal surface ${\mathfrak{S}}_2\left(u,v\right)$ in (6) by using elimination techniques.

$$\begin{array}{ccc}\hfill Q_2(x,y,z)& =& x^2{z}^{10}+y^2{z}^{10}+18x^3{z}^7+18x{y}^2{z}^7+2x{z}^9-135x^4{z}^4-378x^2{y}^2{z}^4+90x^2{z}^6\hfill \\ & & -243y^4{z}^4+54y^2{z}^6+z^8+216x^{5}z+216x^3{y}^{2}z-432x^3{z}^3-648x{y}^2{z}^3\hfill \\ & & +120x{z}^5+432x^4-288x^2{z}^2+48z^4.\hfill \end{array}$$

Then, its degree number is 12. Our findings agree with Richmond’s.

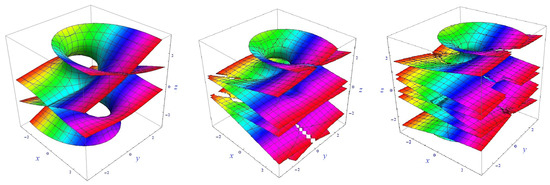
Figure 2. Algebraic minimal surfaces (Left) $Q_2(x,y,z)=0$, (Middle) $Q_3(x,y,z)=0$, (Right) $Q_4(x,y,z)=0$.

Since the real part of the third part of the integral in (1) is $2u$, then $z=2u$ for all the following pairs x and y. We obtain the following parametric equations ${\mathfrak{S}}_m\left(u,v\right)$ for the integers $4\le m\le 7$, respectively,

$$x=-{\rho }^3\frac{1}{15}.\left\{\begin{array}{c}3u^{11}-21u^9{v}^2-66u^7{v}^4-42u^5{v}^6\\ +15u^3{v}^8+5u^3+15u{v}^{10}-15u{v}^2\end{array}\right\},$$

$$y=-{\rho }^3\frac{1}{15}.\begin{array}{c}\left\{\begin{array}{c}15u^{10}v+15u^8{v}^3-42u^6{v}^5-66u^4{v}^7\\ -21u^2{v}^9+15u^{2}v+3v^{11}-5v^3\end{array}\right\}\end{array},$$

$$x=-{\rho }^4\frac{1}{12}.\left\{\begin{array}{c}2u^{14}-22u^{12}{v}^2-78u^{10}{v}^4-54u^8{v}^6\\ +54u^6{v}^8+78u^4{v}^{10}+22u^2{v}^{12}\\ -2v^{14}+3u^4-18u^2{v}^2+3v^4\end{array}\right\},$$

$$y=-{\rho }^4\frac{1}{3}.\left\{\begin{array}{c}3u^{13}v+2u^{11}{v}^3-19u^9{v}^5-36u^7{v}^{79}\\ -19u^{5}v+2u^3{v}^{11}+3u^{3}v+3u{v}^{13}-3u{v}^3\end{array}\right\},$$

$$x=-{\rho }^5\frac{1}{35}.\left\{\begin{array}{c}5u^{17}-80u^{15}{v}^2-300u^{13}{v}^4-160u^{11}{v}^6\\ +550u^9{v}^8+880u^7{v}^{10}+420u^5{v}^{12}\\ +7u^5-70u^3{v}^2-35u{v}^{16}+35u{v}^4\end{array}\right\},$$

$$y=-{\rho }^5\frac{1}{35}.\left\{\begin{array}{c}35u^{16}v-420u^{12}{v}^5-880u^{10}{v}^7-550u^8{v}^9\\ +160u^6{v}^{11}+300u^4{v}^{13}+35u^{4}v\\ +80u^2{v}^{15}-70u^2{v}^3-5v^{17}+7v^5\end{array}\right\},$$

$$x=-{\rho }^6\frac{1}{24}.\left\{\begin{array}{c}3u^{20}-66u^{18}{v}^2-249u^{16}{v}^4-24u^{14}{v}^6\hfill \\ +1014u^{12}{v}^8+1716u^{10}{v}^{10}+1014u^8{v}^{12}\hfill \\ -24u^6{v}^{14}-249u^4{v}^{16}-66u^2{v}^{18}+3v^{20}\hfill \\ +4u^6-60u^4{v}^2+60u^2{v}^4-4v^6\hfill \end{array}\right\},$$

$$y=-{\rho }^6\frac{1}{3}.\left\{\begin{array}{c}3u^{19}v-3u^{17}{v}^3-60u^{15}{v}^5-132u^{13}{v}^7\\ -78u^{11}{v}^9+78u^9{v}^{11}+132u^7{v}^{13}+60u^5{v}^{15}\\ +3u^{5}v+3u^3{v}^{17}-10u^3{v}^3-3u{v}^{19}+3u{v}^5\end{array}\right\}.$$

Here, $\rho ={\left(u^2+v^2\right)}^{-1}.$

Next, we continue our computations to find $Q_m(x,y,z)=0$ for the integers $3\le m\le 7.$ We compute the irreducible algebraic surface equation $Q_3(x,y,z)=0$ (see Figure 2, Middle) of the surface ${\mathfrak{S}}_3\left(u,v\right)$ in (8):

$$\begin{array}{ccc}\hfill Q_3(x,y,z)& =& 2^4{x}^4{z}^{20}+2^5{x}^2{y}^2{z}^{20}+2^4{y}^4{z}^{20}+2^9{x}^5{z}^{16}+2^{10}{x}^{3}y{z}^{16}+2^5{x}^3{z}^{18}+2^{9}x{y}^4{z}^{16}\hfill \\ & & +2^{5}x{y}^2{z}^{18}-2^{12}7x^6{z}^{12}-2^{11}{3}^{2}5x^4{y}^2{z}^{12}+2^{9}7x^4{z}^{14}-2^{15}3x^2{y}^4{z}^{12}\hfill \\ & & +2^{11}3x^2{y}^2{z}^{14}+2^{3}3x^2{z}^{16}-2^{11}17y^6{z}^{12}+2^{9}5y^4{z}^{14}+8y^2{z}^{16}+2^{18}{x}^7{z}^8\hfill \\ & & +2^{15}23x^5{y}^2{z}^8-2^{15}3x^5{z}^{10}+2^{16}11x^3{y}^4{z}^8-2^{12}3\times 17x^3{y}^2{z}^{10}+2^{7}43x^3{z}^{12}\hfill \\ & & +2^{15}7x{y}^6{z}^8-2^{12}{3}^{3}x{y}^4{z}^{10}+2^{7}3\times 13x{y}^2{z}^{12}+2^{3}x{z}^{14}+2^{19}{x}^6{z}^6\hfill \\ & & +2^{16}{x}^4{y}^4{z}^4+2^{15}29x^4{y}^2{z}^6-2^{13}{3}^2{x}^4{z}^8+2^{17}{x}^2{y}^6{z}^4+2^{17}3x^2{y}^4{z}^6\hfill \\ & & -2^{9}3\times 5^2{x}^2{y}^2{z}^8+2^{9}7x^2{z}^{10}+2^{16}{y}^8{z}^4-2^{15}{y}^6{z}^6+2^9{3}^4{y}^4{z}^8+2^{10}{y}^2{z}^{10}\hfill \\ & & +z^{12}+2^{17}{x}^3{y}^4{z}^2-2^{16}5x^3{y}^2{z}^4-2^{14}{x}^3{z}^6+2^{17}x{y}^6{z}^2-2^{15}{3}^{2}x{y}^4{z}^4\hfill \\ & & +{22}^{9}3\times 17x{y}^2{z}^6+2^{6}17x{z}^8-2^{16}{y}^6+2^{13}3y^4{z}^2-2^{10}3y^2{z}^4+2^7{z}^6.\hfill \end{array}$$

Therefore, $Q_3(x,y,z)=0$ is an algebraic minimal surface of the surface ${\mathfrak{S}}_3$. Hence, we get the following irreducible algebraic surface equations (see Figure 2, Right for $Q_4$)

$$\begin{array}{ccc}\hfill Q_4(x,y,z)& =\hfill & 3^7{x}^6{z}^{34}+3^8{x}^4{y}^2{z}^{34}+3^8{x}^2{y}^4{z}^{34}+3^7{y}^6{z}^{34}+2\times 3^7{5}^2{x}^7{z}^{29}\hfill \\ \hfill & \hfill & +106\mathrm{other}\mathrm{lower}\mathrm{degree}\mathrm{terms},\hfill \\ \hfill Q_5(x,y,z)& =\hfill & 2^{16}{x}^8{z}^{52}+2^{18}{x}^6{y}^2{z}^{52}+2^{17}3x^4{y}^4{z}^{52}+2^{18}{x}^2{y}^6{z}^{52}+2^{16}{y}^8{z}^{52}\hfill \\ \hfill & \hfill & +197\mathrm{other}\mathrm{lower}\mathrm{degree}\mathrm{terms},\hfill \\ \hfill Q_6(x,y,z)& =\hfill & 5^{11}{x}^{10}{z}^{74}+5^{12}{x}^8{y}^2{z}^{74}+2\times 5^{12}{x}^6{y}^4{z}^{74}+2\times 5^{12}{x}^4{y}^6{z}^{74}+5^{12}{x}^2{y}^8{z}^{74}\hfill \\ \hfill & \hfill & +332\mathrm{other}\mathrm{lower}\mathrm{degree}\mathrm{terms},\hfill \\ \hfill Q_7(x,y,z)& =\hfill & 2^{12}{3}^{13}{x}^{12}{z}^{100}+2^{13}{3}^{14}{x}^{10}{y}^2{z}^{100}+2^{12}{3}^{14}5x^8{y}^4{z}^{100}+2^{14}{3}^{13}5x^6{y}^6{z}^{100}\hfill \\ \hfill & \hfill & +2^{12}{3}^{14}5x^4{y}^8{z}^{100}+512\mathrm{other}\mathrm{lower}\mathrm{degree}\mathrm{terms}.\hfill \end{array}$$

3.2. Class

Now, we introduce the class of the surfaces ${\mathfrak{S}}_m\left(u,v\right)$ for the integers $2\le m\le 6.$ The case $m=7,$ marked with “*” in Table 2. Before we compute the irreducible algebraic surface equations ${\widehat{Q}}_m(a,b,c)=0,$ we obtain the Gauss maps $e_m\left(u,v\right)$ (see Figure 3 for $e_2,e_3,e_4$) for the integers $2\le m\le 7$ of the surfaces $\mathfrak{S}$${}_m$$\left(u,v\right),$ and we generalize them as follows

$$\begin{array}{ccc}\hfill e_2& =& \left(2\frac{u^2-v^2}{{\lambda }^2+1},2\frac{2uv}{{\lambda }^2+1},\frac{{\lambda }^2-1}{{\lambda }^2+1}\right),\hfill \\ \hfill e_3& =& \left(2\frac{u^3-3u{v}^2}{{\lambda }^3+1},2\frac{3u^{2}v-v^3}{{\lambda }^3+1},\frac{{\lambda }^3-1}{{\lambda }^3+1}\right),\hfill \\ \hfill e_4& =& \left(2\frac{u^4-6u^2{v}^2+v^4}{{\lambda }^4+1},2\frac{4u^{3}v-4u{v}^3}{{\lambda }^4+1},\frac{{\lambda }^4-1}{{\lambda }^4+1}\right),\hfill \\ \hfill e_5& =& \left(2\frac{u^5-10u^3{v}^2+5u{v}^4}{{\lambda }^5+1},2\frac{5u^{4}v-10u^2{v}^3+v^5}{{\lambda }^5+1},\frac{{\lambda }^5-1}{{\lambda }^5+1}\right),\hfill \\ \hfill e_6& =& \left(2\frac{u^6-15u^4{v}^2+15u^2{v}^4-v^6}{{\lambda }^6+1},2\frac{6u^{5}v-20u^3{v}^3+6u{v}^5}{{\lambda }^6+1},\frac{{\lambda }^6-1}{{\lambda }^6+1}\right),\hfill \\ \hfill e_7& =& \left(2\frac{u^7-21u^5{v}^2+35u^3{v}^4-14u{v}^6}{{\lambda }^7+1},2\frac{7u^{6}v-35u^4{v}^3+21u^2{v}^5-v^7}{{\lambda }^7+1},\frac{{\lambda }^7-1}{{\lambda }^7+1}\right),\hfill \\ & & ⋮\hfill \\ \hfill e_m& =& \left(2\frac{Re\left({\zeta }^m\right)}{{\left|\zeta \right|}^m+1},2\frac{Im\left({\zeta }^m\right)}{{\left|\zeta \right|}^m+1},\frac{{\left|\zeta \right|}^m-1}{{\left|\zeta \right|}^m+1}\right),\left(\zeta =u+iv,\left|\zeta \right|=\lambda \right).\hfill \end{array}$$

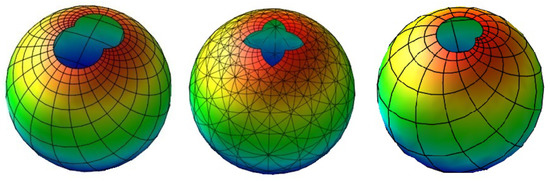
Figure 3. The Gauss maps (Left) $e_2\left(u,v\right)$, (Middle) $e_3\left(u,v\right)$, (Right) $e_4\left(u,v\right)$.

Richmond’s minimal surface ${\mathfrak{S}}_2\left(u,v\right)$ in $\left(\right)$ has class 12. See [23,24] for details. Using (6), (7), (10), and (11), with $P_2(u,v)=-\frac{4u({\lambda }^3-3)}{3\left({\lambda }^2+1\right)},$ we get the surface ${\widehat{\mathfrak{S}}}_2\left(u,v\right)$ in the following inhomogeneous tangential coordinates

$$a=-\frac{3\left(u^2-v^2\right)}{2u({\lambda }^2-3)},b=-\frac{3v}{({\lambda }^2-3)},c=-\frac{3\left({\lambda }^2-1\right)}{4u({\lambda }^2-3)}.$$

Therefore, we obtain the irreducible algebraic surface equation ${\widehat{Q}}_2(a,b,c)=0$ (see Figure 4, Left) of the surface ${\widehat{\mathfrak{S}}}_2\left(u,v\right)$:

$$\begin{array}{ccc}\hfill {\widehat{Q}}_2(a,b,c)& =& 2^{12}{a}^8{b}^4+2^{14}{a}^6{b}^6-2^{14}3a^6{b}^4{c}^2+2^{13}3a^4{b}^8-2^{14}{3}^2{a}^4{b}^6{c}^2+2^{13}{3}^3{a}^4{b}^4{c}^4\hfill \\ & & +2^{14}{a}^2{b}^{10}-2^{14}{3}^2{a}^2{b}^8{c}^2+2^{14}{3}^3{a}^2{b}^6{c}^4-2^{14}{3}^3{a}^2{b}^4{c}^6+2^{12}{b}^{12}-2^{14}3b^{10}{c}^2\hfill \\ & & +2^{13}{3}^3{b}^8{c}^4-2^{14}{3}^3{b}^6{c}^6+2^{12}{3}^4{b}^4{c}^8+2^{11}{3}^3{a}^7{b}^{2}c+2^{11}{3}^4{a}^5{b}^{4}c\hfill \\ & & -2^{11}{3}^{2}19a^5{b}^2{c}^3+2^{11}{3}^4{a}^3{b}^{6}c-2^{12}{3}^{2}19a^3{b}^4{c}^3+2^{11}{3}^{3}11a^3{b}^2{c}^5+2^{11}{3}^{3}a{b}^{8}c\hfill \\ & & -2^{11}{3}^{2}19a{b}^6{c}^3+2^{11}{3}^{3}11a{b}^4{c}^5-2^{11}{3}^{4}a{b}^2{c}^7-2^8{3}^4{a}^8-2^7{3}^{4}7a^6{b}^2\hfill \\ & & +2^9{3}^5{a}^6{c}^2-2^7{3}^6{a}^4{c}^4-2^7{3}^{4}5a^2{c}^6+2^9{3}^5{a}^4{b}^2{c}^2-2^8{3}^6{a}^4{c}^4-2^9{3}^5{a}^2{b}^4{c}^2\hfill \\ & & -2^7{3}^{5}5a^2{b}^2{c}^4-2^7{3}^4{b}^8-2^9{3}^5{b}^6{c}^2+2^7{3}^5{b}^4{c}^4-2^8{3}^4{b}^2{c}^6+2^5{3}^7{a}^{5}c\hfill \\ & & +2^6{3}^7{a}^3{b}^{2}c-2^5{3}^6{a}^3{c}^3+2^5{3}^{7}a{b}^{4}c-2^5{3}^{6}a{b}^2{c}^3+3^8{a}^4+2\times 3^8{a}^2{b}^2+3^8{b}^4.\hfill \end{array}$$

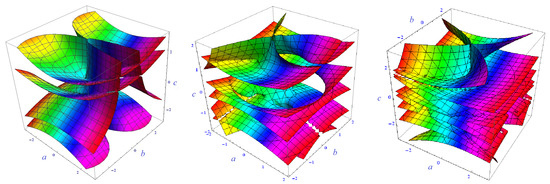
Figure 4. Algebraic surfaces (Left) ${\widehat{Q}}_2(a,b,c)=0$, (Middle) ${\widehat{Q}}_3(a,b,c)=0$, (Right) ${\widehat{Q}}_4(a,b,c)=0$.

Hence, its class number is 12. Our findings agree with that of Richmond’s. Next, we continue our computations to find ${\widehat{Q}}_m$ for integers $3\le m\le 6.$ To find the class of surface ${\mathfrak{S}}_3\left(u,v\right),$ we use (8), (9), (10), and (11). By calculating $P_3(u,v)=-\frac{3u({\lambda }^3-2)}{2\left({\lambda }^3+1\right)},$ we get the surface ${\widehat{\mathfrak{S}}}_3$ inhomogeneous tangential coordinates as follows

$$a=-\frac{4\left(u^2-3v^2\right)u}{3u({\lambda }^3-2)},b=-\frac{4\left(3u^2-v^2\right)v}{3u({\lambda }^3-2)},c=-\frac{2\left({\lambda }^3-1\right)}{3u({\lambda }^3-2)},$$

where $\lambda =u^2+v^2,$${\lambda }^3\ne 2,$$u,v\ne 0.$ In the inhomogeneous tangential coordinates $a,b,c,$ we find the irreducible algebraic surface equation ${\widehat{Q}}_3(a,b,c)=0$ (see Figure 4, Middle) of surface ${\widehat{\mathfrak{S}}}_3(u,v)$ as follows

$$\begin{array}{ccc}\hfill {\widehat{Q}}_3(a,b,c)& =& -3^{18}{a}^{24}-3^{20}{a}^{22}{b}^2+2^3{3}^{20}{a}^{22}{c}^2-2^2{3}^{20}{a}^{20}{b}^4+2^6{3}^{20}{a}^{20}{b}^2{c}^2\hfill \\ & & +229\mathrm{other}\mathrm{lower}\mathrm{degree}\mathrm{terms}.\hfill \end{array}$$

Then, ${\widehat{Q}}_3(a,b,c)=0$ is an algebraic surface of ${\widehat{\mathfrak{S}}}_3(u,v)$. Next, we obtain the following functions $P_i(u,v),$ where $2\le i\le 7$, respectively,

$$\begin{array}{ccc}\hfill P_2& =& -\frac{4u({\lambda }^2-3)}{3\left({\lambda }^2+1\right)},P_4=-\frac{8u\left(3{\lambda }^4-5\right)}{15\left({\lambda }^4+1\right)},P_6=-\frac{12u\left(5{\lambda }^6-7\right)}{35\left({\lambda }^6+1\right)},\hfill \\ \hfill P_3& =& -\frac{3u({\lambda }^3-2)}{2\left({\lambda }^3+1\right)},P_5=-\frac{5u\left(2{\lambda }^5-3\right)}{6\left({\lambda }^5+1\right)},P_7=-\frac{7u\left(3{\lambda }^7-4\right)}{12\left({\lambda }^7+1\right)}.\hfill \end{array}$$

Corollary 2.

Considering the above odd and even integers m of the functions $P_m$, for the integers $k\ge 1$, we have the following generalizations

$$\begin{array}{ccc}\hfill P_{2k}& =& -\frac{4ku\left(\left(2k-1\right){\lambda }^{2k}-\left(2k+1\right)\right)}{\left(2k-1\right)\left(2k+1\right)\left({\lambda }^{2k}+1\right)},\hfill \\ & & \\ \hfill P_{2k+1}& =& -\frac{\left(2k+1\right)u\left(k{\lambda }^{2k+1}-\left(k+1\right)\right)}{k\left(k+1\right)\left({\lambda }^{2k+1}+1\right)}.\hfill \end{array}$$

We reveal the surfaces ${\widehat{\mathfrak{S}}}_2$ and ${\widehat{\mathfrak{S}}}_3$. By using ${\mathfrak{S}}_4-{\mathfrak{S}}_7$, $e_4-e_7,$ respectively, and also (10), (11), we obtain the following surfaces ${\widehat{\mathfrak{S}}}_m(u,v)=\left(a(u,v),b(u,v),c(u,v)\right)$:

$$\begin{array}{ccc}\hfill {\widehat{\mathfrak{S}}}_2& =& -\left(\frac{3\left(u^2-v^2\right)}{2u({\lambda }^2-3)},\frac{3v}{({\lambda }^2-3)},\frac{3\left({\lambda }^2-1\right)}{4u({\lambda }^2-3)}\right),\hfill \\ \hfill {\widehat{\mathfrak{S}}}_3& =& -\left(\frac{4\left(u^3-3u{v}^2\right)}{3u({\lambda }^3-2)},\frac{4\left(3u^{2}v-v^3\right)}{3u({\lambda }^3-2)},\frac{2\left({\lambda }^3-1\right)}{3u({\lambda }^3-2)}\right),\hfill \\ \hfill {\widehat{\mathfrak{S}}}_4& =& -\left(\frac{15\left(u^4-6u^2{v}^2+v^4\right)}{4u\left(3{\lambda }^4-5\right)},\frac{15\left(u^{3}v-u{v}^3\right)}{u\left(3{\lambda }^4-5\right)},\frac{15\left({\lambda }^4-1\right)}{8u\left(3{\lambda }^4-5\right)}\right),\hfill \\ \hfill {\widehat{\mathfrak{S}}}_5& =& -\left(\frac{12\left(u^5-10u^3{v}^2+5u{v}^4\right)}{5u\left(2{\lambda }^5-3\right)},\frac{12\left(5u^{4}v-10u^2{v}^3+v^5\right)}{5u\left(2{\lambda }^5-3\right)},\frac{6\left({\lambda }^5-1\right)}{5u\left(2{\lambda }^5-3\right)}\right),\hfill \\ \hfill {\widehat{\mathfrak{S}}}_6& =& -\left(\frac{35\left(u^6-15u^4{v}^2+15u^2{v}^4-v^6\right)}{6u\left(5{\lambda }^6-7\right)},\frac{35\left(6u^{5}v-20u^3{v}^3+6u{v}^5\right)}{6u\left(5{\lambda }^6-7\right)},\frac{35\left({\lambda }^6-1\right)}{12u\left(5{\lambda }^6-7\right)}\right),\hfill \\ \hfill {\widehat{\mathfrak{S}}}_7& =& -\left(\frac{24\left(u^7-21u^5{v}^2+35u^3{v}^4-14u{v}^6\right)}{7u\left(3{\lambda }^7-4\right)},\frac{24\left(7u^{6}v-35u^4{v}^3+21u^2{v}^5-v^7\right)}{7u\left(3{\lambda }^7-4\right)},\frac{12\left({\lambda }^7-1\right)}{7u\left(3{\lambda }^7-4\right)}\right).\hfill \end{array}$$

Considering equations above, for odd and even numbers m, we get the following:

Corollary 3.

For the surfaces ${\widehat{\mathfrak{S}}}_m(u,v)$, we have the following generalizations

$$\begin{array}{ccc}\hfill {\widehat{\mathfrak{S}}}_{2k}(u,v)& =& -\frac{\left(2k-1\right)\left(2k+1\right)}{4ku\left(\left(2k-1\right){\lambda }^{2k}-\left(2k+1\right)\right)}\left(\begin{array}{c}2Re\left({\zeta }^{2k}\right)\\ 2Im\left({\zeta }^{2k}\right)\\ {\lambda }^{2k}-1\end{array}\right)=\left(\begin{array}{c}a\\ b\\ c\end{array}\right),\hfill \\ \hfill {\widehat{\mathfrak{S}}}_{2k+1}(u,v)& =& -\frac{k\left(k+1\right)}{\left(2k+1\right)u\left(k{\lambda }^{2k+1}-\left(k+1\right)\right)}\left(\begin{array}{c}2Re\left({\zeta }^{2k+1}\right)\\ 2Im\left({\zeta }^{2k+1}\right)\\ {\lambda }^{2k+1}-1\end{array}\right)=\left(\begin{array}{c}a\\ b\\ c\end{array}\right),\hfill \end{array}$$

where the integers $k\ge 1,$$\zeta =u+iv$ and $\left|\zeta \right|=\lambda .$

For the integers $m=4,5,6,$ we obtain the following irreducible algebraic surface equations (see Figure 4, Right for ${\widehat{Q}}_4$):

$$\begin{array}{ccc}\hfill {\widehat{Q}}_4(a,b,c)& =\hfill & 2^{72}{a}^{32}{b}^8+2^{76}{a}^{30}{b}^{10}-2^{76}3\times 5a^{30}{b}^8{c}^2+2^{75}3\times 5a^{28}{b}^{12}\hfill \\ \hfill & \hfill & -2^{76}{3}^2{5}^2{a}^{28}{b}^{10}{c}^2+725\mathrm{other}\mathrm{lower}\mathrm{degree}\mathrm{terms},\hfill \\ \hfill {\widehat{Q}}_5(a,b,c)& =\hfill & =5^{50}{a}^{60}+5^{52}{a}^{58}{b}^2-2^{3}3\times 5^{52}{a}^{58}{c}^2+2^{2}3\times 5^{52}{a}^{56}{b}^4\hfill \\ \hfill & \hfill & -2^6{3}^2{5}^{52}{a}^{56}{b}^2{c}^2+1991\mathrm{other}\mathrm{lower}\mathrm{degree}\mathrm{terms},\hfill \\ \hfill {\widehat{Q}}_6(a,b,c)& =\hfill & 2^{84}{3}^{72}{a}^{72}{b}^{12}+2^{86}{3}^{74}{a}^{70}{b}^{14}-2^{86}{3}^{74}5\times 7a^{70}{b}^{12}{c}^2+2^{85}{3}^{74}5\times 7a^{68}{b}^{16}\hfill \\ \hfill & \hfill & -2^{86}{3}^{74}{5}^2{7}^2{a}^{68}{b}^{14}{c}^2+4390\mathrm{other}\mathrm{lower}\mathrm{degree}\mathrm{terms}.\hfill \end{array}$$

4. Conclusions

We have tried some standard techniques in the elimination theory to reveal the irreducible algebraic surface equations of the surfaces ${\mathfrak{S}}_m\left(u,v\right)$ in ${\mathbb{E}}^3.$ The Sylvester method by hand works for $Q_2(x,y,z)=0$. The projective (Macaulay) and sparse multivariate resultants were implemented on the Maple software [26] package multi-res for $Q_m(x,y,z)=0$ and ${\widehat{Q}}_m(a,b,c)=0$.

Maple’s native implicitization command was Implicitize, and implicitization was based on Maples’ native implementation of Gröbner Basis. Later, we implemented the method in [25] (Chapter 3, p. 128) on Maple. We only succeeded for $m=2,3$ in all above methods under reasonable time.

For $m=4,5,6,7$, the successful method we tried was to compute the equations by defining the elimination ideal using the Gröbner Basis package FGb of Faugère in [27].

The time required to output the irreducible algebraic surface equations $Q_m(x,y,z)=0$ (for integers $2\le m\le 7$) and ${\widehat{Q}}_m(a,b,c)=0$ (for integers $2\le m\le 6$), polynomials defining the elimination ideal, was under reasonable seconds as determined by Table 1 and Table 2.

Calculation of the class for the irreducible algebraic surface equation ${\widehat{Q}}_7(a,b,c)=0$ of ${\mathfrak{S}}_7\left(u,v\right),$ marked with “*” in Table 2, was rejected (i.e., “out of memory”) by Maple 17 on a laptop Pentium Core i5-4310M 2.00 GHz, 4 GB RAM, with the time given in CPU seconds.

Finally, we give the following:

Conjecture 1. 

The degree number of the irreducible algebraic surfaces$Q_m(x,y,z)=0$, and the class number of the irreducible algebraic surfaces${\widehat{Q}}_m(a,b,c)=0$for the$({\zeta }^{-m},{\zeta }^m)$-type real minimal surfaces are equal to the$2m\left(m+1\right)$, where the integers$m\ge 2$.