Quadratic Lyapunov Functions for Stability of the Generalized Proportional Fractional Differential Equations with Applications to Neural Networks
Abstract
:1. Introduction
2. Preliminary Results
- -
- the generalized proportional fractional integral
- -
- the generalized proportional Caputo fractional derivativewhere and are fixed parameters.
3. Quadratic Lyapunov Functions and Their Generalized Proportional Derivatives
- 1.
- The function is a solution of the IVP for the nonlinear system of generalized proportional Caputo fractional differential equations (10);
- 2.
- For any point , the inequalityholds.
- 1.
- The function is a solution of the IVP for the nonlinear system of generalized proportional Caputo fractional differential equations (10);
- 2.
- There exists a positive constant , such that at any point , the inequalityholds.
4. Stability of Neural Networks with a Generalized Proportional Caputo Fractional Derivative
- 1.
- and ;
- 2.
- The functions , ;
- 3.
- There exist positive constants , such that the activation functions satisfy for ;
- 4.
- Equation (23) has an equilibrium ;
- 5.
- The inequalityholds.
- 1.
- Conditions 1–4 of Theorem 1 are satisfied;
- 2.
- There exists a positive constant L, such that inequalityholds.
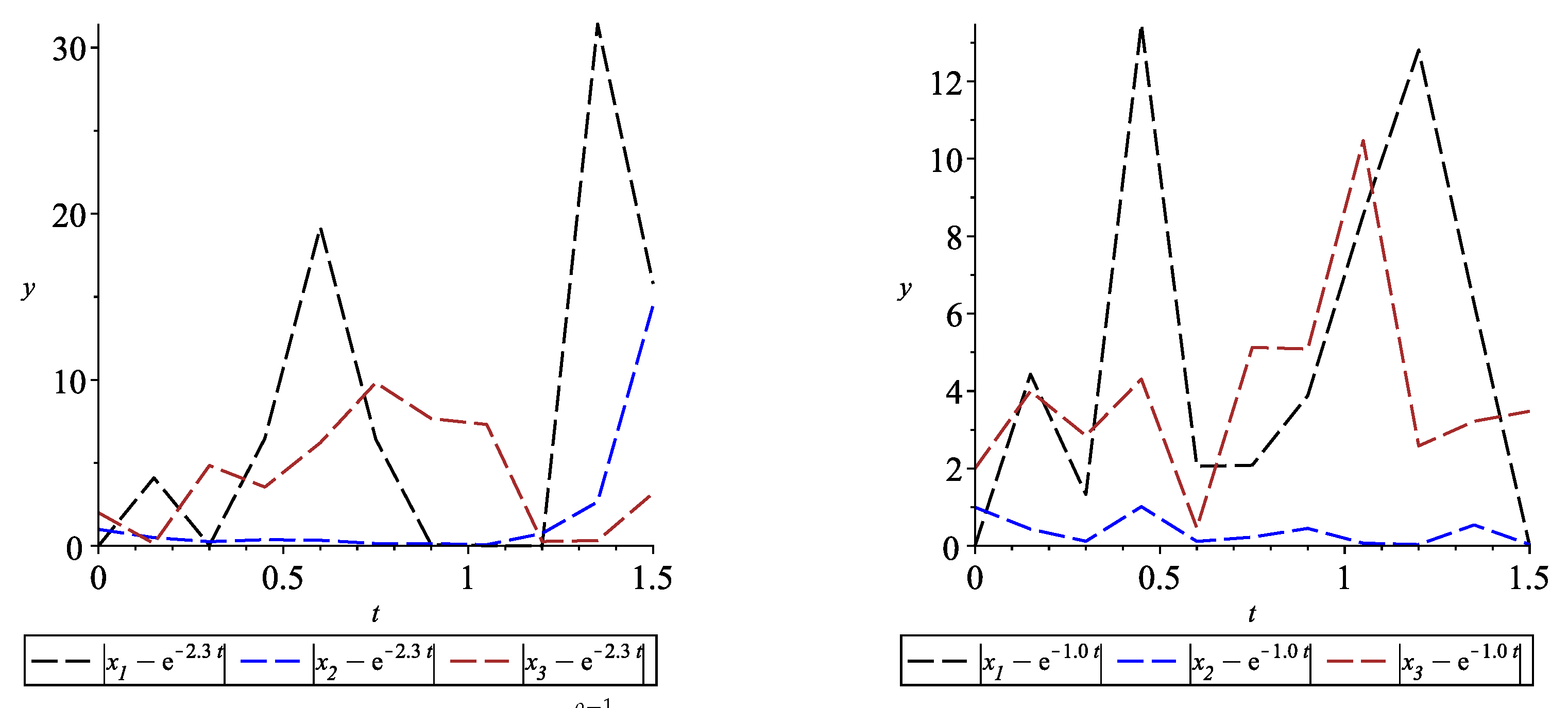
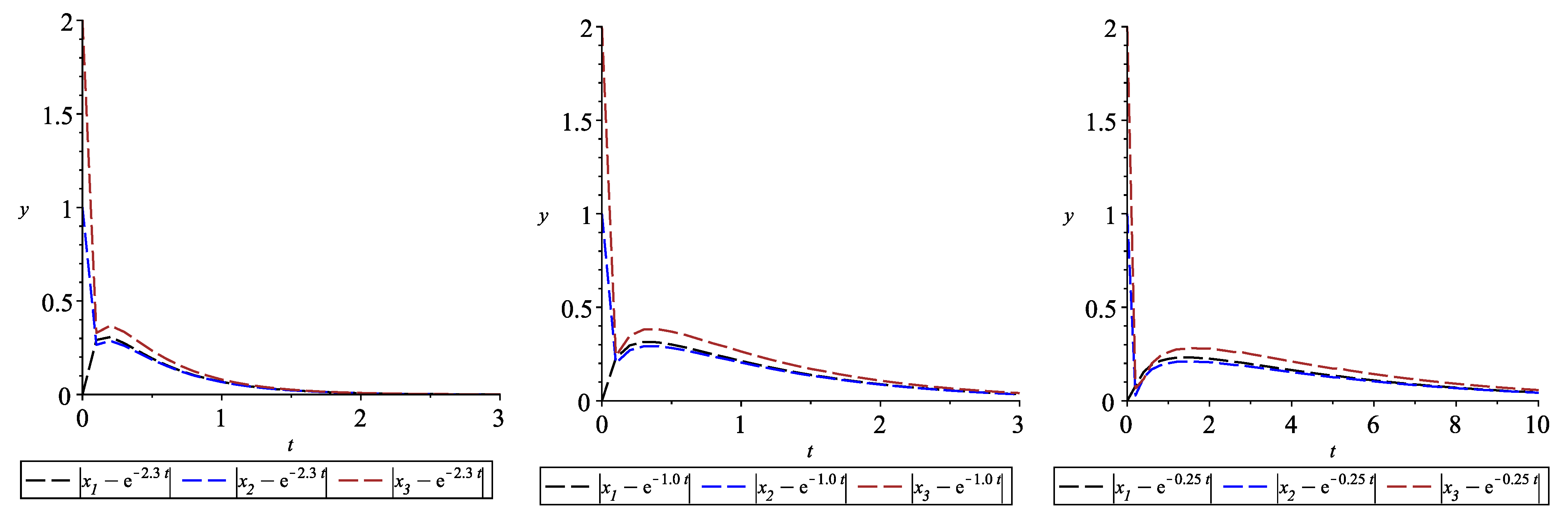
5. Applications
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jarad, F.; Abdeljawad, T.; Alzabut, J. Generalized fractional derivatives generated by a class of local proportional derivatives. Eur. Phys. J. Spec. Top. 2017, 226, 3457–3471. [Google Scholar] [CrossRef]
- Alzabut, J.; Abdeljawad, T.; Jarad, F.; Sudsutad, W. A Gronwall inequality via the generalized proportional fractional derivative with applications. J. Ineq. Appl. 2019, 2019, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Khaminsou, B.; Thaiprayoon, C.; Sudsutad, W.; Jose, S.A. Qualitative analysis of a proportional Caputo fractional differential pantograph differential equations with mixed nonlocal conditions. Nonl. Funct. Anal. Appl. 2021, 26, 197–223. [Google Scholar] [CrossRef]
- Sudsutad, W.; Alzabut, J.; Nontasawatsri, S.; Thaiprayoon, C. Stability analysis for a generalized proportional fractional Langevin equation with variable coefficient and mixed integro-differential boundary conditions. J. Nonlinear Funct. Anal. 2020, 2020, 1–24. [Google Scholar]
- Boroomand, A.; Menhaj, M.B. Fractional-Order Hopfield Neural Networks. In Advances in Neuro-Information Processing; 5506 of Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2009; pp. 883–890. [Google Scholar]
- Kaslik, E.; Sivasundaram, S. Nonlinear dynamics and chaos in fractional-order neural networks. Neural Netw. 2012, 32, 245–256. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Wen, Y.; Gou, Y.; Ye, Z.; Chen, H. Fractional-order gradient descent learning of BP neural networks with Caputo derivative. Neural Netw. 2017, 89, 19–30. [Google Scholar] [CrossRef] [PubMed]
- Deng, J.; Ma, W.; Deng, K.; Li, Y. Tempered Mittag—Leffler stability of tempered fractional dynamical systems. Math. Probl. Eng. 2020, 2020, 7962542. [Google Scholar] [CrossRef]
- Fernandez, A.; Ustaoglu, C. On some analytic properties of tempered fractional calculus. J. Comput. Appl. Math. 2020, 366, 112400. [Google Scholar] [CrossRef] [Green Version]
- Meerschaert, M.M.; Sabzikar, F.; Phanikumar, M.S.; Zeleke, A. Tempered fractional time series model for turbulence in geophysical flows. J. Stat. Mech. Theory Exper. 2014, 9, 9023. [Google Scholar] [CrossRef] [Green Version]
- Aguila–Camacho, N.; Duarte-Mermoud, M.A.; Gallegos, J.A. Lyapunov functions for fractional order systems. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 2951–2957. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.Q.; Podlubny, I. Stability of fractional-order nonlinear dynamic systems: Lyapunov direct method and generalized Mittag—Leffler stability. Comput. Math. Appl. 2010, 59, 1810–1821. [Google Scholar] [CrossRef] [Green Version]
- Rajchakit, G.; Agarwal, P.; Ramalingam, S. Stability Analysis of Neural Networks; Springer: Singapore, 2021. [Google Scholar]
- Tanaka, K. Stability analysis of neural networks via Lyapunov approach. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995. [Google Scholar] [CrossRef]
- Zhang, S.; Yu, Y.; Wang, H. Mittag–Leffler stability of fractional-order Hopfield neural networks. Nonlinear Anal. Hybrid Syst. 2015, 16, 104–121. [Google Scholar] [CrossRef]
- Gu, C.-Y.; Zheng, F.-H.; Shiri, B. Mittag–Leffler stability analysis of tempered fractional neural networks with short memory and variable-order. Fractals 2021, 8, 2140029. [Google Scholar] [CrossRef]
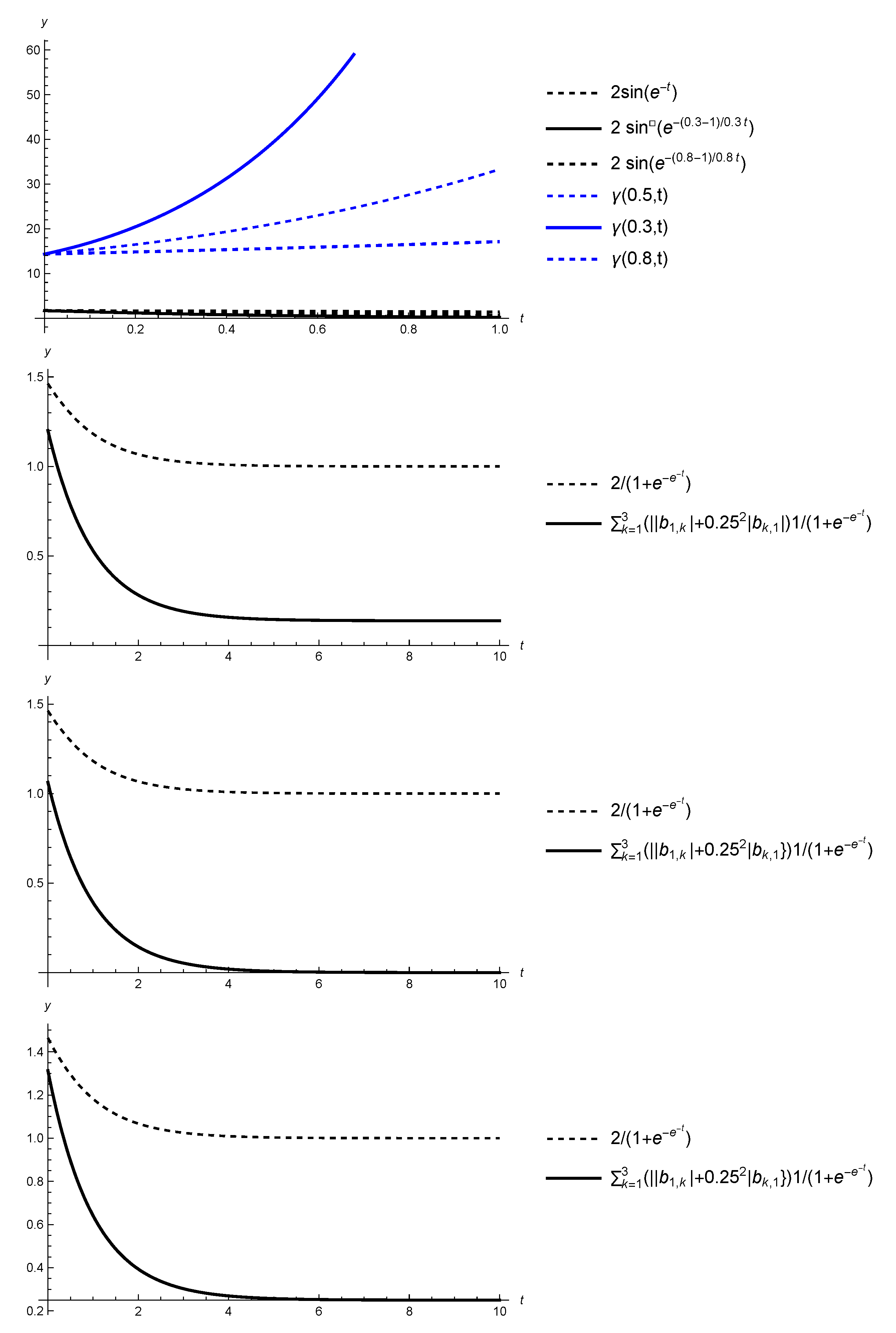
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almeida, R.; Agarwal, R.P.; Hristova, S.; O’Regan, D. Quadratic Lyapunov Functions for Stability of the Generalized Proportional Fractional Differential Equations with Applications to Neural Networks. Axioms 2021, 10, 322. https://doi.org/10.3390/axioms10040322
Almeida R, Agarwal RP, Hristova S, O’Regan D. Quadratic Lyapunov Functions for Stability of the Generalized Proportional Fractional Differential Equations with Applications to Neural Networks. Axioms. 2021; 10(4):322. https://doi.org/10.3390/axioms10040322
Chicago/Turabian StyleAlmeida, Ricardo, Ravi P. Agarwal, Snezhana Hristova, and Donal O’Regan. 2021. "Quadratic Lyapunov Functions for Stability of the Generalized Proportional Fractional Differential Equations with Applications to Neural Networks" Axioms 10, no. 4: 322. https://doi.org/10.3390/axioms10040322
APA StyleAlmeida, R., Agarwal, R. P., Hristova, S., & O’Regan, D. (2021). Quadratic Lyapunov Functions for Stability of the Generalized Proportional Fractional Differential Equations with Applications to Neural Networks. Axioms, 10(4), 322. https://doi.org/10.3390/axioms10040322








