1. Introduction
The complex set is necessary to obtain the roots of all real numbers. It is all too natural to ask whether extensions of complex algebra to higher dimensions introduce more roots: in particular, new roots to the real numbers set. The roots of
in a number system
reduce to the existence and finding of solutions to the equation
. If
, the solutions
will be roots of real numbers, whereas if
, the number and its roots will belong to the
set. In quaternion algebra, there is an infinite number of roots for a real number
if
, whereas there are
m roots for
[
1]. The quaternion roots can be economically obtained by writing quaternions in polar form and using De Moivre’s theorem [
2]. The
equation has been solved in several other number systems: split quaternions [
3], complexified quaternions [
4], and Clifford algebras
with
[
5], to mention some of them.
In contrast with the different versions of quaternions where real quantities have infinitely many roots, the number of possible solutions for the
root of a real or scator number is
, where
n is the number of director dimensions in scator space, as we shall presently see. Not all these roots are necessarily different. In the paper entitled ’
Powers of elliptic scator numbers’, the Victoria equation was established [
6]. This expression can be viewed as a generalization of De Moivre’s formula to scator numbers in
dimensions. The equation’s name and its concomitant winged
sense, were given in homage to chemist Victoria Guasti; for, in the early days of scator algebra, this result revealed the promising route of the scator’s approach. This manuscript draws heavily on, and should be considered as a follow up to the Victoria equation and other results presented in [
6].
This manuscript is organized as follows: In
Section 2, the Victoria equation is inverted to obtain the roots of scators. Two versions exist, one in the multiplicative representation, stated in Theorem 1, and another in the additive representation, Theorem 2, that correspond to the rectangular and polar representations of complex numbers in higher dimensions. An important difference between these two representations is that only in the latter can the product be non-associative and eventually lead to zero scator solutions. The conditions that candidate solutions need to satisfy to be roots of non-zero scators are discussed here. In
Section 3, square roots are considered. No new roots are obtained apart from the complex-like roots present in each scalar-hypercomplex plane. In this and the following sections, a geometrical representation of the roots is presented. Geometric interpretations of hyperbolic scators have been proposed before in terms of higher dimensional spaces [
7,
8,
9] as well as deformed Lorentz metrics [
10]. Elliptic scators and some scator functions of scator variables, in particular the components exponential function, have also been represented geometrically [
11]. Cube roots of one, described in
Section 4, are the first case where new roots of real numbers with two or more non-vanishing director components exist. The two Abelian groups of these roots lie in orthogonal planes revolving around a point that is not the origin. Fourth roots of one, tackled in
Section 5, are relevant because they are the lowest order roots that do not satisfy group properties in the additive representation. Fifth roots, described in
Section 6, are the first case where some Abelian groups of roots no longer lie on planes. Some generalizations for
roots of one are discussed in
Section 7. The conjugation of roots is discussed in this section. Conclusions are drawn in the last section.
3. Square Roots in the Scator Set
In the multiplicative representation, the number one in
is given by a scator with magnitude
, and
n multiplicative director coefficients are equal to zero,
. In the additive representation, one is given by the additive scalar component equal to one,
, and the
n additive director coefficients are equal to zero,
. Recall that real numbers form a subset of the scator set
. From the Victoria Equation (
5), in
, the
roots of one are
where
and the two director axes have been labelled with subindices
x and
y instead of numbers; the latter are usually used for dimensions larger than four. The square roots of 1 in
are
where the scalar component is 1 if
and
when they are unequal; the director components are always zero. The usual
roots of one are thus obtained.
Spurious roots of 1: However, there seems to be another possibility because the number one in the additive representation in
is also attained if
,
. The square root from the Victoria Equation (
5) is
However,
, regardless of the value of the integer
. A zero scator solution is thus obtained. However, from Lemma 1, this solution is not associative and therefore not a root of
. It is instructive to work this example explicitly. The multiplicative to additive transformation of the root
, prior to performing the product of components, is given by Equation (4a) in [
6]:
If this solution were a root of unity, its square should be equal to one. However, the product is clearly not associative, since , while, recalling that the scator product is commutative, . The fact that this non-associative product can be arranged in such a way that the product is 1 explains why this spurious root occurs. It should be noticed that the solution cannot be rearranged so that 1 is the product of two equal expressions, consistent with Corollary 2.
Square roots of : In multiplicative variables, minus one is obtained if
and either
,
, or vice versa. If
and
,
whereas if
and
,
The square roots of minus one in the scator set are the familiar imaginary units of complex algebra, but there is now an imaginary unit for each hypercomplex axis direction. These roots are illustrated in
Figure 1. The scalar component and the two director components have been depicted in orthogonal directions. The director coefficients in multiplicative variables
and
are geometrically represented by the angle between the scalar (real) axis and the corresponding hyperimaginary director axis. The product of the roots
involves a
rotation in the
plane, whereas the product
produces a
rotation. An analogous behaviour occurs in the
plane for the
roots. These two cases exhaust the possibilities in
.
Spurious roots of -1: However, in
, minus one can be written as
. The solution from (
5) is zero:
In terms of the components factors, this solution is
Evaluation of the square is . Depending on the association, this expression is zero or minus one. Thus, this non-associative solution is a spurious root. Notice that the minus one association, , again cannot be written as the product of two equal expressions.
Square roots can be readily generalized to dimensions. Consider four subsets of : (i) the set of positive real numbers , (ii) the set of negative real numbers , (iii) the set of scators with at least one non vanishing director component , and (iv) zero.
(i) For elements in the subset, there are only two different square roots. In additive variables, given a scator with non-zero positive scalar and zero director components, , the two square roots are . In multiplicative variables, given a scator with a non-zero magnitude and director components equal to zero or a multiple of , the square root is , and the two different square roots are , where the ±sign depends on whether there is an even or odd number of director component arguments equal to . The geometrical interpretation of the roots in this case is the familiar cyclotomic division. For example, the root lying on the negative scalar axis makes a angle with respect to the positive scalar (or real) axis. The product of the scator root with itself doubles the angle, thereby mapping onto 1, as in the complex case.
(ii) For elements in the
subset, there exist
square roots. In additive variables, elements with negative additive scalar and zero director components are considered,
. In multiplicative variables, all except one of the director components are zero (mod
). If, for example, the
direction has a
argument, then
The square roots from the Victoria Equation (
5) are
where the only non vanishing term is
There are thus two roots, , for each j from 1 to n. In a geometrical representation, the root lying on the axis makes a angle with respect to the scalar (or real) axis. The product of the scator root with itself doubles the angle, thereby mapping the imaginary unit onto the negative scalar axis. However, there are now n hyper imaginary axes, each of them mapping positive or negative numbers on the line onto the negative scalar axis.
(iii) For elements
, there are only two different square roots in the additive representation, because the possible
phase differences in the
coefficients can only introduce an overall
factor, i.e.,
, and
. The two square roots are
(iv) The square of zero is ; hence, the square root of zero is zero. This is the unique element with only one square root.
The square roots of a scator number
are solutions to the polynomial equation
. In particular, square roots of one satisfy the polynomial
. The second order polynomial with a non-zero linear term is
, where
b is a real coefficient. Surprisingly, this second order polynomial has additional roots that are not present if
. In
, depending on the value of the real number
b, the polynomial
has two, six, or eight scator roots [
13].
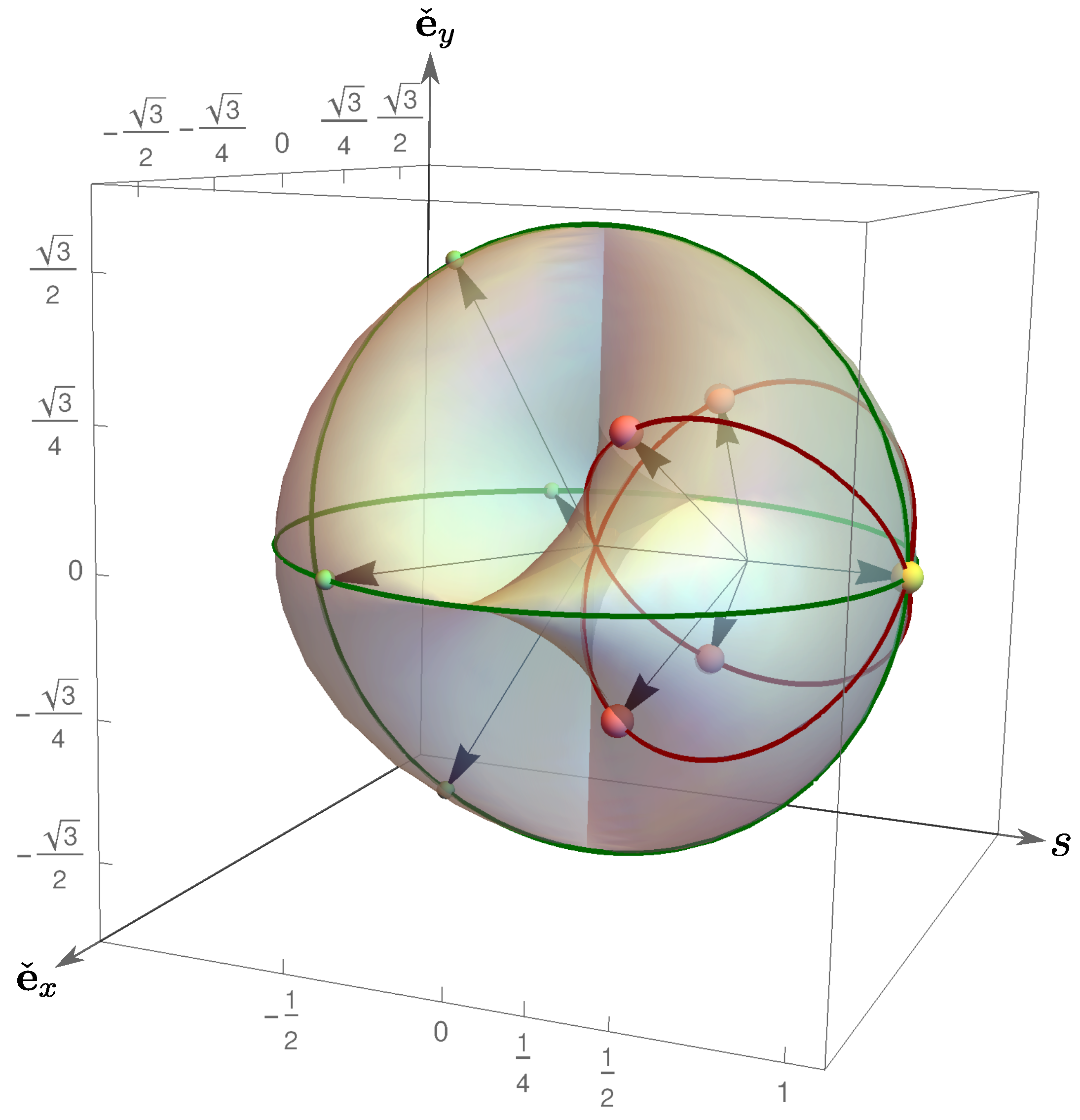
4. Cube Roots of 1
The cube roots of
in
are given by the Victoria equation for
and
:
Labelling the roots
, the
values are shown in
Table 1. The roots
and
are the familiar three cyclotomic complex roots, but there are now two circles, one for each scalar-director mutually orthogonal plane, as depicted in
Figure 2. They account for four roots, in addition, of course, to
. The remaining four hypercomplex roots have non-zero director coefficients with equal magnitude
in both director axes. The roots
,
and
form a group since
and
. These three points lie on the parametric curve
depicted in red in
Figure 2. The two-dimensional surface embedded in three-dimensional space of scators
with unit magnitude is
where zero
is clearly excluded. This surface is known as a cusphere [
11]. The product of the magnitudes is equal to the magnitude of the products since associativity is satisfied, so that all roots have a magnitude equal to one. Therefore, all the roots lie on the isometric surface as shown in
Figure 2.
Perform a Euclidean 45° rotation of the cusphere about the
s axis to bring the hypercomplex roots onto the
and
planes:
At the
plane,
where the positive sign was taken since the magnitude is defined by the positive square root of (
20). Shift
s by
in the negative
s direction,
, to obtain
that is, an equation of an ellipse with semi-axes
and
. The unshifted ellipse is centred at
on the scalar axis. This ellipse and its counterpart, obtained at the
plane in the rotated cusphere, are drawn in red in
Figure 2. The roots
,
, and
, which lie on the ellipse at
with respect to the
axes, also form a group,
,
, and their cubes are equal to
. The parametric curve for this ellipse is
. The 45° Euclidean rotation maps the hypercomplex roots to
and
, but these roots no longer have unit scator magnitude. The Euclidean rotation is an auxiliary procedure to exhibit the types of curves that are being obtained. However, the rotated figures must be treated with much care because a Euclidean rotation does not preserve the scator metric, as may be readily seen from (
20).
The projection of the parametric curve (
19) in the
plane is
=
. The projections of the unrotated ellipses onto the
and
planes are thus circles of radius
, centred at
. The parameter is doubled, so that a 0 to
span describes the complete curve. The hypercomplex root
makes an angle
, measured from the origin (
is superimposed in this projection). However, if the reference point is
, this root makes an angle of
with respect to the scalar axis, as shown in
Figure 3. The
root (and its superimposed projection
) exhibit an analogous behaviour. The parametric curve
, drawn in red in
Figure 3, is therefore trisected by the hypercomplex roots.
There is a
phase increase in each director angle, as the closed curves at 45° with respect to the
axes return to an arbitrary departure point. The geometrical descriptions in
Figure 2,
Figure 3 and Figure 5, as well as in ([
6], Figure 3), suggest that the equal director roots or powers go around the point
. However,
is not a singularity. For
, the parametric curve is equal to
, but this point should not be included in the curve. Recall that zero is not in the cusphere, because the unit magnitude surface cannot include a point that has zero magnitude. Nonetheless, the cusphere points come arbitrarily close to zero. In this sense, the 45° curves come as close as possible to the singularity but jump it, rather than going around it. It is too large a leap to discuss monodromy when many issues, such as giving an unambiguous meaning to ’going around’ in higher dimensional spaces or the topology of the scator space, need to be addressed first. Nonetheless, this part of the discussion aims to show that some of these ideas seem likely to be meaningful in scator algebra.
5. Fourth Roots of 1
Fourth roots of the multiplicative neutral
are a singular case because spurious nilroots are present from the outset. The 16 possible roots in
, obtained from (
5),
are shown in
Table 2.
The (four) roots 1 and are the square roots doubled period. The and roots with and , respectively, correspond to the complex cyclotomic fourth roots, evaluated on the and planes. The and hypercomplex roots with and have minus sign contributions in the products due to the even rs but are otherwise analogous to the previous roots. When are odd, both director coefficients are odd multiples of . A zero scator is thus obtained in the additive representation. These four odd are spurious nilroots (Corollary 2). Recall that lack of associativity arises if the additive scalar component of a product vanishes. In this case, the first warning came from the , (or ) roots that square to , but their cube has a vanishing scalar. Nonetheless, associativity holds because there is only one non-zero director component in either representation. However, when are both odd, there are two non-zero multiplicative director components, and the products no longer associate in the additive representation.
The set of all fourth roots of one does not satisfy group properties in the additive representation even if nilroots are dismissed, because products of orthogonal roots are zero and associativity between different unit orthogonal roots is not satisfied, i.e.,
. Nonetheless, there are four
and three
cyclic groups and a Klein four group, represented graphically in
Figure 4.
In contrast, consider the multiplicative representation where the product satisfies commutative group properties and the exponent distributes over the factors. In
, the fourth roots of unity are
The 16 possible roots in the multiplicative representation are shown in
Table 3. These 16 elements satisfy Abelian group properties. Its proper subgroups are illustrated in
Figure 4.
Remark 1. In the multiplicative representation, the product is irreducible ([6], Definition 2), that is, it cannot be further simplified in this representation since the product has already been performed by having evaluated the sum of arguments. In particular, the multiplicative representation of a scator with multiplicative variables is , and its magnitude is 1. The power series of the
function is actually the additive representation of this function together with the series expansion of the trigonometric functions. If no reference is made to the power series of the
function, as in the previous remark, the question of course arises as to the meaning of this function. The complex exponential can be characterized in several other ways; two of these characterizations have been shown to be also true for the
function in
: (i) the components exponential function
is the scator holomorphic function
of the scator variable
, solution to the differential equation [
11]
, where
. (ii) The components exponential function maps scator addition onto scator multiplication ([
6], Lemma 2.1),
. Therefore, the components exponential function makes sense even if its series representation is not invoked. However, the equivalence between these characterizations in
has not been established.
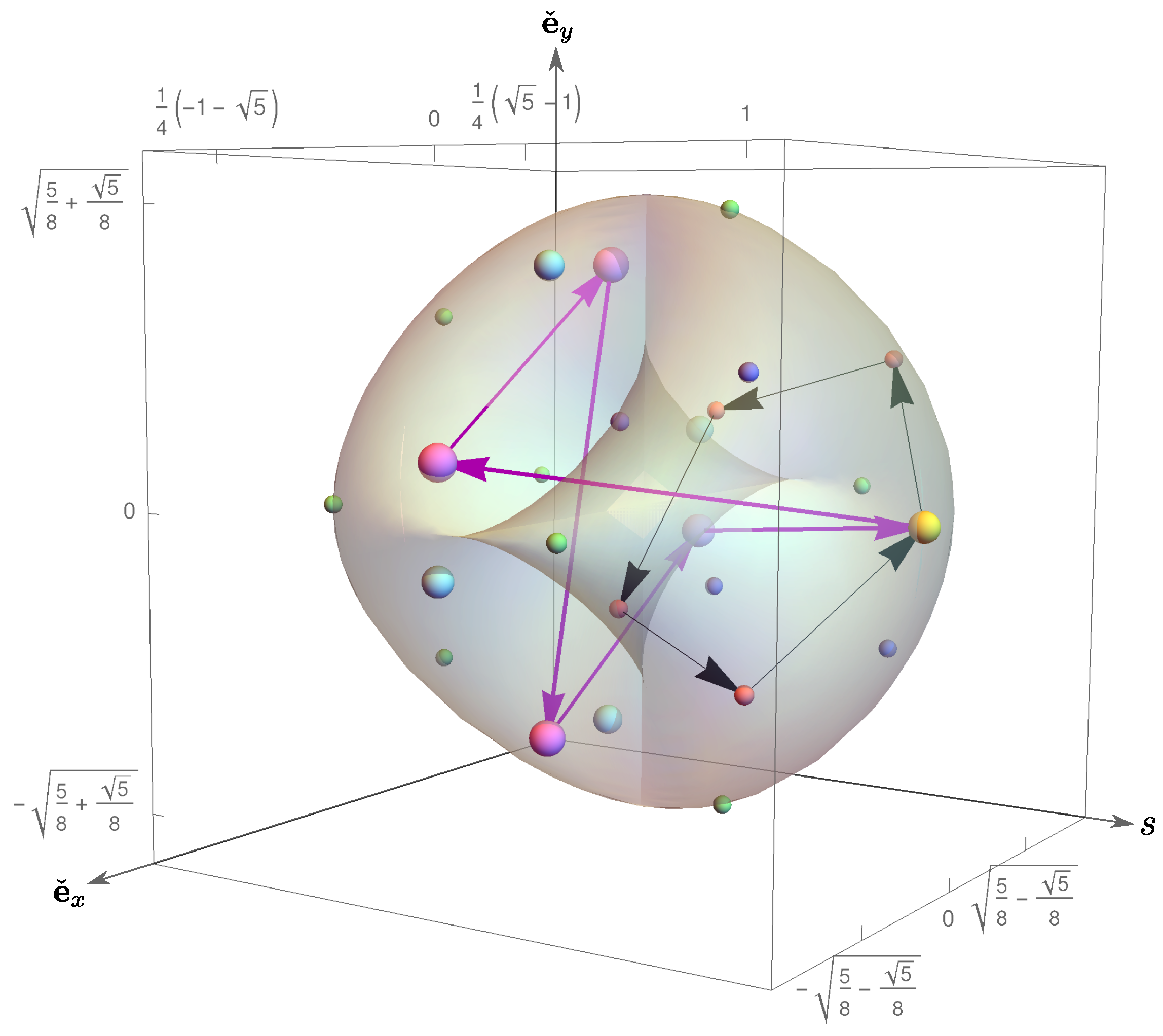
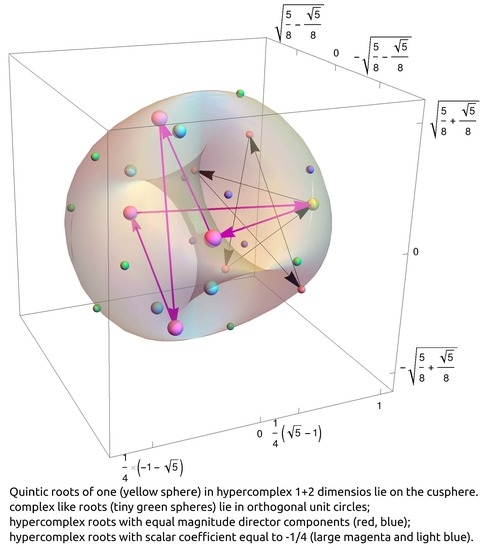
6. Fifth Roots of 1
The Victoria equation for the fifth root of
in
is
There are
possible roots, grouped into six groups with five elements (
), all of them sharing, of course, the neutral element,
. The roots, labelled
with
from 0 to 4, are summarized in
Table 4. Two groups,
and
, correspond to the complex cyclotomic fifth roots, evaluated on the
and
planes. Two other groups correspond to hypercomplex roots with equal magnitude director coefficients that lie on the
planes with respect to the
axes. These roots have positive
s values,
. The group of roots
,
,
,
, and
has director components with equal signs, both positive or both negative. These roots are shown in red in
Figure 5, joined by a pentagon with black arrows. The group
,
,
,
, and
has director components with equal magnitudes but opposite signs (purple in
Figure 5). They exhibit the same structure of the iso-director magnitude groups of the cubic roots. There are now another two sets with a structure that is not present in roots of unity with
,
,
,
,
,
,
,
, and
. All eight roots, depicted in magenta and light blue in
Figure 5, have the same negative additive scalar coefficient,
. These eight roots lie on the
plane, but
does not lie in this plane. Therefore, the five elements of these two groups no longer lie on a plane as in previous cases. The
proper Abelian subgroups of these roots are depicted in
Figure 6.
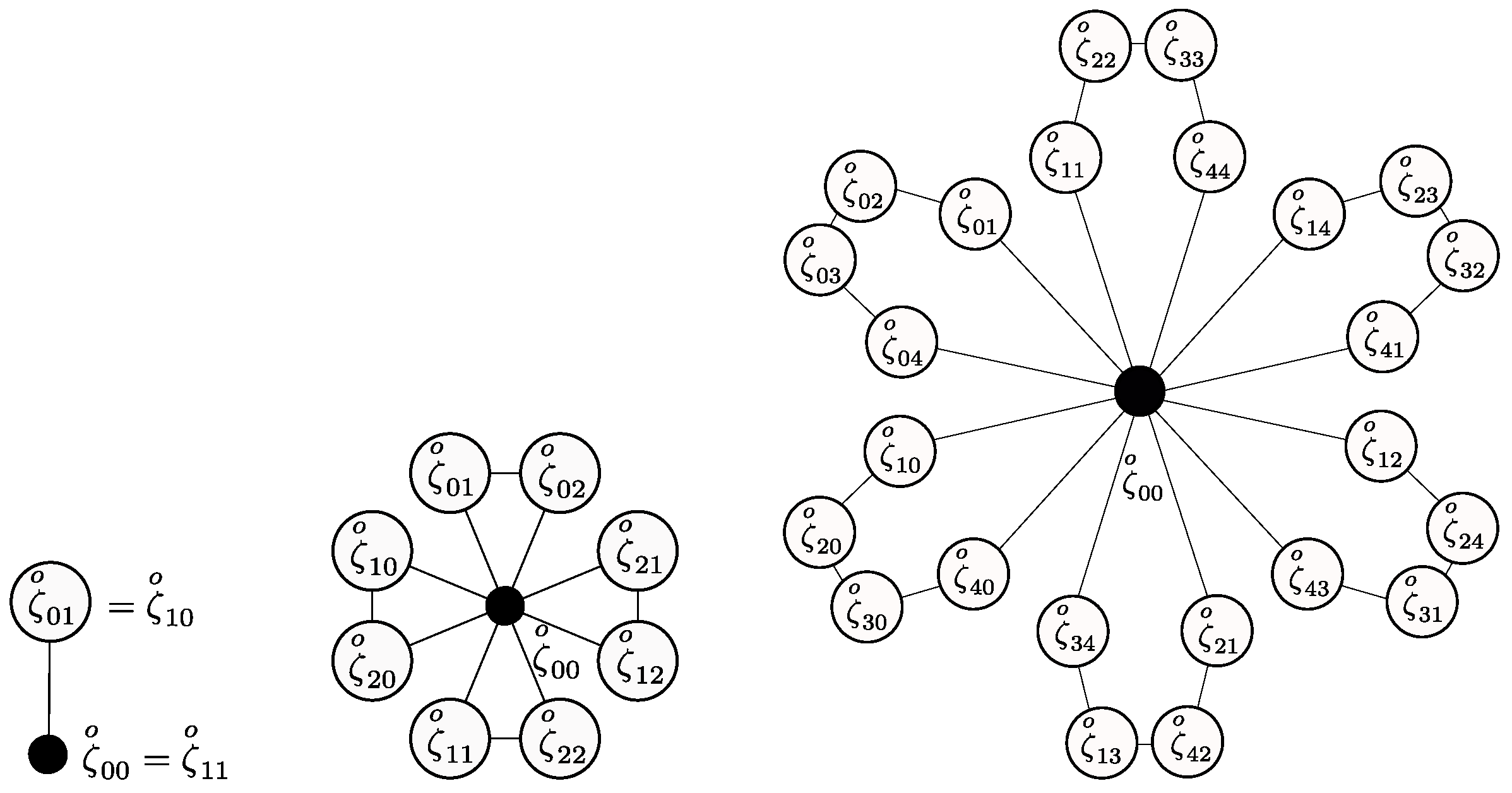
7. qth Roots of 1
A scator raised to the power has possible roots. The roots are obtained from the Victoria root Theorem 2 by evaluation of each of the s, from 0 to q, and for j, from 1 to n. In the multiplicative representation, the roots are obtained from Theorem 1. Label the roots for identification with subindices to , .
The roots of unity, provided that associativity of the factors is ensured, can be grouped in cyclic sets that satisfy Abelian group properties with
q elements in each set.
elements with different
s belong only to one such set, and the element
is the identity element, common to all groups. The
roots are grouped into
g sets; thus,
, the number of cyclic groups with
q elements, is then
For example, for scators in
, there are two director components; then,
. For scators in
,
, there are, in particular,
cube roots that can be grouped into
sets. The elements of a group are obtained by evaluation of the
p powers of any root in the group except the identity, for
p from 0 to
, modulo
q. Examples for
q equalling 2, 3, and 5 are shown in
Figure 6. For example, let
be a fifth root of
: the square is
, the cube
, the fourth power
, and the fifth power
. For
, this sequence produces a pentagon, similar to the one depicted with black arrows in
Figure 5. The sequence
,
,
,
, and
produces a star-like figure, etc. In the multiplicative representation, this scheme is true for any of the
roots of unity, since the product is associative. However, in the additive representation, for even
roots of unity, the number of roots is reduced, and the set of all roots for a given
q does not satisfy group properties. There are, nonetheless, cyclic group subsets within the sets of even
q roots, as shown in
Figure 4.
Director Conjugate Roots
The conjugate of a scator leaves the scalar part invariant and changes the sign of the director coefficients, either in the additive or the multiplicative representation. The
conjugate or
director conjugate of a scator
is defined by the negative of the
director component, while all the remaining components are left unchanged [
14]. In the present context, we refer to the
period conjugate when the
coefficient of a director is left unaltered, but the fundamental periodicity
changes sign,
.
Lemma 2. If is a root of , a period conjugate scator of this root is also a root for any from 1 to n. There are director period conjugate roots for each ordered set of d non-zero elements,.
Proof. Since
is a root, in the multiplicative representation,
so that
Let
in the
term be modified to
,
, so that
. Evaluate
to the power
q using Theorem 1,
but
; thus,
. Therefore,
is also a root. Since any or several
s can be changed by their negative value independently, given a root
,
roots are obtained from the evaluation of
for the ordered sets of
s different from zero from 1 to
n. For
,
For , ;
For , □
Director conjugation is applied independently to each director component. Only
s from 1 to
, if
q is odd, or
, if
q is even, need to be considered, since
is equal to
. For roots of
, period director conjugation and director conjugation give the same expressions since
for all
j. The fifth roots of
are shown as an example in
Figure 7, grouped into nine cyclic sets under director conjugation. These sets clearly do not satisfy group properties, except the trivial single element
set. Nonetheless, they are cyclic under director conjugation, alternating the conjugation components. For the fifth root, it suffices to consider
non-zero values for
. For
,
, there are four possible combinations of
. Each of these four sets have
elements. Take, for instance, the set joined by a horizontal rectangle on the left in
Figure 7; the
element first component conjugation is
. The superstar followed by a number notation means the conjugation of the corresponding number position. Negative indices are mod 5 mapped onto positive indices for ease of comparison with
Figure 6. Subsequent elements of these sets upon director conjugation are
,
, and
. This set of four elements is also depicted on the right in
Figure 7. This clockwise cycle, seen from the positive
s axis, becomes an anticlockwise cycle if director conjugation is initiated with the second component. Scator conjugation alternates between diagonal elements in these sets, i.e.,
. Since conjugation is a second order involution, if applied twice, it leaves the element invariant. For
,
, there are two possible combinations of
. Each of these two sets have
elements. Another two sets of two elements are obtained for
. The multiplicative identity
is invariant under conjugation and is the only element in the remaining set.
To summarize the results in this last section, given a root of in , its scator conjugate (changing signs to all director components) is also a root. This result is analogous to complex conjugate roots of one in . Furthermore, the director conjugate of a root (changing sign only to the director component) is also a root. Since the director conjugate can be subsequently evaluated for any another component, say , and so on, all director conjugate possibilities of a root are also roots. These roots are a higher dimensional generalization of complex conjugate roots in a scator dimensional space.