Oscillation of Repeated Max-Weighted Power Mean Compositions of Fuzzy Matrices

Abstract

In the literature, the powers of a square fuzzy matrix with respect to the max-weighted power mean composition have been shown to always converge. This study considers the max-weighted power mean composition for a sequence of fuzzy matrices. It reveals that the repeated compositions of a sequence of n fuzzy matrices oscillate among n fuzzy matrices once the number of compositions exceeds a certain threshold. The previous finding can be considered as a special case of this study with n = 1.

1. Introduction

In fuzzy set theory, fuzzy relations describe vague relationships among elements. Furthermore, the composition of fuzzy relations provides a way to infer new fuzzy relations. A fuzzy relation can be represented using a fuzzy matrix, where all elements in the fuzzy matrix have values in the closed interval [0,1]. Let “$\odot$” be a binary operator defined on [0,1]² → [0,1]. Then, with “$\odot$”, the composition of an m × n fuzzy matrix $A=\left[a_{ij}\right]$ and an n × s fuzzy matrix $B=\left[b_{jk}\right]$ infers a new fuzzy relation, as given below:

$${\left[A\odot B\right]}_{ik}=\underset{j=1,2,\dots ,n}{\max }\left\{a_{ij}\odot b_{jk}\right\}, i=1,2,\dots ,m \mathrm{and} k=1,2,\dots ,s.$$

(1)

Assuming that $A$ is a square fuzzy matrix, the powers of $A$ with respect to the “$\odot$” operation are defined as follows:

$$A^k=\left\{\begin{array}{cc}A & \mathrm{if} k=1,\\ A^{k-1}\odot A& \mathrm{if} k>1.\end{array}\right.$$

(2)

In the literature, the limiting behavior of consecutive powers of a square fuzzy matrix has been widely studied for various “$\odot$” operations, including max-min [1,2,3,4,5,6], max-product [7,8,9,10], max-Archimedean t-norm [11], max-t-norm [12], max-weighted power mean [13] and a convex combination of max-min and max-arithmetic mean operations [14]. Thomason [6] first proved that the sequence of consecutive powers of a fuzzy matrix with a max-min composition either converges to an idempotent matrix or oscillates with a finite period. Pang and Guu [10] later showed that the limiting behavior of the consecutive powers of a max-product fuzzy matrix relates to the notion of an asymptotic period. Pang [11] further extended this result to develop the sufficient conditions for the powers of a max-Archimedean t-norm fuzzy matrix to converge in finitely many steps. Lur et al. [14] proved that they powers of a fuzzy matrix with respect to a convex combination of max-min and max-arithmetic mean operations are always convergent. Lur et al. [13] also showed that the powers of a fuzzy matrix with respect to the max-weighted power mean composition are always convergent. Notably, the weighted power mean (see Section 2) is more general than the arithmetic mean, and has been used in many applications (e.g., fuzzy information retrieval [15]) to provide more flexibility than the arithmetic mean.

This study investigates the limiting behavior of repeated compositions of a sequence of fuzzy matrices with respect to the max-weighted power mean composition. Given n fuzzy matrices $A_0,A_1,\dots ,A_{n-1}$ and an integer $k\ge n$, the repeated compositions of $A_0,A_1,\dots ,A_{n-1}$ are defined as follows:

$$\mathit{F}\left(A_0,A_1,\dots ,A_{n-1},k\right)=\left\{\begin{array}{cc}{A}_0\otimes A_1\otimes \dots \otimes A_{n-1} & \mathrm{if} k=n\\ \mathit{F}\left(A_0,A_1,\dots ,A_{n-1},k-1\right)\otimes A_{\left(k-1\right)\backslash n}& \mathrm{if} k>n\end{array}\right.$$

(3)

where $k-1$ is the number of compositions, and “$\otimes$” and “\” represent the max-weighted power mean composition and the modulo operation, respectively. Notably, $A_0,A_1,\dots ,A_{n-1}$ are not restricted to square matrices, and the dimensions of these matrices are assumed to be conformable. That is, the number of columns of a matrix $A_i$ equals the number of rows of the matrix $A_{i+1}$ for $i=0$ to n − 2, and the number of columns of the final matrix $A_{n-1}$ in the sequence equals the number of rows of the first matrix $A_0$. This study shows that the repeated compositions of a sequence of n fuzzy matrices oscillate among n fuzzy matrices, each with a period n, once the number of compositions exceeds a certain threshold. If n = 1, then Equation (3) degrades to Equation (2), and the repeated compositions of a square fuzzy matrix converge, same as the results of [13]. Therefore, this study extends the results of Lur et al. [13] from a square fuzzy matrix to a sequence of fuzzy matrices.

Furthermore, this study considers the case of the composition between a square fuzzy matrix $C$ and a repeated sequence of n fuzzy matrices $A_0,A_1,\dots ,A_{n-1}$, as defined below:

$$\mathit{G}\left(C,A_0,A_1,\dots ,A_{n-1},k\right)=\left\{\begin{array}{cc}C\otimes A_0\otimes A_1\otimes \dots \otimes A_{n-1} & \mathrm{if} k=n,\\ \mathit{G}\left(C,A_0,A_1,\dots ,A_{n-1},k-1\right)\otimes A_{\left(k-1\right)\backslash n}& \mathrm{if} k>n.\end{array}\right.$$

(4)

This study shows that $\mathit{G}\left(C,A_0,A_1,\dots ,A_{n-1},k\right)$ and $\mathit{F}\left(A_0,A_1,\dots ,A_{n-1},k\right)$ exhibit the same limiting behavior as k approaches infinity.

2. Preliminaries

The weighted power mean is also called the weighted generalized mean ([16], p. 60). Lur et al. [13] defined the “$\otimes$” operator, based on the weighted power mean, as follows.

Definition 1.

Given$\lambda \in \left(0,1\right)$and$p\in ℝ$, a binary operator“$\otimes$” from [0,1]²→[0,1] is defined as follows:

$$a\otimes b={\left(\mathsf{\lambda }{a}^p+\left(1-\mathsf{\lambda }\right)b^p\right)}^{\frac{1}{p}}, \mathrm{for} \mathrm{all} a,b\in \left[0,1\right].$$

(5)

Notably, to avoid division by zero in Equation (5), if $p<0$, then both a and b must be positive. The value of $a\otimes b$ is shifted toward min{a,b} (or max{a,b}) for small (or large) $p$. As $p$ approaches “$-$∞” and “∞”, $a\otimes b$ is equivalent to “min” and “max”, respectively. If $\mathsf{\lambda }=\frac{1}{2}$ and $p=-1$, then $a\otimes b$ equals the harmonic mean; if $\mathsf{\lambda }=\frac{1}{2}$ and $p\to 0$, then $a\otimes b$ equals the geometric mean; if $\mathsf{\lambda }=\frac{1}{2}$ and $p=1$, then $a\otimes b$ equals the arithmetic mean; and if $\mathsf{\lambda }=\frac{1}{2}$ and $p=1$, then $a\otimes b$ equals the quadratic mean. To calculate the max-weighted power mean composition of two fuzzy matrices, simply use “$\otimes$” for “$\odot$” in Equation (1).

Lemma 1 shows the convergence behavior of the powers of a fuzzy matrix with respect to the max-weighted power mean composition.

Lemma 1.

([13]) Let $A$ be an m × m fuzzy matrix. Then,

(1)

$\underset{k\to \infty }{\lim }{A}^k=\widehat{A}$exists.

(2)

For each$1\le j\le m$,${\widehat{A}}_{rj}={\widehat{A}}_{sj}$for all$1\le r,s\le m$.

3. Oscillation of Repeated Compositions of Two Fuzzy Matrices

3.1. Case of a Repeated Sequence of Two Fuzzy Matrices

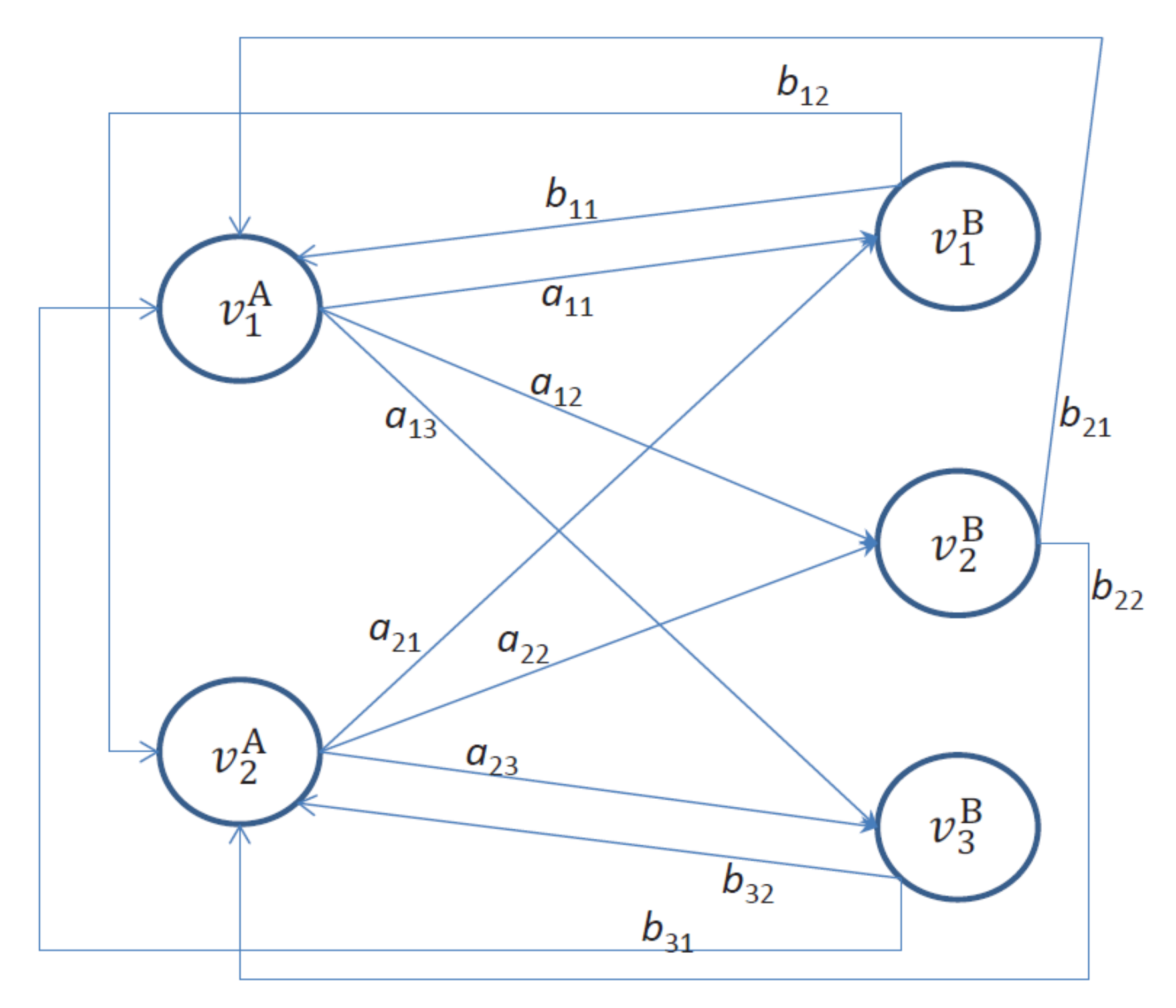
For ease of exposition, first consider the composition of a repeated sequence of two fuzzy matrices $A={\left[a_{ij}\right]}_{mn}$ and $B={\left[b_{ij}\right]}_{nm}$, i.e., the case of Equation (3) with n = 2. A weighted directed graph corresponding to $\mathit{F}\left(A,B,k\right)$ is defined as $\mathit{D}\left(A,B\right)=\left(V,E\right),$ where $V=V^A\cup V^B$ is the set of vertices with $V^A=\left\{v_1^A,v_2^A,\dots ,v_m^A\right\}$ and $V^B=\left\{v_1^B,v_2^B,\dots ,v_n^B\right\}$, and $E$ is the set of edges formed by connecting every vertex in $V^A$ to every vertex in $V^B$, and every vertex in $V^B$ to every vertex in $V^A$. The weight of the edge from any vertex $v_i^A\in V^A$ to any vertex $v_j^B\in V^B$ is the element $a_{ij}$ in matrix $A$, while the weight of the edge from $v_j^B$ to $v_i^A$ is the element $b_{ji}$ in matrix $B$. Obviously, $\mathit{F}\left(A,B,k\right)$ and $\mathit{F}\left(B,A,k\right)$ correspond to the same graph $\mathit{D}\left(A,B\right)$.

Example 1.

Let$A=\left(\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\end{array}\right)$and$B=\left(\begin{array}{cc}{b}_{11}& b_{12}\\ b_{21}& b_{22}\\ b_{31}& b_{32}\end{array}\right)$. The weighted directed graph$\mathit{D}\left(A,B\right)$corresponding to$\mathit{F}\left(A,B,k\right)$is shown inFigure 1.

A k-path L_k is a path of k edges in $\mathit{D}\left(A,B\right)$. Obviously, if k is an even (or odd) number, then a k-path starting from a vertex in $V^A$ must end at a vertex in $V^A$ (or $V^B$). The weight of L_k is denoted as w(L_k) and is defined by performing the “$\otimes$” operation on the weights of the edges in L_k, following the order of the edges along the path. For example, if k is an even number, then the weights of the k-path $v_{i_0}^A⟶v_{i_1}^B⟶v_{i_2}^A⟶\dots ⟶v_{i_{k-1}}^B⟶v_{i_k}^A$ and the k-path $v_{i_0}^B⟶v_{i_1}^A⟶v_{i_2}^B⟶\dots ⟶v_{i_{k-1}}^A⟶v_{i_k}^B$ are $a_{i_0{i}_1}\otimes b_{i_1{i}_2}\otimes a_{i_2{i}_3}\otimes \dots \otimes b_{i_{k-1}{i}_k}$ and $b_{i_0{i}_1}\otimes a_{i_1{i}_2}\otimes b_{i_2{i}_3}\otimes \dots \otimes a_{i_{k-1}{i}_k}$, respectively. If k is an odd number, then the weights of the k-path $v_{i_0}^A⟶v_{i_1}^B⟶v_{i_2}^A⟶\dots ⟶v_{i_{k-1}}^A⟶v_{i_k}^B$ and the k-path $v_{i_0}^B⟶v_{i_1}^A⟶v_{i_2}^B⟶\dots ⟶v_{i_{k-1}}^B⟶v_{i_k}^A$ are $a_{i_0{i}_1}\otimes b_{i_1{i}_2}\otimes a_{i_2{i}_3}\otimes \dots \otimes a_{i_{k-1}{i}_k}$ and $b_{i_0{i}_1}\otimes a_{i_1{i}_2}\otimes b_{i_2{i}_3}\otimes \dots \otimes b_{i_{k-1}{i}_k}$, respectively.

Example 2.

Consider the weighted directed graph$\mathit{D}\left(A,B\right)$inFigure 1. The path$v_2^A⟶v_1^B⟶v_2^A$is a 2-path, and its weight equals$a_{21}\otimes b_{12}$. The path$v_2^B⟶v_1^A⟶v_2^B⟶v_2^A$is a 3-path, and its weight equals$b_{21}\otimes a_{12}\otimes b_{22}$.

Lemma 2 shows that $\mathit{F}\left(A,B,k\right)$ can be calculated using the k-paths in $\mathit{D}\left(A,B\right)$.

Lemma 2.

Let$A={\left[a_{ij}\right]}_{mn}$and$B={\left[b_{ij}\right]}_{nm}$be two fuzzymatrices, and${\left[.\right]}_{ij}$denote the component in the ith row and the jth column of a matrix. Then, [$\mathit{F}\left(A,B,k\right)$]_ij = max{w(L_k): L_k is a k-path from vertex $v_i^A\in V^A$ to vertex $v_j^A\in V^A$ (when k is even) or vertex $v_j^B\in V^B$ (when k is odd)}.

Proof. 

Let M = max{w(L_k): L_k is a k-path from vertex $v_i^A\in V^A$ to vertex $v_j^A$ or vertex $v_j^B$}. Proceed by induction on k. The assertion is true for k = 2. Assume that the assertion is true for k$-$ 1. Consider the case of k being an even number. Choose 1≤ s≤ n such that:

$${\left[\mathit{F}\left(A,B,k-1\right)\right]}_{is}\otimes {\left[B\right]}_{sj}=\underset{1\le t\le n}{\max }{\left[\mathit{F}\left(A,B,k-1\right)\right]}_{it}\otimes {\left[B\right]}_{tj}={\left[\mathit{F}\left(A,B,k\right)\right]}_{ij}$$

By induction hypothesis, there is a (k − 1)-path $L_{k-1}=\left(\left(v_{i_0}^A=v_i^A\right)⟶v_{i_1}^B⟶\dots ⟶\left(v_{i_{k-1}}^B=v_s^B\right)\right)$ such that ${\left[\mathit{F}\left(A,B,k-1\right)\right]}_{is}=w\left(L_{k-1}\right)$. Hence:

$${\left[\mathit{F}\left(A,B,k\right)\right]}_{ij}=w\left(L_{k-1}\right)\otimes b_{sj}=a_{i_0{i}_1}\otimes b_{i_1{i}_2}\otimes \dots \otimes a_{i_{k-2}{i}_{k-1}}\otimes b_{sj}=w\left(L_k\right),$$

where $L_k=\left(\left(v_{i_0}^A=v_i^A\right)⟶v_{i_1}^B⟶\dots ⟶\left(v_{i_{k-1}}^B=v_s^B\right)⟶\left(v_{i_k}^A=v_j^A\right)\right)$. This implies ${\left[\mathit{F}\left(A,B,k\right)\right]}_{ij}\le M.$ On the other hand, let $L_k=\left(\left(v_{i_0}^A=v_i^A\right)⟶v_{i_1}^B⟶\dots ⟶v_{i_{k-1}}^B⟶\left(v_{i_k}^A=v_j^A\right)\right)$ be given arbitrarily, and $L_{k-1}=\left(\left(v_{i_0}^A=v_i^A\right)⟶v_{i_1}^B⟶\dots ⟶v_{i_{k-1}}^B\right)$be derived subsequently. Then:

$$w\left(L_k\right)=a_{i_0{i}_1}\otimes b_{i_1{i}_2}\otimes \dots \otimes a_{i_{k-2}{i}_{k-1}}\otimes b_{i_{k-1}{i}_k}$$

By induction hypothesis:

$${\left[\mathit{F}\left(A,B,k-1\right)\right]}_{i_0{i}_{k-1}}\ge w\left(L_{k-1}\right)=a_{i_0{i}_1}\otimes b_{i_1{i}_2}\otimes \dots \otimes a_{i_{k-2}{i}_{k-1}}$$

Hence:

$$w\left(L_k\right)\le {\left[\mathit{F}\left(A,B,k-1\right)\right]}_{i_0{i}_{k-1}}\otimes b_{i_{k-1}{i}_k}\le {\left[\mathit{F}\left(A,B,k\right)\right]}_{ij}$$

This result implies ${\left[\mathit{F}\left(A,B,k\right)\right]}_{ij}\ge M.$ Hence,${\left[\mathit{F}\left(A,B,k\right)\right]}_{ij}=M$ holds for an even k. The proof for ${\left[\mathit{F}\left(A,B,k\right)\right]}_{ij}=M$ where k is odd is similar, and thus is omitted herein. □

Remark 1.

The above proof extends the proof of Lemma 2 in Lur et al. [14] from powers of a square fuzzy matrix to repeated compositions of a sequence of two fuzzy matrices.

Theorem 1.

Let$A={\left[a_{ij}\right]}_{mn}$and$B={\left[b_{ij}\right]}_{nm}$be two fuzzymatrices and k$\in \mathbb{N}$. Then,

(i)

$\underset{k\to \infty }{\lim }\mathit{F}\left(A,B,2k-\eta \right)={\widehat{E}}_{\eta }$ exists for each $\eta \in \left\{0,1\right\}$.

(ii)

Given$\eta \in \left\{0,1\right\}$and$1\le j\le n$,${\left[{\widehat{E}}_{\eta }\right]}_{rj}={\left[{\widehat{E}}_{\eta }\right]}_{sj}$for all$1\le r,s\le m$.

Proof. 

(i) First, consider the case of $\eta =0$. Fix $1\le r,s\le m$, and let $i_0=r$ and $i_{2k}=s$. Let $L_{2k}=\left(v_{i_0}^A⟶v_{i_1}^B⟶v_{i_2}^A⟶\dots ⟶v_{i_{2k-1}}^B⟶v_{i_{2k}}^A\right)$ be given, and $L_{2k-2}=\left(v_{i_0}^A⟶v_{i_3}^B⟶v_{i_4}^A⟶\dots ⟶v_{i_{2k-1}}^B⟶v_{i_{2k}}^A\right)$ be obtained by removing $v_{i_1}^B$ and $v_{i_2}^A$ from $L_{2k}$. Then:

$$w\left(L_{2k}\right)=a_{i_0{i}_1}\otimes b_{i_1{i}_2}\otimes a_{i_2{i}_3}\otimes b_{i_3{i}_4}\otimes \dots \otimes a_{i_{2k-2}{i}_{2k-1}}\otimes b_{i_{2k-1}{i}_{2k}},$$

and:

$$w\left(L_{2k-2}\right)=a_{i_0{i}_3}\otimes b_{i_3{i}_4}\otimes \dots \otimes a_{i_{2k-2}{i}_{2k-1}}\otimes b_{i_{2k-1}{i}_{2k}}$$

By Definition 1, we have:

$$\begin{array}{l}{\left(w\left(L_{2k}\right)\right)}^p\\ ={\lambda }^{2k-1}{a}_{i_0{i}_1}^p+{\lambda }^{2k-2}\left(1-\lambda \right)b_{i_1{i}_2}^p+{\lambda }^{2k-3}\left(1-\lambda \right)a_{i_2{i}_3}^p+{\lambda }^{2k-4}\left(1-\lambda \right)b_{i_3{i}_4}^p+\dots +\left(1-\lambda \right)b_{i_{2k-1}{i}_{2k}}^p\\ ={\lambda }^{2k-3}{a}_{i_0{i}_3}^p+{\lambda }^{2k-4}\left(1-\lambda \right)b_{i_3{i}_4}^p+\dots +\left(1-\lambda \right)b_{i_{2k-1}{i}_{2k}}^p+{\lambda }^{2k-1}{a}_{i_0{i}_1}^p+{\lambda }^{2k-2}\left(1-\lambda \right)b_{i_1{i}_2}^p+{\lambda }^{2k-3}\left(1-\lambda \right)a_{i_2{i}_3}^p-{\lambda }^{2k-3}{a}_{i_0{i}_3}^p\\ ={\left(w\left(L_{2k-2}\right)\right)}^p+{\lambda }^{2k-1}{a}_{i_0{i}_1}^p+{\lambda }^{2k-2}\left(1-\lambda \right)b_{i_1{i}_2}^p+{\lambda }^{2k-3}\left(1-\lambda \right)a_{i_2{i}_3}^p-{\lambda }^{2k-3}{a}_{i_0{i}_3}^p\\ \le {\left(w\left(L_{2k-2}\right)\right)}^p+{\lambda }^{2k-1}\delta +{\lambda }^{2k-2}\left(1-\lambda \right)\delta +{\lambda }^{2k-3}\left(1-\lambda \right)\delta \\ ={\left(w\left(L_{2k-2}\right)\right)}^p+{\lambda }^{2k-3}\delta ,\end{array}$$

where $\delta =\max \left\{a^p:a \mathrm{is} \mathrm{a} \mathrm{component} \mathrm{in} A \mathrm{or} B\right\}$. Since $L_{2k}$ is an arbitrary path with length 2k, Lemma 2 yields:

$${\left({\left[\mathit{F}\left(A,B,2k\right)\right]}_{rs}\right)}^p\le {\left({\left[\mathit{F}\left(A,B,2k-2\right)\right]}_{rs}\right)}^p+{\lambda }^{2k-3}\delta$$

(6)

Similarly, let $i_0=r$, $i_{2k}=s$, and $L_{2k-2}=\left(v_{i_0}^A⟶v_{i_3}^B⟶v_{i_4}^A⟶\dots ⟶v_{i_{2k-1}}^B⟶v_{i_{2k}}^A\right)$ be a ($2k-2$)-path from vertex $v_r^A$ to $v_s^A$. Choose $1\le i_1\le n$, $1\le i_2\le m$ and set $L_{2k}=\left(v_{i_0}^A⟶v_{i_1}^B⟶v_{i_2}^A⟶v_{i_3}^B⟶v_{i_4}^A⟶\dots ⟶v_{i_{2k-1}}^B⟶v_{i_{2k}}^A\right)$. Then, $L_{2k}$ is a 2k-path from vertex $v_r^A$ to $v_s^A$. Then, we have:

$$\begin{array}{l}{\left(w\left(L_{2k-2}\right)\right)}^p\\ ={\lambda }^{2k-3}{a}_{i_0{i}_3}^p+{\lambda }^{2k-4}\left(1-\lambda \right)b_{i_3{i}_4}^p+\dots +\left(1-\lambda \right)b_{i_{2k-1}{i}_{2k}}^p\\ ={\lambda }^{2k-1}{a}_{i_0{i}_1}^p+{\lambda }^{2k-2}\left(1-\lambda \right)b_{i_1{i}_2}^p+{\lambda }^{2k-3}\left(1-\lambda \right)a_{i_2{i}_3}^p+{\lambda }^{2k-4}\left(1-\lambda \right)b_{i_3{i}_4}^p+\dots +\left(1-\lambda \right)b_{i_{2k-1}{i}_{2k}}^p+{\lambda }^{2k-3}{a}_{i_0{i}_3}^p-{\lambda }^{2k-1}{a}_{i_0{i}_1}^p-{\lambda }^{2k-2}\left(1-\lambda \right)b_{i_1{i}_2}^p-{\lambda }^{2k-3}\left(1-\lambda \right)a_{i_2{i}_3}^p\\ ={\left(w\left(L_{2k}\right)\right)}^p+{\lambda }^{2k-3}{a}_{i_0{i}_3}^p-{\lambda }^{2k-1}{a}_{i_0{i}_1}^p-{\lambda }^{2k-2}\left(1-\lambda \right)b_{i_1{i}_2}^p-{\lambda }^{2k-3}\left(1-\lambda \right)a_{i_2{i}_3}^p\\ \le {\left(w\left(L_{2k}\right)\right)}^p+{\lambda }^{2k-3}\delta \end{array}$$

where $\delta =\max \left\{a^p:a \mathrm{is} \mathrm{a} \mathrm{component} \mathrm{in} A \mathrm{or} B\right\}$. Then, Lemma 2 yields:

$${\left({\left[\mathit{F}\left(A,B,2k-2\right)\right]}_{rs}\right)}^p\le {\left({\left[\mathit{F}\left(A,B,2k\right)\right]}_{rs}\right)}^p+{\lambda }^{2k-3}\delta$$

(7)

Equations (6) and (7) yield:

$$\left|{\left({\left[\mathit{F}\left(A,B,2k\right)\right]}_{rs}\right)}^p-{\left({\left[\mathit{F}\left(A,B,2k-2\right)\right]}_{rs}\right)}^p\right|\le {\lambda }^{2k-3}\delta$$

Fix $\breve{N}$ as an even number. For all even numbers $N>\breve{N}$, we have:

$$\begin{array}{l}\left|{\left({\left[\mathit{F}\left(A,B,N\right)\right]}_{rs}\right)}^p-{\left({\left[\mathit{F}\left(A,B,\breve{N}\right)\right]}_{rs}\right)}^p\right|\\ \le \left|{\left({\left[\mathit{F}\left(A,B,N\right)\right]}_{rs}\right)}^p-{\left({\left[\mathit{F}\left(A,B,N-2\right)\right]}_{rs}\right)}^p\right|\\ +\left|{\left({\left[\mathit{F}\left(A,B,N-2\right)\right]}_{rs}\right)}^p-{\left({\left[\mathit{F}\left(A,B,N-4\right)\right]}_{rs}\right)}^p\right|\\ +\dots +\left|{\left({\left[\mathit{F}\left(A,B,\breve{N}+2\right)\right]}_{rs}\right)}^p-{\left({\left[\mathit{F}\left(A,B,\breve{N}\right)\right]}_{rs}\right)}^p\right|\\ \le {\lambda }^{N-3}\delta +{\lambda }^{N-5}\delta +\dots +{\lambda }^{\breve{N}-1}\delta \\ =\frac{\left({\lambda }^{\breve{N}-1}\delta \right)\left(1-{\lambda }^{\left(N-\breve{N}\right)/2}\right)}{1-{\lambda }^2}\\ \le \frac{{\lambda }^{\breve{N}-1}\delta }{1-{\lambda }^2}\end{array}$$

Since $\mathsf{\lambda }\in \left(0,1\right)$, all sequences $\left\{{\left({\left[\mathit{F}\left(A,B,2k\right)\right]}_{rs}\right)}^p\right\}$ are Cauchy sequences and hence converge. Therefore, there exists a fuzzy matrix ${\widehat{E}}_0$ such that $\underset{k\to \infty }{\lim }\mathit{F}\left(A,B,2k\right)={\widehat{E}}_0.$

To prove the case of $\eta =1$, fix $1\le r\le m$ and $1\le s\le n$, and let $i_0=r$ and $i_{2k-1}=s$. Let $L_{2k-1}=\left(v_{i_0}^A⟶v_{i_1}^B⟶v_{i_2}^A⟶v_{i_3}^B⟶v_{i_4}^A⟶\dots ⟶v_{i_{2k-2}}^A⟶v_{i_{2k-1}}^B\right)$ be given, and $L_{2k-3}=\left(v_{i_0}^A⟶v_{i_3}^B⟶v_{i_4}^A⟶\dots ⟶v_{i_{2k-2}}^A⟶v_{i_{2k-1}}^B\right)$. Then:

$$w\left(L_{2k-1}\right)=a_{i_0{i}_1}\otimes b_{i_1{i}_2}\otimes a_{i_2{i}_3}\otimes b_{i_3{i}_4}\otimes \dots \otimes b_{i_{2k-3}{i}_{2k-2}}\otimes a_{i_{2k-2}{i}_{2k}-1}$$

and:

$$w\left(L_{2k-3}\right)=a_{i_0{i}_3}\otimes b_{i_3{i}_4}\otimes \dots \otimes b_{i_{2k-3}{i}_{2k-2}}\otimes a_{i_{2k-2}{i}_{2k}-1}$$

The rest of the proof is similar to the proof for the case of $\eta =0$, and therefore is omitted herein.

(ii) Only the case of $\eta =0$ is proved here, and the case of $\eta =1$ can be proved similarly. Let $L^{rj}=\left(v_r^A⟶v_{i_1}^B⟶v_{i_2}^A⟶\dots ⟶v_{i_{2k-1}}^B⟶v_j^A\right)$ be a 2k-path from vertex $v_r^A$ to vertex $v_j^A$ and $L^{sj}=\left(v_s^A⟶v_{i_1}^B⟶v_{i_2}^A⟶\dots ⟶v_{i_{2k-1}}^B⟶v_j^A\right)$ be a 2k-path from vertex $v_s^A$ to vertex $v_j^A$. Then:

$$w\left(L^{rj}\right)=a_{r{i}_1}\otimes b_{i_1{i}_2}\otimes a_{i_2{i}_3}\otimes b_{i_3{i}_4}\otimes \dots \otimes a_{i_{2k-2}{i}_{2k-1}}\otimes b_{i_{2k-1}j}$$

and:

$$w\left(L^{sj}\right)=a_{s{i}_1}\otimes b_{i_1{i}_2}\otimes a_{i_2{i}_3}\otimes b_{i_3{i}_4}\otimes \dots \otimes a_{i_{2k-2}{i}_{2k-1}}\otimes b_{i_{2k-1}j}$$

By the same argument as the proof of (i), we have:

$$\left|{\left(w\left(L^{rj}\right)\right)}^p-{\left(w\left(L^{sj}\right)\right)}^p\right|\le {\lambda }^{2k-1}\delta$$

From (i), we deduce ${\left({\left[{\widehat{E}}_0\right]}_{rj}\right)}^p={\left({\left[{\widehat{E}}_0\right]}_{sj}\right)}^p$, which implies ${\left[{\widehat{E}}_0\right]}_{rj}={\left[{\widehat{E}}_0\right]}_{sj}$.  □

Remark 2.

The above proof follows the proof for Theorem 1 of [13], except that in Theorem 1 we consider two fuzzy matrices of the correct sizes instead of just one square fuzzy matrix.

Remark 3.

The sequence of repeated compositions of the two fuzzy matrices $A$and$B$, once the number of compositions exceeds a certain threshold, is formed by two interleaving fuzzy matrices${\widehat{E}}_0$and${\widehat{E}}_1$.

Example 3.

Let$A=\left[\begin{array}{ccc}0.7& 0.8& 0.9\\ 0.3& 0.6& 0.1\end{array}\right]$and$B=\left[\begin{array}{cc}0.1& 0.2\\ 0.5& 0.4\\ 0.3& 0.8\end{array}\right]$. Given“$\otimes$” with$p=2$and$\lambda =0.5$, we have:

$$\begin{array}{l}\mathit{F}\left(A,B,2k\right)={\widehat{E}}_0=\left[\begin{array}{cc}0.6164414003& 0.7858116823\\ 0.6164414003& 0.7858116823\end{array}\right] \mathrm{for} k\ge 17, \mathrm{and} \\ \mathit{F}\left(A,B,2k-1\right)={\widehat{E}}_1=\left[\begin{array}{ccc}0.6595452979& 0.7141428429& 0.7713624310\\ 0.6595452979& 0.7141428429& 0.7713624310\end{array}\right] \mathrm{for} k\ge 19. \end{array}$$

Given“$\otimes$” with$p=1$and$\lambda =0.5$, we have:

$$\begin{array}{l}\mathit{F}\left(A,B,2k\right)={\widehat{E}}_0=\left[\begin{array}{cc}0.6& 0.775\\ 0.6& 0.775\end{array}\right] \mathrm{for} k\ge 16, \mathrm{and}\\ \mathit{F}\left(A,B,2k-1\right)={\widehat{E}}_1=\left[\begin{array}{ccc}0.65& 0.7& 0.75\\ 0.65& 0.7& 0.75\end{array}\right] \mathrm{for} k\ge 17. \end{array}$$

Given“$\otimes$” with$p=0.5$and$\lambda =0.5$, we have:

$$\begin{array}{l}\mathit{F}\left(A,B,2k\right)={\widehat{E}}_0=\left[\begin{array}{cc}0.5922024587& 0.7687276485 \\ 0.5922024587& 0.7687276485\end{array}\right] \mathrm{for} k\ge 17, \mathrm{and} \\ \mathit{F}\left(A,B,2k-1\right)={\widehat{E}}_1=\left[\begin{array}{ccc}0.6449751870& 0.6922024587& 0.7380787687\\ 0.6449751870& 0.6922024587& 0.7380787687\end{array}\right] \mathrm{for} k\ge 18.\end{array}$$

Given“$\otimes$” with$p=-0.5$and$\lambda =0.5$, we have:

$$\begin{array}{l}\mathit{F}\left(A,B,2k\right)={\widehat{E}}_0=\left[\begin{array}{cc}0.5778656157& 0.7542903969\\ 0.5778656157& 0.7542903969\end{array}\right] \mathrm{for} k\ge 17, \mathrm{and} \\ \mathit{F}\left(A,B,2k-1\right)={\widehat{E}}_1=\left[\begin{array}{ccc}0.6345486624& 0.6754446797& 0.7123893035\\ 0.6345486624& 0.6754446797& 0.7123893035\end{array}\right] \mathrm{for} k\ge 18. \end{array}$$

Given“$\otimes$” with$p=-2$and$\lambda =0.5$, we have:

$$\begin{array}{l}\mathit{F}\left(A,B,2k\right)={\widehat{E}}_0=\left[\begin{array}{cc}0.5621250091& 0.7291175068\\ 0.5621250091& 0.7291175068\end{array}\right] \mathrm{for} k\ge 18 \mathrm{and} \\ \mathit{F}\left(A,B,2k-1\right)={\widehat{E}}_1=\left[\begin{array}{ccc}0.6198442739& 0.6552027920& 0.6742550437\\ 0.6198442739& 0.6552027920& 0.6742550437\end{array}\right] \mathrm{for} k\ge 19.\end{array}$$

Notably, the threshold of k in each example above was derived by computing all cases of$k$=1,2,3,… until the value of$\mathit{F}\left(A,B,2k\right)$or$\mathit{F}\left(A,B,2k-1\right)$stopped changing.

Theorem 2.

Let$A=\left[a_{ij}\right]$and$B=\left[b_{ij}\right]$be two$m\times m$fuzzymatrices and k$\in \mathbb{N}$. Then, both$\underset{k\to \infty }{\lim }\mathit{F}\left(A,B,2k\right)=\underset{k\to \infty }{\lim }\mathit{F}\left(B,A,2k-1\right)$and$\underset{k\to \infty }{\lim }\mathit{F}\left(A,B,2k-1\right)=\underset{k\to \infty }{\lim }\mathit{F}\left(B,A,2k\right)$hold.

Proof. 

Fix $1\le r,s\le m$ and $i_{2k}=s$. Let $L_{2k}=\left(v_r^A⟶v_{i_1}^B⟶v_{i_2}^A⟶\dots ⟶v_{i_{2k-1}}^B⟶v_{i_{2k}}^A\right)$ be a given path starting from a vertex $v_r^A\in V^A$. Let $L_{2k-1}=\left(v_r^B⟶v_{i_2}^A⟶v_{i_3}^B⟶v_{i_4}^A⟶\dots ⟶v_{i_{2k-1}}^B⟶v_{i_{2k}}^A\right)$ be obtained by replacing the edges $v_r^A⟶v_{i_1}^B$ and $v_{i_1}^B⟶v_{i_2}^A$ in $L_{2k}$ with the edge $v_r^B⟶v_{i_2}^A$. Then:

$$w\left(L_{2k}\right)=a_{r{i}_1}\otimes b_{i_1{i}_2}\otimes a_{i_2{i}_3}\otimes b_{i_3{i}_4}\otimes \dots \otimes a_{i_{2k-2}{i}_{2k-1}}\otimes b_{i_{2k-1}{i}_{2k}}$$

and:

$$w\left(L_{2k-1}\right)=b_{r{i}_2}\otimes a_{i_2{i}_3}\otimes b_{i_3{i}_4}\otimes \dots \otimes a_{i_{2k-2}{i}_{2k-1}}\otimes b_{i_{2k-1}{i}_{2k}}$$

By the same argument as in the proof of (i) of Theorem 1, we have:

$$\left|{\left(w\left(L_{2k}\right)\right)}^p-{\left(w\left(L_{2k-1}\right)\right)}^p\right|\le {\lambda }^{2k-2}\delta$$

and consequently:

$$\left|{\left({\left[\mathit{F}\left(A,B,2k\right)\right]}_{rs}\right)}^p-{\left({\left[\mathit{F}\left(B,A,2k-1\right)\right]}_{rs}\right)}^p\right|\le {\lambda }^{2k-2}\delta$$

Since $\mathsf{\lambda }\in \left(0,1\right)$, $\underset{k\to \infty }{\lim }\mathit{F}\left(A,B,2k\right)=\underset{k\to \infty }{\lim }\mathit{F}\left(B,A,2k-1\right)$ holds. The proof for $\underset{k\to \infty }{\lim }\mathit{F}\left(A,B,2k-1\right)=\underset{k\to \infty }{\lim }\mathit{F}\left(B,A,2k\right)$ is similar to the proof for $\underset{k\to \infty }{\lim }\mathit{F}\left(A,B,2k\right)=\underset{k\to \infty }{\lim }\mathit{F}\left(B,A,2k-1\right)$ above, and thus is omitted.  □

Remark 4.

Given two square fuzzy matrices $A$and$B$of the same size, the limiting behaviors of repeated compositions of the sequence$\left(AB\right)$and of repeated compositions of the sequence$\left(BA\right)$oscillate between the same two fuzzy matrices.

Example 4.

Let$A=\left[\begin{array}{ccc}0.1& 0.6& 0.7\\ 0.2& 0.5& 0.8\\ 0.3& 0.4& 0.9\end{array}\right]$and$B=\left[\begin{array}{ccc}0.8& 1.0& 0.3\\ 0.2& 0.9& 0.4\\ 1.0& 1.0& 0.5\end{array}\right]$. Given“$\otimes$” with$p=1$and$\lambda =0.5$, we have:

$$\begin{gathered} \underset{k\to \infty }{\lim }\mathit{F}\left(B,A,2k\right)=\underset{k\to \infty }{\lim }\mathit{F}\left(B,A,32\right)=\underset{k\to \infty }{\lim }\mathit{F}\left(A,B,2k-1\right)=\underset{k\to \infty }{\lim }\mathit{F}\left(A,B,35\right) \\ =\left[\begin{array}{ccc}0.5666666667& 0.7666666667& 0.8666666667\\ 0.5666666667& 0.7666666667& 0.8666666667\\ 0.5666666667& 0.7666666667& 0.8666666667\end{array}\right] \end{gathered}$$

and:

$$\begin{gathered} \underset{k\to \infty }{\lim }\mathit{F}\left(B,A,2k-1\right)=\underset{k\to \infty }{\lim }\mathit{F}\left(B,A,33\right)=\underset{k\to \infty }{\lim }\mathit{F}\left(A,B,2k\right)=\underset{k\to \infty }{\lim }\mathit{F}\left(A,B,32\right) \\ =\left[\begin{array}{ccc}0.9333333333& 0.9333333333& 0.6833333333\\ 0.9333333333& 0.9333333333& 0.6833333333\\ 0.9333333333& 0.9333333333& 0.6833333333\end{array}\right] \end{gathered}$$

3.2. Case of a Square Fuzzy Matrix and a Repeated Sequence of Two Fuzzy Matrices

This section considers the compositions of a fuzzy matrix $C={\left[c_{ij}\right]}_{mm}$ and a repeated sequence of two fuzzy matrices $A={\left[a_{ij}\right]}_{mn}$ and $B={\left[b_{ij}\right]}_{nm}$, i.e., the case of Equation (4) with n = 2. By following a similar approach for $\mathit{F}\left(A,B,k\right)$ in Section 3.1, we show that $\mathit{G}\left(C,A,B,k\right)$ also exhibits the same limiting behavior as $\mathit{F}\left(A,B,k\right)$. 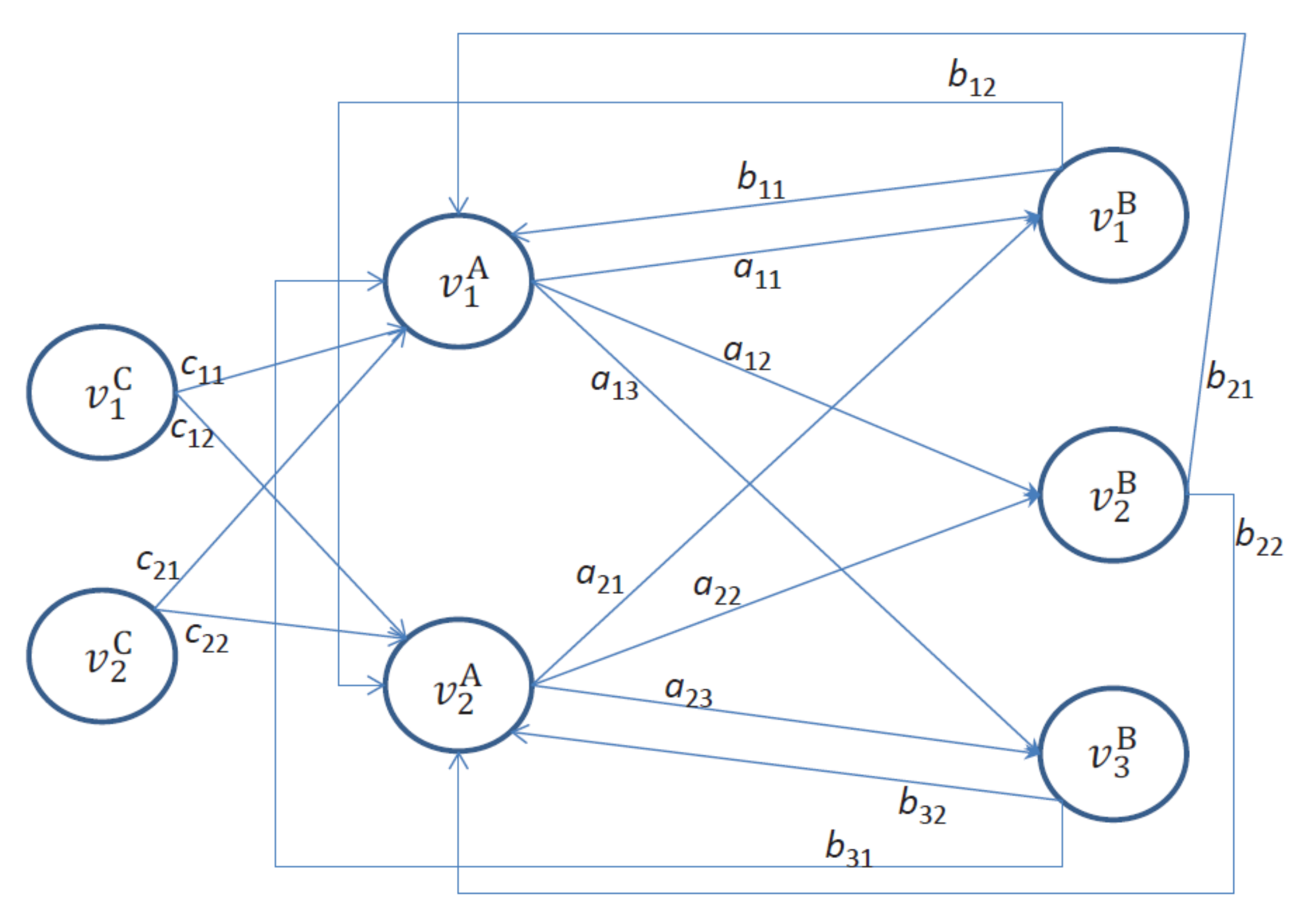First, the weighted directed graph corresponding to $\mathit{G}\left(C,A,B,k\right)$ is denoted as $\overline{\mathit{D}}\left(C,A,B\right)$ and is formed by adding a set of vertices $V^C=\left\{v_1^C,v_2^C,\dots ,v_m^C\right\}$ to the directed graph $\mathit{D}\left(A,B\right)$, along with the edges connecting every vertex $v_i^C\in V^C$ to every vertex $v_j^A\in V^A$ with weight $c_{ij}$, $1\le i,j\le m$.

Example 5.

Consider the fuzzy matrices $A$and$B$in Example 1 and the fuzzy matrix$C=\left[\begin{array}{cc}{c}_{11}& c_{12}\\ c_{21}& c_{22}\end{array}\right]$. The weighted directed graph$\overline{\mathit{D}}\left(C,A,B\right)$corresponding to$\mathit{G}\left(C,A,B,k\right)$is shown inFigure 2.

Similar to Lemma 2, Lemma 3 shows that $\mathit{G}\left(C,A,B,k\right)$ can be calculated using the (k+1)-paths in $\overline{\mathit{D}}\left(C,A,B\right)$. Theorem 3 shows that $\mathit{F}\left(A,B,k\right)$ and $\mathit{G}\left(C,A,B,k\right)$ exhibit the same limiting behavior as k approaches infinity.

Lemma 3.

Let $A={\left[a_{ij}\right]}_{mn}$,$B={\left[b_{ij}\right]}_{nm}$and$C={\left[c_{ij}\right]}_{mm}$be three fuzzy matrices and k$\in \mathbb{N}$. Then,${\left[\mathit{G}\left(C,A,B,k\right)\right]}_{ij}=max\left\{w\left(L_{k+1}\right):L_{k+1}\right.$is a (k+1)-path in$\overline{\mathit{D}}\left(C,A,B\right)$from vertex$v_i^C\in V^C$to vertex$v_j^A\in V^A$(when k is even) or vertex$v_j^B\in V^B$(when k is odd)}.

The proof of Lemma 3 is similar to that of Lemma 2, and thus is omitted herein.

Theorem 3.

Let$A={\left[a_{ij}\right]}_{mn}$,$B={\left[b_{ij}\right]}_{nm}$and$C={\left[c_{ij}\right]}_{mm}$be three fuzzy matrices and k$\in \mathbb{N}$. Then, both$\underset{k\to \infty }{\lim }\mathit{F}\left(A,B,2k\right)=\underset{k\to \infty }{\lim }\mathit{G}\left(C,A,B,2k\right)$and$\underset{k\to \infty }{\lim }\mathit{F}\left(A,B,2k-1\right)=\underset{k\to \infty }{\lim }\mathit{G}\left(C,A,B,2k-1\right)$hold.

Proof. 

Only the equality $\underset{k\to \infty }{\lim }\mathit{F}\left(A,B,2k\right)=\underset{k\to \infty }{\lim }\mathit{G}\left(C,A,B,2k\right)$ is proved here. The equality $\underset{k\to \infty }{\lim }\mathit{F}\left(A,B,2k-1\right)=\underset{k\to \infty }{\lim }\mathit{G}\left(C,A,B,2k-1\right)$ can be proved similarly, and thus is omitted.

Fix $1\le r,s\le m$, and let $s=i_{2k}$. Let $L_{2k+1}=\left(v_r^C⟶v_{i_0}^A⟶v_{i_1}^B⟶v_{i_2}^A⟶\dots ⟶v_{i_{2k-1}}^B⟶v_{i_{2k}}^A\right)$ be a given path starting from a vertex $v_i^C\in V^C$. Let $L_{2k}=\left(v_r^A⟶v_{i_1}^B⟶v_{i_2}^A⟶\dots ⟶v_{i_{2k-1}}^B⟶v_{i_{2k}}^A\right)$ be obtained by replacing the edges $v_r^C⟶v_{i_0}^A$ and $v_{i_0}^A⟶v_{i_1}^B$ in $L_{2k+1}$ with the edge $v_r^A⟶v_{i_1}^B$. Then:

$$w\left(L_{2k+1}\right)=c_{r{i}_0}\otimes a_{i_0{i}_1}\otimes b_{i_1{i}_2}\otimes a_{i_2{i}_3}\otimes b_{i_3{i}_4}\otimes \dots \otimes a_{i_{2k-2}{i}_{2k-1}}\otimes b_{i_{2k-1}{i}_{2k}},$$

and:

$$w\left(L_{2k}\right)=a_{r{i}_1}\otimes b_{i_1{i}_2}\otimes a_{i_2{i}_3}\otimes b_{i_3{i}_4}\otimes \dots \otimes a_{i_{2k-2}{i}_{2k-1}}\otimes b_{i_{2k-1}{i}_{2k}}$$

By Lemma 3 and the same argument as in the proof of (i) of Theorem 1, we have:

$$\left|{\left(w\left(L_{2k+1}\right)\right)}^p-{\left(w\left(L_{2k}\right)\right)}^p\right|\le {\lambda }^{2k-1}\delta$$

and consequently:

$$\left|{\left({\left[\mathit{G}\left(C,A,B,2k\right)\right]}_{rs}\right)}^p-{\left({\left[\mathit{F}\left(A,B,2k\right)\right]}_{rs}\right)}^p\right|\le {\lambda }^{2k-1}\delta$$

where $\delta =\max \left\{a^p:a \mathrm{is} \mathrm{a} \mathrm{component} \mathrm{in} A \mathrm{or} C\right\}$. Since $\mathsf{\lambda }\in \left(0,1\right)$, $\underset{k\to \infty }{\lim }\mathit{F}\left(A,B,2k\right)=\underset{k\to \infty }{\lim }\mathit{G}\left(C,A,B,2k\right)$ holds.  □

Remark 5.

Adding a square fuzzy matrix $C$to a repeated sequence of two fuzzy matrices$A$and$B$does not change the limiting behavior of repeated compositions of the sequence.

Example 6.

Given fuzzy matrices $A$and$B$as in Example 4, let$C=\left[\begin{array}{ccc}0.7& 0.2& 1.0\\ 0.6& 0.8& 0.9\\ 0.5& 0.1& 0.8\end{array}\right]$. Given“$\otimes$” with$p=1$and$\lambda =0.5$, we have:

$$\begin{array}{l}\underset{k\to \infty }{\lim }\mathit{F}\left(A,B,2k\right)=\mathit{F}\left(A,B,32\right)=\underset{k\to \infty }{\lim }\mathit{G}\left(C,A,B,2k\right)=\mathit{G}\left(C,A,B,34\right)=\underset{k\to \infty }{\lim }\mathit{G}\left(A,A,B,2k\right)=\mathit{G}\left(A,A,B,32\right)=\underset{k\to \infty }{\lim }\mathit{G}\left(B,A,B,2k\right)=\mathit{G}\left(B,A,B,32\right), \mathrm{and}\\ \underset{k\to \infty }{\lim }\mathit{F}\left(A,B,2k-1\right)=\mathit{F}\left(A,B,35\right)=\underset{k\to \infty }{\lim }\mathit{G}\left(C,A,B,2k\right)=\mathit{G}\left(C,A,B,31\right)=\underset{k\to \infty }{\lim }\mathit{G}\left(A,A,B,2k\right)=\mathit{G}\left(A,A,B,33\right)=\underset{k\to \infty }{\lim }\mathit{G}\left(B,A,B,2k\right)=\mathit{G}\left(B,A,B,31\right).\end{array}$$

Theorem 4 considers a special case of Theorem 3 where the matrices $A$ and $B$ are the same.

Theorem 4.

Let$A=\left[a_{ij}\right]$and$C=\left[c_{ij}\right]$be two$mm$fuzzymatrices and k$\in \mathbb{N}$. Then, $\underset{k\to \infty }{\lim }{A}^k=\underset{k\to \infty }{\lim }\mathit{G}\left(C,A,A,k\right)$holds.

Proof. 

By Theorem 3, $\underset{k\to \infty }{\lim }\mathit{F}\left(A,A,2k\right)=\underset{k\to \infty }{\lim }\mathit{G}\left(C,A,A,2k\right)$and $\underset{k\to \infty }{\lim }\mathit{F}\left(A,A,2k-1\right)=\underset{k\to \infty }{\lim }\mathit{G}\left(C,A,A,2k-1\right)$ hold. By Lemma 1, $\underset{k\to \infty }{\lim }\mathit{F}\left(A,A,2k\right)=\underset{k\to \infty }{\lim }\mathit{F}\left(A,A,2k-1\right)=\widehat{A}$. Therefore, $\underset{k\to \infty }{\lim }{A}^k=\underset{k\to \infty }{\lim }\mathit{G}\left(C,A,A,k\right)$ holds. □

4. Oscillation of Repeated Compositions of a Sequence of Fuzzy Matrices

This definition of the directed graph corresponding to the expression $\mathit{F}\left(A,B,k\right)$ in Section 3.1 can be generalized for the expression $\mathit{F}\left(A_0,A_1,\dots ,A_{n-1},k\right)$, where $A_0,A_1,\dots ,A_{n-1}$ are n ≥ 1 fuzzy matrices. Let the dimensions of $A_0,A_1,\dots ,A_{n-1}$ be $m_0{m}_1$, $m_1{m}_2$,…,$m_{n-1}{m}_0$, respectively. The directed graph corresponding to the expression $\mathit{F}\left(A_0,A_1,\dots ,A_{n-1},k\right)$ is defined as $\mathit{D}\left(A_0,A_1,\dots ,A_{n-1}\right)=\left(V,E\right),$ where $V={{\displaystyle \cup }}_{i=0,1,\dots ,n-1}{V}^{A_i}$ is the set of vertices with $V^{A_i}=\left\{v_1^{A_i},v_2^{A_i},\dots ,v_{m_i}^{A_i}\right\}$ for i = 0 to n–1, and $E$ is the set of edges formed by connecting each vertex in $V^{A_i}$ to each vertex in $V^{A_{i+1}}$ for i = 0 to n–2 and connecting each vertex in $V^{A_n}$ to each vertex in $V^{A_0}$. Obviously, $\mathit{D}\left(A_0,A_1,\dots ,A_{n-1}\right)=\mathit{D}\left(A_1,A_2,\dots ,A_{n-1},A_0\right)=\dots =\mathit{D}\left(A_{n-1},A_0,A_1,\dots ,A_{n-2}\right)$. Furthermore, Lemma 2 and Theorems 1, 2 and 3 can be extended to a sequence of n ≥ 1 fuzzy matrices, as described in Lemma 4 and Corollaries 1, 2 and 3, respectively.

Lemma 4.

Let $A_0,A_1,\dots ,A_{n-1}$be a sequence of fuzzy matrices and k$\in \mathbb{N}$. Then, ${\left[\mathit{F}\left(A_0,A_1,\dots ,A_{n-1},k\right)\right]}_{ij}=\max \{w\left(L_k\right):L_k$ is a k-path in $\mathit{D}\left(A_0,A_1,\dots ,A_{n-1}\right)$ starting from avertexin$V^A$.}.

Proof. 

Let $\eta =\left(n \mathrm{modulo} k\right)$, then $\eta \in \left\{0,1,\dots ,n-1\right\}.$ For each $\eta \in \left\{0,1,\dots ,n-1\right\}$, Lemma 4 can be proved in the same fashion as the proof of Lemma 2, and therefore the detailed proof is omitted herein. □

Corollary 1.

Let$A_0,A_1,\dots ,A_{n-1}$be a sequence of n fuzzy matrices and k$\in \mathbb{N}$. Then,

(i)

$\underset{k\to \infty }{\lim }\mathit{F}\left(A_0,A_1,\dots ,A_{n-1},nk-\eta \right)={\widehat{E}}_{\eta }$ exists for each $\eta \in \left\{0,1,\dots ,n-1\right\}$.

(ii)

Given $\eta \in \left\{0,1,\dots ,n-1\right\}$ and $1\le j\le n$, ${\left[{\widehat{E}}_{\eta }\right]}_{rj}={\left[{\widehat{E}}_{\eta }\right]}_{sj}$ for all $1\le r,s\le m$, where m is the number of rows in $A_1$.

Proof. 

For each $\eta \in \left\{0,1,\dots ,n-1\right\}$ Corollary 1 can be proved in the same fashion as the proof of Theorem 1, and therefore the detailed proof is omitted herein. □

Remark 6.

The repeated compositions of a sequence of n fuzzy matrices $A_0,A_1,\dots ,A_{n-1}$, once their number of compositions exceeds a certain threshold, oscillate among these n fuzzy matrices,${\widehat{E}}_0, {\widehat{E}}_1,\dots ,{\widehat{E}}_{n-1}$, each with a period of n.

Example 7.

Let$A_0=\left[\begin{array}{ccc}0.7& 0.8& 0.9\\ 0.3& 0.6& 0.1\end{array}\right], A_1=\left[\begin{array}{ccc}0.1& 0.6& 0.7\\ 0.2& 0.5& 0.8\\ 0.3& 0.4& 0.9\end{array}\right]$and$A_2=\left[\begin{array}{cc}0.1& 0.2\\ 0.5& 0.4\\ 0.3& 0.8\end{array}\right]$. Given“$\otimes$” with$p=-2$and$\lambda =0.5$, we have:

$$\begin{array}{l}\mathit{F}\left(A_0,A_1,A_2,3k\right)={\widehat{E}}_0=\left[\begin{array}{cc}0.5446611566& 0.7748500681\\ 0.5446611566& 0.7748500681\end{array}\right], \\ \mathit{F}\left(A_0,A_1,A_2,3k-1\right)={\widehat{E}}_1=\left[\begin{array}{ccc}0.3861342027& 0.6039214949& 0.7519320942\\ 0.3861342027& 0.6039214949& 0.7519320942\end{array}\right],\\ \mathit{F}\left(A_0,A_1,A_2,3k-2\right)={\widehat{E}}_2=\left[\begin{array}{ccc}0.6079208994& 0.6709026617& 0.6589881935\\ 0.6079208994& 0.6709026617& 0.6589881935\end{array}\right]\\ \mathrm{for} k\ge 12.\end{array}$$

Notably, the threshold 12 for k was derived by computing all cases of$k$ =1,2,3,… until the values of$\mathit{F}\left(A,B,3k\right)$,$\mathit{F}\left(A,B,3k-1\right)$, and$\mathit{F}\left(A,B,3k-2\right)$stopped changing.

Corollary 2.

Let$A_0,A_1,\dots ,A_{n-1}$be a sequence of n fuzzy matrices, each with size$mm$and k$\in \mathbb{N}$. Then, $\underset{k\to \infty }{\lim }\mathit{F}\left(A_0,A_1,\dots ,A_{n-1},nk-\eta \right)=\underset{k\to \infty }{\lim }\mathit{F}\left(A_1,A_2,\dots ,A_{n-1},A_0,nk-\eta -1\right)$ for$\eta =0 to n-2$, and $\underset{k\to \infty }{\lim }\mathit{F}\left(A_0,A_1,\dots ,A_{n-1},nk-\left(n-1\right)\right)=\underset{k\to \infty }{\lim }\mathit{F}\left(A_1,A_2,\dots ,A_{n-1},A_0,nk\right).$

The proof of Corollary 2 is similar to that of Theorem 2, and therefore is omitted herein.

Remark 7.

Let$A_0,A_1,\dots ,A_{n-1}$be nsquare fuzzy matricesof the same size. Then, for each of these n sequences ($A_0,A_1,\dots ,A_{n-1}$), ($A_1,A_2,\dots ,A_{n-1},A_0),\dots , and \left(A_{n-1},A_0,A_1,A_2,\dots ,A_{n-2}\right)$, the repeated compositions of the sequence oscillate among the same n fuzzy matrices, once the number of compositions exceeds a certain threshold. Furthermore, each of these n oscillating fuzzy matrices has a period of n.

Example 8.

Let $A_0=\left[\begin{array}{ccc}0.05& 1.0& 0.35\\ 0.16& 0.75& 0.25\\ 0.10& 0.65& 0.16\end{array}\right], A_1=\left[\begin{array}{ccc}0.1& 0.6& 0.7\\ 0.2& 0.5& 0.8\\ 0.3& 0.4& 0.9\end{array}\right]$and $A_2=\left[\begin{array}{ccc}0.75& 0.25& 1.00\\ 0.65& 0.16& 0.52\\ 0.55& 1.00& 0.72\end{array}\right]$. Given “$\otimes$” with $p=1$ and $\mathsf{\lambda }=0.5$, we have:

$$\begin{array}{l}\mathit{F}\left(A_0,A_1,A_2,36+3\check{k}\right)=\mathit{F}\left(A_1,A_2,A_0,35+3\check{k}\right)=\mathit{F}\left(A_2,A_0,A_1,34+3\check{k}\right)=\left[\begin{array}{ccc}0.6857142857& 0.9107142857 & 0.7707142857\\ 0.6857142857& 0.9107142857 & 0.7707142857\\ 0.6857142857& 0.9107142857 & 0.7707142857\end{array}\right],\\ \mathit{F}\left(A_0,A_1,A_2,37+3\check{k}\right)=\mathit{F}\left(A_1,A_2,A_0,36+3\check{k}\right)=\mathit{F}\left(A_2,A_0,A_1,35+3\check{k}\right)=\left[\begin{array}{ccc}0.5353571429& 0.8428571429 & 0.5803571429\\ 0.5353571429& 0.8428571429 & 0.5803571429\\ 0.5353571429& 0.8428571429 & 0.5803571429\end{array}\right] \mathrm{and}\\ \mathit{F}\left(A_0,A_1,A_2,35+3\check{k}\right)=\mathit{F}\left(A_1,A_2,A_0,34+3\check{k}\right)=\mathit{F}\left(A_2,A_0,A_1,33+3\check{k}\right)=\left[\begin{array}{ccc}0.5214285714& 0.6714285714 & 0.8214285714\\ 0.5214285714& 0.6714285714 & 0.8214285714\\ 0.5214285714& 0.6714285714 & 0.8214285714\end{array}\right]\\ \mathrm{for} \mathrm{all} \check{k}\in \mathbb{N}\cup \left\{0\right\}.\end{array}$$

Corollary 3.

Let $C,A_0,A_1,\dots ,A_{n-1}$be n + 1 fuzzy matrices with dimensions $m_0\times m_0$, $m_0\times m_1$, $m_1\times m_2$,…,$m_{n-1}\times m_0$, respectively, and k$\in \mathbb{N}$. Then:

$$\underset{k\to \infty }{\lim }\mathit{G}\left(C,A_0,A_1,\dots ,A_{n-1},nk-\eta \right)=\underset{k\to \infty }{\lim }\mathit{F}\left(A_0,A_1,\dots ,A_{n-1},nk-\eta \right) \mathrm{for} \eta =0 \mathrm{to} n-1.$$

The proof of Corollary 3 resembles that of Theorem 3 and, thus, is omitted here.

Example 9.

Given the fuzzy matrices $A_0$, $A_1$and$A_2$ as in Example 8, $C$ as in Example 6, and“$\otimes$” with$p=1$and$\lambda =0.5$, we have:

$$\begin{array}{l}\mathit{F}\left(A_0,A_1,A_2,36+3\check{k}\right)=\mathit{G}\left(C,A_0,A_1,A_2,33+3\check{k}\right)=\mathit{G}\left(A_0,A_0,A_1,A_2,33+3\check{k}\right)=\mathit{G}\left(A_1,A_0,A_1,A_2,33+3\check{k}\right)=\mathit{G}\left(A_2,A_0,A_1,A_2,33+3\check{k}\right),\\ \mathit{F}\left(A_0,A_1,A_2,37+3\check{k}\right)=\mathit{G}\left(C,A_0,A_1,A_2,37+3\check{k}\right)=\mathit{G}\left(A_0,A_0,A_1,A_2,37+3\check{k}\right)=\mathit{G}\left(A_1,A_0,A_1,A_2,37+3\check{k}\right)=\mathit{G}\left(A_2,A_0,A_1,A_2,34+3\check{k}\right) \mathrm{and}\\ \mathit{F}\left(A_0,A_1,A_2,35+3\check{k}\right)=\mathit{G}\left(C,A_0,A_1,A_2,32+3\check{k}\right)=\mathit{G}\left(A_0,A_0,A_1,A_2,32+3\check{k}\right)=\mathit{G}\left(A_1,A_0,A_1,A_2,32+3\check{k}\right)=\mathit{G}\left(A_2,A_0,A_1,A_2,32+3\check{k}\right)\\ \mathrm{for} \mathrm{all} \check{k}\in \mathbb{N}\cup \left\{0\right\}.\end{array}$$

5. Discussion

The important properties of fuzzy matrices have attracted much attention from the research community. The following examples are mentioned: Jiang et al. [17] studied the transitive of generalized fuzzy matrices, Guo and Shang [18] derived an approximate solution of positive fully fuzzy linear matrix equations, Lee and Hur [19] proposed bipolar fuzzy relations, Di Martino and Sessa [20] evaluated the strength of the fuzzy relation, and Lin et al. [21] studied the solutions of fuzzy relational equations. This work studies the limiting behavior of repeated compositions of a sequence of fuzzy matrices with respect to the max-weighted power mean composition. We show that the repeated compositions of a sequence of n fuzzy matrices oscillate among n fuzzy matrices, each with a period n, once the number of compositions exceeds a certain threshold (see Corollary 1). Furthermore, the repeated compositions of the sequence resulting from moving a sequence of n square fuzzy matrices in a circular fashion oscillate in the same n fuzzy matrices as the repeated compositions of the original sequence of n square fuzzy matrices (see Corollary 2). Additionally, composing additional square matrices before the repeated compositions of a sequence of square fuzzy matrices does not alter the limiting behavior of the repeated compositions of the sequence of square fuzzy matrices (see Corollary 3).

By reducing the sequence of n fuzzy matrices to a sequence of n square fuzzy matrices, the powers of a square fuzzy matrix are demonstrated to be always convergent, which was also proved by Lur et al. [13]. Therefore, this study can be considered as an extension of Lur et al. [13] from a square fuzzy matrix to a sequence of fuzzy matrices.

Although the powers of a square fuzzy matrix always converge, the case of p approaching negative infinity, where p denotes the power in the weighted power mean (see Definition 1), should also be considered. As is well known, the weighted power mean is the min operation if p approaches negative infinity. The max-min powers of a square fuzzy matrix either converge or oscillate, as is also well known. Therefore, theoretically, the oscillation behavior of the powers of a square fuzzy matrix with a max-weighted power mean composition could only occur when p approaches negative infinity. In practice, if p is small enough, then the oscillation behavior might be experienced in the sequence of consecutive powers of a fuzzy matrix with a max-weighted power mean composition due to floating-point imprecision. An example is given below, where the fuzzy matrix is from Buckley [1], and all computations are performed using double-precision floating point variables in the Java programming language.

Example 10.

Let $A=\left[\begin{array}{ccc}0& 0.2& 1\\ 0.4& 0& 1\\ 0& 1& 0.3\end{array}\right]$. Given “$\otimes$” with $p=-774$ and $\mathsf{\lambda }=0.5$, we have:

$\underset{k\to \infty }{\lim }{A}^k=A^{1050}=\left[\begin{array}{ccc}0.4003583760& 1& 1\\ 0.4003583760& 1& 1\\ 0.4003583760& 1& 1\end{array}\right]$. However, if$p=-775$, then we have:

$$A^{2k}=\left[\begin{array}{ccc}0& 1& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right] \mathrm{and} A^{2k-1}=\left[\begin{array}{ccc}0& 0& 1\\ 0& 0& 1\\ 0& 1& 0\end{array}\right]$$

for all k$\in \mathbb{N}$.