Using Free Mathematical Software in Engineering Classes

Abstract

There are many computational applications and engines used in mathematics, with some of the best-known arguably being Maple, Mathematica, MATLAB, and Mathcad. However, although they are very complete and powerful, they demand the use of commercial licences, which can be a problem for some education institutions or in cases where students desire to use the software on an unlimited number of devices or to access it from several of them simultaneously. In this contribution, we show how GeoGebra, WolframAlpha, Python, and SageMath can be applied to the teaching of different mathematical courses in engineering studies, as they are some of the most interesting representatives of free (and mostly open source) mathematical software. As the best way to show a topic in mathematics is by providing examples, this article explains how to make calculations for some of the main topics associated with Calculus, Algebra, and Coding theories. In addition to this, we provide some results associated with the usage of Mathematica in different graded activities. Moreover, the comparison between the results from students that use Mathematica and students that participate in a “traditional” course, solving problems and attending to master classes, is shown.

1. Introduction

The Bologna Accord is an agreement on a common model of higher education reached in 1999 that implies the creation of a common European area of university studies. It emphasizes the creation of a European Area of Higher Education (EAHE) as a key to promoting students’ mobility, aiming to simplify Europe’s educational qualifications and ensuring that credentials granted by an institution in one country are comparable with those earned elsewhere [1].

There are 48 countries currently involved in the Bologna Accord. The cornerstones of such an open space are mutual recognition of degrees and other higher education qualifications, transparency (readable and comparable degrees organized in a three-cycle structure), and European cooperation in quality assurance.

Due to the Bologna Accord, the teaching of mathematics has suffered important changes, such as the necessity to enhance the traditional teaching–learning process with practical cases, the possibility to introduce some key concepts, and the reinforcement of the learning process by using technology and specific mathematical software [2,3]. Nowadays, there are many computational packages focused on mathematics, with Mathematica and MATLAB being two of the best known [4,5]. However, even though they are certainly very complete and powerful, they require the use of commercial licenses, which can be a problem for some education institutions or in cases where students desire to use the software on an unlimited number of devices or to access them from several of them simultaneously.

In this paper, our goal is to show how free mathematical software (which most of the time is also open source software, but not always) can be applied to the teaching of different engineering courses at the University of Salamanca and Centro Universitario U-tad, from first-year algebra or calculus to more specialized topics such as coding theory. The University of Salamanca was founded by King Alfonso IX of León in 1218, which makes it the oldest Spanish university in existence and one of the oldest in Europe. The university offers 81 courses in the first and second cycles spread throughout five branches of knowledge, including Science and Engineering [6]. U-tad is the acronym for Centro Universitario de Tecnología y Arte Digital (Technology and Digital Art University Centre), a private university centre founded in 2011 with a strong focus on the creation, programming, and management of digital content, products, and services [7]. U-tad is based near Madrid, andit currently offers three higher technical education courses, five undergraduate degrees and twelve postgraduate courses.

Learning a programming language is highly important for pre-university and university students. One of the goals of the Europe 2020 growth strategy [8] is the implantation of information and communication technologies at all educational levels. In this sense, Scratch and App Inventor are widely used in Spanish secondary education and high schools, and Python is also included among the technology tools used in formal education institutions [9]. However, the number of students that arrive at university with a fair programming knowledge is still low. In fact, the first contact with a formal programming language for most engineering students takes place during their first semester. At the University of Salamanca and U-tad, for example, C is the first programming language that is taught to students.

In this study, GeoGebra, WolframAlpha, Python, and SageMath have been used for providing actual examples used in class, as they are good representatives of free mathematical software. In addition, we have analysed the relationship between the use of these tools and the final grades obtained by engineering students. We have also included data about a statistical study of two academic courses in which we proposed the use of Mathematica (and as an alternative WolframAlpha) as a tool for solving mathematical problems.

The rest of this contribution is organized as follows: Section 2 describes other articles associated with this topic. Section 3 presents the most relevant information about GeoGebra, WolframAlpha, Python, and SageMath, while Section 4 provides several examples used at class. After that, Section 5 provides some statistics associated with the usage of Mathematica software in some engineering classes. Finally, in Section 6 we offer some conclusions and ideas for future work.

2. Related Work

There are several publications that analyse the use of mathematical software for teaching at different levels and from different points of view. For example, Hillmayr et al. presented a comprehensive analysis about how the use of technology can enhance learning in secondary school mathematics and science in [10]. They compared learning outcomes of students using digital tools to those of a control group taught without the use of digital tools. Their results showed that the use of digital tools had a positive effect on student learning outcomes and that the use of intelligent tutoring systems or simulations (dynamic mathematical tools) was significantly more beneficial than hypermedia systems. Moreover, in [11] a taxonomy of five categories of tool-based mathematics software is considered: (a) review and practice, (b) general, (c) specific, (d) environment, and (e) communication. A description of the affordances and constraints of such categories of software is provided, and how each one facilitates different aspects of student learning is discussed.

Other contributions study the use of different software for teaching mathematics. Among them, we highlight the following: [12,13,14,15,16,17,18,19,20]. In comparison to those articles, this contribution focuses on a specific set of open source engines and provides examples used in actual engineering classes.

3. Computational Engines

Engineering is considered “the application of mathematics and sciences to the building and design of projects for the use of society” [21]. Moreover, mathematical theory and practical engineering challenges are linked to computational procedures [22]. Representation of functions or surfaces, the calculation of the Taylor polynomial for a given function, solving systems of linear equations or making calculations with matrices are some of the examples that engineering students need everyday in their studies [23].

There are arguably three possibilities regarding the usage of computational engines:

• Commercial software: MATLAB, Mathematica, Maple, Mathcad, SPSS, etc.
• Free software: GeoGebra, WolframAlpha, SageMath, Maxima, Scilab, Octave, R, FreeMat, Demetra+, etc.
• Programming languages such as Python or Julia.

Each of these options has its benefits and disadvantages. Applications such as MATLAB or Mathematica are very powerful, but obviously they require commercial licences and the installation of many software packages that in some cases have to be managed manually and need to allocate several gigabytes of hard drive space. In addition to this, those applications sometimes have processor and memory requirements that cannot be satisfied by all type of students. Even though universities usually provide computing resources to students, events such as the coronavirus pandemic have shown that students cannot depend solely on the university infrastructure.

In comparison, the computational capabilities of free software engines are lower in some instances, but for introductory subjects they may be more than enough. Finally, programming languages such as Python are very versatile and allow one to perform symbolic and numeric calculations, but many first-year students are not familiar with them. Even though it could be argued that first-year students are also unfamiliar with the syntaxis of mathematical engines, it is true that many computations can be achieved with a sole command in those mathematical engines, while they would require creating a small application using a programming language, with the difficulties that that option brings (importing the proper libraries, formatting the code in a proper way, etc.).

In this paper, we have focused on GeoGebra, WolframAlpha, Python, and SageMath, not only because they are free to use, but also because as a side effect that freedom allows us to chose the best option for each topic inside a course, preventing educators from being tied to a single solution.

Several authors have analysed the benefits and disadvantages of different educational applications [24,25,26], and they found that all of them have similar characteristics and are suitable for classes. Sometimes, the decision on which application to use depends on the usage of the same software by the teacher in his/her own research activities [27].

It is important to mention other open source applications and libraries of mathematical software different to those considered in detail in this work, which are included in

Table 1. Additional open source mathematical software applications.

Name	Author(s)	Web Page (Accessed on 31 August 2021)	Field
Axiom	Axiom Team	http://www.axiom-developer.org/	CAS
Cadabra	K. Peeters et al.	https://cadabra.science/	CAl
CoCoA	L. Robbiano	http://cocoa.dima.unige.it/	CmA
Demetra+	Eurostat	https://github.com/jdemetra/jdemetra-app	CDm
Flint	W. Hart	http://www.flintlib.org/	ODE
FreeMat	S. Basu	http://freemat.sourceforge.net/	Alg
GAP	Araújo et al.	https://www.gap-system.org/	DAl
Gfan	A. Jensen	http://home.imf.au.dk/jensen/software/gfan/gfan.html	AlG
GiNaC	C. Bauer et al.	https://www.ginac.de/	AlC
Gnuplot	Gnuplot team	http://www.gnuplot.info/	2/3D
Gretl	A. Cottrell	http://gretl.sourceforge.net/	EcA
LiPS	M. Melnick	http://lipside.sourceforge.net/	LiP
Mathics	B. Jones et al.	https://mathics.org/	CAS
Maxima	W. Schelter	https://maxima.sourceforge.io/	CAS
Macaulay 2	D. Grayson et al.	http://www.math.uiuc.edu/Macaulay2/	AlG
MPFR	MPFR team	https://www.mpfr.org/	FPA
MPIR	B. Gladman et al.	https://www.mpir.org/	Art
MuPAD-Combinat	F. Hivert et al.	http://mupad-combinat.sourceforge.net/	CAl
NTL	V. Shoup	http://www.shoup.net/ntl//	NTh
Octave	J.B. Rawlings et al.	https://www.octave.org	SyC
PARI/GP	H. Cohen et al.	http://pari.math.u-bordeaux.fr/	NTh
R	R. Ihaka and R. Gentleman	https://www.r-project.org/	CDm
Reduce	T. Hearn	http://www.reduce-algebra.com/	CAS
Scilab	INRIA	https://www.scilab.org/	NuC
Xcas	B. Parisse	http://xcas.sourceforge.net/fr/index.php	CAS

.

3.1. GeoGebra

GeoGebra is an interactive geometry, algebra, statistics, and calculus application available both as an online resource and a native application in Windows, macOS, and Linux systems [28].

The GeoGebra website includes several services such as a calculator and a graphics plotter, but the most widely used option is what is called GeoGebra Classic, which puts together those individual tools.

Figure 1 shows the GeoGebra Classic interface, where it is possible to find modules for two- and three-dimensional plotting, an input bar, and the CAS (Computer Algebra System) module, among others.

GeoGebra’s interface is easy to use and allows the configuration of several aspects associated with function representation, such as line width, colour, and style. These representations can be integrated into online books that can be shared with students so, for instance, they can navigate through all the examples and solutions associated with a certain topic [29].

3.2. WolframAlpha

WolframAlpha is a computational knowledge engine developed by a subsidiary of Wolfram Research, the company behind Mathematica [30]. Given that WolframAlpha is a reduced version of the Mathematica software, all options must be entered as text in the application’s input box. However, the website provides access to many examples, so students can find the right expression in a relatively short time. Obviously, the advantage of using WolframAlpha instead of Mathematica is that it can be accessed by anyone as a web service free of charge.

One of the most interesting aspects of WolframAlpha is the possibility to use both natural language and Mathematica syntax for computations, so even students with little or no knowledge of the Mathematica syntax can use the engine without effort.

3.3. Python

Python is an interpreted, high-level, and general-purpose programming language that emphasizes code readability [31]. Python was first released in 1991, but it was not until the launch of versions 2.0 and 3.0 in 2000 and 2008, respectively, that Python was really popularized among programmers. Since 1 January 2020, Python 2 is no longer officially supported [32], which means that Python 3 is the only version which is active nowadays.

One of the advantages of Python over other programming languages is the number of modules and extensions that can be used [33]. From an engineering point of view, some of the most useful are NumPy (which defines types for numerical arrays and matrices together with the basic operations that can be applied to them) [34], SymPy (a library for symbolic mathematics) [35], and SciPy (which uses NumPy in order to perform advanced mathematical, signal processing, optimization, and statistics calculations) [36].

3.4. SageMath

SageMath is a computer algebra system with features covering many aspects of mathematics, including algebra, combinatorics, graph theory, numerical analysis, number theory, calculus, and statistics [37].

The first version of SageMath was released in 2005 as free and open source software under the GNU General Public License version 2, with the initial goal of becoming an open source alternative to Magma, Maple, Mathematica, and MATLAB.

Instead of developing another computational engine from scratch, SageMath integrates many already existing open source packages such as NumPy, SciPy, matplotlib, Sympy, Maxima, and R, among others, using a syntax similar to the one provided by Python.

SageMath can be installed as a stand-alone application or run in the cloud using CoCalc [38], a web-based cloud computing service (see Figure 2).

4. Examples

4.1. Calculus

Many Calculus key concepts can be reinforced or at least better understood by students when presented in a graphical way. Allowing students to replicate some model computations in similar problems has the benefit of providing a durable link between what is taught in class and what they study at home [39].

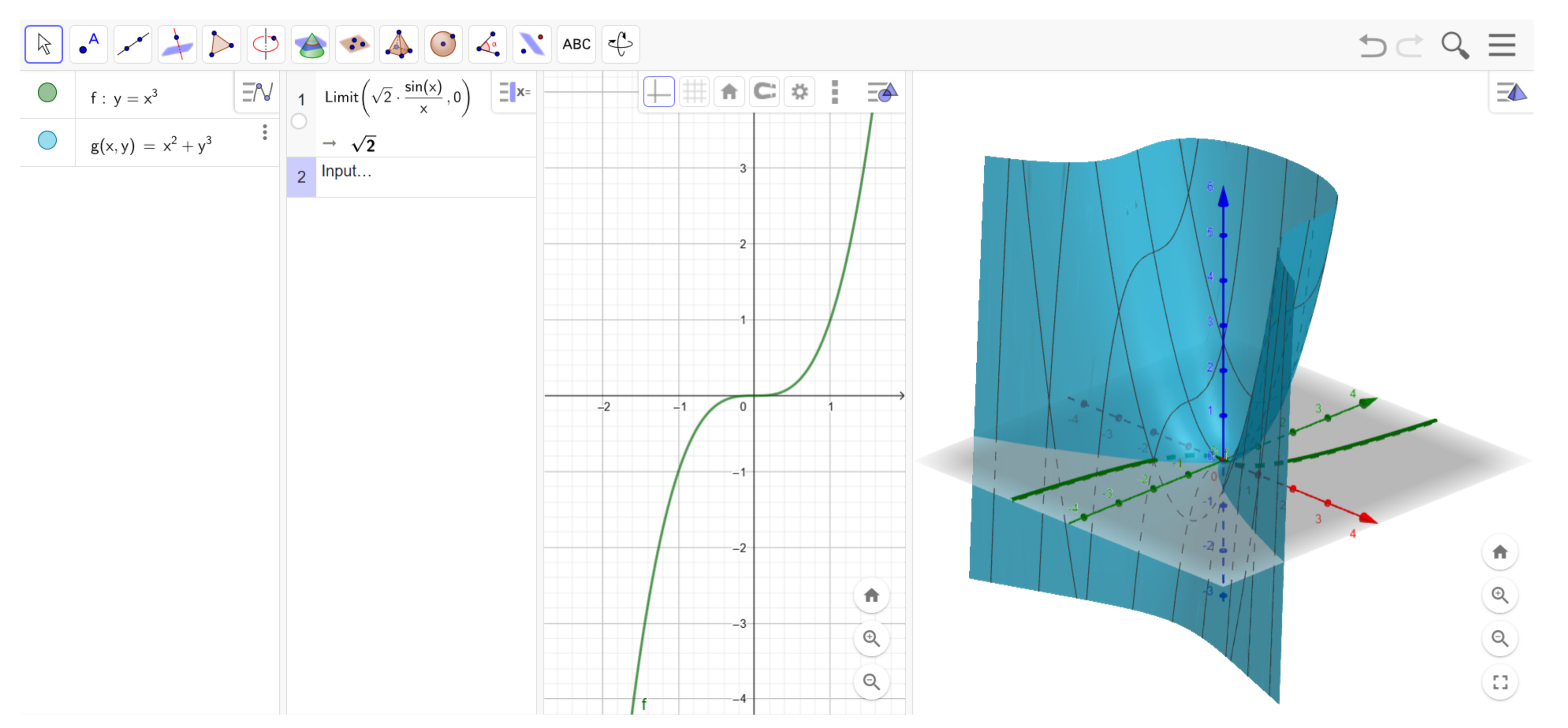
Figure 3 shows an example associated with the graphical representation of a function and its asymptotes. If, for instance, we intend to show how the Taylor polynomials work, we can include in the same solution the initial function and Taylor polynomials of different degrees, so students can realize that a higher degree implies a better approximation for real functions (see Figure 3).

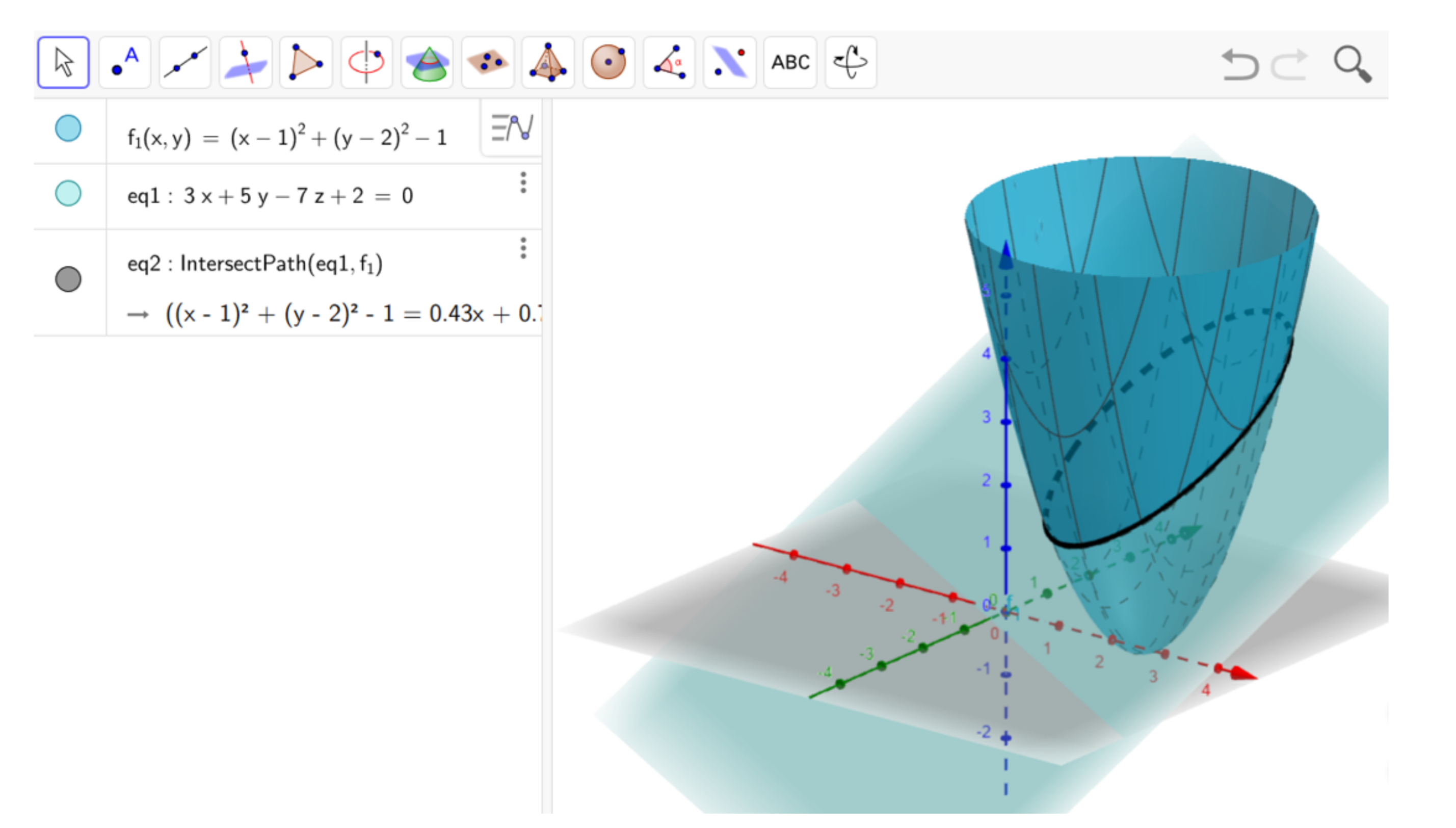
Regarding the calculus of several variables, GeoGebra is a suitable option given that it allows students to rotate three-dimension images in any direction. As an example, Figure 4 shows how to represent the intersection of two surfaces.

Switching to WolframAlpha, it is possible to perform calculations such as performing the second derivative of a function and specializing the resulting expression at a point with a single command.

WolframAlpha can also be very convenient in some instances where, together with the requested calculation, the engine also provides a graphic representation of the solution, as in the case of Figure 5.

Both GeoGebra and WolframAlpha are supported by a large number of developers who make available their work, so it is possible to access many great online demonstrations and practical examples. This feature is particularly interesting when teaching theorems and their applications, as it is a topic where many students face some difficulties. Some examples are [40,41], where Lagrange’s theorem and the Ingetral Mean Value theorem are described using WolframAlpha resources.

4.2. Algebra

This section shows how to use Python for solving different algebra problems using parts of the code developed by Javier García Algarra [42]. In order to correctly execute the following examples, it must be taken into account that NymPy and SymPy modules must be imported through the following commands:

import numpy as np

import sympy as sp

from sympy.matrices import Matrix

For convenience, figures included hereafter have been executed as a worksheet in CoCalc. The first example shows how to represent a polynomial and to obtain its roots (see Figure 6).

If we need to solve a system of linear equations, we can use the code displayed in Figure 7.

In Python, it is possible to define matrices either directly or through a lambda expression, which can be useful sometimes (see Figure 8).

Once we have defined matrix A, Figure 9 shows how to obtain its determinant, inverse matrix, and associated eigenvalues in an easy way.

It is also possible to define and operate matrices with symbolic content, as shown in Figure 10.

4.3. Coding Theory

In this section, we will demonstrate how to operate with linear codes using SageMath. In the first example, we will define a generator matrix with coefficients defined over the Galois field with three elements, GF(3), as shown in Figure 11.

Then, we can use G as the generator matrix of a $(8,5)$ code and request information such as the length, dimension, mininum distance, and weight distribution of the code, as shown in Figure 12.

Quite conveniently, we can obtain the generator matrix in systematic form as well as the code’s parity check matrix (see Figure 13).

We are also able to check if a received vector is a proper codeword or not, in which case its syndrome will be different from the zero vector, as shown in Figure 14.

In the case of cyclic codes, in addition to matrices, it is also possible to work with polynomials, as can be seen in Figure 15.

5. Experimental Study

In the experiment performed at the University of Salamanca, two groups of students were selected. The first group, with 57 students studying for a Chemical Engineering degree, represented the experimental group, while the control group was made up of 63 students studying for an Industrial Engineering degree. In the experimental group, students were allowed to use WolframAlpha (or, alternatively, Mathematica, with the same commands). In both cases, students attended a numerical analysis course with comparable contents, so conclusions could be obtained from the comparison. The study took into account the performance of students during the academic years 2018–2019 and 2019–2020.

For the experimental group, three questionnaires, two software exercises in the computer room, and two exams were conducted during the first year associated with this analysis. In contrast, during the second year, two questionnaires, three software exercises, and two exams were monitored. Students from the control group did not participate in software seminars and their only assessment activity was a final written exam at the end of the semester.

The goal of the statistical study presented in this section is to analyse, firstly, the relation between the different assessment activities and the results obtained when using mathematical software instead of traditional problem-solving methods and, secondly, to compare the results with students that did not participate in similar activities.

5.1. Chemical Engineering Degree

The numerical analysis course in the Chemical Engineering degree has 7.5 credits, and the final mark was calculated over 10 points, where 5% corresponds to questionnaires, 10% to software activities, 15% to team work and solving additional problems, and the remaining 70% corresponds to the grades associated with the written exams.

As has been mentioned before, for this study, data from two academic years was collected. In the case of the 2018–2019 course, out of 57 students, seven students that did not attend the different assessment activities have been discarded. Since the Bologna Accord was put into effect, the number of drop-out students has reduced and every year a fewer number of students leave mathematics courses.

Figure 16 shows the box plot representation for the student marks associated with the different assessment activities, where the stars represent the extreme values.

In the case of software practices, Median > Mean, and Kurtosis = 1.468. In the case of questionnaires and exams, these values are different, as can be seen in

Table 2. Descriptive statistics for the academic year 2018–2019.

Concept	Questionnaire	Software	Exam
N Valid	50	50	50
Missing	0	0	0
Mean	6.0322	3.2210	5.4018
Median	6.4350	7.2000	5.6400
Mode	0.00 a	7.75	5.25
Standard Deviation	2.12767	2.40013	1.73700
Variance	4.527	5.761	3.017
Skewness	−1.038	−1.465	−1.465
Standard Error of Skewness	0.337	0.337	0.337
Kurtosis	0.993	1.468	2.723
Standard Error of Kurtosis	0.662	0.662	0.662
Range	9.22	9.00	8.00
Minimum	0.00	0.00	0.00
Maximum	9.22	9.00	8.00

^a Multiple modes exist, the smallest value is shown.

.

Software activity is clearly what suits students the best. Engineering students usually like to work with their hands, in the laboratory or with computers. Moreover, this activity is typically accomplished by collaborating with their fellows, which usually is not the case of exams and to a lesser extent of questionnaires. A consequence of this fact is the absence of a correlation. The biggest one is between software and questionnaires (the Pearson correlation coefficient is equal to 0.720).

We conducted an ANOVA to check the relation between the three activities: questionnaires, software and exams. We have found out that the data meet the homogeneity of variances (the Levene statistic has a significance that is equal to $0.068$), they are random samples (the test significance is equal to $0.568$), and variables follow a normal distribution (the Kolmogorov–Smirnov test significance is equal to $0.086$).

Table 3. ANOVA test results for the academic year 2018–2019.

Concept	Sum of Squares	df	Mean Square	F	Significance
Between Groups	18.402	2	9.201	2.075	0.129
Within Groups	651.933	147	4.435
Total	670.336	149

shows the results of the analysis of variance that indicates that the hypothesis of equal means is accepted, i.e., the means for questionnaires, software, and exams are equal.

In the 2019–2020 academic year, out of 48 students, eight alumni were discarded as they did not fully participate in all the assessment activities. The statistical analysis is quite similar to the one developed for the previous academic year. In this case, the correlation between activities has been reduced: $0.197$ between software and questionnaires. The final average mark of students is $5.93$ compared to $5.43$ obtained the previous year.

With the goal to avoid the duplication of information we have included Figure 17, where histograms and normal curves for the assessment activities during the 2019–2020 course are displayed.

5.2. Industrial Engineering

The Industrial Engineering mathematics course has six credits and the final mark, which corresponds to the final exam, is calculated over 10 points. In this instance, the marks from 63 students were collected from the 2019–2020 academic year. For the control group, the final marks obtained in the final exam are shown in

Table 4. Final results of Industrial Engineering students.

Mark	Percentage
Not attending	25.40
Between 0 and 4.99	31.75
Between 5 and 6.99	19.05
Between 7 and 8.99	17.46
Between 9 and 10	6.35

.

In this case, only 42.86% of students passed the exam, and the qualification’s mean was 4.74.

5.3. Analysis of the Results

The analysis derived from the data obtained in the Chemical Engineering courses is presented in

Table 5. Mean and Standard Deviation for questionnaires (Q), Software (S) and Exams (E).

Course	Mean			Standard Deviation
	Q	S	E	Q	S	E
2018–2019	6.0322	6.2210	5.4018	2.12767	2.40013	1.73700
2019–2020	5.5441	5.9195	6.5961	2.60838	2.14294	1.32373

.

The independent samples test was performed in order to obtain the relation between the grades in different assessment activities grouped by year. As a result, we found out that the same variance appears in both courses (the Levene’s test for equality of variances coefficient is equal to $0.709$) and the t-test for the equality of means returns the $95\%$ confidence interval of the difference equal to $(-1.83377,-0.55491)$ assuming equal variances and to $(-1.82308,0.56559)$ when equal variances are not assumed, with a significance value of $0.00$ in both cases.

Compared to the data obtained from Industrial Engineering students, it can be seen that the mean is lower than the mean for Chemical Engineering students. This could be interpreted as an indication that, when mathematical software is used at class, students improve their understanding of the contents and obtain better results compared to students that are being taught in the traditional way.

6. Conclusions

In this contribution, we have shown how to use some of the best-known free computational packages in order to enhance the learning process for mathematical courses in engineering studies. The usage of engines such as the ones implemented by GeoGebra, WolframAlpha, Python or SageMath allows students to grasp the key concepts seen in class and to practice problems at their leisure, resulting in better learning outcomes and grades.

Using free software has the additional benefit of allowing educators to choose the best option for each topic inside a course, as they are not tied to a specific product that can be optimal for some subjects but inadequate in some other instances. Some of the examples shown throughout this article could even be used in high schools and academies, which are two institutions less likely to commit themselves to investments in things such as mathematical software licences.

An observation made by the authors of this paper during the elaboration of the research is that first-year students are less inclined to use a programming language than a computational engine in order to solve engineering problems, even if they were previously familiar with the programming language in question. Some reasons for this are that students (incorrectly) do not try to interrelate the knowledge obtained in different subjects and that they prefer to use a command instead of coding a small application to obtain fast results. Another conclusion is that students prefer not to install applications if they can obtain the same results by connecting to a remote service providing online compilers or calculators.

Additionally, an analysis of the results obtained when using mathematical software to an engineering mathematics course is included. This analysis allows one to derive some conclusions about the application of mathematical software to different activities such as questionnaires, problems to be solved, and exams. In our study, students that participated in a course that allowed the completion of some activities with the help of mathematical software obtained better marks than students that attended to a more “traditional” course, composed of master classes and problem solving sessions. In general, we believe that students are able to achieve a better understanding of the contents of mathematical subjects if they are allowed to use computational engines, which benefits both students and teachers.