Powers of Elliptic Scator Numbers

Abstract

Elliptic scator algebra is possible in $1+n$ dimensions, $n\in \mathbb{N}$. It is isomorphic to complex algebra in 1 + 1 dimensions, when the real part and any one hypercomplex component are considered. It is endowed with two representations: an additive one, where the scator components are represented as a sum; and a polar representation, where the scator components are represented as products of exponentials. Within the scator framework, De Moivre’s formula is generalized to $1+n$ dimensions in the so called Victoria equation. This novel formula is then used to obtain compact expressions for the integer powers of scator elements. A scator in ${\mathbb{S}}^{1+n}$ can be factored into a product of n scators that are geometrically represented as its projections onto n two dimensional planes. A geometric interpretation of scator multiplication in terms of rotations with respect to the scalar axis is expounded. The powers of scators, when the ratio of their director components is a rational number, lie on closed curves. For 1 + 2 dimensional scators, twisted curves in a three dimensional space are obtained. Collecting previous results, it is possible to evaluate the exponential of a scator element in 1 + 2 dimensions.

1. Introduction

De Moivre’s formula establishes a relationship between complex algebra and trigonometry through the evaluation of powers of numbers in modulus and angle variables. This type of relationship has been extended to higher dimensional algebras, notably quaternions [1], split quaternions [2], dual complex numbers [3], real and complex $2\times 2$ matrices [4] and other Clifford algebras [5]. De Moivre’s relationship is closely related to Euler’s formula and hence to the exponential function. Advances in De Moivre type expressions have also produced novel results in the exponential mapping, for example in split quaternionic matrices [6]. The exponential function is unique, between other things, because for the real and complex algebras, it maps the additive group onto the multiplicative group, the basic operations of the real and complex fields.

Elliptic scator algebra extends complex numbers to a higher number of dimensions, retaining one real part, labeled scalar part in scator parlance and any number of hypercomplex components [7]. The underlying philosophy of this algebra is to some extent, related to geometric algebras [8,9]. Videlicet, giving a geometric meaning to the algebraic operations from the outset. This, in turn, lends naturally to describe time, space and other properties in the physical world [10]. The set of elliptic scators is akin to split-quaternions in the sense that it contains zero divisors and nilpotent elements. However, the scator product is not bilinear, thus, it cannot be represented as a matrix–matrix product. The scator product provides an interesting route for a unified mathematical description of quantum dynamics, encompassing the quantum system time evolution and its reduction to observed states [11]. Scator algebra has also been successfully applied to other problems, such as a time–space description in deformed Lorentz metrics [12,13,14] and three dimensional fractal structures [15,16].

This algebraic structure has two representations, an additive and a multiplicative representation that corresponds to the rectangular and polar versions of complex numbers. The relationship between the two scator representations is established by a generalized Euler’s type equation. The components exponential function is a scator function of a scator argument that extends the notion of the complex exponential to higher dimensions [17]. This function, labeled ’cexp’, is scator holomorphic and its derivative is the function itself, thus it satisfies the differential equation $f^{\prime }\left(\stackrel{o}{\zeta }\right)=f\left(\stackrel{o}{\zeta }\right)$, where the prime denotes differentiation with respect to $\stackrel{o}{\zeta }$. The set of holomorphic functions according to the differential quotient criterion [18] is somewhat larger than their counterpart in the quaternion set [19]. The additive and multiplicative (rectangular/polar) scator representations allow for a generalization of De Moivre’s formula to $1+n$ dimensions in scator algebra.

In this paper, the essentials of elliptic scator algebra are presented in Section 2. Emphasis is laid on the transformations between representations. Just as in real and complex algebra, the components exponential function, reviewed in this section, maps scator addition onto scator multiplication. This result is used to prove the commutative group properties in the multiplicative representation and its relationship with non-associativity in the additive representation. The relation between a scator raised to an integer power and angle multiplication is established in Section 3. A geometric representation of these results is presented in Section 4. The exponential of a $1+2$ dimensional scator and its relationship with the components exponential function, is obtained in Section 5.

2. Elliptic Scator Algebra

The two scator representations and the fundamental scator addition and scator product operations are reviewed in this section. In the additive representation, scator elements are represented by a sum of components:

$$\stackrel{o}{\phi }=f_0+\sum _{j=1}^n{f}_j{\check{\mathbf{e}}}_j,$$

(1)

where $f_0,f_j\in \mathbb{R}$, j from 1 to $n\in \mathbb{N}$ and ${\check{\mathbf{e}}}_j\notin \mathbb{R}$. The scator coefficients in this representation, named the additive variables, are tagged with lowercase Latin letters. The multiplicative or polar representation of a scator is:

$$\stackrel{o}{\phi }={\phi }_0\prod _{j=1}^n{e}^{{\phi }_j{\check{\mathbf{e}}}_j}={\phi }_0\prod _{j=1}^{n}exp\left({\phi }_j{\check{\mathbf{e}}}_j\right),$$

(2)

where ${\phi }_0\in {\mathbb{R}}^{+},{\phi }_j\in \mathbb{R}$, and ${\check{\mathbf{e}}}_j\notin \mathbb{R}$; ${\mathbb{R}}^{+}$ represents the interval $\left[\left.0,\infty \right)\right.$. The scator variables in the multiplicative representation ${\phi }_0,{\phi }_j$, named multiplicative variables, are labeled with Greek letters. The zero subindex component is the scalar component in either representation. The director components are labeled with subindices 1 to n. For all elements in the ${\mathbb{S}}^{1+n}$ scator set, the additive scalar component must be different from zero if two or more director components are not zero,

$${\mathbb{S}}^{1+n}=\left\{\stackrel{o}{\phi }=f_0+\sum _{j=1}^n{f}_j{\check{\mathbf{e}}}_j:f_0\ne 0\mathrm{if}\exists f_j{f}_l\ne 0,\mathrm{for}j\ne l\mathrm{from}1\mathrm{to}n\right\}.$$

(3)

In the early papers ${\mathbb{E}}^{1+n}$ was used instead of ${\mathbb{S}}^{1+n}$.

2.1. Transformation between Representations

The transformation from the multiplicative to additive representation originates from Euler type relationships for each ${\check{\mathbf{e}}}_j$ director component, $e^{{\phi }_j{\check{\mathbf{e}}}_j}=cos{\phi }_j+sin{\phi }_j{\check{\mathbf{e}}}_j$, where the scator product of a unit director with itself is minus one, ${\check{\mathbf{e}}}_j{\check{\mathbf{e}}}_j=-1$. The scator $\stackrel{o}{\phi }$ given by (2), is then

:

$$\stackrel{o}{\phi }={\phi }_0\prod _{j=1}^n{e}^{{\phi }_j{\check{\mathbf{e}}}_j}⟼{\phi }_0\prod _{j=1}^n\left(cos{\phi }_j+sin{\phi }_j{\check{\mathbf{e}}}_j\right).$$

(4a)

The product of terms involving only orthogonal director components in the factors is requested to distribute over addition. In general, scator multiplication does not distribute over addition [7]. Two unit scators are orthogonal in scator algebra, if their scator product is zero ${\check{\mathbf{e}}}_j{\check{\mathbf{e}}}_k=0$. The n director units are requested to be orthogonal between them, that is, ${\check{\mathbf{e}}}_j{\check{\mathbf{e}}}_k=0$ for all $j\ne k$, for $j,k$ from 1 to n. The product of the scator components is then:

$$\stackrel{o}{\phi }={\phi }_0\prod _{j=1}^n\left(cos{\phi }_j+sin{\phi }_j{\check{\mathbf{e}}}_j\right)={\phi }_0\prod _{k=1}^{n}cos\left({\phi }_k\right)+{\phi }_0\sum _{j=1}^n\prod _{k\ne j}^{n}cos\left({\phi }_k\right)sin\left({\phi }_j\right){\check{\mathbf{e}}}_j.$$

(4b)

The mapping of the multiplicative to additive representations is given by the function ${\mathfrak{f}}_{mar}:\left({\mathbb{R}}^{+};{\mathbb{R}}^n\right)\to {\mathbb{S}}^{1+n}$,

$${\mathfrak{f}}_{mar}:{\phi }_0\prod _{j=1}^n{e}^{{\phi }_j{\check{\mathbf{e}}}_j}⟼\underset{f_0}{\underbrace{{\phi }_0\prod _{k=1}^{n}cos\left({\phi }_k\right)}}+\underset{f_j}{\underbrace{{\phi }_0\sum _{j=1}^n\prod _{k\ne j}^{n}cos\left({\phi }_k\right)sin\left({\phi }_j\right)}}{\check{\mathbf{e}}}_j.$$

(5)

The arguments of the trigonometric functions are, of course, modulus $2\pi$ due to their fundamental period. The inverse mapping is given by the function ${\mathfrak{f}}_{amur}:{\mathbb{S}}^{1+n}\to \left({\mathbb{R}}^{+};{\mathbb{R}}^n\right)$ defined, for scators with $f_0\ne 0$, by

$${\mathfrak{f}}_{amur}:f_0+\stackrel{n}{\sum _{j=1}}{f}_j{\check{\mathbf{e}}}_j⟼\underset{{\phi }_0}{\underbrace{\left|f_0\right|\stackrel{n}{\prod _{j=1}}\sqrt{1+\frac{f_j^2}{f_0^2}}}}exp\left(\underset{{\phi }_j}{\underbrace{arctan\left(\frac{f_j}{f_0}\right)}}{\check{\mathbf{e}}}_j\right),$$

(6a)

for scators with zero additive scalar component and non-zero ${\check{\mathbf{e}}}_j$ director component by:

$${\mathfrak{f}}_{amur}:f_j{\check{\mathbf{e}}}_j⟼\left|f_j\right|exp\left(\mathrm{sgn}\left(f_j\right)\frac{\pi }{2}{\check{\mathbf{e}}}_j\right),$$

(6b)

and for the null scator

$${\mathfrak{f}}_{amur}:0+\sum _{j=1}^{n}0{\check{\mathbf{e}}}_j⟼0\prod _{j=1}^{n}exp\left(0{\check{\mathbf{e}}}_j\right).$$

(6c)

To recap, there are two representations of scator numbers, additive and multiplicative, each of them with their corresponding additive (1) or multiplicative (2) variables. A scator number can also be expressed in the additive representation with multiplicative variables (5) or in the multiplicative representation with additive variables (6a) and (6b). These four possibilities are a higher dimensional analogue of complex numbers that can be written in Cartesian form with real and imaginary parts $z=a+ib$, or polar form $z=r{e}^{i\phi }$ with modulus and angle variables; $z=r\left(cos\phi +isin\phi \right)$ or $z=\sqrt{a^2+b^2}exp\left(iarctan\left(\frac{b}{a}\right)\right)$ being the other two possible ways to write them. The relationships between variables are:

$$f_0={\phi }_0\stackrel{n}{\prod _{k=1}}cos{\phi }_k;f_j={\phi }_0\stackrel{n}{\prod _{k\ne j}}cos{\phi }_{k}sin{\phi }_j,$$

(7a)

and

$${\phi }_0=\left|f_0\right|\stackrel{n}{\prod _{j=1}}\sqrt{1+\frac{f_j^2}{f_0^2}},\mathrm{if}{f}_0\ne 0,{\phi }_0=\left|f_j\right|\mathrm{if}{f}_0=0,{\phi }_0=0\mathrm{if}{f}_0=f_j=0\forall j;$$

(7b)

$${\phi }_j=arctan\left(\frac{f_j}{f_0}\right).$$

(7c)

There is no scator additive to multiplicative representation in the ${\mathbb{R}}^{1+n}\backslash {\mathbb{S}}^{1+n}$ set. In $1+1$ dimensions, there are j subsets ${\mathbb{S}}_j^{1+1}\subseteq {\mathbb{S}}^{1+n}$ where all ${\check{\mathbf{e}}}_l$ coefficients vanish, except for the $j^{th}$ component. These j scator sets are isomorphic to $\mathbb{C}$. Equation (5) reduces to Euler’s formula for any one of these sets, ${\mathfrak{f}}_{mar}:{\phi }_0{e}^{{\phi }_l{\check{\mathbf{e}}}_l}⟼{\phi }_{0}cos\left({\phi }_l\right)+{\phi }_{0}sin\left({\phi }_l\right){\check{\mathbf{e}}}_l$, where ${\check{\mathbf{e}}}_l\notin \mathbb{R}$ represents a hyper-imaginary unit, ${\check{\mathbf{e}}}_l{\check{\mathbf{e}}}_l=-1$.

Scator algebra is endowed with two fundamental operations. The sum of scators $\stackrel{o}{\alpha }=a_0+{\sum }_{j=1}^n{a}_j{\check{\mathbf{e}}}_j\in {\mathbb{R}}^{1+n}$ and $\stackrel{o}{\beta }=b_0+{\sum }_{j=1}^n{b}_j{\check{\mathbf{e}}}_j\in {\mathbb{R}}^{1+n}$ is

$$\stackrel{o}{\alpha }+\stackrel{o}{\beta }=\left(a_0+b_0\right)+\sum _{j=1}^n\left(a_j+b_j\right){\check{\mathbf{e}}}_j.$$

(8)

Scator addition satisfies Abelian group properties.

2.2. Product in the Additive Representation

${\mathbb{S}}^{1+n}$ is the subset of ${\mathbb{R}}^{1+n}$ where multiplication is defined in the additive representation.

Definition 1.

For $\stackrel{o}{\alpha }=a_0+{\sum }_{j=1}^n{a}_j{\check{\mathbf{e}}}_j\in {\mathbb{S}}^{1+n}$ and $\stackrel{o}{\beta }=b_0+{\sum }_{j=1}^n{b}_j{\check{\mathbf{e}}}_j\in {\mathbb{S}}^{1+n}$, the product $\stackrel{o}{\alpha }\stackrel{o}{\beta }$ is: if $a_0{b}_0\ne 0$,

$$\stackrel{o}{\alpha }\stackrel{o}{\beta }=a_0{b}_0\prod _{k=1}^n\left(1-\frac{a_k{b}_k}{a_0{b}_0}\right)+a_0{b}_0\sum _{j=1}^n\left[\prod _{k\ne j}^n\left(1-\frac{a_k{b}_k}{a_0{b}_0}\right)\left(\frac{a_j}{a_0}+\frac{b_j}{b_0}\right)\right]{\check{\mathbf{e}}}_j.$$

(9a)

If $a_0=0$ and $b_0\ne 0$, $\stackrel{o}{\alpha }=a_l{\check{\mathbf{e}}}_l$ has a single non-vanishing director component,

$$\stackrel{o}{\alpha }\stackrel{o}{\beta }=-a_l{b}_l+a_l{b}_0{\check{\mathbf{e}}}_l-\sum _{j\ne l}^n\left(a_l\frac{b_l{b}_j}{b_0}\right){\check{\mathbf{e}}}_j.$$

(9b)

If $a_0=b_0=0$, $\stackrel{o}{\alpha }=a_l{\check{\mathbf{e}}}_l$ and $\stackrel{o}{\beta }=b_j{\check{\mathbf{e}}}_j$,

$$\stackrel{o}{\alpha }\stackrel{o}{\beta }=-a_l{b}_j{\delta }_{lj},$$

(9c)

where ${\delta }_{lj}$ is a Kroneker delta. The (9b) and (9c) product definitions can be obtained from the appropriate limits of (9a). Evaluation of the director components limits should always be performed prior to the scalar component limit, in order to remain within the ${\mathbb{S}}^{1+n}$ set [11]. Conjugation of $\stackrel{o}{\phi }=f_0+{\sum }_{j=1}^n{f}_j{\check{\mathbf{e}}}_j$ is defined by ${\stackrel{o}{\phi }}^{*}\equiv f_0-{\sum }_{j=1}^n{f}_j{\check{\mathbf{e}}}_j$. The magnitude is given by the positive square root of the scator times its conjugate $∥\stackrel{o}{\phi }∥=\sqrt{\stackrel{o}{\phi }{\stackrel{o}{\phi }}^{*}}$. For a scator with non-vanishing additive scalar component:

$$∥\stackrel{o}{\phi }∥=\sqrt{\stackrel{o}{\phi }{\stackrel{o}{\phi }}^{*}}=\left|f_0\right|\prod _{k=1}^n\sqrt{1+\frac{f_k^2}{f_0^2}},$$

(10)

and if the additive scalar component is zero there is only one director component, say the $l^{th}$ component, $∥\stackrel{o}{\phi }∥=\left|f_l\right|$. The multiplicative inverse of a scator $\stackrel{o}{\phi }$ is ${\stackrel{o}{\phi }}^{-1}={\stackrel{o}{\phi }}^{*}/{∥\stackrel{o}{\phi }∥}^2$.

Multiplication is commutative and, if zero is avoided, all elements have inverse in ${\mathbb{S}}^{1+n}$. A previous communication has been devoted to the conditions when the product is or is not associative in the additive representation [11]. The two main results are:

Theorem 1

(Fernandez-Guasti, 2018). “The scator product in ${\mathbb{S}}^{1+n}$ is associative in the additive representation if all possible product pairs have a non vanishing additive scalar component, $\left(\stackrel{o}{\alpha }\stackrel{o}{\beta }\right)\stackrel{o}{\phi }=\stackrel{o}{\alpha }\left(\stackrel{o}{\beta }\stackrel{o}{\phi }\right)=\stackrel{o}{\beta }\left(\stackrel{o}{\alpha }\stackrel{o}{\phi }\right)$ if $\stackrel{o}{\alpha }\stackrel{o}{\beta },\stackrel{o}{\beta }\stackrel{o}{\phi },\stackrel{o}{\alpha }\stackrel{o}{\phi }\in {\mathbb{S}}_{\ne 0}^{1+n}$.”

The set ${\mathbb{S}}_{\ne 0}^{1+n}\subseteq {\mathbb{S}}^{1+n}$ is the subset of ${\mathbb{S}}^{1+n}$ with a non zero additive scalar component.

Theorem 2

(Fernandez-Guasti, 2018). The scator product in ${\mathbb{S}}^{1+n}$ is in general not associative for $n>1$ in the additive representation, if one or more of the possible product pairs has a vanishing additive scalar component, $\left(\stackrel{o}{\alpha }\stackrel{o}{\beta }\right)\stackrel{o}{\phi }\ne \stackrel{o}{\alpha }\left(\stackrel{o}{\beta }\stackrel{o}{\phi }\right)\ne \stackrel{o}{\beta }\left(\stackrel{o}{\alpha }\stackrel{o}{\phi }\right)$ if $\stackrel{o}{\alpha }\stackrel{o}{\beta }\mathrm{or}\stackrel{o}{\beta }\stackrel{o}{\phi }\mathrm{or}\stackrel{o}{\alpha }\stackrel{o}{\phi }\in {\mathbb{S}}_0^{1+n}$.

Elements in ${\mathbb{S}}_0^{1+n}$ can only have a single non-vanishing director component, say the j component from the n director components, $f_j{\check{\mathbf{e}}}_j\in {\mathbb{S}}_j^{1+n}$. The set of elements that have zero additive scalar component is ${\mathbb{S}}_0^{1+n}={\bigcup }_{j=1}^n{\mathbb{S}}_j^{1+n}$. In the associative case, for $n>1$, all products invoke (9a), whereas in the non-associative case, a product rule other than (9a) is invoked in at least one of the products. Theorem (1) establishes a sufficient condition for the scator product to be associative in the additive representation, whereas Theorem (2) establishes a necessary condition for non-associativity.

2.3. Product in the Multiplicative Representation

In the multiplicative representation, the product of two scators is evaluated by performing the multiplicative scalars product and the addition of the multiplicative director coefficients with the same director unit,

$$\stackrel{o}{\alpha }\stackrel{o}{\beta }=\left({\alpha }_0\prod _{j=1}^{n}exp\left({\alpha }_j{\check{\mathbf{e}}}_j\right)\right)\left({\beta }_0\prod _{j=1}^{n}exp\left({\beta }_j{\check{\mathbf{e}}}_j\right)\right)={\alpha }_0{\beta }_0\prod _{j=1}^{n}exp\left[\left({\alpha }_j+{\beta }_j\right){\check{\mathbf{e}}}_j\right].$$

(11)

The multiplicative scator components having the same director ${\check{\mathbf{e}}}_j$, satisfy the addition theorem for exponents. The conjugate of the scator $\stackrel{o}{\phi }={\phi }_0{\prod }_{j=1}^n{e}^{{\phi }_j{\check{\mathbf{e}}}_j}$, is obtained by the negative of the director components, leaving the multiplicative scalar component unchanged ${\stackrel{o}{\phi }}^{*}\equiv {\phi }_0{\prod }_{j=1}^n{e}^{-{\phi }_j{\check{\mathbf{e}}}_j}$. The magnitude of a scator $∥\stackrel{o}{\phi }∥=\sqrt{\stackrel{o}{\phi }{\stackrel{o}{\phi }}^{*}}$, in the multiplicative representation from (11), is $∥\stackrel{o}{\phi }∥={\phi }_0$. The multiplicative scalar represents the scator magnitude. The multiplicative inverse ${\stackrel{o}{\phi }}^{-1}={\stackrel{o}{\phi }}^{*}{∥\stackrel{o}{\phi }∥}^{-2}$ exists if the scator magnitude is not zero.

The product in the multiplicative representation is closely related to the components exponential function [17]. The $\stackrel{o}{\mathrm{c}}\exp$ function is a scator function $\stackrel{o}{\mathrm{c}}\exp :{\mathbb{R}}^{1+n}\to {\mathbb{S}}^{1+n}$ of scator variable, say $\stackrel{o}{\zeta }=z_0+{\sum }_{j=1}^n{z}_j{\check{\mathbf{e}}}_j$, given in the multiplicative representation, by the product of the exponential of each component,

$$\stackrel{o}{\mathrm{c}}\exp \left(\stackrel{o}{\zeta }\right)\equiv \stackrel{o}{\mathrm{c}}\exp \left(z_0+\sum _{j=1}^n{z}_j{\check{\mathbf{e}}}_j\right)\equiv exp\left(z_0\right)\prod _{j=1}^{n}exp\left(z_j{\check{\mathbf{e}}}_j\right).$$

(12a)

The $\stackrel{o}{\mathrm{c}}\exp$ function is scator holomorphic in the entire ${\mathbb{R}}^{1+n}$ domain according to the differential quotient criterion [17]. In the additive representation, the $\stackrel{o}{\mathrm{c}}\exp$ function is:

$$\stackrel{o}{\mathrm{c}}\exp \left(z_0+\sum _{j=1}^n{z}_j{\check{\mathbf{e}}}_j\right)\equiv \underset{{\mathrm{cexp}}_0\left(\stackrel{o}{\zeta }\right)}{\underbrace{e^{z_0}\prod _{k=1}^{n}cos\left(z_k\right)}}+\sum _{j=1}^n\underset{{\mathrm{cexp}}_j\left(\stackrel{o}{\zeta }\right)}{\underbrace{e^{z_0}\prod _{k\ne j}^{n}cos\left(z_k\right)sin\left(z_j\right)}}{\check{\mathbf{e}}}_j.$$

(12b)

Lemma 1.

The $\stackrel{o}{\mathrm{c}}\exp :{\mathbb{R}}^{1+n}\to {\mathbb{S}}^{1+n}$ function maps scator addition onto scator multiplication.

Proof. 

For scators $\stackrel{o}{\alpha }+\stackrel{o}{\beta }$,

$$\stackrel{o}{\mathrm{c}}\exp \left(\stackrel{o}{\alpha }+\stackrel{o}{\beta }\right)=exp\left(a_0+b_0\right)\prod _{j=1}^{n}exp\left(\left(a_j+b_j\right){\check{\mathbf{e}}}_j\right).$$

Since the exponential addition theorem is satisfied component-wise,

$$\stackrel{o}{\mathrm{c}}\exp \left(\stackrel{o}{\alpha }+\stackrel{o}{\beta }\right)=exp\left(a_0\right)exp\left(b_0\right)\prod _{j=1}^{n}exp\left(a_j{\check{\mathbf{e}}}_j\right)exp\left(b_j{\check{\mathbf{e}}}_j\right),$$

this expression can be rearranged to obtain:

$$\stackrel{o}{\mathrm{c}}\exp \left(\stackrel{o}{\alpha }+\stackrel{o}{\beta }\right)=\stackrel{o}{\mathrm{c}}\exp \left(\stackrel{o}{\alpha }\right)\stackrel{o}{\mathrm{c}}\exp \left(\stackrel{o}{\beta }\right).$$

(13)

□

The multiplicative scator representation in terms of the $\stackrel{o}{\mathrm{c}}\exp$ function is:

$$\stackrel{o}{\phi }={\phi }_0\stackrel{o}{\mathrm{c}}\exp \left(\sum _{j=1}^n{\phi }_j{\check{\mathbf{e}}}_j\right),$$

(14)

as can be seen from (2) and (12a).

Corollary 1.

The scator product satisfies commutative group properties in the multiplicative representation.

Proof. 

The commutative group properties of addition for the director components are mapped onto the commutative group properties of the director components in the multiplicative representation. The product of the multiplicative scalar components is a product of two real numbers; provided that the scator with zero magnitude is excluded, commutative group properties are satisfied. □

In particular, product associativity is satisfied in the multiplicative representation,

$$\begin{array}{c}\stackrel{o}{\alpha }\stackrel{o}{\beta }\stackrel{o}{\phi }=\left(\stackrel{o}{\alpha }\stackrel{o}{\beta }\right)\stackrel{o}{\phi }=\stackrel{o}{\alpha }\left(\stackrel{o}{\beta }\stackrel{o}{\phi }\right)=\stackrel{o}{\beta }\left(\stackrel{o}{\phi }\stackrel{o}{\alpha }\right)\hfill \\ =\left({\alpha }_0\prod _{j=1}^{n}exp\left({\alpha }_j{\check{\mathbf{e}}}_j\right)\right)\left({\beta }_0\prod _{j=1}^{n}exp\left({\beta }_j{\check{\mathbf{e}}}_j\right)\right)\left({\beta }_0\prod _{j=1}^{n}exp\left({\beta }_j{\check{\mathbf{e}}}_j\right)\right)\\ \hfill ={\alpha }_0{\beta }_0{\phi }_0\prod _{j=1}^{n}exp\left[\left({\alpha }_j+{\beta }_j+{\phi }_j\right){\check{\mathbf{e}}}_j\right].\end{array}$$

Remark 1.

The product of non zero factors is never zero in the multiplicative representation, for example, let ${\alpha }_j+{\beta }_j=\frac{\pi }{2}$ for all j from 1 to n,

$$\stackrel{o}{\alpha }\stackrel{o}{\beta }=\left({\alpha }_0\prod _{j=1}^{n}exp\left({\alpha }_j{\check{\mathbf{e}}}_j\right)\right)\left({\beta }_0\prod _{j=1}^{n}exp\left({\beta }_j{\check{\mathbf{e}}}_j\right)\right)={\alpha }_0{\beta }_0\prod _{j=1}^{n}exp\left(\frac{\pi }{2}{\check{\mathbf{e}}}_j\right).$$

The magnitude of this scator is $∥\stackrel{o}{\alpha }\stackrel{o}{\beta }∥={\left({\alpha }_0{\beta }_0{\prod }_{j=1}^{n}exp\left(\frac{\pi }{2}{\check{\mathbf{e}}}_j\right){\alpha }_0{\beta }_0{\prod }_{j=1}^{n}exp\left(-\frac{\pi }{2}{\check{\mathbf{e}}}_j\right)\right)}^{\frac{1}{2}}$ $={\alpha }_0{\beta }_0$. In the multiplicative representation, the product of the magnitudes is always equal to the magnitude of the products.

The group properties of the scator product in 1 + 2 and 1 + 3 dimensions, have been discussed in an embedding of scator algebra in a higher dimensional space [20].

Definition 2.

The product of exponentials with different ${\check{\mathbf{e}}}_j$ components is irreducible in the multiplicative representation, that is, it is not possible to express such a scator with fewer factors. The product ${\varphi }_0{\prod }_{j=1}^{n}exp\left({\phi }_j{\check{\mathbf{e}}}_j\right)$ can no longer be simplified, regardless of the values of the ${\phi }_j$ coefficients. Inasmuch as the sum, $f_0+{\sum }_{j=1}^n{f}_j{\check{\mathbf{e}}}_j$, is irreducible in the additive representation, for it cannot be written with fewer addends.

2.4. Product in the Additive Representation with Multiplicative Variables

The product can be written with multiplicative variables in the additive representation from (5) and (11),

$$\begin{array}{c}\stackrel{o}{\alpha }\stackrel{o}{\beta }={\alpha }_0{\beta }_0\prod _{j=1}^n{e}^{\left({\alpha }_j+{\beta }_j\right){\check{\mathbf{e}}}_j}⟼\hfill \\ \hfill {\alpha }_0{\beta }_0\prod _{k=1}^{n}cos\left({\alpha }_k+{\beta }_k\right)+{\alpha }_0{\beta }_0\sum _{j=1}^n\prod _{k\ne j}^{n}cos\left({\alpha }_k+{\beta }_k\right)sin\left({\alpha }_j+{\beta }_j\right){\check{\mathbf{e}}}_j.\end{array}$$

(15)

The conditions for a product to give a zero scalar component or a null scator in terms of the additive variables have been discussed before ([11], Section 3.1). Consider these conditions using multiplicative variables.

Zero additive scalar component: If any one of the cosine arguments is zero, the scalar component of $\stackrel{o}{\alpha }\stackrel{o}{\beta }$ is zero. Let it be the argument of the $l^{\mathrm{th}}$ component

$$cos\left({\alpha }_l+{\beta }_l\right)=cos\left(\frac{\pi }{2}\right)=0.$$

This is condition $a_0{b}_0=a_l{b}_l$ in additive variables, since $1=\frac{a_l{b}_l}{a_0{b}_0}=tan{\alpha }_{l}tan{\beta }_l$ and $cos{\alpha }_{l}cos{\beta }_l=sin{\alpha }_{l}sin{\beta }_l$ can be rewritten as the cosine of the sum of angles, $cos\left({\alpha }_l+{\beta }_l\right)=0$. A particular value of the previous case is ${\alpha }_l=\frac{\pi }{2}$, then ${\beta }_l=0$, that corresponds, in additive variables, to $\stackrel{o}{\alpha }=a_l{\check{\mathbf{e}}}_l$ when the ${\check{\mathbf{e}}}_l$ component of $\stackrel{o}{\beta }$ is zero, $b_l=0$.

Zero products: If two or more director arguments are equal to $\frac{\pi }{2}$ $\mathrm{mod}\pi$, a scator is zero in the additive representation. Let the ${\check{\mathbf{e}}}_l$ and ${\check{\mathbf{e}}}_q$ arguments be $\frac{\pi }{2}$, from (15), the scalar component and all director components with $j\ne l,q$ involve a ${cos}^2\left(\frac{\pi }{2}\right)$ factor, the ${\check{\mathbf{e}}}_l$ and ${\check{\mathbf{e}}}_q$ coefficients involve a $cos\left(\frac{\pi }{2}\right)$ factor,

$$\begin{array}{c}\stackrel{o}{\alpha }\stackrel{o}{\beta }={\alpha }_0{\beta }_0\prod _{k\ne l,q}^{n}cos\left({\alpha }_k+{\beta }_k\right){cos}^2\left(\frac{\pi }{2}\right)\hfill \\ \hfill +{\alpha }_0{\beta }_0\sum _{j=1}^n\prod _{k\ne j,l,q}^{n}cos\left({\alpha }_k+{\beta }_k\right){cos}^{2-{\delta }_{jl}-{\delta }_{jq}}\left(\frac{\pi }{2}\right)sin\left({\alpha }_j+{\beta }_j\right){\check{\mathbf{e}}}_j=0+\sum _{j=1}^{n}0{\check{\mathbf{e}}}_j.\end{array}$$

(16)

The multiplicative (11) and additive (9a)–(9c) definitions of the product are equivalent. In the early papers, this equivalence led us to a wrong statement regarding the product associativity in the additive representation, that has now been corrected [11]. The lack of associativity in the additive representation arises because the single multiplication rule in the polar representation is mapped into three different rules in the additive representation. When different rules in the additive representation have to be used, product associativity becomes an issue. Some examples will be given in the next sections.

3. Victoria Equation

The main theorems, stated in this section, establish the relationship between a scator raised to an integer power and angle multiplication by the integer number. Examples are worked out to become familiar with the theorems in the multiplicative and additive representations. The post-evaluation criterion is introduced to exhibit the equivalence between representations when the product is not associative in the additive representation. The conditions for a nilpotent element and a scator raised to a given power with zero scalar component are considered in Section 3.1. The exponential addition theorem is satisfied component wise in the multiplicative representation of scator algebra, thus the following proposition.

Theorem 3.

In the multiplicative representation, for a scator $\stackrel{o}{\phi }\in {\mathbb{S}}^{1+n}$ raised to the power $m\in \mathbb{Z}$, the exponent m distributes over the scator factors:

$${\stackrel{o}{\phi }}^m={\left({\phi }_0\prod _{j=1}^n{e}^{{\phi }_j{\check{\mathbf{e}}}_j}\right)}^m={\phi }_0^m\prod _{j=1}^n{e}^{m{\phi }_j{\check{\mathbf{e}}}_j}.$$

(17)

Proof. 

From (11), if $\stackrel{o}{\alpha }=\stackrel{o}{\beta }$

$${\stackrel{o}{\alpha }}^2=\left({\alpha }_0\prod _{j=1}^n{e}^{{\alpha }_j{\check{\mathbf{e}}}_j}\right)\left({\alpha }_0\prod _{j=1}^n{e}^{{\alpha }_j{\check{\mathbf{e}}}_j}\right)={\alpha }_0^2\prod _{j=1}^n{e}^{2{\alpha }_j{\check{\mathbf{e}}}_j},$$

by induction, for $m\in \mathbb{N}$, the m^th power of a scator in the multiplicative representation is

$${\stackrel{o}{\phi }}^m={\left({\phi }_0\prod _{j=1}^n{e}^{{\phi }_j{\check{\mathbf{e}}}_j}\right)}^m={\phi }_0^m\prod _{j=1}^n{e}^{m{\phi }_j{\check{\mathbf{e}}}_j}.$$

(18)

The multiplicative inverse is:

$${\stackrel{o}{\phi }}^{-1}={∥\stackrel{o}{\phi }∥}^{-2}{\stackrel{o}{\phi }}^{*}={\phi }_0^{-1}\prod _{j=1}^n{e}^{-{\phi }_j{\check{\mathbf{e}}}_j}.$$

Replace ${\phi }_0\to {\phi }_0^{-1}$ and ${\phi }_j\to -{\phi }_j$ in (18),

$${\left({\stackrel{o}{\phi }}^{-1}\right)}^m={\left({\phi }_0^{-1}\prod _{j=1}^n{e}^{{\phi }_j{\check{\mathbf{e}}}_j}\right)}^m={\left({\phi }_0^{-1}\right)}^m\prod _{j=1}^n{e}^{m\left(-{\phi }_j\right){\check{\mathbf{e}}}_j},$$

but since ${\phi }_0,{\phi }_j\in \mathbb{R}$, ${\left({\phi }_0^{-1}\right)}^m={\phi }_0^{-m}$ and $m\left(-{\phi }_j\right)=-m{\phi }_j$, thus ${\stackrel{o}{\phi }}^{-m}={\phi }_0^{-m}{\prod }_{j=1}^n{e}^{-m{\phi }_j{\check{\mathbf{e}}}_j}$.

Therefore, (18) is satisfied for integer m, where ${\left(\stackrel{o}{\phi }\right)}^0\equiv \stackrel{0}{1}$. □

Since the scator product is associative in the multiplicative representation, there is no need to place an explicit association in the products, that is, ${\stackrel{o}{\phi }}^3=\stackrel{o}{\phi }\stackrel{o}{\phi }\stackrel{o}{\phi }$. For example, consider the unit magnitude scator $\stackrel{o}{\phi }=exp\left(\frac{\pi }{4}{\check{\mathbf{e}}}_1\right)exp\left(2{\check{\mathbf{e}}}_2\right)$, then ${\stackrel{o}{\phi }}^3=exp\left(\frac{3\pi }{4}{\check{\mathbf{e}}}_1\right)exp\left(6{\check{\mathbf{e}}}_2\right)$.

The multiplicative to additive transformation together with Theorem 3, allow for the following generalization of De Moivre formula in scator algebra.

Theorem 4.

Provided that the product of the factors and its components are associative, a scator $\stackrel{o}{\phi }\in {\mathbb{S}}^{1+n}$ raised to the power $m\in \mathbb{Z}$, can be written in the additive representation as:

$$\begin{array}{c}{\left({\phi }_0\prod _{k=1}^{n}cos{\phi }_k+\sum _{j=1}^n{\phi }_0\prod _{k\ne j}^{n}cos{\phi }_{k}sin{\phi }_j{\check{\mathbf{e}}}_j\right)}^m\hfill \\ \hfill ={\phi }_0^m\prod _{k=1}^{n}cos\left(m{\phi }_j\right)+\sum _{j=1}^n{\phi }_0^m\prod _{k\ne j}^{n}cos\left(m{\phi }_k\right)sin\left(m{\phi }_j\right){\check{\mathbf{e}}}_j.\end{array}$$

(19)

Proof. 

From the multiplicative to additive transformation (5) applied to both sides of Equation (17), Equation (19) is obtained. While (17) is valid for any arguments, the possible lack of associativity in the additive representation could mar (19), because the left side of the equation is product associativity dependent while the right side is not. Theorem 1 establishes the associativity sufficient condition in the additive representation, namely, that none of the possible product associations give a scator with zero scalar additive component for $n>1$. The multiplicative to additive transformation (5), involves the product of the scator components (4a). Equation (19) in terms of the director components factors is:

$${\left({\phi }_0\prod _{j=1}^n\left(cos{\phi }_j+sin{\phi }_j{\check{\mathbf{e}}}_j\right)\right)}^m={\phi }_0^m\prod _{j=1}^n\left(cos\left(m{\phi }_j\right)+sin\left(m{\phi }_j\right){\check{\mathbf{e}}}_j\right).$$

(20)

This equation and thus Equation (19) is satisfied if none of the $m\times n$ products on the left of (20), produce a scator with zero additive scalar component for $n>1$. If there is only a single one non-zero director component, the scator product becomes a bilinear operation in the additive representation (9a)–(9c), associativity of the product is then insured even if the additive scalar component is zero. □

For historical reasons, we shall refer to (19) as the victoria equation.

Example 1.

Consider the victoria equation in $1+2$ dimensions with $m=2$,

$$\begin{array}{c}{\left(cos{\phi }_{1}cos{\phi }_2+cos{\phi }_{2}sin{\phi }_1{\check{\mathbf{e}}}_1+cos{\phi }_{1}sin{\phi }_2{\check{\mathbf{e}}}_2\right)}^2=\hfill \\ \hfill cos\left(2{\phi }_1\right)cos\left(2{\phi }_2\right)+cos\left(2{\phi }_2\right)sin\left(2{\phi }_1\right){\check{\mathbf{e}}}_1+cos\left(2{\phi }_1\right)sin\left(2{\phi }_2\right){\check{\mathbf{e}}}_2,\end{array}$$

(21)

where ${\phi }_0^2$ has been canceled on both sides of the equation. The squaring operation on the LHS of (21) can be evaluated from (9a),

$$\begin{array}{c}{\left(f_0+f_1{\check{\mathbf{e}}}_1+f_2{\check{\mathbf{e}}}_2\right)}^2=f_0^2\left(1-\frac{f_1^2}{f_0^2}\right)\left(1-\frac{f_2^2}{f_0^2}\right)+2f_0{f}_1\left(1-\frac{f_2^2}{f_0^2}\right){\check{\mathbf{e}}}_1\hfill \\ \hfill +2f_0{f}_2\left(1-\frac{f_1^2}{f_0^2}\right){\check{\mathbf{e}}}_2,\end{array}$$

(22)

replacement in terms of the multiplicative variables from comparison with (21) gives:

$$\begin{array}{c}{\left(cos{\phi }_{1}cos{\phi }_2+cos{\phi }_{2}sin{\phi }_1{\check{\mathbf{e}}}_1+cos{\phi }_{1}sin{\phi }_2{\check{\mathbf{e}}}_2\right)}^2\hfill \\ ={cos}^2{\phi }_1{cos}^2{\phi }_2\left(1-{tan}^2{\phi }_1\right)\left(1-{tan}^2{\phi }_2\right)\\ \hfill +2cos{\phi }_1{cos}^2{\phi }_{2}sin{\phi }_1\left(1-{tan}^2{\phi }_2\right){\check{\mathbf{e}}}_1+2cos{\phi }_2{cos}^2{\phi }_{1}sin{\phi }_2\left(1-{tan}^2{\phi }_1\right){\check{\mathbf{e}}}_2.\end{array}$$

This result is substituted in (21), and equating term to term:

scalar components: $\left({cos}^2{\phi }_1-{sin}^2{\phi }_1\right)\left({cos}^2{\phi }_2-{sin}^2{\phi }_2\right)=cos\left(2{\phi }_1\right)cos\left(2{\phi }_2\right),$

${\check{\mathbf{e}}}_1$ components: $2cos{\phi }_{1}sin{\phi }_1\left({cos}^2{\phi }_2-{sin}^2{\phi }_2\right)=cos\left(2{\phi }_2\right)sin\left(2{\phi }_1\right),$and the ${\check{\mathbf{e}}}_2$ equality: $2cos{\phi }_{2}sin{\phi }_2\left({cos}^2{\phi }_1-{sin}^2{\phi }_1\right)=cos\left(2{\phi }_1\right)sin\left(2{\phi }_2\right).$

These expressions are products of familiar double angle trigonometric identities.

Definition 3.

If the Victoria equation (19), is evaluated symbolically, that is, without entering any specific values for the arguments, the (9a) product rule should always be used. If thereafter, particular scator component values are inserted, the procedure is known as the postevaluation algorithm.

The Victoria equation is satisfied if the post-evaluation algorithm is adopted, even if associativity of the factors is not fulfilled. In this case, associativity in the additive representation should not have any precedence parenthesis if the product is evaluated symbolically prior to entering specific values.

Example 2.

Evaluate ${\stackrel{o}{\phi }}^3$ from repeated use of (9a),

$$\begin{array}{c}{\stackrel{o}{\phi }}^3=\stackrel{o}{\phi }\stackrel{o}{\phi }\stackrel{o}{\phi }={\left(f_0+f_1{\check{\mathbf{e}}}_1+f_2{\check{\mathbf{e}}}_2\right)}^3=f_0^3\left(1-\frac{3f_1^2}{f_0^2}\right)\left(1-\frac{3f_2^2}{f_0^2}\right)\hfill \\ \hfill +f_1\left(1-\frac{3f_2^2}{f_0^2}\right)\left(3f_0^2-f_1^2\right){\check{\mathbf{e}}}_1+f_2\left(1-\frac{3f_1^2}{f_0^2}\right)\left(3f_0^2-f_2^2\right){\check{\mathbf{e}}}_2.\end{array}$$

(23)

For ${\phi }_0=1$, ${\phi }_1=\frac{\pi }{4}$, ${\phi }_2=2$, the additive variables are $f_0=f_1=\frac{1}{\sqrt{2}}cos\left(2\right)$, and $f_2=\frac{1}{\sqrt{2}}sin\left(2\right)$. The post-evaluated expression, from (23) is ${\left(f_0+f_1{\check{\mathbf{e}}}_1+f_2{\check{\mathbf{e}}}_2\right)}^3\approx -0.679+0.679{\check{\mathbf{e}}}_1+0.198{\check{\mathbf{e}}}_2$. The same result is obtained from the RHS of (19), $-\frac{1}{\sqrt{2}}cos\left(6\right)+\frac{1}{\sqrt{2}}cos\left(6\right){\check{\mathbf{e}}}_1-\frac{1}{\sqrt{2}}sin\left(6\right){\check{\mathbf{e}}}_2$. The outcome is identical in the multiplicative representation. The post-evaluation procedure avoids, in this case, the zero scalar singularity. However, evaluate ${\stackrel{o}{\phi }}^2=\stackrel{o}{\phi }\stackrel{o}{\phi }$ in the additive representation with the specific values. Since $f_0=f_1$ from (9a), ${\stackrel{o}{\phi }}^2=\left(\stackrel{o}{\phi }\stackrel{o}{\phi }\right)=2\left(f_0^2-f_2^2\right){\check{\mathbf{e}}}_1$. The product $\left(\stackrel{o}{\phi }\stackrel{o}{\phi }\right)\stackrel{o}{\phi }$, since $\left(\stackrel{o}{\phi }\stackrel{o}{\phi }\right)$ has zero additive scalar component, has to be evaluated with (9b),

$$\left(\stackrel{o}{\phi }\stackrel{o}{\phi }\right)\stackrel{o}{\phi }=\left(2\left(f_0^2-f_2^2\right){\check{\mathbf{e}}}_1\right)\left(f_0+f_0{\check{\mathbf{e}}}_1+f_2{\check{\mathbf{e}}}_2\right)=2\left(f_0^2-f_2^2\right)\left(-f_0+f_0{\check{\mathbf{e}}}_1-f_2{\check{\mathbf{e}}}_2\right),$$

an altogether different expression is obtained compared with ${\stackrel{o}{\phi }}^3=\stackrel{o}{\phi }\stackrel{o}{\phi }\stackrel{o}{\phi }$, given by (23). The numerical value of the non associative product in this example is $\left(\stackrel{o}{\phi }\stackrel{o}{\phi }\right)\stackrel{o}{\phi }\approx -0.19+0.19{\check{\mathbf{e}}}_1-0.42{\check{\mathbf{e}}}_2.$ If the products are not associative, the way the m products in ${\stackrel{o}{\phi }}^m$ are associated, has to be stated explicitly.

Corollary 2.

If the coefficients of the director components in multiplicative variables of a scator $\stackrel{o}{\phi }$ are algebraic real numbers, then ${\stackrel{o}{\phi }}^m$, $m\in \mathbb{Z}$ is associative in the additive representation.

Proof. 

The multiplicative coefficients ${\phi }_j$ of a scator raised to the power $m\in \mathbb{Z}$ are $m{\phi }_j$. Since the product $m{\phi }_j$ is also algebraic but $\pi$ is transcendental, $m{\phi }_j$ cannot be equal to $\frac{\pi }{2}$. At least one component $m{\phi }_j=\frac{\pi }{2}$ is necessary for a scator product to have a null scalar component. This, in turn, is a necessary condition for non-associativity. □

Corollary 3.

If none of the director coefficients in multiplicative variables of a scator $\stackrel{o}{\phi }$ is of the form $\frac{\pi }{2p}$, $\left|p\right|>\left|m\right|$, $p,m\in \mathbb{Z}$, then ${\stackrel{o}{\phi }}^m$, is associative in the additive representation.

Proof. 

This result follows from the Victoria equation (19), the zero additive scalar component condition in Section 2.4 and Theorem 1. □

3.1. Nilpotent and Nil-Scalar-Potent Elements

Elements whose three components have equal absolute value in the additive representation, are the only non trivial square nilpotent elements in 1 + 2 dimensional imaginary scator algebra ([15], Lemma 1). The present formalism permits a more encompassing proposition.

Lemma 2.

A scator $\stackrel{o}{\phi }={\phi }_0{\prod }_{k=1}^{n}cos\left({\phi }_k\right)+{\sum }_{j=1}^n{\phi }_0{\prod }_{k\ne j}^{n}cos\left({\phi }_k\right)sin\left({\phi }_j\right){\check{\mathbf{e}}}_j$, is power m nilpotent in the additive representation, if ${\phi }_l={\phi }_q=\pm \frac{\pi }{2m}$ mod π, for any two different director components, $l\ne q$ and none of the ${\phi }_j$’s different from ${\phi }_l,{\phi }_q$ are of the form $\frac{\pi }{2p}$ with $p<m$.

Proof. 

The scator

$$\stackrel{o}{\phi }={\phi }_0\prod _{k\ne l,q}^{n}cos\left({\phi }_k\right){cos}^2\left(\frac{\pi }{2m}\right)+{\phi }_0\sum _{j=1}^n\prod _{k\ne j}^{n}cos\left({\phi }_k\right)cos\left(\frac{\pi }{2m}\right)sin\left({\phi }_j\right){\check{\mathbf{e}}}_j,$$

evaluated to the $m^{th}$ power from (19) is,

$$\begin{array}{c}{\stackrel{o}{\phi }}^m={\phi }_0^m\prod _{k\ne l,q}^{n}cos\left(m{\phi }_k\right){cos}^2\left(\frac{\pi }{2}\right)\hfill \\ \hfill +{\phi }_0^m\sum _{j\ne l}^n\prod _{k\ne j,l,q}^{n}cos\left(m{\phi }_k\right){cos}^{2-{\delta }_{jl}-{\delta }_{jq}}\left(\frac{\pi }{2}\right)sin\left(m{\phi }_j\right){\check{\mathbf{e}}}_j.\end{array}$$

However, all terms involve at least a $cos\left(\frac{\pi }{2}\right)=0$ factor, thus ${\stackrel{o}{\phi }}^m=0$. The condition on the ${\phi }_{j\ne l,q}$ director coefficients insures that the scator is not nilpotent for any smaller m. □

Definition 4.

A scator $\stackrel{o}{\phi }$ is power m nil-scalar potent if the additive scalar component of ${\stackrel{o}{\phi }}^m$ is zero.

Corollary 4.

A scator $\stackrel{o}{\phi }\in {\mathbb{S}}^{1+n}\setminus {\mathbb{S}}_j^{1+1}$ is power m nil-scalar potent, if ${\phi }_l=\pm \frac{\pi }{2m}$ mod π and none of the ${\phi }_j$’s different from ${\phi }_l$ are of the form $\frac{\pi }{2p}$ with $p<m$. The products of ${\stackrel{o}{\phi }}^{m+1}$ are not associative in the additive representation.

Proof. 

The proof is analogous to Lemma 2, but only one director component is requested to satisfy ${\phi }_l=\pm \frac{\pi }{2m}$ mod $\pi$,

$$\stackrel{o}{\phi }={\phi }_0\prod _{k\ne l}^{n}cos\left({\phi }_k\right)cos\left(\frac{\pi }{2m}\right)+{\phi }_0\sum _{j=1}^n\prod _{k\ne j}^{n}cos\left({\phi }_k\right)sin\left({\phi }_j\right){\check{\mathbf{e}}}_j,$$

then, the ${\check{\mathbf{e}}}_l$ director component will not vanish

$${\stackrel{o}{\phi }}^m={\phi }_0^m\prod _{k\ne l}^{n}cos\left(m{\phi }_k\right)sin\left(\pm \frac{\pi }{2}\right){\check{\mathbf{e}}}_l.$$

Since $\stackrel{o}{\phi }$ has two or more non zero director components and ${\stackrel{o}{\phi }}^m$ has a vanishing additive scalar component, from Theorem 2, the product ${\stackrel{o}{\phi }}^m\stackrel{o}{\phi }$ is in general, not associative. □

It is not straight forward to state whether a scator number in the additive representation with additive variables, that is, $\stackrel{o}{\phi }=f_0+{\sum }_{j=1}^n{f}_j{\check{\mathbf{e}}}_j$, is nil-scalar-potent for some exponent m. A possible route to giving an answer without a direct calculation is to evaluate the multiplicative director coefficients via (7a), ${\phi }_j=arctan\left(\frac{f_j}{f_0}\right)$. An m nil-scalar-potent scator requires that ${\phi }_j=\pm \frac{\pi }{2m}$ for any j from 1 to n. Thus, for each component, evaluate

$$\frac{\pi }{2arctan\left(\frac{f_j}{f_0}\right)}=m,\mathrm{if}m\in \mathbb{Z},$$

(24)

if m is an integer, the scator will be power m nil-scalar-potent. It is of course possible that different director components have different ms that satisfy (24), then for each $m_j\in \mathbb{Z}$ the scator will be power $m_j$ nil-scalar-potent. If two or more components satisfy the condition (24), the scator is power m nilpotent.

Example 3.

Consider the scator,

$$\stackrel{o}{\phi }=f_0+f_0\sum _{j\ne l,q}^{n}tan\left({\phi }_j\right){\check{\mathbf{e}}}_j+f_0\left(2-\sqrt{3}\right){\check{\mathbf{e}}}_l-f_0\left(2-\sqrt{3}\right){\check{\mathbf{e}}}_q,$$

(25)

where $f_0={\prod }_{k=1}^{n}cos\left({\phi }_k\right)$. In the additive representation, identify the different director components with equal (absolute value) coefficients. For each pair, evaluate

$$\frac{\pi }{2arctan\left(\frac{f_l}{f_0}\right)}=\frac{\pi }{2arctan\left(2-\sqrt{3}\right)}=\frac{\pi }{2\frac{\pi }{12}}=6.$$

Thus the scator (25) is power 6 nilpotent.

In contrast with split-quaternions, only the identity element is idempotent in elliptic scators. To prove it, consider ${\stackrel{o}{\phi }}^2=\stackrel{o}{\phi }$ in the multiplicative form:

$${\phi }_0^2\prod _{j=1}^n{e}^{2{\phi }_j{\check{\mathbf{e}}}_j}={\phi }_0\prod _{j=1}^n{e}^{{\phi }_j{\check{\mathbf{e}}}_j},$$

${\phi }_0^2={\phi }_0$ only for ${\phi }_0=1$, and ${\phi }_j=2{\phi }_j$ only if ${\phi }_j=0$, thus only the identity is idempotent.

4. Geometric Interpretation

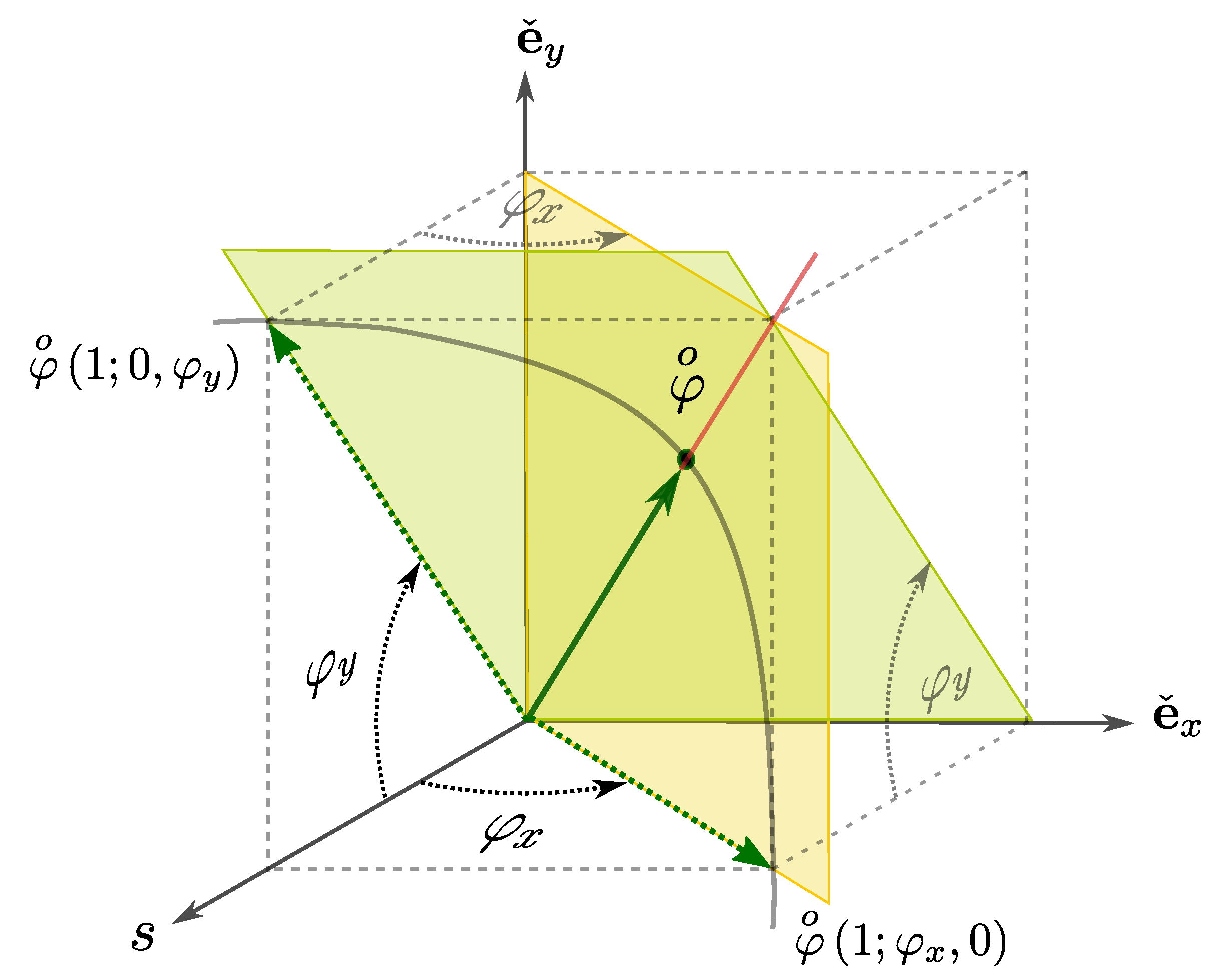
The scalar component and two director components can be depicted in orthogonal directions in a three dimensional plot. The director coefficients in multiplicative variables ${\phi }_x$ and ${\phi }_y$ are geometrically represented by the angle between the scalar (real) axis and the projection onto the corresponding hyperimaginary director axis as shown in Figure 1. Notice that these angles are neither spherical coordinate angles nor direction cosines, nor Euler angles. Positive scator angles are measured taking the scalar axis as reference and measuring towards the corresponding positive director axis. In low dimensional cases, letters are sometimes used for the director coefficient subindices instead of numbers.

The product of two scators with constant coefficients involves a scaling and a rotation in each scalar-hypercomplex plane. Consider the product of unit magnitude scators so that scaling is not an issue in the following discussion. The magnitude of a product is equal to the product of the magnitudes provided that the products are associative [11]. Therefore, for $n>1$, the product of unit magnitude scators will remain unitary if the scalar component of the products and its scator conjugates do not vanish. In particular, the powers of associative unit scators lie on the isometric scator surface, called a cusphere [17]. The unit cusphere is an n dimensional surface embedded in a $1+n$ dimensional space that satisfies the condition $∥\stackrel{o}{\phi }∥=\stackrel{o}{1}$. The additive representation with multiplicative variables of a unit scator is:

$$\stackrel{o}{\phi }=\prod _{k=1}^{n}cos{\phi }_k+\sum _{j=1}^n\prod _{k\ne j}^{n}cos{\phi }_{k}sin{\phi }_j{\check{\mathbf{e}}}_j,$$

where ${\phi }_0=1$. If $\stackrel{o}{\phi }\in {\mathbb{S}}^{1+2}$,

$$\stackrel{o}{\phi }\left(1;{\phi }_x,{\phi }_y\right)=cos{\phi }_{x}cos{\phi }_y+cos{\phi }_{y}sin{\phi }_x{\check{\mathbf{e}}}_x+cos{\phi }_{x}sin{\phi }_y{\check{\mathbf{e}}}_y,$$

(26)

where, on the left, the scator components are explicitly shown, the scalar component is separated by a semicolon from the director components that are separated by commas. Recall that Greek letters with subindices represent multiplicative variables whereas Latin letters, that is, $\stackrel{o}{\phi }\left(f_0;f_x,f_y\right)$, represent additive variables. The scator (26) can be factored as $\stackrel{o}{\phi }=\left(cos{\phi }_x+sin{\phi }_x{\check{\mathbf{e}}}_x\right)cos{\phi }_y+cos{\phi }_{x}sin{\phi }_y{\check{\mathbf{e}}}_y$, so that the angle ${\phi }_x$ in the $s,{\check{\mathbf{e}}}_x$ projection (the scalar axis is labeled s for short) is preserved regardless of the ${\phi }_y$ angle. The plane defined by the unit scators $\stackrel{o}{\phi }\left(1;{\phi }_x,0\right)$ and ${\check{\mathbf{e}}}_y$ is depicted in yellow in Figure 1. Similarly, $\stackrel{o}{\phi }=cos{\phi }_{y}sin{\phi }_x{\check{\mathbf{e}}}_x+\left(cos{\phi }_y+sin{\phi }_y{\check{\mathbf{e}}}_y\right)cos{\phi }_x$, evinces that the angle in $s,{\check{\mathbf{e}}}_y$ is preserved regardless of the ${\phi }_x$ angle, as shown in Figure 1. The plane defined by the scators $\stackrel{o}{\phi }\left(1;0,{\phi }_y\right)$ and ${\check{\mathbf{e}}}_x$ is depicted in green. The scator (26) can then be viewed as the intersection of these two planes.

Lemma 3.

There is a unique decomposition of a scator in terms of its magnitude and the product of unit scators with single non-vanishing orthogonal director components.

Proof. 

The proof follows from Equation (4b) proceeding in the inverse direction. The multiplicative scalar ${\phi }_0$ represents the scator magnitude. If ${\phi }_0$ is factored, the remaining unit magnitude scator in ${\mathbb{S}}^{1+n}$ is:

$$\prod _{k=1}^{n}cos\left({\phi }_k\right)+\sum _{j=1}^n\prod _{k\ne j}^{n}cos\left({\phi }_k\right)sin\left({\phi }_j\right){\check{\mathbf{e}}}_j.$$

each ${\check{\mathbf{e}}}_j$ director component can be factored with a Euler type expression $\left(cos{\phi }_j+sin{\phi }_j{\check{\mathbf{e}}}_j\right)$,

$$\stackrel{o}{\phi }={\phi }_0\prod _{j=1}^n\left(cos{\phi }_j+sin{\phi }_j{\check{\mathbf{e}}}_j\right).$$

Since ${\phi }_j=arctan\left(\frac{f_j}{f_0}\right)$ and ${\phi }_0=\left|f_0\right|\stackrel{n}{\prod _{j=1}}\sqrt{1+\frac{f_j^2}{f_0^2}}$, an arbitrary scator in additive variables $\stackrel{o}{\phi }=f_0+{\sum }_{j=1}^n{f}_j{\check{\mathbf{e}}}_j\in {\mathbb{S}}^{1+n}$, can then be factored as:

$$\stackrel{o}{\phi }=\left|f_0\right|\stackrel{n}{\prod _{j=1}}\sqrt{1+\frac{f_j^2}{f_0^2}}\prod _{j=1}^n\left(cos\left(arctan\left(\frac{f_j}{f_0}\right)\right)+sin\left(arctan\left(\frac{f_j}{f_0}\right)\right){\check{\mathbf{e}}}_j\right).$$

□

The products in the above expression can be evaluated to recover the original scator,

$$cos\left(arctan\left(\frac{f_j}{f_0}\right)\right)=\frac{\mathrm{Sgn}\left(cos{\phi }_j\right)\left|f_0\right|}{\sqrt{f_0^2+f_j^2}}=\frac{\mathrm{Sgn}\left(cos{\phi }_j\right)}{\sqrt{1+\frac{f_j^2}{f_0^2}}}$$

and

$$sin\left(arctan\left(\frac{f_j}{f_0}\right)\right)=\frac{f_j}{\sqrt{f_0^2+f_j^2}}=\frac{f_j/\left|f_0\right|}{\sqrt{1+\frac{f_j^2}{f_0^2}}};$$

thus,

$$\stackrel{o}{\phi }=\left|f_0\right|\prod _{j=1}^n\left(\mathrm{Sgn}\left(cos{\phi }_j\right)+\frac{f_j}{\left|f_0\right|}{\check{\mathbf{e}}}_j\right).$$

This product can then be readily written as a sum for scators since all director components are orthogonal Equation(12) [17],

$$\stackrel{o}{\phi }=\left|f_0\right|\left(\mathrm{Sgn}\left(f_0\right)+\sum _{j=1}^n\frac{f_j}{\left|f_0\right|}{\check{\mathbf{e}}}_j\right),$$

where $\mathrm{Sgn}\left(f_0\right)={\prod }_{j=1}^n\mathrm{Sgn}\left(cos{\phi }_j\right)$. Thus

$$\stackrel{o}{\phi }=\left|f_0\right|\mathrm{Sgn}\left(f_0\right)+\frac{\left|f_0\right|}{\left|f_0\right|}\sum _{j=1}^n{f}_j{\check{\mathbf{e}}}_j=f_0+\sum _{j=1}^n{f}_j{\check{\mathbf{e}}}_j.$$

The ${\mathbb{S}}^{1+n}$ scator decomposition can be geometrically represented as the projection onto n planes. Each of these $\left(s,{\check{\mathbf{e}}}_j\right)\in {\mathbb{S}}_j^{1+1}$ planes, share the scalar axis but have a single director component orthogonal to the remaining director units.

The projections of the ${\mathbb{S}}^{1+2}$ dimensional scator (26), depicted in Figure 1 are,

$$\stackrel{o}{\phi }\left(1;{\phi }_x,0\right)=cos{\phi }_x+sin{\phi }_x{\check{\mathbf{e}}}_x,\stackrel{o}{\phi }\left(1;0,{\phi }_y\right)=cos{\phi }_y+sin{\phi }_y{\check{\mathbf{e}}}_y.$$

Scator elements (unlike other objects like vectors) can be written as the product of its projections; In this example, $\stackrel{o}{\phi }\left(1;{\phi }_x,{\phi }_y\right)=\stackrel{o}{\phi }\left(1;{\phi }_x,0\right)\stackrel{o}{\phi }\left(1;0,{\phi }_y\right)$. Notice that the $1+2D$ scator as well as its $1+1D$ projections are unitary scators. This is only possible because the scator magnitude (10) is not a quadratic Euclidean form.

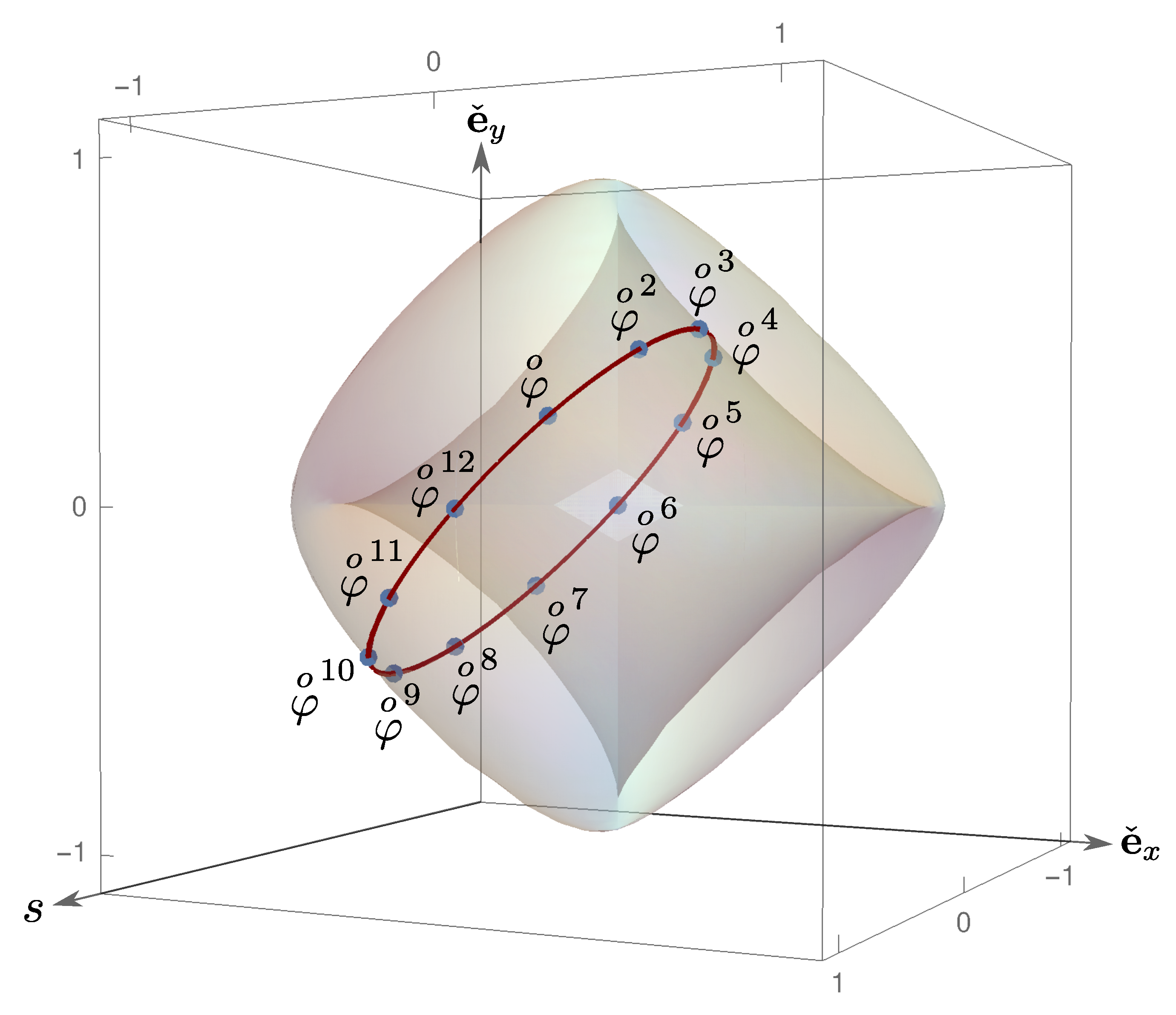
The representation (26) lends nicely to parametrically plotting the cusphere as shown in Figure 2. The square magnitude of $\stackrel{o}{\phi }\left(1;{\phi }_x,{\phi }_y\right)$ in terms of additive components, from (10), is ${∥\stackrel{o}{\phi }∥}^2={\stackrel{o}{1}}^2={cos}^2{\phi }_x{cos}^2{\phi }_y\left(1+{tan}^2{\phi }_x\right)\left(1+{tan}^2{\phi }_y\right).$ The Pythagorean identity in ${\mathbb{S}}^{1+2}$ scator space is:

$$1=\left({sin}^2{\phi }_x+{cos}^2{\phi }_x\right)\left({sin}^2{\phi }_y+{cos}^2{\phi }_y\right).$$

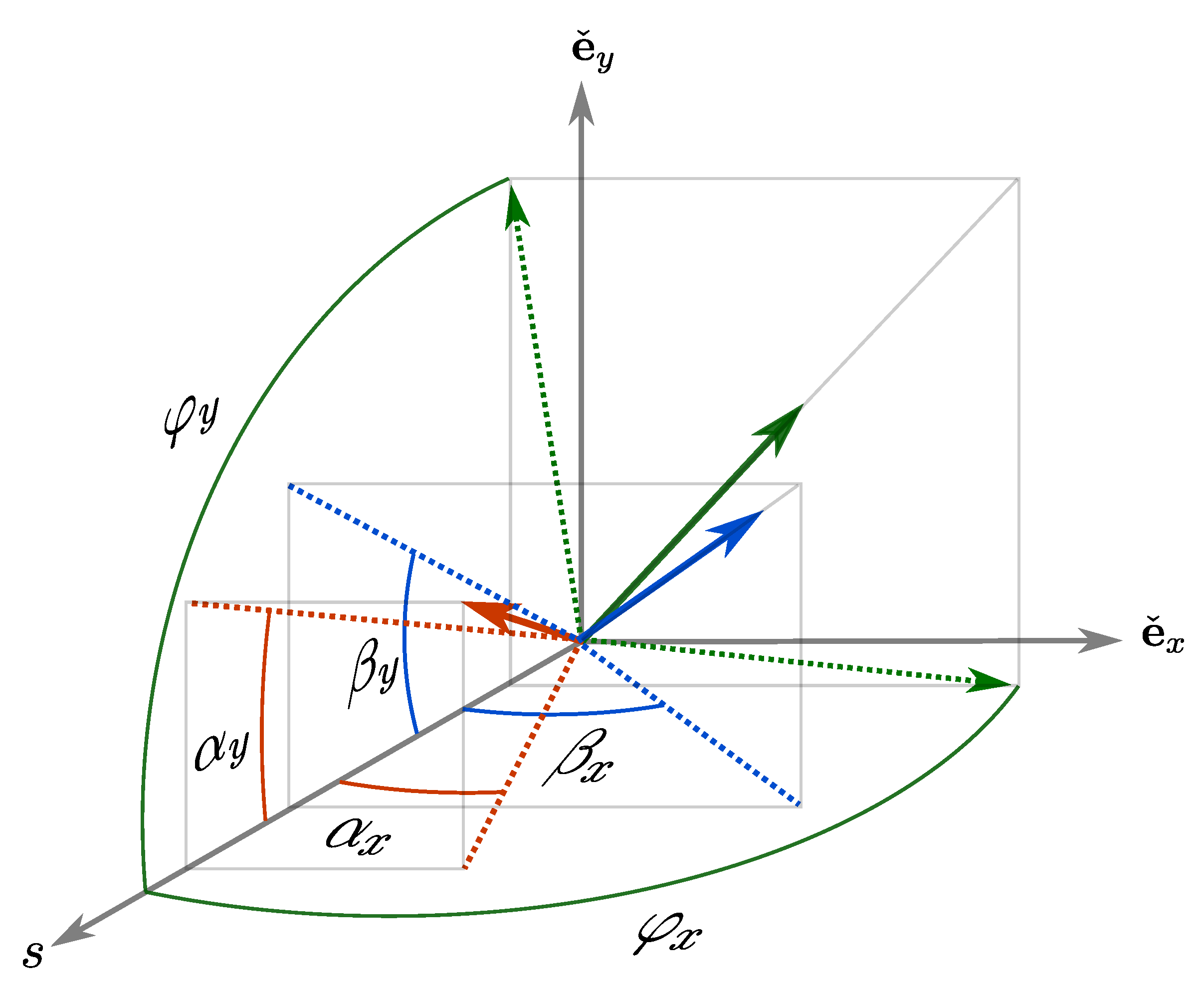
The geometric interpretation of the product for arbitrary unit scators is rather rich and complex. The product requires the sum of scator angles in each direction measured with respect to the scalar axis. A qualitative geometrical representation is depicted in Figure 3. Notice that both angles are involved in each additive component as evinced in (11).

In ${\mathbb{S}}^{1+2}$, there are three degrees of freedom, $f_0;f_x,f_y$ in additive variables or ${\phi }_0;{\phi }_1,{\phi }_2$ in multiplicative variables. Unit magnitude scators, $∥\stackrel{o}{\phi }∥=\stackrel{o}{1}={\phi }_0$, leave two independent quantities: in multiplicative variables, the director coefficients ${\phi }_x,{\phi }_y$, whereas the additive variables are related by $1=f_0^{-2}\left(f_0^2+f_x^2\right)\left(f_0^2+f_y^2\right)$. The $\stackrel{o}{\phi }\in {\mathbb{S}}^{1+2}$ unit scator raised to the power m, from the Victoria equation is:

$${\stackrel{o}{\phi }}^m=cos\left(m{\phi }_x\right)cos\left(m{\phi }_y\right)+cos\left(m{\phi }_y\right)sin\left(m{\phi }_x\right){\check{\mathbf{e}}}_x+cos\left(m{\phi }_x\right)sin\left(m{\phi }_y\right){\check{\mathbf{e}}}_y.$$

(27)

The product of unit scators in the scalar $s,{\check{\mathbf{e}}}_x$ plane or the $s,{\check{\mathbf{e}}}_y$ plane, represents proper rotations in these planes. This is expected, since ${\mathbb{S}}_j^{1+1}$ is isomorphic to complex algebra for any one j from 1 to n. The novel part comes from scators that do not lie on these planes.

4.1. Scators with Equal Hypercomplex Components

Consider, to begin with, unit magnitude scators with equal hypercomplex director components, ${\phi }_x={\phi }_y$, from (26)

$$\stackrel{o}{\phi }={cos}^2{\phi }_x+\frac{1}{2}sin\left(2{\phi }_x\right){\check{\mathbf{e}}}_x+\frac{1}{2}sin\left(2{\phi }_x\right){\check{\mathbf{e}}}_y.$$

This scator lies on the 45 degree plane with respect to the ${\check{\mathbf{e}}}_x,{\check{\mathbf{e}}}_y$ directions. The square of this scator is:

$${\stackrel{o}{\phi }}^2={cos}^2\left(2{\phi }_x\right)+\frac{1}{2}sin\left(4{\phi }_x\right){\check{\mathbf{e}}}_x+\frac{1}{2}sin\left(4{\phi }_x\right){\check{\mathbf{e}}}_y,$$

that again lies on the $\frac{\pi }{4}$ director–director plane and must be on the cusphere surface, since unit magnitude invariance holds if associativity is satisfied. The same is true for higher order powers,

$${\stackrel{o}{\phi }}^m={cos}^2\left(m{\phi }_x\right)+\frac{1}{2}sin\left(2m{\phi }_x\right){\check{\mathbf{e}}}_x+\frac{1}{2}sin\left(2m{\phi }_x\right){\check{\mathbf{e}}}_y.$$

Thus, all integer powers of a scator with equal director components lie on the equal director’s coefficients plane. For example, let ${\phi }_x={\phi }_y=\frac{\pi }{6}$,

$$\stackrel{o}{\phi }={cos}^2\left(\frac{\pi }{12}\right)+\frac{1}{2}sin\left(\frac{\pi }{6}\right){\check{\mathbf{e}}}_x+\frac{1}{2}sin\left(\frac{\pi }{6}\right){\check{\mathbf{e}}}_y,$$

that in additive variables is

$$\stackrel{o}{\phi }=\frac{1}{4}\left(2+\sqrt{3}\right)+\frac{1}{4}{\check{\mathbf{e}}}_x+\frac{1}{4}{\check{\mathbf{e}}}_y.$$

The angles in the ${\check{\mathbf{e}}}_x$ and ${\check{\mathbf{e}}}_y$ directions increase by $\frac{\pi }{6}$ every time a product with $\stackrel{o}{\phi }$ is performed, the $12+1$ power returns to the original position ${\stackrel{o}{\phi }}^{13}=\stackrel{o}{\phi }$. The integer powers of this scator are depicted in Figure 2. For a scator where the ${\phi }_x$ director coefficient is a trigonometric number, that is, equal to a rational multiple of $\pi$, the powers will repeat. Since all trigonometric numbers are algebraic numbers [21], the power of scators $\stackrel{o}{\phi }=f_0+f_x{\check{\mathbf{e}}}_x+f_x{\check{\mathbf{e}}}_y$ with real algebraic additive coefficients $f_0,f_x$ will eventually repeat. The converse is also true, if a director coefficient in the multiplicative representation is not a rational multiple of $\pi$, ${\stackrel{o}{\phi }}^m$ will never be equal to $\stackrel{o}{\phi }$ for integer m. Consider the curve where all powers of unit scators with equal directors lie, be them eventually periodic or not. To this end, let $t={\phi }_x={\phi }_y$, the parametric curve is:

$$\stackrel{o}{\phi }\left(1;t,t\right)=\frac{1}{2}+\frac{1}{2}cos\left(2t\right)+\frac{1}{2}sin\left(2t\right){\check{\mathbf{e}}}_x+\frac{1}{2}sin\left(2t\right){\check{\mathbf{e}}}_y.$$

(28)

This function is mod $\pi$ periodic since all arguments involve the double angle. The projections in the $s,{\check{\mathbf{e}}}_1$ plane and the $s,{\check{\mathbf{e}}}_2$ plane are circles with radius $\frac{1}{2}$ centerd at $s=\frac{1}{2}$. The curve is centered at $s=\frac{1}{2}$ and at this s, the maximum value of the director components is obtained. The curve is shown in Figure 2. The powers of the equal director components scator are thus not revolving about the origin, but about the point $\frac{1}{2}+0{\check{\mathbf{e}}}_x+0{\check{\mathbf{e}}}_y$, as can be seen from the above expression. If the scator coefficients have equal magnitude but opposite sign, an analogous scheme is obtained but in the plane at $-45{}^{\circ }$ with respect to the ${\check{\mathbf{e}}}_x,{\check{\mathbf{e}}}_y$ axes.

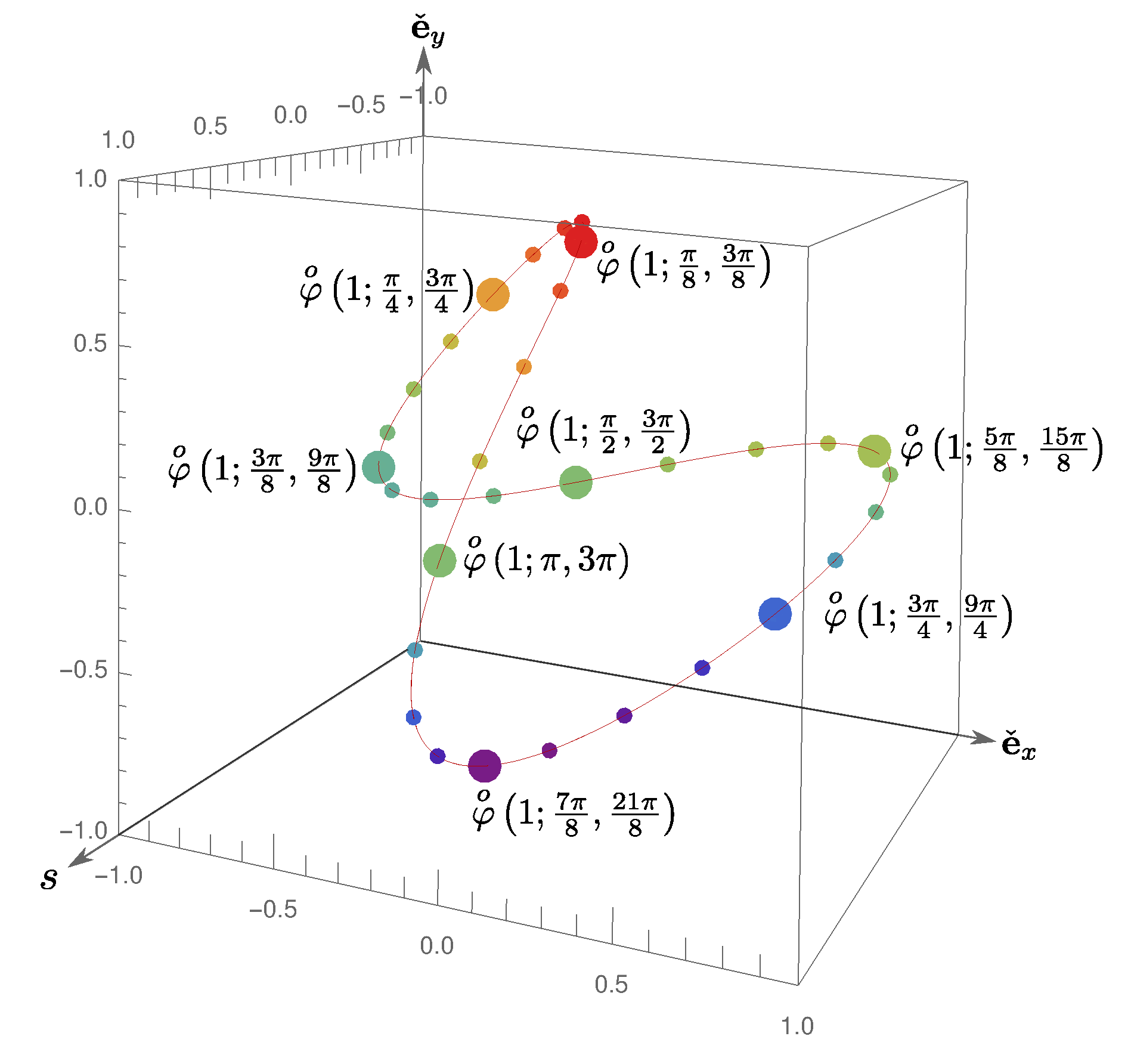
4.2. Unit Magnitude Scators with $\lambda$ Ratio of Scator Coefficients

In order to generalize to arbitrary hypercomplex director components, let ${\phi }_y=\lambda {\phi }_x$, where $\lambda$ is an arbitrary real number. Any unit magnitude scator in ${\mathbb{S}}^{1+2}\backslash \left({\mathbb{S}}_x^{1+1}\cup {\mathbb{S}}_y^{1+1}\right)$ can be obtained with this scheme. From (26),

$$\stackrel{o}{\phi }\left(1;{\phi }_x,\lambda {\phi }_x\right)=cos\left({\phi }_x\right)cos\left(\lambda {\phi }_x\right)+cos\left(\lambda {\phi }_x\right)sin\left({\phi }_x\right){\check{\mathbf{e}}}_x+cos\left({\phi }_x\right)sin\left(\lambda {\phi }_x\right){\check{\mathbf{e}}}_y.$$

This function, with continuous arguments, also arises from the components exponential mapping of line segments with constant scalar, inclined in the ${\check{\mathbf{e}}}_x,{\check{\mathbf{e}}}_y$ plane [17].

The power mapping $\stackrel{o}{\phi }⟶{\stackrel{o}{\phi }}^m$ may thus be viewed as a discrete version of the continuous components exponential mapping

$$\stackrel{o}{\mathrm{c}}\exp \left(t{\check{\mathbf{e}}}_x+\lambda t{\check{\mathbf{e}}}_y\right)=cos\left(t\right)cos\left(\lambda t\right)+sin\left(t\right)cos\left(\lambda t\right){\check{\mathbf{e}}}_1+cos\left(t\right)sin\left(\lambda t\right){\check{\mathbf{e}}}_2.$$

These curves no longer lie on a plane, as in the equal directors case, but a curve in three dimensional space lying on the cusphere surface. The curves are closed for rational $\lambda$. For integer $\lambda$, the function has periodicity $\pi$ for $\lambda$ odd; whereas there is a $2\pi$ period if $\lambda$ is even. In the $s,{\check{\mathbf{e}}}_x$ plane, the curves exhibit $\lambda$ loops for odd $\lambda$ and 2$\lambda$ loops for even $\lambda$. For example, the curve with $\lambda =3$ is depicted in Figure 4. Powers of $\stackrel{o}{\phi }\left(1;\frac{\pi }{8},\frac{3\pi }{8}\right)$ are shown in large dots, whereas powers of $\stackrel{o}{\phi }\left(1;\frac{\pi }{32},\frac{3\pi }{32}\right)$ are shown in the smaller dots. Some other curves with $\lambda$ up to four are shown in [17]. These examples do not pretend to be exhaustive but to give a taste of the geometric representation of powers of scators.

5. Exponential of a Scator

The component’s exponential function mentioned in Section 2.3, is defined in terms of products of exponentials with single component scator arguments. The question arises as to whether the exponential of a scator, rather than the exponentials of its components, is possible. The affirmative answer and its form in terms of elementary functions is given by the following Lemma. A conjecture regarding a generalization of this result and limiting cases are undertaken once the proof is completed.

Lemma 4.

The exponential of a scator $z_0+z_x{\check{\mathbf{e}}}_x+z_y{\check{\mathbf{e}}}_y\in {\mathbb{S}}^{1+2}$ is

$$\begin{array}{c}{e}^{z_0+z_x{\check{\mathbf{e}}}_x+z_y{\check{\mathbf{e}}}_y}=e^{z_0}{e}^{z_x{\check{\mathbf{e}}}_x}{e}^{z_y{\check{\mathbf{e}}}_y}cosh\left(\frac{z_x{z}_y}{z_0}\right)\hfill \\ \hfill -e^{z_0}\left(e^{z_y{\check{\mathbf{e}}}_x}{e}^{z_x{\check{\mathbf{e}}}_y}-cos\left(z_x-z_y\right)\right)sinh\left(\frac{z_x{z}_y}{z_0}\right).\end{array}$$

(29)

Proof. 

Commence with the exponential of a scator with only one director component,

$$e^{z_0+z_l{\check{\mathbf{e}}}_l}=e^{z_0}{e}^{z_l{\check{\mathbf{e}}}_l}=e^{z_0}\left(cos{z}_l+sin{z}_l{\check{\mathbf{e}}}_l\right).$$

(30a)

The above equalities are immediate from the general addition theorem and Euler’s relationship for the imaginary unit ${\check{\mathbf{e}}}_l$. However, it is necessary to recreate this result through a lengthier procedure to establish two equations needed to obtain the exponential of a scator in 1+2 dimensions. The transformation from multiplicative to additive (polar to Cartesian) variables in ${\mathbb{S}}_l^{1+1}$, from (5) is:

$$z_0={\zeta }_{0}cos{\zeta }_l,z_l={\zeta }_{0}sin{\zeta }_l{\check{\mathbf{e}}}_l.$$

(30b)

The series definition of the exponential function is:

$$e^{z_0+z_l{\check{\mathbf{e}}}_l}=\sum _{m=0}^{\infty }\frac{{\left(z_0+z_l{\check{\mathbf{e}}}_l\right)}^m}{m!},$$

and in multiplicative variables

$$e^{z_0+z_l{\check{\mathbf{e}}}_l}=e^{{\zeta }_{0}cos{\zeta }_l+{\zeta }_{0}sin{\zeta }_l{\check{\mathbf{e}}}_l}=\sum _{m=0}^{\infty }\frac{{\left({\zeta }_{0}cos{\zeta }_l+{\zeta }_{0}sin{\zeta }_l{\check{\mathbf{e}}}_l\right)}^m}{m!}.$$

From the Victoria equation in ${\mathbb{S}}_l^{1+n}$, which in this 1 + 1 dimensional case is identical to De Moivre formula,

$$e^{{\zeta }_{0}cos{\zeta }_l+{\zeta }_{0}sin{\zeta }_l{\check{\mathbf{e}}}_l}=\sum _{m=0}^{\infty }\frac{{\zeta }_0^{m}cos\left(m{\zeta }_l\right)}{m!}+\sum _{m=0}^{\infty }\frac{{\zeta }_0^{m}sin\left(m{\zeta }_l\right){\check{\mathbf{e}}}_l}{m!}.$$

(30c)

From the sum of (30c) and its conjugate:

$$\sum _{m=0}^{\infty }\frac{{\zeta }_0^{m}cos\left(m{\zeta }_l\right)}{m!}=\frac{1}{2}\left(e^{{\zeta }_{0}cos{\zeta }_l+{\zeta }_{0}sin{\zeta }_l{\check{\mathbf{e}}}_l}+e^{{\zeta }_{0}cos{\zeta }_l-{\zeta }_{0}sin{\zeta }_l{\check{\mathbf{e}}}_l}\right).$$

Factor $e^{{\zeta }_{0}cos{\zeta }_l}$ and use the cosine definition in terms of exponentials,

$$\sum _{m=0}^{\infty }\frac{{\zeta }_0^{m}cos\left(m{\zeta }_l\right)}{m!}=e^{{\zeta }_{0}cos{\zeta }_l}cos\left({\zeta }_{0}sin{\zeta }_l\right).$$

(31)

The difference of (30c) minus its conjugate is:

$$\sum _{m=0}^{\infty }\frac{{\zeta }_0^{m}sin\left(m{\zeta }_l\right){\check{\mathbf{e}}}_l}{m!}=\frac{1}{2}\left(e^{{\zeta }_{0}cos{\zeta }_l+{\zeta }_{0}sin{\zeta }_l{\check{\mathbf{e}}}_l}-e^{{\zeta }_{0}cos{\zeta }_l-{\zeta }_{0}sin{\zeta }_l{\check{\mathbf{e}}}_l}\right).$$

An analogous procedure gives the series involving the sine function

$$\sum _{m=0}^{\infty }\frac{{\zeta }_0^{m}sin\left(m{\zeta }_l\right)}{m!}=e^{{\zeta }_{0}cos{\zeta }_l}sin\left({\zeta }_{0}sin{\zeta }_l\right).$$

(32)

So that:

$$e^{{\zeta }_{0}cos{\zeta }_l+{\zeta }_{0}sin{\zeta }_l{\check{\mathbf{e}}}_l}=e^{{\zeta }_{0}cos{\zeta }_l}cos\left({\zeta }_{0}sin{\zeta }_l\right)+e^{{\zeta }_{0}cos{\zeta }_l}sin\left({\zeta }_{0}sin{\zeta }_l\right){\check{\mathbf{e}}}_l.$$

Returning to the additive variables using (30b), (30a) is recovered.

Consider the exponential of a scator with two director components in the additive representation but with multiplicative variables:

$$\begin{array}{c}{e}^{z_0+z_x{\check{\mathbf{e}}}_x+z_y{\check{e}}_y}=exp\left({\zeta }_{0}cos{\zeta }_{x}cos{\zeta }_y+{\zeta }_{0}sin{\zeta }_{x}cos{\zeta }_y{\check{\mathbf{e}}}_x+{\zeta }_{0}sin{\zeta }_{y}cos{\zeta }_x{\check{\mathbf{e}}}_y\right)\hfill \\ \hfill =\sum _{m=0}^{\infty }\frac{{\left({\zeta }_{0}cos{\zeta }_{x}cos{\zeta }_y+{\zeta }_{0}sin{\zeta }_{x}cos{\zeta }_y{\check{\mathbf{e}}}_x+{\zeta }_{0}sin{\zeta }_{y}cos{\zeta }_x{\check{\mathbf{e}}}_y\right)}^m}{m!},\end{array}$$

from the multiplicative to additive transformation (7a),

$$z_0={\zeta }_{0}cos{\zeta }_{x}cos{\zeta }_y,z_x={\zeta }_{0}sin{\zeta }_{x}cos{\zeta }_y,z_y={\zeta }_{0}sin{\zeta }_{y}cos{\zeta }_x.$$

(33)

From the Victoria equation, a scator raised to the power m is equal to:

$$\begin{array}{c}{\left({\zeta }_{0}cos{\zeta }_{x}cos{\zeta }_y+{\zeta }_{0}sin{\zeta }_{x}cos{\zeta }_y{\check{\mathbf{e}}}_x+{\zeta }_{0}sin{\zeta }_{y}cos{\zeta }_x{\check{\mathbf{e}}}_y\right)}^m=\hfill \\ \hfill {\zeta }_0^{m}cos\left(m{\zeta }_x\right)cos\left(m{\zeta }_y\right)+{\zeta }_0^{m}sin\left(m{\zeta }_x\right)cos\left(m{\zeta }_y\right){\check{\mathbf{e}}}_x+{\zeta }_0^{m}sin\left(m{\zeta }_y\right)cos\left(m{\zeta }_x\right),{\check{\mathbf{e}}}_y\end{array}$$

so that

$$\begin{array}{c}exp\left({\zeta }_{0}cos{\zeta }_{x}cos{\zeta }_y+{\zeta }_{0}sin{\zeta }_{x}cos{\zeta }_y{\check{\mathbf{e}}}_x+{\zeta }_{0}sin{\zeta }_{y}cos{\zeta }_x{\check{\mathbf{e}}}_y\right)=\hfill \\ \hfill \sum _{m=0}^{\infty }{\zeta }_0^m\frac{cos\left(m{\zeta }_x\right)cos\left(m{\zeta }_y\right)+sin\left(m{\zeta }_x\right)cos\left(m{\zeta }_y\right){\check{\mathbf{e}}}_x+sin\left(m{\zeta }_y\right)cos\left(m{\zeta }_x\right){\check{\mathbf{e}}}_y}{m!}.\end{array}$$

(34)

Let us evaluate each component in this expression.

Scalar component. The product of cosine functions is rewritten as a sum of cosines, $cos\left(m{\zeta }_x\right)cos\left(m{\zeta }_y\right)=cos\left[m\left({\zeta }_x+{\zeta }_y\right)\right]+cos\left[m\left({\zeta }_x-{\zeta }_y\right)\right]$, so that the series can be evaluated from (31),

$$\sum _{m=0}^{\infty }\frac{{\zeta }_0^{m}cos\left[m\left({\zeta }_x\pm {\zeta }_y\right)\right]}{m!}=e^{{\zeta }_{0}cos\left({\zeta }_x\pm {\zeta }_y\right)}cos\left[{\zeta }_{0}sin\left({\zeta }_x\pm {\zeta }_y\right)\right].$$

The series of the product of cosine functions is then

$$\begin{array}{c}\sum _{m=0}^{\infty }\frac{{\zeta }_{0}cos\left(m{\zeta }_x\right)cos\left(m{\zeta }_y\right)}{m!}=\frac{1}{2}{e}^{{\zeta }_{0}cos\left({\zeta }_x+{\zeta }_y\right)}cos\left[{\zeta }_{0}sin\left({\zeta }_x+{\zeta }_y\right)\right]\hfill \\ \hfill +\frac{1}{2}{e}^{{\zeta }_{0}cos\left({\zeta }_x-{\zeta }_y\right)}cos\left[{\zeta }_{0}sin\left({\zeta }_x-{\zeta }_y\right)\right].\end{array}$$

To recover the expression in terms of additive variables, expand the sum of angles and use (30b),

$${\zeta }_{0}cos\left({\zeta }_x\pm {\zeta }_y\right)={\zeta }_{0}cos\left({\zeta }_x\right)cos\left({\zeta }_y\right)\mp {\zeta }_{0}sin\left({\zeta }_x\right)sin\left({\zeta }_y\right)=z_0\mp \frac{z_x{z}_y}{z_0}$$

(35a)

$${\zeta }_{0}sin\left({\zeta }_x\pm {\zeta }_y\right)={\zeta }_{0}sin\left({\zeta }_x\right)cos\left({\zeta }_y\right)\pm {\zeta }_{0}sin\left({\zeta }_y\right)cos\left({\zeta }_x\right)=z_x\pm z_y$$

(35b)

to obtain,

$$\sum _{m=0}^{\infty }\frac{{\zeta }_{0}cos\left(m{\zeta }_x\right)cos\left(m{\zeta }_y\right)}{m!}=\frac{1}{2}{e}^{z_0}\left(e^{-\frac{z_x{z}_y}{z_0}}cos\left(z_x+z_y\right)+e^{\frac{z_x{z}_y}{z_0}}cos\left(z_x-z_y\right)\right).$$

The sum of angles in additive variables can again be expanded and regrouped in order to rewrite the exponentials in terms of hyperbolic trigonometric functions:

$$\begin{array}{c}\frac{1}{2}{e}^{z_0}\left(e^{-\frac{z_x{z}_y}{z_0}}cos\left(z_x+z_y\right)+e^{\frac{z_x{z}_y}{z_0}}cos\left(z_x-z_y\right)\right)=\hfill \\ \hfill e^{z_0}cosh\left(\frac{z_x{z}_y}{z_0}\right)cos{z}_{x}cos{z}_y+e^{z_0}sinh\left(\frac{z_x{z}_y}{z_0}\right)sin{z}_{x}sin{z}_y.\end{array}$$

The series of the product of cosine functions is then:

$$\begin{array}{c}\sum _{m=0}^{\infty }\frac{{\zeta }_{0}cos\left(m{\zeta }_x\right)cos\left(m{\zeta }_y\right)}{m!}=\hfill \\ \hfill e^{z_0}cosh\left(\frac{z_x{z}_y}{z_0}\right)cos{z}_{x}cos{z}_y+e^{z_0}sinh\left(\frac{z_x{z}_y}{z_0}\right)sin{z}_{x}sin{z}_y.\end{array}$$

(36a)

${\check{\mathbf{e}}}_x$director component. Rewrite the product $sin\left(m{\zeta }_x\right)cos\left(m{\zeta }_y\right){\check{\mathbf{e}}}_x$ in terms of the sum of sine functions $sin\left(m{\zeta }_x\right)cos\left(m{\zeta }_y\right)=sin\left[m\left({\zeta }_x+{\zeta }_y\right)\right]+sin\left[m\left({\zeta }_x-{\zeta }_y\right)\right]$.

Each series can then be evaluated from (32):

$$\sum _{m=0}^{\infty }\frac{{\zeta }_0^{m}sin\left[m\left({\zeta }_x\pm {\zeta }_y\right)\right]}{m!}=e^{{\zeta }_{0}cos\left({\zeta }_x\pm {\zeta }_y\right)}sin\left[{\zeta }_{0}sin\left({\zeta }_x\pm {\zeta }_y\right)\right],$$

so that

$$\begin{array}{c}\sum _{m=0}^{\infty }\frac{{\zeta }_0^{m}sin\left(m{\zeta }_x\right)cos\left(m{\zeta }_y\right)}{m!}=\frac{1}{2}{e}^{{\zeta }_{0}cos\left({\zeta }_x+{\zeta }_y\right)}sin\left[{\zeta }_{0}sin\left({\zeta }_x+{\zeta }_y\right)\right]\hfill \\ \hfill +\frac{1}{2}{e}^{{\zeta }_{0}cos\left({\zeta }_x-{\zeta }_y\right)}sin\left[{\zeta }_{0}sin\left({\zeta }_x-{\zeta }_y\right)\right].\end{array}$$

Expand the sum of angles from (35a) and (35b),

$$\sum _{m=0}^{\infty }\frac{{\zeta }_0^{m}sin\left(m{\zeta }_x\right)cos\left(m{\zeta }_y\right)}{m!}=\frac{1}{2}{e}^{z_0-\frac{z_x{z}_y}{z_0}}sin\left(z_x+z_y\right)+\frac{1}{2}{e}^{z_0+\frac{z_x{z}_y}{z_0}}sin\left(z_x-z_y\right).$$

Expand again the sum of angles and regroup to obtain:

$$\begin{array}{c}\sum _{m=0}^{\infty }\frac{{\zeta }_0^{m}sin\left(m{\zeta }_x\right)cos\left(m{\zeta }_y\right)}{m!}=\hfill \\ \hfill e^{z_0}cosh\left(\frac{z_x{z}_y}{z_0}\right)sin{z}_{x}cos{z}_y-e^{z_0}sinh\left(\frac{z_x{z}_y}{z_0}\right)sin{z}_{y}cos{z}_x.\end{array}$$

(36b)

${\check{\mathbf{e}}}_y$director component. The product $sin\left(m{\zeta }_y\right)cos\left(m{\zeta }_x\right){\check{\mathbf{e}}}_y$ is written in an analogous fashion:

$$\sum _{m=0}^{\infty }\frac{{\zeta }_0^{m}sin\left(m{\zeta }_y\right)cos\left(m{\zeta }_x\right)}{m!}=\frac{1}{2}{e}^{z_0-\frac{z_x{z}_y}{z_0}}sin\left(z_x+z_y\right)-\frac{1}{2}{e}^{z_0+\frac{z_x{z}_y}{z_0}}sin\left(z_x-z_y\right).$$

In terms of hyperbolic functions:

$$\begin{array}{c}\sum _{m=0}^{\infty }\frac{{\zeta }_0^{m}sin\left(m{\zeta }_y\right)cos\left(m{\zeta }_x\right)}{m!}=\hfill \\ \hfill e^{z_0}cosh\left(\frac{z_x{z}_y}{z_0}\right)sin{z}_{y}cos{z}_x-e^{z_0}sinh\left(\frac{z_x{z}_y}{z_0}\right)sin{z}_{x}cos{z}_y.\end{array}$$

(36c)

Collecting results from (36a), (36b) and (36c) in (34),

$$\begin{array}{c}{e}^{z_0+z_x{\check{\mathbf{e}}}_x+z_y{\check{\mathbf{e}}}_y}=cosh\left(\frac{z_x{z}_y}{z_0}\right)e^{z_0}\left(cos{z}_{x}cos{z}_y+sin{z}_{x}cos{z}_y{\check{\mathbf{e}}}_x+sin{z}_{y}cos{z}_x{\check{\mathbf{e}}}_y\right)\hfill \\ \hfill +sinh\left(\frac{z_x{z}_y}{z_0}\right)e^{z_0}\left(sin{z}_{x}sin{z}_y-cos{z}_{x}sin{z}_y{\check{\mathbf{e}}}_x-sin{z}_{x}cos{z}_y{\check{\mathbf{e}}}_y\right).\end{array}$$

(37)

Rewritten in terms of products of exponentials from Equation (16) [17], the exponential of $z_0+z_x{\check{\mathbf{e}}}_x+z_y{\check{\mathbf{e}}}_y$ is

$$\begin{array}{c}{e}^{z_0+z_x{\check{\mathbf{e}}}_x+z_y{\check{\mathbf{e}}}_y}=e^{z_0}{e}^{z_x{\check{\mathbf{e}}}_x}{e}^{z_y{\check{\mathbf{e}}}_y}cosh\left(\frac{z_x{z}_y}{z_0}\right)\hfill \\ \hfill -\left(e^{z_0}{e}^{z_y{\check{\mathbf{e}}}_x}{e}^{z_x{\check{\mathbf{e}}}_y}-e^{z_0}cos\left(z_x-z_y\right)\right)sinh\left(\frac{z_x{z}_y}{z_0}\right).\end{array}$$

□

The generalization to higher dimensions is carried out in a similar fashion, although the algebra becomes considerably more elaborate.

The exponential of a scator $\stackrel{o}{\phi }\in {\mathbb{S}}^{1+2}$, in terms of the components exponential function is:

$$\begin{array}{c}{e}^{\stackrel{o}{\phi }}=e^{f_0+f_x{\check{\mathbf{e}}}_x+f_y{\check{\mathbf{e}}}_y}=\stackrel{o}{\mathrm{c}}\exp \left(\stackrel{o}{\phi }\right)cosh\left(\frac{f_x{f}_y}{f_0}\right)\hfill \\ \hfill -\left(\stackrel{o}{\mathrm{c}}\exp \left(f_0+f_y{\check{\mathbf{e}}}_x+f_x{\check{\mathbf{e}}}_y\right)-e^{f_0}cos\left(f_x-f_y\right)\right)sinh\left(\frac{f_x{f}_y}{f_0}\right).\end{array}$$

(38)

Corollary 5.

In the limit when the additive scalar component is much larger than the director components $f_0^2\gg f_x^2,f_y^2$, the exponential of a scator in ${\mathbb{S}}^{1+2}$ is equal to the component’s exponential function of the scator, $\underset{f_0^2\gg f_x^2,f_y^2}{\lim }\left[\exp \left(\stackrel{o}{\phi }\right)\right]=\stackrel{o}{\mathrm{c}}\exp \left(\stackrel{o}{\phi }\right)$.

Proof. 

If the argument is much smaller than one, the hyperbolic functions are:

$\underset{\left|f_0\right|\gg \left|f_x{f}_y\right|}{\lim }\left[cosh\left(\frac{f_x{f}_y}{f_0}\right)\right]\approx 1$ and $\underset{\left|f_0\right|\gg \left|f_x{f}_y\right|}{\lim }\left[sinh\left(\frac{f_x{f}_y}{f_0}\right)\right]\approx 0$, from (38),

$$\underset{f_0^2\gg f_x^2,f_y^2}{\lim }\left(e^{f_0+f_x{\check{\mathbf{e}}}_x+f_y{\check{\mathbf{e}}}_y}\right)=e^{f_0}{e}^{f_x{\check{\mathbf{e}}}_x}{e}^{f_y{\check{\mathbf{e}}}_y}=\stackrel{o}{\mathrm{c}}\exp \left(f_0+f_x{\check{\mathbf{e}}}_x+f_y{\check{\mathbf{e}}}_y\right).$$

□

It is conjectured that this corollary should be true in $1+n$ dimensions: The exponential of a scator $\stackrel{o}{\phi }\in {\mathbb{S}}^{1+n}$ is equal to the components exponential function of $\stackrel{o}{\phi }$ in the limit when the additive scalar component is much larger than any of the j director components, $\underset{f_0^2\gg f_j^2}{\lim }\exp \left(\stackrel{o}{\phi }\right)=\stackrel{o}{\mathrm{c}}\exp \left(\stackrel{o}{\phi }\right)$.

In this $f_0^2\gg f_x^2,f_y^2$ limit, the scator magnitude becomes an Euclidean quadratic form, since the product ${\displaystyle \prod _{j=1}^n}\left(1+\frac{f_j^2}{f_0^2}\right)$ in (10) is then approximated by the sum,

$$\underset{f_0^2\gg f_x^2,f_y^2}{\lim }{\phi }_0^2=f_0^2\left(\stackrel{n}{\prod _{j=1}}\left(1+\frac{f_j^2}{f_0^2}\right)\right)\approx f_0^2\left(1+\stackrel{n}{\sum _{j=1}}\frac{f_j^2}{f_0^2}\right)\approx f_0^2+\stackrel{n}{\sum _{j=1}}{f}_j^2.$$

Geometrically, this limit corresponds to scators paraxial to the s axis. The intersection of the cusphere and a constant s plane in this limit is ${\displaystyle \stackrel{n}{\sum _{j=1}}}{f}_j^2={\phi }_0^2-f_0^2$. This equation represents an $S^{n-1}$ dimensional hypersphere embedded in an n dimensional space. For two director components, $S^1$ is a circle in the ${\check{\mathbf{e}}}_x,{\check{\mathbf{e}}}_y$ plane with radius $\sqrt{{\phi }_0^2-f_0^2}$.

In the limit when $f_0\to 0$, if $f_x{f}_y\ne 0$, $sinh\left(\frac{f_x{f}_y}{f_0}\right)\approx cosh\left(\frac{f_x{f}_y}{f_0}\right)\approx \frac{1}{2}exp\left(\frac{f_x{f}_y}{f_0}\right)$, the exponential function

$$\underset{f_0\to 0}{\lim }\left[exp\left(f_0+f_x{\check{\mathbf{e}}}_x+f_y{\check{\mathbf{e}}}_y\right)\right]=\frac{1}{2}\underset{f_0\to 0}{\lim }\left[cos\left(f_x-f_y\right)exp\left(\frac{f_x{f}_y}{f_0}\right)\right]$$

diverges as $f_0\to 0$. This result is not unexpected because the scator product is defined in ${\mathbb{S}}^{1+2}$, where $f_0$ cannot be zero if there are two non-vanishing director components. The series representation of the exponential with scator argument is

$$exp\left(f_0+f_x{\check{\mathbf{e}}}_x+f_y{\check{\mathbf{e}}}_y\right)=\sum _{m=0}^{\infty }\frac{{\left(f_0+f_x{\check{\mathbf{e}}}_x+f_y{\check{\mathbf{e}}}_y\right)}^m}{m!},$$

this expression involves products of scators. For the second and third terms in the series, from Equations (22) and (23), respectively, all three components of ${\left(f_0+f_x{\check{\mathbf{e}}}_x+f_y{\check{\mathbf{e}}}_y\right)}^2$ diverge as $f_0\to 0$. Therefore, the domain of the exponential function of scator argument is ${\mathbb{S}}^{1+2}$. However, the image of the exponential function is not restricted to the ${\mathbb{S}}^{1+2}$ set. For example:

$$exp\left(f_0+\frac{\pi }{2}{\check{\mathbf{e}}}_x+\pi {\check{\mathbf{e}}}_y\right)=-e^{f_0}cosh\left(\frac{{\pi }^2}{2f_0}\right){\check{\mathbf{e}}}_x+e^{f_0}sinh\left(\frac{{\pi }^2}{2f_0}\right){\check{\mathbf{e}}}_y,$$

this scator has vanishing scalar but two non zero director components. The exponential function mapping of a scator goes from the scator set onto the real set, $\exp \left(\stackrel{o}{\phi }\right):{\mathbb{S}}^{1+n}\to {\mathbb{R}}^{1+n}$. In contrast, the component’s exponential function mapping is $\stackrel{o}{\mathrm{c}}\exp \left(\stackrel{o}{\phi }\right):{\mathbb{R}}^{1+n}\to {\mathbb{S}}^{1+n}$.