Criteria for the Oscillation of Solutions to Linear Second-Order Delay Differential Equation with a Damping Term
Abstract
1. Introdiction
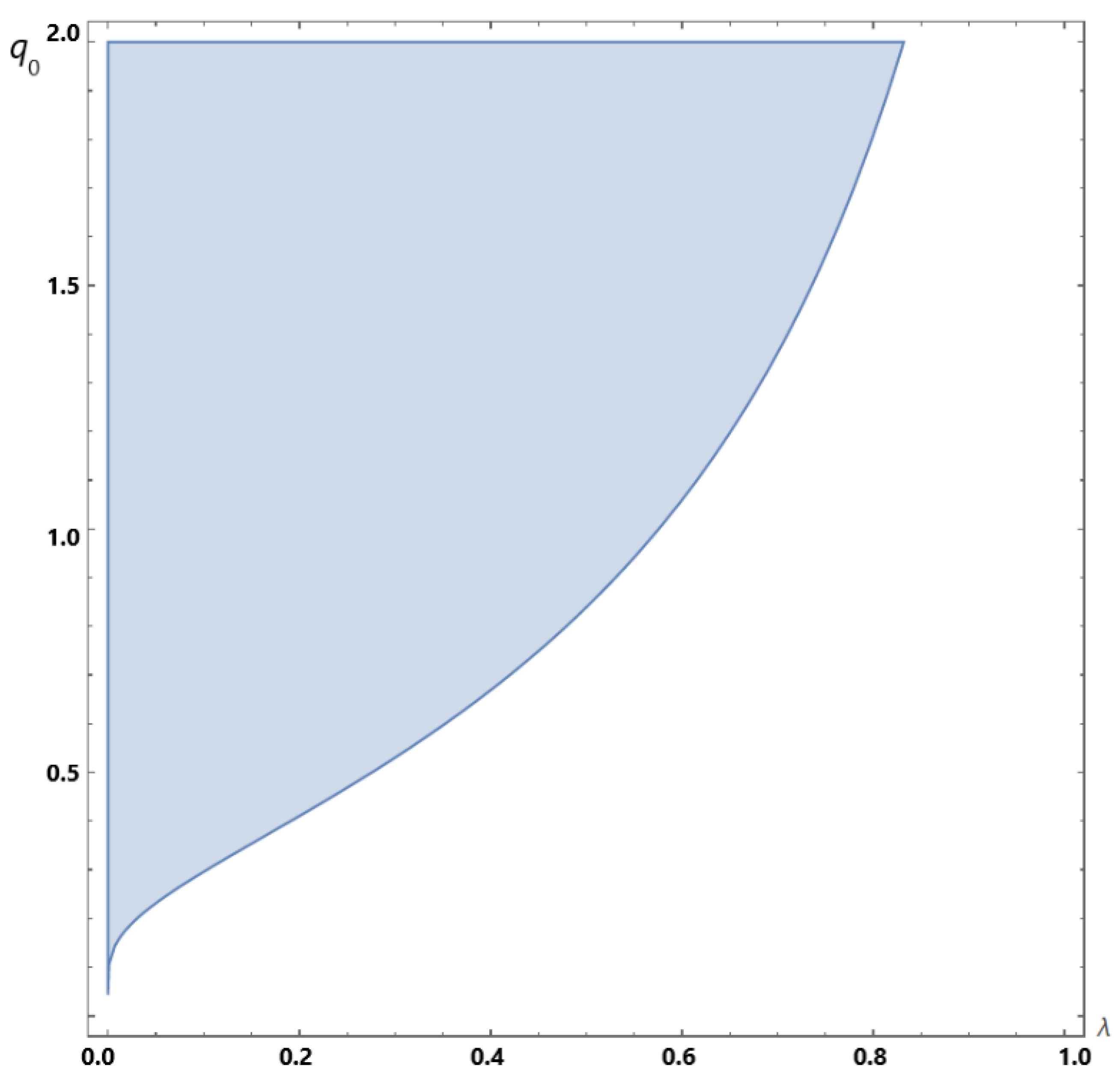
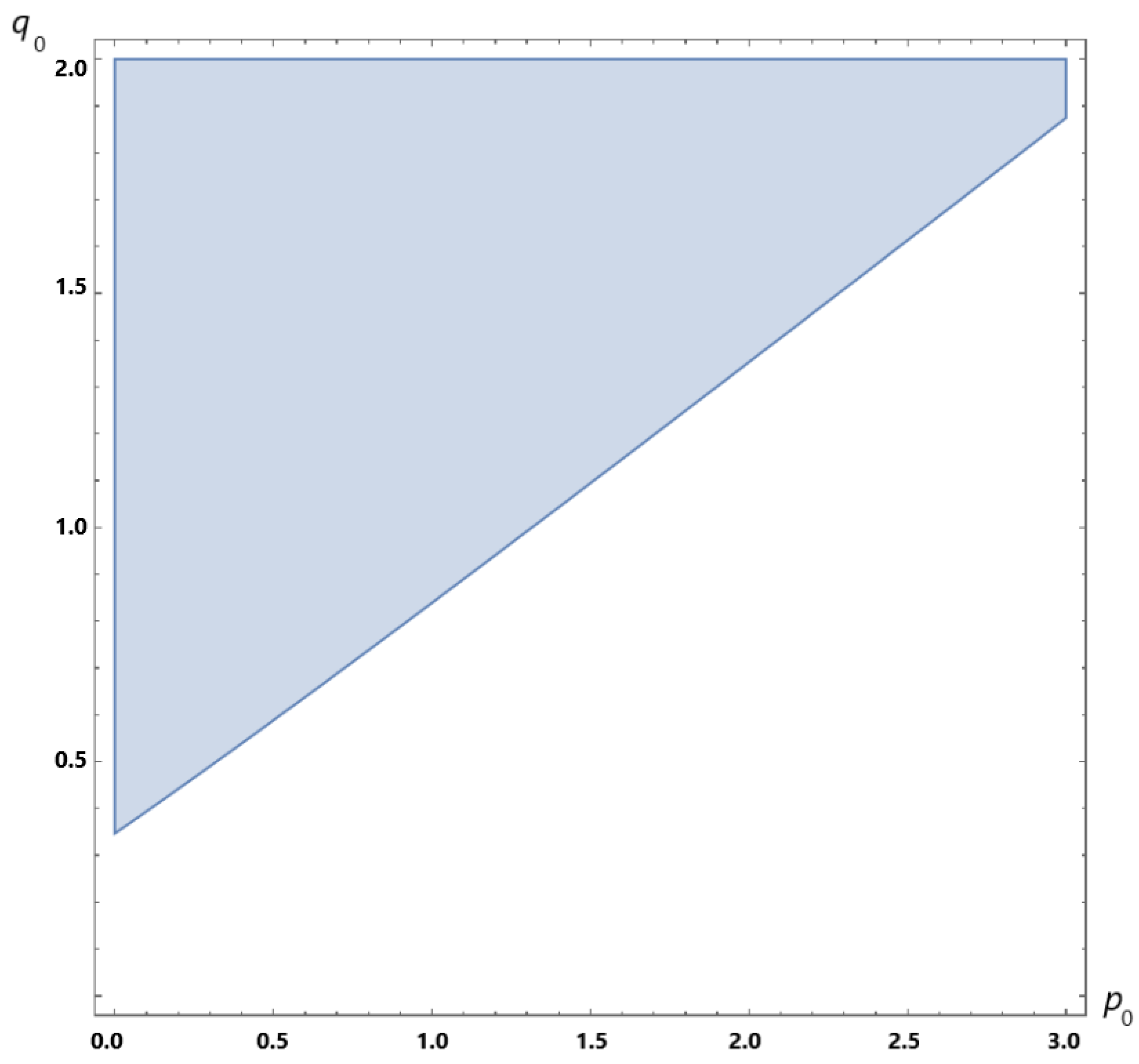
2. Main Results I: Delay Equation
- for
3. Main Results II: Advanced Equation
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Agarwal, R.P.; Grace, S.R.; O’Regan, D. Oscillation Theory for Difference and Functional Differential Equations; Marcel Dekker: New York, NY, USA; Kluwer Academic: Dordrecht, The Netherlands, 2000. [Google Scholar]
- Hale, J.K. Theory of Functional Differential Equations; Springer: NewYork, NY, USA, 1977. [Google Scholar]
- Kocic, V.L.; Ladas, G. Global Behavior of Nonlinear Difference Equations of Higher Order with Applications; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1993. [Google Scholar]
- Dzurina, J.; Grace, S.R.; Jadlovska, I.; Li, T. Oscillation criteria for second-order Emden—Fowler delay differential equations with a sublinear neutral term. Math. Nachr. 2020, 293, 910–922. [Google Scholar] [CrossRef]
- Moaaz, O.; Anis, M.; Baleanu, D.; Muhib, A. More effective criteria for oscillation of second-order differential equations with neutral arguments. Mathematics 2020, 8, 986. [Google Scholar]
- Moaaz, O.; Baleanu, D.; Muhib, A. New aspects for non-existence of kneser solutions of neutral differential equations with odd-order. Mathematics 2020, 8, 494. [Google Scholar] [CrossRef]
- Moaaz, O.; Furuichi, S.; Muhib, A. New comparison theorems for the nth order neutral differential equations with delay inequalities. Mathematics 2020, 8, 454. [Google Scholar] [CrossRef]
- Saker, S.H.; Pang, P.Y.; Agarwal, R.P. Oscillation theorem for second-order nonlinear functional differential equation with damping. Dyn. Syst. Appl. 2003, 12, 307–322. [Google Scholar]
- Grace, S.R. Oscillation theorems for second order nonlinear differential equations with damping. Math. Nachr. 1989, 141, 117–127. [Google Scholar] [CrossRef]
- Grace, S.R. On the oscillatory and asymptotic behavior of damping functional differential equations. Math. Jpn. 1991, 36, 220–237. [Google Scholar]
- Grace, S.R. Oscillation of nonlinear differential equations of second order. Publ. Math. 1992, 40, 143–153. [Google Scholar] [CrossRef][Green Version]
- Graef, J.R.; Özdemir, O.; Kaymaz, A.; Tunc, E. Oscillation of damped second-order linear mixed neutral differential equations. Monatshefte Math. 2021, 194, 85–104. [Google Scholar] [CrossRef]
- Ladde, G.S.; Lakshmikantham, V.; Zhang, B.G. Oscillation Theory of Differential Equations with Deviating Arguments; Marcel Dekker: New York, NY, USA, 1987. [Google Scholar]
- Baculikova, B. Oscillatory behavior of the second order noncanonical differential equa tions. Electron. J. Qual. Theory Differ. Equ. 2019. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moaaz, O.; Elabbasy, E.M.E.; Awrejcewicz, J.; Abdelnaser, A. Criteria for the Oscillation of Solutions to Linear Second-Order Delay Differential Equation with a Damping Term. Axioms 2021, 10, 246. https://doi.org/10.3390/axioms10040246
Moaaz O, Elabbasy EME, Awrejcewicz J, Abdelnaser A. Criteria for the Oscillation of Solutions to Linear Second-Order Delay Differential Equation with a Damping Term. Axioms. 2021; 10(4):246. https://doi.org/10.3390/axioms10040246
Chicago/Turabian StyleMoaaz, Osama, Elmetwally M. E. Elabbasy, Jan Awrejcewicz, and Aml Abdelnaser. 2021. "Criteria for the Oscillation of Solutions to Linear Second-Order Delay Differential Equation with a Damping Term" Axioms 10, no. 4: 246. https://doi.org/10.3390/axioms10040246
APA StyleMoaaz, O., Elabbasy, E. M. E., Awrejcewicz, J., & Abdelnaser, A. (2021). Criteria for the Oscillation of Solutions to Linear Second-Order Delay Differential Equation with a Damping Term. Axioms, 10(4), 246. https://doi.org/10.3390/axioms10040246








