Abstract
Quantum characteristics of a mass-accreting oscillator are investigated using the invariant operator theory, which is a rigorous mathematical tool for unfolding quantum theory for time-dependent Hamiltonian systems. In particular, the quantum energy of the system is analyzed in detail and compared to the classical one. We focus on two particular cases; one is a linearly mass-accreting oscillator and the other is an exponentially mass-accreting one. It is confirmed that the quantum energy is in agreement with the classical one in the limit . We showed that not only the classical but also the quantum energy oscillates with time. It is carefully analyzed why the energy oscillates with time, and a reasonable explanation for that outcome is given.
MSC:
81-08; 81V22; 37J06; 70G60
1. Introduction
Hamiltonians of most actual physical systems such as forced oscillators [1,2,3,4,5], mass-accreting oscillators [6,7,8,9,10,11], and damped oscillators [11,12,13,14,15] are a function of time. For this reason, these systems are called time-dependent Hamiltonian systems (TDHSs). Deriving not only numerical but also analytical solutions of TDHSs has become one of main tasks that deserve to be carried out in the context of theoretical physics. Sometimes, to achieve such a purpose, the time variations of parameters of a system are assumed to be sufficiently slow for simplicity. In this study, we are interested in time behavior of quantized energy for mass-accreting nanomechanical oscillatory systems. Knowledge of mass-accreting oscillators can be applied to analyzing the oscillation of an accretion disc (diskoseismology) [2,16,17,18,19,20] and multiple crystal oscillator used for measuring density of a particular gas [21].
The rate of increase in mass in the above-mentioned systems may vary with time in general in an arbitrary fashion. As is well known, for a simple case in which the rate of mass-accretion is constant with time, the system is described by the Caldirola-Kanai Hamiltonian [22,23]. The description of a quantum system via such a Hamiltonian is in fact a phenomenological method for single particle motion instead of the entire description of the system and reservoir as a whole. Although we consider a quantum problem of a linear oscillator model in this work, there are also many works from a long time ago devoted to nonlinear oscillators and their quantum-classical-correspondence problem [24,25,26,27].
A useful tool for describing dynamical systems with time-dependent parameters is invariant operator methods [28,29]. These methods have been widely used when unfolding quantum theory of TDHSs. There may be many kinds of invariants for a system. For instance, linear and quadratic invariant operators for an oscillator-like Hamiltonian system are reported in Reference [30]. We will introduce a linear invariant operator in this research. From quantum theory associated with the linear invariant operator, we can easily identify the relation between the quantum and the classical theory of a dynamical system.
In this work, we investigate how to develop quantum theory of a mass-accreting oscillator on the basis of invariant operator method. General quantum theory of oscillators with time-varying mass are used to analyze two particular systems such as the linearly mass-accreting oscillator and the oscillator with exponentially increasing mass. We focus on time behavior of quantum energy and compare it with the classical one. In classical mechanics, the energy of the mass-accreting oscillator oscillates with time. We determine whether quantum energy also oscillates over time with the same pattern as the classical one and analyze why the energy oscillates. The similarity and difference between classical and quantum states of the system are also addressed.
2. Preliminary Analysis in Classical Domain
We first note the classical aspect of mass-accreting oscillators as a preliminary. Basically, a mass-accreting oscillator is understood from the pail-rain model [7,11] or a time-dependent mass system described in Reference [31]. Like many cases of TDHSs, the action of the environment on the system can be replaced by a time-dependent term in the Hamiltonian, allowing a standard approach for a single particle motion.
If we express the time-dependent mass as in this case, the Hamiltonian can be represented in the form
where is a natural frequency. The corresponding classical equation of motion is given by
If we consider that this is a second-order differential equation, there may be two linearly independent solutions. If we call them and , respectively, the general solution can be represented as
where and are arbitrary constants. Once is known, the expression of momentum can also be derived from a basic relation between them in mechanics. Among the many classical quantities that can be analyzed in terms of Equation (3), we consider classical energy, which is of the form
For a particular case where the type of is chosen in a way that the solution of Equation (2) is known or solved, we can completely describe the time behavior of this classical energy. From the next section, we will analyze the system quantum mechanically with the explicit choice of .
3. Quantum Analysis
We consider two types of in order to analyze the quantum features of the system depending on the pattern of mass-accreting. We first choose the time dependence of so that it represents a linearly accreting mass, and the other choice in the next corresponds to the exponentially mass-accreting one. As with the case of the classical analysis given in the previous section, we also focus on the time evolution of mechanical energy but in view of quantum theory.
3.1. Linearly Mass-Accreting Oscillator
Let us first consider the case in which mass of the system is given by , where m is the initial mass and k is a positive constant. Then, the equation of motion given in Equation (2) becomes
The solutions of this equation are easily derived to be
where is an arbitrary real constant and and are the first- and the second-kind 0th order Bessel functions, respectively. Of course, the general solution is obtained by inserting these two equations into Equation (3).
The quantum Hamiltonian of the system is given by replacing canonical variables of the classical Hamiltonian with their corresponding operators. Thus, we have
Through an inspection, we confirm that the separation of variables method for solving the Schrödinger equation of the system with this Hamiltonian cannot be applicable. Hence, we need another mathematical tool for solving quantum solutions of the system. One of several methods useful for this purpose is the invariant operator method. A large part of mechanical properties of dynamical physical systems can be clarified and understood from this method. As is well known, the invariant operator should satisfy the Liouville–von Neumann equation which is of the form
By solving this equation for the linearly mass-accreting oscillator in a straightforward way [9,30,32], we derive a linear operator as
where
Notice that is a complex variable and its Hermitian adjoint is also an invariant operator. The commutation relation between them is . This means that we can regard and as an annihilation and creation operators of the system, respectively. In the simple-harmonic-oscillator limit where and , the invariant operator reduces to
which is the familiar annihilation operator where a time-dependent phase is chosen.
Let us express the eigenvalue equation of the invariant operator in the form
Then, the eigenvalue is given by
Among many physical quantities that can be analyzed from a quantum point of view, we are interested in the development of quantum energy of the TDHS, which has attracted considerable concern in theoretical physics. Unlike that of classical energy, the expression of quantum energy differs depending on given quantum states. For instance, the spectrum of allowed quantum energies in the Fock state is discrete, whereas quantum energy in the coherent state that we consider here is represented in terms of and .
From fundamental quantum dynamics, quantum energy is the expectation value of the Hamiltonian
where is the eigenstate of . Because we can also chose a different form of the invariant operator instead of the one given in Equation (10), there may be many quantum expressions of energy, which correspond to those of different quantum states. For the case of the present work where Equation (10) is chosen as the invariant operator, the quantum state corresponds to the coherent state.
To evaluate Equation (17), let us express the quantum Hamiltonian in terms of and such that
where
Now a direct evaluation leads to the explicit formula of the quantum energy in the coherent state:
Notice that this oscillates with time like a classical energy as illustrated in Figure 1. The amplitude of such an oscillation diminishes as time goes by. If we consider that quantum energy is represented in terms of ℏ, quantum energy is different from the corresponding classical one. It is expected that, when we neglect the value of ℏ, quantum energy may agree well with the classical one. From Figure 2, we see that the time behavior of the expectation value of quantum energy under the limit follows a trajectory that is quite similar to the classical one.
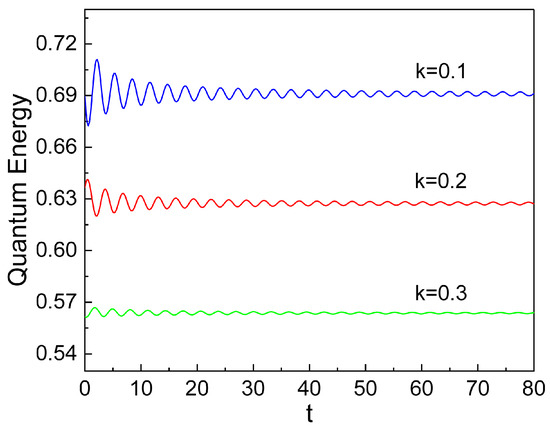
Figure 1.
Quantum energy of a linearly mass-accreting oscillator with various values of k. We used , , , , and .
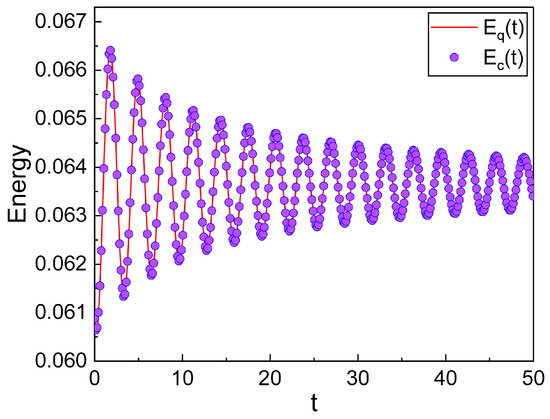
Figure 2.
Detailed comparison of the quantum energy (solid red line) with the classical energy (thick dotted blue line) for linearly mass-accreting oscillator, under the limit for the quantum energy. We used , , , , and .
3.2. Comparison with the Exponentially Mass-Accreting Oscillator
Now let us compare our results for the linear mass-accreting oscillator to those of the exponentially mass-accreting oscillator which was treated in Reference [9]. In this case, the time-dependent mass is given by where m is the initial mass and is a constant. Here, the mass exponentially increases with time depending on the value of . The classical equation of motion corresponding to this system is given by
This is the same as that of the damped harmonic oscillator. In fact, the classical trajectory of exponentially mass-accreting oscillator in one-dimensional space is the same as that of the damped harmonic oscillator. However, the energy of the system is different from that of the damped harmonic oscillator and does not dissipate over time [6]. In this case, two linearly independent solutions of the classical equation of motion are given by
where . In this case, a general solution given in Equation (3) is represented as
where and . Then, the corresponding classical energy given in Equation (4) is expressed in the form
This can be divided into kinetic and potential energies:
The time behavior of mechanical energy together with and is plotted in Figure 3. This energy oscillates as time goes by, but the envelope of the energy oscillation does not vary with time. The energy of the oscillator increases around its turning points and decreases around the equilibrium position where it attains maximum velocity.
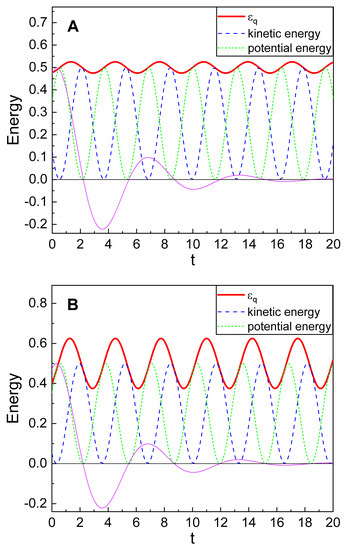
Figure 3.
Quantum mechanical energy (solid red line), (under the limit ), of exponentially mass-accreting oscillator given in Equation (29) with for (A) and for (B). The long dashed blue line is the corresponding kinetic energy, whereas the short dashed green line is the potential energy. A slim violet curve is the relative position of the oscillator. We used , , , and .
Through the same procedure as that of the previous section, we can also obtain quantum solution of energy as
which agrees well with that of Reference [9]. This energy also oscillates with time like a classical one. From Figure 3, we see that the energy decreases with time near the equilibrium position and increases at the turning points of the oscillator.
While the amplitude of the energy oscillation of the linearly mass-accreting oscillator diminishes with time, the amplitude of the energy oscillation for the exponentially mass-accreting oscillator does not vary. This is the main difference of the energy evolution between the two oscillatory systems.
4. Conclusions
The time behavior of quantum energy of mass-accreting oscillatory nanosystems is investigated through rigorous analytical analyses. The expression of quantum energy is different depending on quantum states. The quantum energy that we have treated in this work is associated with the coherent state. We confirmed that quantum energy of the system oscillates with time like classical energy. This leads to quantum and classical correspondence for the system, which is a fundamental concept in modern physics.
Now we analyze why the energies of the considered systems oscillate with time. To interpret the results of our developments, let us compare them with the case of a mass-accreting free particle. For this, we consider the Hamiltonian of a mass-accreting free particle, which has the form . This can be obtained by removing the potential term from Equation (1). We can see that the corresponding classical energies for linearly mass-accreting and exponentially mass-accreting free particles are given by
respectively, where is the initial velocity of the particle. Hence, the mechanical energies in this case decay with time in proportion to
respectively.
When the oscillatory systems attain the highest velocity near the equilibrium position, the systems act like a free particle because we can neglect the force acting on the oscillator through a spring at that moment. Since we can approximate the systems as a mass-accreting free particle in that case, the oscillatory energy may dissipate in a manner similar to those given in Equations (32) and (33), respectively, for linearly and exponentially mass-accreting oscillators. This is the reason why the energies of the systems decay around the equilibrium position.
On the other hand, the accretion of mass at the turning points of the oscillator results in the increase in the potential energy due to a high displacement of the oscillator at those instants of time. This is the reason why the energy increases at the turning points of the oscillator.
Funding
This work was supported by the National Research Foundation of Korea(NRF) grant funded by the Korea government (MSIT) (No.: NRF-2021R1F1A1062849).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
References
- Choi, J.R. Unitary transformation approach for the phase of the damped driven harmonic oscillator. Mod. Phys. Lett. B 2003, 17, 1365–1376. [Google Scholar] [CrossRef]
- Pétri, J. Forced oscillations in a hydrodynamical accretion disk and QPOs. Astrophys. Space Sci. 2006, 302, 117–139. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.-H.; Yan, Z.-Y. Frequency dependence of the entanglement entropy production in a system of coupled driven nonlinear oscillators. Entropy 2019, 21, 889. [Google Scholar] [CrossRef] [Green Version]
- Golovinski, P.A. Dynamics of driven Brownian inverted oscillator. Phys. Lett. A 2020, 384, 126203. [Google Scholar] [CrossRef]
- Kenfack, S.C.; Nguimeya, G.P.; Talla, P.K.; Fotue, A.J.; Fobasso, M.F.C.; Tiotsop, M.; Djomou, J.R.D.; Ekosso, C.M.; Fai, L.C. Decoherence of driven coupled harmonic oscillator. J. Nanosci. Curr. Res. 2016, 1, 1000104. [Google Scholar]
- Marchiolli, M.A.; Mizrahi, S.S. Dissipative mass-accreting quantum oscillator. J. Phys. A Math. Gen. 1997, 30, 2619–2635. [Google Scholar] [CrossRef]
- Ray, J.R. Dissipation and quantum theory. Lett. Al Nuovo Cimento 1979, 25, 47–50. [Google Scholar] [CrossRef]
- Choi, J.R.; Song, J.N.; Hong, S.J. Wigner distribution function of superposed quantum states for a time-dependent oscillator-like Hamiltonian system. J. Theor. Appl. Phys. 2012, 6, 26. [Google Scholar] [CrossRef] [Green Version]
- Choi, J.R. Analysis of quantum energy for Caldirola-Kanai Hamiltonian systems in coherent states. Results Phys. 2013, 3, 115–121. [Google Scholar] [CrossRef] [Green Version]
- González-Acosta, E.; Corona-Galindo, M.G. Noether’s theorem and the invariants for dissipative and driven dissipative like systems. Rev. Mex. Fis. 1992, 38, 511–517. [Google Scholar]
- Dekker, H. Classical and quantum mechanics of the damped harmonic oscillator. Phys. Rep. 1981, 80, 1–110. [Google Scholar] [CrossRef]
- Rosenau da Costa, M.; Caldeira, A.O.; Dutra, S.M.; Westfahl, H., Jr. Exact diagonalization of two quantum models for the damped harmonic oscillator. Phys. Rev. A 2000, 61, 022107. [Google Scholar] [CrossRef] [Green Version]
- Schuch, D. Some remarks on analytical solutions for a damped quantum parametric oscillator. J. Phys. Conf. Ser. 2019, 1275, 012033. [Google Scholar] [CrossRef]
- Aguiar, V.; Guedes, I. Fisher information of quantum damped harmonic oscillators. Phys. Scr. 2015, 90, 045207. [Google Scholar] [CrossRef]
- Lawson, L.M.; Avossevou, G.Y.H.; Gouba, L. Lewis-Riesenfeld quantization and SU(1,1) coherent states for 2D damped harmonic oscillator. J. Math. Phys. 2018, 59, 112101. [Google Scholar] [CrossRef] [Green Version]
- Nowak, M.A.; Wagoner, R.V. Diskoseismology: Probing accretion disks. I. Trapped adiabatic oscillations. Astrophys. J. 1991, 378, 656–664. [Google Scholar] [CrossRef]
- Lubow, S.H.; Prinole, J.E. Wave propagation in accretion disks: Axisymmetric case. Astrophys. J. 1993, 409, 360–371. [Google Scholar] [CrossRef]
- Wagoner, R.V. Relativistic and Newtonian diskoseismology. New Astron. Rev. 2008, 51, 828–834. [Google Scholar] [CrossRef]
- Cox, J.P. Adiabatic oscillations of accretion disks. Astrophys. J. 1981, 247, 1070–1077. [Google Scholar] [CrossRef]
- Li, L.-X.; Goodman, J.; Narayan, R. Nonaxisymmetric g-mode and p-mode instability in a hydrodynamic thin accretion disk. Astrophys. J. 2003, 593, 593–980. [Google Scholar] [CrossRef] [Green Version]
- California Institute of Technology CalTech. Multiple Crystal Oscillator Measuring Apparatus. U.S. Patent 3879992 A, 29 April 1975. [Google Scholar]
- Caldirola, P. Porze non conservative nella meccanica quantistica. Nuovo Cimento 1941, 18, 393–400. [Google Scholar] [CrossRef]
- Kanai, E. On the quantization of dissipative systems. Prog. Theor. Phys. 1948, 3, 440–442. [Google Scholar] [CrossRef]
- Milburn, G.J.; Holmes, C.A. Quantum coherence and classical chaos in a pulsed parametric oscillator with a Kerr nonlinearity. Phys. Rev. A 1991, 44, 4704–4711. [Google Scholar] [CrossRef] [Green Version]
- Wielinga, B.; Milburn, G.J. Chaos and coherence in an optical system subject to photon nondemolition measurement. Phys. Rev. A 1992, 46, 762–770. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Leoński, W. Quantum and classical dynamics for a pulsed nonlinear oscillator. Physica A 1996, 233, 365–378. [Google Scholar] [CrossRef]
- Kowalewska-Kudłaszyk, A.; Kalaga, J.K.; Leoński, W. Wigner-function nonclassicality as indicator of quantum chaos. Phys. Rev. E 2008, 78, 066219. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lewis, H.R., Jr. Classical and quantum systems with time-dependent harmonic-oscillator-type Hamiltonians. Phys. Rev. Lett. 1967, 18, 510–512. [Google Scholar] [CrossRef]
- Lewis, H.R., Jr.; Riesenfeld, W.B. An exact quantum theory of the time-dependent harmonic oscillator and of a charged particle in a time-dependent electromagnetic field. J. Math. Phys. 1969, 10, 1458–1473. [Google Scholar] [CrossRef]
- Abdalla, M.S.; Choi, J.R. Propagator for the time-dependent charged oscillator via linear and quadratic invariants. Ann. Phys. 2007, 322, 2795–2810. [Google Scholar] [CrossRef]
- Choi, J.R. Exact quantum theory of noninteracting electrons with time-dependent effective mass in a time-dependent magnetic field. J. Phys. Condens. Matter 2003, 15, 823–832. [Google Scholar] [CrossRef]
- Choi, J.R. An approach to dark energy problem through linear invariants. Chin. Phys. C 2011, 35, 233–242. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).