Abstract
Here we describe eight new methods, arisen in the last 60 years, to study solutions of a Hamiltonian system with n degrees of freedom. The first six of them are intended for systems with small parameters or without them. The methods allow to find families of periodic solutions and families of invariant n-dimensional tori by means of analytic computation near a stationary solution, near a periodic solution and near an invariant torus, using the corresponding normal form of a Hamiltonian. Then we can continue the founded families by means of numerical computation. In a Hamiltonian system without parameters, only periodic solutions and invariant n-dimensional tori form one-parameter families. The last two methods are intended for systems with not small parameters, which do not depend on time. They allow computing sets of parameters, which guarantee the stability of some solutions for linear (method seven) and nonlinear (method eight) systems. We do not consider chaotic behaviors, but only regular ones.
1. Introduction
The following methods, arisen in the last 60 years, are considered here.
- A normal form method that allows one to study regular perturbations near a stationary solution [1] (Ch. I), near a periodic solution [1] (Ch. II) [2,3], near the invariant torus [1] (Ch. II) and near families of such solutions [1] (Ch. VII, VIII), as well as bifurcations of periodic solutions and invariant tori and their stability.
- The method of truncated systems obtained with the help of Newton polyhedra, which allows the study of singular perturbations. For the theory and three applications, see [4] (Ch. IV). Other applications: Beletskiy’s equation on satellite oscillations [5,6], problems of periodic flyby of the Moon and planets.
- The method of generating families of periodic solutions (regular and singular). Generating families are the limits of families of periodic solutions as the perturbing parameters tend to zero. The solutions of the generating families consist of certain parts of the solutions to the limit problem. If the limit problem is integrable, then the generating families are found analytically. Applications: the restricted three-body problem, where the limit problem is the two-body problem and the generating families are one-parameter [1] (Ch. III–V) [7,8,9]; Hill’s problem [10], where the limit problem is an intermediate Henon problem and each generating family consists of one solution [11,12]. This approach can be applied to families of invariant tori as well.
- Methods of numerical computation of families of periodic solutions and of families of invariant tori.
- The method of generalized problems admitting in Celestial Mechanics bodies with negative masses [13]. Such problems have unified complete families of periodic solutions, which facilitates their calculation. Example: generalized Hill’s problem [13].
- Calculation of the network of families of periodic solutions and families of invariant tori as a “skeleton” of a part of the phase space. Poincaré [14] wrote about the benefits of such “skeletons”. Examples: the Hill problem [13] and partly the restricted three-body problem [9,15].
- Method of computation of a set of stability of stationary solutions of a linear multi-parameter Hamiltonian system combines modern techniques of elimination theory and power geometry [4]. It can be applied in the case when the Hamiltonian function depends on parameters in a polynomial way and gives the description of the boundary of the set of stability in the parameter space [16], and breaking it into cells in which nonlinear terms cannot impact the type of stability [17]. Examples: one gyroscopic problem with three-dimensional space of parameters [16], a double pendulum with a following force.
- Application of the q-analog of the classical subresultant for the characteristic polynomial of the matrix of a linear multi-parameter Hamiltonian system allows one to find resonant manifolds [18] and invariant coordinate subspace of the normal form of a Hamiltonian system. Resonant manifolds together with normal form in the vicinity of a stationary solution provide the method of dividing the set of stability into cells where formal stability takes place. The invariant coordinate subspaces allow reducing the phase flow of the initial system to a subspace of essentially less dimension.
2. Normal Form
2.1. A Vicinity of Stationary Solution
2.1.1. Resonant Normal Form
Consider an autonomous Hamiltonian system
with n degrees of freedom in the vicinity of a stationary point (SP)
If the Hamilton function is analytic at this point, then it can be expanded in a power series
where , , , . Since point (2) is stationary, expansion (3) begins with quadratic terms. The linear part of system (1) corresponds to them. The eigenvalues of its matrix A are split into pairs
Let . Canonical coordinate changes
keep the system Hamiltonian.
Theorem 1
([1] (Ch. I)). There is a canonical formal transformation (4), which reduces the Hamiltonian (3) to the normal form
where the series contains only resonant terms with
and the quadratic part of has its normal form (so that the matrix of the linear part of the system is the Hamiltonian analog of the Jordan normal form).
Here is the scalar product.
If , then the normal form (5) is equivalent to a system with fewer degrees of freedom and additional parameters. Normalizing transformation (4) preserves linear automorphisms
For the real original system (1), the coefficients of the complex normal form (5) satisfy special realness relations, and under the standard canonical linear change of coordinates , the system with Hamiltonian (5) goes over into the real system. There are several ways to calculate the coefficients of the normal form (5). The simplest is described in the book [19] by Zhuravlev, Petrov, Shunderyuk. The resonant normal form of the autonomous Hamiltonian system near the stationary solution, which takes into account only the eigenvalues of the matrix A of its linear part and without restrictions on this matrix A, was introduced in 1972. Previous variants of normal form were proposed by Birkhoff [20], Cherry [21], Gustavson [22] and others. They assumed some restrictions on the matrix of linear parts of the system. Later, a slightly simpler superresonant normal form was introduced, which took into account the Jordan cells of the normal form of the matrix A [23]. However, these additional simplifications did not allow an additional decrease in the number of degrees of freedom. For a more general approach to the normal form, see [24].
Suppose that the Hamiltonian function
depends on the small parameter and that when , the origin is a stationary point. The Hamiltonian (6) is assumed to be analytic in all of its arguments in some neighborhood of the point , . The following question arises: What is the simplest form to which we can reduce (6) by using a canonical change of variables
where and ?
Let be the eigenvalues of the matrix
when , . We write .
Theorem 2.
We point out some features of this theorem. First, the parameter does not change under a normalizing transformation. Second, the -dependence of the normal form lies in the fact that for resonant indices , the coefficient depends on in an arbitrary fashion. Third, the eigenvalues do not depend on and are computed for the value .
The theory of a resonant normal form near a stationary solution is described in detail in the book [1] (Chapter I).
Usually the normalizing transformation diverges in the whole neighborhood of the stationary point. However, near the point there are such analytical families of stationary points, of periodic solutions and of n-dimensional invariant tori, which adjoin the point. Next we describe these families in coordinates of the normal form and small parameters.
2.1.2. Families of Stationary Points
Let there be zeros among eigenvalues . Let them be and other . Then, stationary points satisfy the following system of equations
Here . The coordinate subspace (9), we denote as .
2.1.3. Families of Periodic Solutions
All non-zero imaginary eigenvalues , we divide into such blocks that all eigenvalues from the same block are pairwise commensurable, and they are not commensurable with from other blocks. A block can consist of one eigenvalue.
Let one such block correspond to a set of indices .
Then is a set of increasing natural indices . Here . Consider the coordinate subspace
Then in the coordinate subspace , a family of periodic solutions satisfies the following system [25]
From its solutions, we have to exclude the family of stationary points (8), (9). In (10) a is a free parameter. We can exclude it and obtain the system (8) and
In total, we obtain equations for unknowns, which describes a one-parameter family of periodic solutions.
2.1.4. Families of n-Dimensional Irreducible Invariant Tori
Such family can go through the stationary point only if all n eigenvalues are purely imaginary
and equation does not have integer solution , . Then in the normal form (5),
We put
We consider the set in the cartesian coordinates . In the generic case, each coordinate subspace (with respect to ) contains one one-dimensional (with respect to ) component of the set that does not lie in a smaller coordinate subspace. Consequently, the set consists of such components; for each there are exactly of these components situated in d-dimensional (with respect to ) coordinate subspaces. In particular, there is one component,
situated outside the coordinate subspaces.
It is the formal family of the tori.
Let
where T is a symmetric matrix. In the generic case, and the system of equations in (11) has a one-dimensional solution,
System (11) can be written in the form
The formal family will be analytical if eigenvalues satisfy the following condition on small divisors [25].
Condition
Let over , , , where . Then
It is a very weak numerical restriction on the eigenvalues .
2.1.5. Stability
The stationary point can be stable if all eigenvalues are pure imaginary.
Condition . Equation
has no integer solutions with .
This condition means that there are no resonances up to and including the order k. If it is satisfied, then in the normal form (5)
where are homogeneous polynomials from
of degree l, and is a series from starting with powers above k and is an integer part of number .
Thus it is possible to obtain a Hamiltonian of the form (12) with partial normalization only up to order k, when contains not only resonance terms.
In particular, under the condition we have
Under the condition , we have
Definition 1.
A fixed point of a real Hamiltonian system (1) is stable by Lyapunov if for every in “cube”
there exists a closed integral -dimensional manifold surrounding the point from all sides.
Lemma 1.
A stationary point is Lyapunov stable if there exists sign-definite real integral
of the system (1), where is the homogeneous form of degree l. In other words,
and does not return to zero at any except the point .
Stability is possible only if . If the condition is satisfied, then all are different and non-zero. In this case, the complex coordinates are related to the real coordinates by the canonical substitution
Suppose
Then in real coordinates , is real,
Theorem 3
([26]). If the condition is satisfied and the numbers are of the same sign, then the fixed point is stable according to Lyapunov.
Here, the role of the integral f is played by the Hamiltonian itself, for it is an integral, the notation (13) has the form (12) with and the form is of constant sign, for .
By formal we will mean power series, about the convergence of which nothing is known.
Definition 2
Formal stability means that the departure of solutions from the fixed point, if anything, is very slow: slower than any finite degree t.
Definition 3
Since , then under the condition the entry (14) takes the form
Hence, all the coefficients of are real.
Let be a linear hull of integers satisfying the equation , and is a non-negative orthant without origin.
Theorem 4
([29]). If the condition is met and in (19)
then the point is formally stable in the sense of the Definition 2
Here, the normal form of the Hamiltonian (5) is used to construct the formal integral.
According to (17) in real coordinates, the normal form (12) is
where the homogeneous polynomials are real. The following generalization of Theorem 4 is proved verbatim as well.
Theorem 5.
If the condition is satisfied and in the normal form (21)
then the point is formally stable in the sense of the Definition 3.
Condition M2 ([28] (Ch. 8, § 3)). System of equations
has no solution , i.e., , .
Under conditions and M2, the conditions of Theorem 4 are fulfilled and there is formal stability. However, the condition M2 is easier to check than the (20) condition.
If , the M2 takes the form:
system of two equations
has no solution with .
However, the solutions of the first equation have the form . For them, only when , i.e., the first equation has no solutions with under the condition of Theorem 3 . Substituting them into the second equation and reducing by , we obtain the condition
which is called the Arnold–Moser condition.
Under this condition there is not only formal stability, but also Lyapunov stability, because there are one-parameter families of two-dimensional invariant tori with similar sets of frequencies that lock the origin of coordinates. However, J. Moser [30] in 1968 and V.I. Arnold [31] in 1963 made mistakes in proving this fact. At the end of the article [25] there is a criticism of the first proof of Theorem 7 in [30].
On formal stability for , see also [32,33,34].
Most works on stability use conditions such as condition M2, where the number-theoretic character of frequencies is not taken into account. However, the structure of the normal form depends on them. For example, if the equation
has no solutions in integer , then the condition is satisfied and the normal form of the Hamiltonian (5) is . Then any is a formal integral and the fixed point is formally stable. In particular, at this is satisfied if the ratio is an irrational number.
Example 1.
In the book [28] (Ch. 7), the stability of the libration points of the planar circular restricted three-body problem is studied. There , the frequencies , with satisfy the equation
where μ is the ratio of the masses of the two bodies and the only parameter of the problem (). In this case, the stability is studied for
It is shown in § 4 that according to (4.7) in the normal form (21) at
Let us show that at these values the frequencies of and are incommensurable, i.e., there is formal stability.
From Equation (25), we obtain
The product can have two values
However, on the interval (23), the function takes the largest value at the right end at . There
Therefore, it follows from equality (27) that
Assume , i.e., . Here z is the ratio of the squares of the frequencies. According to (26) we obtain
Substituting this and in (28), we obtain
Consequently, z satisfies the quadratic equation
Its roots are
Given (28), we see that both values of z are irrational. Consequently, the ratio of frequencies is also irrational. □
Example 2.
In the book [28] (Ch. 8), the stability of libration points of a spatial circular restricted three-body problem is studied. There , the frequencies and are the same as in Example 1, and . In § 3 on p. 136, the formal stability theorem is formulated for all values of μ such that , except where there is double resonance. Let us show that in this problem, the double resonance is impossible.
Indeed, in the case of double resonance, the frequencies and are commensurate with each other and commensurate with unity. Let
where —are integers,
According to (26)
That is, , or , or
Let us put
Then the Equation (30) takes the form
As we know, all solutions to the Equation (32) in integer non-negative numbers have the form
where ϰ is a non-negative integer. According to (29) and (31) . Therefore, the Equations (33) will apply when , and when , and we put
By direct verification, we make sure that when , the Equations (31) and (34) are impossible for integers. When , the Equations (31) and (33) follow
Therefore,
The numbers , ϰ, have no common factor, and the numbers and have no common factor other than 2. Therefore, the ratio (35) cannot be an integer.
2.2. A Neighborhood of a Periodic Solution
2.2.1. Local Coordinates
Let a real Hamiltonian system with degrees of freedom have a real -periodic solution and the Hamiltonian function is analytic in some neighborhood of it.
According to [1] (Ch. II, Sect. 2.1) near the solution we can introduce such real local canonical coordinates that the solution is given by equations
and the Hamiltonian has the form
where integers , integer , real analytic functions have the period and they are expanded in the Fourier series.
Then the Hamiltonian system is
2.2.2. Normal Form
For and quadratic in part of the Hamiltonian (36) defines -periodic linear in system
Let be eigenvalues of its monodromy matrix, i.e., matrix of substitution of the fundamental matrix of solutions to the system (38) in the period . Let all . We put
Using correct numeration one obtains
Let us denote .
Theorem 6
([1] (Ch. II); [3]). There exists a complex formal invertible -periodic in ψ and φ canonical transformation of coordinates in the form of Poisson series
which reduces the Hamiltonian γ into normal form
where , , and m are integers, and all terms of the second sum are resonant, i.e.,
The normal form preserves small parameters and linear automorphisms of the initial system.
Let , , , , and , , are rational numbers.
Theorem 7.
A similar theorem is in [3].
Variable s is now a formal integral of the following system
If the initial Hamiltonian is real for real coordinates , then in Theorem 6 variables are complex but variables and are real. Here according to [1] (Chs. I, II) variables are connected with real variables , by the linear standard transformation
2.2.3. Families of Periodic Solutions
Let all imaginary numbers among eigenvalues be , i.e., , . Let all rational numbers have eigenvalues . Then the family of periodic solutions going through the solution satisfies the following system [25]
where a is a free parameter. Excluding it, we obtain the system
2.2.4. Families of -Dimensional Irreducible Invariant Tori
Such a family goes through the periodic solution only if all eigenvalues are pure imaginary, i.e., , and equation has no integral solutions , . Then in normal form , and our family is defined by the system
where a is a free parameter. Excluding it, we obtain the system
That formal family is analytic if eigenvalues satisfy the following condition on small divisors [25].
Condition
Let over , , , . Then
2.2.5. Stability
The periodic solution is stable only if all eigenvalues have .
Here there is a notion of Lyapunov stability, but at the conditions for its existence coincide with those for formal stability.
Definition 4.
Periodic solution
of a Hamiltonian system
orbitally formally stable if there exists such a power real series on , , ρ almost periodic on ψ
which may diverge, but is a formal sign-defined integral of the system (49).
In other words, all the coefficients of a power series
must convert to zero and the homogeneous in form , with only when , .
Recall that a function is periodic if it has a single frequency, conditionally (or quasi) periodic if it has a finite number of frequencies, and almost periodic if it has a countable number of frequencies. In our case, there will be quasi-periodic functions .
Definition 4 is similar to Definition 2, but one can also define formal orbital stability similar to Definition 3.
Put .
Condition . For all integer with the scalar products are not integers, i.e., the comparison has no solutions with such .
Theorem 8
([1,3]). Under the condition , there exists a complex formal reversible -periodic on ψ and ϕ canonical coordinate transformation
which brings the Hamiltonian γ to the normal form
where , , and m are integers, all terms of the second sum have order in above two and resonant, that is,
Let us put
Theorem 9
Note that the returns from the variables to the original variables are given by formal power series on with quasi-periodic coefficients on . Let us call the Hamiltonian (56) a reduced normal form.
The variable s is now the formal integral of the system
The orbital stability problem of the periodic solution has now been reduced to the stability problem of the fixed point , in the system (57).
2.2.6. Real Case
If the original Hamiltonian is real under the real variables , then in Theorem 8 the variables are complex and the variables and are real.
If the condition is satisfied, then according to [1] (Chapters I and II) the complex variables are related to the real variables , by the formulae
The complex variables and their conjugate variables are related by the relations
With complex conjugation, the Hamiltonian (51) is preserved:
Indeed, , and we can show that
Note that according to (60)
Therefore, in (53), all and are real, and all are purely imaginary. Assume .
According to (59)
Now (58) takes the form
All quantities here are real.
All integer vectors that satisfy the comparison , form in the lattice L. Let M be its linear hull and is a non-negative orthant in with no origin.
2.3. The Neighborhood of an Invariant Torus
2.3.1. Reduction to Normal Form
Let a real analytic Hamiltonian system
have an invariant torus of dimension k. Using the normal form, we can study the solutions of the system (63) in a neighborhood of the torus for any [25]. Here we confine ourselves to the most important case . We call a torus regular if in its neighborhood there are local coordinates , that have the following properties.
- The coordinates and are canonically conjugate and are analytic functions of and .
- The coordinates are -periodic.
- The torus is specified by the equations .
- On the system (63) induces the system
Then, in the neighborhood of the regular torus the system (63) takes the form
In the neighborhood under consideration, the Hamiltonian function g is -periodic in each and is expanded in a convergent series
where the integer vectors are non-negative and the coefficients are analytic -periodic functions. By hypothesis, on the torus , the system (65) takes the form (64), that is,
where is its frequency basis.
Now we try to simplify the system (65) by means of a formal canonical local coordinate transformation
where , and we have not written out terms of higher degrees in . As a result of such a transformation, let . We expand in a Poisson series
We call the Hamiltonian function h a normal form if in (68) only those coefficients are nonzero for which
The -condition:
where the limit is taken over the integers such that .
2.3.2. Families of n-Dimensional Irreducible Regular Tori
Torus is irreducible, if equation
has no integer solutions . Then normal form in (68) does not depend on , i.e., .The formal family of our tori satisfies the system [25]
where a is a free parameter, i.e.,
Let the MacLaurin series for h have the form
where T is a symmetric square matrix. In our case, , and so the system (70) is
In the generic case, , and so the system has a unique one-parametric solution
that is, the set is a one-parameter family of n-dimensional regular tori with frequency basis .
The formal family (58) is analytic, if frequencies satisfy the following condition on small divisors.
Condition
Let for , . Then
Thus, we have proved the following result.
Corollary 3.
In a generic Hamiltonian system with n degrees of freedom, an invariant regular torus , whose frequency basis is non-resonant and satisfies the ω-condition, lies on an analytic one-parameter family of n-dimensional tori, filled by conditionally-periodic solutions with frequency basis . The Hamiltonian function changes monotonically in this family. Torus is not bifurcating, if .
2.3.3. Stability
Non-resonant torus is formally stable.
3. The Truncated Systems Method
If an equation (or a system of equations) contains a linear part, then sometimes it can be reduced to normal form. However, if the equation does not have a linear part, then the question arises: what should be considered as the first approximation of the equation (or the system)? The answer to it is given by the method of truncated equations, which makes it possible to write out several first approximations and for each indicate the region in the space of variables and parameters where it dominates.
3.1. Truncated Hamilton Function
Let the vectors , and be canonical variables and small parameters, respectively. Let the autonomous (time-independent) Hamilton function be expanded in a power series
where , and are constant coefficients. Each term of series (72) is associated with its vector exponent . The set of all points Q with in the sum (72) is called the support of the sum (72). The convex hull of the support is called the Newton polyhedron of the sum (72). Its boundary consists of vertices , edges and faces of dimensions . The intersection is called the boundary subset of the set . Each generalized face (including vertices and edges) corresponds to:
- Normal cone
- Truncated sum
It is the first approximation to the sum (72) when
along . Thus, using truncated Hamiltonian functions, we can find approximate problems.
3.2. Restricted Three Bodies Problem (RTBP)
Let two bodies and with masses and , respectively, revolve around their common center of mass with a period of . The plane circular restricted three-body problem studies the plane motion of a body of infinitesimal mass under the action of the Newtonian attraction of bodies and . In a rotating (synodic) coordinate system, the problem is described by an autonomous Hamiltonian system with two degrees of freedom and one parameter . It was introduced by Euler in 1772 [35]. The Hamilton function has the form [1]
Here body and body , where , . Consider small values of the mass ratio . For the problem becomes the problem of two bodies and . However, here it is necessary to remove from the phase space the points corresponding to the collisions of bodies and . Collision points split the solutions of the problem of two bodies and into parts. For small near the body there is a singular perturbation of the case .
In order to find all the first approximations of the restricted three-body problem, it is necessary to introduce local coordinates
near the body and expand the Hamiltonian function in a power series in these coordinates. After expanding in a Maclaurin series, Hamilton’s function (73) takes the form
where f is a convergent power series that does not contain terms of order less than three. Let
The set of these points consists of the points
where The convex hull of the set is the polyhedron . Surface of the polyhedron consists of faces , edges and vertices . To each such element there corresponds a truncated Hamiltonian , which is the sum of those terms of series (74) whose points belong to . Truncated Hamiltonian functions are different first approximations of function (74), valid in different regions of the space . Figure 1 depicts a polyhedron for series (74) in , coordinates, which is a semi-infinite trihedral prism with an oblique base. It has four faces and six edges. Let us consider them.
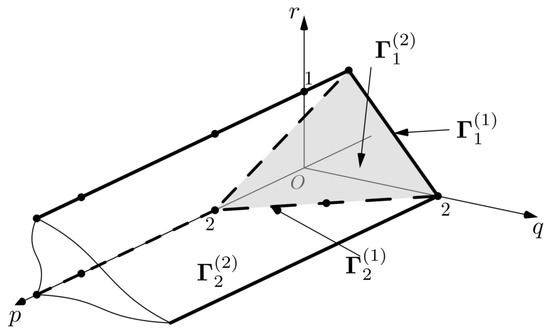
Figure 1.
The polyhedron for the Hamiltonian function (74) in coordinates .
The face , which is the oblique base of the prism , contains the vertices
It corresponds to the truncated Hamilton function
It describes Hill’s problem [10], found in 1878, which is non-integrable. A power transformation
reduces the corresponding Hamiltonian system to the Hamiltonian system with the Hamiltonian function of the form (75), where must be replaced by , respectively.
Face contains points
It corresponds to the truncated Hamiltonian function , which is obtained from the function h at 0. It describes the problem of two bodies and , which is integrable.
Consider the edges. Of the six edges, one is improper. It passes through the point parallel to the vector . On three edges, , that is, for them the truncated Hamiltonian functions do not depend on , and the solutions of the corresponding truncated Hamiltonian systems have , which is not interesting. Two edges remain.
Edge . It contains the points and of the set . The corresponding truncated Hamilton function is
It describes the problem of two bodies and . Power transformation (76) reduces it into a Hamilton system with a Hamilton function of the form (77), where is replaced by , respectively.
The edge contains points , , of the set . It corresponds to the truncated Hamilton function (3.4) with . It describes an intermediate problem (between the Hill problem and the problem of two bodies and ), which is integrable. This first approximation was introduced by Hénon [36,37] in 1969.
Therefore, very close to the body the first approximation of the original restricted problem with the Hamiltonian function (74) is the problem of two bodies and with Hamiltonian (77), just close is the Hill problem with Hamiltonian (75), further from the body is the intermediate problem, and far from the body is the problem of two bodies and . Near the body , the periodic solutions of the restricted problem are perturbations of both periodic solutions of all the above four first approximations and the results of gluing the hyperbolic orbits of the two-body problem with arc-solutions of either the two-body problem , or an intermediate problem. In [38,39,40,41,42], periodic solutions of the intermediate problem were used as generators for finding periodic quasi-satellite orbits of the restricted problem.
Therefore, the restricted three-body problem was stated by L. Euler in 1772, one of its first approximations was found by G. Hill in 1878 as a result of long work, another of its first approximations was found by M. Hénon in 1969 again as a result of non-trivial work. However, using the polyhedron, these approximations and the others can be found without difficulty.
3.3. Truncated Algebraic Systems
Consider now the set of polynomials
Each has its own support and all accompanying objects: Newton’s polyhedron its generalized faces , their normal cones , boundary sets , truncated polynomials . Moreover, for every non-empty intersection
there corresponds to a set of truncations
which is the first approximation of the set (78), for
near the intersection (79) and is called the truncation of the set (78).
Consider now the system of equations
corresponding to the set (78). System (81) corresponds to all the objects indicated for the set (78), as well as the truncated systems of equations
each of which corresponds to one set of truncations (80). Each truncated system (82) is the first approximation of the complete system (81).
3.4. Analytical Computation of Local Families
In Section 2, we obtained systems of equations of the form (78), (81), the roots of which are families of stationary points, of periodic solutions and of invariant tori, when coordinates tend to zero. The method, described in Section 3.3, allows to calculate such roots in the form of power series from some parameters. Examples of such computations are shown in [43]. The method of truncated equations and systems allows to calculate asymptotic solutions for ordinary differential equations: the Beletskii equation of satellite oscillations [5], the problem of periodic flyby of planets with a close approach to the Earth and for partial differential equations: boundary layer on a needle.
4. Generating Families of Periodic Solutions and Generating Families of Invariant Tori
As soon as electronic computers appeared, scientists began to calculate families of periodic solutions of the restricted three-body problem for different cases: Sun–Jupiter , Earth–Moon , etc. It turned out that these families are very similar, and their periodic solutions resemble solutions to the two-body problem. In 1968, M. Hénon [44] realized that it was necessary to consider the limits of these families for . Generating families allow to understand and to prescribe by analytic computation singularities of families for small parameter .
4.1. Method
Let the Hamilton function depend analytically on small parameters and the corresponding Hamiltonian system has families of periodic solutions . Some of these families may have limits at . Families are called generating. Their solutions are formed by parts of solutions of the Hamilton limit system with .
If this limit system is integrable, then the generating families can be described analytically. This approach was proposed by Hénon [44]. It was used for the Hill problem and for the restricted three-body problem [1] (Ch. III-V), [7,8].
4.2. The Hill Problem
Its Hamilton function has the form
The corresponding system
describes the motion of the Moon with zero mass under the influence of the attraction of the Sun , located at infinity, and the Earth with mass 1, located at the origin of coordinates. The Hamilton function (83) is analytic in
We apply the canonical coordinate transformation
and we obtain the Hamiltonian system
where
Let and . Then, in the limit, we obtain system (4.2) with
This is the Hénon problem [36]. For , system (84) is linear and, therefore, integrable. Since the Hamiltonian is homogeneous, it suffices to consider it for . It has one regular periodic solution
If the orbit of the solution to the Henon problem passes through the point
then the body collides with the body and the solution cannot be continued through the collision. Therefore, point (4.3) divides the solution into independent parts. Hénon [36] found all the arc-solutions that start and end with such collisions. They form a countable set of two types. The arc-solutions of the first type are denoted by the symbols , and their orbits are epicycloids. For they are shown in Figure 2. The orbits of arc-solutions with negative j values are symmetric to them about the axis.
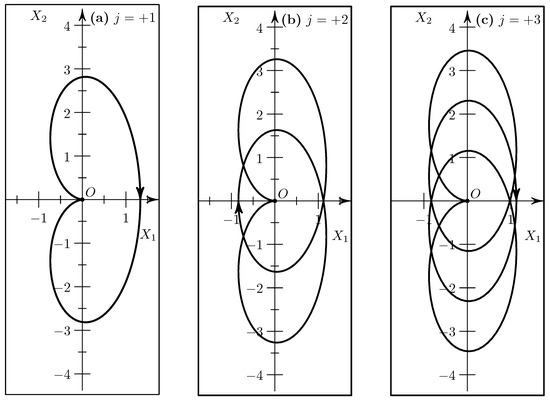
Figure 2.
Arc-solutions of the first type for j: (a), (b) and (c).
The arc-solutions of the second type are denoted by the letters i and e, their orbits are ellipses passing through the point (85). They are shown in Figure 3.
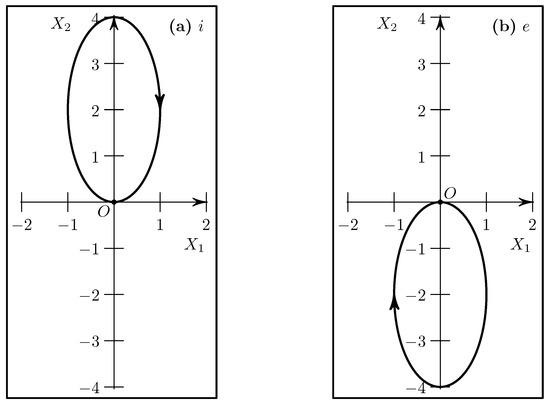
Figure 3.
Arc-solutions of the second type i (a) and e (b).
Theorem 12.
([45]) A sequence of arc-solutions that does not contain two successively identical arc-solutions of the second type is a generating solution to the Hill problem.
Here the generating family of periodic solutions consists of one solution. All known families of periodic solutions to the Hill problem include at least one generating solution.
In the restricted three-body problem, there is a countable set of one-parameter generating families of periodic solutions. Some of them are quite complex [7].
The same approach is applicable to families of n-dimensional invariant tori. The Hill problem has no generating families of them, but the RTBP has an infinite amount: indeed all solutions to the two-body problem with fixed irrational mean motion form such a family [1]. However, generating families of invariant tori are not studied yet.
5. Numerical Computation of Families of Periodic Solutions and of Invariant Tori
In Section 2 and Section 3, we describe a way for computation of local such families near a stationary point, near a periodic solution and near n-dimensional invariant torus. For periodic solutions, there are many methods for numerical continuation of their families (see [46,47,48,49]) and a lot applications of these methods.
For invariant tori, there is one method for numerical computation of their family proposed by C. Simó [50] (see also [51]). Therefore, the method of computation of families of invariant tori appeared only since 1998.
6. Generalized Problems
Usually in celestial mechanics, bodies with non-negative masses are considered. However, Batkhin [13] proposed to consider problems where some masses are negative. In the Hill problem with body mass equal to (called the anti-Hill problem), families of periodic solutions are extensions of families of periodic solutions to the classical Hill problem. Therefore, it is more convenient to calculate families of periodic solutions for both problems at once: for the Hill problem and for the anti-Hill ones. This approach provides new families of periodic solutions for the classical Hill problem.
Figure 4 shows a diagram of the connections between these families of the Hill (left) and the anti-Hill (right) problems. The center column gives the generating solutions for these families.
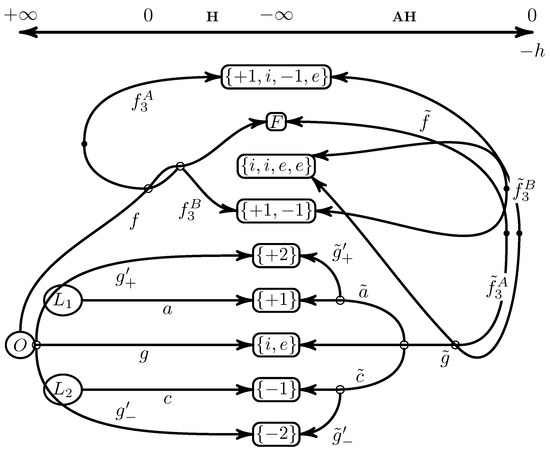
Figure 4.
Diagram of connection between main families of the Hill and anti-Hill problems. The upper axis shows the change of value of the Hamiltonian function (83).
The usefulness of negative masses in Celestial Mechanics was only realized after 2014.
7. Skeletons
In some parts of the phase space of the Hamilton system, there are many families of periodic solutions, invariant tori and they form the “skeleton” of this part of the phase space. Therefore, the calculation of such families is very useful for studying the structure of the phase space.
In some problems, there are many computed families of periodic solutions, but their number is not yet sufficient to form a skeleton. For recent results in this direction for the restricted three-body problem, see [9,15,52,53]. For the Hill problem, see [54] (§ 10.4), [55] (§ 19), [11,12,13,36,37,45,56,57,58]. However, families of invariant tori were not studied yet.
8. Stability in a Linear Multi-Parameter Hamiltonian System
The last two sections presented the description of methods providing an investigation of stability for the case of a Hamiltonian that depends in a polynomial way on the parameter vector P of the parameter space . Assuming a generic case, we describe in Section 8 the method which allows finding in the parameter space such domains that SP is Lyapunov stable either in the full problem or in the linear approximation of the full problem. This method essentially explores modern elimination theory and can be implemented in any computer algebra system.
The study of Lyapunov stability of the SP of a Hamiltonian system in the case in which the number of degrees of freedom is greater than two requires considerable effort. This is due, on the one hand, to the fact that the stability of the equilibrium position in the linear approximation can be destroyed by any arbitrarily small perturbation of higher order. On the other hand, the Arnold-Mozer theorem on the stability of the equilibrium position is inapplicable for large dimensions. However, for many applications, the formal stability proposed by J. Moser [27] is quite sufficient.
Let us consider the simplest invariant manifold of dimension 0, namely, the stationary points of a Hamiltonian function depending in a polynomial way on the parameter vector , where s is the dimension of the parameter space . The proposed methods can be applied to the case of manifolds of large dimensions, i.e., in the case of studying Hamiltonian phase flow near a periodic solution or near an invariant torus.
In the generic case, an analytic time-independent Hamiltonian function in the vicinity of the SP, coinciding with the origin, is expanded into a convergent series of homogeneous polynomials of degree k of its phase variables
The well-known Lagrange–Dirichlet theorem [26] and [55] (§ 29) states that SP is stable if the quadratic form is sign-determined (see Theorem 3).
If the number of degrees of freedom is not more than two
- Stability is determined by the Arnold–Moser theorem in the absence of resonances of order four or less, which requires normalizing H to order four;
- For resonances of order less than four, the stability conditions are derived in the works of A. P. Markeev and A. G. Sokolsky (see [28] and also Section 2.1.5).
The series (86) starts with the quadratic Hamiltonian defining the local dynamics near the SP. The behavior of the phase flow in the first approximation is described by a linear Hamiltonian system
Let us recall here the main properties of a linear Hamiltonian system.
- If is an eigenvalue of the matrix B, then is also its eigenvalue. All eigenvalues , , of the matrix B can be reordered in such a way that , .
- The characteristic polynomial of the matrix B contains only even powers of , so it is a polynomial in . The following [16] polynomialis called semi-characteristic.
- If for any j, i.e., the SP is hyperbolic, then it is structurally stable according to the Hartman–Grobman theorem.
- For an elliptic SP, the behavior of the phase flow in its vicinity can only be obtained by taking into account the nonlinear terms. Usually this is performed using KAM-theory, but here such study is performed using the Hamiltonian normal form described in Section 2.
Definition 5.
The stability set Σ of the system (87) is the set of all values of parameter for which the SP is Lyapunov stable.
In terms of roots of a semi-characteristic polynomial (88), the condition of stability of the SP is given by
Theorem 13
([16]). The SP of the linear Hamiltonian system (87) is Lyapunov-stable if and only if
- All the roots of the semi-characteristic polynomial (88) are real and non-positive;
- All elementary divisors of the matrix B are simple.
Let us first briefly recall the definition of a k-th order subdiscriminant of an arbitrary monic polynomial of n degree (for more details, see [59]).
Definition 6.
Let
be some monic polynomial from the x variable. Then its k-th subdiscriminant ,
where are roots of the polynomial (89), I is any non empty subset of the set , is its cardinality (number of elements in I). For we put and for we put . For we obtain the classical discriminant.
The criteria of reality and negativity of roots is given by the following statement.
Proposition 1.
For all roots of a polynomial of degree n to be real, negative, and distinct, it is necessary and sufficient that the conditions
where is the k-th sub-discriminant of the polynomial .
Checking the simplicity of elementary divisors of matrix B is provided by calculating the rank of matrix for multiple roots of polynomial .
Proposition 2.
If is a root of of multiplicity l, then all corresponding elementary divisors of matrix are simple if and only if .
If is a root of of multiplicity l, then all corresponding elementary divisors of matrix are simple if and only if .
The boundary of the stability set consists of parts of surfaces satisfying
- The condition of zero roots ;
- The condition of multiple roots , where is the discriminant of the polynomial .
Assuming that functions and are polynomials in , we obtain the problem of description of the affine varieties and , which divide the space of parameters into cells. The appropriate cells are included in the stability set according to Proposition 1. The boundaries of these cells are selected according to Proposition 2 with the help of multiple roots founded from (94).
Remark 1.
According to Proposition 1 the set of stability Σ is a solution of the system (90), i.e., it is a semi-algebraic set. It can be computed with the algorithm of cylindrical algebraic decomposition (CAD) [59] (Sect. 5). The CAD algorithm usually demonstrates rather high computational complexity.
For the system (87), let the stability set be calculated. Then for each value of the eigenvalues of the matrix are purely imaginary , and elementary divisors are simple. In this case, the Hamiltonian is reduced to the normal form with a set of invariants , ,
The change of the signature of the quadratic form can occur while crossing the hypersurface , which divides the stability set into regions with the same signature value . Let us distinguish those regions for which , i.e., for them the Lagrange–Dirichlet theorem is inapplicable. The formal stability of the SP should be studied in these regions of the stability set .
Remark 2.
To determine the invariants and consequently the signature of the normal form (91), it is not necessary to perform a normalization procedure. It is sufficient to use the method described in [17].
9. Studying of Formal Stability of Stationary Point
Here, we give a schematic description of the method for studying the formal stability of the SP. This method is based on the following key results: normal form of the Hamiltonian at the SP, Bruno’s Theorem 4 on formal stability and q-analog of the classical elimination theory.
In the absence of strong resonances between eigenvalues of a linearized Hamiltonian system in the neighborhood of the SP, the condition for its formal stability is formulated by the Bruno theorem [29]. In the paper [17], a scheme for investigating formal stability was proposed. This scheme assumes, firstly, that the set of stability of the SP in linear approximation is computed, and secondly, that the so-called resonant sets of the characteristic polynomial corresponding to strong resonances 2:1, 3:1 between eigenvalues are found. Here we consider a method for investigating the stability of the SP of a multi-parameter Hamiltonian system with more than two degrees of freedom, based on the description of the discriminant and resonant sets of the real polynomial proposed in [18].
One of the earliest results on the formal stability of the SP is
Theorem 14
(Birkhoff). If for some value of the parameter vector all components of the vector of eigenvalues are rationally incommensurable, i.e., the equation has no integer solution , , then there exists a formal canonical transformation w of the variables such that the Hamiltonian is a power series over . Here are action-angle variables.
The Birkhoff theorem is difficult to apply because resonance sets are dense everywhere in the parameter space .
Let the condition from Section 2.1.5 take place, i.e., for , then it is known that there exists an analytic canonical transformation such that the new Hamiltonian g has the form
where , , , and is a polynomial of variables of degree three or higher in .
Theorem 15
(Bruno [29]). If on any pair of nonzero integer vectors and of ortant , , which are solutions to the equation
bilinear form at , then the SP of the Hamilton system is formally stable.
Note that the condition (92) of the Bruno theorem is equivalent to the fact that the semi-algebraic system is incompatible.
Thus, to apply the Bruno theorem on formal stability, it is necessary to find the boundaries of regions in the parameter space defined by resonance sets.
Here we consider a scheme for studying the formal stability of the equilibrium position of a Hamiltonian system under the following assumptions:
- Number of degrees of freedom more than two;
- The quadratic form in the expansion (86) is nondegenerate and not sign-defined;
- Hamiltonian function smoothly depends on the parameter vector .
The proposed research scheme essentially uses the normal form of the Hamiltonian system near the SP, a method for computing the stability set of a linear multi-parameter Hamiltonian system [16] and a method for computing the resonance set of a real polynomial [18]. These methods, in the case of polynomial dependence on the parameter , essentially use so-called quantum calculus [60].
The application of q-subdiscriminants of the characteristic polynomial allows not only to find out if it has commensurable roots, but also, under certain conditions, to find these roots without having to calculate all its eigenvalues. If the coefficients of polynomial (89) depend on parameters, both q-subdiscriminants are functions of these parameters, which makes it possible to determine at what values of q resonance takes place and to find its multiplicity and order.
To determine the rational comparability of the roots of the polynomial, we will use q-analogs of the classic derivative and subdiscriminant.
Definition 7.
Jackson derivative (q-derivative, q-differential Jackson operator):
The Jackson derivative has all the properties of an ordinary derivative. In addition to the above properties, we note that the q-derivative function is equal to , and applying q-derivative to q-binomial of degree n again gives q-binomial of degree multiplied by .
With the q-derivative, the q-analog of the classic polynomial discriminant is now determined.
Definition 8.
Define q-discriminant of polynomial as the resultant of a polynomial pair and :
The equality to zero of the q-discriminant of polynomial with fixed q is a signature of the existence of at least one pair of q-commensurable roots; however, the detailed structure of all commensurable roots can be obtained using the sequence of q-subdiscriminants of various orders of the polynomial .
Theorem 16
([18]). The polynomial has exactly different sequences of q-commensurable roots if and only if the first non-zero q-subdiscriminant in sequence (93) of k-th q-subdiscriminants , , has the index d.
All commensurable roots of the polynomial are the roots of the largest common polynomial divisor of and its q-derivative :
Theorem 16 states that the degree of the polynomial is equal to the number d of the first non-zero q-subdiscriminant in the sequence .
Note that q-subdiscriminants are calculated using any of the matrix methods to calculate the classical subresultants of the polynomial pair and [61].
Let, in the conditions of Theorem 16, the first non-zero q-discriminant have the index d, . Let us denote with , , d the modified q-Sylvester matrix , where the column with the number is replaced by its column with the number and with which is the determinant of this inner. Then, as shown in [18], the following proposition takes place.
Proposition 3.
If in the sequence (93) the first one different from zero q-subdiscriminant has the index d, then
The roots of polynomial (94) are either q-commensurable roots for or multiple roots for of the initial polynomial (89).
Let us describe schematically the procedure of formal stability studying.
In the first step, the stability set of the linear Hamiltonian system (87) is computed. Then the open regions in which the signature of the quadratic form is not equal to , i.e., the Lagrange–Dirichlet theorem on Lyapunov stability is not applicable.
In the next step, the resonance sets and are computed for the semi-characteristic polynomial (88), dividing each region into subregions that have resonances of order four and higher. Then, in these regions, the procedure of reducing the Hamiltonian (86) to the fourth-order normal form is applied. After normalization, we check whether the condition of the Bruno theorem is satisfied.
On sections of resonance sets , , where there is a single resonance, the theorems of [28] (Ch. 4, §§ 2, 3) are applied. For the case of multiple resonance, as well as for resonance of order two, the formal stability study can be carried out using a different approach.
On the one hand, the presence of resonance leads to additional first formal integrals, which allows decreasing the number of degrees of freedom of the normalized system [1] (Ch. I, §3), and in some cases even to integrate it. On the other hand, finding the invariant coordinate subspaces of the Hamiltonian normal form reduces the phase flow to subspaces of fewer dimensions, on which one can search the realization of conditions of analyticity of the normalizing transformation.
Author Contributions
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SP | stationary point |
| RTBP | restricted three body problem |
References
- Bruno, A.D. The Restricted 3–Body Problem: Plane Periodic Orbits; Walter de Gruyter: Berlin, Germany, 1994. [Google Scholar]
- Bruno, A.D. Normal form of a Hamiltonian system with a periodic perturbation. Comput. Math. Math. Phys. 2020, 60, 36–52. [Google Scholar] [CrossRef]
- Bruno, A.D. Normalization of the periodic Hamiltonian system. Program. Comput. Softw. 2020, 46, 76–83. [Google Scholar] [CrossRef]
- Bruno, A.D. Power Geometry in Algebraic and Differential Equations; Elsevier Science: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Bruno, A.D.; Varin, V.P. The limit problems for the equation of oscillations of a satellite. Celest. Mech. Dyn. Astron. 1997, 67, 1–40. [Google Scholar] [CrossRef]
- Beletsky, V.V. Essays on the Motion of Celestial Bodies, 1st ed.; Birkhäuser Verlag: Basel, Switzerland, 2001. [Google Scholar]
- Hénon, M. Generating Families in the Restricted Three-Body Problem; Number 52 in Lecture Note in Physics. Monographs; Springer: Berlin/Heidelber, Germany; New York, NY, USA, 1997. [Google Scholar]
- Hénon, M. Generating Families in the Restricted Three-Body Problem. II. Quantitative Study of Bifurcations; Number 65 in Lecture Note in Physics. Monographs; Springer: Berlin/Heidelber, Germany; New York, NY, USA, 2001. [Google Scholar]
- Bruno, A.D.; Varin, V.P. Periodic solutions of the restricted three-body problem for small mass ratio. J. Appl. Math. Mech. 2007, 71, 933–960. [Google Scholar] [CrossRef]
- Hill, G.W. Researches in the Lunar Theory. Amer. J. Math. 1878, 1, 5–26, 129–147, 245–260. [Google Scholar] [CrossRef]
- Batkhin, A.B. Symmetric Periodic Solutions of the Hill’s Problem. I. Cosm. Res. 2013, 51, 275–288. [Google Scholar] [CrossRef]
- Batkhin, A.B. Symmetric Periodic Solutions of the Hill’s Problem. II. Cosm. Res. 2013, 51, 452–464. [Google Scholar] [CrossRef]
- Batkhin, A.B. Web of Families of Periodic Orbits of the Generalized Hill Problem. Dokl. Math. 2014, 90, 539–544. [Google Scholar] [CrossRef]
- Poincaré, H. Les Métods Nouvelles de la Mécanique Céleste; Gauthier-Villars: Paris, France, 1899; Volume 3. [Google Scholar]
- Bruno, A.D.; Varin, V.P. Periodic solutions of the restricted three body problem for small μ and the motion of small bodies of the Solar system. Astron. Astrophys. Trans. (AApTr) 2012, 27, 479–488. [Google Scholar]
- Batkhin, A.B.; Bruno, A.D.; Varin, V.P. Stability sets of multiparameter Hamiltonian systems. J. Appl. Math. Mech. 2012, 76, 56–92. [Google Scholar] [CrossRef]
- Batkhin, A.B. Segregation of stability domains of the Hamilton nonlinear system. Autom. Remote Control. 2013, 74, 1269–1283. [Google Scholar] [CrossRef]
- Batkhin, A.B. Parameterization of a Set Determined by the Generalized Discriminant of a Polynomial. Program. Comput. Softw. 2018, 44, 75–85. [Google Scholar] [CrossRef]
- Zhuravlev, V.F.; Petrov, A.G.; Shunderyuk, M.M. Selected Problems of Hamiltonian Mechanics; LENAND: Moscow, Russia, 2015; p. 304. (In Russian) [Google Scholar]
- Birkhoff, G.D. Dynamical Systems. In Colloquim Publications, revised ed.; AMS: Providence, RI, USA, 1966; Volume 9. [Google Scholar]
- Cherry, T.M. On the Solution of Hamiltonian Systems of Differential Equations in the Neighbourhood of a Singular Point. Proc. Lond. Math. Soc. 1928, s2, 151–170. [Google Scholar] [CrossRef]
- Gustavson, F.G. On constructing formal integrals of a Hamiltonian system near an equilibrium point. Astron. J. 1966, 71, 670–688. [Google Scholar] [CrossRef]
- Baider, A.; Sanders, J.A. Unique normal forms: The nilpotent Hamiltonian case. J. Differ. Equations 1991, 92, 282–304. [Google Scholar] [CrossRef][Green Version]
- Belitskii, G.R. Normal forms with respect to filtering action of a group. Trans. Moscow Math. Soc. 1979, 40, 3–46. [Google Scholar]
- Bruno, A.D. Families of periodic solutions and invariant tori of Hamiltonian systems. In Formal and Analytic Solutions of Differential Equations; Filipuk, G., Lastra, A., Michalik, S., Eds.; World Scientific (Europe): Singapore, 2020. [Google Scholar] [CrossRef]
- Lejeune-Dirichlet, J.P.G. Über die Stabilität des Gleichgewichts. J. Die Reine Und Angew. Math. 1846, 32, 85–88. [Google Scholar]
- Moser, J. New aspects in the theory of stability in Hamiltonian systems. Comm. Pure Appl. Math. 1958, 11, 81–114. [Google Scholar] [CrossRef]
- Markeev, A.P. Libration Points in Celestial Mechanics and Cosmodynamics; Nauka: Moscow, Russia, 1978. (In Russian) [Google Scholar]
- Bruno, A.D. Formal stability of Hamiltonian systems. Math. Notes 1967, 1, 216–219. [Google Scholar] [CrossRef]
- Moser, J. Lectures on Hamiltonian systems. Mem. Amer. Math. Soc. 1968, 81, 87. [Google Scholar]
- Arnold, V.I. Small denominators and problems of stability of motion in classical and celestial mechanics. Russ. Math. Surv. 1963, 18, 85–191. [Google Scholar] [CrossRef]
- Cárcamo-Díaz, D.; Palacián, J.F.; Vidal, C.; Yangus, P. Nonlinear stability of elliptic equilibria in Hamiltonian systems with exponential time estimates. Discret. Contin. Dyn. Syst. 2021, 41, 5183–5208. [Google Scholar] [CrossRef]
- Bounemoura, A.; Fayad, B.; Niederman, L. Super-exponential stability for generic real-analytic elliptic equilibrium points. Adv. Math. 2020, 366, 107088. [Google Scholar] [CrossRef]
- dos Santos, F.; Vidal, C. Stability of equilibrium solutions of Hamiltonian systems with n-degrees of freedom and single resonance in the critical case. J. Differ. Equations 2018, 264, 5152–5179. [Google Scholar] [CrossRef]
- Euler, L. Theoria Motuum Lunae Nova Methoda Pertractata; Typis Academiae Imperialis Scientiarum: Petropolis, Brazil, 1772. [Google Scholar]
- Hénon, M. Numerical exploration of the restricted problem. V. Hill’s case: Periodic prbits and their stability. Astron. Astrophys. 1969, 1, 223–238. [Google Scholar]
- Hénon, M. Numerical exploration of the restricted problem. VI. Hill’s case: Non-periodic orbits. Astron. Astrophys. 1970, 9, 24–36. [Google Scholar]
- Benest, D. Libration effects for retrograde satellitesin the restricted three-body problem. I: Circular plane Hill’s case. Celest. Mech. 1976, 13, 203–215. [Google Scholar] [CrossRef]
- Kogan, A.Y. Distant satellite orbits in the restricted circular three-body problem. Cosm. Res. 1989, 26, 705–710. [Google Scholar]
- Lidov, M.L.; Vashkov’yak, M.A. Quasisatellite periodic orbits. In Analytical Celestial Mechanics; Kholshevnikov, K.V., Ed.; Kasan University: Kazan, Russia, 1990; pp. 53–57. (In Russian) [Google Scholar]
- Lidov, M.L.; Vashkov’yak, M.A. Perturbation theory and analysis of evolution of quasisatellite orbits in the restricted three-body problem. Cosm. Res. 1993, 31, 187–207. [Google Scholar]
- Lidov, M.L.; Vashkov’yak, M.A. On quasi-satellite orbits in a restricted elliptic three-body problem. Astron. Lett. 1994, 20, 676–690. [Google Scholar]
- Bruno, A.D.; Batkhin, A.B. Resolution of an algebraic singularity by power geometry algorithms. Program. Comput. Softw. 2012, 38, 57–72. [Google Scholar] [CrossRef]
- Hénon, M. Sur les orbites interplanetaires qui rencontrent deux fois la terre. Bull. Astron. Ser. 3 1968, 3, 377–402. [Google Scholar]
- Hénon, M. New families of periodic orbits in Hill’s problem of three bodies. Celest. Mech. Dyn. Astr. 2003, 85, 223–246. [Google Scholar] [CrossRef]
- Parker, T.S.; Chua, L.O. Practical Numerical Algorithms for Chaotic Systems; Springer: New York, NY, USA, 1989. [Google Scholar]
- Simó, C. Analitycal and numerical computation of invariant manifolds. In Modern Methods in Celestial Mechanics; Editions Froniéres: Paris, France, 1990; pp. 285–330. [Google Scholar]
- Lara, M.; Peláez, J. On the numerical continuation of periodic orbits. An intrinsic, 3-dimensional, differential, predictor-corrector algorithm. Astron. Astrophys. 2002, 389, 692–701. [Google Scholar] [CrossRef]
- Galan-Vioque, J.; Almaraz, F.J.M.; Macías, E.F. Continuation of periodic orbits in symmetric Hamiltonian and conservative systems. Eur. Phys. J. Spec. Top. 2014, 223, 2705–2722. [Google Scholar] [CrossRef]
- Simó, C. Effective Computations in Celestial Mechanics and Astrodynamics. In Modern Methods of Analytical Mechanics and Their Applications; Rumyantsev, V.V., Karapetyan, A.V., Eds.; Springer: Vienna, Austria, 1998; Volume 387, pp. 55–102. [Google Scholar] [CrossRef]
- Jorba, A. Efficient numerical computation of Normal forms, Center manifolds and First integrals of Hamiltonian Systems. Exp. Math. 1999, 8, 155–195. [Google Scholar] [CrossRef]
- Voyatzis, G.; Kotoulas, T. Planar periodic orbits in exterior resonances with Neptune. Planet. Space Sci. 2005, 53, 1189–1199. [Google Scholar] [CrossRef]
- Voyatzis, G.; Kotoulas, T.; Hadjidemetriou, J.D. Symmetric and Nonsymmetric Periodic Orbits in the Exterior Mean Motion Resonances with Neptune. Celest. Mech. Dyn. Astron. 2005, 91, 191–202. [Google Scholar] [CrossRef]
- Szebehely, V. Theory of Orbit: The Restricted Problem of Three Bodies; Academic Press: New York, NY, USA; London, UK, 1967. [Google Scholar]
- Siegel, C.L.; Moser, J.K. Lectures on Celestial Mechanics; Springer: Berlin/Heidelber, Germany; New York, NY, USA, 1971. [Google Scholar]
- Simó, C.; Stuchi, T.J. Central stable/unstable manifolds and the destruction of KAM tori in the planar Hill problem. Phys. D 2000, 140, 1–32. [Google Scholar] [CrossRef]
- Hénon, M. Families of asymmetric periodic orbits in Hill’s problem of three bodies. Celest. Mech. Dyn. Astr. 2005, 93, 87–100. [Google Scholar] [CrossRef]
- Tsirogiannis, G.A.; Perdios, E.A.; Markellos, V.V. Improved grid search method: An efficient tool for global computation of periodic orbits. Application to Hill’s problem. Celest. Mech. Dyn. Astr. 2009, 103, 49–78. [Google Scholar] [CrossRef]
- Basu, S.; Pollack, R.; Roy, M.F. Algorithms in Real Algebraic Geometry; Algorithms and Computations in Mathematics 10; Springer: Berlin/Heidelber, Germany; New York, NY, USA, 2006. [Google Scholar]
- Kac, V.; Cheung, P. Quantum Calculus; Springer: Berlin/Heidelber, Germany; New York, NY, USA, 2002. [Google Scholar]
- von zur Gathen, J.; Lücking, T. Subresultants revisited. Theor. Comput. Sci. 2003, 297, 199–239. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).