New Procedures of a Fractional Order Model of Novel Coronavirus (COVID-19) Outbreak via Wavelets Method
Abstract
1. Introduction
2. Preliminaries
3. A Brief Review of Wavelets
3.1. Sine–Cosine Wavelets and Their Properties
3.1.1. Sine–Cosine Wavelets
3.1.2. Function Approximation
3.1.3. Sine–Cosine Wavelet Operational Matrix of the Fractional Integration
Block Pulse Functions (BPFs)
3.2. Bernoulli Wavelets and Their Properties
3.2.1. Bernoulli Wavelets
3.2.2. Function Approximation
3.2.3. Bernoulli Wavelet Operational Matrix of the Fractional Integration
4. Description of Numerical Method
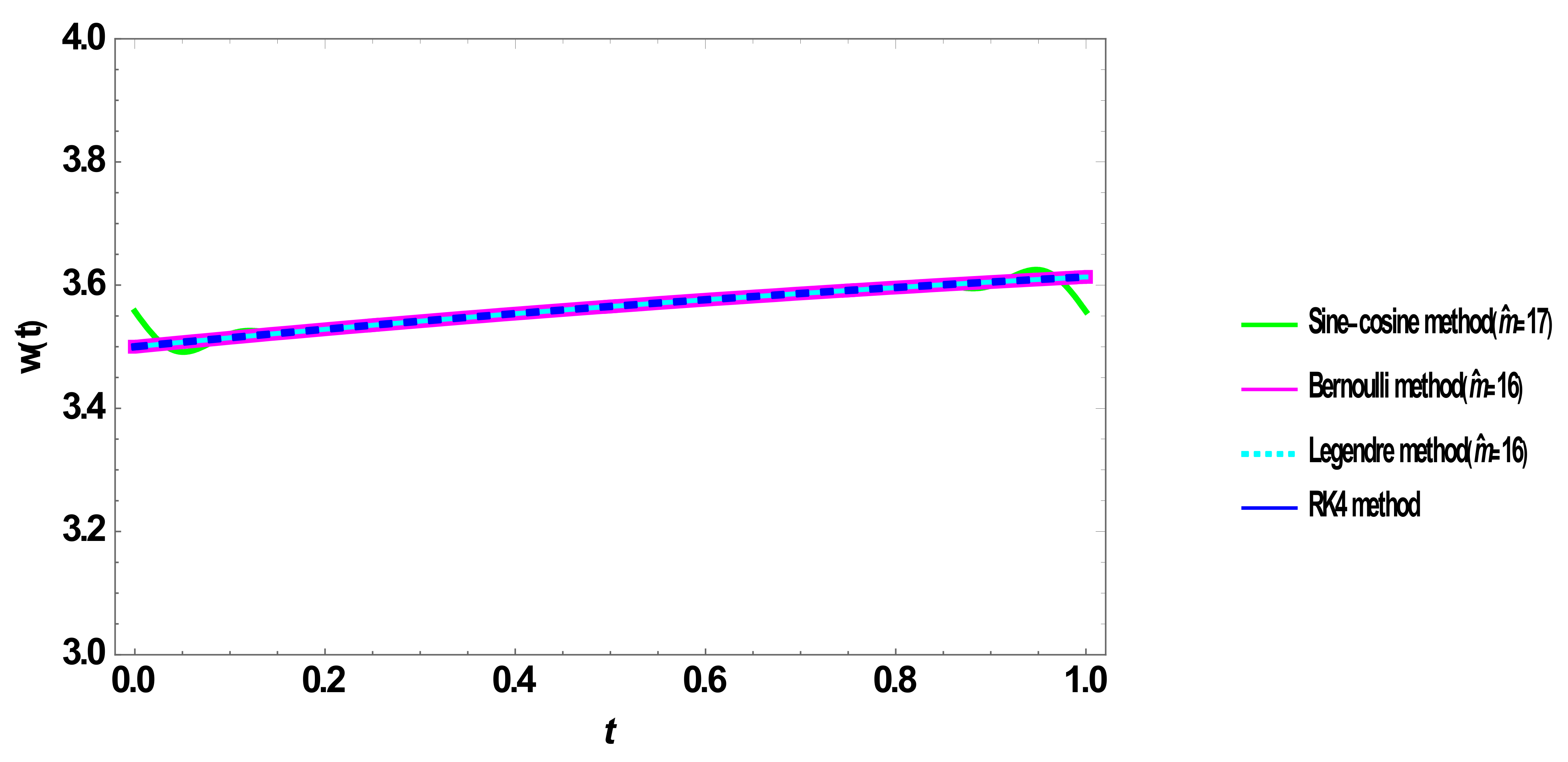
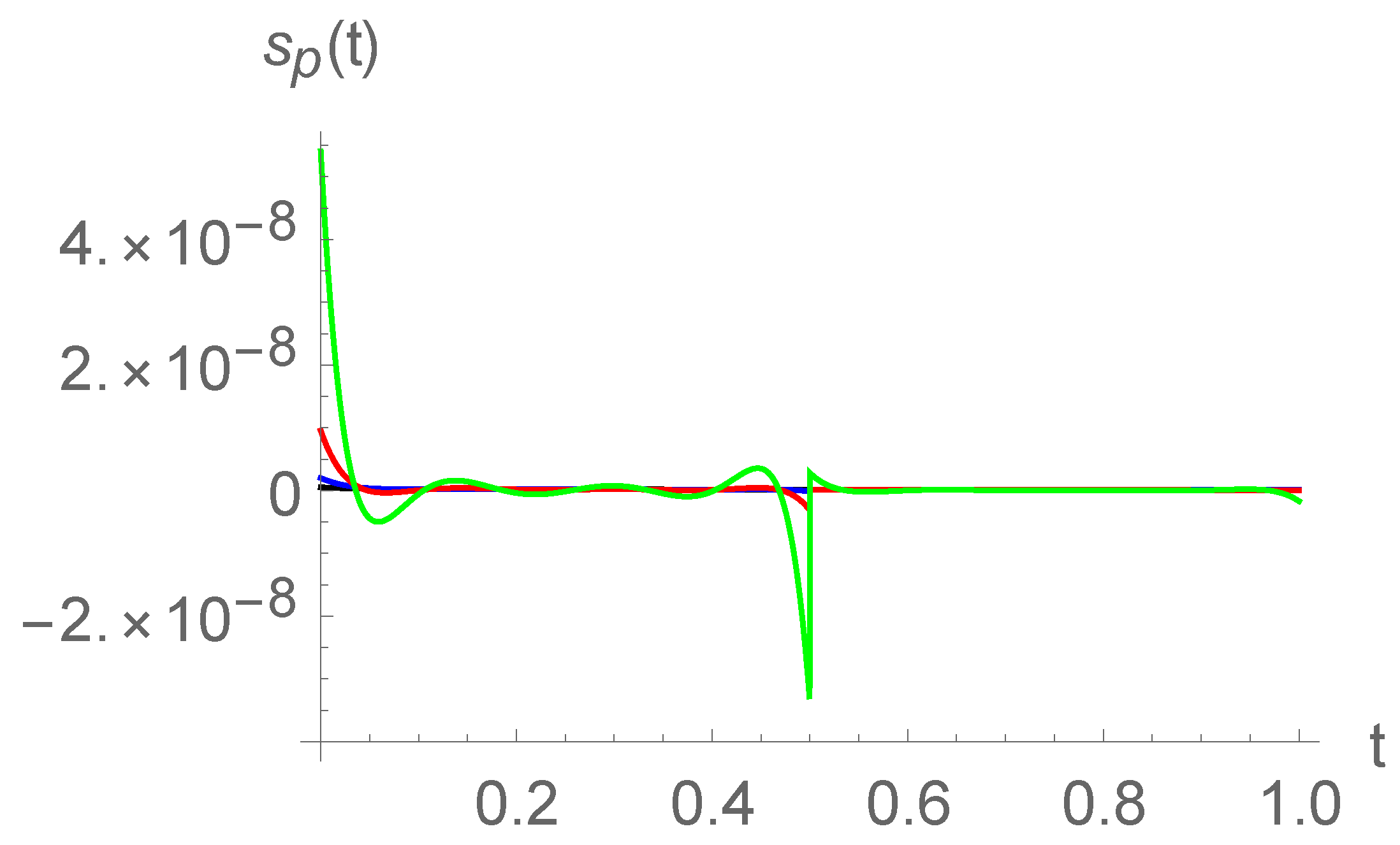
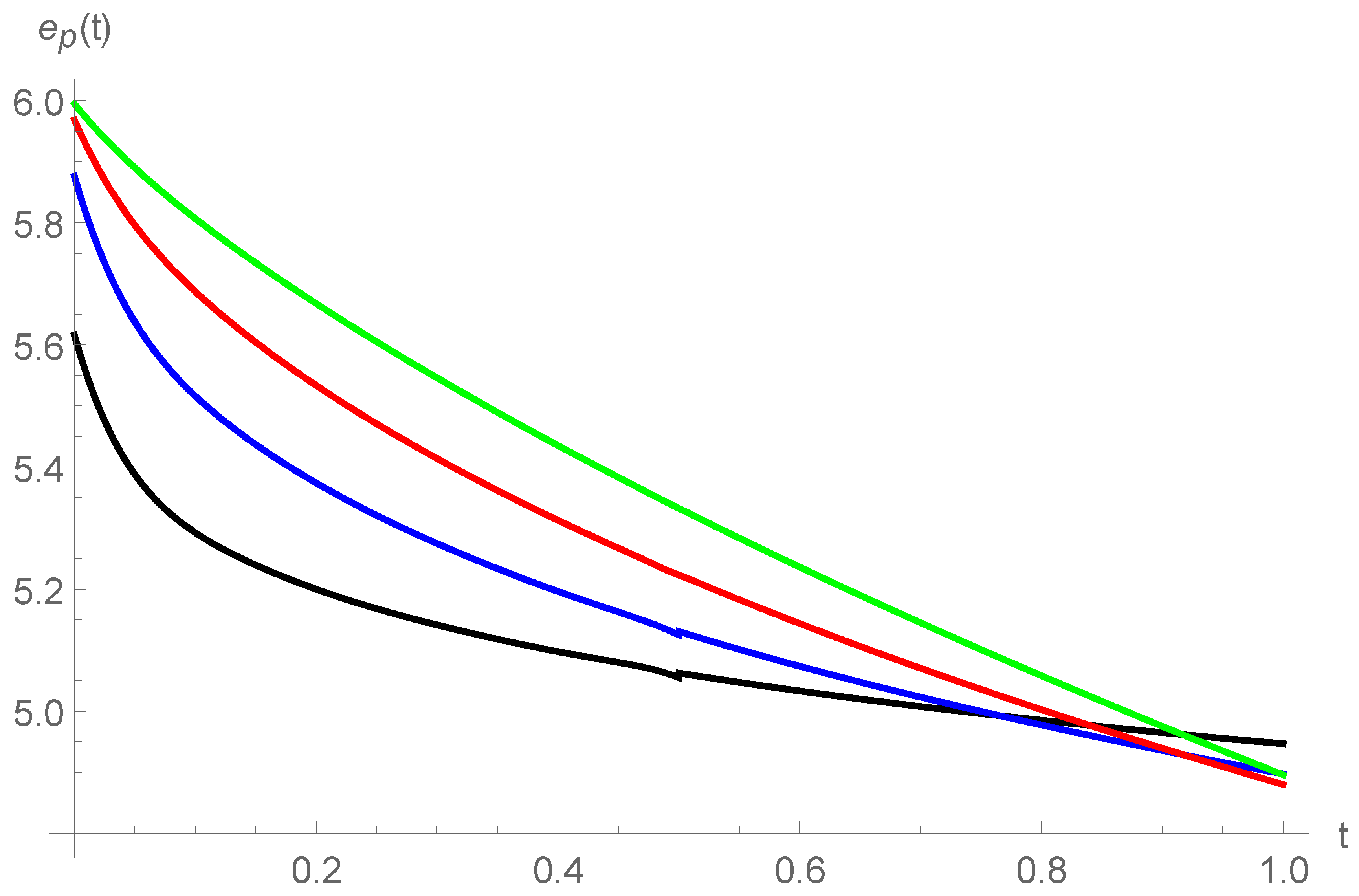
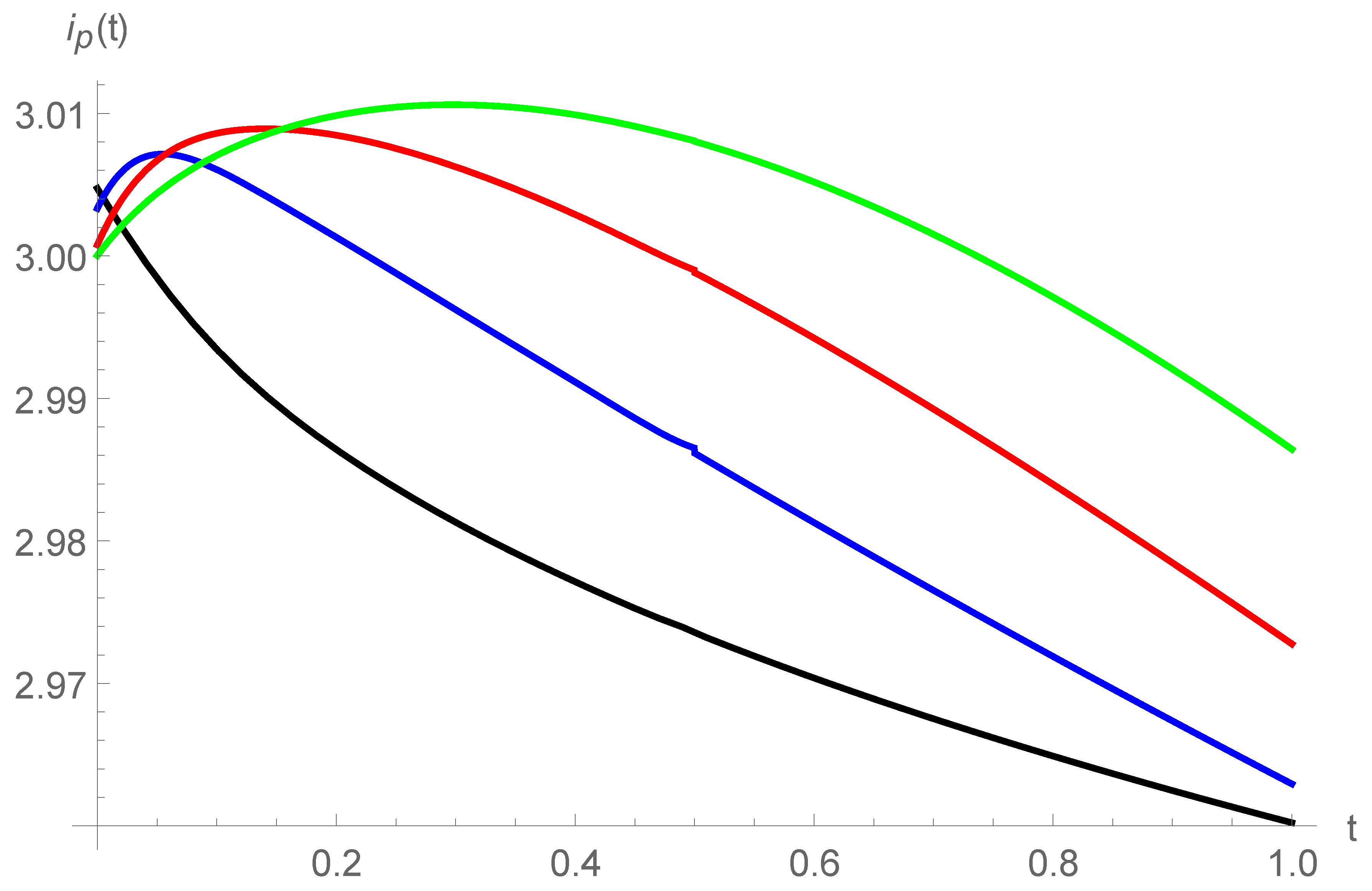
5. Results and Discussion
5.1. Convergence of the Solution
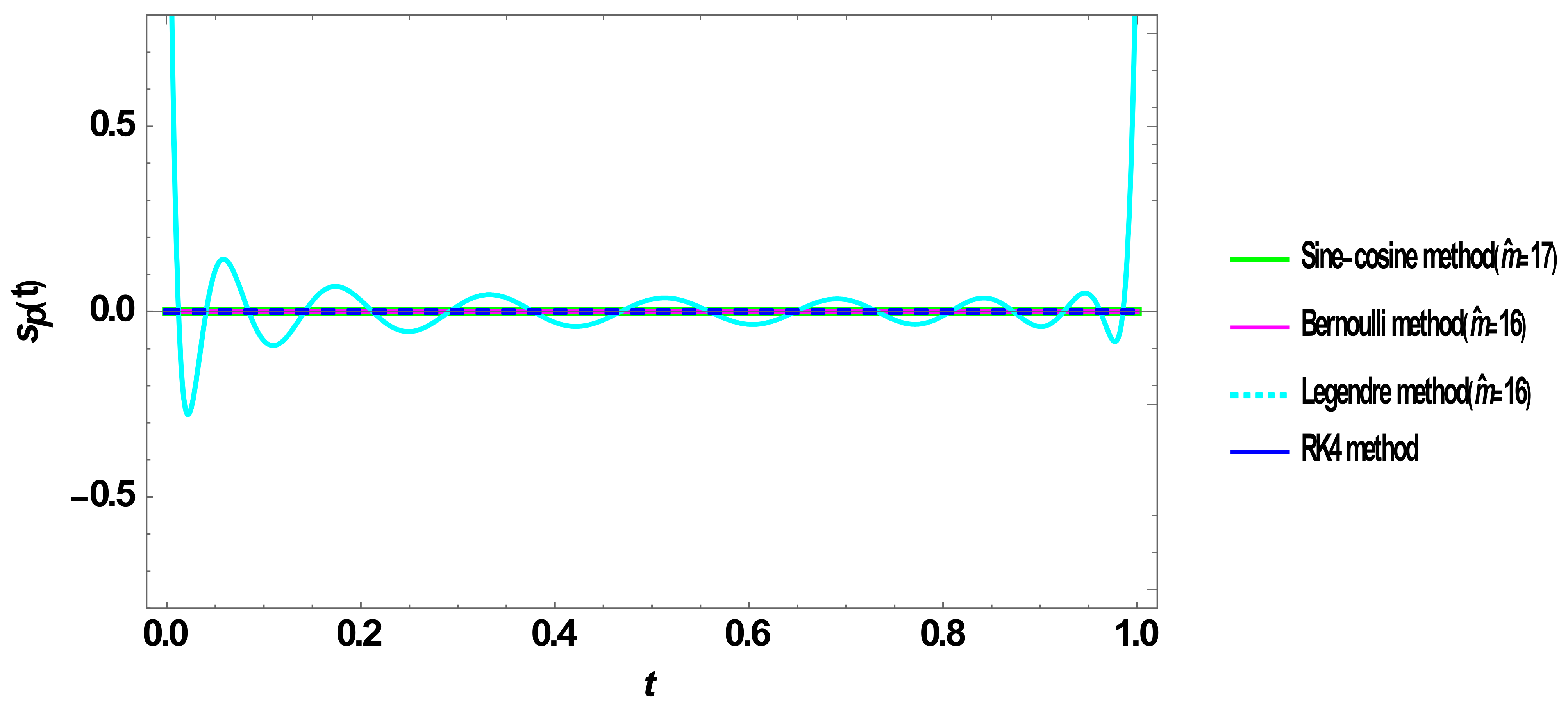
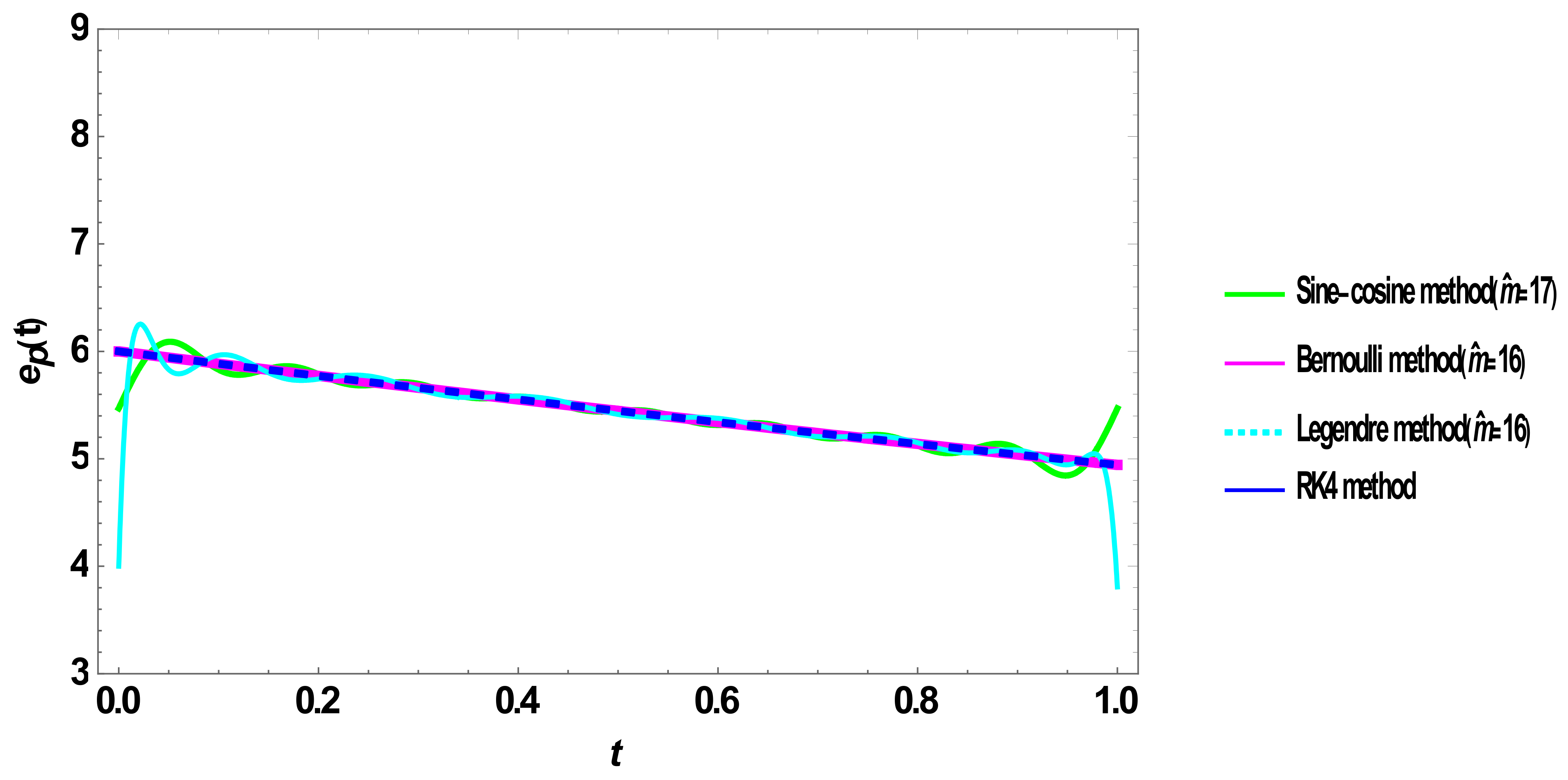
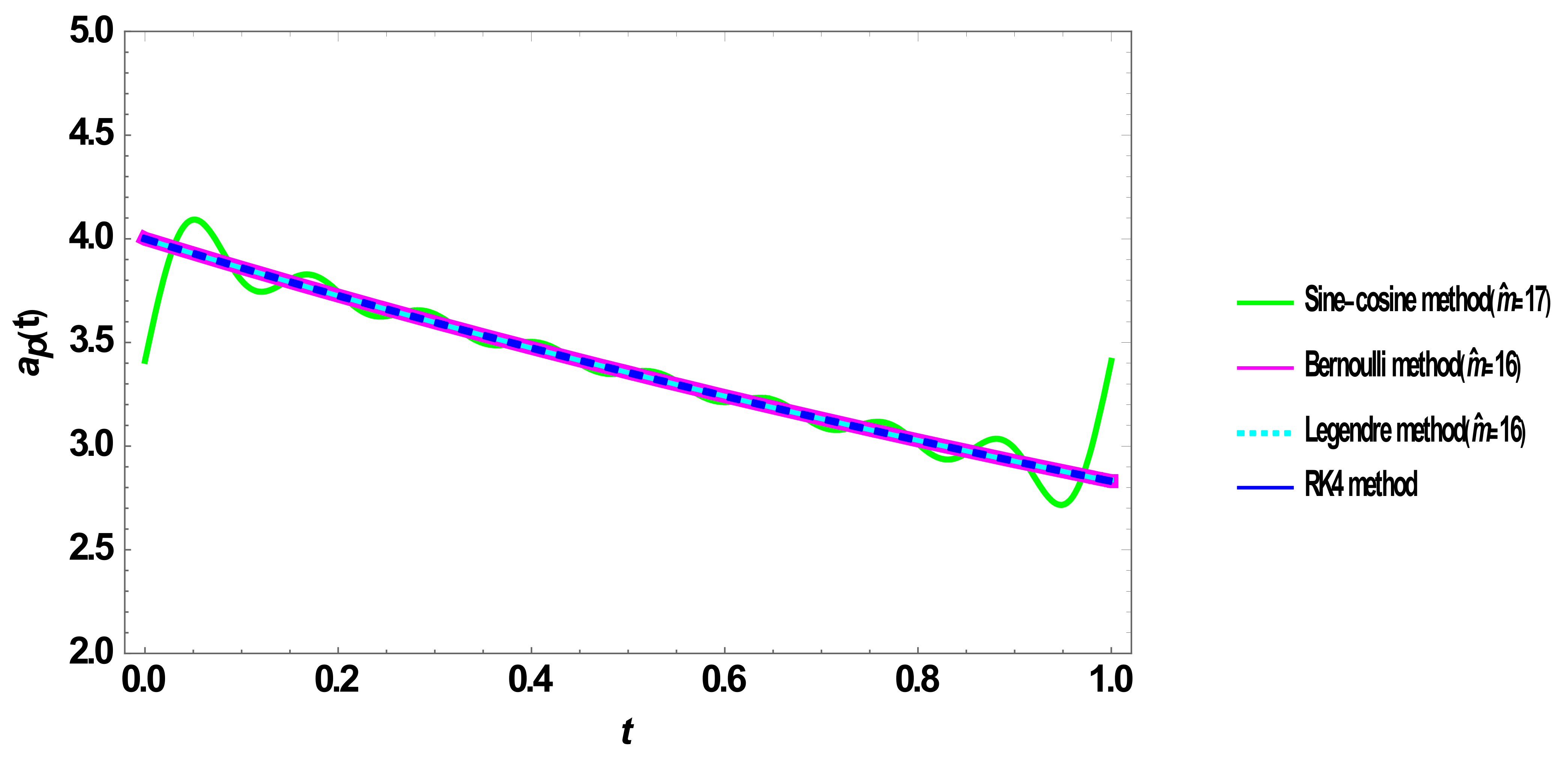
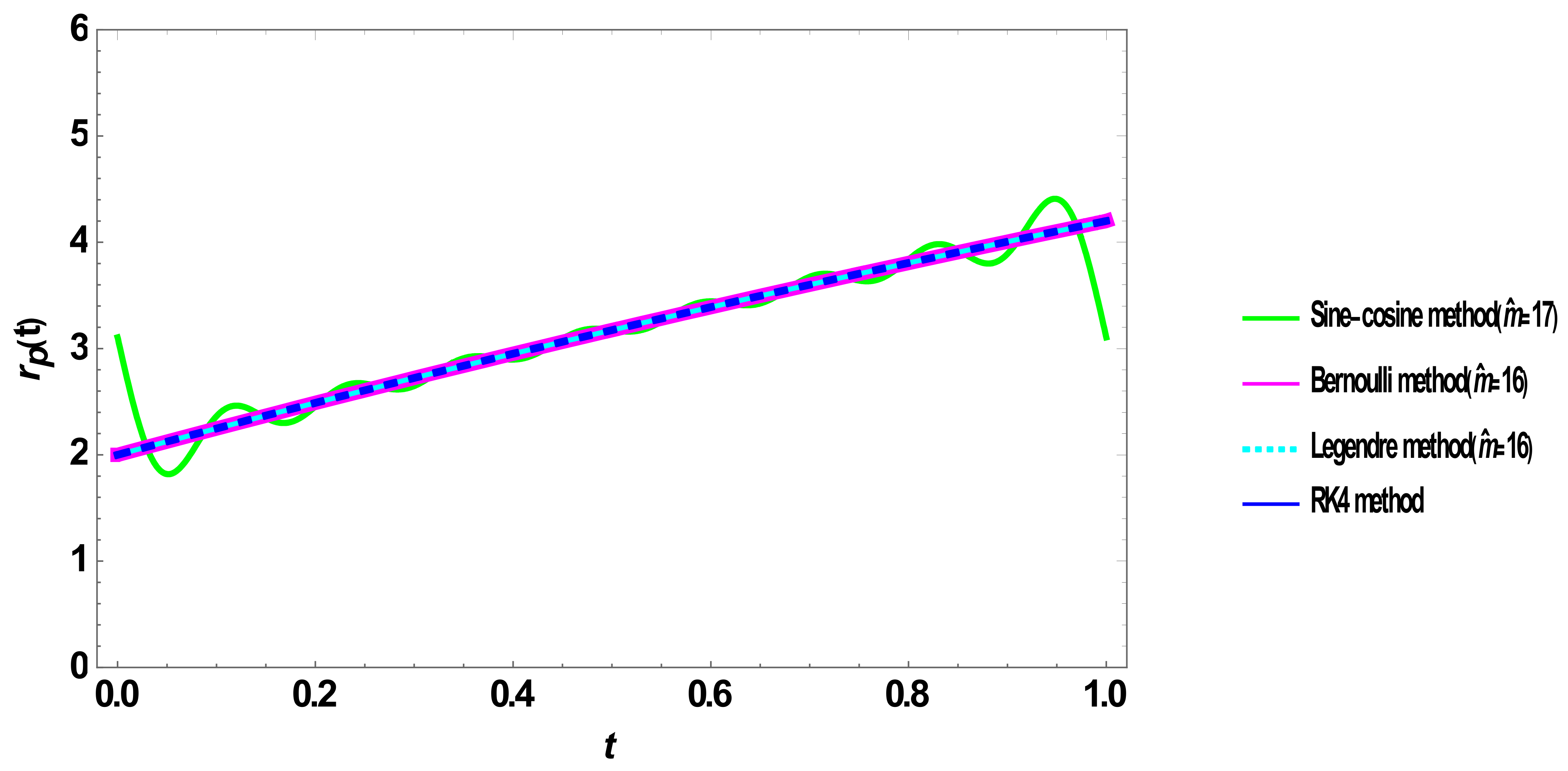
5.2. Verification of the Solution
5.3. Computational Cost
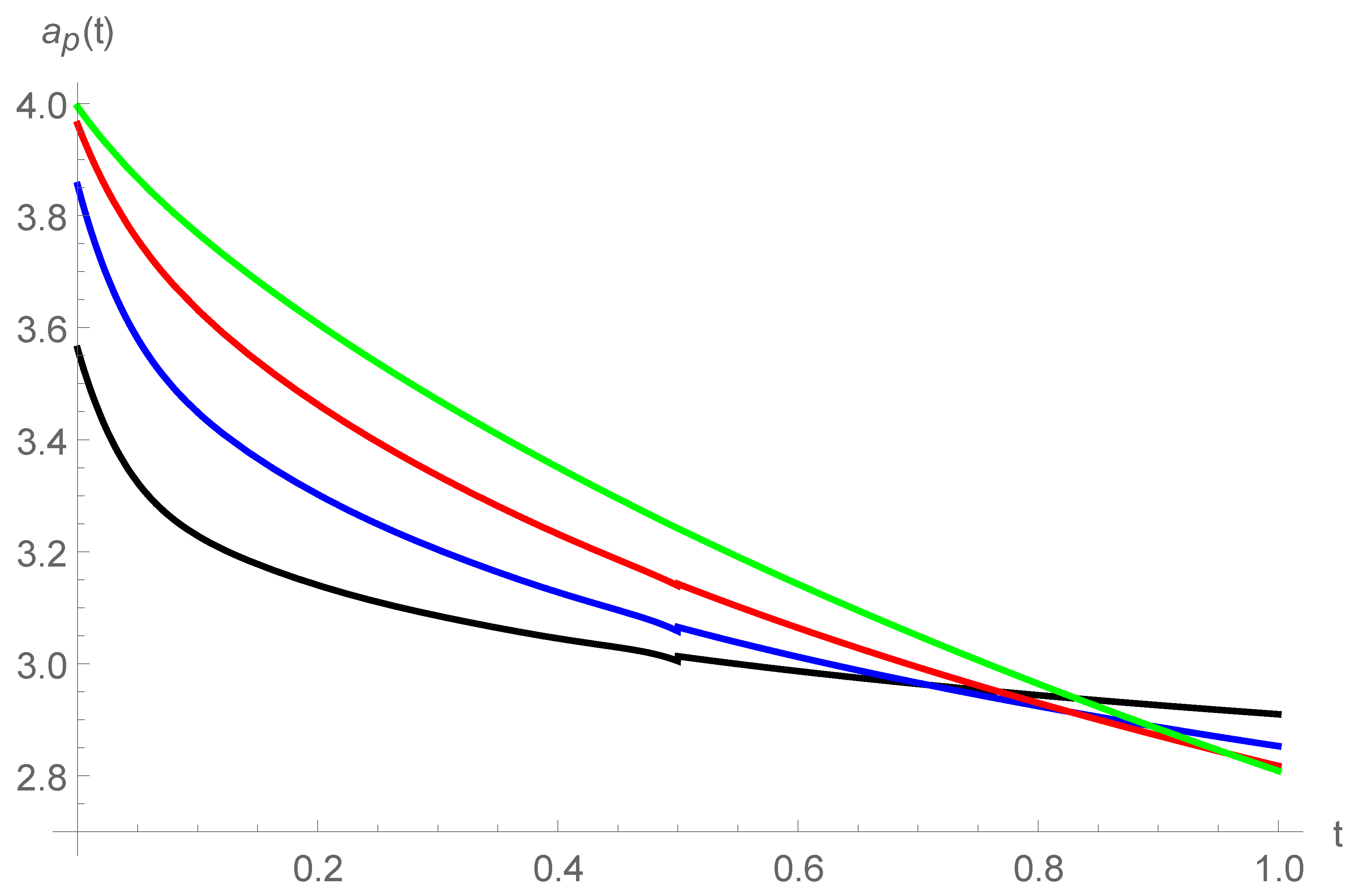
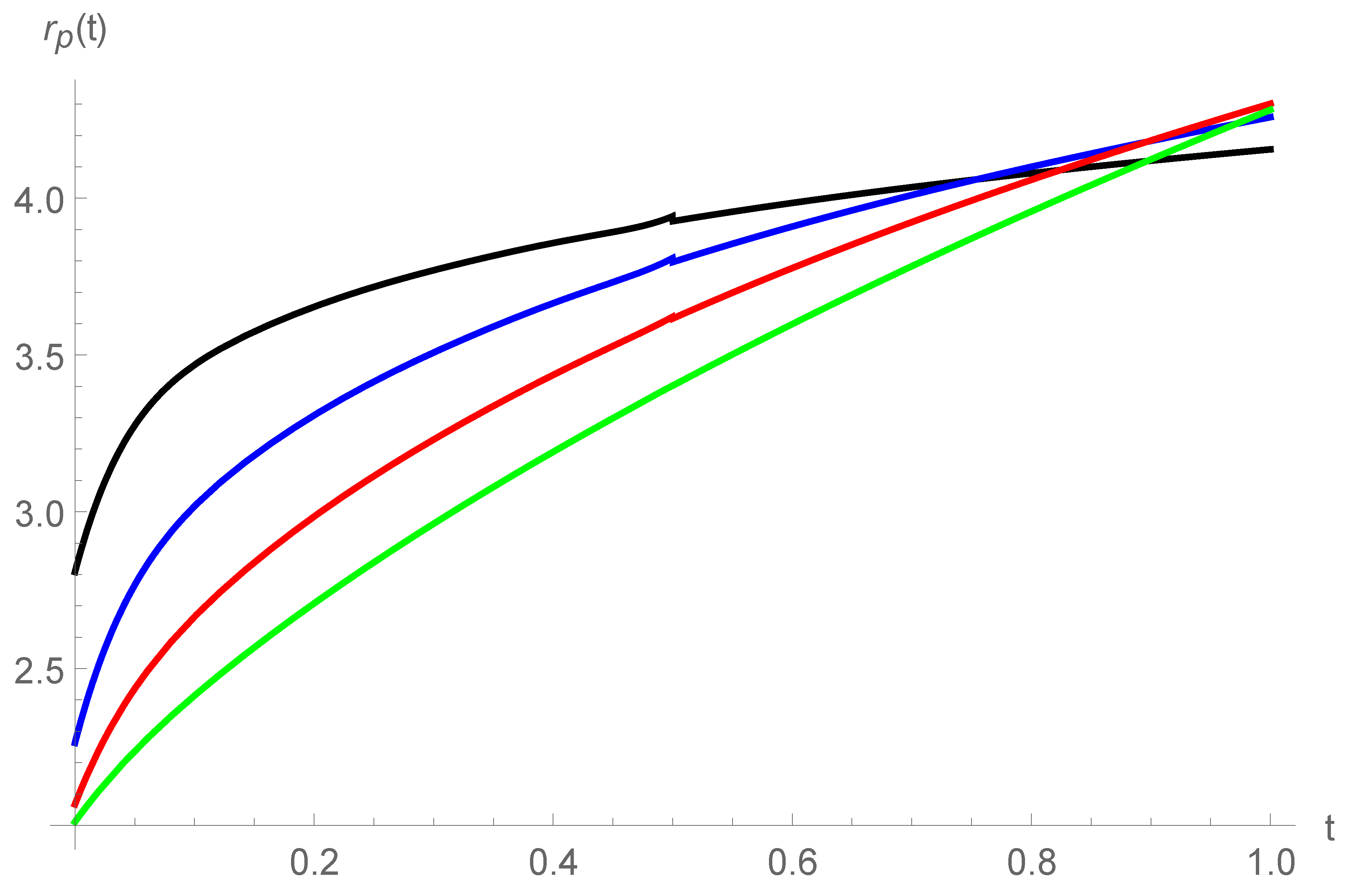
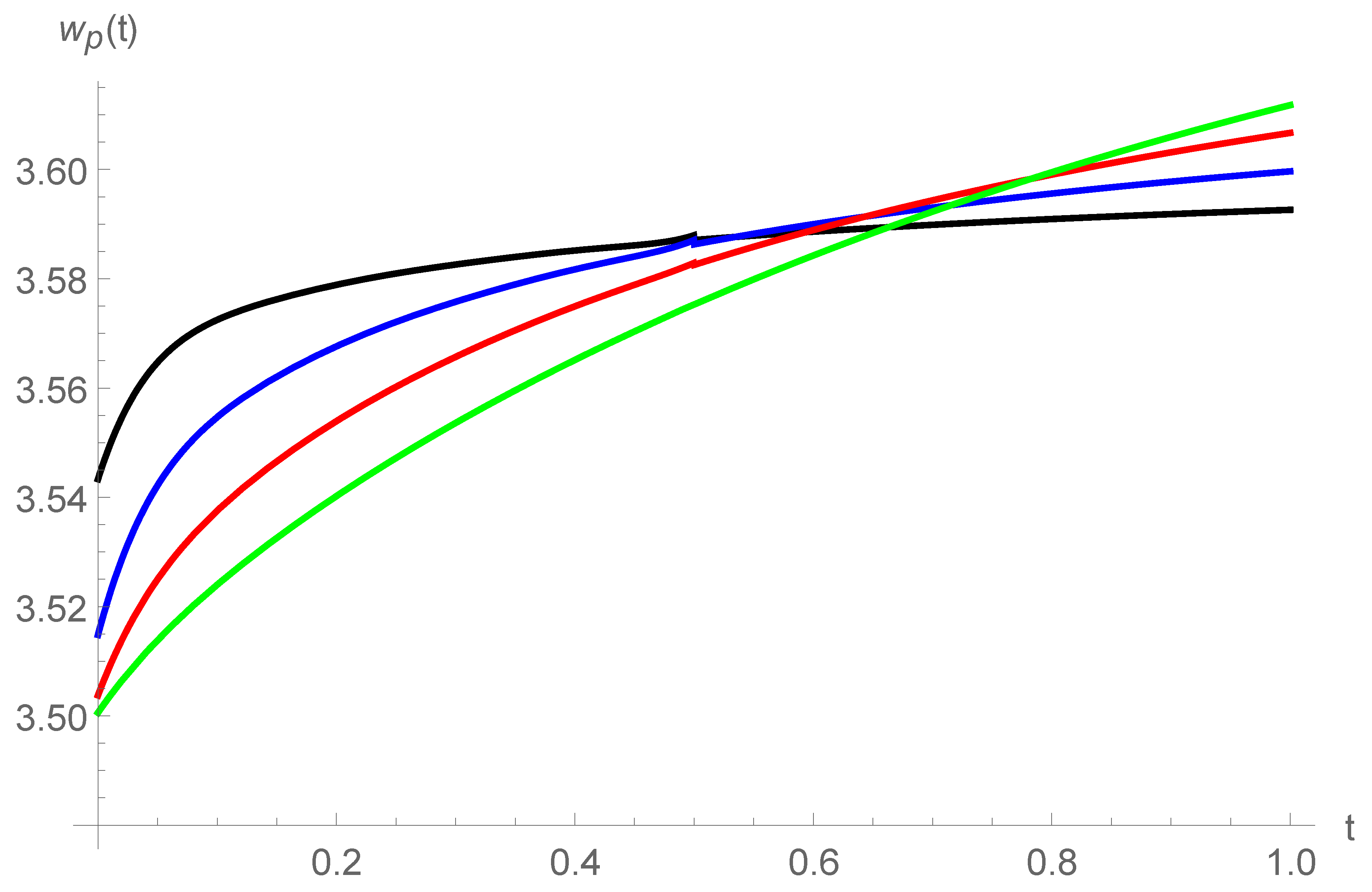
5.4. The Effects of Fractional Orders
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Alluwaimi, A.M.; Alshubaith, I.H.; Al-Ali, A.M.; Abohelaika, S. The Coronaviruses of Animals and Birds: Their Zoonosis, Vaccines, and Models for SARS-CoV and SARS-CoV2. Front. Vet. Sci. 2020, 7, 655. [Google Scholar] [CrossRef] [PubMed]
- Madjid, M.; Safavi-Naeini, P.; Solomon, S.D.; Vardeny, O. Potential effects of coronaviruses on the cardiovascular system: A review. JAMA Cardiol. 2020, 5, 840–931. [Google Scholar] [CrossRef] [PubMed]
- WHO. Novel Coronavirus (2019-nCoV): Situation Report 3; WHO: Geneva, Switzerland, 2020. [Google Scholar]
- Chen, T.M.; Rui, J.; Wang, Q.P.; Zhao, Z.Y.; Cui, J.A.; Yin, L. A mathematical model for simulating the phase-based transmissibility of a novel coronavirus. Infect. Dis. Poverty 2020, 9, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.A.; Atangana, A. Modeling the dynamics of novel coronavirus (2019-nCov) with fractional derivative. Alex. Eng. J. 2020, 59, 2379–2389. [Google Scholar] [CrossRef]
- Rajagopal, K.; Hasanzadeh, N.; Parastesh, F.; Hamarash, I.I.; Jafari, S.; Hussain, I. A fractional-order model for the novel coronavirus (COVID-19) outbreak. Nonlinear Dyn. 2020, 101, 711–718. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Li, J.; Xiao, C.; Yang, P. Numerical solution and parameter estimation for uncertain SIR model with application to COVID-19. Fuzzy Optim. Decis. Mak. 2021, 20, 189–208. [Google Scholar] [CrossRef]
- Hashemizadeh, E.; Ebadi, M.A. A numerical solution by alternative Legendre polynomials on a model for novel coronavirus (COVID-19). Adv. Differ. Equ. 2020, 2020, 527. [Google Scholar] [CrossRef]
- Kisela, T. Fractional Differential Equations and Their Applications; Faculty of Mechanical Engineering Institute of Mathematics: Brno-střed, Czech Republic, 2008. [Google Scholar]
- Solís-Pérez, J.E.; Gómez-Aguilar, J.F.; Atangana, A. A fractional mathematical model of breast cancer competition model. Chaos Solitons Fractals 2019, 127, 38–54. [Google Scholar] [CrossRef]
- Hussain, A.; Baleanu, D.; Adeel, M. Existence of solution and stability for the fractional order novel coronavirus (nCoV-2019) model. Adv. Differ. Equ. 2020, 2020, 1–9. [Google Scholar] [CrossRef]
- Atangana, A. Modelling the spread of COVID-19 with new fractal-fractional operators: Can the lockdown save mankind before vaccination? Chaos Solitons Fractals 2020, 136, 109860. [Google Scholar] [CrossRef]
- Wang, B.H.; Wang, Y.Y.; Dai, C.Q.; Chen, Y.X. Dynamical characteristic of analytical fractional solitons for the space-time fractional Fokas-Lenells equation. Alex. Eng. J. 2020, 59, 4699–4707. [Google Scholar] [CrossRef]
- Yu, L.J.; Wu, G.Z.; Wang, Y.Y.; Chen, Y.X. Traveling wave solutions constructed by Mittag–Leffler function of a (2 + 1)-dimensional space-time fractional NLS equation. Results Phys. 2020, 17, 103156. [Google Scholar] [CrossRef]
- Fang, J.J.; Mou, D.S.; Wang, Y.Y.; Zhang, H.C.; Dai, C.Q.; Chen, Y.X. Soliton dynamics based on exact solutions of conformable fractional discrete complex cubic Ginzburg–Landau equation. Results Phys. 2021, 20, 103710. [Google Scholar] [CrossRef]
- Wang, B.-H.; Wang, Y.-Y. Fractional white noise functional soliton solutions of a wick-type stochastic fractional NLSE. Appl. Math. Lett. 2020, 110, 106583. [Google Scholar] [CrossRef]
- Wang, B.-H.; Wang, Y.-Y.; Dai, C.-Q. Fractional optical solitons with stochastic properties of a wick-type stochastic fractional NLSE driven by the Brownian motion. Waves Random Complex Media 2021, 1–14. [Google Scholar]
- Noeiaghdam, S. A novel technique to solve the modified epidemiological model of computer viruses. SEMA J. 2019, 76, 97–108. [Google Scholar] [CrossRef]
- Noeiaghdam, S.; Micula, S. Dynamical Strategy to Control the Accuracy of the Nonlinear Bio-Mathematical Model of Malaria Infection. Mathematics 2021, 9, 1031. [Google Scholar] [CrossRef]
- Noeiaghdam, S.; Suleman, M.; Budak, H. Solving a modified nonlinear epidemiological model of computer viruses by homotopy analysis method. Math. Sci. 2018, 12, 211–222. [Google Scholar] [CrossRef]
- Tuan, N.H.; Mohammadi, H.; Rezapour, S. A mathematical model for COVID-19 transmission by using the Caputo fractional derivative. Chaos Solitons Fractals 2020, 140, 110107. [Google Scholar] [CrossRef] [PubMed]
- Yi, M.; Huang, J. Wavelet operational matrix method for solving fractional differential equations with variable coefficients. Appl. Math. Comput. 2014, 230, 383–394. [Google Scholar] [CrossRef]
- Yi, M.; Wang, L.; Huang, J. Legendre wavelets method for the numerical solution of fractional integro-differential equations with weakly singular kernel. Appl. Math. Model. 2016, 40, 3422–3437. [Google Scholar] [CrossRef]
- Razzaghi, M.; Yousefi, S. Sine-cosine wavelets operational matrix of integration and its applications in the calculus of variations. Int. J. Syst. Sci. 2002, 33, 805–810. [Google Scholar] [CrossRef]
- Saeed, A.; Saeed, U. Sine-cosine wavelet method for fractional oscillator equations. Math. Methods Appl. Sci. 2019, 42, 6960–6971. [Google Scholar] [CrossRef]
- Wang, Y.; Yin, T.; Zhu, L. Sine-cosine wavelet operational matrix of fractional order integration and its applications in solving the fractional order Riccati differential equations. Adv. Differ. Equ. 2017, 2017, 222. [Google Scholar] [CrossRef]
- Kajani, M.T.; Ghasemi, M.; Babolian, E. Numerical solution of linear integro-differential equation by using sine–cosine wavelets. Appl. Math. Comput. 2006, 180, 569–574. [Google Scholar] [CrossRef]
- Kilicman, A.; Al Zhour, Z.A.A. Kronecker operational matrices for fractional calculus and some applications. Appl. Math. Comput. 2007, 187, 250–265. [Google Scholar] [CrossRef]
- Keshavarz, E.; Ordokhani, Y. Bernoulli wavelets method for solution of fractional differential equations in a large interval. Math. Res. 2016, 2, 17–32. [Google Scholar] [CrossRef]
- Rahimkhani, P.; Ordokhani, Y.; Babolian, E. Numerical solution of fractional pantograph differential equations by using generalized fractional-order Bernoulli wavelet. J. Comput. Appl. Math. 2017, 309, 493–510. [Google Scholar] [CrossRef]
- Tohidi, E.; Bhrawy, A.; Erfani, K. A collocation method based on Bernoulli operational matrix for numerical solution of generalized pantograph equation. Appl. Math. Model. 2013, 37, 4283–4294. [Google Scholar] [CrossRef]
- Soltanpour Moghadam, A.; Arabameri, M.; Baleanu, D.; Barfeie, M. Numerical solution of variable fractional order advection-dispersion equation using Bernoulli wavelet method and new operational matrix of fractional order derivative. Math. Methods Appl. Sci. 2020, 43, 3936–3953. [Google Scholar] [CrossRef]

| Variables and Parameters | Definition | Variables and Parameters | Definition |
|---|---|---|---|
| np | The birth rate of people. | µ’p | The shedding coefficients from Ap to W. |
| mp | The death rate of people. | δp | The proportion of asymptomatic infection rate of people. |
| The incubation period of people. | βp | The transmission rate from Ip to Sp. | |
| The latent period of people. | βW | The transmission rate from W to Sp. | |
| The infectious period of symptomatic infection in people. | k | The multiple of the transmissibility of Ap to that of Ip. | |
| The infectious period of asymptomatic infection in people. | The lifetime of the virus in W. | ||
| µp | The shedding coefficients from Ip to W. | c | The relative shedding rate of Ap compared to Ip. |
| t | 1010 Sp M = 4 | 1010 Sp M = 5 | 1010 Sp M = 6 | 1010 Sp M = 7 | ROC M = 7 | 1010 Sp M = 8 | ROC M = 8 | 1010 Sp M = 9 | ROC M = 9 | 1010 Sp M = 10 | ROC M = 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.2 | 1.08 | 1.77 | 2.57 | 2.62 | −18.95 | 2.24 | −0.73 | 2.03 | −0.29 | 2.13 | 1.16 |
| 0.4 | 2.28 | 0.804 | 2.09 | 1.42 | 4.69 | 1.47 | 3.83 | 1.81 | −0.73 | 1.35 | 0.16 |
| 0.6 | 1.30 | 1.29 | 1.29 | 1.29 | −0.01 | 1.29 | −234 | 1.29 | 0.02 | 1.29 | −20 |
| 0.8 | 1.12 | 1.12 | 1.12 | 1.12 | 3.30 | 1.12 | 1.10 | 1.12 | −0.86 | 1.12 | 1.30 |
| t | ep M = 4 | ep M = 5 | ep M = 6 | ep M = 7 | ROC M = 7 | ep M = 8 | ROC M = 8 | ep M = 9 | ROC M = 9 | ep M = 10 | ROC M = 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.2 | 5.4570 | 5.4560 | 5.4565 | 5.4564 | 3.17 | 5.4562 | −0.77 | 5.4560 | −0.17 | 5.4559 | 2.09 |
| 0.4 | 5.2560 | 5.2519 | 5.2535 | 5.2529 | 0.94 | 5.2529 | 3.79 | 5.2529 | −0.25 | 5.2528 | 0.94 |
| 0.6 | 5.1056 | 5.1054 | 5.1053 | 5.1053 | 0.72 | 5.1052 | 0.79 | 5.1052 | 0.85 | 5.1052 | 0.88 |
| 0.8 | 4.9861 | 4.9860 | 4.9859 | 4.9859 | 1.13 | 4.9859 | 0.79 | 4.9859 | 0.87 | 4.9859 | 0.88 |
| t | ip M = 4 | ip M = 5 | ip M = 6 | ip M = 7 | ROC M = 7 | ip M = 8 | ROC M = 8 | ip M = 9 | ROC M = 9 | ip M = 10 | ROC M = 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.2 | 3.0058 | 3.0058 | 3.0058 | 3.0057 | −0.88 | 3.0058 | 0.39 | 3.0058 | 0.45 | 3.0058 | 5.47 |
| 0.4 | 2.9974 | 2.9976 | 2.9975 | 2.9975 | 1.79 | 2.9975 | 1.59 | 2.9975 | −0.025 | 2.9975 | −0.8 |
| 0.6 | 2.9878 | 2.9878 | 2.9878 | 2.9878 | 0.95 | 2.9877 | 0.90 | 2.9877 | 0.88 | 2.9877 | 0.89 |
| 0.8 | 2.9775 | 2.9775 | 2.9775 | 2.9775 | 0.74 | 2.9775 | 0.88 | 2.9775 | 0.87 | 2.9775 | 0.88 |
| t | ap M = 4 | ap M = 5 | ap M = 6 | ap M = 7 | ROC M = 7 | ap M = 8 | ROC M = 8 | ap M = 9 | ROC M = 9 | ap M = 10 | ROC M = 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.2 | 3.0058 | 3.0058 | 3.0058 | 3.0057 | −0.88 | 3.0058 | 0.39 | 3.0058 | 0.45 | 3.0058 | 5.47 |
| 0.4 | 2.9974 | 2.9976 | 2.9975 | 2.9975 | 1.79 | 2.9975 | 1.59 | 2.9975 | −0.025 | 2.9975 | −0.8 |
| 0.6 | 2.9878 | 2.9878 | 2.9878 | 2.9878 | 0.95 | 2.9877 | 0.90 | 2.9877 | 0.88 | 2.9877 | 0.88 |
| 0.8 | 2.9775 | 2.9775 | 2.9775 | 2.9775 | 0.74 | 2.9775 | 0.88 | 2.9775 | 0.87 | 2.9775 | 0.89 |
| t | rp M = 4 | rp M = 5 | rp M = 6 | rp M = 7 | ROC M = 7 | rp M = 8 | ROC M = 8 | rp M = 9 | ROC M = 9 | rp M = 10 | ROC M = 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.2 | 3.1403 | 3.1422 | 3.1412 | 3.1412 | 6.15 | 3.1417 | −0.80 | 3.1421 | −0.11 | 3.1423 | 2.20 |
| 0.4 | 3.5476 | 3.5563 | 3.5529 | 3.5542 | 1.00 | 3.5543 | 4.18 | 3.5542 | −0.38 | 3.5544 | 0.47 |
| 0.6 | 3.8494 | 3.8497 | 3.8499 | 3.8500 | 0.72 | 3.8501 | 0.78 | 3.8501 | 0.85 | 3.8501 | 0.88 |
| 0.8 | 4.0869 | 4.0870 | 4.0871 | 4.0871 | 1.21 | 4.0872 | 0.78 | 4.0872 | −0.87 | 4.0872 | 0.89 |
| t | wp M = 4 | wp M = 5 | wp M = 6 | wp M = 7 | ROC M = 7 | wp M = 8 | ROC M = 8 | wp M = 9 | ROC M = 9 | wp M = 10 | ROC M = 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.2 | 3.5608 | 3.5609 | 3.5609 | 3.5609 | 9.39 | 3.5609 | −0.77 | 3.5609 | −0.10 | 3.5609 | 2.31 |
| 0.4 | 3.5783 | 3.5789 | 3.5786 | 3.5787 | 1.06 | 3.5787 | 5.1 | 3.5787 | −0.53 | 3.5787 | 0.21 |
| 0.6 | 3.5898 | 3.5898 | 3.5898 | 3.5898 | 0.71 | 3.5898 | 0.78 | 3.5898 | 0.85 | 3.5898 | 0.88 |
| 0.8 | 3.5975 | 3.5976 | 3.5976 | 3.5976 | 1.36 | 3.5976 | 0.76 | 3.5976 | −0.87 | 3.5976 | 0.89 |
| t | 1010 Sp L = 4 | 1010 Sp L = 5 | 1010 Sp L = 6 | 1010 Sp L = 7 | ROC L = 7 | 1010 Sp L = 8 | ROC L = 8 | 1010 Sp L = 9 | ROC L = 9 | 1010 Sp L = 10 | ROC L = 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.2 | 0.368 | 1.26 | 3.06 | 3.62 | −1.68 | 2.44 | −0.63 | 1.17 | 0.10 | 1.37 | −24.1 |
| 0.4 | 1.16 | 1.36 | 2.20 | 0.874 | 0.31 | 2.11 | −0.13 | 1.39 | 8.58 | 1.40 | 7.31 |
| 0.6 | 1.53 | 1.52 | 0.753 | 0.92 | 0.08 | 0.821 | −0.14 | 1.47 | 8.87 | 1.46 | 8.38 |
| 0.8 | 1.96 | 1.91 | 0.840 | 0.246 | −0.19 | 0.865 | −0.07 | 0.78 | 9.24 | 1.75 | −9.38 |
| t | ep L = 4 | ep L= 5 | ep L = 6 | ep L = 7 | ROC L = 7 | ep L = 8 | ROC L = 8 | ep L = 9 | ROC L = 9 | ep L = 10 | ROC L = 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.2 | 5.3833 | 5.3951 | 5.4766 | 5.5134 | −0.41 | 5.4717 | 15 | 5.4189 | 1.91 | 5.4222 | −11.6 |
| 0.4 | 5.2357 | 5.2385 | 5.2857 | 5.2175 | 0.12 | 5.2783 | −0.31 | 5.2441 | 4.96 | 5.2449 | 6.59 |
| 0.6 | 5.1227 | 5.1198 | 5.0729 | 5.1403 | 0.13 | 5.0800 | −0.30 | 5.1139 | 5.18 | 5.1131 | 6.50 |
| 0.8 | 5.0548 | 5.0443 | 4.9666 | 4.9308 | −0.38 | 4.9707 | −0.13 | 5.0219 | 2.35 | 8.0187 | −11.0 |
| t | ip L = 4 | ip L = 5 | ip L = 6 | ip L = 7 | ROC L = 7 | ip L = 8 | ROC L = 8 | ip L = 9 | ROC L = 9 | ip L = 10 | ROC L = 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.2 | 3.0032 | 3.0036 | 3.0065 | 3.0077 | −0.40 | 3.0063 | −0.14 | 3.0045 | 2.09 | 3.0046 | −11.5 |
| 0.4 | 2.9969 | 2.9970 | 2.9987 | 2.9962 | 0.13 | 2.9984 | −0.34 | 2.9972 | 4.69 | 2.9972 | 6.39 |
| 0.6 | 2.9884 | 2.9883 | 2.9865 | 2.9890 | 0.13 | 2.9868 | −0.35 | 2.9810 | 4.78 | 2.9880 | 6.22 |
| 0.8 | 2.9803 | 2.9798 | 2.9768 | 2.9754 | −0.45 | 2.9769 | −0.14 | 2.9788 | 1.81 | 2.9787 | −12.1 |
| t | ap L = 4 | ap L = 5 | ap L = 6 | ap L = 7 | ROC L = 7 | ap L = 8 | ROC L = 8 | ap L = 9 | ROC L = 9 | ap L = 10 | ROC L = 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.2 | 3.080 | 3.3203 | 3.4046 | 3.4426 | −0.41 | 3.3996 | −0.15 | 3.3449 | 1.91 | 3.3483 | −11.6 |
| 0.4 | 3.1595 | 3.1624 | 3.2111 | 3.1408 | 0.12 | 3.2035 | −0.31 | 3.1682 | 5.00 | 3.1690 | 6.60 |
| 0.6 | 3.0527 | 3.0497 | 3.0015 | 3.0709 | 0.13 | 3.0088 | −0.30 | 3.0437 | 5.20 | 3.0429 | 6.53 |
| 0.8 | 2.9942 | 3.9835 | 2.9040 | 2.8672 | −0.38 | 2.9082 | −0.13 | 2.9609 | 2.39 | 2.9577 | −11.0 |
| t | rp L = 4 | rp L = 5 | rp L = 6 | rp L = 7 | ROC L = 7 | rp L = 8 | ROC L = 8 | rp L = 9 | ROC L = 9 | rp L = 10 | ROC L = 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.2 | 3.2907 | 3.2666 | 3.1000 | 3.0248 | −0.41 | 3.1099 | −0.15 | 3.2178 | 1.91 | 3.2111 | −11.6 |
| 0.4 | 3.5893 | 3.5836 | 3.4872 | 3.6263 | 0.12 | 3.5023 | −0.31 | 3.5721 | 4.97 | 3.5706 | 6.59 |
| 0.6 | 3.8144 | 3.8204 | 3.9160 | 3.7785 | 0.13 | 3.9016 | −0.30 | 3.8324 | 5.18 | 3.8340 | 6.51 |
| 0.8 | 4.9469 | 4.9683 | 4.1265 | 4.1995 | −0.38 | 4.1182 | −0.13 | 4.0137 | 2.36 | 4.0201 | −11.0 |
| t | wp L = 4 | wp L = 5 | wp L = 6 | wp L = 7 | ROC L = 7 | wp L = 8 | ROC L = 8 | wp L = 9 | ROC L = 9 | wp L = 10 | ROC L = 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.2 | 3.5675 | 3.5664 | 3.5591 | 3.5557 | −0.41 | 3.5595 | −0.15 | 3.5643 | 1.88 | 3.5640 | −11.6 |
| 0.4 | 3.5802 | 3.5800 | 3.5758 | 3.5819 | 0.12 | 3.5764 | −0.30 | 3.5795 | 5.01 | 3.5794 | 6.64 |
| 0.6 | 3.5883 | 3.5885 | 3.5927 | 3.5867 | 0.13 | 3.5921 | −0.29 | 3.5890 | 5.28 | 3.5891 | 6.55 |
| 0.8 | 3.5915 | 3.5924 | 3.5993 | 3.9024 | −0.37 | 3.5989 | −0.13 | 3.5943 | 2.448 | 3.5946 | −10.8 |
| Bernoulli Wavelets | M = 4 | M = 5 | M = 6 | L = 7 | M = 8 | M = 9 | M = 10 |
|---|---|---|---|---|---|---|---|
| CPU running time | 0.28 | 0.67 | 1.71 | 2.55 | 3.91 | 9.00 | 67.9 |
| Sine-cosine wavelets | L = 4 | L = 5 | L = 6 | L = 7 | L = 8 | L = 9 | L = 10 |
| CPU running time | 0.82 | 1.73 | 3.08 | 5.35 | 8.86 | 9.67 | 13.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hedayati, M.; Ezzati, R.; Noeiaghdam, S. New Procedures of a Fractional Order Model of Novel Coronavirus (COVID-19) Outbreak via Wavelets Method. Axioms 2021, 10, 122. https://doi.org/10.3390/axioms10020122
Hedayati M, Ezzati R, Noeiaghdam S. New Procedures of a Fractional Order Model of Novel Coronavirus (COVID-19) Outbreak via Wavelets Method. Axioms. 2021; 10(2):122. https://doi.org/10.3390/axioms10020122
Chicago/Turabian StyleHedayati, Maryamsadat, Reza Ezzati, and Samad Noeiaghdam. 2021. "New Procedures of a Fractional Order Model of Novel Coronavirus (COVID-19) Outbreak via Wavelets Method" Axioms 10, no. 2: 122. https://doi.org/10.3390/axioms10020122
APA StyleHedayati, M., Ezzati, R., & Noeiaghdam, S. (2021). New Procedures of a Fractional Order Model of Novel Coronavirus (COVID-19) Outbreak via Wavelets Method. Axioms, 10(2), 122. https://doi.org/10.3390/axioms10020122








