On Λ-Fractional Viscoelastic Models
Abstract
1. Introduction
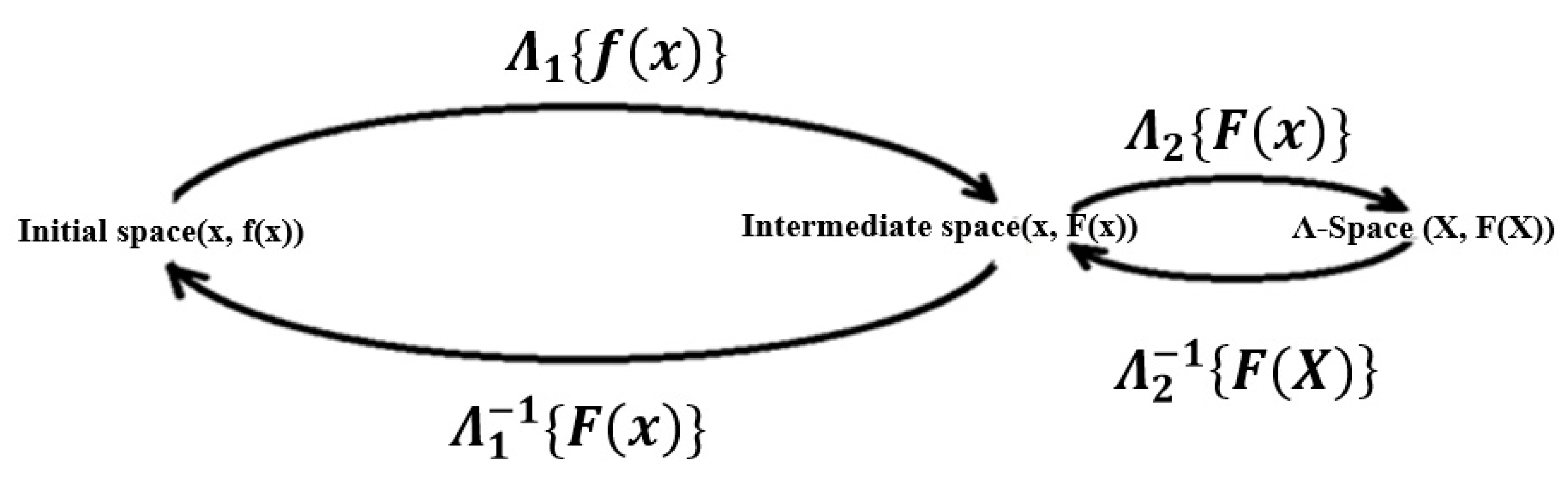
2. Outline of Λ-Fractional Derivative, Λ-Transform, and Dual Λ-Space
3. Models of Viscoelasticity-The Conventional Zener Model
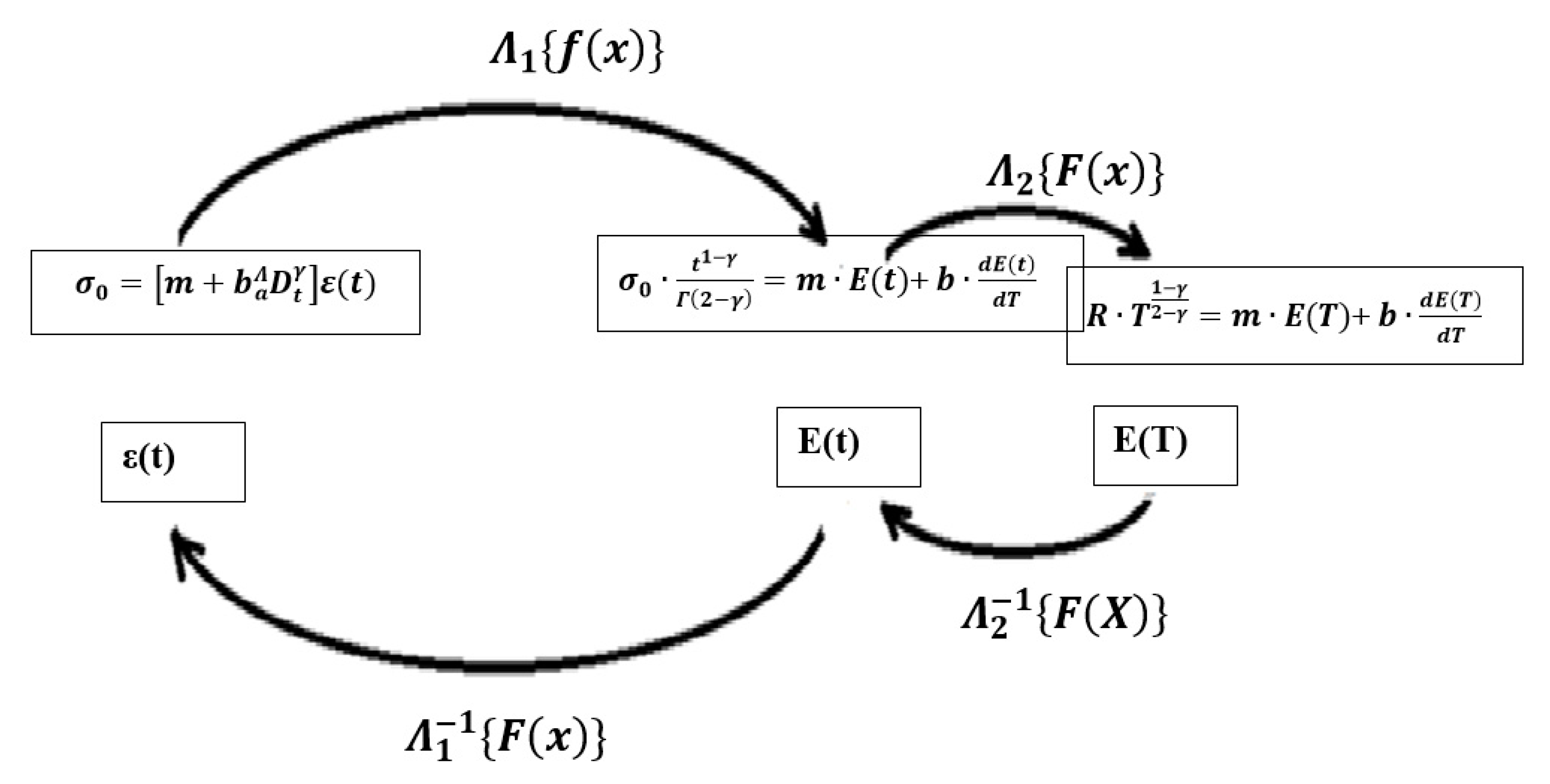
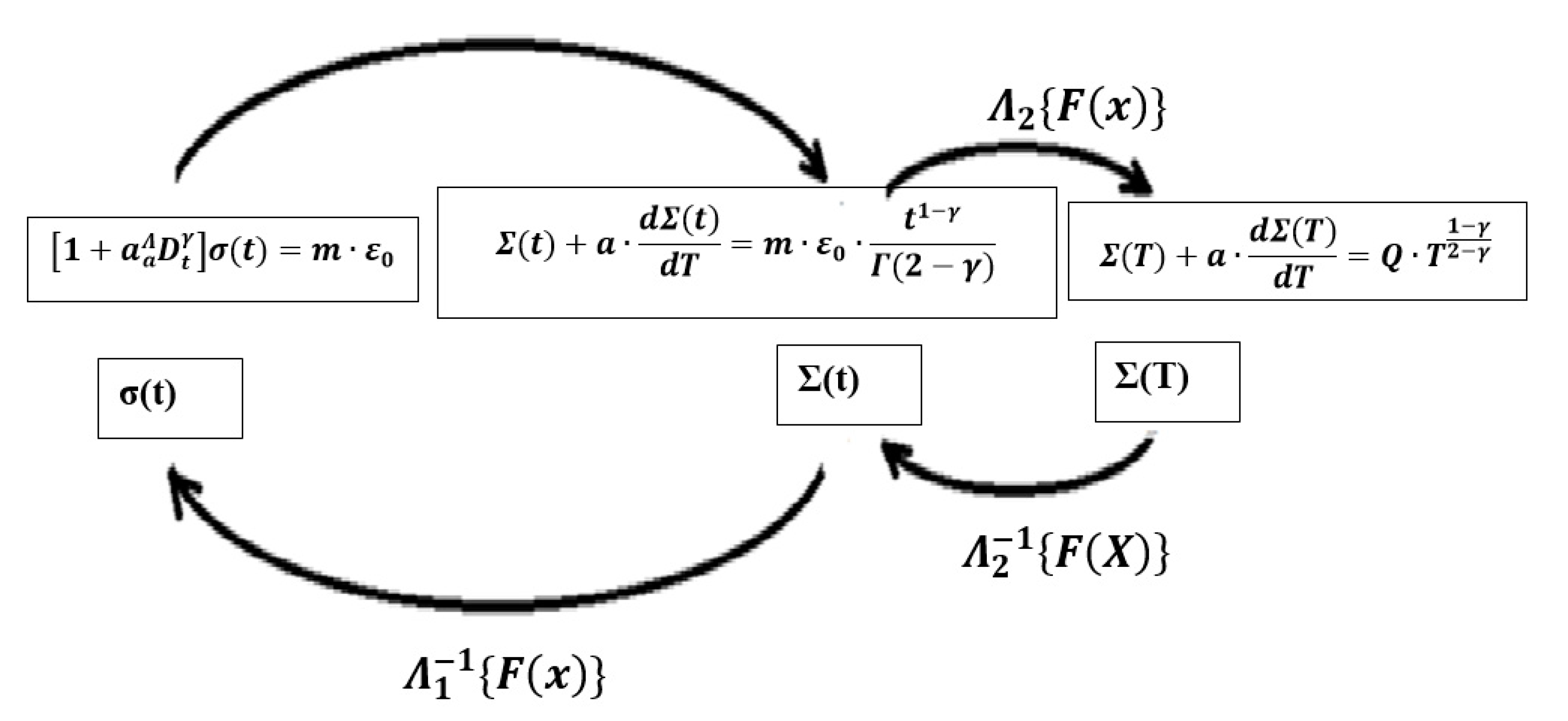
4. The Λ-Fractional Zener Viscoelastic Model
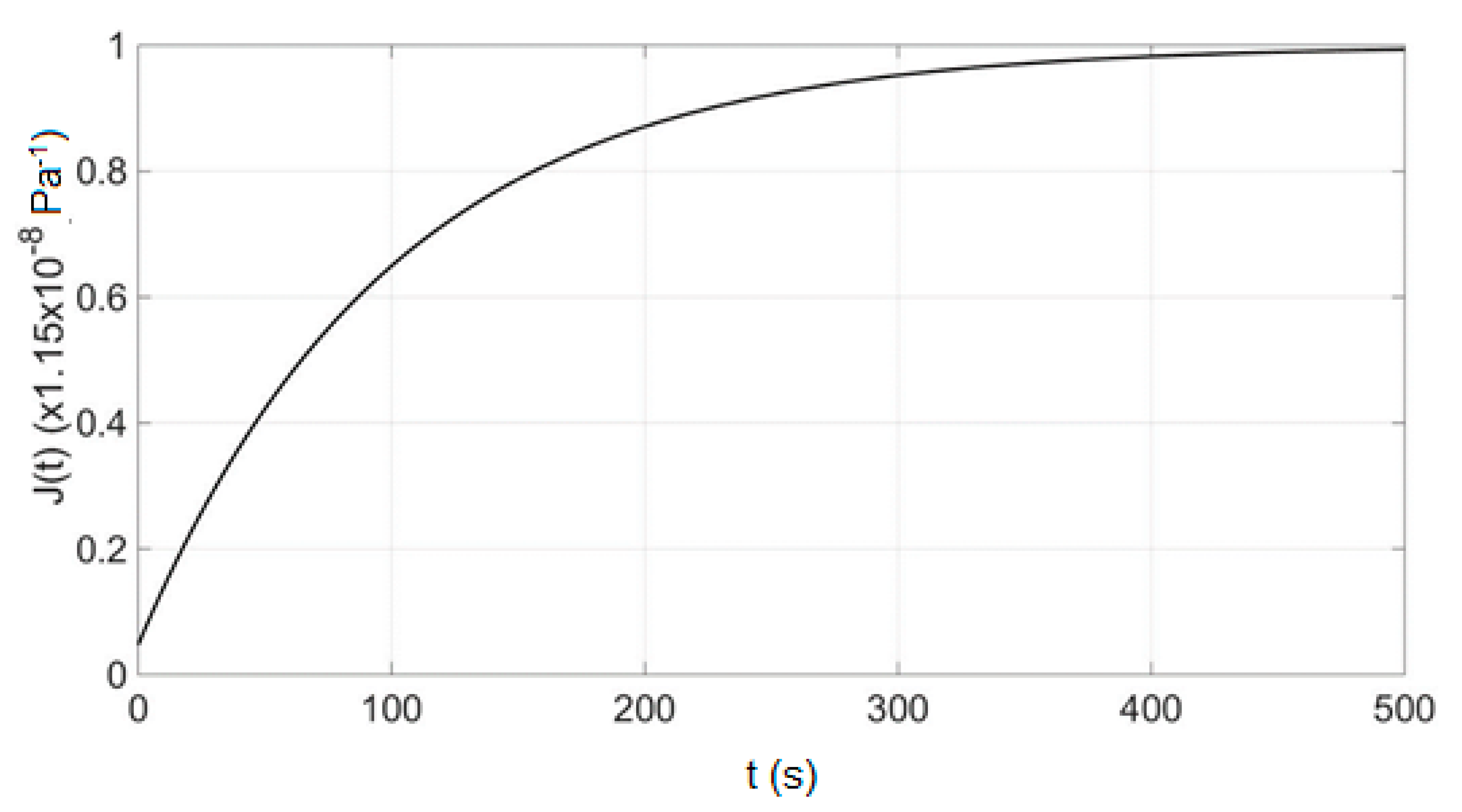
4.1. Creep
4.1.1. Setup of Fractional Differential Equation in the Initial Space
4.1.2. Λ1-Transform of Fractional Differential Equation from the Initial to the Intermediate Space
4.1.3. Λ2-Transform of Fractional Differential Equation from the Intermediate to the Λ-Space
4.1.4. Inverse Λ−12-Transform and Λ−11-Transform of Results in Λ-Space to the Initial Space
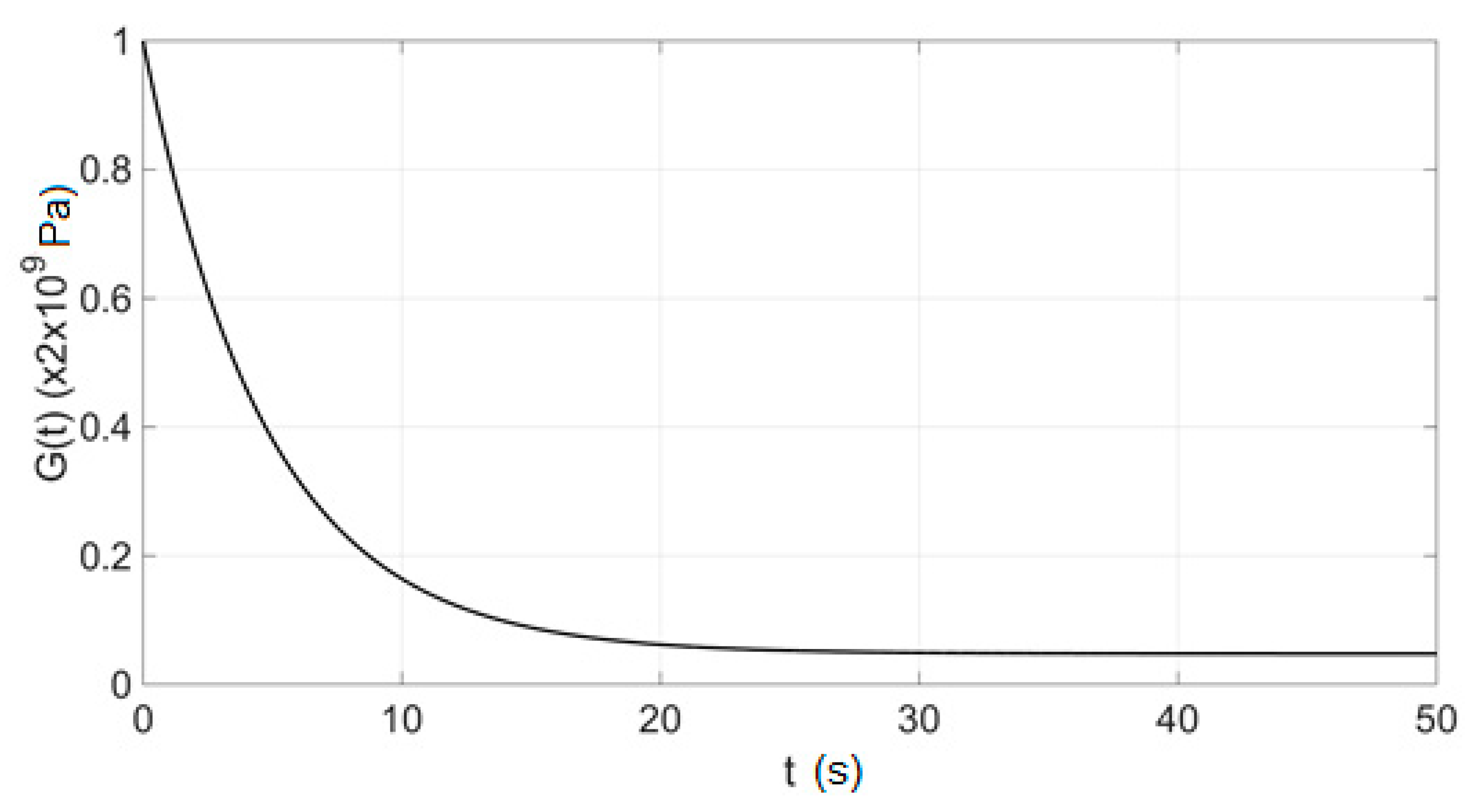
4.2. Relaxation
4.2.1. Setup of Fractional Differential Equation in the Initial Space
4.2.2. Λ1-Transform of Fractional Differential Equation from the Initial to the Intermediate Space
4.2.3. Λ2-Transform of Fractional Differential Equation from the Intermediate to the Λ-Space
4.2.4. Inverse Λ−12-Transform and Λ−11-Transform of Results in Λ-Space to the Initial Space
5. Application of Λ-Derivative to the Zener Model
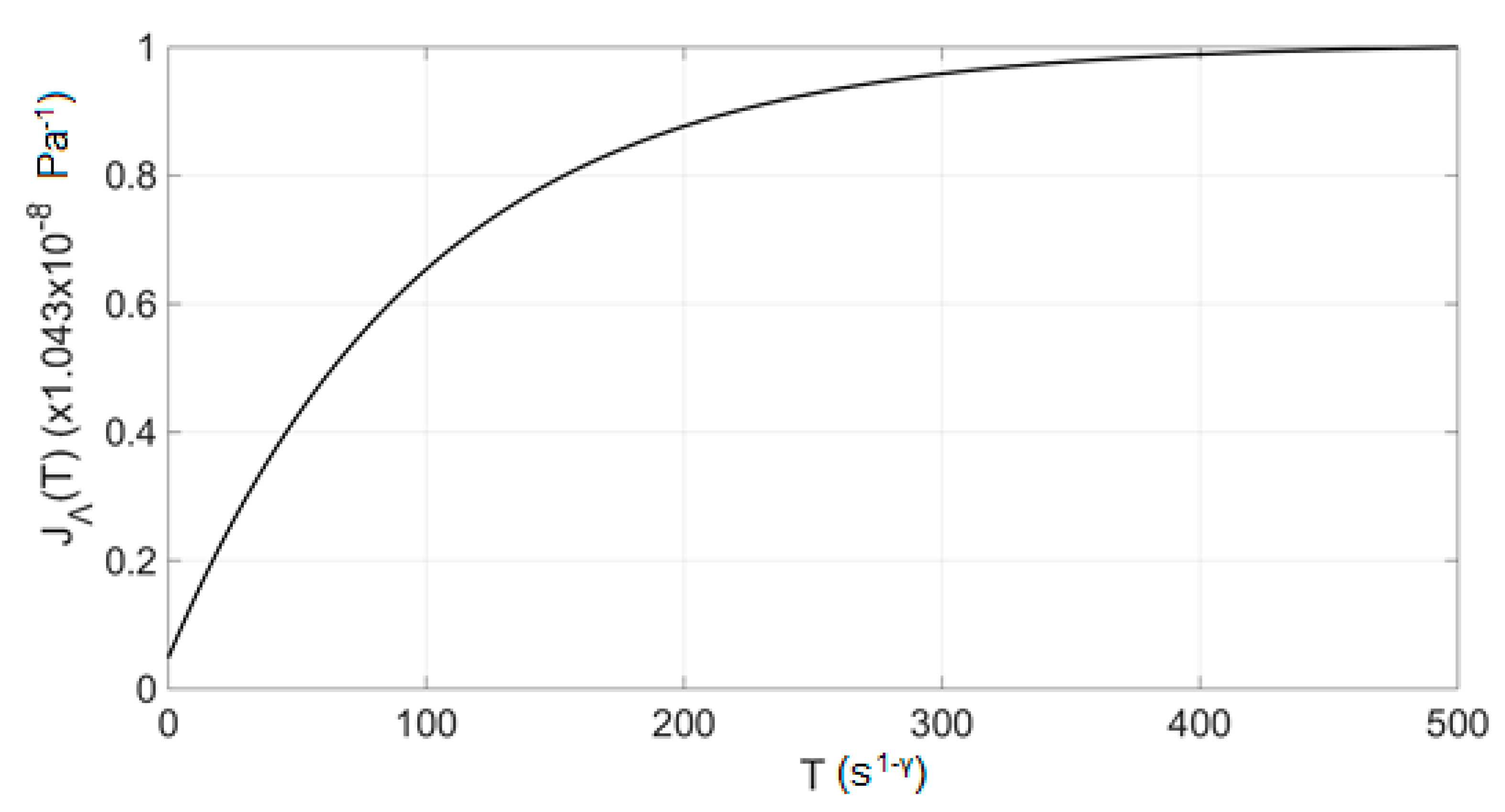
5.1. Creep
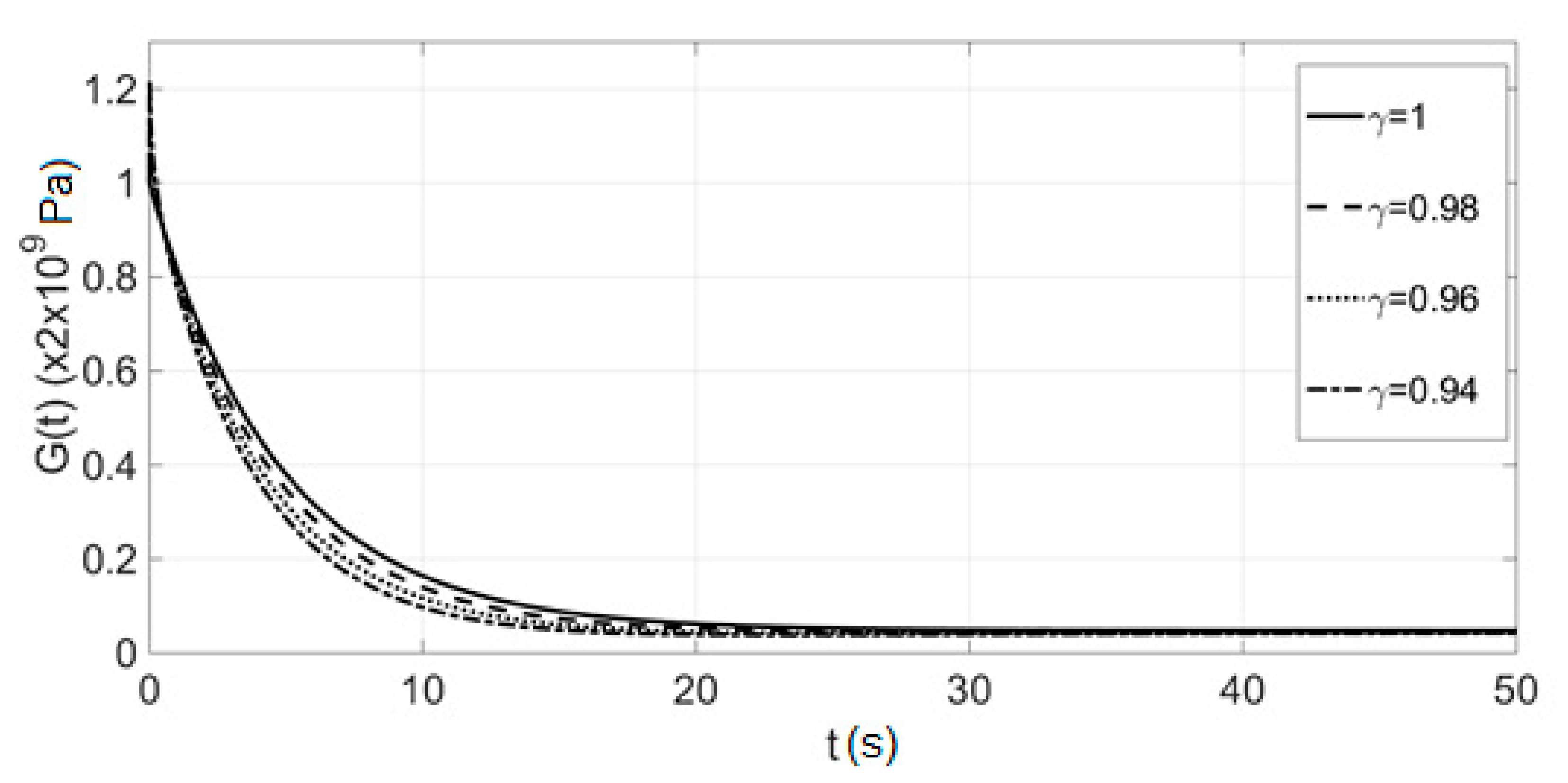
5.2. Relaxation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Eringen, A.C. Non-Local Continuum Field Theories; Springer: New York, NY, USA, 2002. [Google Scholar]
- Carpinteri, A.; Chiaia, B.; Cornetti, P. A Fractional calculus approach to the mechanics of fractal media. Rend. Semin. Mat. 2000, 58, 57–68. [Google Scholar]
- Butera, S.; Di Paola, M. A physically-based connection between Fractional Calculus and fractal geometry. Ann. Phys. 2014, 350, 146–158. [Google Scholar] [CrossRef]
- Tatom, F. The relationship between Fractional Calculus and Fractals. Fractals 1995, 3, 217–229. [Google Scholar] [CrossRef]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Hackensack, NJ, USA, 2000. [Google Scholar]
- West, B.J.; Bologna, M.; Grigolini, P. Physics of Fractal Operators; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Drapaca, C.S.; Sivaloganathan, S.A. Fractional model of continuum mechanics. J. Elast. 2012, 107, 107–123. [Google Scholar] [CrossRef]
- Di Paola, M.; Failla, G.; Zingales, M. Physically-based approach to the mechanics of strong non-local linear elasticity theory. J. Elast. 2009, 97, 103–130. [Google Scholar] [CrossRef]
- Carpinteri, A.; Cornetti, P.; Sapora, A. A Fractional calculus approach to non-local elasticity. Eur. Phys. J. Sp. Top. 2011, 193, 193–204. [Google Scholar] [CrossRef]
- Lazopoulos, K.A. Fractional vector calculus and Fractional continuum mechanics. In Proceedings of the Conference Mechanics Through Mathematical Modelling, Celebrating the 70th Birthday of Prof. T. Atanackovic, Novi Sad, Serbia, 6–11 September 2015; p. 40. [Google Scholar]
- Baleanu, D.; Muslih, S.; Rabei, E. On Fractional Euler-Lagrange and Hamilton Equations and the Fractional generalization of total time Derivatives. Non. Dyn. 2008, 53, 67–74. [Google Scholar] [CrossRef]
- Sumelka, W. Fractional Viscoplasticity. Mech. Res. Commun. 2014, 56, 31–36. [Google Scholar]
- Magin, R.L. Fractional calculus in bioengineering, Parts 1–3. Crit. Rev. Biomed. Eng. 2004, 32, 1–377. [Google Scholar] [CrossRef] [PubMed]
- Atanackovic, T.M. A Modified Zener model of a viscoelastic body. Con. Mech. Ther. 2002, 14, 137–148. [Google Scholar] [CrossRef]
- Atanackovic, T.M. A generalized model for the uniaxial isothermal deformation of a viscoelastic body. Acta Mech. 2002, 159, 77–86. [Google Scholar] [CrossRef]
- Lazopoulos, K.A.; Karaoulanis, D.; Lazopoulos, Α.Κ. On Fractional modeling of viscoelastic mechanical systems. Mech. Res. Commun. 2016, 78, 1–5. [Google Scholar] [CrossRef]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity; Imperial College Press: London, UK, 2010. [Google Scholar]
- Yang, X.J.; Gao, F.; Ju, Y. General Fractional Derivatives with Applications in Viscoelasticity; Academic Press: Cambridge, MA, USA, 2020. [Google Scholar]
- Olivar-Romero, F.; Rosas-Ortiz, O. Transition from the Wave Equation to either the Heat or the Transport Equations through Fractional Differential Expressions. Symmetry 2018, 10, 524. [Google Scholar] [CrossRef]
- Di Paola, M.; Alotta, G.; Burlon, A.; Failla, G. A novel approach to nonlinear variable-order fractional viscoelasticity. Philos. Trans. R. Soc. A 2020, 378, 20190296. [Google Scholar] [CrossRef] [PubMed]
- Chillingworth, D.R.J. Differential Topology with a View to Applications; Pitman: London, UK; San Francisco, CA, USA, 1976. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach: Amsterdam, The Netherlands, 1993. [Google Scholar]
- König, H.; Milman, V. Characterizing the Derivative and the entropy function by the Leibniz rule. J. Funct. Anal. 2011, 261, 1325–1344. [Google Scholar] [CrossRef][Green Version]
- König, H.; Milman, V. Operator Relations Characterizing Derivatives; Birkhäuser: Basel, Switzerland, 2018. [Google Scholar]
- Cresson, J.; Szafrańska, A. Comments on various extensions of the Riemann–Liouville Fractional derivatives: About the Leibniz and chain rule properties. Commun. Nonlinear Sci. Numer. Simul. 2020, 82, 104903. [Google Scholar] [CrossRef]
- Jumarie, G. Modified Riemann-Liouville Derivative and Fractional Taylor series of nondifferentiable functions further results. Math. Comp. App. 2006, 51, 1367–1376. [Google Scholar] [CrossRef]
- Jumarie, G. Table of some basic Fractional calculus formulae derived from a modified Riemann-Liouville Derivative for nondifferentiable functions. App. Math. Lett. 2009, 22, 378–385. [Google Scholar] [CrossRef]
- Yang, X.J. Advanced Local Fractional Calculus and Its Applications; World Scientific: New York, NY, USA, 2012. [Google Scholar]
- Gauld, D. Differential Topology, an Introduction; Dover: New York, NY, USA, 2006. [Google Scholar]
- Atangana, A. Derivative with a New Parameter: Methods and Applications; Elsevier: London, UK, 2016. [Google Scholar]
- Lazopoulos, K.A.; Lazopoulos, A.K. On the Mathematical Formulation of Fractional Derivatives. Prog. Fract. Differ. Appl. 2019, 5, 261–267. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Podlubny, I. Fractional Differential Equations (An Introduction to Fractional Derivatives, Fractional Differential Equations, Some Methods of Their Solution and Some of Their Applications); Academic Press: San Diego, CA, USA; Boston, MA, USA; New York, NY, USA; London, UK; Tokyo, Japan; Toronto, ON, Canada, 1999. [Google Scholar]
- Oldham, K.B.; Spanier, J. The Fractional Calculus; Academic Press: New York, NY, USA; London, UK, 1974. [Google Scholar]
- Li, C.; Cai, M. Theory and Numerical Approximations of Fractional Integrals and Derivatives; Society for Industrial and Applied Mathematics (SIAM): Philadelphia, PA, USA, 2020. [Google Scholar]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lazopoulos, A.K.; Karaoulanis, D. On Λ-Fractional Viscoelastic Models. Axioms 2021, 10, 22. https://doi.org/10.3390/axioms10010022
Lazopoulos AK, Karaoulanis D. On Λ-Fractional Viscoelastic Models. Axioms. 2021; 10(1):22. https://doi.org/10.3390/axioms10010022
Chicago/Turabian StyleLazopoulos, Anastassios K., and Dimitrios Karaoulanis. 2021. "On Λ-Fractional Viscoelastic Models" Axioms 10, no. 1: 22. https://doi.org/10.3390/axioms10010022
APA StyleLazopoulos, A. K., & Karaoulanis, D. (2021). On Λ-Fractional Viscoelastic Models. Axioms, 10(1), 22. https://doi.org/10.3390/axioms10010022





