Foundations of Inference

Abstract

We present a simple and clear foundation for finite inference that unites and significantly extends the approaches of Kolmogorov and Cox. Our approach is based on quantifying lattices of logical statements in a way that satisfies general lattice symmetries. With other applications such as measure theory in mind, our derivations assume minimal symmetries, relying on neither negation nor continuity nor differentiability. Each relevant symmetry corresponds to an axiom of quantification, and these axioms are used to derive a unique set of quantifying rules that form the familiar probability calculus. We also derive a unique quantification of divergence, entropy and information.

1. Introduction

The quality of an axiom rests on it being both convincing for the application(s) in mind, and compelling in that its denial would be intolerable.

We present elementary symmetries as convincing and compelling axioms, initially for measure, subsequently for probability, and finally for information and entropy. Our aim is to provide a simple and widely comprehensible foundation for the standard quantification of inference. We make minimal assumptions—not just for aesthetic economy of hypotheses, but because simpler foundations have wider scope.

It is a remarkable fact that algebraic symmetries can imply a unique calculus of quantification. Section 2 gives the background and outlines the procedure and major results. Section 3 lists the symmetries that are actually needed to derive the results, and the following Section 4 writes each required symmetry as an axiom of quantification. In Section 5, we derive the sum rule for valuation from the associative symmetry of ordered combination. This sum rule is the basis of measure theory. It is usually taken as axiomatic, but in fact it is derived from compelling symmetry, which explains its wide utility. There is also a direct-product rule for independent measures, again derived from associativity. Section 6 derives from the direct-product rule a unique quantitative divergence from source measure to destination.

In Section 7 we derive the chain product rule for probability from the associativity of chained order (in inference, implication). Probability calculus is then complete. Finally, Section 8 derives the Shannon entropy and information (a.k.a. Kullback–Leibler) as special cases of divergence of measures. All these formulas are uniquely defined by elementary symmetries alone.

Our approach is constructivist, and we avoid unnecessary formality that might unduly confine our readership. Sets and quantities are deliberately finite since it is methodologically proper to axiomatize finite systems before any optional passage towards infinity. R.T. Cox [1] showed the way by deriving the unique laws of probability from logical systems having a mere three elementary “atomic” propositions. By extension, those same laws applied to Boolean systems with arbitrarily many atoms and ultimately, where appropriate, to well-defined infinite limits. However, Cox needed to assume continuity and differentiability to define the calculus to infinite precision. Instead, we use arbitrarily many atoms to define the calculus to arbitrarily fine precision. Avoiding infinity in this way yields results that cover all practical applications, while avoiding unobservable subtleties.

Our approach unites and significantly extends the set-based approach of Kolmogorov [2] and the logic-based approach of Cox [1], to form a foundation for inference that yields not just probability calculus, but also the unique quantification of divergence and information.

2. Setting the Scene

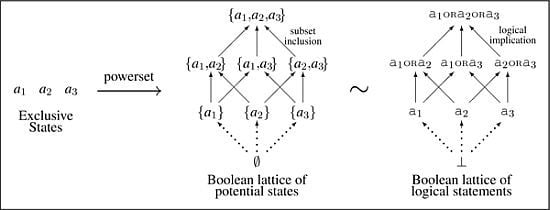
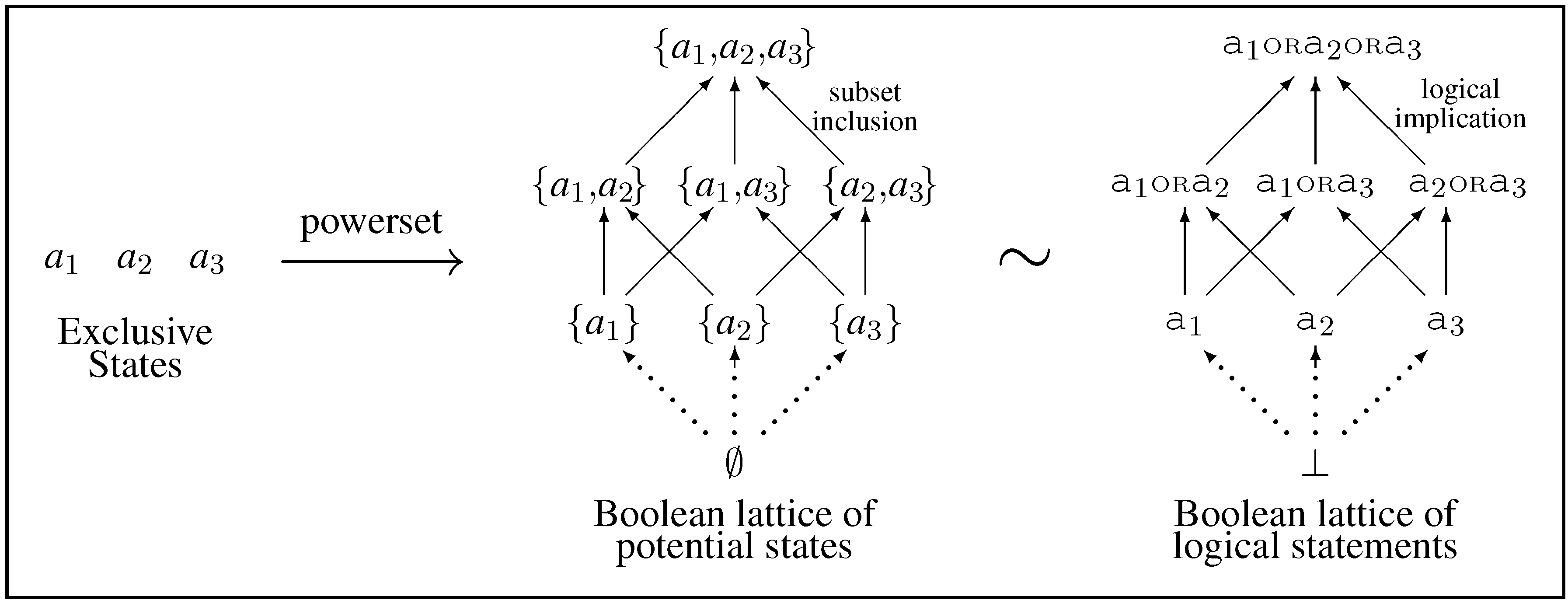
We model the world (or some interesting aspect of it) as being in a particular state out of a finite set of mutually exclusive states (as in Figure 1, left). Since we and our tools are finite, a finite set of states, albeit possibly very large in number, suffices for all practical modeling.

As applied to inference, each state of the world is associated, via isomorphism, with a statement about the world. This results in a set of mutually exclusive statements, which we call atoms. Atoms are combined through logical OR to form compound statements comprising the elements of a Boolean lattice (Figure 1, right), which is isomorphic to a Boolean lattice of sets (Figure 1, center). Although carrying different interpretations, the mathematical structures are identical. Set inclusion “⊂” is equivalent to logical implication “⇒”, which we abstract to lattice order “<”. It is a matter of choice whether to include the null set ∅, equivalent to the logical absurdity ⊥. The set-based view is ontological in character and associated with Kolmogorov, while the logic-based view is epistemological in character and associated with Cox.

Figure 1. The Boolean lattice of potential states (center) is constructed by taking the $2^N$ powerset of an antichain of N mutually exclusive atoms (in this case $a_1,a_2,a_3$, left). This lattice is isomorphic to the Boolean lattice of logical statements ordered by logical implication (right).

Figure 1. The Boolean lattice of potential states (center) is constructed by taking the $2^N$ powerset of an antichain of N mutually exclusive atoms (in this case $a_1,a_2,a_3$, left). This lattice is isomorphic to the Boolean lattice of logical statements ordered by logical implication (right).

Quantification proceeds by assigning a real number $m\left(\mathtt{x}\right)=x$, called a valuation, to elements $\mathtt{x}$. (Typewriter font denotes lattice elements $\mathtt{x}$, whereas their associated valuations (real numbers) x are shown in italic.) We require valuations to be faithful to the lattice, in the sense that

$$\underset{\mathrm{lattice}\mathrm{elements}}{\underbrace{\mathtt{x}<\mathtt{y}}}⟹\underset{\mathrm{real}\mathrm{numbers}}{\underbrace{x<y}}$$

(1)

so that compound elements carry greater value than any of their components. Clearly, this by itself is only a weak restriction on the behavior of valuation.

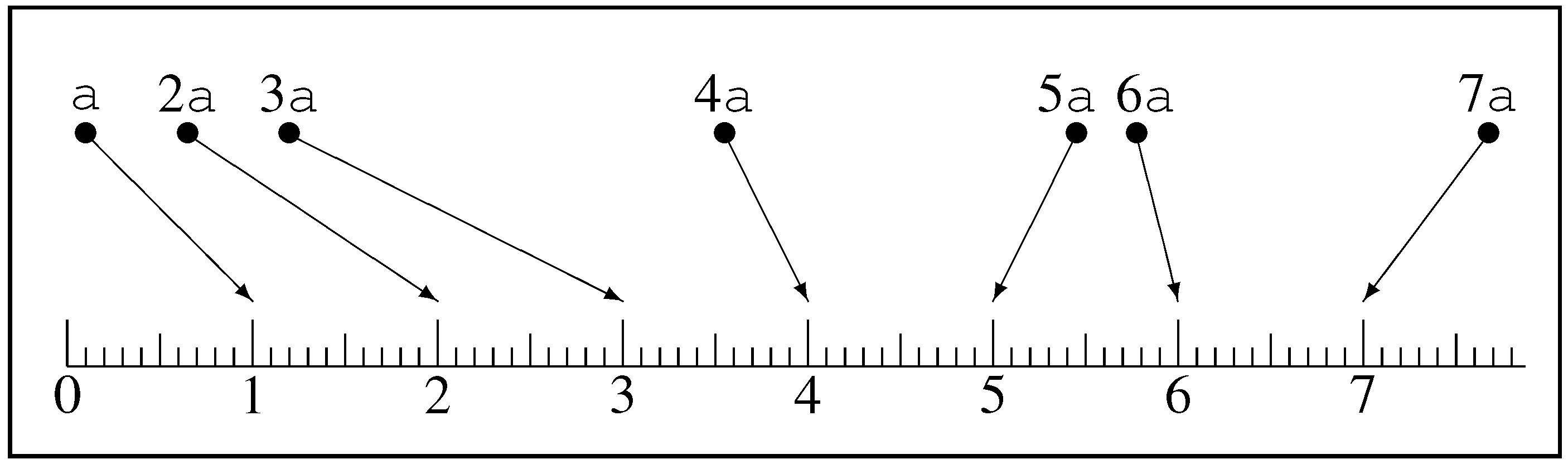
Combination of two atoms (or disjoint compounds) into their compound is written as the operator ⊔, for example $\mathtt{z}=\mathtt{x}\bigsqcup \mathtt{y}$. Our first step is to quantify the combination of disjoint elements through an operator ⊕ that combines values (Table 1 below lists such operators and their eventual identifications).

$$\underset{\mathrm{real}\mathrm{numbers}}{\underbrace{z=x\oplus y}}\mathrm{representing}\underset{\mathrm{joined}\mathrm{elements}}{\underbrace{\mathtt{z}=\mathtt{x}\bigsqcup \mathtt{y}}}$$

(2)

We find that the symmetries underlying ⊔ place constraints on ⊕ that effectively require it to be addition +. At this stage, we already have the foundation of measure theory, and the generalization of combination (of disjoint elements) to the lattice join (of arbitrary elements) is straightforward. The wide applicability of these underlying symmetries explains the wide utility of measure theory, which might otherwise be mysterious.

Table 1. Operators and their symbols.

Operation	Symbol	Quantification	(Eventual form)
ordering	<	<
combination	⊔	⊕	(addition)
direct product	×	⊗	(multiplication)
chaining	,	⊙	(multiplication)

Table 1. Operators and their symbols.

Operation	Symbol	Quantification	(Eventual form)
ordering	<	<
combination	⊔	⊕	(addition)
direct product	×	⊗	(multiplication)
chaining	,	⊙	(multiplication)

We can consider the atoms ${\mathtt{a}}_1,{\mathtt{a}}_2,{\mathtt{a}}_3,\cdots ,{\mathtt{a}}_N$ and ${\mathtt{b}}_1,{\mathtt{b}}_2,\cdots ,{\mathtt{b}}_M$ from separate problems as $NM$ composite atoms ${\mathtt{c}}_{ij}={\mathtt{a}}_i\times {\mathtt{b}}_j$ in an equivalent composite problem. The direct-product operator ⊗ quantifies the composition of values:

$$\underset{\mathrm{real}\mathrm{numbers}}{\underbrace{c=a\otimes b}}\mathrm{representing}\underset{\mathrm{composite}\mathrm{element}}{\underbrace{\mathtt{c}=\mathtt{a}\times \mathtt{b}}}$$

(3)

We find that the symmetries of × place constraints on ⊗ that require it to be multiplication.

It is common in science to acquire numerical assignments by optimizing a variational potential. By requiring consistency with the numerical assignments of ordinary multiplication, we find that there is a unique variational potential $H(\mathbf{p}\mid \mathbf{q})$, of “$plogp$” form, known as the (generalized Kullback–Leibler) Bregman divergence of measure $\mathbf{p}$ from measure $\mathbf{q}$.

Inference involves the relationship of one logical statement (predicate $\mathtt{x}$) to another (context $\mathtt{t}$), initially in a situation where $\mathtt{x}\Rightarrow \mathtt{t}$ so that the context includes subsidiary predicates. To quantify inference, we assign real numbers $p(\mathtt{x}\mid \mathtt{t})$, ultimately recognised as probability, to predicate–context intervals $[\mathtt{x},\mathtt{t}]$. Such intervals can be chained (concatenated) so that $[\mathtt{x},\mathtt{z}]=\left[\right[\mathtt{x},\mathtt{y}],[\mathtt{y},\mathtt{z}\left]\right]$, with ⊙ representing the chaining of values.

$$\underset{\mathrm{real}\mathrm{numbers}}{\underbrace{p(\mathtt{x}\mid \mathtt{z})=p(\mathtt{x}\mid \mathtt{y})\odot p(\mathtt{y}\mid \mathtt{z})}}\mathrm{representing}\underset{\mathrm{chained}\mathrm{intervals}}{\underbrace{[\mathtt{x},\mathtt{z}]=\left[\right[\mathtt{x},\mathtt{y}],[\mathtt{y},\mathtt{z}\left]\right]}}$$

(4)

We find that the symmetries of chaining require ⊙ to be multiplication, yielding the product rule of probability calculus. When applied to probabilities, the divergence formula reduces to the information, also known as the Kullback–Leibler formula, with entropy being a variant.

2.1. The Order-Theoretic Perspective

The approach we employ can be described in terms of order-preserving (monotonic) maps between order-theoretic structures. Here we present our approach, described above, from this different perspective.

Order-theoretically, a finite set of exclusive states can be represented as an antichain, illustrated in Figure 1(left) as three states $a_1$, $a_2$, and $a_3$ situated side-by-side. Our state of knowledge about the world (more precisely, of our model of it—we make no ontological claim) is often incomplete so that we can at best say that the world is in one of a set of potential states, which is a subset of the set of all possible states. In the case of total ignorance, the set of potential states includes all possible states. In contrast, perfect knowledge about our model is represented by singleton sets consisting of a single state. We refer to the singleton sets as atoms, and note that they are exclusive in the sense that no two can be true.

The space of all possible sets of potential states is given by the partially-ordered set obtained from the powerset of the set of states ordered by set inclusion. For an antichain of mutually exclusive states, the powerset is a Boolean lattice (Figure 1, center), with the bottom element optional. By conceiving of a statement about our model of the world in terms of a set of potential states, we have an order-isomorphism from the Boolean lattice of potential states ordered by set inclusion to the Boolean lattice of statements ordered by logical implication (Figure 1, right). This isomorphism maps each set of potential states to a statement, while mapping the algebraic operations of set union ∪ and set intersection ∩ to the logical OR and AND, respectively.

The perspective provided by order theory enables us to focus abstractly on the structure of a Boolean lattice with its generic algebraic operations join ∨ and meet∧. This immediately broadens the scope from Boolean to more general distributive lattices — the first fruit of our minimalist approach. For additional details on partially ordered sets and lattices in particular, we refer the interested reader to the classic text by Birkhoff [3] or the more recent text by Davey & Priestley [4].

Quantification proceeds by assigning valuations $m\left(\mathtt{x}\right)=x$ to elements $\mathtt{x}$, to form a real-valued representation. For this to be faithful, we require an order-preserving (monotonic) map between the partial order of a distributive lattice and the total order of the chains that are to be found within. Thus $\mathtt{x}<\mathtt{y}$ is to imply that $x<y$, a relationship that we call fidelity. The converse is not true: the total order imposed by quantification must be consistent with but can extend the partial order of the lattice structure.

We write the combination of two atoms into a compound element (and more generally any two disjoint compounds into a compound element) as ⊔, for example $\mathtt{z}=\mathtt{x}\bigsqcup \mathtt{y}$. Derivation of the calculus of quantification starts with this disjoint combination operator, where we find that its symmetries place constraints on its representation ⊕ that allow us the convention of ordinary addition “$\oplus =+$”. This basic result generalizes to the standard join lattice operator ∨ for elements that (possibly having atoms in common) need not be disjoint, for which the sum rule generalizes to its standard inclusion/exclusion form [5], which involves the meet ∧ for any atoms in common.

There are two mathematical conventions concerning the handling the nothing-is-true null element ⊥ at the bottom of the lattice known as the absurdity. Some mathematicians opt to include the bottom element on aesthetic grounds, whereas others opt to exclude it because of its paradoxical interpretation [4]. If it is included, its quantification is zero. Either way, fidelity ensures that other elements are quantified by positive values that are positive (or, by elementary generalization, zero). At this stage, we already have the foundation of measure theory.

Logical deduction is traditionally based on a Boolean lattice and proceeds “upwards” along a chain (as in the arrows sketched in Figure 1). Given some statement $\mathtt{x}$, one can deduce that $\mathtt{x}$ implies $\mathtt{x}\mathtt{OR}\mathtt{y}$ since $\mathtt{x}\mathtt{OR}\mathtt{y}$ includes $\mathtt{x}$. Similarly, $\mathtt{x}\mathtt{AND}\mathtt{y}$ implies $\mathtt{x}$ since $\mathtt{x}$ includes $\mathtt{x}\mathtt{AND}\mathtt{y}$. The ordering relationships among the elements of the lattice are encoded by the zeta function of the lattice [6]

$$\begin{array}{c}\hfill \mathrm{zeta}\mathrm{function}:\zeta (\mathtt{x},\mathtt{y})=\left\{\begin{array}{cc}1& \mathrm{if}\mathtt{x}\le \mathtt{y}\hfill \\ 0& \mathrm{if}\mathtt{x}\nleqq \mathtt{y}\hfill \end{array}\right.\phantom{\}}\end{array}$$

(5)

Deduction is definitive.

Inference, or logical induction, is the inverse of deduction and proceeds “downwards” along a chain, losing logical certainty as knowledge fragments. Our aim is to quantify this loss of certainty, in the expectation of deriving probability calculus. This requires generalization of the binary zeta function $\zeta (\mathtt{x},\mathtt{y})$ to some real-valued function $p(x\mid y)$ which will turn out to be the standard probability of x GIVEN y. However, a firm foundation for inference must be devoid of a choice of arbitrary generalizations. By viewing quantification in terms of an order-preserving map between the partial order (Boolean lattice) and a total order (chain) subject to compelling symmetries alone, we obtain a firm foundation for inference, devoid of further assumptions of questionable merit.

By considering atoms (singleton sets, which are the join-irreducible elements of the Boolean lattice) as precise statements about exclusive states, and composite lattice elements (sets of several exclusive states) as less precise statements involving a degree of ignorance, the two perspectives of logic and sets, on which the Cox and Kolmogorov foundations are based, become united within the order-theoretic framework.

In summary, the powerset comprises the hypothesis space of all possible statements that one can make about a particular model of the world. Quantification of join using + is the sum rule of probability calculus, and is required by adherence to the symmetries we list. It fixes the valuations assigned to composite elements in terms of valuations assigned to the atoms. Those latter valuations assigned to the atoms remain free, unconstrained by the calculus. That freedom allows the calculus to apply to inference in general, with the mathematically-arbitrary atom valuations being guided by insight into a particular application.

2.2. Commentary

Our results—the sum rule and divergence for measures, and the sum and product rules with information for probabilities—are standard and well known (their uniqueness perhaps less so). The matter we address here is which assumptions are necessary and which are not. A Boolean lattice, after all, is a special structure with special properties. Insofar as fewer properties are needed, we gain generality. Wider applicability may be of little value to those who focus solely on inference. Yet, by showing that the basic foundations of inference have wider scope, we can thereby offer extra—and simpler—guidance to the scientific community at large.

Even within inference, distributive problems may have relationships between their atoms such that not all combinations of states are allowed. Rather than extend a distributive lattice to Boolean by padding it with zeros, the tighter framework immediately empowers us to work with the original problem in its own right. Scientific problems (say, the propagation of particles, or the generation of proteins) are often heavily conditional, and it could well be inappropriate or confusing to go to a full Boolean lattice when a sparser structure is a more natural model.

We also confirm that commutativity is not a necessary assumption. Rather, commutativity of measure is imposed by the associativity and order required of a scalar representation. Conversely, systems that are not commutative (matrices under multiplication, for example) cannot be both associative and ordered.

3. Symmetries

Here, we list the relevant symmetries on which our axioms are based. All are properties of distributive lattices, and our descriptions are styled that way so that a reader wary of further generality does not need to move beyond this particular, and important, example. However, one may note that not all the properties of a distributive lattice (such as commutativity of the join) are listed, which implies that these results are applicable to a broader class of algebraic structures that includes distributive lattices.

Valuation assignments rank statements via an order-preserving map which we call fidelity .

$$\begin{array}{c}\hfill \mathrm{Symmetry}0:\underset{\mathrm{lattice}\mathrm{elements}}{\underbrace{\mathtt{x}<\mathtt{y}}}⟹\underset{\mathrm{real}\mathrm{numbers}}{\underbrace{x<y}}\end{array}$$

(6)

It is a matter of convention that we choose to order the valuations in the same sense as the lattice order (“more is bigger”). Reverse order would be admissible and logically equivalent, though less convenient.

In the specific case of Boolean lattices of logical statements, the binary ordering relation, represented generically by <, is equivalent to logical implication (⇒) between different statements, or equivalently, proper subset inclusion (⊂) in the powerset representation. Combination preserves order from the right and from the left

$$\begin{array}{c}\hfill \mathrm{Symmetry}1:\mathtt{x}<\mathtt{y}⟹\left\{\begin{array}{c}\mathtt{x}\bigsqcup \mathtt{z}<\mathtt{y}\bigsqcup \mathtt{z}\\ \mathtt{z}\bigsqcup \mathtt{x}<\mathtt{z}\bigsqcup \mathtt{y}\end{array}\right.\phantom{\}}\end{array}$$

(7)

for any $\mathtt{z}$ (a property that can be viewed as distributivity of ⊔ over <) on the grounds that ordering needs to be robust if it is to be useful. Combination is also taken to be associative

$$\begin{array}{c}\hfill \mathrm{Symmetry}2:(\mathtt{x}\bigsqcup \mathtt{y})\bigsqcup \mathtt{z}=\mathtt{x}\bigsqcup (\mathtt{y}\bigsqcup \mathtt{z})\end{array}$$

(8)

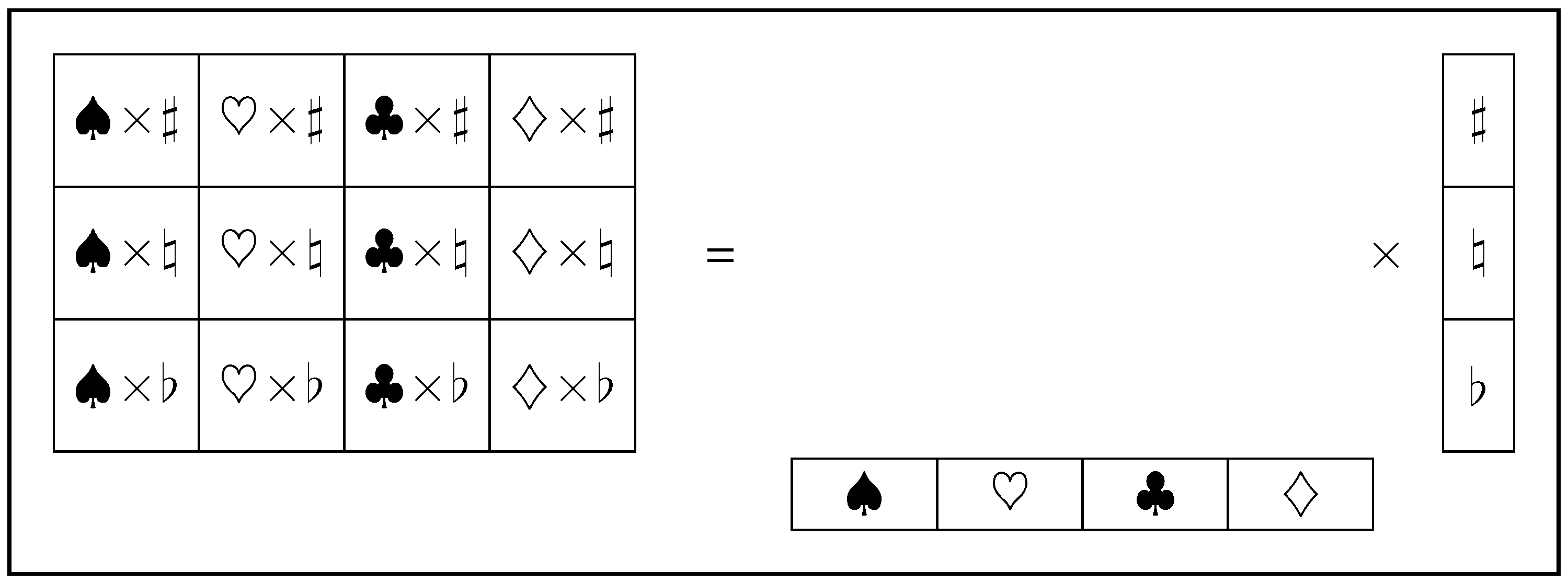
Independent systems can be considered together (Figure 2).

Figure 2. One system might, for example, be playing-card suits $\mathtt{x}\in \{♠,♡,♣,♢\}$, while another independent system might be music keys $\mathtt{t}\in \{♭,♮,♯\}$. The direct-product combines the spaces of$\mathtt{x}$ and $\mathtt{t}$ to form the joint space of$\mathtt{x}\times \mathtt{t}$ with atoms like $♡\times ♮$.

Figure 2. One system might, for example, be playing-card suits $\mathtt{x}\in \{♠,♡,♣,♢\}$, while another independent system might be music keys $\mathtt{t}\in \{♭,♮,♯\}$. The direct-product combines the spaces of$\mathtt{x}$ and $\mathtt{t}$ to form the joint space of$\mathtt{x}\times \mathtt{t}$ with atoms like $♡\times ♮$.

The direct-product operator × is taken to be (right-)distributive over ⊔

$$\begin{array}{c}\hfill \mathrm{Symmetry}3:(\mathtt{x}\times \mathtt{t})\bigsqcup (\mathtt{y}\times \mathtt{t})=(\mathtt{x}\bigsqcup \mathtt{y})\times \mathtt{t}\end{array}$$

(9)

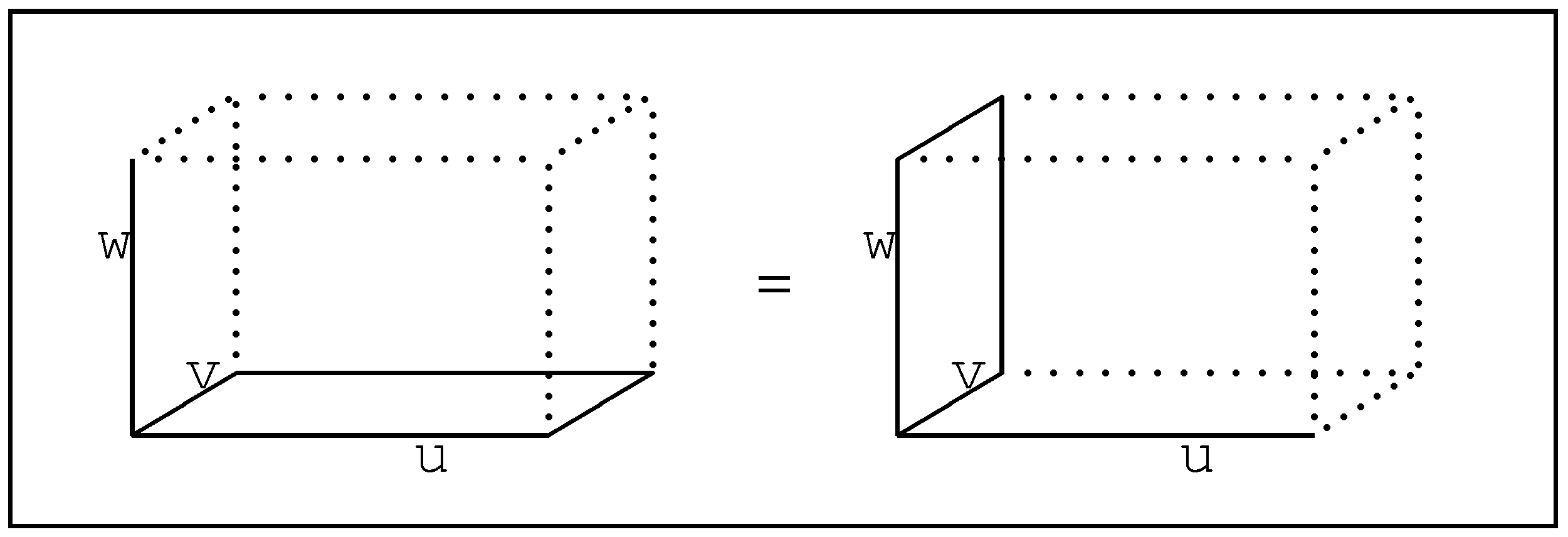
so that relationships in one set, such as perhaps $♣\bigsqcup ♡$, remain intact whether or not an independent element from the other, such as perhaps ♮, is appended. Left distributivity may well hold but is not needed. The direct product of independent lattices is also taken to be associative (Figure 3).

$$\begin{array}{c}\hfill \mathrm{Symmetry}4:(\mathtt{u}\times \mathtt{v})\times \mathtt{w}=\mathtt{u}\times (\mathtt{v}\times \mathtt{w})\end{array}$$

(10)

Figure 3. Associativity of direct product can be viewed geometrically.

Figure 3. Associativity of direct product can be viewed geometrically.

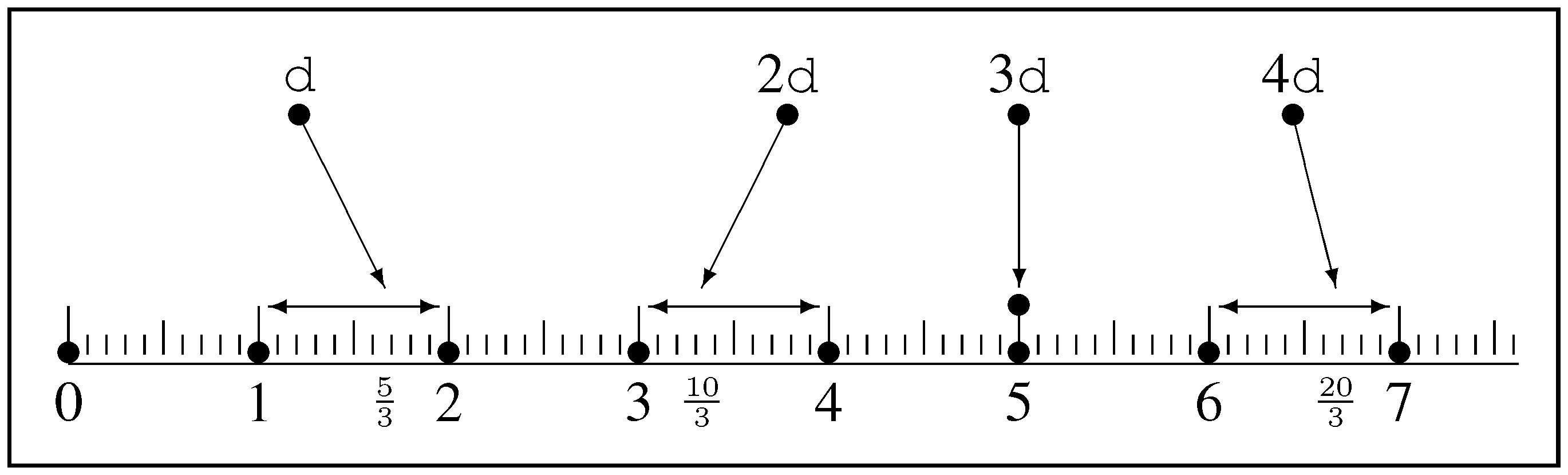
Finally, we consider a totally ordered set of logical statements that form a chain $\mathtt{x}<\mathtt{y}<\mathtt{z}<\mathtt{t}$. We focus on an interval on the chain, which is defined by an ordered pair of logical statements $[\mathtt{x},\mathtt{t}]$. Adjacent intervals can be chained, as in $\left[[\mathtt{x},\mathtt{y}],[\mathtt{y},\mathtt{z}]\right]=[\mathtt{x},\mathtt{z}]$, and chaining is associative

$$\left[[\mathtt{x},\mathtt{y}],[\mathtt{y},\mathtt{z}]\right],[\mathtt{z},\mathtt{t}]=[\mathtt{x},\mathtt{y}],\left[[\mathtt{y},\mathtt{z}],[\mathtt{z},\mathtt{t}]\right]$$

(11)

Using Greek symbols to represent an interval, $\alpha =[\mathtt{x},\mathtt{y}]$, $\beta =[\mathtt{y},\mathtt{z}]$, $\gamma =[\mathtt{z},\mathtt{t}]$, we have

$$\begin{array}{c}\hfill \mathrm{Symmetry}5:(\alpha ,\beta ),\gamma =\alpha ,(\beta ,\gamma )\end{array}$$

(12)

These and these alone are the symmetries we need for the axioms of quantification. They are presented as a cartoon in the “Conclusions” section below.

4. Axioms

We now introduce a layer of quantification. Our axioms arise from the requirement that any quantification must be consistent with the symmetries indicated above. Therefore, each symmetry gives rise to an axiom. We seek scalar valuations to be assigned to elements of a lattice, while conforming to the above symmetries (#0—#5)for disjoint elements.

Fidelity (symmetry #0) requires us to choose an increasing measure so that, without loss of generality, we may set $m\left(\perp \right)=0$ and thereafter

$$\begin{array}{c}\hfill \mathrm{Axiom}0:x>0\end{array}$$

(13)

To conform to the ordering symmetry #1, we require ⊕ as set up in Equation 2 to obey

$$\begin{array}{c}\hfill \mathrm{Axiom}1:x<y⟹\left\{\begin{array}{c}x\oplus z<y\oplus z\\ z\oplus x<z\oplus y\end{array}\right.\phantom{\}}\end{array}$$

(14)

To conform to the associative symmetry #2, we also require ⊕ to obey

$$\begin{array}{c}\hfill \mathrm{Axiom}2:(x\oplus y)\oplus z=x\oplus (y\oplus z)\end{array}$$

(15)

These equations are to hold for arbitrary values x, y, z assigned to the disjoint $\mathtt{x}$, $\mathtt{y}$, $\mathtt{z}$. Appendix A will show that these order and associativity axioms are necessary and sufficient to determine the additive calculus of measure.

To conform to the distributive symmetry #3, we require ⊗ as set up in Equation 3 to obey

$$\begin{array}{c}\hfill \mathrm{Axiom}3:(x\otimes t)\oplus (y\otimes t)=(x\oplus y)\otimes t\end{array}$$

(16)

for disjoint $\mathtt{x}$ and $\mathtt{y}$ combined with any $\mathtt{t}$ from the second lattice. Presence of $\mathtt{t}$ may change the measures, but does not change their underlying additivity. To conform to the associative symmetry #4, we also require ⊗ to obey

$$\begin{array}{c}\hfill \mathrm{Axiom}4:(u\otimes v)\otimes w=u\otimes (v\otimes w)\end{array}$$

(17)

These axioms determine the multiplicative form of ⊗ and also lead to a unique divergence between measures.

To conform to the associative symmetry #5, we require ⊙ as set up in Equation 4 to obey

$$\begin{array}{c}\hfill \mathrm{Axiom}5:\left(p\left(\alpha \right)\odot p\left(\beta \right)\right)\odot p\left(\gamma \right)=p\left(\alpha \right)\odot \left(p\left(\beta \right)\odot p\left(\gamma \right)\right)\end{array}$$

(18)

where $\alpha =[\mathtt{x},\mathtt{y}]$, $\beta =[\mathtt{y},\mathtt{z}]$, $\gamma =[\mathtt{z},\mathtt{t}]$ are individual steps concatenated along the chain $\alpha ,\beta ,\gamma$, which is $\left[\right[\mathtt{x},\mathtt{y}],[\mathtt{y},\mathtt{z}],[\mathtt{z},\mathtt{t}\left]\right]=[\mathtt{x},\mathtt{t}]$. This final axiom will let us pass from measure to probability and Bayes’ theorem, and from divergence to information and entropy. For each operator (Table 1), the eventual form satisfies all relevant axioms, which assures existence. Uniqueness remains to be demonstrated.

5. Measure

Preliminary to investigating probability, we attend to the foundation of measure.

5.1. Disjoint arguments

According to the scalar associativity theorem (Appendix A), an operator ⊕ obeying axioms 1 and 2 exists and can without loss of generality be taken to be addition +, giving the sum rule.

$$\begin{array}{c}\hfill \mathrm{Sum}\mathrm{rule}:x\oplus y=x+y\end{array}$$

(19)

Commutativity $x\oplus y=y\oplus x$, though not explicitly assumed, is an unsurprising property. In accordance with fidelity (axiom 0), element values are strictly positive $x>0$. In this form, positive-valued valuation $m\left(\mathtt{x}\right)=x$ of lattice elements is known as a measure. If the null element is included as the bottom of the lattice, it has zero value.

Whilst we are free to adopt additivity as a convenient convention, we are also free to adopt any order-preserving regrade Θ for which the rule would be

$$x\oplus y={\Theta }^{-1}\left(\Theta \left(x\right)+\Theta \left(y\right)\right)$$

(20)

This carries no extra generality because this form can be reverted to additivity by applying Θ, but we need such alternative grading later to avoid inconsistency between different assignments. There is no other freedom. If the linear form of sum rule is to be maintained, the only freedom is linear rescaling $\Theta \left(x\right)=Kx$, with $K>0$ to retain positivity.

Measure theory (see for example [7]) is usually introduced with additivity (countably additive or σ-additive) and non-negativity as “obvious” basic assumptions, with emphasis on the technical control of infinity in unbounded applications. Here we emphasize the foundation, and discover the reason why measure theory is constructed as it is. The symmetries of combination require it. Any other formulation would break these basic properties of associativity and order, and would not yield a widely useful theory.

5.2. Arbitrary Arguments

For elements $\mathtt{x}$ and $\mathtt{y}$ that need not be disjoint, their join ∨ is defined as comprising all their constituent atoms counted once only, and the meet ∧ as comprising those atoms they have in common. In inference, ∨ is logical OR and ∧ is logical AND.

By putting $\mathtt{x}=\mathtt{u}\bigsqcup \mathtt{v}$ and $\mathtt{y}=\mathtt{v}\bigsqcup \mathtt{w}$ for disjoint $\mathtt{u},\mathtt{v},\mathtt{w}$, we reach the general “inclusion/exclusion” sum rule for arbitrary $\mathtt{x}$ and $\mathtt{y}$

$${\displaystyle \boxed{\phantom{(}m(\mathtt{x}\vee \mathtt{y})+m(\mathtt{x}\wedge \mathtt{y})=m\left(\mathtt{x}\right)+m\left(\mathtt{y}\right)\phantom{)}}}$$

(21)

Commutativity of join and meet follow:

$$m(\mathtt{x}\vee \mathtt{y})=m(\mathtt{y}\vee \mathtt{x}),m(\mathtt{x}\wedge \mathtt{y})=m(\mathtt{y}\wedge \mathtt{x}).$$

(22)

5.3. Independence

From the associativity of direct product (axiom 4), the associativity theorem (Appendix A again) assures the existence of an additivity relationship of the form

$$\Theta (x\otimes t)=\Theta \left(x\right)+\Theta \left(t\right)$$

(23)

for some invertible function Θ of the measures $x=m\left(\mathtt{x}\right)$, $t=m\left(\mathtt{t}\right)$ and $x\otimes t=m(\mathtt{x}\times \mathtt{t})$. We can not proceed as before to re-grade in terms of $\Theta \left(m\right)$ to supersede m, because we are already using additivity

$$x\otimes t+y\otimes t=(x+y)\otimes t$$

(24)

(axiom 3, distributivity of ⊗ over $\oplus =+$) to define the grade. Instead, we require consistency with the sum-rule behavior for $x\otimes t$ and $y\otimes t$. Defining $\Psi ={\Theta }^{-1}$ gives, term by term,

$$\Psi (\xi +\tau )+\Psi (\eta +\tau )=\Psi \left(\zeta \right(\xi ,\eta )+\tau )$$

(25)

where

$$\xi =\Theta \left(x\right),\eta =\Theta \left(y\right),\zeta =\Theta (x+y),\tau =\Theta \left(t\right).$$

(26)

Among these variables, $\xi ,\eta ,\tau$ are independent, but (through the sum rule), ζ depends on ξ and η but not τ. This is the product equation. By definition, Ψ returns a measure, so it is positive.

The product theorem (Appendix B) shows Θ to be logarithmic, with Equation 23 reading

$$\frac{1}{A}log\frac{x\otimes t}{C}=\frac{1}{A}log\frac{x}{C}+\frac{1}{A}log\frac{t}{C}$$

(27)

with A and C universal constants (A cancelling out), and C being positive. The obvious convention $C=1$ loses no generality, and shows ⊗ to be simple multiplication

$$\begin{array}{c}\hfill \mathrm{Direct}-\mathrm{product}\mathrm{rule}:x\otimes t=xt\end{array}$$

(28)

Measures are required to multiply, because of associativity of direct product, and the “$\otimes t$” operation is represented by “scale by t”. This is consistent with linear rescaling (here depending on the second factor t) being the only allowed freedom for the measure assigned to the first factor x.

6. Variation

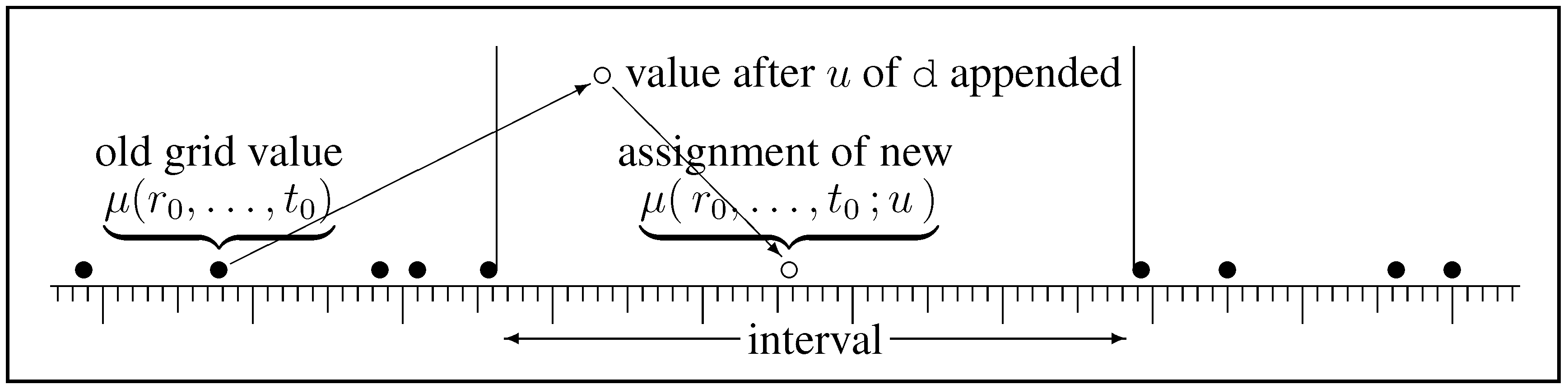
Variational principles are common in science—minimum energy for equilibrium, Hamilton’s principle for dynamics, maximum entropy for thermodynamics, and so on—and we seek one for measures. The aim is to discover a variational potential $H\left(\mathbf{m}\right)$ whose constrained minimum allows the valuations $\mathbf{m}=(m_1,m_2,\cdots ,m_N)$ of N atoms to be assigned subject to appropriate constraints of the form $f\left(\mathbf{m}\right)=\mathrm{constant}$. (The vectors which appear in this section are shown in bold-face font.)

The variational potential is required to be general, applying to arbitrary constraints. Just like values themselves, constraints on individual atom values can be combined into compound constraints that influence several values: indeed the constraints could simply be imposition of definitive values. Such combination allows a Boolean lattice, entirely analogous to Figure 1, to be developed from individual atomic constraints. The variational potential H is to be a valuation on the measures resulting from these constraints, combination being represented by some operator $◯$ so that

$$H\left(x\mathtt{WITH}y\right)=H\left(x\right)◯H\left(y\right)$$

(29)

for constraints acting on disjoint atoms or compounds.

Adding extra constraints always increases H, otherwise the variational requirement would be broken, so H must be faithful to chaining in the lattice.

$$\underset{\mathrm{chained}}{\underbrace{x<y}}⟹\underset{\mathrm{real}\mathrm{numbers}}{\underbrace{H\left(x\right)<H\left(y\right)}}$$

(30)

We also have order

$$H\left(x\right)<H\left(y\right)⟹\left\{\begin{array}{c}H\left(x\right)◯H\left(z\right)<H\left(y\right)◯H\left(z\right)\\ H\left(z\right)◯H\left(x\right)<H\left(z\right)◯H\left(y\right)\end{array}\right.$$

(31)

because if y is a “harder” constraint than x (meaning $H\left(y\right)>H\left(x\right)$), that ranking should not be affected by some other constraint on something else. Associativity

$$\left(H\right(x\left)◯H\right(y\left)\right)◯H\left(z\right)=H\left(x\right)◯\left(H\right(y\left)◯H\right(z\left)\right)$$

(32)

is likewise required and expresses the combination of three constraints. It would also be natural to assume commutativity, $H\left(x\right)◯H\left(y\right)=H\left(y\right)◯H\left(x\right)$, but that is not necessary because we already recognize Equations 30–32 as our axioms 0, 1, 2. Hence, using Appendix A again, there exists a “$◯$ = +” grade on which H is additive.

$$H\left(\mathbf{m}\right)=\sum _{\mathrm{atoms}i}{H}_i\left(m_i\right)$$

(33)

We have now justified additivity, thus filling a gap in traditional accounts of the calculus of variations.

Under perturbation, the minimization requirement is

$$\delta H\left(\mathbf{m}\right)\ge 0\mathrm{when}\delta f_1\left(\mathbf{m}\right)=\delta f_2\left(\mathbf{m}\right)=\cdots =0$$

(34)

The standard “$\oplus =+$” form of the sum rule happens to be continuous and differentiable, so is applicable to valuation of systems that differ arbitrarily little. We adopt it, and can then justifiably require the variational potential to be valid for arbitrarily small perturbations:

$$dH\left(\mathbf{m}\right)=0\mathrm{when}d{f}_1\left(\mathbf{m}\right)=d{f}_2\left(\mathbf{m}\right)=\cdots =0$$

(35)

This limit Equation 35 is weaker than the original Equation 34 not only because of the restricted context, but also because the nature of the extremum (maximum or minimum or saddle) is lost in the discarded second-order effects. However, it still needs to be satisfied. It also shows that any variational potential must by its nature be differentiable at least once.

One now invents supposedly constant “Lagrange multiplier” coefficients ${\lambda }_1,{\lambda }_2,\cdots$ and considers what appears at first to be the different problem of solving

$$d\left(\phantom{(}H\left(\mathbf{m}\right)-{\lambda }_1{f}_1\left(\mathbf{m}\right)-{\lambda }_2{f}_2\left(\mathbf{m}\right)-\cdots \right)=0\mathrm{under}\mathrm{arbitrary}\mathrm{perturbation}$$

(36)

for $\mathbf{m}$. Clearly, Equation 36 is equivalent to Equation 35 for perturbations that happen to hold the f’s constant ($df=0$). However, the values those f’s take may well be wrong. The trick is to choose the λ’s so that the f’s take their correct constraint values. That being done, Equation 36 solves the variational problem Equation 35.

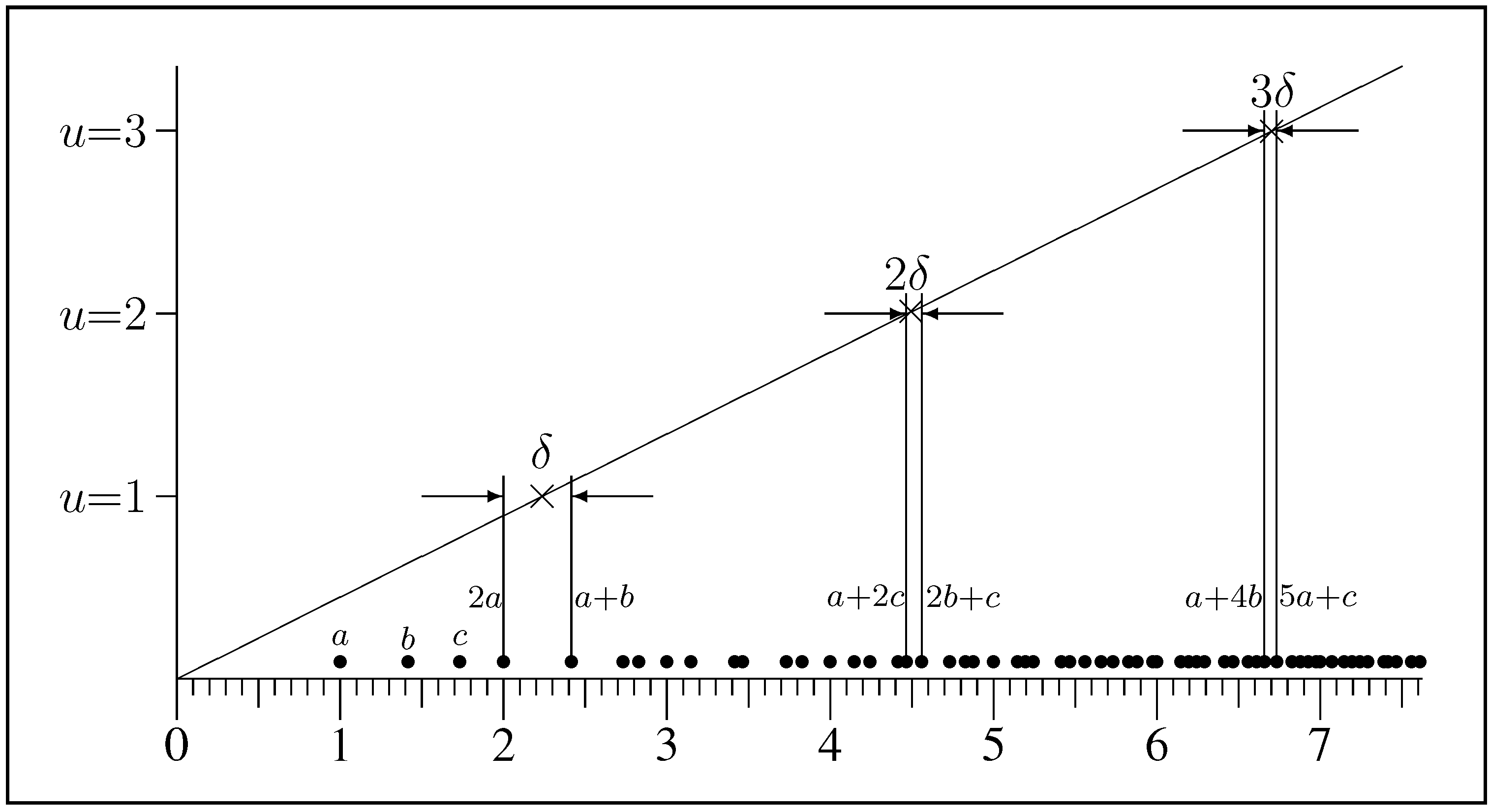
Let the application be two-dimensional, x-by-y, in the sense of applying to values $m(\mathtt{x}\times \mathtt{y})$ of elements on a direct-product lattice. Suppose we have x-dependent constraints that yield $m\left(\mathtt{x}\right)=m_x$ on one factor (say the card suits in Figure 2 above), and similar y-dependent constraints that yield $m\left(\mathtt{y}\right)=m_y$ on the other factor (say music keys in Figure 2). Both factors being thus controlled, their direct-product is implicitly controlled by the those same constraints. Here, we already know the target value $m(\mathtt{x}\times \mathtt{y})=m_x{m}_y$ from the direct-product rule Equation 28. Hence the variational assignment for the particular value $m(\mathtt{x}\times \mathtt{y})$ derives from

$$H_{xy}^{\prime }\left(m_x{m}_y\right)={\lambda }_1{f}_1\left(m_x\right)+{\lambda }_2{f}_2\left(m_y\right)$$

(37)

(where′ indicates derivative). The variational theorem (Appendix C) gives the solution of this functional equation as

$$H_i\left(m_i\right)=A_i+B_i{m}_i+C_i(m_{i}log{m}_i-m_i)$$

(38)

for the individual valuation being considered, where $A_i,B_i,C_i$ are constants. Combining all the atoms yields

$${\displaystyle \boxed{H\left(\mathbf{m}\right)=\sum _{\mathrm{atoms}i}^{}\left(A_i+B_i{m}_i+C_i(m_{i}log{m}_i-m_i)\right)}}$$

(39)

The coefficient $C_i$ represents the intrinsic importance of atom ${\mathtt{a}}_i$ in the summation, but usually the atoms are a priori equivalent so that the C’s take a common value. The scaling of a variational potential is arbitrary (and is absorbed in the Lagrange multipliers), so we may set $C=1$, ensuring that H has a minimum rather than a maximum. Alternatively, $C=-1$ would ensure a maximum. However, the settings of A and B depend on the application.

6.1. Divergence and Distance

One use of H is as a quantifier of the divergence of destination values $\mathbf{w}$ from source values $\mathbf{u}$ that existed before the constraints that led to $\mathbf{w}$ were applied. For this, we set $C=1$ to get a minimum, $B_i=-log{u}_i$ to place the unconstrained minimizing $\mathbf{w}$ at $\mathbf{u}$, and $A_i=u_i$ to make the minimum value zero. This form is

$$\begin{array}{c}\hfill \mathrm{Divergence}:H(\mathbf{w}\mid \mathbf{u})=\sum _{\mathrm{atoms}i}\left(\phantom{(}{u}_i-w_i+w_{i}log(w_i/u_i)\right)\end{array}$$

(40)

This formula is unique: none other has the properties Equations 33,37 that elementary applications require. Equivalently, any different formula would give unjustifiable answers in those applications. Plausibly, H is non-negative, $H(\mathbf{w}\mid \mathbf{u})\ge 0$ with equality if and only if $\mathbf{w}=\mathbf{u}$, so that it usefully quantifies the separation of destination from source.

In general, H obeys neither commutativity nor the triangle inequality, $H(\mathbf{w}\mid \mathbf{u})\ne H(\mathbf{u}\mid \mathbf{w})$ and $H(\mathbf{w}\mid \mathbf{u})\nleqq H(\mathbf{w}\mid \mathbf{v})+H(\mathbf{v}\mid \mathbf{u})$. Hence it cannot be a geometrical “distance”, which is required to have both those properties. In fact, there is no definition of geometrical measure-to-measure distance that obeys the basic symmetries, because H is the only candidate, and it fails.

Here again we see our methodology yielding clear insight. “From–to” can be usefully quantified, but “between” cannot. A space of measures may have connectedness, continuity, even differentiability, but it cannot become a metric space and remain consistent with its foundation.

In the limit of many small values, H admits a continuum limit

$$H(\mathbf{w}\mid \mathbf{u})=\int \left(\phantom{(}u\left(\theta \right)-w\left(\theta \right)+w\left(\theta \right)log\left(w\right(\theta )/u(\theta \left)\right)\right)d\theta$$

(41)

The constraints that force a measure away from the original source may admit several destinations, but minimizing H is the unique rule that defines a defensibly optimal choice. This is the rationale behind maximum entropy data analysis [8].

7. Probability Calculus

In inference, we seek to impose on the hypothesis space a quantified degree of implication $p(\mathtt{x}\mid \mathtt{t})$, to represent the plausibility of predicate $\mathtt{x}$ conditional on current knowledge that excludes all hypotheses outside the stated context $\mathtt{t}$. This is accomplished via a bivaluation, which is a functional that takes a pair of lattice elements to a real number. This bivaluation should depend on both $\mathtt{x}$ (obviously) and $\mathtt{t}$ (otherwise it would be just the measure assigned to $\mathtt{x}$). The natural conjecture is that probability should be identified with a normalized measure, and we proceed to prove this—measures can have arbitrary total but probabilities will (according to standard convention) sum to unity.

At the outset, though, we simply wish to set up a bivaluation for predicate $\mathtt{x}$ within context $\mathtt{t}$.

7.1. Chained Arguments

Within given context $\mathtt{t}$, we require $p(\mathtt{x}\mid \mathtt{t})$ to have the order and associative symmetries #1 and #2 that define a measure. Consequently, p obeys the sum rule

$$p(\mathtt{x}\bigsqcup \mathtt{y}\mid \mathtt{t})=p(\mathtt{x}\mid \mathtt{t})+p(\mathtt{y}\mid \mathtt{t})$$

(42)

for disjoint $\mathtt{x}$ and $\mathtt{y}$ with $\mathtt{x}\bigsqcup \mathtt{y}<\mathtt{t}$. It is the dependence on $\mathtt{t}$ that remains to be determined.

Associativity of chaining (axiom 5) for $\mathtt{a}<\mathtt{b}<\mathtt{c}<\mathtt{d}$ is represented by

$$\left(\underset{p(\alpha ,\beta )}{\underbrace{\underset{p\left(\alpha \right)}{\underbrace{p(\mathtt{a}\mid \mathtt{b})}}\odot \underset{p\left(\beta \right)}{\underbrace{p(\mathtt{b}\mid \mathtt{c})}}}}\right)\odot \underset{p\left(\gamma \right)}{\underbrace{p(\mathtt{c}\mid \mathtt{d})}}=\underset{p\left(\alpha \right)}{\underbrace{p(\mathtt{a}\mid \mathtt{b})}}\odot \left(\underset{p(\beta ,\gamma )}{\underbrace{\underset{p\left(\beta \right)}{\underbrace{p(\mathtt{b}\mid \mathtt{c})}}\odot \underset{p\left(\gamma \right)}{\underbrace{p(\mathtt{c}\mid \mathtt{d})}}}}\right)$$

(43)

We do not have commutativity, $(\alpha ,\beta )=\left[\right[\mathtt{a},\mathtt{b}],[\mathtt{b},\mathtt{c}\left]\right]=[\mathtt{a},\mathtt{c}]$ not being the same as $(\beta ,\alpha )$ (which is meaningless), but we do have associativity and we do have order along the chain. By the associativity theorem, ⊙ exists and there is a scale on which it is simple addition. However, we can not regrade to that scale and discard the original because we have already fixed the grade of p to be additive with respect to its first argument. Instead, we infer additivity on some other grade $\Theta \left(p\right)$

$$\Theta \left(\underset{p\left(\alpha \right)\odot p\left(\beta \right)}{\underbrace{p(\mathtt{a}\mid \mathtt{c})}}\right)=\Theta \left(\underset{p\left(\alpha \right)}{\underbrace{p(\mathtt{a}\mid \mathtt{b})}}\right)+\Theta \left(\underset{p\left(\beta \right)}{\underbrace{p(\mathtt{b}\mid \mathtt{c})}}\right)$$

(44)

required to be consistent with the sum-rule behavior of p. Defining $\Psi ={\Theta }^{-1}$ gives

$$\underset{p\left(\alpha \right)\odot p\left(\beta \right)}{\underbrace{p(\mathtt{a}\mid \mathtt{c})}}=\Psi \left(\Theta \left(\underset{p\left(\alpha \right)}{\underbrace{p(\mathtt{a}\mid \mathtt{b})}}\right)+\Theta \left(\underset{p\left(\beta \right)}{\underbrace{p(\mathtt{b}\mid \mathtt{c})}}\right)\right)$$

(45)

Substituting this in the sum rule Equation 42, term by term, yields the same “product Equation” 25

$$\Psi \left(\zeta \right(\xi ,\eta )+\tau )=\Psi (\xi +\tau )+\Psi (\eta +\tau )$$

(46)

as before, where

$$\xi =\Theta \left(p(\mathtt{x}\mid \mathtt{z})\right),\eta =\Theta \left(p(\mathtt{y}\mid \mathtt{z})\right),\zeta =\Theta \left(p(\mathtt{x}\bigsqcup \mathtt{y}\mid \mathtt{z})\right),\tau =\Theta \left(p(\mathtt{z}\mid \mathtt{t})\right).$$

(47)

Through the sum rule, ζ depends as shown on ξ and η but not τ. The independent variables are $\xi ,\eta ,\tau$.

The solution (Appendix B again) shows Θ to be logarithm, so that ⊙ was multiplication and

$$p(\mathtt{x}\mid \mathtt{z})=p(\mathtt{x}\mid \mathtt{y})p(\mathtt{y}\mid \mathtt{z})/C$$

(48)

in which p (positive by virtue of being a measure on predicates) takes the sign of a universal constant C. Without loss of generality, we assign the scale of p by fixing $C=1$, giving the standard product rule for conditioning.

$$\begin{array}{c}\hfill \mathrm{Chain}-\mathrm{product}\mathrm{rule}:p(\mathtt{x}\mid \mathtt{z})=p(\mathtt{x}\mid \mathtt{y})p(\mathtt{y}\mid \mathtt{z})\end{array}$$

(49)

7.2. Arbitrary Arguments

The chain-product rule, which as written above is valid for any chain, can be generalized to accommodate arbitrary elements. This is accomplished by noting that $\mathtt{x}\wedge \mathtt{y}=\mathtt{x}$ in a chain where $\mathtt{x}<\mathtt{y}$, so that $p(\mathtt{x}\wedge \mathtt{y}\mid \mathtt{y})=p(\mathtt{x}\mid \mathtt{y})$. The general form

$$p(\mathtt{a}\wedge \mathtt{b}\mid \mathtt{c})=p(\mathtt{a}\mid \mathtt{b}\wedge \mathtt{c})p(\mathtt{b}\mid \mathtt{c})$$

(50)

follows by observing that $\mathtt{x}=\mathtt{a}\wedge \mathtt{b}\wedge \mathtt{c}$, $\mathtt{y}=\mathtt{b}\wedge \mathtt{c}$ and $\mathtt{z}=\mathtt{c}$ form a chain and hence are subject to the chain rule.

The special case $p(\mathtt{t}\mid \mathtt{t})=1$ is obtained by setting $\mathtt{y}=\mathtt{z}=\mathtt{t}$ in the chain-product rule. For any $\mathtt{x}\le \mathtt{t}$, ordering requires $p(\mathtt{x}\mid \mathtt{t})\le p(\mathtt{t}\mid \mathtt{t})=1$, so that the range of values is $0\le p\le 1$ and we recognize p as probability, hereafter denoted Pr.

Probability calculus is now proved:

$$\begin{array}{c}\mathrm{Range}\hfill \\ \mathrm{Sum}\mathrm{rule}\hfill \\ \mathrm{Chain}-\mathrm{product}\hfill \end{array}\boxed{{\displaystyle \begin{array}{c}0=Pr(\perp \mid \mathtt{t})<Pr(\mathtt{x}\mid \mathtt{t})\le Pr(\mathtt{t}\mid \mathtt{t})=1\\ Pr(\mathtt{x}\vee \mathtt{y}\mid \mathtt{t})+Pr(\mathtt{x}\wedge \mathtt{y}\mid \mathtt{t})=Pr(\mathtt{x}\mid \mathtt{t})+Pr(\mathtt{y}\mid \mathtt{t})\\ Pr(\mathtt{x}\wedge \mathtt{y}\mid \mathtt{t})=Pr(\mathtt{x}\mid \mathtt{y}\wedge \mathtt{t})Pr(\mathtt{y}\mid \mathtt{t})\end{array}}}$$

The top element of the current lattice, $\mathtt{t}$, is the (provisional) truth, often written ⊤.

From the commutativity $Pr(\mathtt{x}\wedge \mathtt{y}\mid \mathtt{t})=Pr(\mathtt{y}\wedge \mathtt{x}\mid \mathtt{t})$ associated with ∧, we obtain Bayes’ Theorem

$$Pr(\mathtt{x}\mid \theta \wedge \mathtt{t})Pr(\theta \mid \mathtt{t})=Pr(\theta \mid \mathtt{x}\wedge \mathtt{t})Pr(\mathtt{x}\mid \mathtt{t})$$

(51)

which can be simplified by making the common context implicit and writing

$$\underset{\mathrm{Likelihood}}{\underbrace{Pr(\mathtt{x}\mid \theta )}}\underset{\mathrm{Prior}}{\underbrace{Pr\left(\theta \right)}}=\underset{\mathrm{Posterior}}{\underbrace{Pr(\theta \mid \mathtt{x})}}\underset{\mathrm{Evidence}}{\underbrace{Pr\left(\mathtt{x}\right)}}\parallel \mathtt{t}$$

(52)

to relate data $\mathtt{x}$ and parameter θ (with context $\mathtt{t}$ understood). Do not misinterpret the abbreviated notation. Probability is always and necessarily, by construction, a bivaluation that assigns a real number to a pair of elements in a Boolean lattice. In addition, one does not need to differentiate between likelihood, prior, posterior, and evidence by giving each one a different notation. The terms that comprise Bayes’ Theorem represent the same bivaluation applied to different pairs of elements.

7.3. Probability as a Ratio

The equations of probability calculus (range, sum rule, and chain-product rule) can all be subsumed in the single expression

$$Pr(\mathtt{x}\mid \mathtt{t})=\frac{m(\mathtt{x}\wedge \mathtt{t})}{m\left(\mathtt{t}\right)}\forall \mathtt{x},\forall \mathtt{t}\ne \perp$$

(53)

for probability as a ratio of measures. Thus the calculus of probability is nothing more than the elementary calculus of proportions of measure. As anticipated, within its context $\mathtt{t}$, a probability distribution is simply the shape of the confined measure, automatically normalized to unit mass.

This is, essentially, the original discredited frequentist definition (see [9]) of probability, as the ratio of number of successes to number of trials. However, it is here retrieved at an abstract level, which bypasses the catastrophic difficulties of literal frequentism when faced with isolated non-reproducible situations. Just as ordinary addition is forced for measures in $[0,\infty )$, so ordinary proportions in $[0,1]$ are forced for probability calculus.

Whereas the sum rule for measure and probability generalizes to the inclusion/exclusion form for general elements which need not be disjoint, so does the ratio form of probability allow generalization from intervals [3] to generalized intervals, consisting of arbitrary pairs $[\mathtt{x},\mathtt{t}]$ which need not be in a chain. The bivaluation form Equation 53 still holds but now represents a general degree of implication between arbitrary elements.

8. Information and Entropy

Here, we take special cases of the variational potential H, appropriate for probability distributions instead of arbitrary measures.

8.1. Information

Within a given context, probability is a measure, normalized to unit mass. The divergence H of destination probability $\mathbf{p}$ from source probability $\mathbf{q}$ then simplifies to

$$\begin{array}{c}\hfill \mathrm{Information}:\boxed{{\displaystyle H(\mathbf{p}\mid \mathbf{q})=\sum _k^{}{p}_{k}log\frac{p_k}{q_k}}}\end{array}$$

In statistics, this is known as the Kullback–Leibler formula [10].

If the final destination is a fully determined state, with a single p equal to 1 while all the others are necessarily 0, then we have the extreme case

$$H(\mathbf{p}\mid \mathbf{q})=-log{q}_k\mathrm{when}{p}_k=1.$$

(55)

This represents the information gained on acquiring the knowledge that the specific k was true—equivalently the surprise at finding k instead of any available alternative. Generally, H is the amount of compression (logarithmically, with respect to the source) induced by the constraints that modulate source into destination.

In the limit of many small values, H admits a continuum limit

$$H(\mathbf{p}\mid \mathbf{q})=\int p\left(x\right)log\frac{p\left(x\right)}{q\left(x\right)}dx$$

(56)

sometimes (with a minus sign) known as the cross-entropy.

8.2. Entropy

The variational potential

$$H\left(\mathbf{p}\right)=\sum _k\left(A_k+B_k{p}_k+C(p_{k}log{p}_k-p_k)\right)$$

(57)

can also quantify uncertainty. For this, we require zero uncertainty when one probability value equals to 1 (definitely present) and all the others are necessarily 0 (definitely not present). This is accomplished by setting $A_k=0$ and $B_k=C$. Setting $C=-1$ gives the conventional scale, and yields

$$\begin{array}{c}\hfill \mathtt{Entropy}:{\displaystyle \boxed{S\left(\mathbf{p}\right)=-\sum _k^{}{p}_{k}log{p}_k}}\end{array}$$

(58)

We call this “entropy”, and give it a separate symbol S as well as a separate name, to distinguish it from the previous “information” special case of divergence.

Entropy happens to be the expectation value of the information gained by deciding on one particular cell instead of any of the others in a partition.

$$S\left(\mathbf{p}\right)={〈-log{p}_k〉}_k$$

(59)

It is a function of the partitioning as well as the probability distribution, which is why it does not have a continuum limit. Plausibly, entropy has the following three properties:

• S is a continuous function of its arguments.
• If there are n equal choices, so that $p_k=1/n$, then S is monotonically increasing in n.
• If a choice is broken down into subsidiary choices, then
  S adds according to probabilistic expectation, meaning
  $S(p_1,p_2,p_3)=S(p_1,p_2+p_3)+(p_2+p_3)S(p_2,p_3)$.

These are the three properties from which Shannon [11] originally proved the entropy formula. Here, we see that those properties, like that formula, are inevitable consequences of seeking a variational quantity for probabilities.

Information and entropy are near synonyms, and are often used interchangeably. As seen here, though, entropy S is different from H. It is a property of just one partitioned probability distribution, it has a maximum not a minimum, and it does not have a continuum limit. Its least value, attained when a single probability is 1 and all the others are 0, is zero. Its value generally diverges upwards as the partitioning deepens, whereas H usually tends towards a continuum limit.

9. Conclusions

9.1. Summary

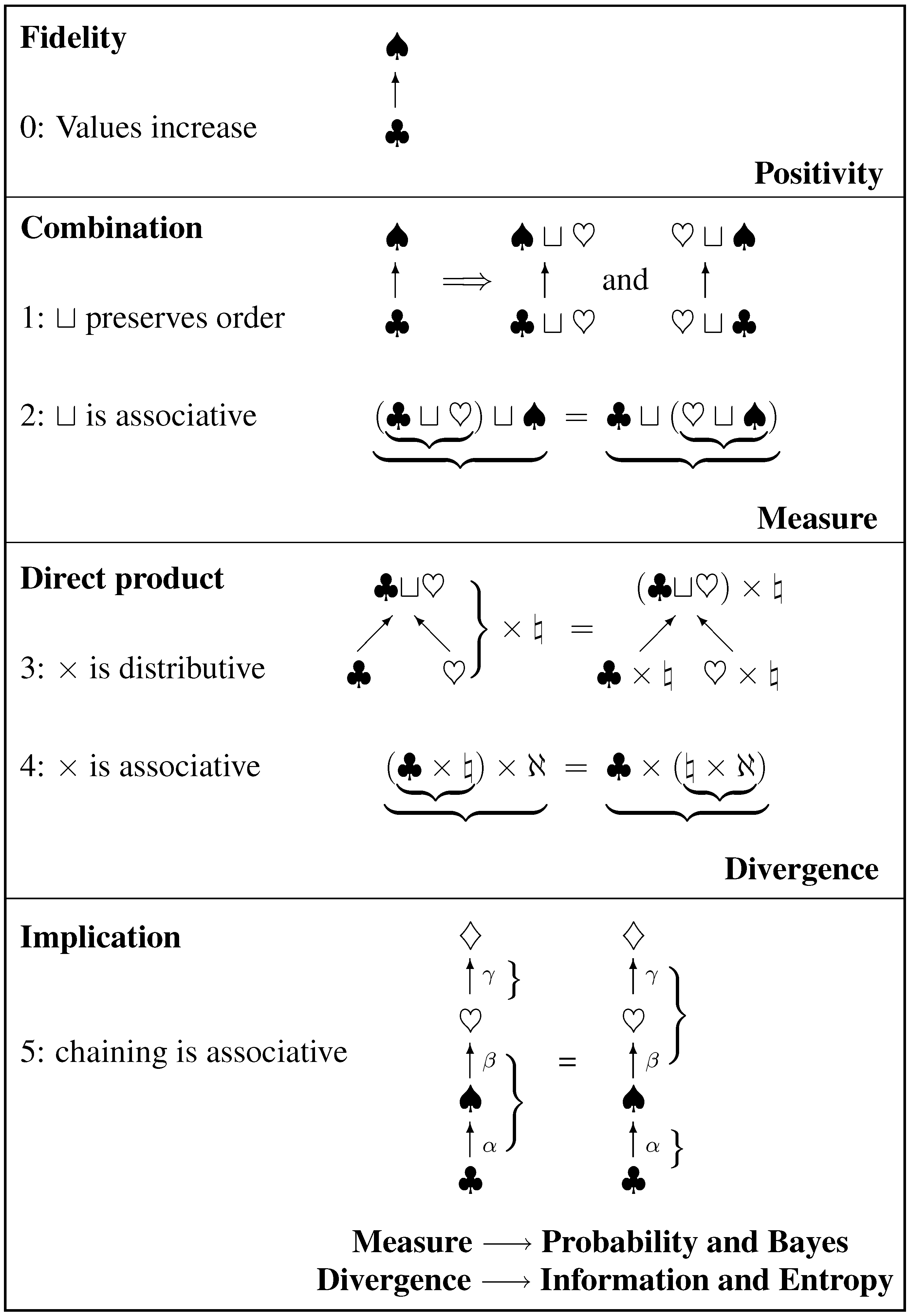
We start with a set $\{{\mathtt{a}}_1,{\mathtt{a}}_2,{\mathtt{a}}_3,\cdots ,{\mathtt{a}}_N\}$ of “atomic” elements which in inference represent the most fundamental exclusive statements we can make about the states (of our model) of the world. Atoms combine to form a Boolean lattice which in inference is called the hypothesis space of statements. This structure has rich symmetry, but other applications may have less and we have selected only what we needed, so that our results apply more widely and to distributive lattices in particular. The minimal assumptions are so simple that they can be drawn as the cartoon below (Figure 4).

Axiom 1 represents the order property that is required of the combination operator ⊔. Axiom 2 says that valuation must conform to the associativity of ⊔. These axioms are compelling in inference. By the associativity theorem (Appendix A — see the latter part for a proof of minimality) they require the valuation to be a measure $m\left(\mathtt{x}\right)$, with ⊔ represented by addition (the sum rule). Any 1:1 regrading is allowed, but such change alters no content so that the standard linearity can be adopted by convention. This is the rationale behind measure theory.

The direct product operator × that represents independence is distributive (axiom 3) and associative (axiom 4), and consequently independent measures multiply (the direct-product rule). There is then a unique form of variational potential for assigning measures under constraints, yielding a unique divergence of one measure from another.

Probability $Pr(x\mid t)$ is to be a bivaluation, automatically a measure over predicate $\mathtt{x}$ within any specified context $\mathtt{t}$. Axiom 5 expresses associativity of ordering relations (in inference, implications) and leads to the chain-product rule which completes probability calculus. The variational potential defines the information (Kullback–Leibler) carried by a destination probability relative to its source, and also yields the Shannon entropy of a partitioned probability distribution.

9.2. Commentary

We have presented a foundation for inference that unites and significantly extends the approaches of Kolmogorov [2] and Cox [1], yielding not just probability calculus, but also the unique quantification of divergence and information. Our approach is based on quantifying finite lattices of logical statements in such a way that quantification satisfies minimal required symmetries. This generalizes algebraic implication, or equivalently subset inclusion, to a calculus of degrees of implication. It is remarkable that the calculus is unique.

Our derivations have relied on a set of explicit axioms based on simple symmetries. In particular, we have made no use of negation (NOT), which in applications other than inference may well not be present. Neither have we assumed any additive or multiplicative behavior (as did Kolmogorov [2], de Finetti [12], and Dupré & Tipler [13]). On the contrary, we find that sum and product rules follow from elementary symmetry alone.

Figure 4. Cartoon graphic of the symmetries invoked, and where they lead. Ordering is drawn as upward arrows.

Figure 4. Cartoon graphic of the symmetries invoked, and where they lead. Ordering is drawn as upward arrows.

We find that associativity and order provide minimal assumptions that are convincing and compelling for scalar additivity in all its applications. Associativity alone does not force additivity, but associativity with order does. Positivity was not assumed, though it holds for all applications in this paper.

Commutativity was not assumed either, though commutativity of the resulting measure follows as a property of additivity. Associativity and commutativity do not quite force additivity because they allow degenerate solutions such as $a\oplus b=max(a,b)$. To eliminate these, strict order is required in some form, and if order is assumed then commutativity does not need to be. Hence scalar additivity rests on ordered sequences rather than the disordered sets for which commutativity would be axiomatic.

$$\begin{array}{ccccc}\mathrm{Associativity}+\mathrm{Order}\hfill & ⟹& \mathrm{Additivity}\mathrm{allowed}\hfill & ⟹\hfill & \mathrm{Commutativity}\hfill \\ \mathrm{Associativity}\mathrm{alone}\hfill & \nRightarrow & \mathrm{Additivity}\mathrm{allowed}\hfill & & \\ \mathrm{Associativity}+\mathrm{Commutativity}\hfill & \nRightarrow & \mathrm{Additivity}\mathrm{allowed}\hfill & \end{array}$$

Aczél [14] assumes order in the form of reducibility, and he too derives commutativity. However, his analysis assumes the continuum limit already attained, which requires him to assume continuity.

$$\begin{array}{ccccc}\mathrm{Associativity}+\mathrm{Order}+\mathrm{Continuity}\hfill & ⟹& \mathrm{Additivity}\mathrm{allowed}\hfill & ⟹\hfill & \mathrm{Commutativity}\hfill \end{array}$$

Our constructivist approach uses a finite environment in which continuity does not apply, and proceeds directly to additivity. Here, continuity and differentiability are merely emergent properties of + as the continuum limit is approached by allowing arbitrarily many atoms of different type.

Yet there can be no requirement of continuity, which is merely a convenient convention. For example, re-grading could take the binary representations of standard arguments ($101.{011}_2$ representing $5\frac{3}{8}$) and interpret them in base-3 ternary (with $101.{011}_3$ representing $10\frac{4}{27}$), so that $\Theta \left(10\frac{4}{27}\right)=5\frac{3}{8}$. Valuation becomes discontinuous everywhere, but the sum rule still works, albeit less conveniently. Indeed, no finite system can ever demonstrate the infinitesimal discrimination that defines continuity, so continuity cannot possibly be a requirement of practical inference.

At the cost of lengthening the proofs in the appendices, we have avoided assuming continuity or differentiability. Yet we remark that such infinitesimal properties ought not influence the calculus of inference. If they did, those infinitesimal properties would thereby have observable effects. But detecting whether or not a system is continuous at the infinitesimal scale would require infinite information, which is never available. So assuming continuity and differentiability, had that been demanded by the technicalities of mathematical proof (or by our own professional inadequacy), would in our view have been harmless. As it happens, each appendix touches on continuity, but the arguments are appropriately constructed to avoid the assumption, so any potential controversy over infinite sets and the rôle of the continuum disappears.

Other than reversible regrading, any deviation from the standard formulas must inevitably contradict the elementary symmetries that underlie them, so that popular but weaker justifications (e.g., de Finetti [12]) in terms of decisions, loss functions, or monetary exchange can be discarded as unnecessary. In fact, the logic is the other way round: such applications must be cast in terms of the unique calculus of measure and probability if they are to be quantified rationally. Indeed, we hold generally that it is a tactical error to buttress a strong argument (like symmetry) with a weak argument (like betting, say). Doing that merely encourages a skeptic to sow confusion by negating the weak argument, thereby casting doubt on the main thesis through an illogical impression that the strong argument might have been circumvented too.

Finally, the approach from basic symmetry is productive. Goyal and ourselves [15] have used just that approach to show why quantum theory is forced to use complex arithmetic. Long a deep mystery, the sum and product rules of complex arithmetic are now seen as inevitably necessary to describe the basic interactions of physics. Elementary symmetry thus brings measure, probability, information and fundamental physics together in a remarkably unified synergy.