Introduction to the Yang-Baxter Equation with Open Problems
Abstract
:1. Introduction
2. Preliminaries
 is a solution of the Yang-Baxter equation (sometimes called the braid relation), if the equality
is a solution of the Yang-Baxter equation (sometimes called the braid relation), if the equality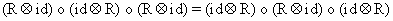 (1)
(1)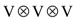 .
.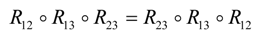 (2)
(2) . Then R satisfies (1) if and only if R ο T satisfies (2) if and only if T ο R satisfies (2).
. Then R satisfies (1) if and only if R ο T satisfies (2) if and only if T ο R satisfies (2).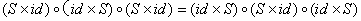 (3)
(3)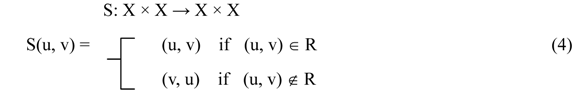
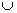 Rop is an equivalence relation on X and the complement relation of R is a strict partial order on each class of R
Rop is an equivalence relation on X and the complement relation of R is a strict partial order on each class of R 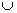 Rop (where Rop is the opposite relation of R).
Rop (where Rop is the opposite relation of R).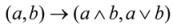 is a solution for the set-theoretical Yang-Baxter equation.
is a solution for the set-theoretical Yang-Baxter equation.3. Main Results and Discussion
 k-{0}. We define the k-linear map
k-{0}. We define the k-linear map .
. such that
such that 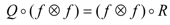 .
.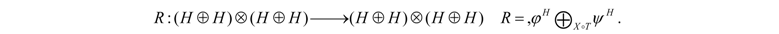
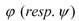 are non-isomorphic operators. It follows that for non-isomorphic Hopf algebras we obtain non-isomorphic YB operators.
are non-isomorphic operators. It follows that for non-isomorphic Hopf algebras we obtain non-isomorphic YB operators.4. Conclusions and Directions for Future Research
Acknowledgments
References and Notes
- Yang, C.N. Some exact results for the many-body problem in one dimension with repulsive delta-function interaction. Phys. Rev. Lett. 1967, 19, 1312–1315. [Google Scholar]
- Baxter, R.J. Partition function for the eight-vertex lattice model. Ann. Phys. 1972, 70, 193–228. [Google Scholar]
- Baxter, R.J. Exactly Solved Models in Statistical Mechanics; Academic Press: London, UK, 1982. [Google Scholar]
- Caenepeel, S.; Militaru, G.; Zhu, S. Frobenius and separable functors for generalized Hopf modules and Nonlinear equations. In Lecture Notes in Mathematics 1787; Springer: Berlin, Germany, 2002. [Google Scholar]
- Gateva-Ivanova, T. A combinatorial approach to the set-theoretical solutions of the Yang-Baxter equation. J. Math. Phys. 2004, 45, 3828–3859. [Google Scholar]
- Kassel, C. Quantum groups. In Graduate Texts in Mathematics; Springer Verlag: Berlin, Germany, 1995. [Google Scholar]
- Lambe, L.; Radford, D. Introduction to the quantum Yang-Baxter equation and quantum groups: An algebraic approach. In Mathematics and Its Applications 423; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1997. [Google Scholar]
- Nichita, F.F. Non-Linear Equations, Quantum Groups, and Duality Theorems; VDM Verlag: Saarbrücken, Germany, 2009. [Google Scholar]
- Drinfeld, V.G. On some unsolved problems in quantum group theory. In Quantum Groups, Lecture Notes in Mathematics; Kulish, P.P., Ed.; Springer-Verlag: Berlin, Germany, 1992; Volume 1510, pp. 1–8. [Google Scholar]
- Hobby, D.; Nichita, F.F. Solutions of the set-theoretical Yang-Baxter equation derived from relations. Acta Universitatis Apulensis 2012, in press.. [Google Scholar]
- Dascalescu, S.; Nichita, F.F. Yang-Baxter operators arising from (co)algebra structures. Commun. Algebra 1999, 27, 5833–5845. [Google Scholar]
- Brzezinski, T.; Nichita, F.F. Yang-baxter systems and entwining structures. Commun. Algebra 2005, 33, 1083–1093. [Google Scholar]
- Turaev, V. The Yang-Baxter equation and invariants of links. Invent. Math. 1988, 92, 527–553. [Google Scholar]
- Massuyeau, G.; Nichita, F.F. Yang-Baxter operators arising from algebra structures and the Alexander polynomial of knots. Commun. Algebra 2005, 33, 2375–2385. [Google Scholar]
- Nichita, F.F.; Parashar, D. Spectral-parameter dependent Yang-Baxter operators and Yang-Baxter systems from algebra structures. Commun. Algebra 2006, 34, 2713–2726. [Google Scholar]
- Andruskiewitsch, N.; Schneider, H.J. Lifting of quantum linear spaces and pointed Hopf algebras of order p3. J. Algebra 1998, 209, 658–691. [Google Scholar]
- Beattie, M.; Dascalescu, S.; Grünenfelder, L. On the number of types of finite dimensional Hopf algebras. Invent. Math. 1999, 136, 1–7. [Google Scholar]
- Gelaki, S. Pointed Hopf algebras and Kaplansky’s 10-th conjecture. J. Algebra 1998, 209, 635–657. [Google Scholar]
- Nichita, F.F. Self-inverse Yang-Baxter operators from (co)algebra structures. J. Algebra 1999, 218, 738–759. [Google Scholar]
- Hlavaty, L.; Snobl, L. Solutions of a Yang-Baxter system. Available online: http://arxiv.org/pdf/math/9811016.pdf (accessed on 24 April 2012). 1998, arXiv:math.QA/9811016v2. arXiv.org e-Print archive..
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Nichita, F. Introduction to the Yang-Baxter Equation with Open Problems. Axioms 2012, 1, 33-37. https://doi.org/10.3390/axioms1010033
Nichita F. Introduction to the Yang-Baxter Equation with Open Problems. Axioms. 2012; 1(1):33-37. https://doi.org/10.3390/axioms1010033
Chicago/Turabian StyleNichita, Florin. 2012. "Introduction to the Yang-Baxter Equation with Open Problems" Axioms 1, no. 1: 33-37. https://doi.org/10.3390/axioms1010033
APA StyleNichita, F. (2012). Introduction to the Yang-Baxter Equation with Open Problems. Axioms, 1(1), 33-37. https://doi.org/10.3390/axioms1010033



