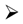Gradings, Braidings, Representations, Paraparticles: Some Open Problems
Abstract
:1. Introduction
1.1. Structure of the Paper
2. The Algebras, in Terms of Generators and Relations
3. Braided Group, Ordinary Hopf and -Lie Structures for the Mixed Paraparticle Algebras: An Attempt at Classification
3.1. Historical and Conceptual Introduction—Literature Review
- 1.
- is a -graded algebra (the term superalgebra appears often in physics literature when ) in the sense that and for any .
- 2.
- is a (left) -module algebra.
- 3.
- is a (right) -comodule algebra.
- 4.
- is an algebra in the Category of representations (modules) of the group Hopf algebra .
- 5.
- is an algebra in the Category of corepresentations (comodules) of the group Hopf algebra .
- 1.
- is a -graded coalgebra (the term supercoalgebra seems also appropriate when ) in the sense that for any and for all . ( and are assumed to be the comultiplication and the counity respectively).
- 2.
- is a (left) -module coalgebra.
- 3.
- is a (right) -comodule coalgebra.
- 4.
- is a coalgebra in the Category of representations (modules) of the group Hopf algebra .
- 5.
- is a coalgebra in the Category of corepresentations (comodules) of the group Hopf algebra .

- 1.
- is a -graded, -braided Hopf algebra or a -Hopf algebra.
- 2.
- is a Hopf algebra in the braided Monoidal Category of representations of .
- 3.
- is a braided group for which the braiding is given by the function .
- 4.
- is simultaneously an algebra, a coalgebra and a -module, all its structure functions (multiplication, comultiplication, unity, counity and antipode) are -module morphisms. The comultiplication and the counity are algebra morphisms in the braided monoidal Category . ( stands for the braided tensor product algebra). At the same time, the antipode is a “twisted” or “braided” anti-homomorphism in the sense that for any homogeneous .
- 5.
- The -module is an algebra in (equiv.: a -module algebra) and a coalgebra in (equiv.: a -module coalgebra), the comultiplication and the counity are algebra morphisms in the braided monoidal Category and at the same time, the antipode is an algebra anti-homomorphism in the braided monoidal Category .
3.2. Description of the Problem–Research Objectives
- Given the ()-grading described in [14,15,34,35] we intend to check whether it is compatible with other commutation factors (i.e.,: other braidings for the Category of modules) than the one presented in these works. In other words, we are going to determine possible alternative braided group structures, corresponding to the single ()-graded structure for PBF described in the above works. It will also be interesting to examine, which of these alternatives—if any—are directly associated to some particular color-graded Lie structure (directly in the sense that they may stem from the UEA).
- We are going to determine possible alternative -gradings for the PBF, PFB (co)algebras where the group may either be itself (with some grading inequivalent to the previous, in the sense formerly described) or some other suitable group, for ex. or . In each case, we will further investigate the possible braidings (in the sense analyzed in the former paragraph).
- We are going to collect the results of the previous two steps and develop Theorems and Propositions which establish the possible braided group structures of PBF and PFB independently of the possible color-graded Lie structures. For each of the above cases, we intend to explicitly compute: (a) The group action (i.e., the grading); (b) The braiding (i.e., the family of isomorphisms), the commutation factor (i.e., the bicharacter or equiv: the color function), (c) The (quasi)triangular structure (i.e., the -matrix) of the corresponding group Hopf algebra.
4. An Attempt to Approach the Fock-like Representations for the Algebras Utilizing Their Braided Group Structures
4.1. Conceptual Introduction–Methodological Review
-
- regarding (the usual Weyl algebra or: boson algebra) as a superalgebra with odd generators, and proving that it is isomorphic (as an assoc. superalgebra) to a quotient superalgebra of PB,
-
- constructing the graded tensor product representations, of (graded) tensor powers of the form (-copies),
-
- pulling back the module structure to a representation of PB through suitable (homogeneous) homomorphisms of the form , which are constructed via the braided comultiplication of PB (see [103]),
-
- prove that the -modules thus obtained, are isomorphic (as -modules) to -graded tensor product modules, between -copies, of the first () Fock-like representation of ,
-
- prove that the parabosonic -Fock-like module, corresponding to arbitrary value of the positive integer , is contained as an irreducible direct summand of the above constructed -graded tensor product representation,
-
- compute explicitly the action of the PB generators and the corresponding matrix elements, on the above mentioned -Fock-like modules and finally,
-
- decompose the obtained -graded tensor product representations into irreducible components and investigate whether more irreducible summands arise, non-isomorphic to the -Fock-like submodule.
4.2. Description of the Problem–Research Objectives
- We first intend to proceed to the explicit construction of the Fock-like representations in the case of the (inf. deg. of freedom) parabosonic PB and parafermionic PF algebra following the methodology developed in [103] and outlined above. Starting from the parabosonic algebra, this involves computations of expressions of the following formwhere: , denotes the action, the -fold tensor product of the bosonic ground state, the CCR generator lies in the -th entry of the tensor product and there are a finite only number of non-zero exponents in the above product. The mathematical problem here, which is necessary to be solved in order to explicitly perform the computation is the development of a suitable multinomial theorem in the anticommuting variables . The corresponding problem appears to be easier for the case of PF, since the corresponding variables ( is the CAR generator) appear to be commuting (the exact choice of the braiding and the grading depends of course on the results of the previous part of the project). What we are actually describing here, are the steps for the explicit calculation of the action of the generators on the tensor product representations of—suitably—graded versions of CCR and CAR and the subsequent decomposition of these representations in irreducible components. In [103] we have proved that the -Fock-like modules are contained as irreducible factors of such graded, tensor product representations. However, it remains to see whether such decompositions can produce as direct summands or more generally as submodules other non-equivalent representations as well.

- Next, we intend to compare our obtained (according to the above described method) results with those obtained in [6,7,8] (where a totally different approach, based on induced representations and chains of inclusions of Lie superalgebras contained as subalgebras, has been adopted). It is expected that the identification of the representations may lead us to valuable insight, relative to the interrelations between the various, diversified analytical tools used.
- The next step will consist of generalizing the above calculations for the case of the mixed paraparticle algebras PBF and PFB. The philosophy of the method is based on the same idea: The Fock-like representations of PBF and PFB will be extracted as irreducible submodules arising in the decomposition of the graded tensor product representations of and . In this case, is a mixture of commuting (symmetric mixture) bosons and fermions and a mixture of anticommuting (antisymmetric mixture) of bosonic and fermionic generators (see also [54] § 6.2 pp. 199–207, [31] for more details on the structure of these algebras). Just as the CCR may be considered a graded quotient algebra of PB (see [103]) , and the CAR a graded quotient algebra of PF, in the same spirit we will consider as a suitable graded quotient of PBF and as a graded quotient of PFB. These are exactly the algebras we intend to employ, in order to generalize the formerly described method for the case of the mixed paraparticle algebras PBF (Relative Parabose Set algebra) and PFB (Relative Parafermi Set algebra). The results of the previous part of the project (i.e., Section 3.) are expected to lead us in suitable choices for the grading and the braiding of and (in the same manner that the results of [69,70,71] led us to the use of odd-bosons in [103]). Finally it is worth mentioning, that the computational problem we expect to reveal here is the development of a suitable multinomial theorem mixing commuting and anticommuting variables.
5. A Proposal for the Development of an Algebraic Model for the Description of the Interaction between Monochromatic Radiation and a Multiple Level System
5.1. Review of Recent Work
5.2. Description of the Problem–Research Objectives
6. Conclusions
Acknowledgments
References
- Green, H.S. A generalized method of field quantization. Phys. Rev. 1953, 90, 2, 270–273. [Google Scholar]
- Volkov, D.V. On the quantization of half-integer spin fields. Sov. Phys.-JETP 1959, 9, 1107–1111. [Google Scholar]
- Volkov, D.V. S-matrix in the generalized quantization method. Sov. Phys.-JETP 1960, 11, 375–378. [Google Scholar]
- Wigner, E.P. Do the equations of motion determine the quantum mechanical commutation relations? Phys. Rev. 1950, 77, 5, 711–712. [Google Scholar]
- Greenberg, O.W.; Messiah, A.M.L. Selection rules for Parafields and the absence of Paraparticles in nature. Phys. Rev. 1965, 138, 1155–1167. [Google Scholar] [CrossRef]
- Lievens, S.; Stoilova, N.I.; Van der Jeugt, J. The paraboson Fock space and unitary irreducible representations of the Lie superalgebra osp(1/2n). Commun. Math. Phys. 2008, 281, 805–826. [Google Scholar] [CrossRef]
- Stoilova, N.I.; Van der Jeugt, J. The parafermion Fock space and explicit so(2n+1) representations. J. Phys. Math. Gen. 2008, 41, 075202:1–075202:13. [Google Scholar] [CrossRef]
- Stoilova, N.I.; Van der Jeugt, J. Parafermions, parabosons and representations of so(∞) and osp(1/∞). Int. J. Math. 2009, 20, 693–715. [Google Scholar] [CrossRef]
- Ganchev, A.C.; Palev, T.D. A lie superalgebraic interpretation of the Parabose statistics. J. Math. Phys. 1980, 21, 797–799. [Google Scholar] [CrossRef]
- Ryan, C.; Sudarshan, E.C.G. Representations of Parafermi rings. Nucl. Phys. 1963, 47, 207–211. [Google Scholar] [CrossRef]
- Kamefuchi, S.; Takahashi, Y. A generalization of field quantization and statistics. Nucl. Phys. 1962, 36, 177–206. [Google Scholar] [CrossRef]
- Palev, T.D. Parabose and Parafermi operators as generators of orthosymplectic Lie superalgebras. J. Math. Phys. 1982, 23, 1100–1102. [Google Scholar] [CrossRef]
- Palev, T.D. A description of the superalgebra osp(2n+1/2m) via Green generators. J. Phys. Math. Gen. 1996, 29, L171–L176. [Google Scholar] [CrossRef]
- Yang, W.; Jing, S. Graded lie algebra generating of parastatistical algebraic structure. Commun. Theor. Phys. 2001, 36, 647–650. [Google Scholar]
- Yang, W.; Jing, S. A new kind of graded Lie algebra and parastatistical supersymmetry. Sci. China (Series A) 2001, 44, 1167–1173. [Google Scholar] [CrossRef]
- Jaynes, E.T.; Cummings, F.W. Comparison of Quantum and semi-classical radiation theories with application to the beamer-maser. Proc. IEEE 1963, 51, 89–109. [Google Scholar] [CrossRef]
- Nicolai, H. Supersymmetry and spin systems. J. Phys. Math. Gen. 1976, 9, 1497–1506. [Google Scholar] [CrossRef]
- Aragone, C.; Zypman, F. Supercoherent states. J. Phys. Math. Gen. 1986, 19, 2267–2279. [Google Scholar] [CrossRef]
- Alvarez-Moraga, N.; Hussin, V. Sh(2/2) superalgebra eigenstates and generalized supercoherent and supersqueezed states. Intern. J. Theor. Phys. 2004, 43, 179–218. [Google Scholar] [CrossRef]
- Fatyga, B.W.; Kostelecky, V.A.; Nieto, M.M.; Truax, D.R. Supercoherent states. Phys. Rev. 1991, 43, 1403–1412. [Google Scholar] [CrossRef]
- Shore, B.W.; Knight, P.L. Topical Review: The Jaynes-Cummings model. J. Mod. Opt. 1993, 40, 1195–1238. [Google Scholar] [CrossRef]
- Buzano, C.; Rasseti, M.G.; Rastelo, M.L. Dynamical superalgebra of the “dressed” Jaynes-Cummings model. Phys. Rev. Lett. 1989, 62, 137–139. [Google Scholar] [CrossRef] [PubMed]
- Floreanini, R.; Spiridonov, V.P.; Vinet, L. Q-Oscillator realizations of the quantum superalgebras slq(m/n) and ospq(m,2n). Comm. Math. Phys. 1991, 137, 149–160. [Google Scholar] [CrossRef]
- Frappat, L.; Sorba, P.; Sciarrino, A. Dictionary on Lie Algebras and Superalgebras; Academic Press: London, UK, 2000. [Google Scholar]
- Liao, L.; Song, X.C. Q-deformation of Lie superalgebras B(m,n), B(0,n), C(1+n) and D(m,n) in their boson-fermion representations. J. Phys. Math. Gen. 1991, 24, 5451–5463. [Google Scholar] [CrossRef]
- Tang, D.S. Formal relations between classical superalgebras and fermion-boson creation and annihilation operators. J. Math. Phys. 1984, 25, 2966–2973. [Google Scholar] [CrossRef]
- Sun, C.P. Boson-fermion realization of indecomposable representations for Lie superalgebras. J. Phys. Math. Gen. 1987, 20, 5823–5829. [Google Scholar] [CrossRef]
- Palev, T.D. Canonical realizations of Lie superalgebras: Ladder representations of the Lie superalgebra A(m,n). J. Math. Phys. 1981, 22, 2127–2131. [Google Scholar] [CrossRef]
- Fu, H.C.; Sun, C.P. New inhomogeneous boson realizations and inhomogeneous differential realizations of Lie algebras. J. Math. Phys. 1990, 31, 2797–2802. [Google Scholar] [CrossRef]
- Fu, H.C. Inhomogeneous differential realization, boson-fermion realization of Lie superalgebras and their indecomposable representations. J. Math. Phys. 1991, 32, 767–775. [Google Scholar] [CrossRef]
- Palev, T.D. A superalgebra Uq[osp(3/2)] generated by deformed paraoperators and its morphism onto a Wq(1/1) Clifford-Weyl algebra. J. Math. Phys. 1993, 34, 4872–4883. [Google Scholar] [CrossRef]
- Ky, N.A.; Palev, T.D.; Stoilova, N.I. Transformations of some induced osp(3/2) modules in an so(3)⊕sp(2) basis. J. Math. Phys. 1992, 33, 1841–1863. [Google Scholar] [CrossRef]
- Biswas, S.N.; Soni, S.K. Supersymmetry, Parastatistics and operator realizations of a Lie algebra. J. Math. Phys. 1988, 29, 16–20. [Google Scholar] [CrossRef]
- Kanakoglou, K.; Daskaloyannis, C.; Herrera-Aguilar, A. Mixed paraparticles, colors, braidings and a new class of realizations for Lie superalgebras. Available online: http://arxiv.org/abs/0912.1070 (accessed on 13 June 2012).
- Kanakoglou, K.; Daskaloyannis, C.; Herrera-Aguilar, A. Super-Hopf realizations of Lie superalgebras: Braided paraparticle extensions of the Jordan-Schwinger map. AIP Conf. Proc. 2010, 1256, 193–200. [Google Scholar]
- Yang, W.; Jing, S. Fock space structure for the simplest parasupersymmetric System. Mod. Phys. Lett. 2001, 16, 963–971. [Google Scholar] [CrossRef]
- Kanakoglou, K.; Herrera-Aguilar, A. Ladder operators, Fock-spaces, irreducibility and group gradings for the Relative Parabose Set algebra. Intern. J. Algebra 2011, 5, 413–428. [Google Scholar]
- Kanakoglou, K.; Herrera-Aguilar, A. Graded Fock-like representations for a system of algebraically interacting paraparticles. J. Phys. Conf. Ser. 2011, 287, 012037:1–012037:4. [Google Scholar] [CrossRef]
- Beckers, J.; Deberg, N. On supersymmetric harmonic oscillators and the Green-Cusson Ansätze. J. Math. Phys. 1991, 32, 3094–3100. [Google Scholar] [CrossRef]
- Beckers, J.; Deberg, N. Parastatistics, supersymmetry and parasupercoherent states. J. Math. Phys. 1990, 31, 1513–1523. [Google Scholar] [CrossRef]
- Beckers, J.; Deberg, N. Parastatistics and supersymmetry in Quantum Mechanics. Nucl. Phys. 1990, 340, 767–776. [Google Scholar] [CrossRef]
- Beckers, J.; Deberg, N. On parasupersymmetric coherent states. Mod. Phys. Lett. 1989, 4, 1209–1215. [Google Scholar] [CrossRef]
- Beckers, J.; Deberg, N. Coherent states in parasupersymmetric Quantum Mechanics. Mod. Phys. Lett. 1989, 4, 2289–2293. [Google Scholar] [CrossRef]
- Rubakov, V.A.; Spiridonov, V.P. Parasupersymmetric Quantum Mechanics. Mod. Phys. Lett. 1988, 3, 1337–1347. [Google Scholar] [CrossRef]
- Milnor, J.; Moore, J. On the structure of Hopf algebras. Ann. Math. 1965, 81, 211–264. [Google Scholar] [CrossRef]
- Kostant, B. Graded Manifolds, Graded Lie Theory and Prequantization. In Differential Geometrical Methods in Mathematical Physics Lecture Notes in Mathematics; Dold, A., Eckman, A., Eds.; Springer: Berlin, Germany, 1975; Volume 570, pp. 177–306. [Google Scholar]
- Montgomery, S. Hopf algebras and their actions on Rings; The NSF-CBMS Regional Conference Series in Mathematics 82; AMS: Providence, RI, USA, 1993; Chapters 4, 10; pp. 40–43, 178–217. [Google Scholar]
- Majid, S. Foundations of Quantum Group Theory; Cambridge University Press: Cambridge, UK, 1995; Chapters 2, 9; pp. 35–68, 414–499. [Google Scholar]
- Majid, S. A Quantum Groups Primer; London Mathematical Society, Lecture Notes Series, 292; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Dascalescu, S.; Nastasescu, C.; Raianu, S. Hopf Algebras, an Introduction; Pure and Applied Mathematics 235; Marcel Dekker: New York, NY, USA, 2001. [Google Scholar]
- Kassel, C. Quantum Groups; Graduate texts in Mathematics 155; Springer: New York, NY, USA, 1995; Chapters III, XIII. [Google Scholar]
- Abe, E. Hopf Algebras; Cambridge University Press: Cambridge, UK, 1980; Chapters 2, 3; pp. 91–92, 137–144. [Google Scholar]
- Sweedler, M.E. Hopf Algebras; W.A. Benjamin, Inc: New York, NY, USA, 1969; Chapter XI; pp. 227–228, 237–238. [Google Scholar]
- Kanakoglou, K. Hopf and Graded Hopf Structures in Parabosonic and Parafermionic Algebras and applications in Physics. Ph.D. Thesis, Aristotle University of Thessaloniki (AUTh), 2009. [Google Scholar]
- Steenrod, N.E. The cohomology algebra of a space. Enseign. Math. 1961, 7, 153–178. [Google Scholar]
- Cohen, M.; Montgomery, S. Group graded rings, smash products and group actions. Trans. Am. Math. Soc. 1984, 282, 237–258. [Google Scholar] [CrossRef]
- Năstăsescu, C.; Torrecillas, B. Graded Coalgebras. Tsukuba J. Math. 1993, 17, 461–479. [Google Scholar]
- Năstăsescu, C.; Torrecillas, A. Clifford Theory for Graded Coalgebras: Applications. J. Algebra 1995, 174, 573–586. [Google Scholar] [CrossRef]
- Dăscălescu, S.; Năstăsescu, C.; Raianu, S.; Van Oystaeyen, F. Graded Coalgebras and Morita-Takeuchi contexts. Tsukuba J. Math. 1995, 20, 395–407. [Google Scholar]
- Dăscălescu, S.; Năstăsescu, C.; Raianu, S. Strongly graded coalgebras and crossed coproducts. In Proceedings Dedicated to A. Orsatti, Lecture notes in Applied Mathematics; Marcel Dekker: New York, NY, USA; Volume 201, pp. 131–141.
- Scheunert, M. Generalized Lie algebras. J. Math. Phys. 1979, 20, 712–720. [Google Scholar] [CrossRef]
- Scheunert, M. Graded tensor calculus. J. Math. Phys. 1983, 24, 2658–2670. [Google Scholar] [CrossRef]
- Scheunert, M. The theory of lie superalgebras. Lect. Notes Math. 1978, 716, 1–270. [Google Scholar]
- Scheunert, M. Universal R-matrices for finite abelian groups—a new look at graded multilinear algebra. Available online: http://arxiv.org/abs/q-alg/9508016 (accessed on 13 June 2012).
- Kang, S.J.; Kwon, J.H. Graded Lie superalgebras, supetrace formula and orbit Lie superalgebras. Proc. Lond. Math. Soc. 2000, 81, 675–724. [Google Scholar] [CrossRef]
- Kang, S.J. Graded Lie Superalgebras and the Superdimension Formula. J. Algebra 1998, 204, 597–655. [Google Scholar] [CrossRef]
- Mikhalev, A.A.; Zolotykh, A.A. Combinatorial Aspects of Lie Superalgebras; CRC Press: Boca Raton, FL, USA, 1995; pp. 7–29. [Google Scholar]
- Majid, S. Quasitriangular Hopf algebras and the Yang-Baxter equation. Intern. J. Mod. Phys. 1990, 5, 1–91. [Google Scholar] [CrossRef]
- Kanakoglou, K.; Daskaloyannis, C. Variants of bosonization in Parabosonic algebra: The Hopf and super-Hopf structures in Parabosonic algebra. J. Phys. Math. Theor. 2008, 41, 105203:1–105203:18. [Google Scholar] [CrossRef]
- Kanakoglou, K.; Daskaloyannis, C. Bosonization and Parastatistics: An Example and an Alternative Approach. In Generalized Lie Theory in Mathematics, Physics and beyond; Silvestrov, S.D., Paal, E., Abramov, V., Stolin, A., Eds.; Springer: Berlin, Germany, 2008; Chapter 18; pp. 207–218. [Google Scholar]
- Kanakoglou, K.; Daskaloyannis, C. Graded Structure and Hopf Structures in Parabosonic Algebra: An Alternative Approach to Bosonization. In New Techniques in Hopf Algebras and Graded Ring Theory; Caenepeel, S., Van Oystaeyen, F., Eds.; Royal Flemish Academy of Belgium (KVAB): Brussels, Belgium, 2007; pp. 105–116. [Google Scholar]
- Majid, S. Cross-products by braided groups and bosonization. J. Algebra 1994, 163, 165–190. [Google Scholar] [CrossRef]
- Khazal, R.; Boboc, C.; Dascalescu, S. Group Gradings of M2(k). Bull. Austral. Math. Soc. 2003, 68, 285–293. [Google Scholar] [CrossRef]
- Boboc, C. Gradings of matrix algebras by the Klein Group. Commun. Algebra 2003, 31, 2311–2326. [Google Scholar] [CrossRef]
- Bahturin, Y.; Zaicev, M. Group gradings on matrix algebras. Canad. Math. Bull. 2002, 45, 499–508. [Google Scholar] [CrossRef]
- Bahturin, Y.; Zaicev, M. Gradings on simple algebras of finitary matrices. J. Algebra 2010, 324, 1279–1289. [Google Scholar] [CrossRef]
- Bahturin, Y.; Zaicev, M. Gradings on simple Lie algebras of type A. J. Lie Theory 2006, 16, 719–742. [Google Scholar]
- Bahturin, Y.; Tvalavadze, M.V. Group gradings on G2. Comm. Algebra 2009, 37, 885–893. [Google Scholar] [CrossRef]
- Bahturin, Y.; Kochetov, M. Group gradings on the Lie algebra psln in positive characteristic. J. Pure Appl. Algebra 2009, 213, 1739–1749. [Google Scholar] [CrossRef]
- Bahturin, Y.; Kochetov, M.; Montgomery, S. Group gradings on simple Lie algebras in positive characteristic. Proc. Amer. Math. Soc. 2009, 137, 1245–1254. [Google Scholar] [CrossRef]
- Bahturin, Y.; Kochetov, M. Classification of group gradings on simple Lie algebras of types A, B, C and D. J. Algebra 2010, 324, 2971–2989. [Google Scholar] [CrossRef]
- Bahturin, Y.; Bresar, M.; Kochetov, M. Group Gradings on finitary simple Lie algebras. Available online: http://arxiv.org/abs/1106.2638 (accessed on 13 June 2012).
- Elduque, A. Fine gradings on simple classical Lie algebras. J. Algebra 2010, 324, 3532–3571. [Google Scholar] [CrossRef]
- Elduque, A.; Kochetov, M. Gradings on the exceptional Lie algebras F4 and G2 revisited. Available online: http://arxiv.org/abs/1009.1218 (accessed on 13 June 2012).
- Elduque, A.; Kochetov, M. Weyl groups of fine gradings on simple Lie algebras of types A, B, C and D. Available online: http://arxiv.org/abs/1109.3540 (accessed on 13 June 2012).
- Draper, C.; Elduque, A.; Martín-González, C. Fine gradings on exceptional Lie superalgebras. Intern. J. Math. 2011, 22, 1823–1855. [Google Scholar] [CrossRef]
- Draper, C. A non computational approach to gradings on f4. Jordan Theory Prepr. Arch. Available online: http://molle.fernuni-hagen.de/~loos/jordan/archive/f4gradings/f4gradings.pdf (accessed on 13 June 2012).
- Draper, C.; Martín-González, C. Gradings on g2. Linear Algebra Appl. 2006, 418, 85–111. [Google Scholar] [CrossRef]
- Draper, C.; Martín-González, C. Gradings on the Albert algebra and on f4. Rev. Mat. Iberoam. 2009, 25, 841–908. [Google Scholar]
- Draper, C.; Viruel, A. Gradings on o (8, ℂ). Linear Algebra Appl. Available online: http://arxiv.org/abs/0709.0194 (accessed on 13 June 2012).
- Patera, J.; Zassenhaus, H. On Lie gradings I. Linear Algebra Appl. 1989, 112, 87–159. [Google Scholar] [CrossRef]
- Havliček, M.; Patera, J.; Pelantová, E. On Lie gradings II. Linear Algebra Appl. 1998, 277, 97–125. [Google Scholar] [CrossRef]
- Havliček, M.; Patera, J.; Pelantová, E. On Lie gradings III. Gradings of the real forms of classical Lie algebras. Linear Algebra Appl. 2000, 314, 1–47. [Google Scholar] [CrossRef]
- Kochetov, M. Gradings on finite dimensional simple Lie algebras. Acta Appl. Math. 2009, 108, 101–127. [Google Scholar] [CrossRef]
- Calderón-Martín, A.J. On the structure of Graded Lie algebras. J. Math. Phys. 2009, 50, 103513:1–103513:8. [Google Scholar] [CrossRef]
- Bahturin, Y.; Shestakov, I.; Zaicev, M. Gradings on simple Jordan and Lie algebras. J. Algebra 2005, 283, 849–868. [Google Scholar] [CrossRef]
- Bahturin, Y.; Sehgal, S.; Zaicev, M. Group gradings on associative algebras. J. Algebra 2001, 241, 677–698. [Google Scholar] [CrossRef]
- Elduque, A. Gradings on octonions. J. Algebra 1998, 207, 342–354. [Google Scholar] [CrossRef]
- Makhsoos, F.; Bashour, M. Z3-Graded Geometric Algebra. Adv. Stud. Theory Phys. 2010, 4, 383–392. [Google Scholar]
- Wakui, M. On the Universal R-matrices of the Dihedral groups. RIMS Kōkyuroku 1998, 1057, 41–53. [Google Scholar]
- Wakui, M. Triangular structures of Hopf Algebras and Tensor Morita Equivalences. Rev. de la Unión Mat. Argent. 2010, 51, 193–200. [Google Scholar]
- Nichita, F.F.; Popovici, B. Yang-Baxter operators from (G,θ) -Lie algebras. Rom. Rep. Phys. 2011, 63, 641–650. [Google Scholar]
- Kanakoglou, K.; Daskaloyannis, C. A braided look at Green ansatz for parabosons. J. Math. Phys. 2007, 48, 113516:1–113516:19. [Google Scholar] [CrossRef]
- Yang, L.M. A note on the Quantum rule of the harmonic oscillator. Phys. Rev. 1951, 84, 788–790. [Google Scholar] [CrossRef]
- Ohnuki, Y.; Kamefuchi, S. On the wave mechanical representation of a bose-like oscillator. J. Math. Phys. 1978, 19, 67–79. [Google Scholar] [CrossRef]
- Sharma, J.K.; Mehta, C.L.; Sudarshan, E.C.G. Parabose coherent states. J. Math. Phys. 1978, 19, 2089–2094. [Google Scholar] [CrossRef]
- Daskaloyannis, C.; Kanakoglou, K.; Tsohantzis, I. Hopf algebraic structure of the Parabosonic and Parafermionic algebras and paraparticle generalizations of the Jordan-Schwinger map. J. Math. Phys. 2000, 41, 652–660. [Google Scholar] [CrossRef]
- Jordan, P. Der Zusammenhang der symmetrischen und linearen Gruppen und das Mehrkörperproblem. Z. Physik 1935, 94, 531. [Google Scholar] [CrossRef]
- Schwinger, J. Selected Papers in Quantum Theory of Angular Momentum; Biedenharn, L.C., Van Dam, H., Eds.; Academic Press: New York, NY, USA, 1965. [Google Scholar]
- Kanakoglou, K.; Herrera-Aguilar, A. On a class of Fock-like representations for Lie Superalgebras. Available online: http://arxiv.org/abs/0709.0194 (accessed on 13 June 2012).
- Palev, T.D. SL(3|N) Wigner quantum oscillators: Examples of ferromagnetic-like oscillators with noncommutative, square-commutative geometry. Available online: http://arxiv.org/abs/hep-th/0601201 (accessed on 13 June 2012).
Appendix: Sketch of the Proof of Proposition 3.2
- a.
- is a right -comodule (with the coaction denoted by ).
- b.
- Its structure maps i.e., the comultiplication and the counity , are H-comodule morphisms.

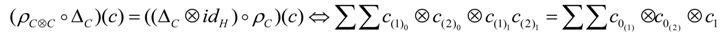
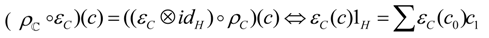
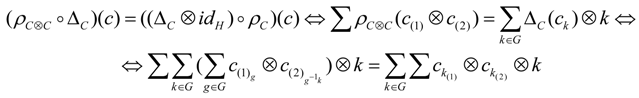
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Kanakoglou, K. Gradings, Braidings, Representations, Paraparticles: Some Open Problems. Axioms 2012, 1, 74-98. https://doi.org/10.3390/axioms1010074
Kanakoglou K. Gradings, Braidings, Representations, Paraparticles: Some Open Problems. Axioms. 2012; 1(1):74-98. https://doi.org/10.3390/axioms1010074
Chicago/Turabian StyleKanakoglou, Konstantinos. 2012. "Gradings, Braidings, Representations, Paraparticles: Some Open Problems" Axioms 1, no. 1: 74-98. https://doi.org/10.3390/axioms1010074
APA StyleKanakoglou, K. (2012). Gradings, Braidings, Representations, Paraparticles: Some Open Problems. Axioms, 1(1), 74-98. https://doi.org/10.3390/axioms1010074