Integrating Geological Domains into Machine Learning for Ore Grade Prediction: A Case Study from a Porphyry Copper Deposit
Abstract
1. Introduction
2. Proposed Workflow
3. Theoretical Background
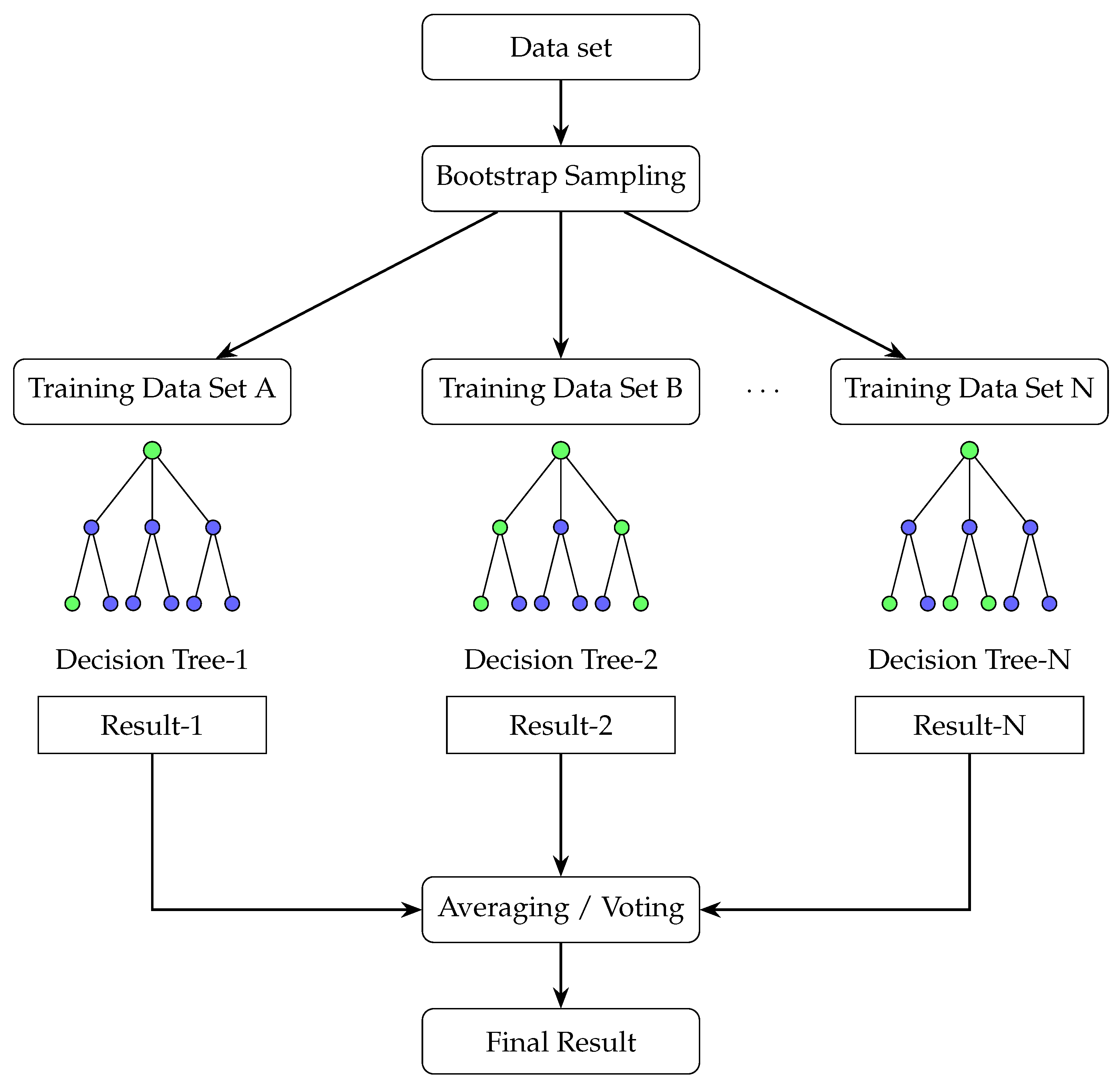
3.1. Random Forest
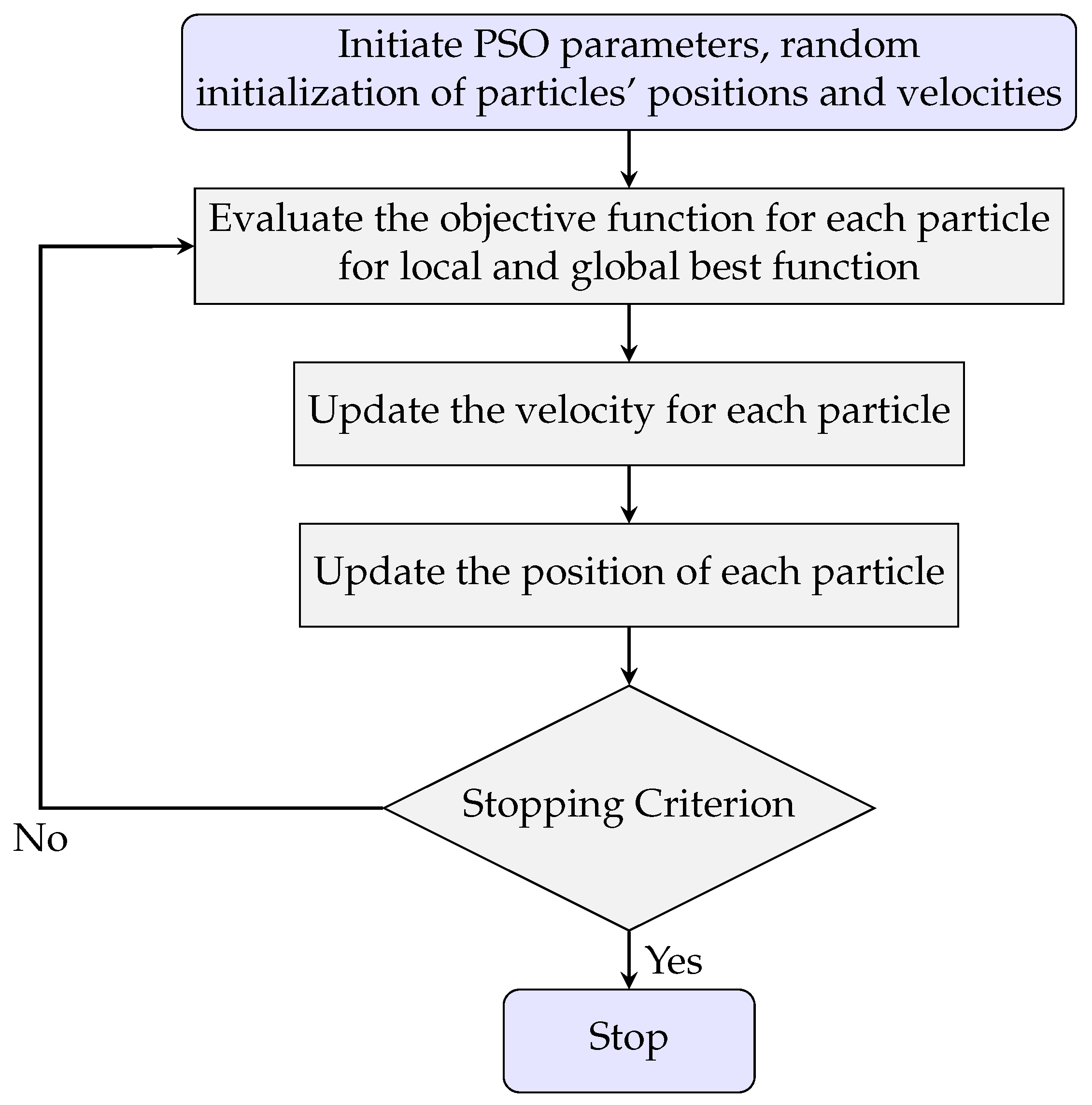
3.2. Particle Swarm Optimization
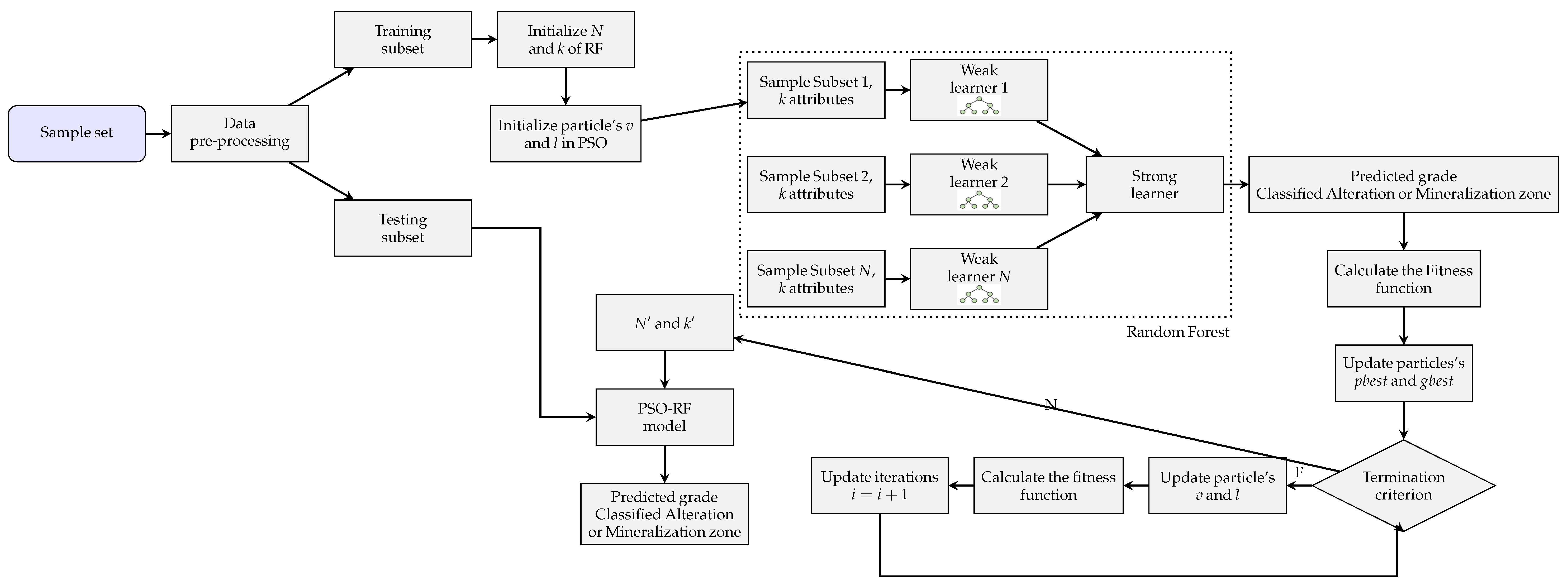
3.3. PSO-RF Algorithm
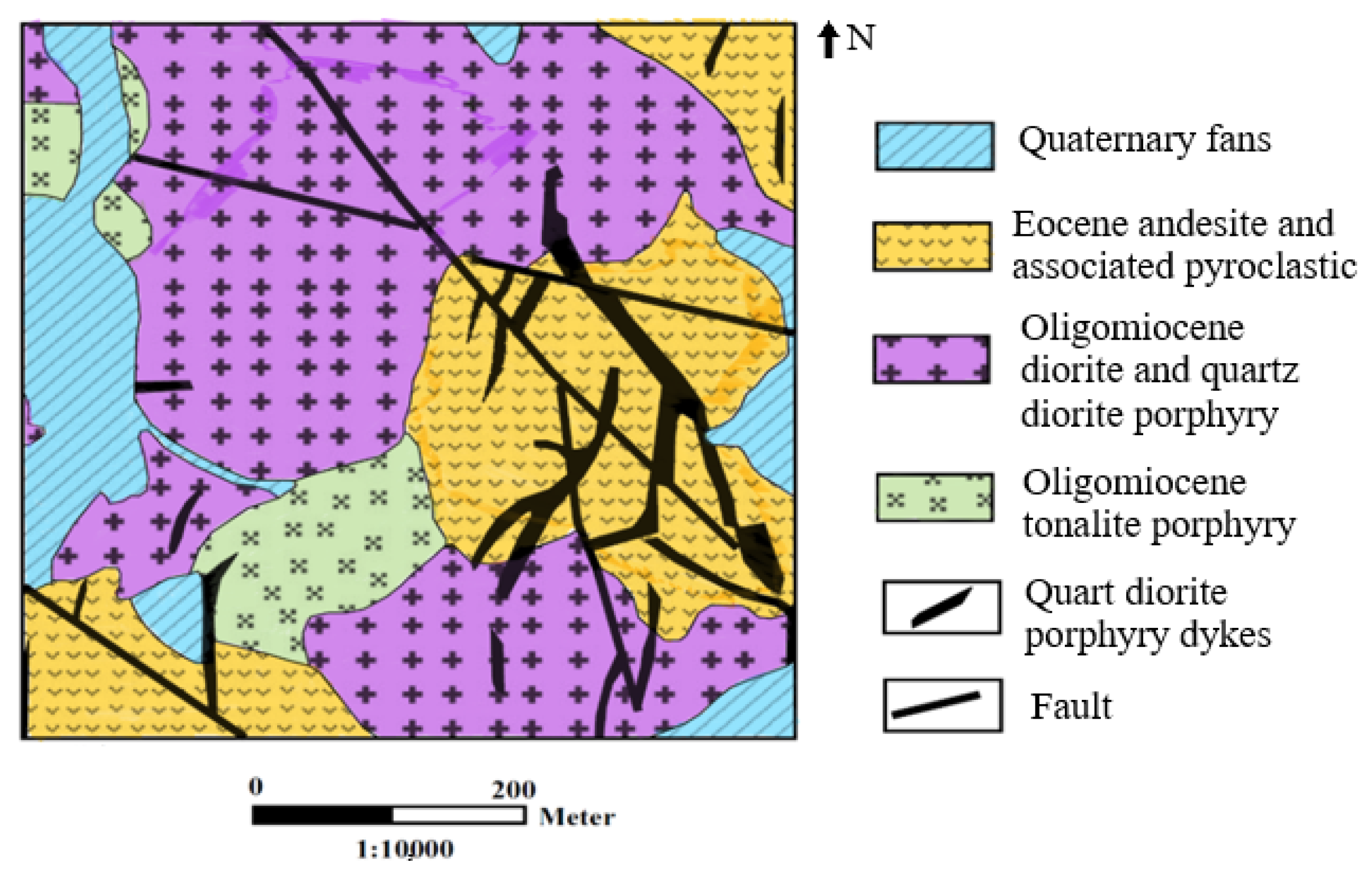
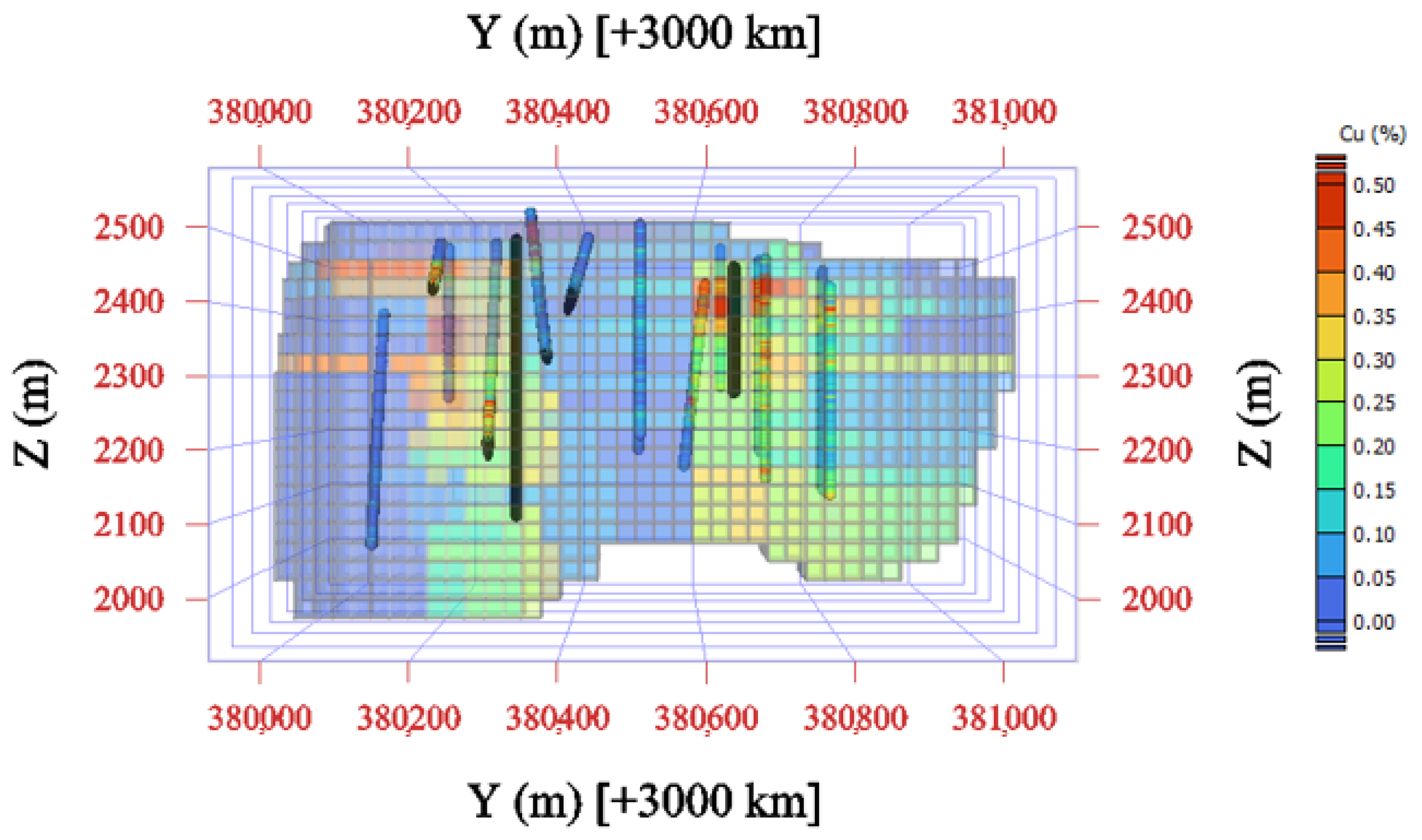
4. Dataset and Geological Context
5. Results and Discussion
5.1. Validating the PSO-RF Approach
5.2. Incorporating Geological Inputs into Ore Grade Predictions
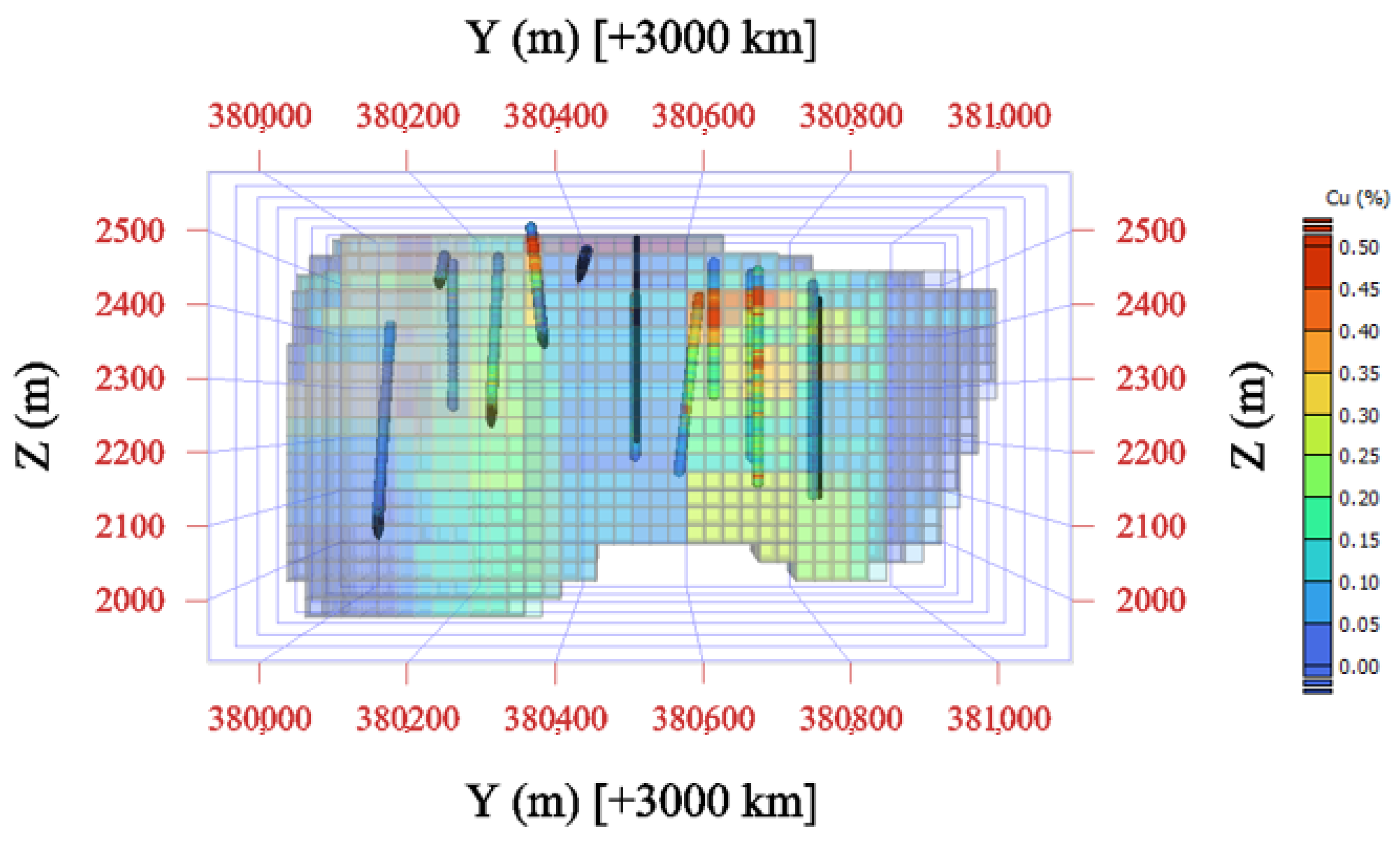
- Case A: Spatial coordinates only. In this scenario, the spatial coordinates of the sample data were used as the sole input features for training the PSO-RF model and for estimating copper grade.
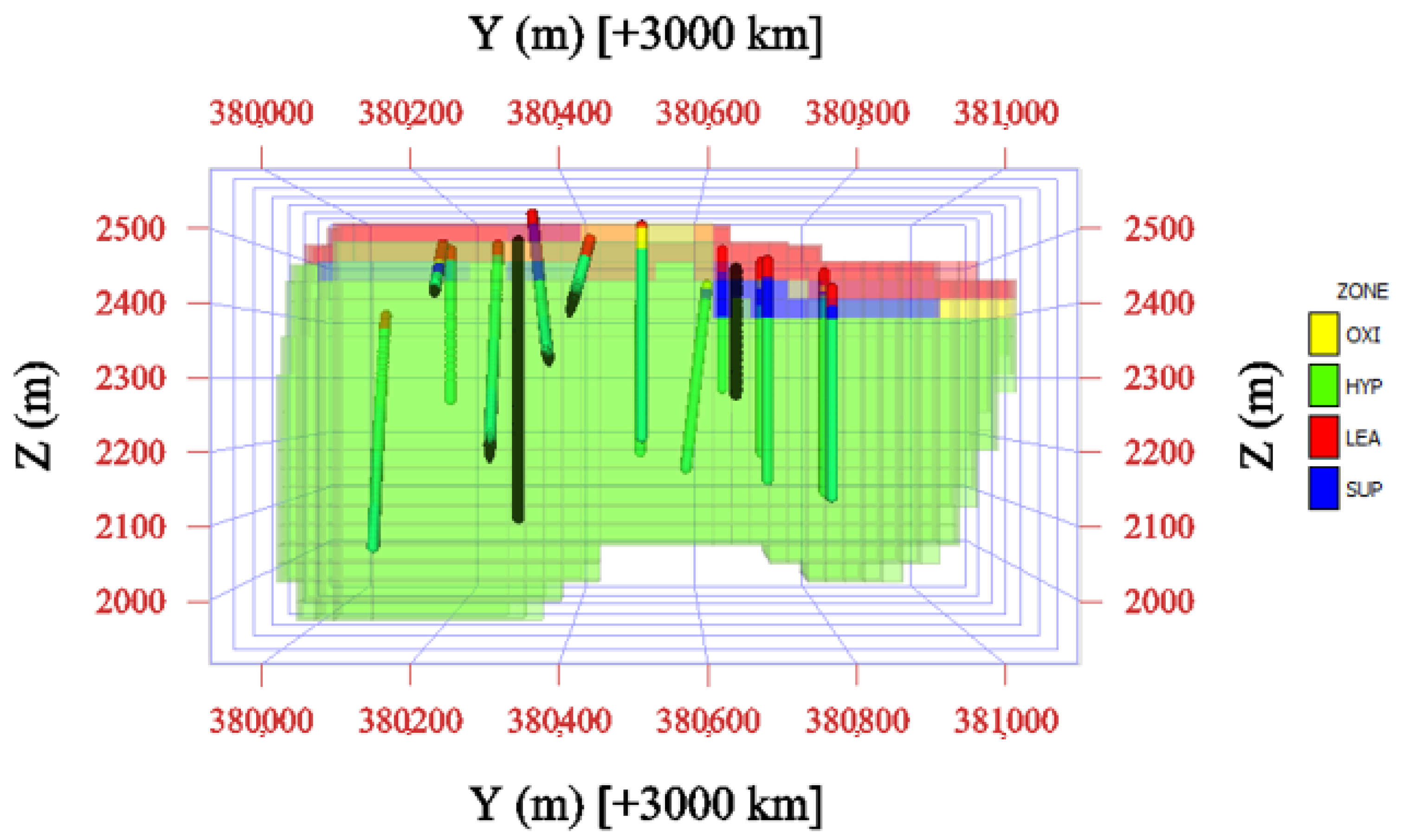
- Case B: Spatial coordinates and alteration zones. In this case, the PSO-RF model was first applied to classify the alteration zones in the study area. The resulting classified alteration zones, together with the spatial coordinates, were then used as input features for training the PSO-RF model and estimating copper grade.
- Case C: Spatial coordinates and mineralization zones. Similar to Case B, the mineralization zones were first classified, and the classified zones, along with the spatial coordinates, were used as input features for training the PSO-RF model and estimating copper grade.
- Case D: Spatial coordinates, alteration zones, and mineralization zones. In this scenario, both the classified alteration zones and mineralization zones obtained from the previous steps were combined with the spatial coordinates. These three types of information were then used jointly as input features for training the PSO-RF model and estimating copper grade.
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Emery, X.; Séguret, S.A. Geostatistics for the Mining Industry: Applications to Porphyry Copper Deposits; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Dumakor-Dupey, N.K.; Arya, S. Machine learning—A review of applications in mineral resource estimation. Energies 2021, 14, 4079. [Google Scholar] [CrossRef]
- Lantuéjoul, C. Geostatistical Simulation: Models and Algorithms; Springer: Berlin, Germany, 2002. [Google Scholar]
- Rossi, M.E.; Deutsch, C.V. Mineral Resource Estimation; Springer: Nw York, NY, USA, 2014. [Google Scholar]
- Bassani, M.A.A.; Coimbra Leite Costa, J.F.; Deutsch, C.V. Multivariate geostatistical simulation with sum and fraction constraints. Appl. Earth Sci. 2018, 127, 83–93. [Google Scholar] [CrossRef]
- Abulkhair, S.; Dowd, P.A.; Xu, C. Geostatistics in the presence of multivariate complexities: Comparison of multi-Gaussian transforms. Math. Geosci. 2023, 55, 713–734. [Google Scholar] [CrossRef]
- Battalgazy, N.; Valenta, R.; Gow, P.; Spier, C.; Forbes, G. Addressing geological challenges in mineral resource estimation: A comparative study of deep learning and traditional techniques. Minerals 2023, 13, 982. [Google Scholar] [CrossRef]
- Mahboob, M.; Celik, T.; Genc, B. Review of machine learning-based Mineral Resource estimation. J. South. Afr. Inst. Min. Metall. 2022, 122, 655–664. [Google Scholar] [CrossRef]
- Plaza-Carvajal, J.; Maleki, M.; Khorram, F.; Emery, X. Assessing the Accuracy of Gaussian Transformations for Reproducing Statistical and Spatial Dependence Relationships in Multivariate Simulation: Plaza-Carvajal, Maleki, Khorram and Emery. Nat. Resour. Res. 2025, 24, 2993–3012. [Google Scholar] [CrossRef]
- Tsae, N.B.; Adachi, T.; Kawamura, Y. Application of artificial neural network for the prediction of copper ore grade. Minerals 2023, 13, 658. [Google Scholar] [CrossRef]
- Kaplan, U.E.; Topal, E. A new ore grade estimation using combine machine learning algorithms. Minerals 2020, 10, 847. [Google Scholar] [CrossRef]
- Jain, G.; Pathak, P.; Bhatawdekar, R.M.; Kainthola, A.; Srivastav, A. Evaluation of machine learning models for ore grade estimation. In Proceedings of the International Conference on Geotechnical Challenges in Mining, Tunneling and Underground Infrastructures, Virtual, 20 December 2021; Springer: Singapore, 2021; pp. 613–624. [Google Scholar]
- Mery, N.; Marcotte, D. Quantifying mineral resources and their uncertainty using two existing machine learning methods. Math. Geosci. 2022, 54, 363–387. [Google Scholar] [CrossRef]
- Marquina Araujo, J.J.; Cotrina Teatino, M.A.; Mamani Quispe, J.N.; Noriega Vidal, E.M.; Vega Gonzalez, J.A.; Vega-Gonzalez, J.; Cruz-Galvez, J. Copper ore grade prediction using machine learning techniques in a copper deposit. J. Min. Environ. 2024, 15, 1011–1027. [Google Scholar]
- Li, Z.; Zhan, Z.; Hu, J.; Yi, S.; Zhang, X.; Weng, Z.; Zhang, Z.; Ding, K. An Adaptive Generalized Regression Neural Network Approach for Ore Grade Estimation Considering Spatial Anisotropy. Nat. Resour. Res. 2025, 34, 2423–2442. [Google Scholar] [CrossRef]
- Nasretdinova, M.; Madani, N.; Maleki, M. A stepwise cosimulation framework for modeling critical elements in copper porphyry deposits. Nat. Resour. Res. 2024, 33, 1439–1469. [Google Scholar] [CrossRef]
- Erdogan Erten, G.; Yavuz, M.; Deutsch, C.V. Combination of machine learning and kriging for spatial estimation of geological attributes. Nat. Resour. Res. 2022, 31, 191–213. [Google Scholar] [CrossRef]
- Dutta, P.J.; Emery, X. Classifying rock types by geostatistics and random forests in tandem. Mach. Learn. Sci. Technol. 2024, 5, 025013. [Google Scholar] [CrossRef]
- Mery, N.; Marcotte, D. Assessment of recoverable resource uncertainty in Multivariate deposits through a simple machine learning technique trained using geostatistical simulations. Nat. Resour. Res. 2022, 31, 767–783. [Google Scholar] [CrossRef]
- Maniteja, M.; Samanta, G.; Gebretsadik, A.; Tsae, N.B.; Rai, S.S.; Fissha, Y.; Okada, N.; Kawamura, Y. Advancing iron ore grade estimation: A comparative study of machine learning and ordinary kriging. Minerals 2025, 15, 131. [Google Scholar] [CrossRef]
- Zaki, M.; Chen, S.; Zhang, J.; Feng, F.; Khoreshok, A.A.; Mahdy, M.A.; Salim, K.M. A novel approach for resource estimation of highly skewed gold using machine learning algorithms. Minerals 2022, 12, 900. [Google Scholar] [CrossRef]
- Jafrasteh, B.; Fathianpour, N.; Suárez, A. Comparison of machine learning methods for copper ore grade estimation. Comput. Geosci. 2018, 22, 1371–1388. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Breiman, L. Using iterated bagging to debias regressions. Mach. Learn. 2001, 45, 261–277. [Google Scholar] [CrossRef]
- Ho, T.K. The random subspace method for constructing decision forests. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 832–844. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Wang, M.; Zhao, G.; Liang, W.; Wang, N. A comparative study on the development of hybrid SSA-RF and PSO-RF models for predicting the uniaxial compressive strength of rocks. Case Stud. Constr. Mater. 2023, 18, e02191. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the MHS’95 Proceedings Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; Available online: http://www.ppgia.pucpr.br/alceu/mestrado/aula3/PSO_2.pdf (accessed on 10 October 2025).
- Maleki, M.; Baeza, D.; Soltani-Mohammadi, S.; Madani, N.; Díaz, E.; Anguita, F. Optimising the placement of additional drill holes to enhanced mineral resource classification: A case study on a porphyry copper deposit. Int. J. Min. Reclam. Environ. 2025, 39, 134–151. [Google Scholar] [CrossRef]
- Sahab, M.G.; Toropov, V.V.; Gandomi, A.H. A review on traditional and modern structural optimization: Problems and techniques. In Metaheuristic Applications in Structures and Infrastructures; Elsevier: Amsterdam, The Netherlands, 2013; pp. 25–47. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE: Piscataway, NJ, USA, 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Freitas, D.; Lopes, L.G.; Morgado-Dias, F. Particle swarm optimisation: A historical review up to the current developments. Entropy 2020, 22, 362. [Google Scholar] [CrossRef]
- Cheng, Y.M.; Li, L.; Chi, S.c.; Wei, W. Particle swarm optimization algorithm for the location of the critical non-circular failure surface in two-dimensional slope stability analysis. Comput. Geotech. 2007, 34, 92–103. [Google Scholar] [CrossRef]
- Ferland, J.A.; Amaya, J.; Djuimo, M.S. Application of a particle swarm algorithm to the capacitated open pit mining problem. In Autonomous Robots and Agents; Springer: Berlin/Heidelberg, Germany, 2007; pp. 127–133. [Google Scholar]
- Fernández-Martínez, J.; García-Gonzalo, E.; Fernández-Alvarez, J. Theoretical analysis of particle swarm trajectories through a mechanical analogy. Int. J. Comput. Intell. Res. 2008, 4, 93–105. [Google Scholar] [CrossRef]
- Qi, C.; Fourie, A.; Chen, Q. Neural network and particle swarm optimization for predicting the unconfined compressive strength of cemented paste backfill. Constr. Build. Mater. 2018, 159, 473–478. [Google Scholar] [CrossRef]
- Mirnejad, H.; Mathur, R.; Hassanzadeh, J.; Shafie, B.; Nourali, S. Linking Cu mineralization to host porphyry emplacement: Re-Os ages of molybdenites versus U-Pb ages of zircons and sulfur isotope compositions of pyrite and chalcopyrite from the Iju and Sarkuh porphyry deposits in Southeast Iran. Econ. Geol. 2013, 108, 861–870. [Google Scholar] [CrossRef]
- Mirnejad, H.; Raeisi, D.; Heidari, F. Geochemistry and petrogenesis of tonalite from Iju area, northwest of Shahr-e Babak (Kerman province), with emphasis on adakitic magmatism. Petrol. J. 2015, 6, 197–210. [Google Scholar]
- Zarasvandi, A.; Rezaei, M.; Pourkaseb, H.; Asadi, S.; Azimzadeh, A.M. Characterization of potassic alteration in the Iju porphyry copper deposit using mineral chemistry of biotite and chlorite. Petrol. J. 2018, 8, 67–86. [Google Scholar]
- Aghazadeh, M.; Hou, Z.; Badrzadeh, Z.; Zhou, L. Temporal–spatial distribution and tectonic setting of porphyry copper deposits in Iran: Constraints from zircon U–Pb and molybdenite Re–Os geochronology. Ore Geol. Rev. 2015, 70, 385–406. [Google Scholar] [CrossRef]
- Golestani, M.; Karimpour, M.H.; Shafaroudi, A.M.; Shahri, M.R.H. Geochemistry, U-Pb geochronology and Sr-Nd isotopes of the Neogene igneous rocks, at the Iju porphyry copper deposit, NW Shahr-e-Babak, Iran. Ore Geol. Rev. 2018, 93, 290–307. [Google Scholar] [CrossRef]
- Guilbert, J.M.; Park, C.F., Jr. The Geology of Ore Deposits; Waveland Press: Long Grove, IL, USA, 2007. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Noble, W.S. What is a support vector machine? Nat. Biotechnol. 2006, 24, 1565–1567. [Google Scholar] [CrossRef] [PubMed]
- Sillitoe, R.H. Porphyry copper systems. Econ. Geol. 2010, 105, 3–41. [Google Scholar] [CrossRef]
- Soltani-Mohammadi, S.; Hoseinian, F.S.; Abbaszadeh, M.; Khodadadzadeh, M. Grade estimation using a hybrid method of back-propagation artificial neural network and particle swarm optimization with integrated samples coordinate and local variability. Comput. Geosci. 2022, 159, 104981. [Google Scholar] [CrossRef]




| Mineralization | Alteration | |||||||
|---|---|---|---|---|---|---|---|---|
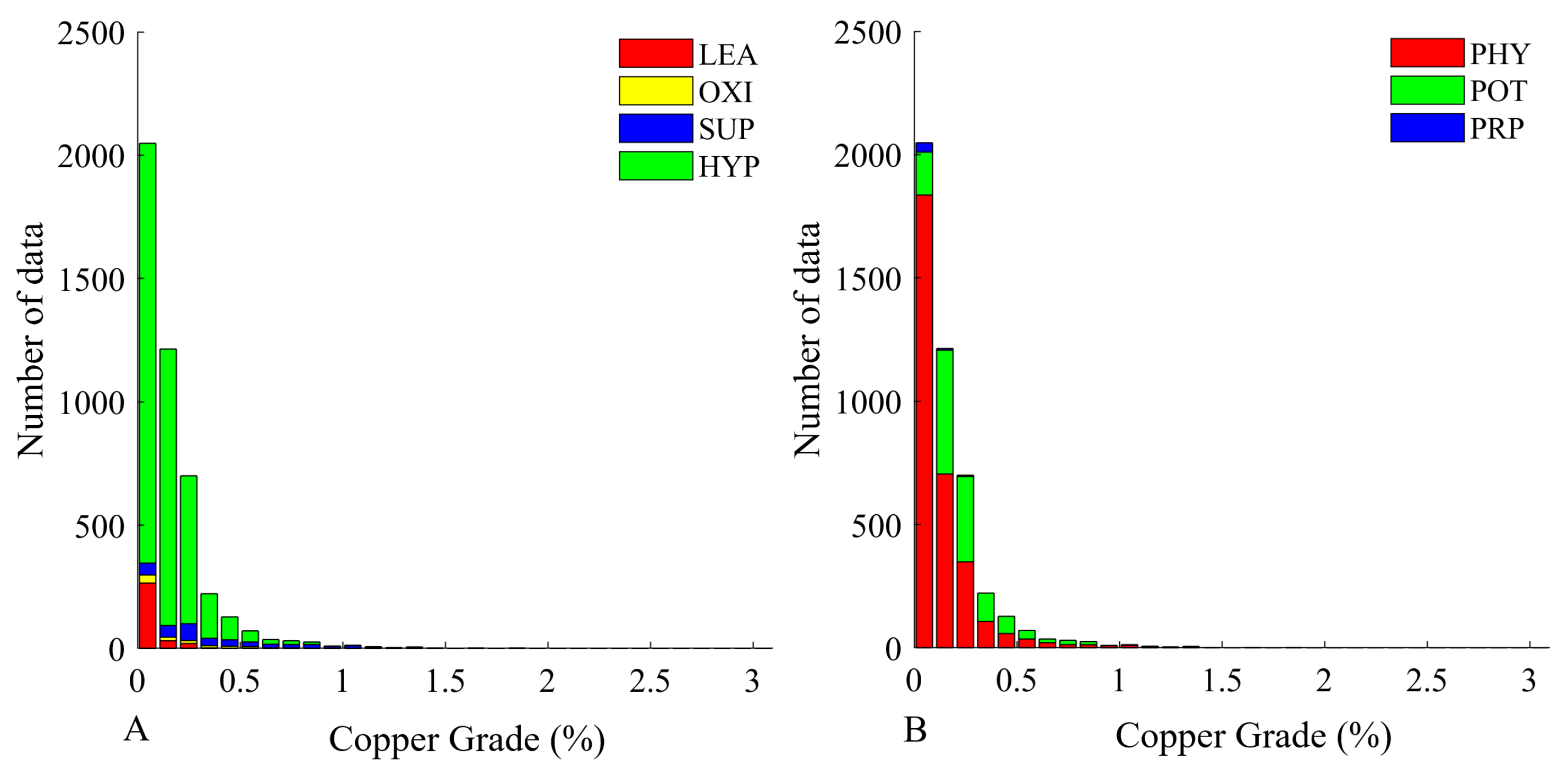
| Global | LEA | OXI | SUP | HYP | PHY | POT | PRP | |
| Number of data | 4526 | 320 | 90 | 322 | 3794 | 3173 | 1303 | 50 |
| Mean value | 0.164 | 0.058 | 0.259 | 0.445 | 0.147 | 0.134 | 0.239 | 0.072 |
| Variance | 0.036 | 0.009 | 0.074 | 0.169 | 0.018 | 0.033 | 0.036 | 0.004 |
| Minimum | 0.00 | 0.000 | 0.000 | 0.006 | 0.000 | 0.000 | 0.020 | 0.010 |
| Lower quartile | 0.050 | 0.010 | 0.060 | 0.170 | 0.050 | 0.040 | 0.130 | 0.030 |
| Median | 0.110 | 0.023 | 0.180 | 0.300 | 0.110 | 0.080 | 0.190 | 0.050 |
| Upper quartile | 0.210 | 0.070 | 0.380 | 0.620 | 0.200 | 0.160 | 0.290 | 0.090 |
| Maximum | 3.430 | 1.210 | 1.540 | 3.430 | 1.390 | 3.430 | 1.880 | 0.260 |
| Mineralization Zones | Alteration Zones | |||
|---|---|---|---|---|
| p-Value | Statistics | p-Value | Statistics | |
| Fligner–Killeen test | 220.09 | 88.05 | ||
| Levene test | 577.69 | 10.82 | ||
| PSO-RF | SVM | ||||||
|---|---|---|---|---|---|---|---|
| Train | Test | Train | Test | ||||
| MSE | R2 | MSE | R2 | MSE | R2 | MSE | R2 |
| 0.0034 | 0.91 | 0.0071 | 0.74 | 0.0021 | 0.93 | 0.0083 | 0.61 |
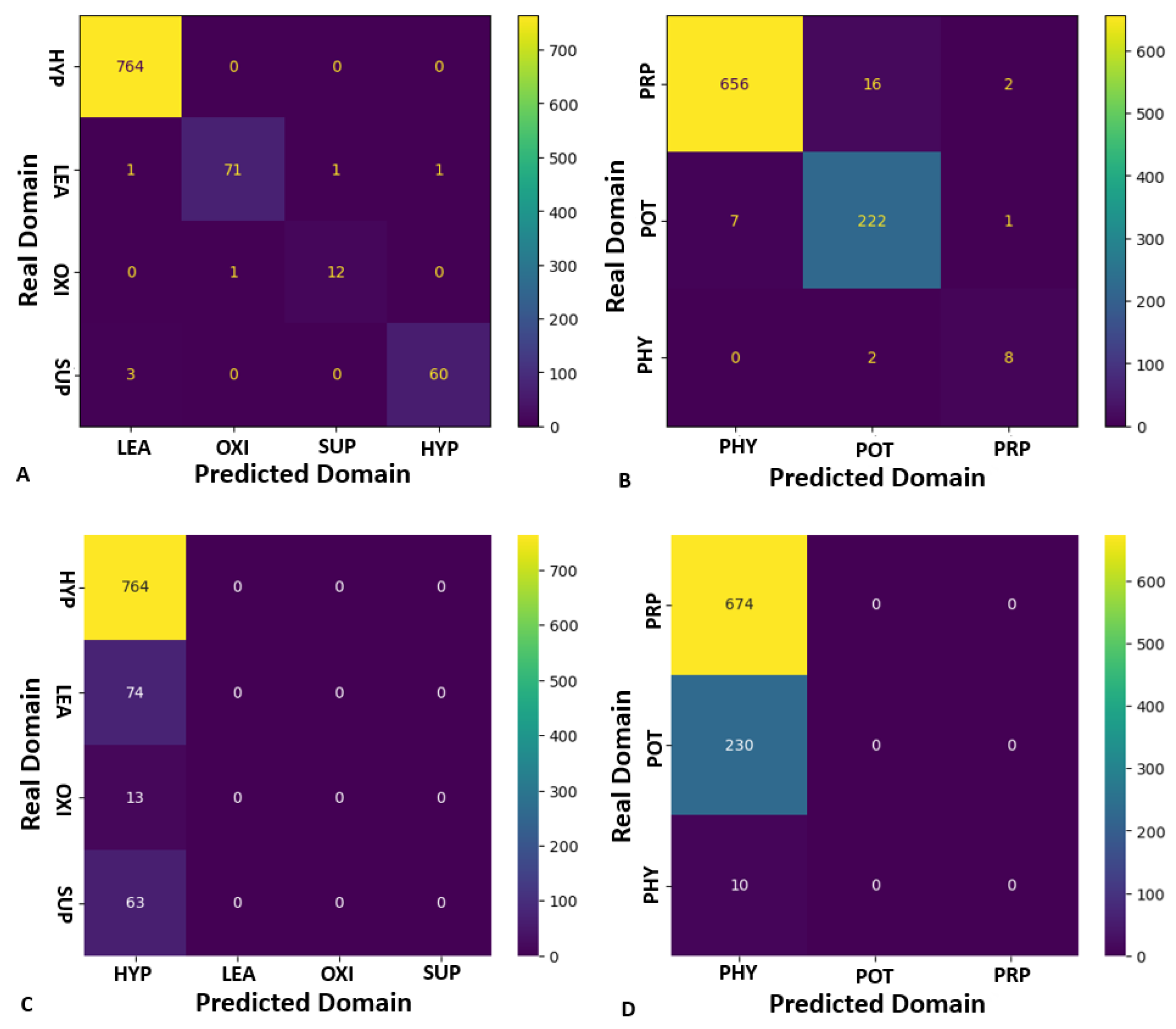
| Model/Task | OA | BA | Macro F1 | Weighted F1 | |
|---|---|---|---|---|---|
| RF—Alteration (A) | 0.99 | 0.98 | 0.98 | 0.99 | 0.98 |
| RF—Mineralization (B) | 0.96 | 0.70 | 0.70 | 0.96 | 0.90 |
| SVM—Alteration (C) | 0.84 | 0.25 | 0.23 | 0.76 | 0.00 |
| SVM—Mineralization (D) | 0.74 | 0.33 | 0.28 | 0.63 | 0.00 |
| Model | MSE | R2 |
|---|---|---|
| Model A | 0.0073 | 0.73 |
| Model B | 0.0073 | 0.72 |
| Model C | 0.0072 | 0.73 |
| Model D | 0.0065 | 0.78 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maleki, M.; Mery, N.; Soltani-Mohammadi, S.; Plaza-Carvajal, J.; Varouchakis, E.A. Integrating Geological Domains into Machine Learning for Ore Grade Prediction: A Case Study from a Porphyry Copper Deposit. Minerals 2025, 15, 1175. https://doi.org/10.3390/min15111175
Maleki M, Mery N, Soltani-Mohammadi S, Plaza-Carvajal J, Varouchakis EA. Integrating Geological Domains into Machine Learning for Ore Grade Prediction: A Case Study from a Porphyry Copper Deposit. Minerals. 2025; 15(11):1175. https://doi.org/10.3390/min15111175
Chicago/Turabian StyleMaleki, Mohammad, Nadia Mery, Saed Soltani-Mohammadi, Jordan Plaza-Carvajal, and Emmanouil A. Varouchakis. 2025. "Integrating Geological Domains into Machine Learning for Ore Grade Prediction: A Case Study from a Porphyry Copper Deposit" Minerals 15, no. 11: 1175. https://doi.org/10.3390/min15111175
APA StyleMaleki, M., Mery, N., Soltani-Mohammadi, S., Plaza-Carvajal, J., & Varouchakis, E. A. (2025). Integrating Geological Domains into Machine Learning for Ore Grade Prediction: A Case Study from a Porphyry Copper Deposit. Minerals, 15(11), 1175. https://doi.org/10.3390/min15111175









