Original Calibration of a Garnet Geobarometer in Metapelite
Abstract
1. Introduction
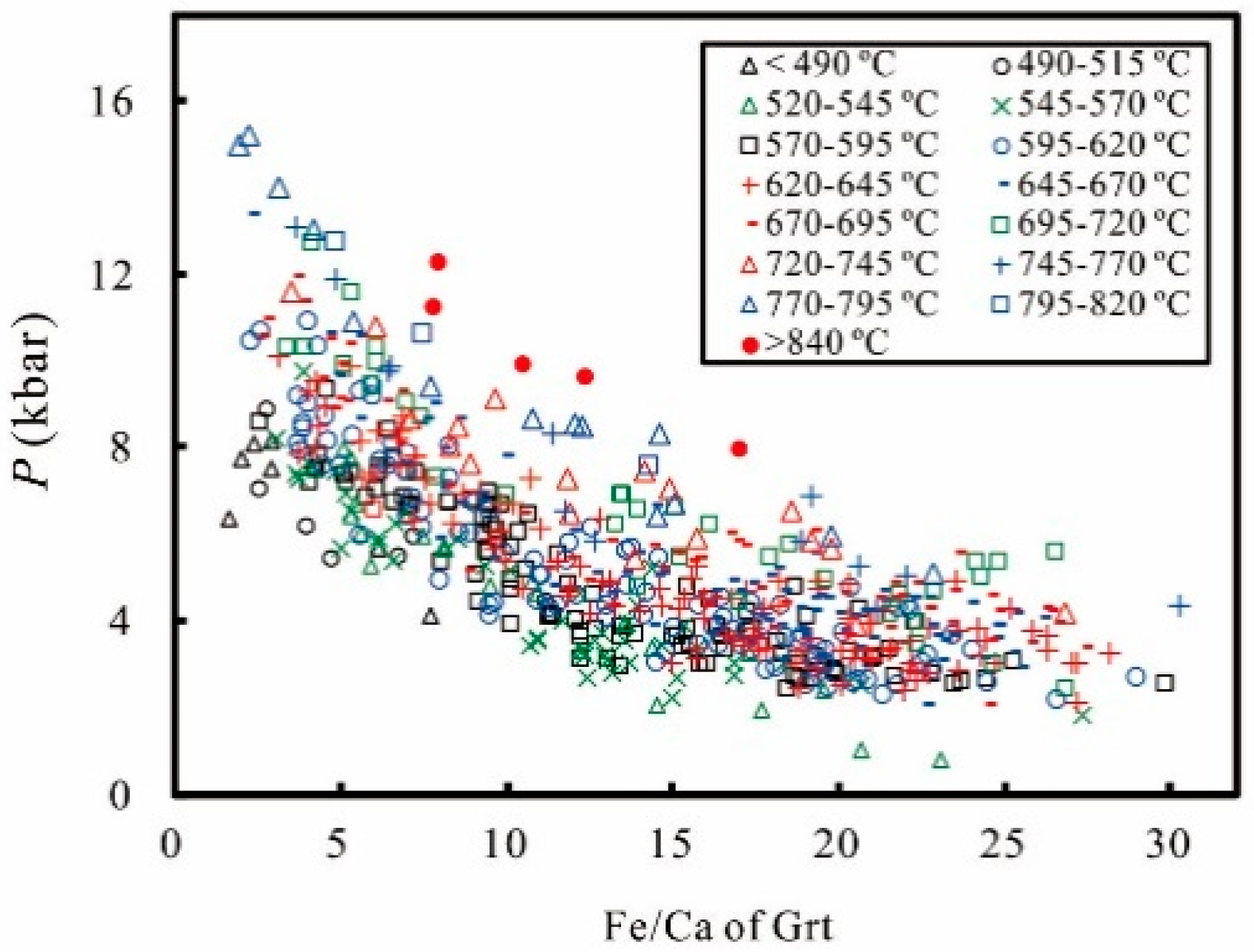
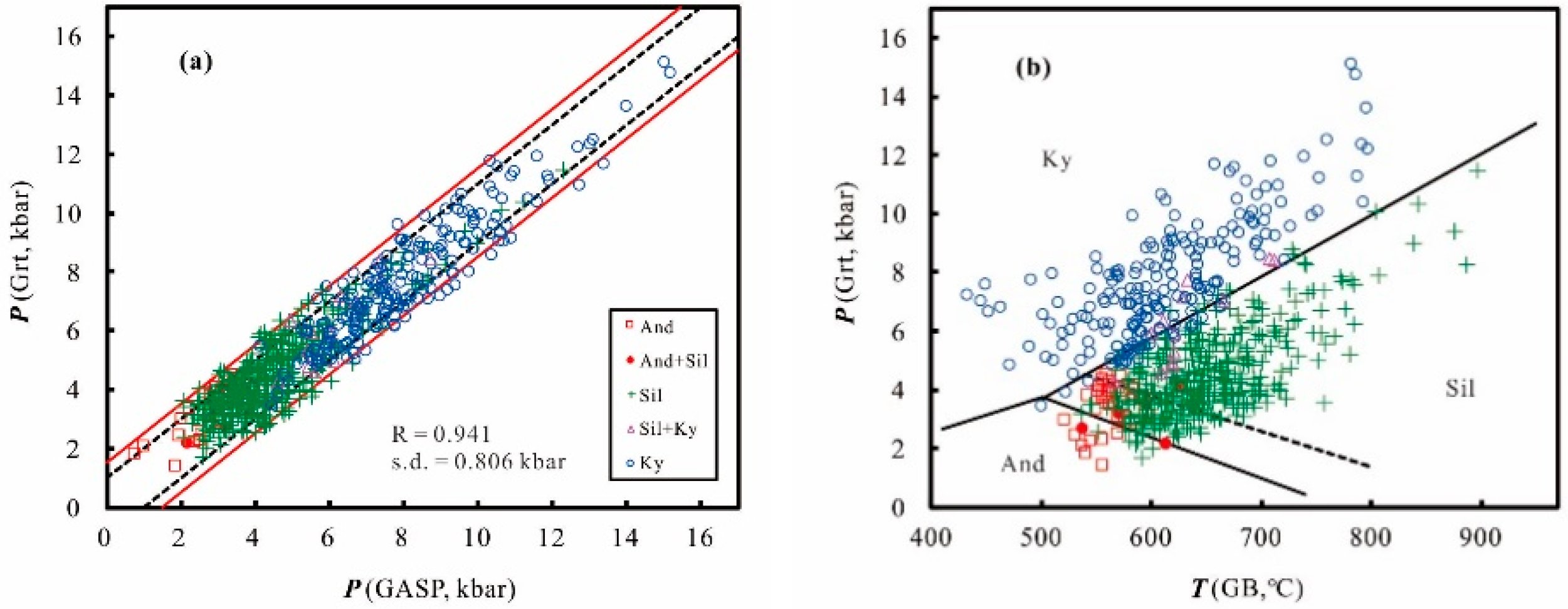
2. Calibration
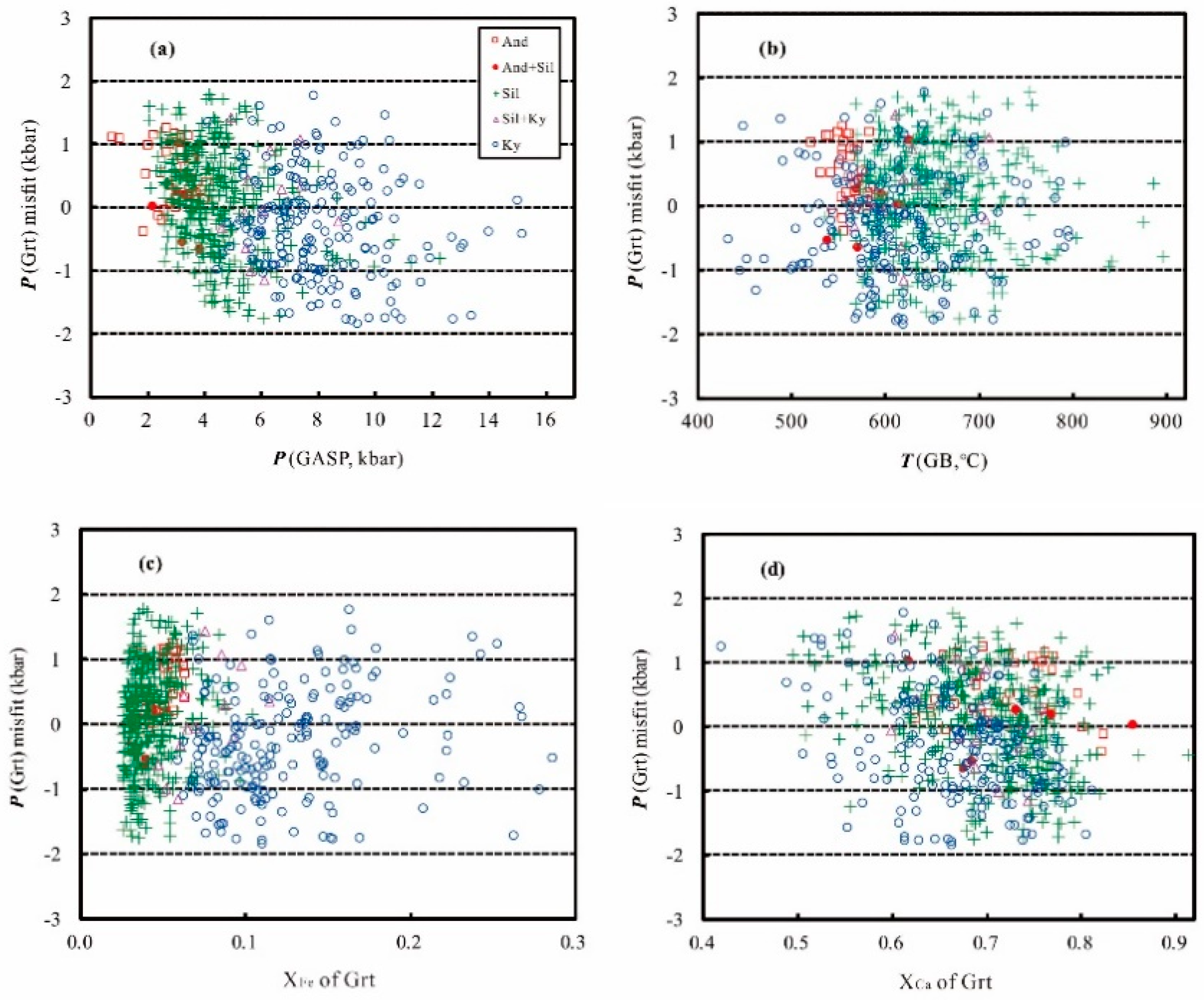
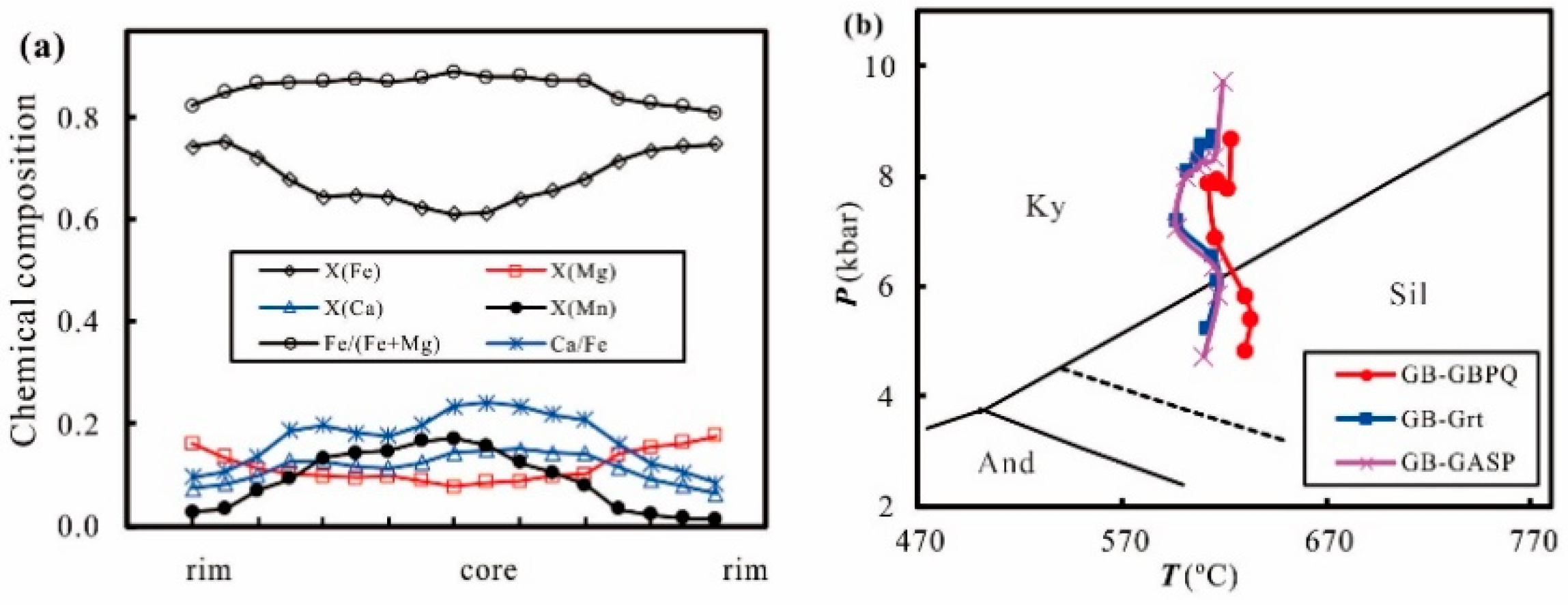
3. Error Consideration
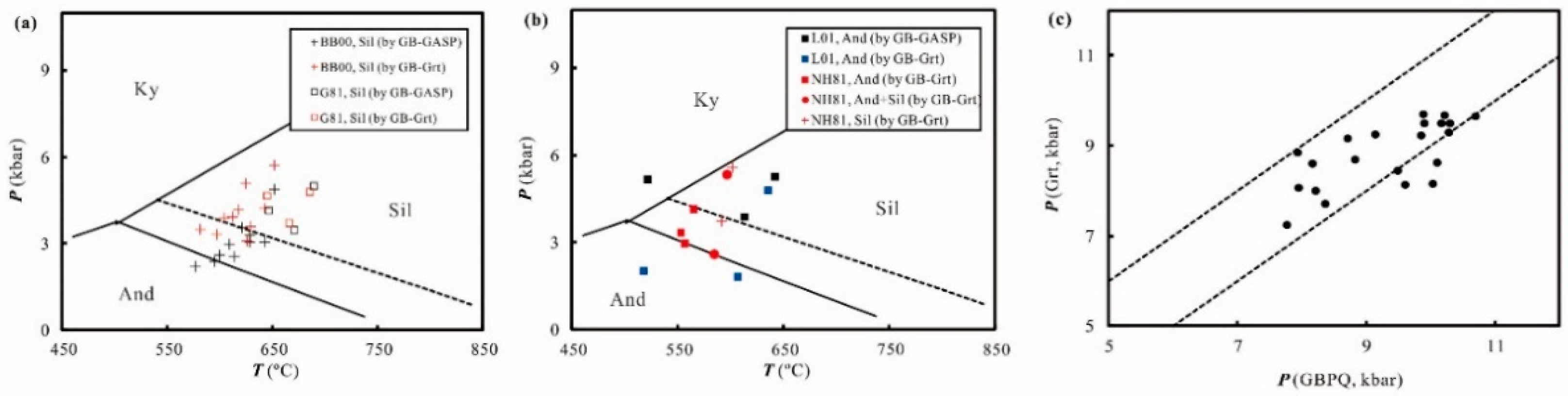
4. Application
5. Discussion
6. Conclusions
Supplementary Materials
Funding
Acknowledgments
Conflicts of Interest
References
- Hammarstrom, J.M.; Zen, E.-A. Aluminum in hornblende: An empirical igneous geobarometer. Am. Miner. 1986, 71, 1297–1313. [Google Scholar]
- Johnson, M.C.; Rutherford, M.J. Experimental calibration of the aluminum-in-hornblende geobarometer with application to Long Valley caldera (California) volcanic rocks. Geology 1989, 17, 837–841. [Google Scholar] [CrossRef]
- Anderson, L.J.; Smith, R.D. The effects of temperature and fO2 on the Al-in-hornblende barometer. Am. Miner. 1995, 80, 549–559. [Google Scholar] [CrossRef]
- Mutch, E.J.F.; Blundy, J.D.; Tattitch, B.C.; Cooper, F.J.; Brooker, R.A. An experimental study of amphibole stability in low-pressure granitic magmas and a revised Al-in-hornblende geobarometer. Contrib. Miner. Petrol. 2016, 171, 85. [Google Scholar] [CrossRef]
- Putirka, K. Amphibole thermometers and barometers for igneous systems and some implications for eruption mechanisms of felsic magmas at arc volcanoes. Am. Miner. 2016, 101, 841–858. [Google Scholar] [CrossRef]
- Massonne, H.J.; Schreyer, W. Phengite geobarometry based on the limiting assemblage with k-feldspar, phlogopite, and quartz. Contrib. Miner. Petrol. 1987, 96, 212–224. [Google Scholar] [CrossRef]
- Massonne, H.J.; Schreyer, W. Stability field of the high-pressure assemblage talc + phengite and two new phengite barometers. Eur. J. Miner. 1989, 1, 391–410. [Google Scholar] [CrossRef]
- Wark, D.A.; Watson, E.B. TitaniQ: A titanium-in-quartz geothermometer. Contrib. Miner. Petrol. 2006, 152, 743–754. [Google Scholar] [CrossRef]
- Thomas, J.B.; Watson, E.B.; Spear, F.S.; Shemella, P.T.; Nayak, S.K.; Lanzirotti, A. TitaniQ under pressure: The effect of pressure and temperature on the solubility of Ti in quartz. Contrib. Miner. Petrol. 2010, 160, 743–759. [Google Scholar] [CrossRef]
- Zack, T.; Moraes, R.; Kronz, A. Temperature dependence of Zr in rutile: Empirical calibration of a rutile thermometer. Contrib. Miner. Petrol. 2004, 148, 471–488. [Google Scholar] [CrossRef]
- Spear, F.S.; Wark, D.A.; Cheney, J.T.; Schumacher, J.C.; Watson, E.B. Zr-in-rutile thermometry in blueschists from Sifnos, Greece. Contrib. Miner. Petrol. 2006, 152, 375–385. [Google Scholar] [CrossRef]
- Ferry, J.M.; Watson, E.B. New thermodynamic models and revised calibrations for the Ti-in-zircon and Zr-in-rutile thermometers. Contrib. Miner. Petrol. 2007, 154, 429–437. [Google Scholar] [CrossRef]
- Tomkins, H.S.; Powell, R.; Ellis, D.J. The pressure dependence of the zirconium-in-rutile thermometer. J. Metamorph. Geol. 2007, 25, 703–713. [Google Scholar] [CrossRef]
- Pape, J.; Mezger, K.; Robyr, M. A systematic evaluation of the Zr-in-rutile thermometer in ultra-high temperature (UHT) rocks. Contrib. Miner. Petrol. 2016, 171, 44. [Google Scholar] [CrossRef]
- Watson, E.B.; Wark, D.A.; Thomas, J.B. Crystallization thermometers for zircon and rutile. Contrib. Miner. Petrol. 2006, 151, 413–433. [Google Scholar] [CrossRef]
- Enami, M.; Nishtyama, T.; Mouri, T. Laser Raman microspectrometry of metamorphic quartz: A simple method for comparison of metamorphic pressures. Am. Miner. 2007, 92, 1303–1315. [Google Scholar] [CrossRef]
- Korsakov, A.V.; Zhukov, V.P.; Vandenabeele, P. Raman-based geobarometry of ultrahigh-pressure metamorphic rocks: Applications, problems, and perspectives. Anal. Bioanal. Chem. 2010, 397, 2739–2752. [Google Scholar] [CrossRef] [PubMed]
- Kohn, M. Thermoba-Raman-try: Calibration of spectroscopic barometers and thermometers for mineral inclusions. Earth Planet Sci. Lett. 2014, 388, 187–196. [Google Scholar] [CrossRef]
- Murri, M.; Mazzucchelli, M.L.; Campomenosi, N.; Korsakov, A.V.; Prencipe, M.; Mihailova, B.D.; Scambelluri, M.; Angel, R.J.; Alvaro, M. Raman elastic geobarometry for anisotropic mineral inclusions. Am. Miner. 2018, 103, 1869–1872. [Google Scholar]
- Murri, M.; Alvaro, M.; Angel, R.J.; Prencipe, M.; Mihailova, B.D. The effects of non-hydrostatic stress on the structure and properties of alpha-quartz. Phys. Chem. Miner. 2019, 46, 487–499. [Google Scholar] [CrossRef]
- Anzolini, C.; Nestola, F.; Mazzucchelli, M.L.; Alvaro, M.; Nimis, P.; Gianese, A.; Morganti, S.; Marone, F.; Campione, M.; Harris, J. Depth of diamond formation obtained from single periclase inclusions. Geology 2019, 47, 219–226. [Google Scholar] [CrossRef]
- Nimis, P.; Angel, R.J.; Alvaro, M.; Nestola, F.; Harris, J.W.; Casati, N.; Marone, F. Crystallographic orientations of magnesiochromite inclusions in diamonds: What do they tell us? Contrib. Miner. Petrol. 2019, 174, 29. [Google Scholar] [CrossRef]
- Stangarone, C.; Angel, R.J.; Prencipe, M.; Campomenosi, N.; Mihailova, B.; Alvaro, M. Measurement of strains in zircon inclusions by Raman spectroscopy. Eur. J. Miner. 2019, in press. [Google Scholar]
- Stangarone, C.; Angel, R.J.; Prencipe, M.; Mihailova, B.; Alvaro, M. New insights into the zircon-reidite phase transition. Am. Miner. 2019, 104, 830–837. [Google Scholar] [CrossRef]
- Zaffiro, G.; Angel, R.J.; Alvaro, M. Constraints on the equations of state of stiff anisotropic minerals: Rutile, and the implications for rutile elastic barometry. Miner. Mag. 2019, 83, 339–347. [Google Scholar] [CrossRef]
- Gonzalez, J.P.; Thomas, J.B.; Baldwin, S.L.; Alvaro, M. Quartz-in-garnet and Ti-in-Quartz (QuiG-TiQ) thermobarometry: Methodology and first application to a quartzofeldspathic gneiss from the (ultra)high-pressure terrane in eastern Papua New Guinea. J. Metamorph. Geol. 2019, 37. [Google Scholar]
- Tracy, R.T. Compositional zoning and inclusions in metamorphic minerals. Rev. Miner. 1982, 10, 355–397. [Google Scholar]
- Xiao, L.L.; Wu, C.M.; Zhao, G.C.; Guo, J.H.; Ren, L.D. Metamorphic P-T paths of the Zanhuang amphibolites and metapelites: Constraints on the tectonic evolution of the Paleoproterozoic Trans-North China Orogen. Int. J. Earth Sci. 2011, 100, 717–739. [Google Scholar] [CrossRef]
- Harley, S.L. The origins of granulites: A metamorphic perspective. Geol. Mag. 1989, 126, 215–247. [Google Scholar] [CrossRef]
- Spear, F.S.; Kohn, M.J.; Florence, F.P.; Menard, T. A model for garnet and plagioclase growth in pelitic schists: Implications for thermobarometry and P-T path determinations. J. Metamorph. Geol. 1990, 8, 683–696. [Google Scholar] [CrossRef]
- Chen, Y.; Ye, K.; Liu, J.B.; Sun, M. Multistage metamorphism of the Huangtuling granulite, Northern Dabie Orogen, eastern China: Implications for the tectonometamorphic evolution of subducted lower continental crust. J. Metamorph. Geol. 2006, 24, 633–654. [Google Scholar] [CrossRef]
- Gaidies, F.; de Capitani, C.; Abart, R.; Schuster, R. Prograde garnet growth along complex P-T-t paths: results from numerical experiments on polyphase garnet from the Wölz Complex (Austroalpine basement). Contrib. Miner. Petrol. 2008, 155, 673–688. [Google Scholar] [CrossRef]
- Kelsey, D.E. On ultrahigh-temperature crustal metamorphism. Gondwana Res. 2008, 13, 1–29. [Google Scholar] [CrossRef]
- Sommer, H.; Hauzenberger, C.; Kröner, A.; Muhongo, S. Isothermal decompression history in the ‘‘Western Granulite” terrain, central Tanzania: Evidence from reaction textures and trapped fluids in metapelites. J. Afr. Earth Sci. 2008, 51, 123–144. [Google Scholar] [CrossRef]
- Guo, J.H.; Peng, P.; Chen, Y.; Jiao, S.J.; Windley, B.F. UHT sapphirine granulite metamorphism at 1.93–1.92Ga caused by gabbronorite intrusions: Implications for tectonic evolution of the northern margin of the North China Craton. Precambrian Res. 2012, 222–223, 124–142. [Google Scholar] [CrossRef]
- Li, B.T.; Massonne, H.J. Two tertiary metamorphic events recognized in high-pressure metapelites of the Nevado-Fil_abride Complex (Betic Cordillera, Spain). J. Metamorph. Geol. 2018, 36, 603–630. [Google Scholar] [CrossRef]
- Wolfe, O.M.; Spear, F.S. Determining the amount of overstepping required to nucleate garnet during Barrovian regional metamorphism, Connecticut Valley Synclinorium. J. Metamorph. Geol. 2018, 36, 79–94. [Google Scholar] [CrossRef]
- Ghent, E.D.; Stout, M.Z. Geobarometry and geothermometry of plagioclase-biotite-garnet-muscovite assemblages. Contrib. Miner. Petrol. 1981, 76, 92–97. [Google Scholar] [CrossRef]
- Bohlen, S.R.; Wall, V.J.; Boettcher, A.L. Experimental investigations and geological applications of equilibria in the system FeO-TiO2-Al2O3-SiO2-H2O. Am. Miner. 1983, 68, 1049–1058. [Google Scholar]
- Robinson, G.R. Calibration of the muscovite–biotite–quartz–garnet–aluminosilicate geothermobarometer. EOS 1983, 64, 351. [Google Scholar]
- Hodges, K.V.; Crowley, P.D. Error estimation and empirical geothermobarometry for pelitic systems. Am. Miner. 1985, 70, 702–709. [Google Scholar]
- Bohlen, S.R.; Liotta, J.J. A barometer for garnet amphibolites and garnet granulites. J. Petrol. 1986, 27, 1025–1034. [Google Scholar] [CrossRef]
- Holdaway, M.J.; Dutrow, B.L.; Hinton, R.W. Devonian and carboniferous metamorphism in west-central Maine: The muscovite-almandine geobarometer and the staurolite problem revisited. Am. Miner. 1988, 73, 20–47. [Google Scholar]
- Koziol, A.M.; Newton, R.C. Redetermination of the anorthite breakdown reaction and improvement of the plagioclase-garnet-Al2SiO5-quartz geobarometer. Am. Miner. 1988, 73, 216–223. [Google Scholar]
- Hoisch, T.D. Equilibria within the mineral assemblage quartz + muscovite + biotite + garnet + plagioclase, and implications for the mixing properties of octahedrally-coordinated cations in muscovite and biotite. Contrib. Miner. Petrol. 1991, 108, 43–54. [Google Scholar] [CrossRef]
- Mukhopadhyay, B.; Holdaway, M.J. Cordierite-garnet-sillimanite-quartz equilibrium: I. New experimental calibration in the system FeO-Al2O3-SiO2-H2O and certain P-T-XH2O relations. Contrib. Miner. Petrol. 1994, 116, 462–472. [Google Scholar] [CrossRef]
- Koziol, A.M.; Bohlen, S.R. Solution properties of almandine-pyrope garnet as determined by phase equilibrium experiments. Am. Miner. 1992, 77, 765–773. [Google Scholar]
- Nichols, G.T.; Berry, R.F.; Green, D.H. Internally consistent gahnitic spinel-cordierite-garnet equilibria in the FMASHZn system: Geothermobarometry and applications. Contrib. Miner. Petrol. 1992, 111, 362–377. [Google Scholar] [CrossRef]
- Holdaway, M.J. Recalibration of the GASP geobarometer in light of recent garnet and plagioclase activity models and versions of the garnet-biotite geothermometer. Am. Miner. 2001, 86, 1117–1129. [Google Scholar] [CrossRef]
- Wu, C.M.; Zhang, J.; Ren, L.D. Empirical garnet–biotite–plagioclase–quartz (GBPQ) geobarometry in medium- to high-grade metapelites. J. Petrol. 2004, 45, 1907–1921. [Google Scholar] [CrossRef]
- Wu, C.M.; Zhang, J.; Ren, L.D. Empirical garnet–muscovite–plagioclase–quartz geobarometry in medium- to high-grade metapelites. Lithos 2004, 78, 319–332. [Google Scholar] [CrossRef]
- Wu, C.M.; Zhao, G.C. Recalibration of the garnet–muscovite (GM) geothermometer and the garnet–muscovite–plagioclase–quartz (GMPQ) geobarometer for metapelitic assemblages. J. Petrol. 2006, 47, 2357–2368. [Google Scholar] [CrossRef]
- Wu, C.M.; Zhao, G.C. The applicability of the GRIPS geobarometry in metapelitic assemblages. J. Metamorph. Geol. 2006, 24, 297–307. [Google Scholar] [CrossRef]
- Wu, C.M. Revised empirical garnet-biotite-muscovite-plagioclase geobarometer in metapelites. J. Metamorph. Geol. 2015, 33, 167–176. [Google Scholar] [CrossRef]
- Holdaway, M.J. Application of new experimental and garnet Margules data to the garnet-biotite geothermometer. Am. Miner. 2000, 85, 881–892. [Google Scholar] [CrossRef]
- Todd, C.S. Limits on the precision of geobarometry at low grossular and anorthite content. Am. Miner. 1998, 83, 1161–1167. [Google Scholar] [CrossRef]
- Wu, C.M.; Cheng, B.H. Valid garnet–biotite (GB) geothermometry and garnet–aluminum silicate–plagioclase–quartz (GASP) geobarometry in metapelitic rocks. Lithos 2006, 89, 1–23. [Google Scholar] [CrossRef]
- Dyar, M.D. Mössbauer spectra of biotite from metapelites. Am. Miner. 1990, 75, 656–666. [Google Scholar]
- Guidotti, C.V.; Dyar, M.D. Ferric iron in metamorphic biotite and its petrologic and crystallochemical implications. Am. Miner. 1991, 76, 161–175. [Google Scholar]
- Williams, M.L.; Grambling, J.A. Manganese, ferric iron, and the equilibrium between garnet and biotite. Am. Miner. 1990, 75, 886–908. [Google Scholar]
- Berman, R.G. Mixing properties of Ca-Mg-Fe-Mn garnets. Am. Miner. 1990, 75, 328–344. [Google Scholar]
- Berman, R.G.; Aranovich, L.Y. Optimized standard state and solution properties of minerals. I. Model calibration for olivine, orthopyroxene, cordierite, garnet, and ilmenite in the system FeO-MgO-CaO-Al2O3-TiO2-SiO2. Contrib. Miner. Petrol. 1996, 126, 1–24. [Google Scholar] [CrossRef]
- Ganguly, J.; Cheng, W.; Tirone, M. Thermodynamics of aluminosilicate garnet solid solution: New experimental data, an optimized model, and thermometric applications. Contrib. Miner. Petrol. 1996, 126, 137–151. [Google Scholar] [CrossRef]
- Mukhopadhyay, B.; Holdaway, M.J.; Koziol, A.M. A statistical model of thermodynamic mixing properties of Ca-Mg-Fe2+ garnets. Am. Miner. 1997, 82, 165–181. [Google Scholar] [CrossRef]
- Holdaway, M.J.; Mukhopadhyay, B. A re-evaluation of the stability relations of andalusite: Thermochemical data and phase diagram for the alumino silicates. Am. Miner. 1993, 78, 298–315. [Google Scholar]
- Pattison, D.R.M. Stability of andalusite and sillimanite and the Al2SiO5 triple point: Constraints from the Ballachulish aureole, Scotland. J. Geol. 1992, 100, 423–446. [Google Scholar] [CrossRef]
- Kohn, M.J.; Spear, F.S. Error propagation for barometers: 2. Application to rocks. Am. Miner. 1991, 76, 138–147. [Google Scholar]
- Barboza, S.A.; Bergantz, G.W. Metamorphism and anatexis in the mafic complex contact aureole, Ivrea Zone, Northern Italy. J. Petrol. 2000, 41, 1307–1327. [Google Scholar] [CrossRef]
- Grew, E.S. Granulite-facies metamorphism at Molodezhnaya Station, eastern Antarctica. J. Petrol. 1981, 22, 297–336. [Google Scholar] [CrossRef]
- Likhanov, I.I.; Reverdatto, V.V.; Sheplev, V.S.; Verschinin, A.E.; Kozlov, P.S. Contact metamorphism of Fe- and Al-rich graphitic metapelites in the Transangarian region of the Yenisei Ridge, eastern Siberia, Russia. Lithos 2001, 58, 55–80. [Google Scholar] [CrossRef]
- Novak, J.M.; Holdaway, M.J. Metamorphic petrology, mineral equilibria, and polymetamorphism in the Augusta quadrangle, south-central Maine. Am. Miner. 1981, 66, 51–69. [Google Scholar]
- Boyle, A.P.; Westhead, R.K. Metamorphic peak geothermobarometry in the Furulund Group, Sulitjelma, Scandinavian Caledonides: Implications for uplift. J. Metamorph. Geol. 1992, 10, 615–626. [Google Scholar] [CrossRef]
- St-Onge, M.R. Zoned poikiloblastic garnets: P-T paths and syn-metamorphic uplift through 30 km of structural depth, Wopmay Orogen, Canada. J. Petrol. 1987, 28, 1–21. [Google Scholar] [CrossRef]
- Wood, B.J. Activity measurements and excess entropy-volume relationships for pyrope-grossular garnets. J. Geol. 1988, 96, 721–729. [Google Scholar] [CrossRef]
- Koziol, A.M.; Newton, R.C. Grossular activity-composition relationships in ternary garnets determined by reversed displaced-equilibrium experiments. Contrib. Miner. Petrol. 1989, 103, 423–433. [Google Scholar] [CrossRef]
- McKenna, L.W.; Hodges, K.V. Accuracy versus precision in locating reaction boundaries: Implications for the garnet-plagioclase-aluminum silicate-quartz geobarometer. Am. Miner. 1988, 73, 1205–1208. [Google Scholar]
- Koziol, A.M. Activity-composition relationships of binary Ca-Fe and Ca-Mn garnets determined by reversed displaced equilibrium experiments. Am. Miner. 1990, 75, 319–327. [Google Scholar]
- Holland, T.J.B.; Powell, R. An improved and extended internally consistent thermodynamic dataset for phases of petrological interest, involving a new equation of state for solids. J. Metamorph. Geol. 2011, 29, 333–383. [Google Scholar] [CrossRef]
- Wu, C.M.; Chen, H.X. Estimation of minimum or maximum pressure or temperature conditions in metamorphic rocks. Acta Petrol. Sin. 2013, 29, 1499–1510. [Google Scholar]
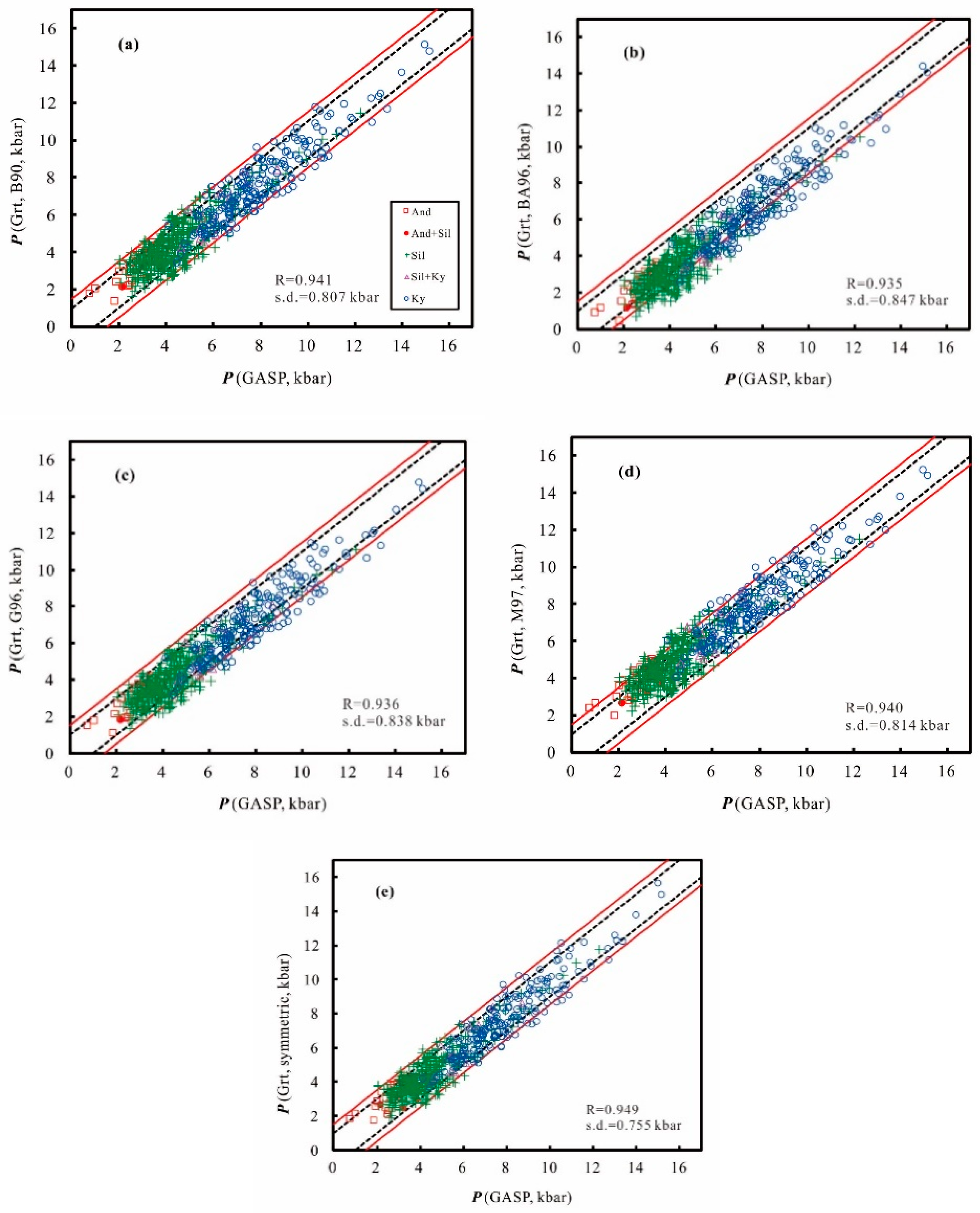
| Model | Solution | Symmetry | ΔH/ΔV | ΔS/ΔV | 1/ΔV | R |
|---|---|---|---|---|---|---|
| (bar) | (bar/K) | (bar/J) | ||||
| H01 | Fe–Mg–Ca–Mn | asymmetric | 8905.5 | 24.542 | −0.150 | 0.941 |
| (±454.1) | (±0.528) | (±0.002) | ||||
| B90 | Fe–Mg–Ca–Mn | asymmetric | 8974.4 | 24.634 | −0.151 | 0.941 |
| (±454.5) | (±0.529) | (±0.002) | ||||
| BA96 | Fe–Mg–Ca | asymmetric | 9626.3 | 24.605 | −0.155 | 0.935 |
| (±478.5) | (±0.556) | (±0.003) | ||||
| G96 | Fe–Mg–Ca–Mn | asymmetric | 9076 | 24.365 | −0.150 | 0.936 |
| (±472.6) | (±0.549) | (±0.002) | ||||
| M97 | Fe–Mg–Ca | asymmetric | 7331.8 | 23.160 | −0.148 | 0.940 |
| (±457.1) | (±0.527) | (±0.002) | ||||
| W | Fe–Mg–Ca–Mn | symmetric | 7815.3 | 25.663 | −0.142 | 0.949 |
| (±925.9) | (±0.659) | (±0.007) |
| Model | Solution | Symmetry | ±1.0 kbar | ±1.0~1.5 kbar | ±1.5~1.8 kbar | >±1.8 kbar |
|---|---|---|---|---|---|---|
| H01 | Fe–Mg–Ca–Mn | asymmetric | 76.6% | 17.7% | 5.7% | 0.0% |
| B90 | Fe–Mg–Ca–Mn | asymmetric | 77.3% | 16.6% | 6.1% | 0.3% |
| BA96 | Fe–Mg–Ca | asymmetric | 56.4% | 18.3% | 10.4% | 14.9% |
| G96 | Fe–Mg–Ca–Mn | asymmetric | 73.0% | 19.3% | 3.9% | 3.9% |
| M97 | Fe–Mg–Ca | asymmetric | 70.0% | 19.7% | 7.0% | 3.3% |
| W | Fe–Mg–Ca–Mn | symmetric | 80.3% | 15.4% | 4.3% | 0.0% |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, C.-M. Original Calibration of a Garnet Geobarometer in Metapelite. Minerals 2019, 9, 540. https://doi.org/10.3390/min9090540
Wu C-M. Original Calibration of a Garnet Geobarometer in Metapelite. Minerals. 2019; 9(9):540. https://doi.org/10.3390/min9090540
Chicago/Turabian StyleWu, Chun-Ming. 2019. "Original Calibration of a Garnet Geobarometer in Metapelite" Minerals 9, no. 9: 540. https://doi.org/10.3390/min9090540
APA StyleWu, C.-M. (2019). Original Calibration of a Garnet Geobarometer in Metapelite. Minerals, 9(9), 540. https://doi.org/10.3390/min9090540





