Bubble Size Distribution Characteristics of a Jet-Stirring Coupling Flotation Device
Abstract
1. Introduction
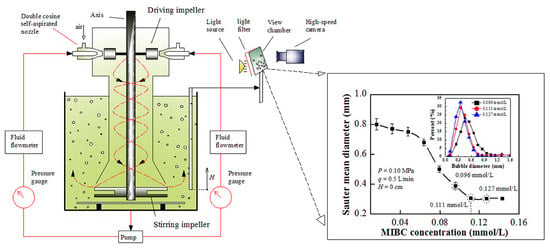
2. Jet-Stirring Coupling Flotation Device
2.1. Device Structure
2.2. Working Process of Flotation Device
3. Experimental Evaluation
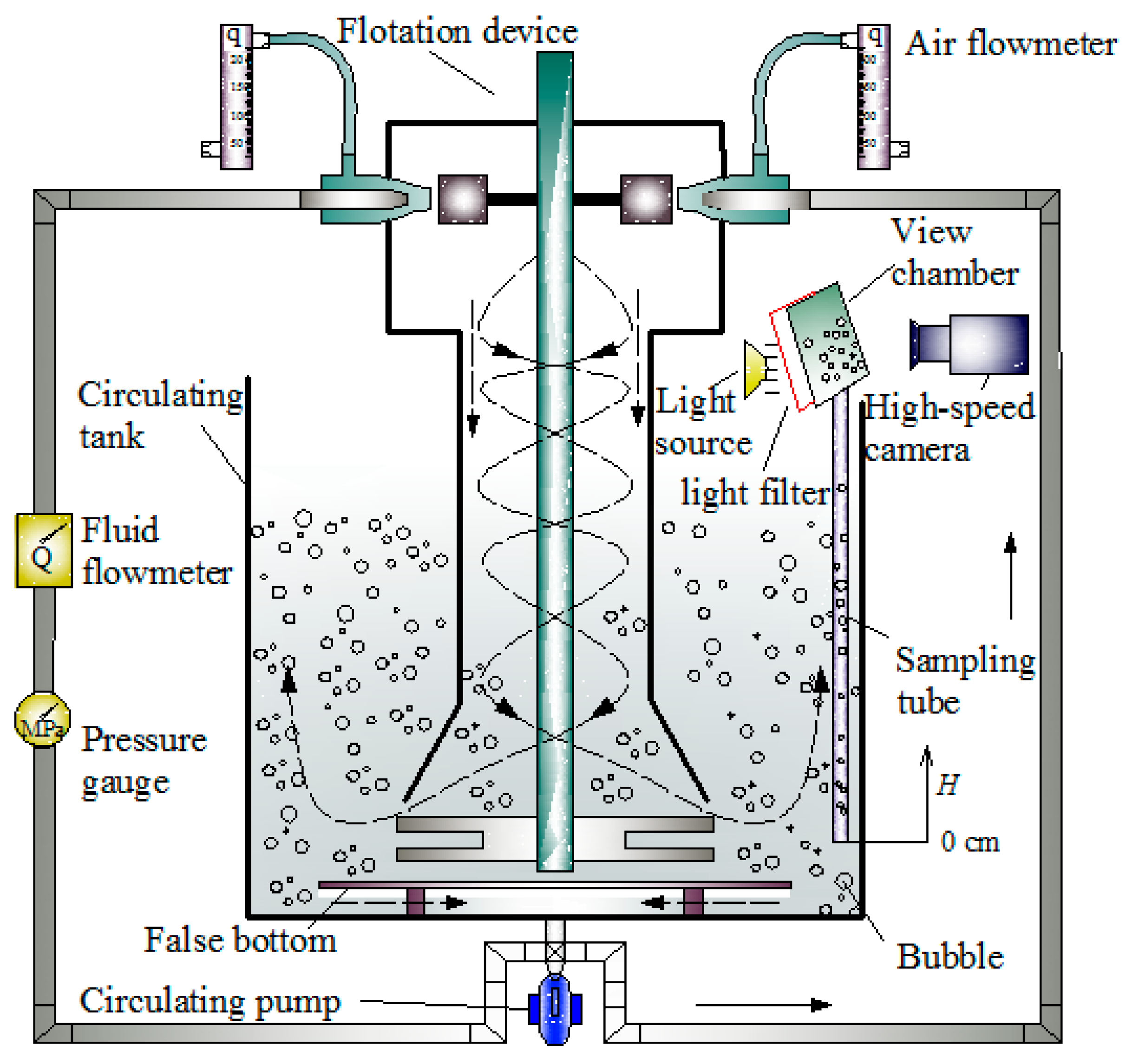
3.1. Experimental System
3.2. Experimental Conditions and Methods
3.3. Data Processing
4 Results and Discussion
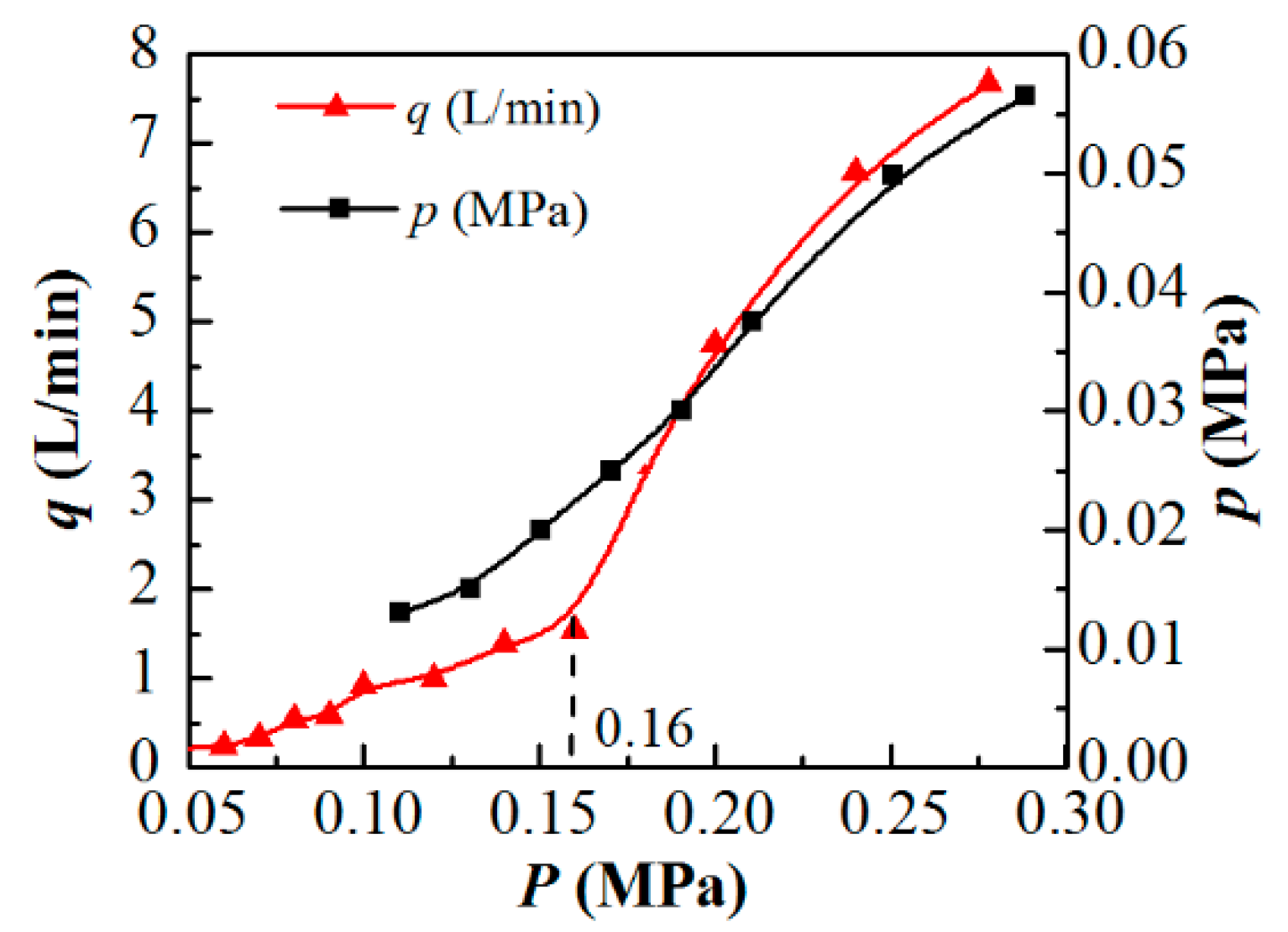
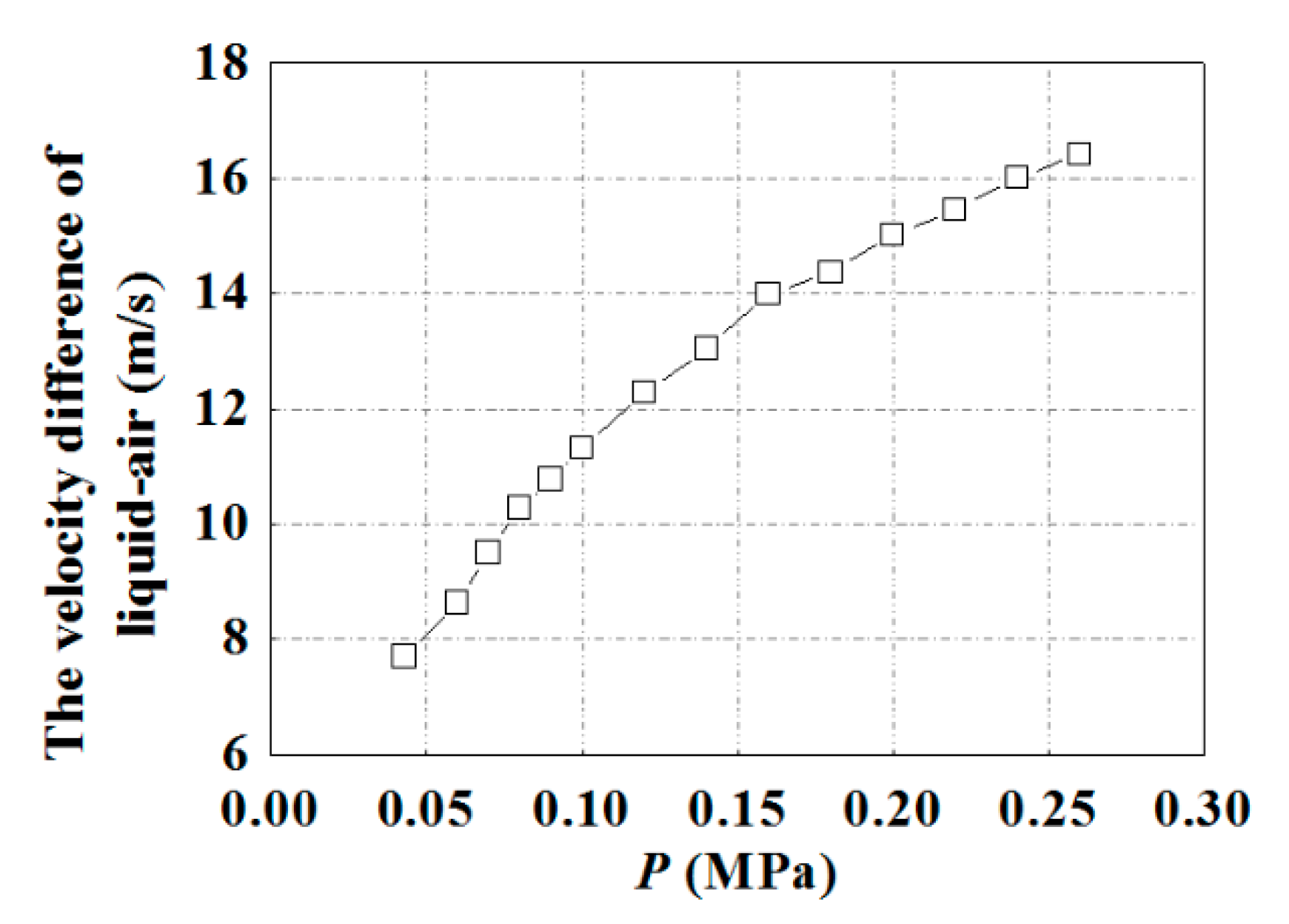
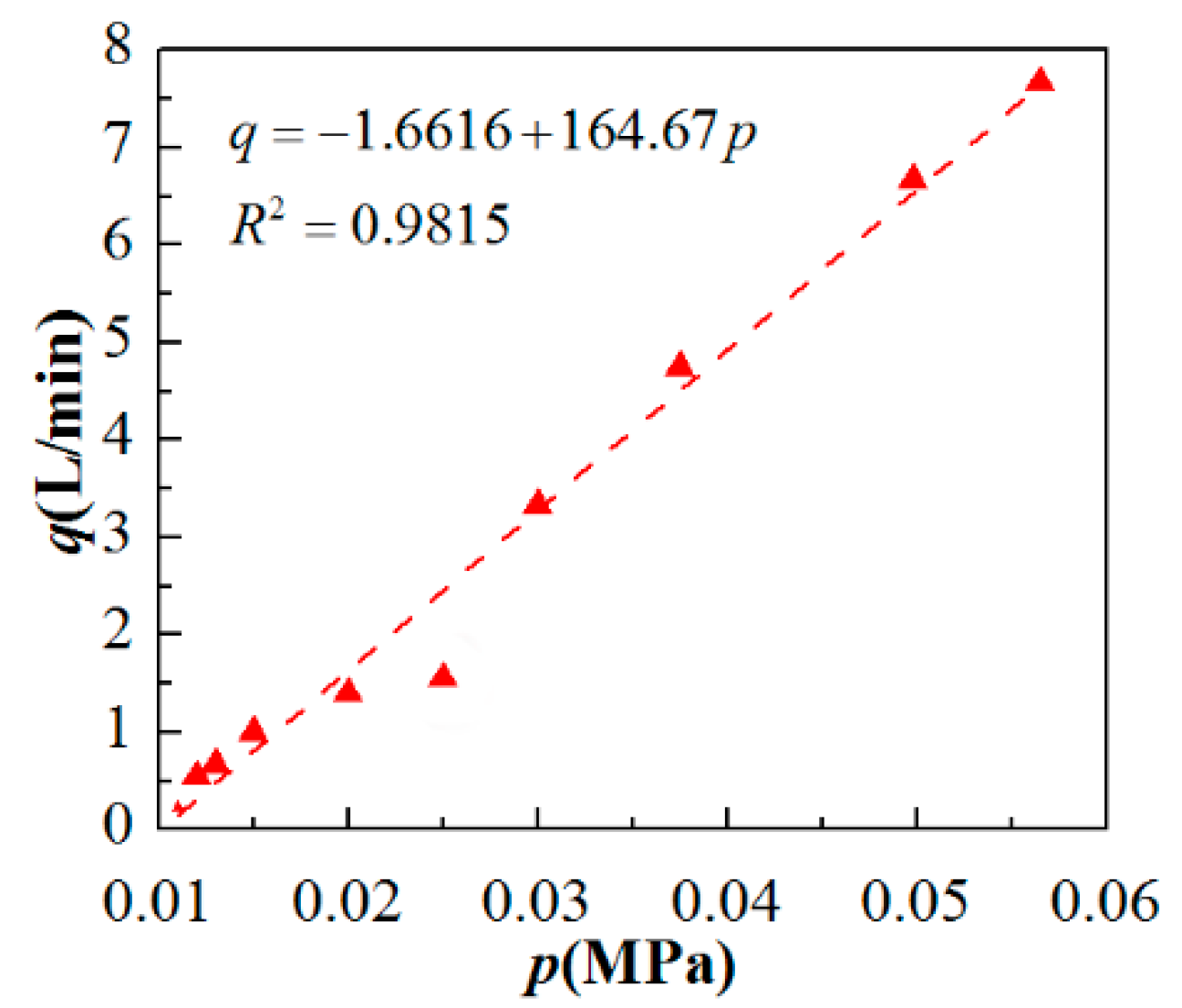
4.1. Effect of Feeding Pressure on Suction Capacity and Negative Pressure in a Double Cosine Self-Aspirated Nozzle
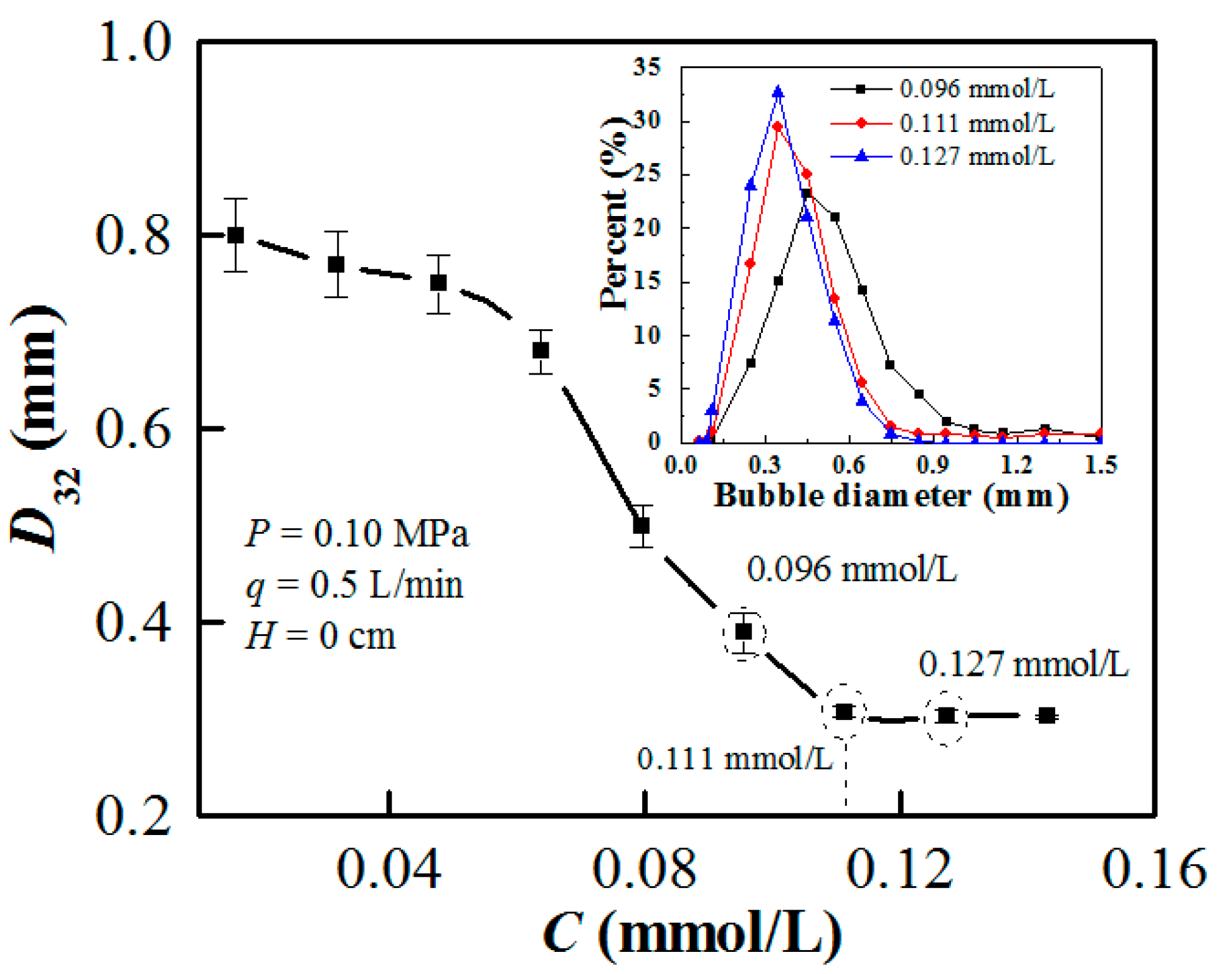
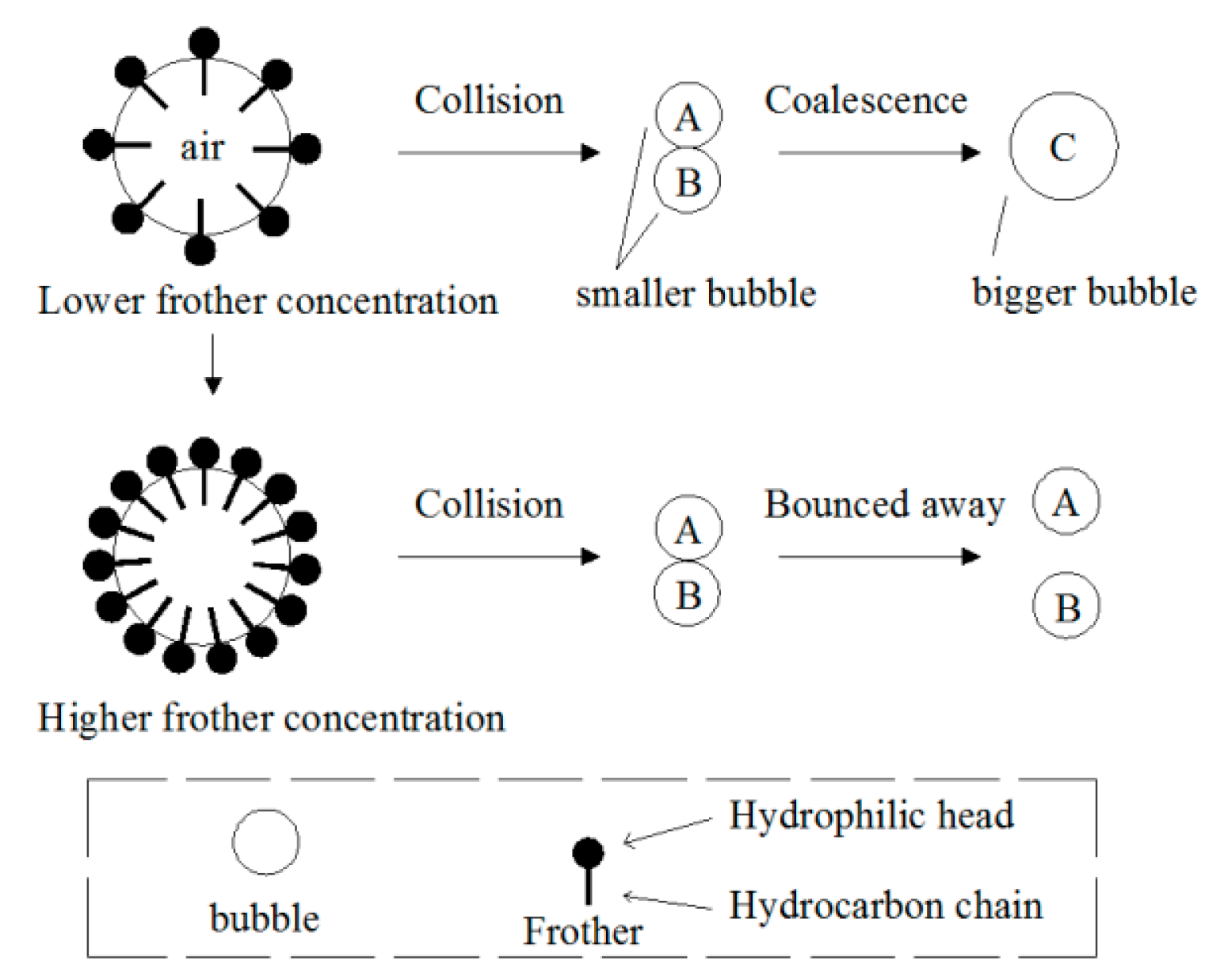
4.2. Effect of Frother Concentration on Bubble Size Distribution
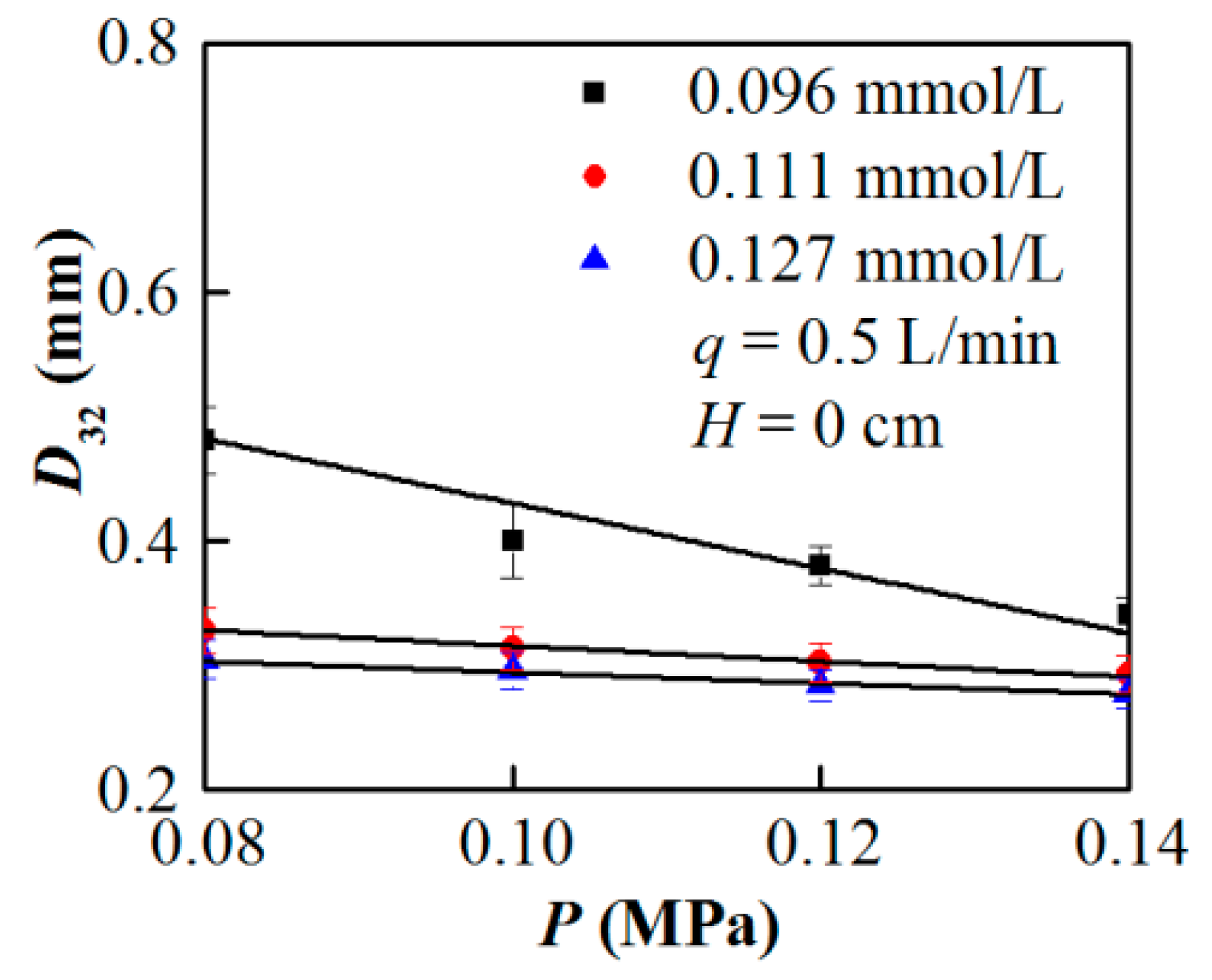
4.3. Effect of Feeding Pressure on Bubble Size
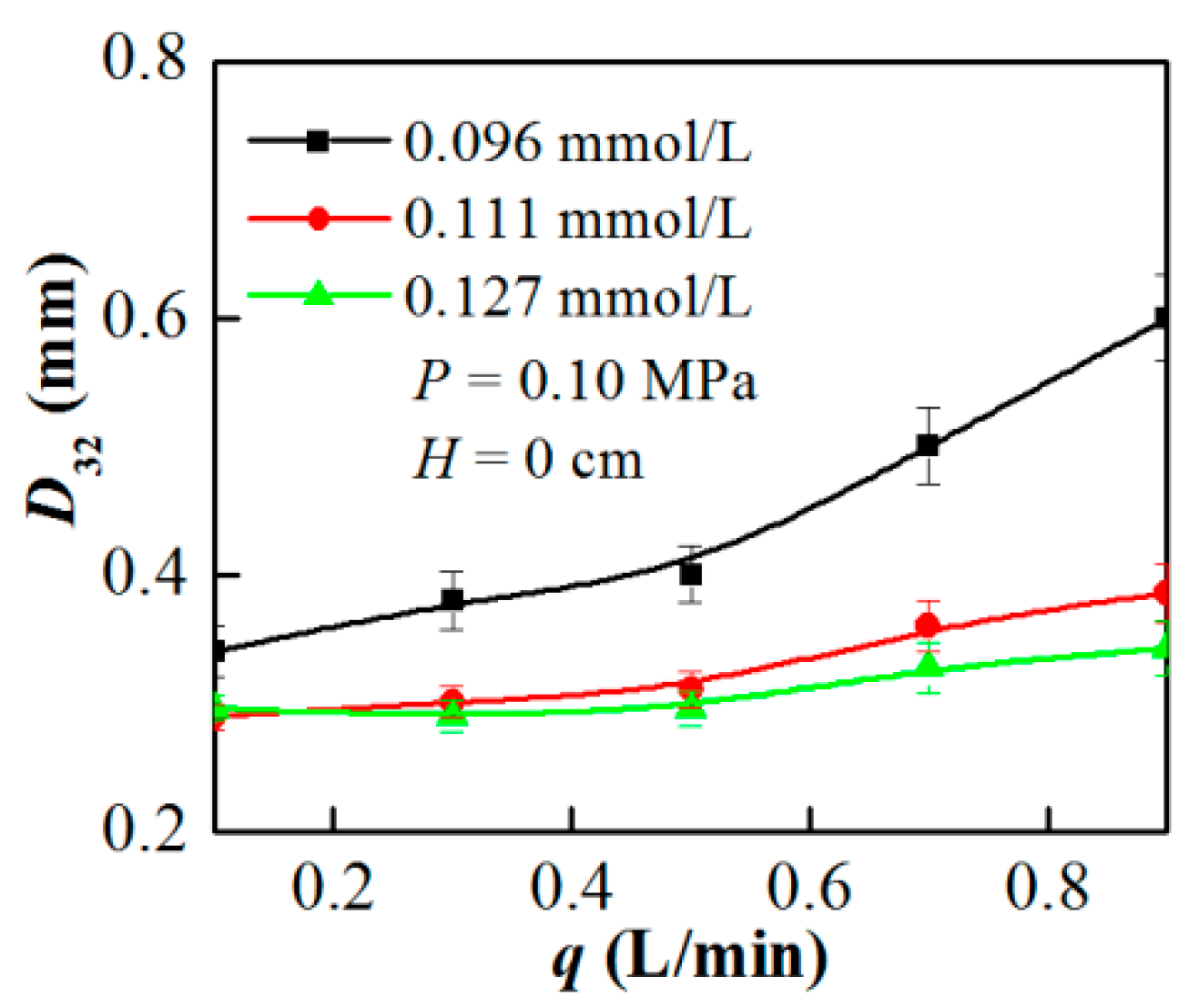
4.4. Effect of Suction Capacity on Bubble Size
4.5. Effect of Sampling Location on Bubble Size
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mesa, D.; Brito-Parada, P.R. Scale-up in froth flotation: A state-of-the-art review. Sep. Purif. Technol. 2019, 210, 950–962. [Google Scholar] [CrossRef]
- Xing, Y.; Xu, M.; Li, M.; Jin, W.; Cao, Y.; Gui, X. Role of DTAB and SDS in bubble-particle attachment: AFM force measurement, attachment behaviour visualization, and contact angle study. Minerals 2018, 8, 349. [Google Scholar] [CrossRef]
- Harris, C.C.; Khandrika, S.M. Flotation machine design: Impeller—Stator interaction. Powder Technol. 1985, 43, 273–278. [Google Scholar] [CrossRef]
- Jameson, G.J. New directions in flotation machine design. Miner. Eng. 2010, 23, 835–841. [Google Scholar] [CrossRef]
- Dey, S.; Paul, G.M.; Pani, S. Flotation behaviour of weathered coal in mechanical and column flotation cell. Powder Technol. 2013, 246, 689–694. [Google Scholar] [CrossRef]
- Li, S.; Lu, D.; Chen, X.; Zheng, X.; Li, X.; Chu, H.; Wang, Y. Industrial application of a modified pilot-scale Jameson cell for the flotation of spodumene ore in high altitude area. Powder Technol. 2017, 320, 358–361. [Google Scholar] [CrossRef]
- Şahbaz, O.; Uçar, A.; Öteyaka, B.; Taş, O.Ö.; Özdemir, O. Separation of colemanite from tailings using the pilot scale flotation column. Powder Technol. 2017, 309, 31–36. [Google Scholar] [CrossRef]
- Shen, Z.; Zhang, M.; Fan, X.; Shi, S.; Han, D. Hydrodynamic and flotation kinetic analysis of a large scale mechanical agitated flotation cell with the typical impeller and the arc impeller. Minerals 2019, 9, 79. [Google Scholar] [CrossRef]
- Zhang, W. Evaluation of effect of viscosity changes on bubble size in a mechanical flotation cell. Trans. Nonferrous Met. Soc. China 2014, 24, 2964–2968. [Google Scholar] [CrossRef]
- Sobhy, A.; Tao, D. Nanobubble column flotation of fine coal particles and associated fundamentals. Int. J. Miner. Process. 2013, 124, 109–116. [Google Scholar] [CrossRef]
- Lin, L.L.; Liu, J.; Wang, L.; Yu, H. Numerical simulation of a self-absorbing microbubble generator for a cyclonic-static microbubble flotation column. Min. Sci. Technol. 2010, 20, 88–92. [Google Scholar]
- Karagüzel, C.; Çobanoğlu, G. Stage-wise flotation for the removal of colored minerals from feldspathic slimes using laboratory scale Jameson cell. Sep. Purif. Technol. 2010, 74, 100–107. [Google Scholar] [CrossRef]
- Gordiychuk, A.; Svanera, M.; Benini, S.; Poesio, P. Size distribution and Sauter mean diameter of micro bubbles for a Venturi type bubble generator. Exp. Therm. Fluid Sci. 2016, 70, 51–60. [Google Scholar] [CrossRef]
- Uçurum, M. Influences of Jameson flotation operation variables on the kinetics and recovery of unburned carbon. Powder Technol. 2009, 191, 240–246. [Google Scholar] [CrossRef]
- Zhang, M.; Li, T.; Wang, G. A CFD study of the flow characteristics in a packed flotation column: Implications for flotation recovery improvement. Int. J. Miner. Process. 2017, 159, 60–68. [Google Scholar] [CrossRef]
- Yan, X.; Shi, R.; Xu, Y.; Wang, A.; Liu, Y.; Wang, L.; Cao, Y. Bubble behaviors in a lab-scale cyclonic-static micro-bubble flotation column. Asia-Pac. J. Chem. Eng. 2016, 11, 939–948. [Google Scholar] [CrossRef]
- Li, Y.; Pan, H.; Li, N.; Jiang, W.; Li, Y.; Zhang, W.; Peng, Z. Design and experimental study of a modified cyclonic microbubble flotation column system. Int. J. Coal Prep. Util. 2017, 37, 1–9. [Google Scholar] [CrossRef]
- Wang, C. The Structure Optimization and Bubble Production Mechanism Study of Annular Jet Suction Mixing Device; Anhui University of Science and Technology: Huainan, China, 2016. [Google Scholar]
- Xing, Y.; Gui, X.; Pan, L.; Pinchasik, B.-E.; Cao, Y.; Liu, J.; Kappl, M.; Butt, H.-J. Recent experimental advances for understanding bubble-particle attachment in flotation. Adv. Colloid Interface Sci. 2017, 246, 105–132. [Google Scholar] [CrossRef]
- Albijanic, B.; Ozdemir, O.; Hampton, M.A.; Nguyen, P.T.; Nguyen, A.V.; Bradshaw, D. Fundamental aspects of bubble–particle attachment mechanism in flotation separation. Miner. Eng. 2014, 65, 187–195. [Google Scholar] [CrossRef]
- Zangooi, A.; Gomez, C.O.; Finch, J.A. Mapping frother distribution in industrial flotation circuits. Miner. Eng. 2017, 113, 36–40. [Google Scholar] [CrossRef]
- Besagni, G.; Inzoli, F. Bubble size distributions and shapes in annular gap bubble column. Exp. Therm. Fluid Sci. 2016, 74, 27–48. [Google Scholar] [CrossRef]
- Alam, R.; Shang, J.Q.; Khan, A.H. Bubble size distribution in a laboratory-scale electroflotation study. Environ. Monit. Assess. 2017, 189, 193. [Google Scholar] [CrossRef] [PubMed]
- Finch, J.A.; Nesset, J.E.; Acuña, C. Role of frother on bubble production and behaviour in flotation. Miner. Eng. 2008, 21, 949–957. [Google Scholar] [CrossRef]
- Zhang, W.; Nesset, J.E.; Finch, J.A. Effect of some operational variables on bubble size in a pilot-scale mechanical flotation machine. J. Cent. South Univ. 2014, 21, 1077–1084. [Google Scholar] [CrossRef]
- Sovechles, J.M.; Lepage, M.R.; Johnson, B.; Waters, K.E. Effect of gas rate and impeller speed on bubble size in frother-electrolyte solutions. Miner. Eng. 2016, 99, 133–141. [Google Scholar] [CrossRef]
- Besagni, G.; Brazzale, P.; Fiocca, A.; Inzoli, F. Estimation of bubble size distributions and shapes in two-phase bubble column using image analysis and optical probes. Flow Meas. Instrum. 2016, 52, 190–207. [Google Scholar] [CrossRef]
- Szyszka, D. Critical Coalescence Concentration (CCC) for surfactants in aqueous solutions. Minerals 2018, 8, 431. [Google Scholar] [CrossRef]
- Grau, R.A.; Laskowski, J.S.; Heiskanen, K. Effect of frothers on bubble size. Int. J. Miner. Process. 2005, 76, 225–233. [Google Scholar] [CrossRef]
- Grau, R.A.; Heiskanen, K. Gas dispersion measurements in a flotation cell. Miner. Eng. 2003, 16, 1081–1089. [Google Scholar] [CrossRef]
- Gomez, C.O.; Finch, J.A. Gas dispersion measurements in flotation cells. Int. J. Miner. Process. 2007, 84, 51–58. [Google Scholar] [CrossRef]
- Acuña, C.A.; Finch, J.A. Tracking velocity of multiple bubbles in a swarm. Int. J. Miner. Process. 2010, 94, 147–158. [Google Scholar] [CrossRef]
- Prakash, R.; Majumder, S.K.; Singh, A. Particle-laden bubble size and its distribution in microstructured bubbling bed in the presence and absence of a surface active agent. Ind. Eng. Chem. Res. 2019, 58, 3499–3522. [Google Scholar] [CrossRef]
- Zhu, H.; Valdivieso, A.L.; Zhu, J.; Song, S.; Min, F.; Arroyo, M.A.C. A study of bubble size evolution in Jameson flotation cell. Chem. Eng. Res. Des. 2018, 137, 461–466. [Google Scholar] [CrossRef]
- Vinnett, L.; Contreras, F.; Yianatos, J. Gas dispersion pattern in mechanical flotation cells. Miner. Eng. 2012, 26, 80–85. [Google Scholar] [CrossRef]
- Laskowski, J.S.; Tlhone, T.; Williams, P.; Ding, K. Fundamental properties of the polyoxypropylene alkyl ether flotation frothers. Int. J. Miner. Process. 2003, 72, 289–299. [Google Scholar] [CrossRef]
- Quinn, J.J.; Sovechles, J.M.; Finch, J.A.; Waters, K.E. Critical coalescence concentration of inorganic salt solutions. Miner. Eng. 2014, 58, 1–6. [Google Scholar] [CrossRef]
- Corona-Arroyo, M.A.; López-Valdivieso, A.; Laskowski, J.S.; Encinas-Oropesa, A. Effect of frothers and dodecylamine on bubble size and gas holdup in a downflow column. Miner. Eng. 2015, 81, 109–115. [Google Scholar] [CrossRef]
- Tan, Y.H.; Rafiei, A.A.; Elmahdy, A.; Finch, J.A. Bubble size, gas holdup and bubble velocity profile of some alcohols and commercial frothers. Int. J. Miner. Process. 2013, 119, 1–5. [Google Scholar] [CrossRef]
- Azgomi, F.; Gomez, C.O.; Finch, J.A. Correspondence of gas holdup and bubble size in presence of different frothers. Int. J. Miner. Process. 2007, 83, 1–11. [Google Scholar] [CrossRef]
- Chu, P.; Waters, K.E.; Finch, J.A. Break-up in formation of small bubbles: Break-up in a confined volume. Colloids Surf. A Physicochem. Eng. Asp. 2016, 503, 88–93. [Google Scholar] [CrossRef]

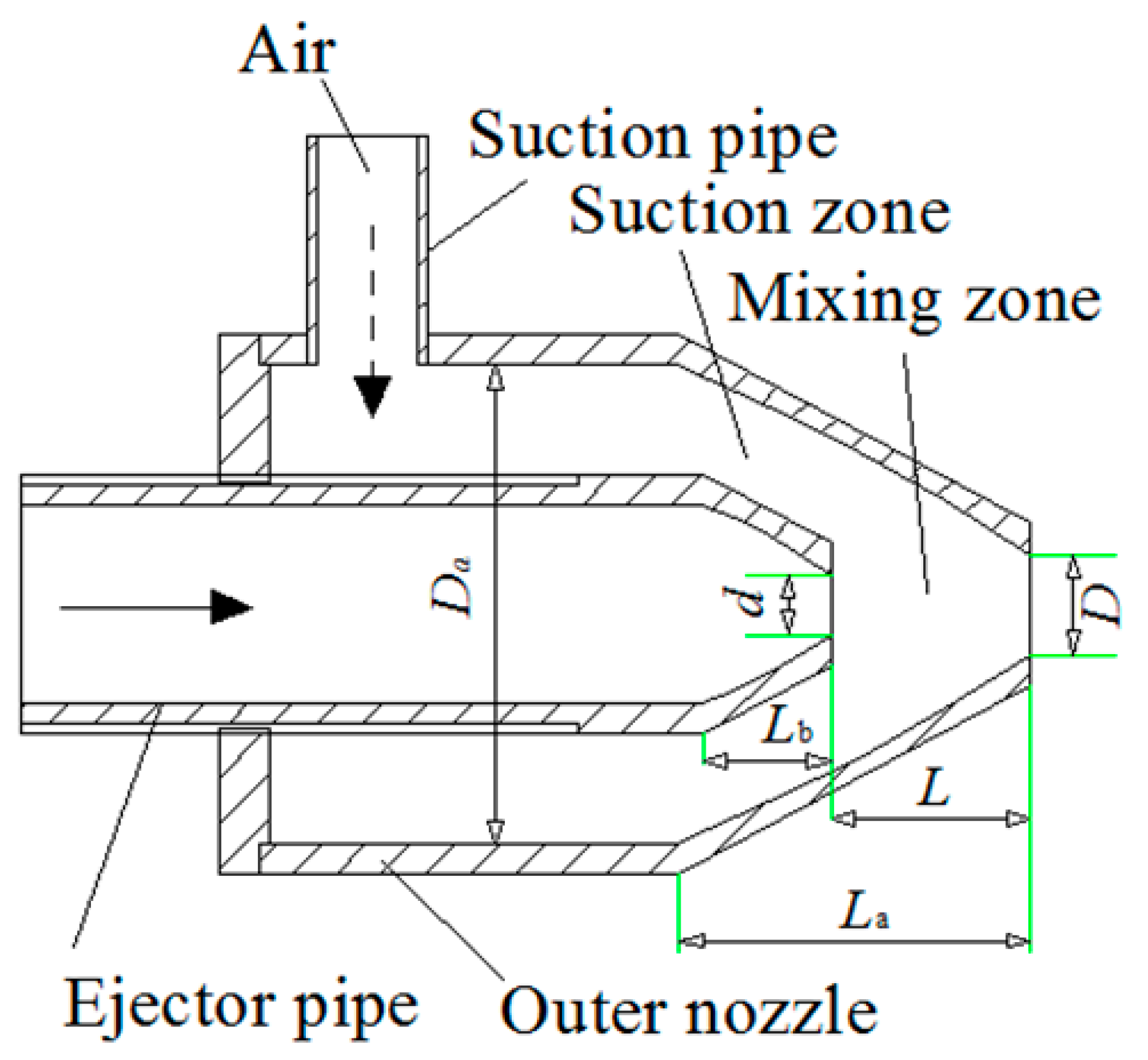


| Length of Outer Nozzle Cosine Section | Diameter of Outer Nozzle Circular Tube Section | Diameter of Outer Nozzle Cosine Section Outlet | Length of Ejector Pipe Cosine Section |
|---|---|---|---|
| La/mm | Da/mm | D/mm | Lb/mm |
| 35 | 48 | 7 | 13 |
| Diameter of Ejector Pipe Cosine Section Outlet | Outlet Distance between Ejector Pipe and Outer Nozzle | Cone Angle of Ejector Pipe Cosine Section | Cone Angle of Outer Nozzle Cosine Section |
| d/mm | L/mm | β/° | d/mm |
| 6 | 20 | 28 | 6 |
| Driving Impeller | Stirring Impeller | Circulating Tank | Diameter of Draft Tube/mm | Distance between Stirring Impeller and False Bottom/mm | Diameter of Mixing Tank/mm | ||
|---|---|---|---|---|---|---|---|
| Length × Width/mm | Diameter/mm | Length × Width /mm | Diameter/mm | Length × Width × Height/mm | |||
| 30 × 35 | 150 | 30 × 75 | 150 | 250 × 250 × 600 | 70 | 25 | 160 |
| The Feeding Pressure | The Volumetric Flow Rate of Air | The Volumetric Flow Rate of Liquid | The Air Flow Velocity | The Liquid Flow Velocity | The Velocity Difference of Liquid-Air |
|---|---|---|---|---|---|
| MPa | m3/h | m3/h | m/s | m/s | m/s |
| 0.04 | 0.012 | 0.788 | 0.044 | 7.746 | 7.70 |
| 0.06 | 0.014 | 0.883 | 0.050 | 8.679 | 8.63 |
| 0.07 | 0.020 | 0.974 | 0.070 | 9.574 | 9.50 |
| 0.08 | 0.032 | 1.058 | 0.115 | 10.399 | 10.28 |
| 0.09 | 0.035 | 1.109 | 0.123 | 10.901 | 10.78 |
| 0.10 | 0.055 | 1.172 | 0.195 | 11.520 | 11.32 |
| 0.12 | 0.060 | 1.271 | 0.212 | 12.493 | 12.28 |
| 0.14 | 0.084 | 1.357 | 0.297 | 13.338 | 13.04 |
| 0.16 | 0.093 | 1.456 | 0.329 | 14.312 | 13.98 |
| 0.18 | 0.200 | 1.534 | 0.708 | 15.078 | 14.37 |
| 0.20 | 0.285 | 1.631 | 1.008 | 16.032 | 15.02 |
| 0.22 | 0.340 | 1.695 | 1.203 | 16.661 | 15.46 |
| 0.24 | 0.400 | 1.772 | 1.415 | 17.418 | 16.00 |
| 0.26 | 0.460 | 1.836 | 1.628 | 18.047 | 16.42 |
| Flotation Machine | D32/mm | References |
|---|---|---|
| Mechanical flotation cell | 0.80–0.90 | [26,28] |
| Jameson cell | 0.65–0.70 | [34,38] |
| Column flotation | 0.75–0.80 | [39,40] |
| Frother Concentration/(mmol/L) | Slope of Fitting | Intercept | ∆D32 a | R2 |
|---|---|---|---|---|
| 0.096 | −2.60 | 0.690 | 0.213 | 0.9742 |
| 0.111 | −0.62 | 0.378 | 0.050 | 0.9861 |
| 0.127 | −0.44 | 0.338 | 0.033 | 0.9787 |
| Frother Concentration/(mmol/L) | Fitting Equations |
|---|---|
| 0.096 | D32 = 0.02060H + 0.39801 |
| 0.111 | D32 = 0.00857H + 0.30337 |
| 0.127 | D32 = 0.00476H + 0.29760 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Y.; Zhu, J.; Shen, L.; Zhou, W.; Ling, Y.; Yang, X.; Wang, S.; Dong, Q. Bubble Size Distribution Characteristics of a Jet-Stirring Coupling Flotation Device. Minerals 2019, 9, 369. https://doi.org/10.3390/min9060369
Han Y, Zhu J, Shen L, Zhou W, Ling Y, Yang X, Wang S, Dong Q. Bubble Size Distribution Characteristics of a Jet-Stirring Coupling Flotation Device. Minerals. 2019; 9(6):369. https://doi.org/10.3390/min9060369
Chicago/Turabian StyleHan, Youli, Jinbo Zhu, Liang Shen, Wei Zhou, Yunjia Ling, Xinyue Yang, Shuo Wang, and Qiao Dong. 2019. "Bubble Size Distribution Characteristics of a Jet-Stirring Coupling Flotation Device" Minerals 9, no. 6: 369. https://doi.org/10.3390/min9060369
APA StyleHan, Y., Zhu, J., Shen, L., Zhou, W., Ling, Y., Yang, X., Wang, S., & Dong, Q. (2019). Bubble Size Distribution Characteristics of a Jet-Stirring Coupling Flotation Device. Minerals, 9(6), 369. https://doi.org/10.3390/min9060369