1. Introduction
Numerous studies were carried out on spinels because of their chemical and structural simplicity, their geological importance, and their use as geothermometers, geobarometers, and geospeedometers (e.g., [
1,
2]). Spinel-supergroup minerals have the general formula, AB
2O
4. The A and B cation charges may be either +2 and +3 (e.g., spinel, MgAl
2O
4, and magnesioferrite, MgFe
2O
4), or +4 and +2 (e.g., ulvöspinel, TiFe
2O
4, and qandilite, TiMg
2O
4). The formal charge of A and B constituents can range from 0 to +6 [
3]. In “normal” spinels, the A constituent occupies the 4-coordinated tetrahedral
T site and the B constituent occupies the 6-coordinated octahedral metal
M site [
4]. In “inverse” spinels, the
T site contains only B cations and the
M site contains an equal number of A and B cations, so the
M site is fully disordered. Intermediate spinels may be expressed as a mix of normal and inverse end-members, with the general formula,
[4][A
1−xB
x]
[6](A
xB
2−x)O
4, where the variable
x is referred to as the “inversion parameter”. This
x is the fraction of B cations at the
T site. In normal spinels
x = 0, and in inverse spinels
x = 1. A value of
x = 2/3 corresponds to a random distribution of A and B atoms. Alternatively, an order parameter,
Q, is used to express the degree of order [
5]. The order parameter,
Q, varies from
Q = 1 for a completely ordered normal spinel to
Q = 0 (where
x = 2/3) for a random arrangement of cations to
Q = −0.5 in inverse spinel. The relationship between
Q and
x is:
Q = 1 – (3/2)
x. Magnesioferrite, MgFe
2O
4, is partly inverse and partly normal, so it is one of the most interesting ferrite spinels [
6,
7,
8].
The structure of cubic spinels consists of T cations at 8a (1/8, 1/8, 1/8), M cations at 16d (½, ½, ½), and O atoms on the body diagonals of a cube at 32e (u, u, u), where u is approximately ¼ in space group Fdm. In a cubic spinel structure, there are only two structural variables (except displacement parameters): the a unit-cell parameter and the O atom positional parameter, u.
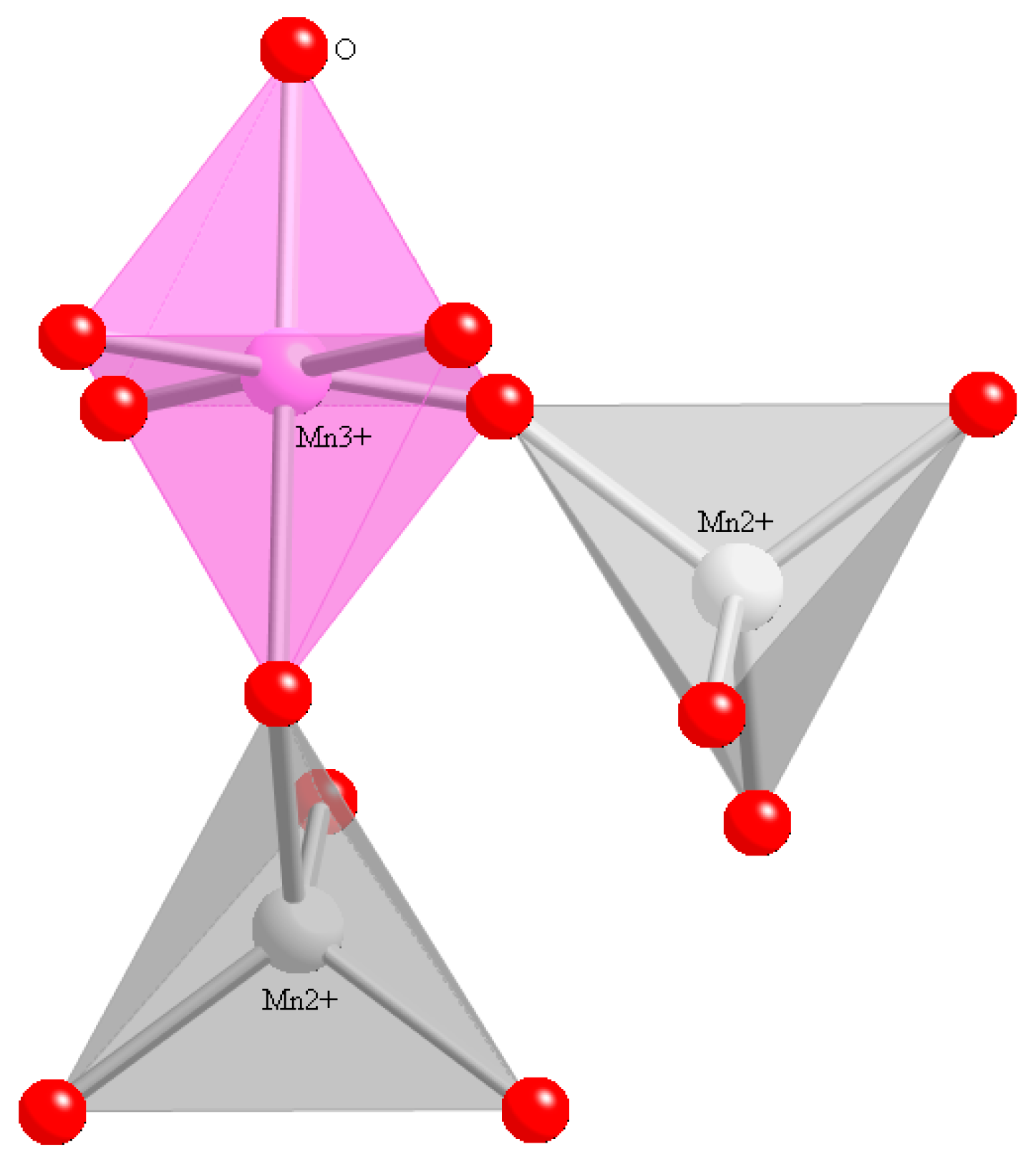
Hausmannite, ideally Mn
3O
4, is a normal spinel with a distorted tetragonal structure (
Figure 1). End-member hausmannite structural formula is
[4][Mn
2+]
[6](Mn
23+)O
4. The
T site may be occupied by divalent cations (e.g., Mn
2+, Mg
2+, Zn
2+, or Fe
2+), and the Jahn–Teller elongated
MO
6 octahedron may be occupied by trivalent cations (e.g., Mn
3+, Fe
3+, or Al
3+). These two types of substitutions should give rise to different structural features. Hetaerolite, ideally ZnMn
2O
4, is isostructural with hausmannite [
9]. Many natural samples belong to the hausmannite–hetaerolite series [MnMn
2O
4–ZnMn
2O
4], where the main substitution is between Mn
2+and Zn
2+ cations. Such series gives rise to well-defined structural variations in hausmannite solid solutions because the divalent cations have similar sizes (e.g., [
10,
11]).
Gutzmer et al. [
13] reported both magnetic and non-magnetic hausmannite samples from Kalahari manganese field (KMF; samples-2 and -3 in
Table 1). It seems that substitution of Fe
3+ cations at the
M site give rise to a magnetic sample. Substitution of Mn
3+ (0.645 Å, HS) by Fe
3+ (0.645 Å, HS) cations results in minor, but measurable changes in unit-cell parameters, and a decrease of Jahn–Teller distortion with increasing Fe
3+ concentrations [
14]. Neutron diffraction results at 10 K from Baron et al. [
14] indicate that Fe-rich hausmannite is not the source for high-temperature (Curie temperature of 750 K) ferrimagnetism in hausmannite-rich ores from the KMF that was described by Gutzmer et al. [
13]. The authors indicated that minor amounts of Mn-bearing hematite in the hausmannite-rich ores may be the source for the unusual magnetic properties, but this was not confirmed. There appear to be two different types of hausmannite samples from the KMF. One type has substitution of divalent cations at the
T site, and the other type has substitution of trivalent cations at the
M site as well as at the
T site. These different types of samples are investigated further in this study.
The crystal structure of hausmannite is that of a tetragonally-deformed cubic spinel structure [
15]. Satomi [
16] reported unit-cell parameters for a synthetic Mn
3O
4 (sample-1;
Table 1). The magnetic structure of hausmannite from a polycrystalline sample was examined by neutron methods and aspects of the structure were discussed [
14,
17,
18]. Thereafter, several structural studies were carried out on hausmannite (
Table 1). Structural data for ZnMn
2O
4 [
19] and MgMn
2O
4 [
20] are also available.
In hausmannite, the
T and
M sites are at fixed positions and the O-atom coordinate is at (0,
x,
y). The O atom is positioned to balance between the co–Operative Jahn–Teller distortion around the Mn
3+ site, stretching of the Mn
3+O
6 octahedron along [001], countered by the force of the tetrahedron preserving its regular form against the tetragonal deformation of the structure [
16,
22]. The chemical bonds in spinels influence the cation ordering, the structural distortion, and the magnetic-exchange interactions [
23]. In hausmannite, the four short Mn
3+–O bonds around the octahedrally-co–Ordinated Mn
3+ cations are covalent, and the two longest bonds have an ionic character [
23]. In contrast, the four Mn
2+–O bonds around the tetrahedral
T sites have characteristics that are between ionic and covalent.
Under normal pressure conditions, hausmannite has two crystallographic forms: a tetragonal low-temperature form and a cubic high-temperature form [
24,
25]. The cubic-tetragonal transition occurs at 1170 °C where there is no Jahn–Teller distortion. The structure is deformed during the transition to the tetragonal structure that contains Jahn–Teller elongation [
24]. In the tetragonal hausmannite structure, the O atoms form a tetragonally distorted cubic close-packed structure where the tetrahedral and octahedral sites are occupied by Mn
2+ and Mn
3+ cations, respectively [
24]. The tetragonal hausmannite crystal structure has space group
I4
1/
amd [
24]. The structure of a hausmannite from Langbån, Sweden is known [
21].
Hausmannite is relatively uncommon, but it has a wide field of stability. It is usually found with other manganese oxide minerals in metamorphosed or hydrothermal manganese ores [
24], but euhedral crystals are rare. Hausmannite occurs in a few localities such as Ilmanau, Thuringia, Germany and the Kalahari manganese field (KMF), South Africa [
14]. It is typically ferrimagnetic, but a strong magnetic sample was discovered in the hydrothermally altered KMF [
13]. In the KMF, the manganese ores are interbedded with the iron-rich Hotazel formation and are preserved in erosional relict basins [
13]. Within the high-grade Wessels type manganese ore, normal faults acted as conduits for hydrothermal fluids which caused hematitization of the manganese ores. This high-grade manganese ore is coarse grained and contains hausmannite, bixbyite, marokite, and hematite [
13].
The unit-cell parameters of Mn
3−xFe
xO
4 hausmannite indicate decreasing Jahn–Teller distortion with increasing Fe content, which also causes an increase in the Curie temperature [
14]. Their study seems to indicate that Fe-rich hausmannite causes the unusual high-temperature ferrimagnetic behavior in the KMF. Iron-rich hausmannite, containing up to 11.3 wt % of Fe
2O
3, has unit-cell parameters that are smaller along the
a axis and larger along the
c axis than pure Mn
3O
4. These parameters shrink along the
a axis and expand along the
c axis, proportional to increasing Fe content [
14].
This study examines the crystal chemistry of two different hausmannite samples from the KMF using electron-probe microanalysis (EPMA). The crystal structure of sample-a was obtained with single-crystal X-ray diffraction (SCXRD) data, whereas that for samples-b and -c were obtained from Rietveld structure refinement using synchrotron high-resolution powder X-ray diffraction (HRPXRD) data. These results are compared with data from the literature (
Table 1).
3. Results and Discussion
Backscattered electron (BSE) images of sample-a revealed the presence of hausmannite within henritermierite garnet (see Figure 8 in [
12]). The chemical composition for sample-a is [Mn
2+0.88Mg
0.11Fe
2+0.01]
Σ2.00(Mn
3+)
2.00O
4, where the substitution is mainly between divalent Mn
2+and Mg
2+ cations at the
T site. In general, the Mn
2+ cation may be replaced by Mg
2+ or Fe
2+ cations. Among trivalent cations, Mn
3+ is the most abundant and may be replaced by Fe
3+ cations, but the amount of Mn
3+ cation is nearly constant at its maximum value of 2 for sample-a (
Table 2). The single-crystal structure refinement indicates that sample-a is close to pure Mn
3O
4 because both the
T and
M site occupancy factors (
sofs) refine to 1 (
Table 5). Consequently, both the M and O
sofs were fixed at 1.0 in the final refinement and
T(
sof) still refined to 1.0. The bond-valence sums around the three atom sites are close to the expected value for pure Mn
3O
4, where the
M site has 3.03 vu that corresponds to the Mn
3+ cation, the
T site has 2.05 vu that corresponds to the Mn
2+ cation, and the O site has 2.03 vu that corresponds to the O atom (
Table 8).
The chemical composition for sample-b is [Mn
0.99Mg
0.01](Mn
1.52Fe
0.48)O
4 (
Table 2) whereas the Rietveld structure refinement give the formula [Mn
0.82Fe
0.18](Mn
1.88Fe
0.12)O
4 (
Table 5), where the total amount of Fe atoms is 0.30, compared to 0.48 obtained by EPMA. The substitution of Fe
3+ for Mn
3+ cations at the
M site indicates that samples-a and -b should have different structural features. Sample-a has a shorter
T–O distance because some Mg
2+ (0.57 Å) replace Mn
2+ (0.66 Å) cations at the
T site. The Jahn–Teller elongation, Δ(
M–O), is larger in sample-a than sample-b (
Table 7). The difference in Jahn–Teller elongation of 0.034(1) Å between samples-a and -b is one of the most significant structural difference between these two samples.
Structural Trends for Hausmannite Solid Solutions
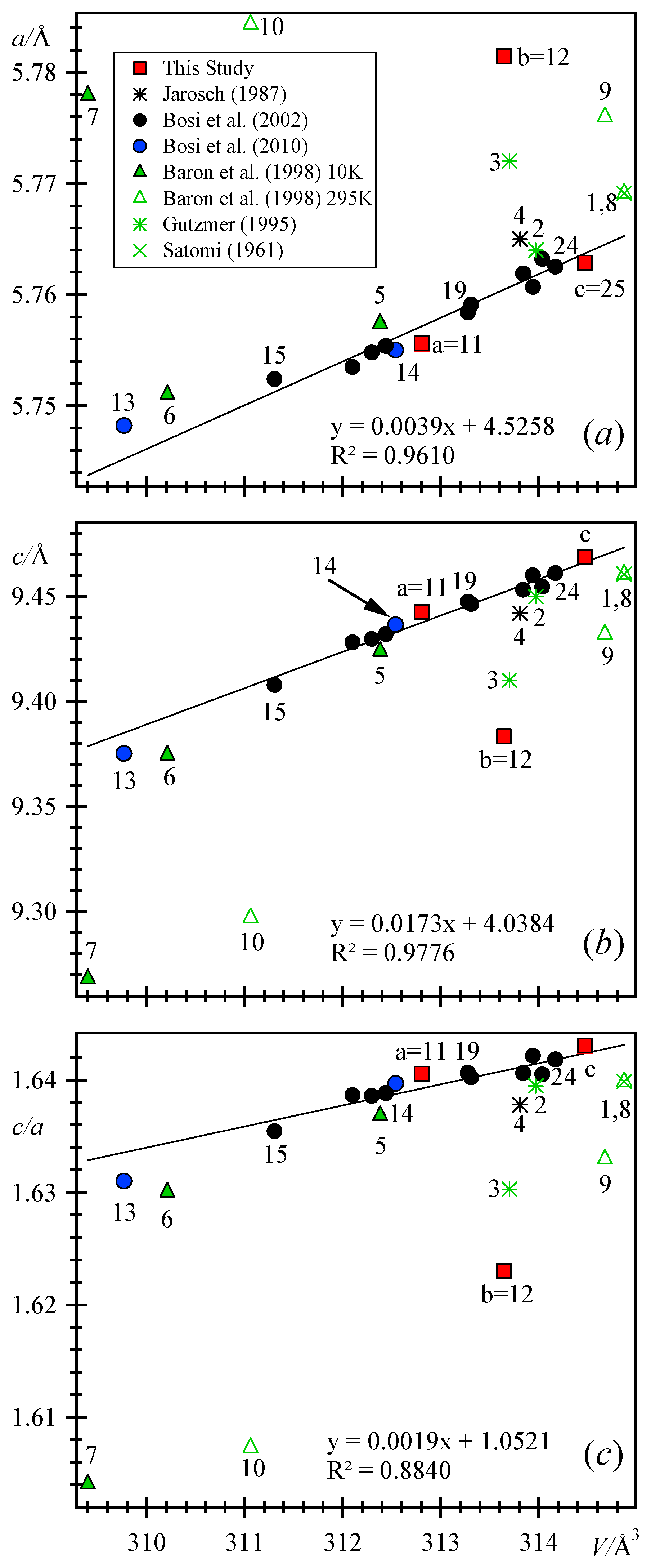
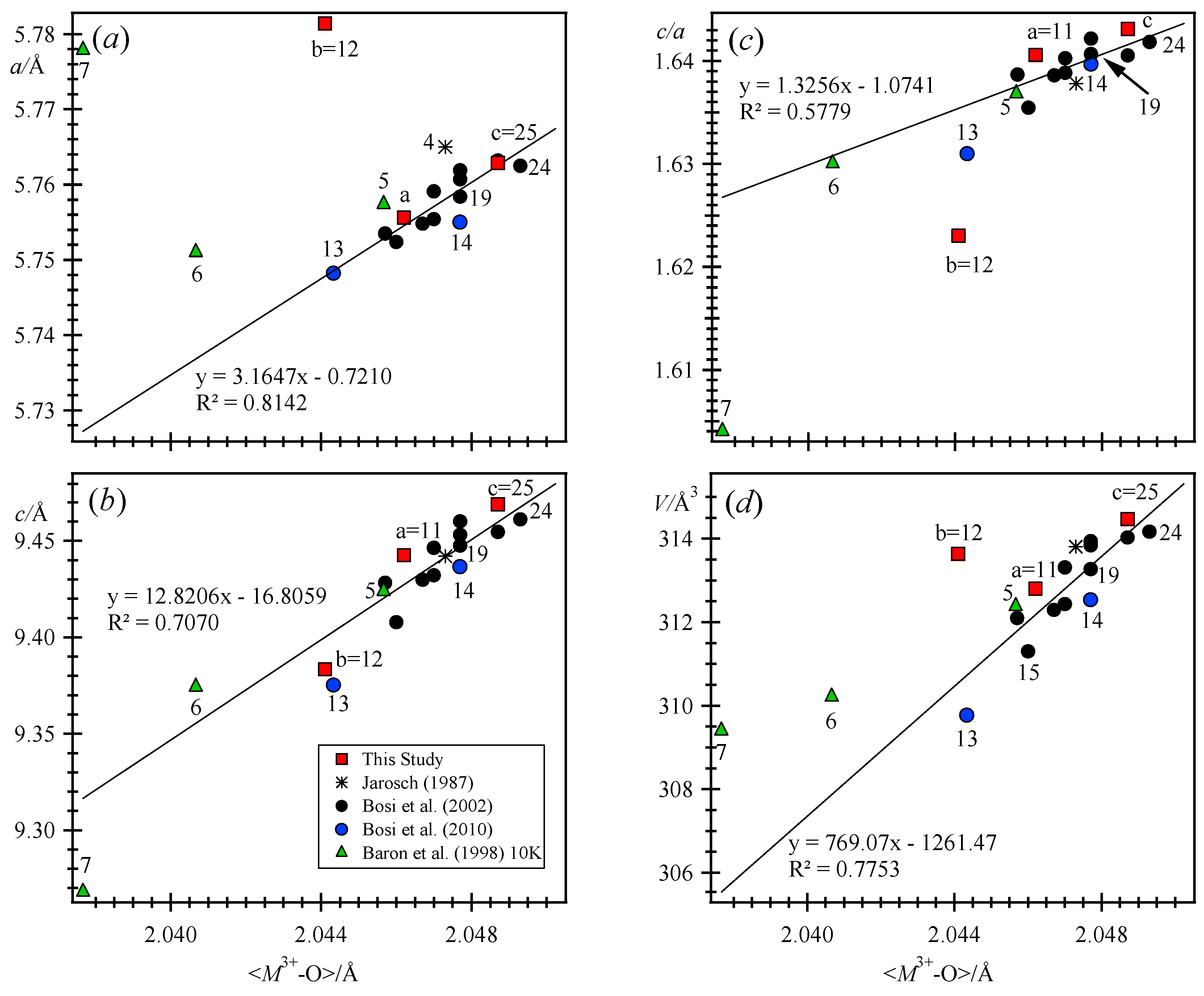
Chemical compositions, unit-cell parameters, and bond distances for 25 hausmannite samples are listed and their variations are shown graphically (
Table 1,
Figure 3,
Figure 4 and
Figure 5). Using data for samples-13 to -24 from Bosi et al. [
10,
11], linear trend lines were constructed. The equations for the linear lines and their R
2 values are given as inserts in each figure. The linear lines represent solid solutions incorporating Mg
2+, Fe
2+, or Zn
2+ cations in the place of Mn
2+ cations at the
T site (
Figure 3,
Figure 4 and
Figure 5). Substitution of Fe
3+ for Mn
3+ cations occur at the
M site in sample-b. The following cation radii from Shannon [
50] are of relevance for hausmannite solid solutions: tetrahedral four-coordinated Mn
2+ (0.66 Å), Fe
2+ (0.63 Å), Zn
2+ (0.60 Å), and Mg
2+ (0.57 Å) cations have similar sizes and may replace each other at the
T site. Similarly, octahedral six-coordinated Mn
3+ (0.645 Å, HS), Fe
3+ (0.645 Å, HS), and less likely Al
3+ (0.535 Å) cations may substitute for each other at the
M site.
Neutron data from Baron et al. [
14] gave structural data at 10 K for three samples (5–7;
Table 1). These neutron data appear to be incorrectly calculated and reported in the American Mineralogist Crystal Structure Database at 295 K (8 to 10;
Table 1). Unit-cell parameters (sample-1) from Satomi [
16] are unreliable because it does not plot close to pure hausmannite that corresponds to samples-24 and -c. The neutron data at 295 K (sample-8) assume sample-1 values in its calculations. Structural data for some nearly pure Mn
3O
4 are given (1, 4, 5, 8, and 21–23). Their deviations in values from nearly pure samples-24 and -c show what datasets are unreliable (1, 8–10 are unreliable;
Figure 3), so these four data points are not considered further.
Gutzmer et al. [
13] presented chemical compositions and unit-cell parameters for two samples from the KMF (2 is non-magnetic and 3 is magnetic;
Table 1). Sample-2 seems similar to pure Mn
3O
4 sample-c (
Figure 3). Sample-a (= 11) plots between samples-14 and -19 (
Figure 3). Sample-b has unit-cell parameters that are different from samples-3 and -7 (10 K data), but it seems plausible that both of these samples are similar to sample-b because all three samples are off the trend lines (
Figure 3). The magnetic property of samples-3 and -7, if present, may arise from the incorporation of Fe
3+ for Mn
3+ cations in hausmannite solid solutions [
14]. However our sample-b is not magnetic when tested with a hand magnet. Based on room-temperature data, sample-c has the largest
V among samples for which structures are available, whereas the Mg-rich sample-13 has the smallest
V.
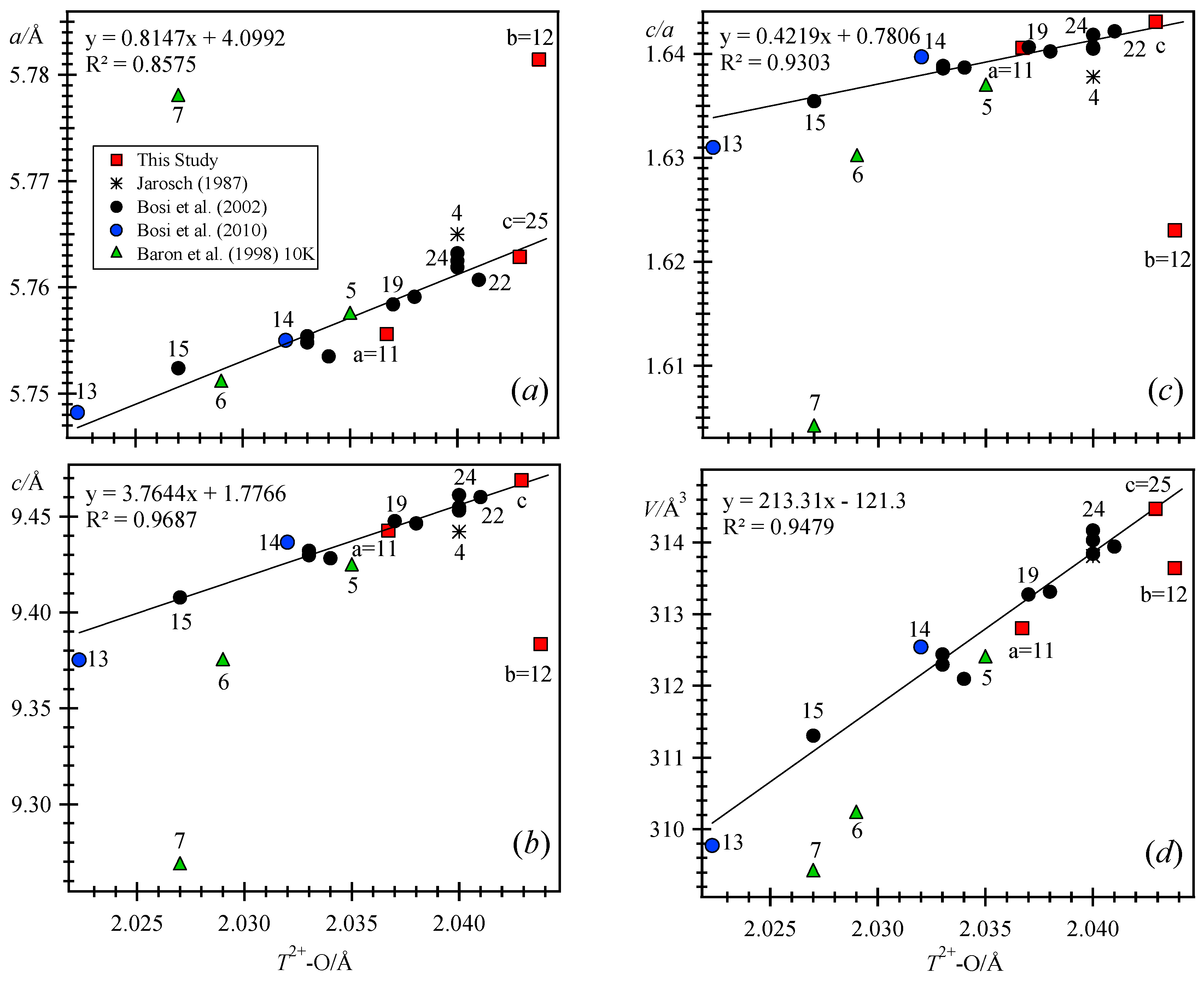
Figure 4 displays the <
T–O> distance against unit-cell parameters. Data for sample-a plots close to sample-19, but samples-b and -7 (10 K) are off the linear trend lines. Samples-b and -c have the largest but similar
T–O distances, whereas the Mg-rich sample-13 has the smallest
T–O distance. The trend lines correspond to substitution of divalent cations at the
T site. Substitution of smaller divalent cations for Mn
2+ at the
T site causes contraction of the
T–O distances, where sample-13 has the shortest distance (
Figure 4;
Table 1). Sample-13 also has the smallest unit-cell parameters because it contains the highest amount of Mg
2+ cations at the
T site. Samples-b and -7 contain a significant amount of Fe
3+ cations at the octahedral
M site, which affects the unit-cell parameters and
T–O distances (
Figure 4).
The average <
M–O> distance varies linearly with unit-cell parameters (
Figure 5). Data for samples-a and -c falls near the linear trend lines, but samples-b and -7 are off those lines. The trend lines correspond to substitution of divalent cations at the
T site. Substitution of trivalent cations at the
M site causes these samples to plot off the trend lines. The presence of Fe
3+ cations at the
M site causes less Jahn–Teller distortion in sample-b compared to sample-a, so the average <
M–O> is shorter in sample-b (
Table 7).
Substitution of cations at the octahedral
M site causes a change in the average <
M3+–O> distance and unit-cell parameters (
Figure 5). For the samples (13 to 24;
Table 1) for which the trend lines are based, the
M site is completely filled with Mn
3+ cations. Therefore, variations in the <
M3+–O> distance arise from the influence of the
T site cations. However, samples-b and -7 contain a significant amount of Fe
3+ cations at the
M site, so these samples are off the trend lines (
Figure 5). With respect to pure Mn
3O
4 (samples-24, -c), sample-b shows an enlargement of
a and contraction of the
c unit-cell parameter. Samples-c and -24 have the largest average <
M–O> distance, whereas the Mg-rich sample-13 has the smallest average <
M–O> distance.
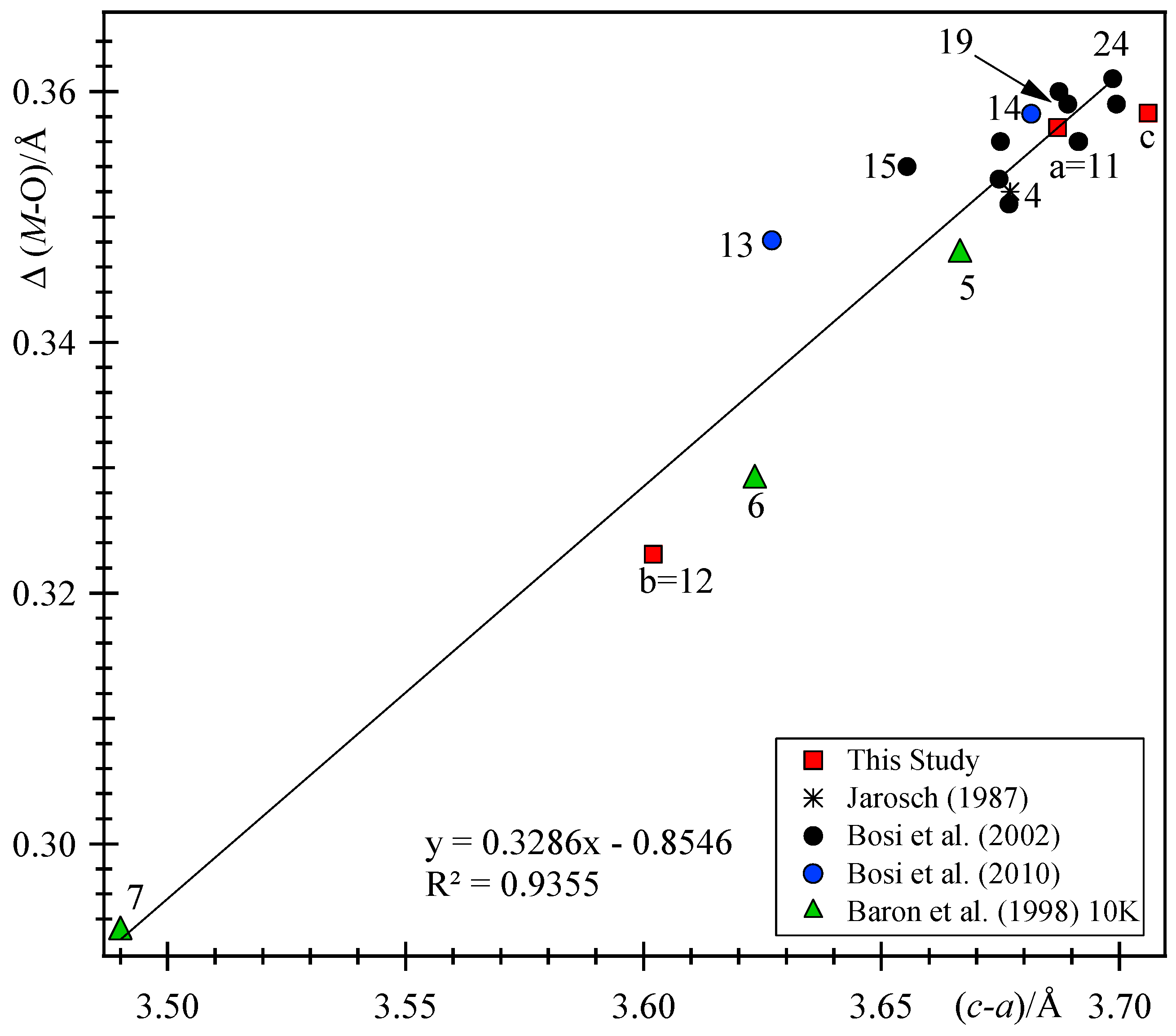
The Jahn–Teller elongation, Δ(
M–O), is less for sample-b compared to sample-a (
Table 6;
Figure 6). As the difference between the
a and
c unit-cell parameters, (
c-
a), becomes smaller, the Jahn–Teller elongation, Δ(
M–O), also becomes smaller (
Figure 6). For the samples in this study, sample-c has the highest Δ(
M–O), whereas sample-b has the lowest Δ(
M–O). At low temperature (10 K), sample-7 has the least distortion. The Mg-rich sample-13 has a small distortion. In the case of the tetragonal to cubic transition of hausmannnite, with increasing temperature, the
a and
c unit-cell parameters approach equality and Δ(
M–O) also approaches 0 towards the transition at 1170 °C.