1. Introduction
A hydrocyclone is a representative device that utilizes the principle of centrifugal sedimentation to effectively separate two-phase or multi-phase liquid-liquid, liquid-solid, and liquid-gas mixtures having components of different densities [
1,
2]. It has many applications such as separation [
3], sorting [
4], liquid concentration [
5], and liquid clarification [
6]. The greatest advantage of the hydrocyclone is that unlike other centrifugal separation devices, no moving components are required. The separation process is completed by the fluid itself, which forms a vortex within the hydrocyclone. Hydrocyclones have the characteristics of high separation efficiency, low space requirements, large processing capacity, low separation cost, and continuous operation. Therefore, among the various solid-liquid separation technologies and equipment, the hydrocyclone is currently one of the most widely used equipment in industry. So far, the hydrocyclone is widely used in many industries such as mineral processing [
7], petroleum [
8], chemical industry [
9], coal, mining [
10], metallurgy [
11], and tailings disposal [
12].
In the rotating flow field of the hydrocyclone, under the condition of force balance, the bigger the particle diameter, the larger the radius of gyration. Thus, under the influence of the centrifugal force field, particles with different diameters follow a certain distribution rule along the radial direction inside the hydrocyclone. The coarse particles will be discharged from the underflow outlet with the external swirl, and the fine particles will be discharged from the overflow outlet with the internal swirl, thereby completing the classification of the coarse and fine particles.
From the perspective of practical application, the flow field study of the hydrocyclone does not seem important, because normally the focus is on the properties of the product obtained after hydrocyclone separation. As stated in the black-box theory, what matters in this case is usually the result, and not the process. However, in order to achieve greater separation efficiency and classification accuracy, it is necessary to improve the separation process, and the internal flow field of the hydrocyclone is an important factor that affects the separation process. Therefore, the importance of flow field research is self-evident. The flow field research, on the one hand, helps to understand the internal black-box theory inside the hydrocyclone and the separation mechanism of the hydrocyclone. On the other hand, the internal structure of the hydrocyclone can be improved and the influence rule of the structural parameters on the separation performance can be obtained.
The separation performance of the hydrocyclone can be improved by efficiently augmenting the structural parameters and form of the hydrocyclone [
13]. Both experimental and theoretical studies by domestic and foreign scholars have generated a series of landmark research results in terms of research methods and content. In terms of the optimization of the structural parameters of the hydrocyclone, the representative studies include experimental studies on the hydrocyclone column height and diameter [
14,
15], feed inlet type and size [
16,
17], overflow pipe diameter, length, and shape, overflow pipe thickness [
18,
19,
20], underflow outlet diameter, and shape, ratio relationship between the underflow outlet and overflow outlet [
21,
22,
23]. A series of new hydrocyclone types have been designed, such as the built-in structural hydrocyclone [
24,
25], underflow outlet filled with flushing water [
26], multi-stage series or parallel hydrocyclone [
27,
28,
29], and three-product cyclone [
30,
31]. Mainza is one of the earliest researchers who put forward the three-product hydrocyclone, and the three-product hydrocyclone has been successfully tested in the Platinum industry for classifying UG2 ore which contains a high density chromite and a low density PGM carrying silica component. The emergence of these new technologies has promoted the further application of hydrocyclones in separation, however, all the aforementioned studies did not consider the influence of structural parameters on the separation efficiency.
Because the experiment is subject to different conditions, the numerical simulation method based on computational fluid dynamics (CFD) is getting more and more attention in the study of the internal flow field of the hydrocyclone. During the research, most scholars agree to use the Reynolds stress model (RSM) [
32,
33,
34,
35,
36] to deal with the turbulence inside the hydrocyclone. For two-phase flow or multi-phase flow, most scholars prefer the discrete particle model (DPM) [
37] to process the particle flow and use the volume of fluid (VOF) [
38] model to process the gas-liquid contact surface, with the result that the simulation is consistent with the experiment is obtained.
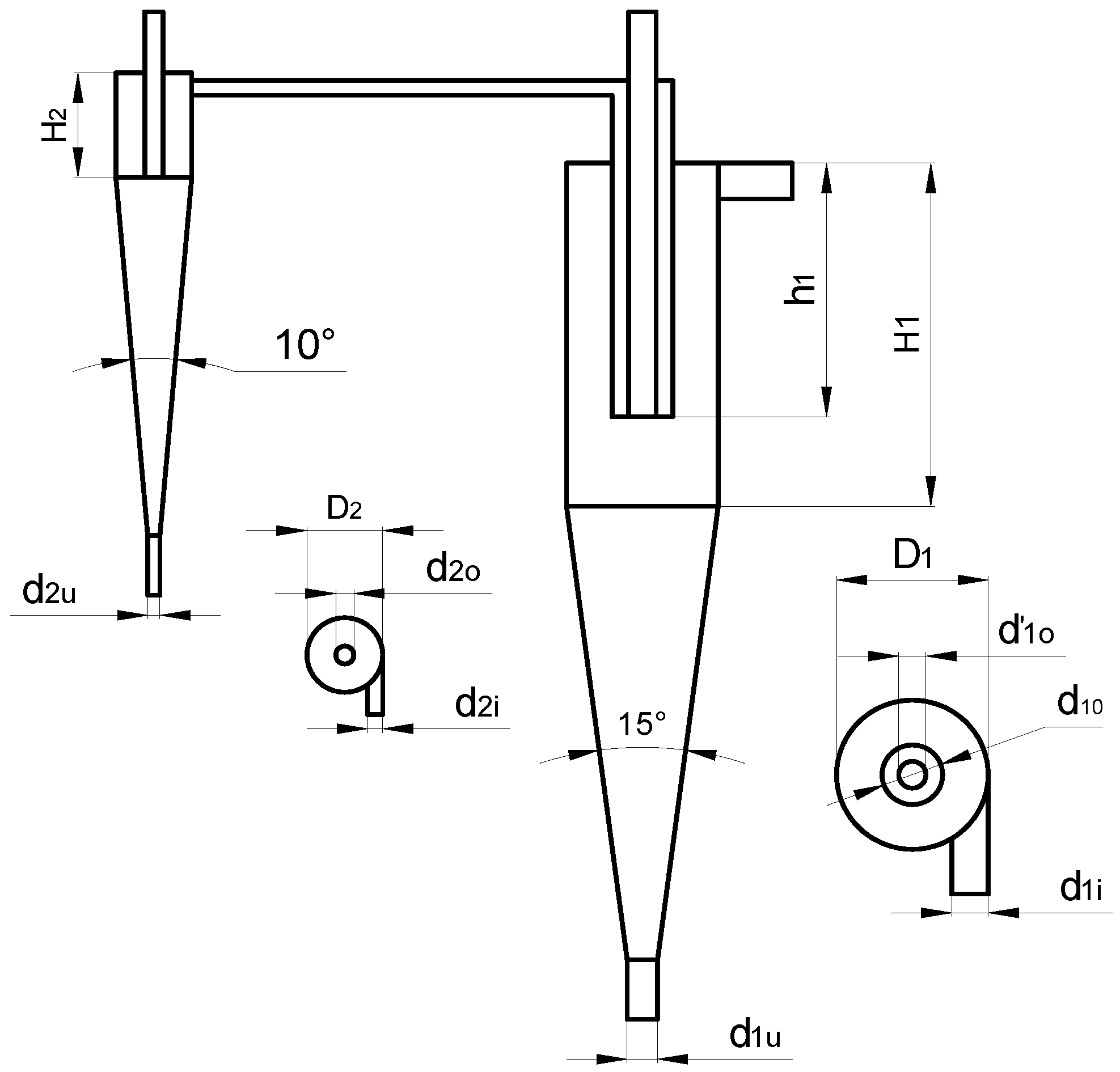
Summarizing the latest domestic and foreign research progress on hydrocyclone structure, the consistent conclusion is that the structural parameters, especially the diameter of the underflow outlet, are the main factors that affect the separation performance of the flow field. However, most of the previous research focused on the separation performance, which could not overcome the shortcomings of existing hydrocyclones in which one classification cannot satisfy the requirements for fine classification with narrow size fraction. The conventional hydrocyclone can only obtain two products through the overflow of the fine particles and underflow of the coarse particles. However, in addition to these two products, there must be an intermediate product between the fine particles and the coarse particles. If the intermediate product enters the underflow, it will cause a loss in concentration. And if the intermediate product enters the overflow, it will cause the concentrate pollution. Therefore, effectively processing the intermediate material to obtain multiple products with narrow size fractions through a single classification that further meets the requirement for the fine classification of the feeding materials in the following sorting operation is key to improving concentrate yield and grade. Thus, a two-stage multi-product hydrocyclone that operates in series was designed in this work. The first stage of the hydrocyclone was designed as a coaxial double-overflow-pipe structure. The finest particle is discharged from the internal overflow pipe and the particle with the intermediate size is discharged from the external overflow pipe, which then relies on the residual pressure to enter the second stage of the hydrocyclone for subsequent fine grading. Thus, a single classification can obtain multiple products with different size fractions resulting from the first stage underflow, first stage overflow, second stage underflow, and second stage overflow. However, due to the special structure of the double-overflow-pipe, the vortex domain, boundary layer and flow regime change. Therefore, it is necessary to study the flow field performance. In this study, numerical analysis and experimental methods were used to study the internal flow field characteristics of the double-overflow-pipe hydrocyclone and the particle size distribution characteristics of the different products. The influence rule of the diameter of the underflow outlet on the flow field and particle size fraction distribution was also studied in this work.
4. Conclusions
In this study, a two-stage series multi-product hydrocyclone was designed so that different particle size fractions could be obtained as the first stage internal overflow, first stage external overflow, first stage underflow, second stage overflow, and second stage underflow after one classification.
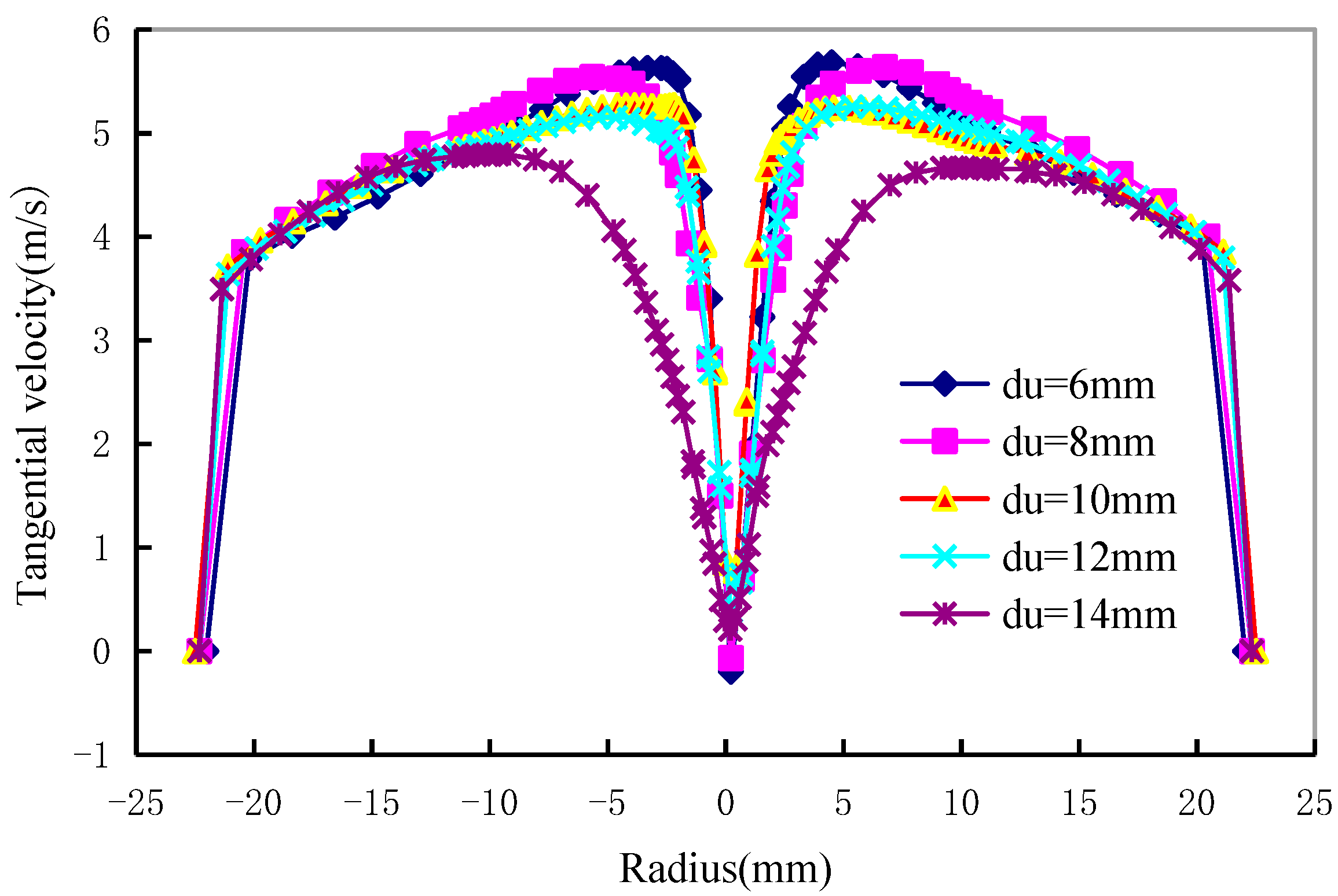
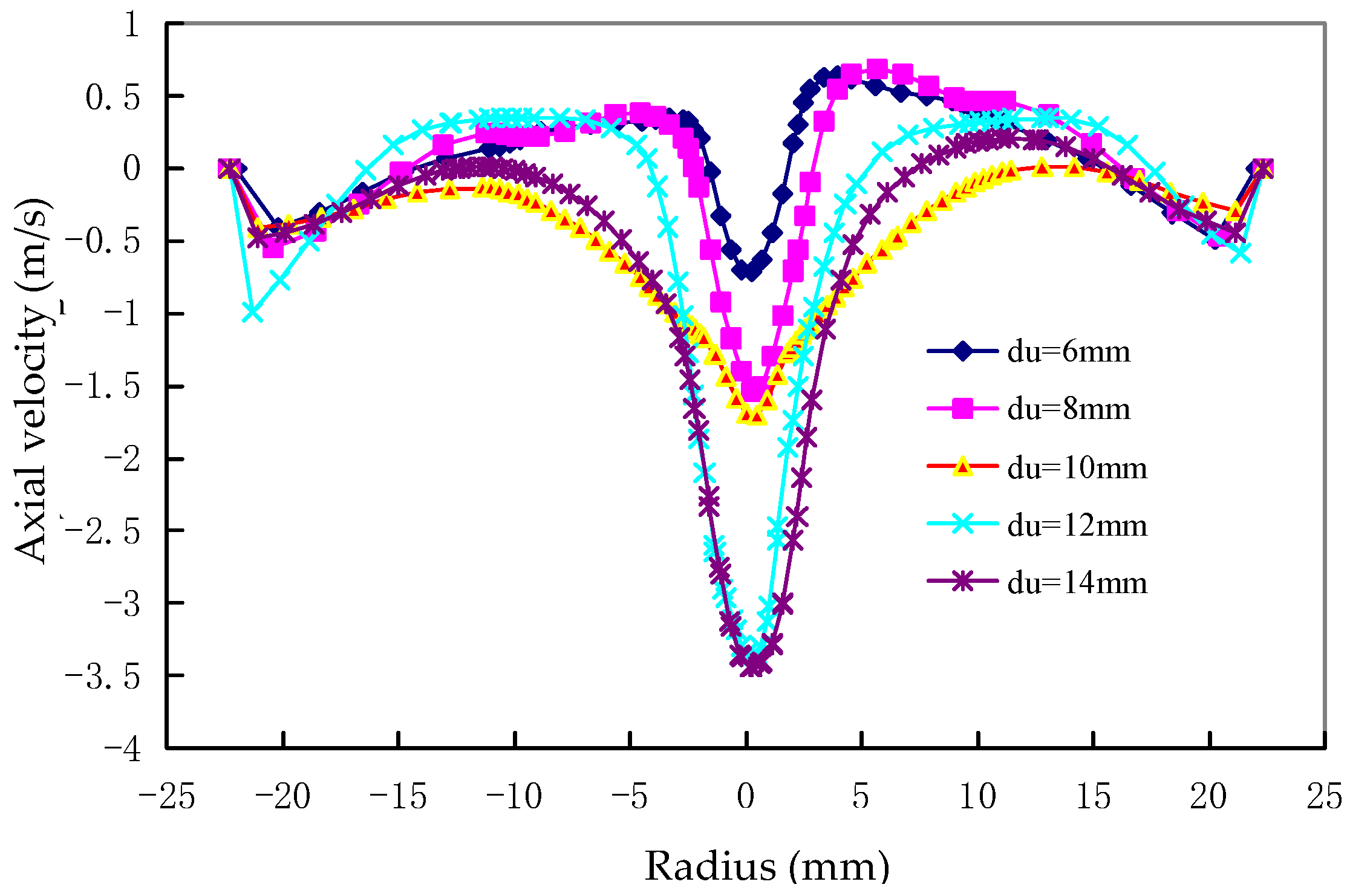
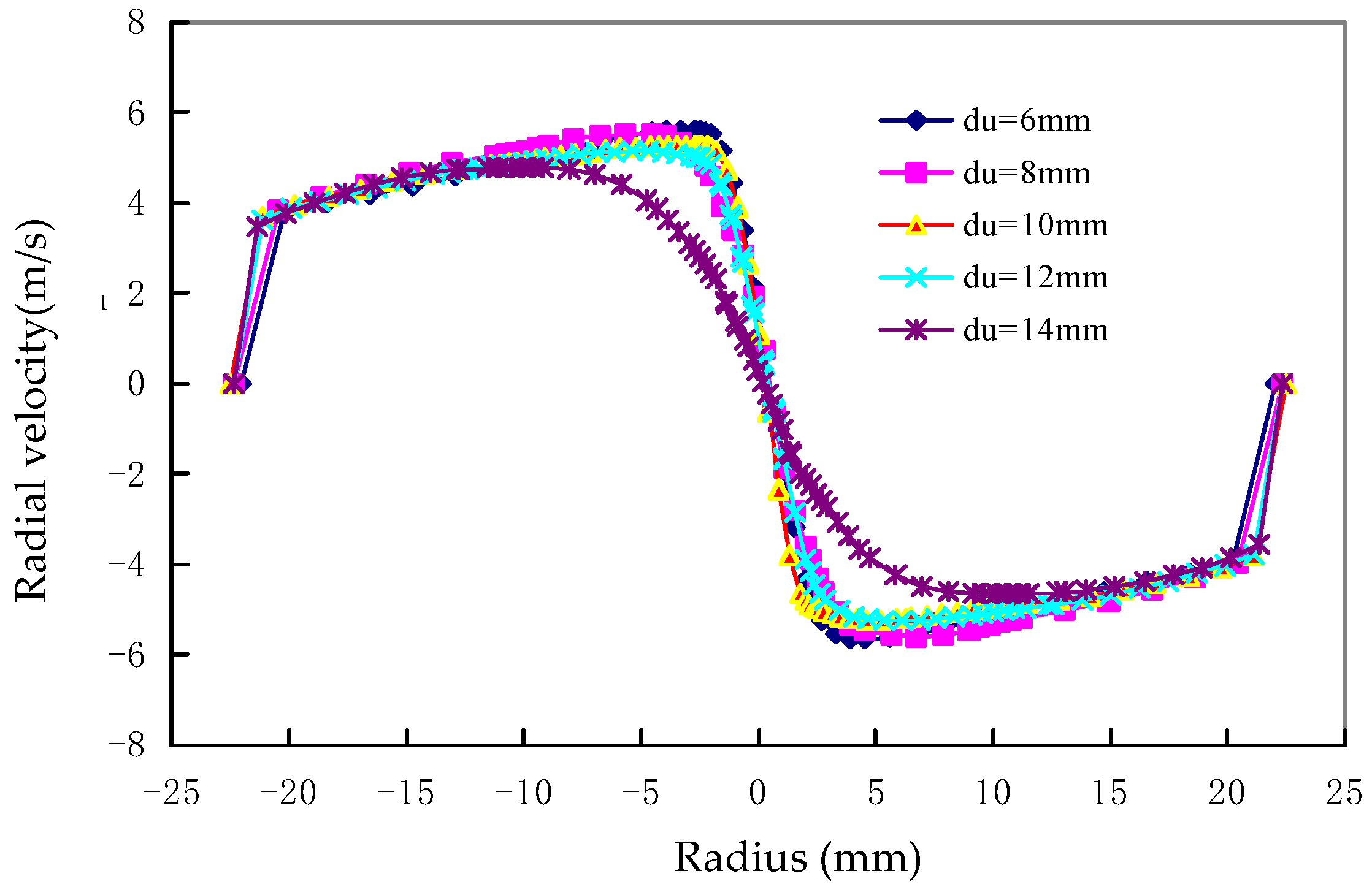
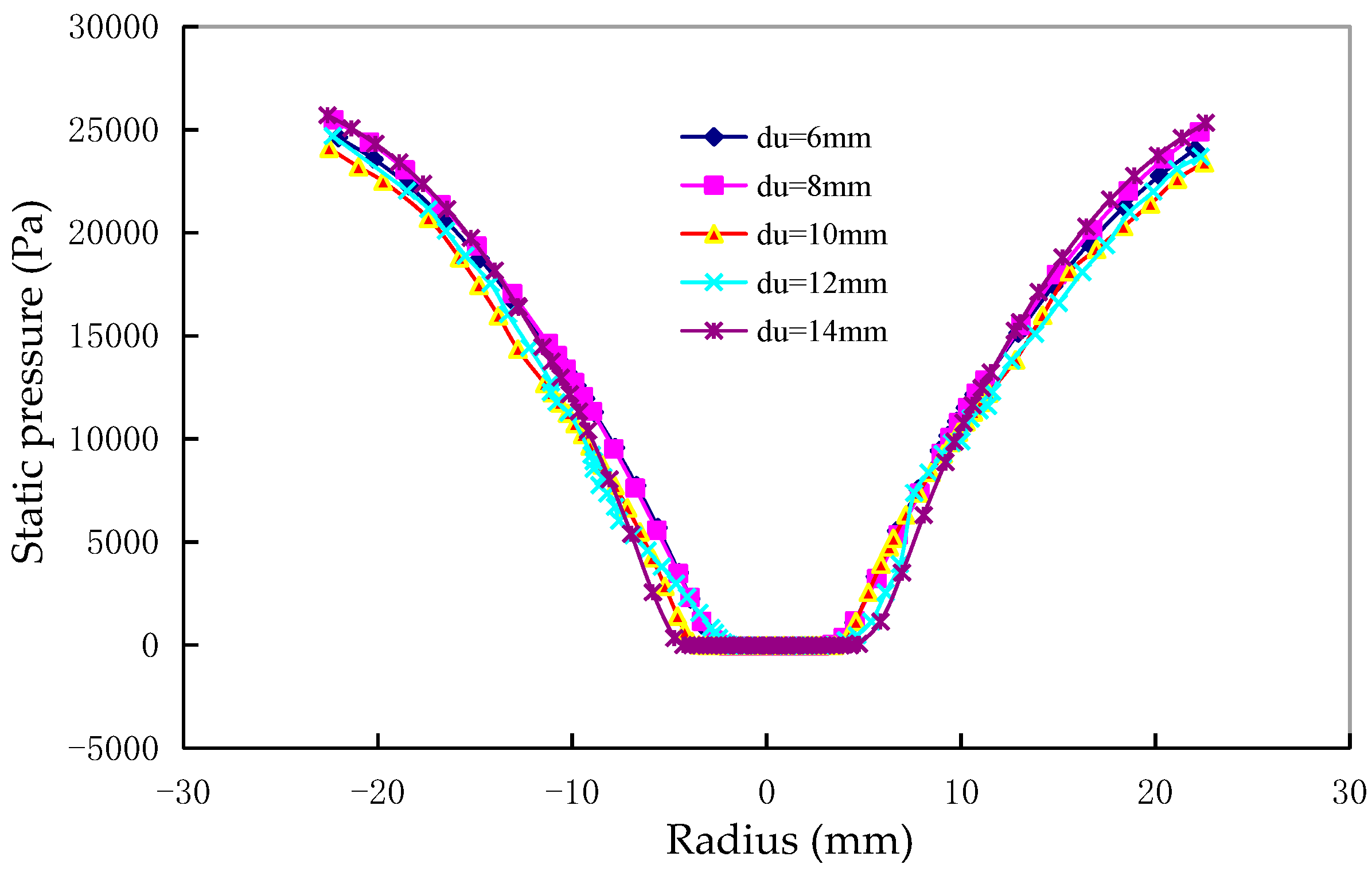
The axial velocity of the double-overflow-pipe changed direction twice along the radial direction, thus enclosing an area between the coaxial overflow pipes. The axial velocity was small in this area, which was not conducive to the particle separation. The diameter of the underflow outlet had little effect on the pressure field and radial velocity field, but had a greater influence on the tangential velocity and axial velocity. The axial velocity increased with the diameter of the underflow, which indicated that an optimal increase in the diameter of the underflow was beneficial to improving the classification efficiency. The tangential velocity increased with the decrease in the diameter of the underflow outlet, which was beneficial for increasing the centrifugal force of the internal swirl of the hydrocyclone, reducing the separation granularity, and improving the classification accuracy of the fine particles.
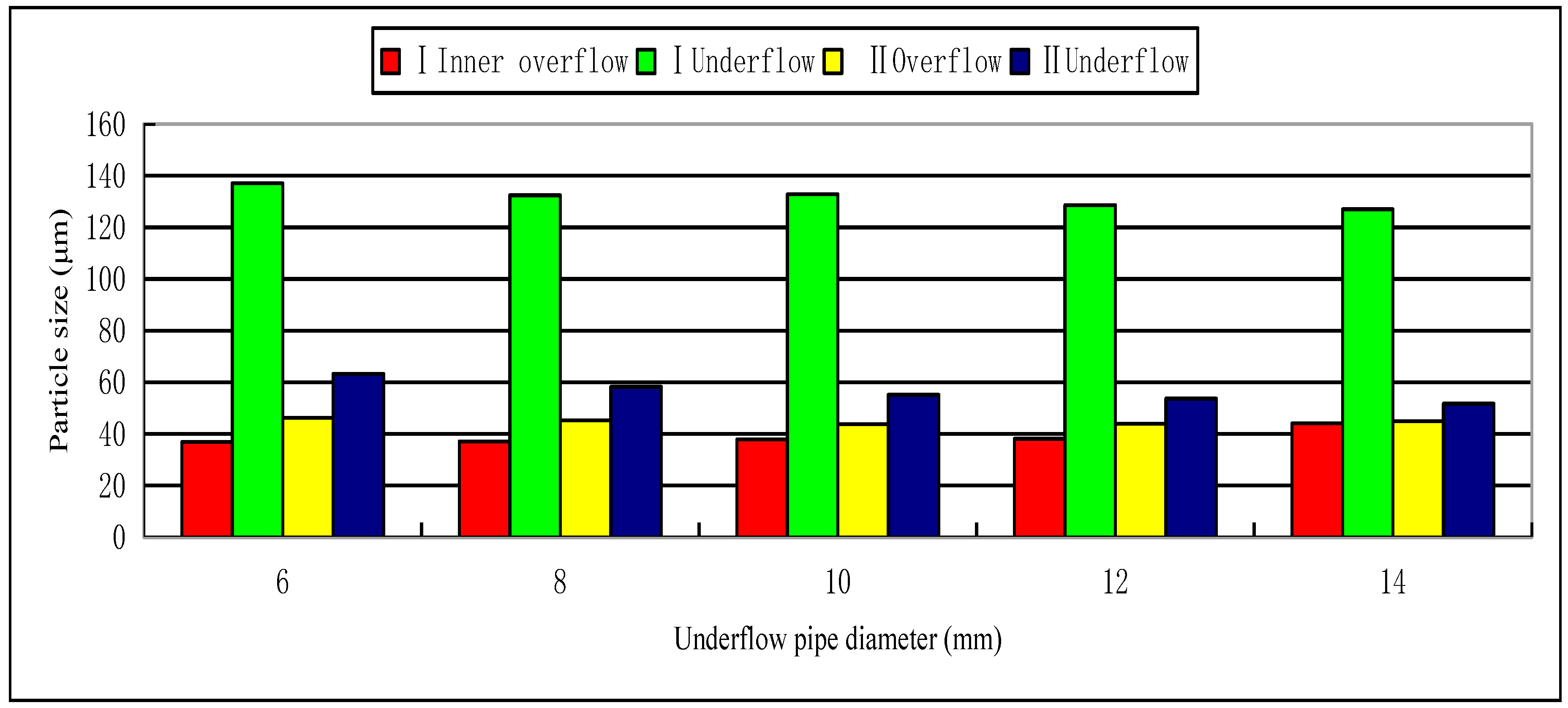
The first stage internal overflow was the finest while the first stage external overflow was the coarsest. The particle size of the second stage overflow was between that of the first stage internal and external overflows. The diameter of the underflow outlet had an opposite influence on the particle size of the first stage internal and external overflows. When the diameter of the underflow outlet increased, the particles of the first stage internal overflow became coarser and the particles of the first stage external overflow became finer.
The results of this study have a certain guiding role in the study of the flow field characteristics of the multi-product hydrocyclone. However, there are still many aspects that need to be addressed, such as the influence rule of the overflow pipe diameter and depth of insertion of the overflow pipe on the flow field and the distribution of the particle size fraction. In addition, the scale-up in engineering application is also an important issue to be discussed and highlight in the next step. These can be used to obtain the optimal structural parameters of the hydrocyclone for the best separation performance.