Abstract
The effect of alkali metal chlorides on the viscoelastic behavior and yielding properties of silica suspensions was studied through creep-recovery and dynamic oscillatory tests with stress control. Then, the viscoelasticity of the pulps was correlated with the silica zeta potential, aggregate size, and the percentage of cations adsorbed on the surface of the ore. The results indicate that larger cations are more prone to adhere to the silica surface, which increases the number of ionic bonds that bind the particles. This generates stronger particle networks and a greater agglomeration of particles, especially those smaller than 10 µm. As the size of the bare cations increases, the rheological response provides higher values of yield stress, complex viscosity, and viscoelastic moduli, but in turn, pulps undergo minor deformations under the application of stress. Dynamic oscillatory tests suggest structural changes, with the phase angle following the inverse relationship with the bare cation size, indicating that the liquid-like character of the pulps increases as the size of the cations increases.
1. Introduction
Elucidating the behavior and stability of colloidal suspensions requires a deep understanding of the principles governing the interactions between surfaces. It is generally considered that the total interaction energy corresponds to the addition of van der Waals forces with double-layer electrostatic interactions, which make up the classical DLVO theory. However, this theory generally fails when two surfaces or particles approach distances of a few nanometers. Other non-DLVO forces appear, such as hydration, hydrophobic, and steric forces, which determine the fate of the interaction. These forces arise in most practical cases, such as in metal oxides in highly saline media. For example, Parson et al. [1] indicate that at salt concentrations higher than 0.01 M, specific ion effects are expected [2,3,4,5,6,7]; that is, the macroscopic properties of suspensions carry the effect generated by the ions in the structure of the water that surrounds them. Small ions such as Li+ are known as maker ions because they attract water molecules more strongly than water molecules do to each other, forming a layer of structured water around the ions. On the other hand, large ions such as Cs+ are known as breakers; they interact weakly with water, generating a layer of structureless water around them. This implies that the hydrated size of ions in solution follows the trend Li+ > Na+ > K+, which is opposite to the bare ion size.
More than a century ago, Hofmeister related the precipitation of proteins with the size of bare ions in solution [8]; interestingly, the order established by Hofmeister has been found in various systems, such as colloidal suspensions of tungsten trioxide, magnetite, alumina, titanium, hematite, and silica [9,10,11,12,13]. Here, we focus on silica, which has been studied extensively due to its relevance in numerous industrial applications [14,15,16]; however, it has not been studied combining rheological and physicochemical results in the presence of a series of alkali metal chloride salts. A particularly important result for our work is that of Franks [9], who measured the zeta potential and yield stress of quartz suspensions in concentrated solutions of monovalent electrolytes, finding that poorly hydrated ions, such as Cs+ and K+, have a greater impact in reducing the absolute value of the zeta potential than highly hydrated ions, such as Li+ and Na+. Franks found a higher yield stress when the pulp was in the presence of breaker ions, although the results were highly dependent on the pH. A challenge that is not yet fully resolved is that of high isoelectric point minerals, such as alumina, the properties of which follow a trend with the size of ions opposite to silica; for example, maker ions generate stronger alumina networks [17,18,19,20,21]. Parson et al. [19] developed a Poisson–Boltzmann electrolyte model that has been particularly successful in capturing trends in minerals with an isoelectric point that is either high or low. The model that includes ionic size, hydration, and dispersion shows that near the surface of alumina (high iep), the ions can dehydrate at the point of contact to be better adsorbed; however, this phenomenon would not occur near the surface of silica (low iep). More recently, through simulation of molecular dynamics, we have confirmed these conclusions (Quezada et al. [22]). Another important work was developed by Peula-García et al. [21], who considered a characteristic not studied before, that is, the degree of anisotropy or the shape of the ions. Strictly speaking, a quantitative description of hydration interactions should include the finite size of ions, discrete nature of solvent, many-body dispersion forces, and polarization effects. Morag et al. [23] measured interaction force curves (AFM) between silica surfaces in the presence of different monovalent salts, finding that at pH < 7.5, Cs+ is better adsorbed due possibly to poor hydration of silanol groups and the hydrophobic ejection of poorly hydrated Cs+ ions from the bulk to the interface. This last principle keeps the strongly hydrated ions in solution. On the other hand, Dishon et al. [24] showed that at pH 5.5, Na+ neutralizes the silica surface between 0.5 and 1 M, K+ between 0.2 and 0.5 M, and Cs+ at a concentration close to 0.1 M.
The relationship between interactions at the colloidal scale and the macroscopic characteristics of silica suspensions is of great practical interest [25]. For example, the management of tailings (mainly quartz) in the mining industry is determined by the flow properties of the pulps and, in recent times, the presence of salts due to the boom in the use of seawater in regions with water shortages [26,27,28,29,30]. Rheology knowledge makes it possible to optimize the tailings management and defines the amount of water and energy that must be used to transport the pulps from the exit of thickeners to the tailings deposit. For this, the rheological parameters from flow curves are most commonly used, which are then adjusted to viscoplastic models such as Bingham or Herschel–Bulkley, where the yield stress represents the strength of the particle network. Although yield stress has been successfully used to describe, design, and control mining processes, it is not enough to describe the complex interactions arising when studying different salts that change the structure of water in metal oxide suspensions. In this sense, creep-recovery tests consist of applying a defined stress to a specific material and measuring its strain. Then, the stress is removed and the material recovers part of its original form, or possibly, it is completely restored. If the latter occurs, the behavior is defined as elastic. If the material does not recover part of its original form, then the behavior is defined as viscous. Meanwhile, viscoelastic behavior simultaneously manifests both elastic and viscous properties. These tests are useful for determining the strengths of particle networks since generally stronger structures deform less [31,32]. Additionally, dynamic methods such as oscillatory rheology tests complement the interpretation of viscoelastic materials. These tests are carried out by subjecting the sample to an oscillatory strain and then measuring the resulting stress as a time function, which is . and are, respectively, the elastic storage modulus and the loss modulus. is a material measure of the energy stored and is therefore related to molecular events of an elastic nature, while is a material measure of the energy dissipated as heat and is related to molecular events of a viscous nature [32,33]. These tests are very useful because they allow interpreting the structure of materials without damaging them. For example, Michot et al. [34] and Paineau et al. [35] used the dynamic method to analyze the degree of gelation of suspensions of nontronite and smectite, respectively. The authors indicated that a gel-like characteristic appears when is much greater than , but in addition, both exhibit a limited dependence on frequency. Additionally, the phase angle, δ, defined as , is an indicator of the solid-like or liquid-like character of the material. A higher value of δ means that the pulp has a higher viscous component.
There has been an important advancement in the understanding of the effect of monovalent salts on the interactions between silica surfaces and their effect on the macroscopic properties that interest the industry. However, there are still no systematic studies analyzing the viscoelasticity of silica pulps. The objective of this work was to study the effect of monovalent chloride salts with cations with different bare sizes (LiCl, NaCl, and KCl) on the viscoelastic properties of silica suspensions. The tests were performed through creep-recovery and dynamic oscillatory tests. Subsequently, the results are related to zeta potential, quantity of cations adsorbed on the solid surface, and size of particle aggregates. The results are of special interest for tailings handling with seawater, as it is or partially desalinated.
2. Materials and Methods
2.1. Materials
Silica particles, from Sigma-Aldrich (Santiago, Chile), with a shape close to spherical, a density of 2.6 g/cm3, and an average size of 24 µm were used. The salts used were alkali metal chlorides of LiCl, NaCl, and KCl (analytical chemical grade, Merck, Santiago, Chile).
2.2. Rheology
Solutions of 100 g of silica powder in 50 mL of water at natural pH (approximately 6.2) were prepared for each test, which were suitably mixed for 1 h with magnetic stirring. When necessary, chloride salt was added at a concentration of 0.5 M. The experiments were carried out in a Haake RheoStress 1 rheometer (Thermo Fisher Scientific, Waltham, MA, USA). The vane-in-cup technique was chosen with a cup-to vane diameter ratio of 1.6 to minimize wall effects [31]. The vane diameter was 2.23 cm and the cup diameter was 3.5 cm.
In the creep-recovery test, a constant stress was applied to the sample for 600 s, which caused an increase in the creep angle, θ, as a function of time. As in previous studies [16,27,31], the shear strain was obtained from Equation (1) for linear materials:
where is the vane diameter and is the cup diameter. Given that Equation (1) corresponds to the model for a standard linear solid (SLS), it would not apply exactly to the systems used in this study. Therefore, the values obtained were considered as “apparent shear strain”. The apparent compliance, , is the apparent shear strain normalized by the applied stress and is given by Equation (2):
when is constant, the material presents linear behavior; on the contrary, if varies with stress, the material has a nonlinear viscoelastic behavior. For the oscillatory tests, a small sinusoidal stress (1 Pa) was applied and then the resulting strain was measured. The stress used was small enough to ensure that the pulp response was in the linear viscoelastic range within which the strain is proportional to the applied stress and the viscoelastic moduli have physical meaning.
2.3. Size Distribution
A stock silica pulp of 10% by weight was prepared for each system, adding the corresponding amount of salt to achieve 0.5 M (if applicable). The pulp was stirred for 5 h under mechanical agitation. Then, 300 mL were taken and emptied into a vessel under controlled agitation at 100 rpm. A variety of techniques are available to determine particle size distributions; however, measurement by focused beam reflectance (FBRM, ParticleTrack G400, Metter-Toledo, Columbus, OH, USA) has an important advantage, since it can be applied to feed suspensions without a high dilution of solids. In this work, the probe was introduced directly into the suspension, and the evolution of the size of the aggregates was recorded. The results presented in this work correspond to the size registered after 5 min since the beginning of the experiment.
2.4. Zeta Potential
A 1% by weight silica suspension in distilled water was prepared. After homogenizing the sample, 0.01 M salt was added (if applicable) and the pH was adjusted with either HCl or hydroxide of the cation corresponding to the salt present in the suspension. The zeta potentials of the suspended silica particles were measured using Zetameter System 4.0 (Zeta-meter, Staunton, VA, USA).
2.5. Ion Adsorption Determination
Three hundred grams of silica pulp were prepared with 33% by weight and 0.01 M of each of the three chloride salts in cylinders of 41.5 cm in height, 3.5 cm in diameter, and 400 cm3 in volume. After a vigorous agitation to achieve homogeneity of the pulps, they were allowed to settle for 24 h. After this time, the supernatant was removed and centrifuged to remove the particles in suspension. Then, an aliquot was extracted for the water analysis. The quantity of cations adsorbed on the surface of the silica particles was calculated by mass balance, considering the concentration of ions in solution, before and after sedimentation. These concentrations were determined by direct-aspiration atomic absorption spectrophotometry (Varian 220 FS Atomic Absorption Spectrophotometer, Varian, Palo Alto, CA, USA). By means of the argentometric method, it was found that the chloride concentration in the supernatant remained constant after sedimentation, which showed that this anion was not adsorbed to the silica surface.
3. Results
3.1. Creep-Recovery Tests
Figure 1 shows the fluency test results of silica suspensions in the presence of single salts, in which the time evolution of the apparent shear strain was measured under fixed applied loads for 600 s. In all cases, a delayed elasticity appeared when the applied stress was less than certain critical stress, so-called (apparent) yield stress. It is interesting to note that the delayed elasticity increased as the character of the salts that increase the structure of the water increased. Thus, the elasticity delayed in the time lapse from 10 to 600 s, and just before the collapse of the particle network, was 53% in the presence of LiCl, with a yield stress of 11 Pa; 17% in NaCl, with a yield stress of 16 Pa; and only 10% in KCl, with a yield stress of 33 Pa.
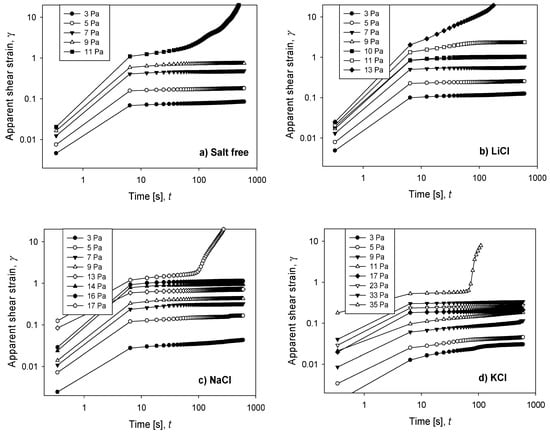
Figure 1.
Apparent shear strain as a function of time for increasing values of applied stress on silica suspensions formulated at natural pH and different salts (ca. 0.5 M): (a) salt-free, (b) LiCl, (c) NaCl, and (d) KCl.
After 600 s of creep tests, the load was removed, and after an additional 600 s, the recovery of the suspensions was measured again. The results are shown in Figure 2. For any applied load, recovery was slightly higher in the presence of breaker salts. At first glance, this result can be misleading, because the recovery in the presence of LiCl was from a much smaller deformation of the particle network than that which occurred in the presence of NaCl and KCl. In any case, the dominant effect shown in Figure 2 was clearly the load applied in the creep test; that is, the higher the load, the greater the deformation and vice versa. In general terms, suspensions lose elasticity when they approach the creep zone.
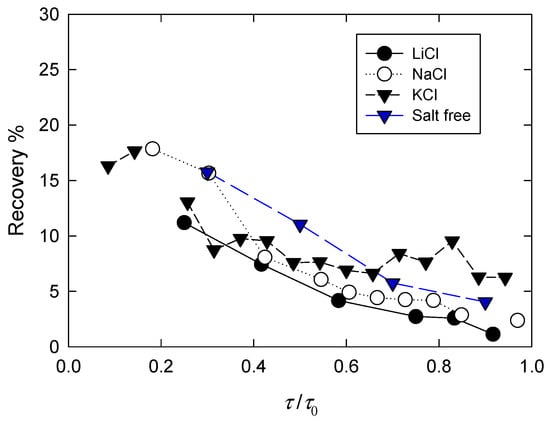
Figure 2.
Recovery of suspensions after creep tests of 600 s as function of applied load τ (normalized by yield stress τ0) and different salts (0.5 M).
Figure 3 shows the effect of applied stress on compliance (calculated from Equation (2)) for each of the 600-s creep tests. A key feature of the viscoelastic behavior was that it did not depend on the applied load. Clearly, the suspensions of silica in the presence of KCl followed linear behavior, whereas the suspensions of silica in freshwater and in the presence of NaCl and LiCl followed nonlinear behavior. The aggregates of silica in the presence of small cations such as Na+ and Li+ were susceptible to being reordered by the applied load and also the water order that, in the presence of these small cations, had gained in structure. This reordering that depends on the history of the applied load led to the nonlinear viscoelastic behavior shown by the silica suspensions in freshwater and in the presence of NaCl and LiCl salts. The K cation was much larger than the Na and Li cations and, therefore, it was more difficult to relocate in the aggregates even if the applied load increased.
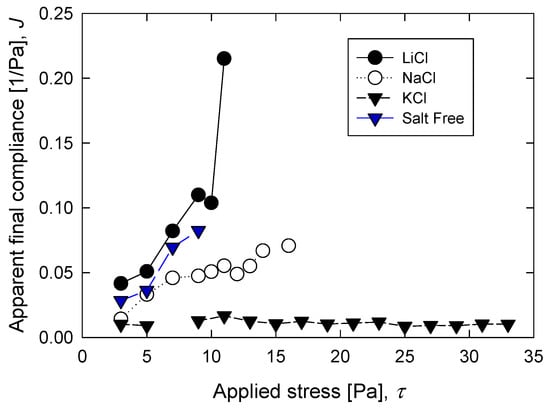
Figure 3.
Apparent final compliance of silica suspensions after creep tests of 600 s as function of applied load τ and different salts (0.5 M).
Figure 4 and Figure 5 show, respectively, the apparent yield stress and critical shear strain of silica suspensions formulated at natural pH in the presence of alkali metal chlorides. In mineral pulps, high values of yield stress are associated with strong interparticle bonds, and pulps of this class bear higher loads before starting to drain. Suspensions of silica in the presence of K+ are a good example, and according to Figure 4, the yield stress of these suspensions was significantly higher, 33 Pa, than that of the other suspensions, 16 and 11 Pa for suspensions with Na+ and Li+, respectively. For a pulp in fresh water, the yield stress was the lowest, 9 Pa. It can be anticipated that the suspensions of silica in the presence of breaker salts with large cations such as K+ are the most resistant, as they deformed little for any load applied in the range studied here. On the other hand, silica suspensions in the presence of small maker cations such as Na+ and Li+ form networks that are less resistant but more deformable than when in the presence of K+. The structural rearrangements of silica agglomerates in the presence of Na+ and Li+ and the ordering induced by these cations in the water structure suggest a greater resistance of the silica interparticle network, but the yield stress results showed the opposite. These results are only reconciled if the referred reordering is spatially short range, so that a silica suspension with any small cation will not offer great resistance to the applied load. Critical shear strain is another fundamental material descriptor for yielding since it is directly related to the strength and energy of the bonds that form particle networks just before collapsing to liquid. Figure 5 shows that silica suspensions in KCl had the lowest critical shear strain, and the order was LiCl > NaCl > KCl, suggesting that the suspensions in KCl, which are those that resist higher applied loads, at the time of collapse had the weakest bonds.
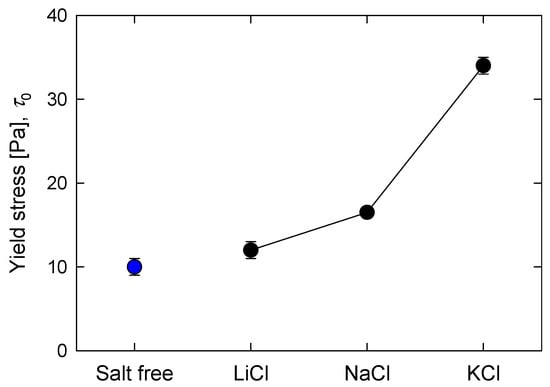
Figure 4.
Effect of salt type (0.5 M) on yield stress of silica suspensions formulated at natural pH.
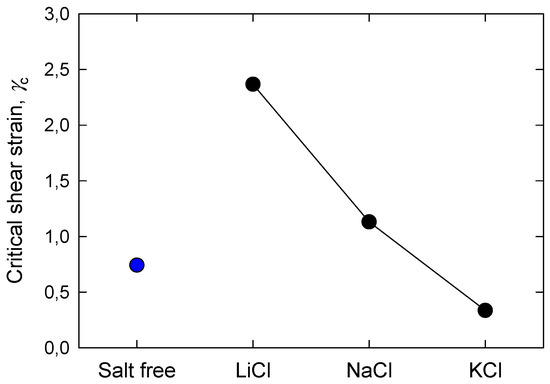
Figure 5.
Effect of salt type (0.5 M) on critical shear strain of silica suspensions formulated at natural pH.
3.2. Dynamic Oscillatory Tests
Figure 6 shows the results of the oscillatory frequency sweep tests, in which a sinusoidal stress with an amplitude of 1 Pa was applied. The viscoelastic moduli ( and ) had the lowest values when the silica pulp had no salt, which indicates that the particle network had the weakest resistance. In the presence of salt, the moduli increased progressively according to the bare size of the cation, again according to the Hofmeister series; that is, larger cations generated larger viscoelastic moduli. These results were supported by the complex viscosity (Figure 7), which also increased progressively according to the bare size of the cation. The results show that the oscillatory tests were consistent with the creep-recovery tests since, in both cases, the resistance of the particle networks increased with the bare size of cations of the alkali metal series. The appearance of a critical strain in the transition from solid-like to liquid-like behavior (Figure 1) indicated the elasto-viscoplastic nature of the material [36]. In addition, Figure 6 shows that for any pulp with salt, the elastic modulus was larger than the viscous modulus, and that both moduli were weakly dependent on the oscillation frequency. This is a typical pulp response with gel behavior.
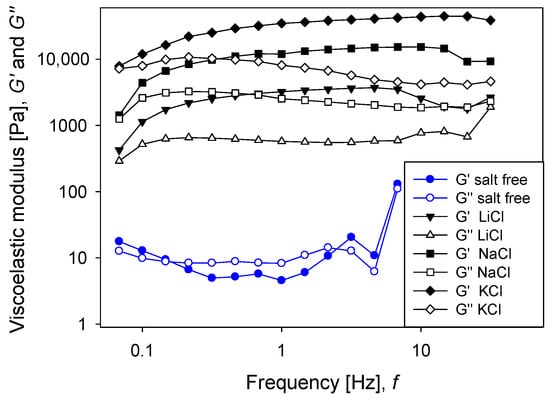
Figure 6.
Effect of salt type on dynamic moduli as a function of frequency for silica suspensions formulated at natural pH. Salt concentration is 0.5 M.
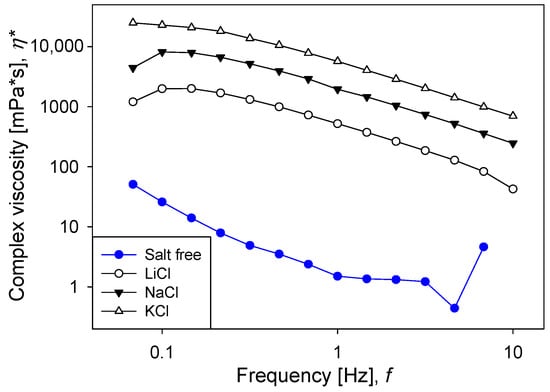
Figure 7.
Effect of salt type on complex viscosity as a function of frequency for silica suspensions formulated at natural pH. Salt concentration is 0.5 M.
A good indicator of the liquid-like or solid-like character of the pulps is the phase angle (). High values of δ indicate that the pulp has a significant viscous component and, therefore, behaves like a liquid. Figure 8 shows that the value of δ for silica suspensions was between 40° and 60°. The addition of salt to the system, independently of the type, modified the internal structure of the particle networks and induced the domain of the elastic component in the pulp, which was reflected in a decrease of δ. When the results obtained for the different salts were compared, it was found that the pulps behaved less as a solid when the size of the cation increased.
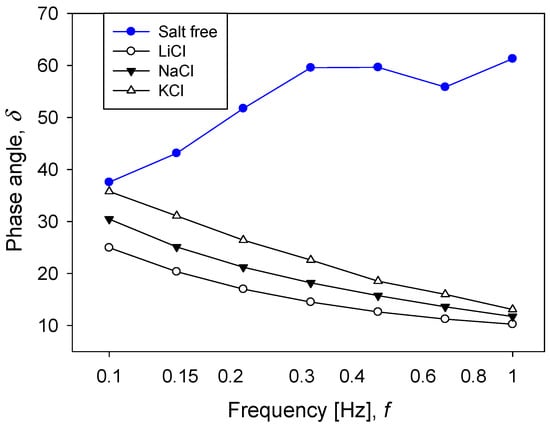
Figure 8.
Effect of salt type on phase angle as a function of frequency for silica suspensions formulated at natural pH. Salt concentration is 0.5 M.
By means of creep-recovery and oscillatory dynamics tests, it was inferred that the silica pulps were more resistant in the presence of salts. The effect was that they increased the yield stress, the viscoelastic modules, and the complex viscosity, although the shear stress decreased, but in turn, increased the elastic ratio (the phase angle decreased). Notable was that greater resistance and greater liquid character of the networks of silica particles were obtained with salts with large cations.
3.3. Size Distribution
The results of the tests with the FBRM probe (Figure 9) showed that the presence of salt favored the aggregation of silica particles and that breaker salts, such as KCl, did so more clearly. The size of the aggregates followed the Hofmeister series, that is, KCl > NaCl > LiCl, between 25.4 µm in KCl and 27.1 µm in KCl, which was only slightly larger than the average size of the silica particles in fresh water (24.1 µm). Figure 10 shows that the silica used in the experiments had an important fraction of 67% of small particles, <10 µm, and that these particles were prone to aggregate in the presence of salts. The results are interesting because they show that, in the presence of breaker salts, there is a greater propensity to form larger silica aggregates. However, in the presence of a maker salt, such as LiCl, such a propensity is lower.
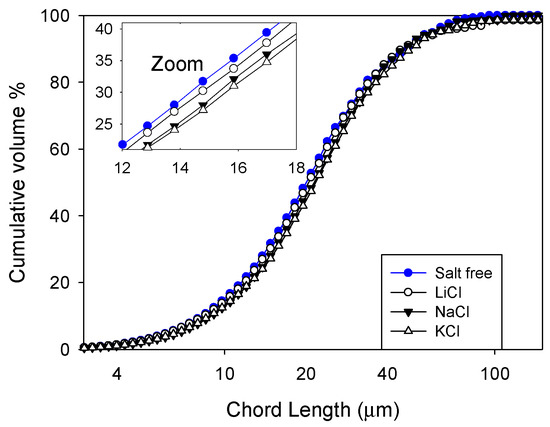
Figure 9.
Effect of the type of salt (0.01 M) on cumulative volume distribution. Pulps are formulated at 10% by weight and natural pH. The mean sqrt size for each system is salt-free: 24.1 µm, LiCl: 25.4 µm, NaCl: 26.3 µm, and KCl: 27.1 µm.
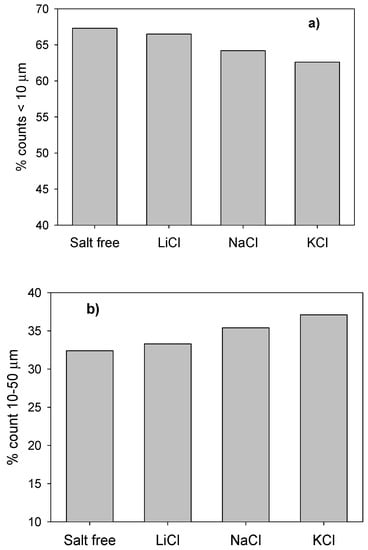
Figure 10.
Distribution of silica particles classified into two segments: (a) counts <10 µm and (b) counts 10–50 µm.
3.4. Zeta Potential and Cation Adsorption
In general, the electrolyte ions that were added to the pulps were attracted around the silica particles, forming a double layer that screened surface anionic charges. At a low salt concentration (0.01 M), Figure 11 shows that the magnitude of the negative zeta potential as a function of pH followed the inverse Hofmeister series, that is, Li+ > Na+ > K+, implying that cation adsorption on the silica surfaces followed the Hofmeister series K+ > Na+ > Li+. Therefore, the cation with the highest charge density of all the alkali metals, that is, Li+, was not the cation that most compressed the double electric layer of silica. The water molecules within the first hydration shell of Li+ were so tightly bound that the effective surface charge density was reduced and so was the screening power. The result was a low adsorption of Li+, lower than Na+ and K+, as Figure 12 shows.
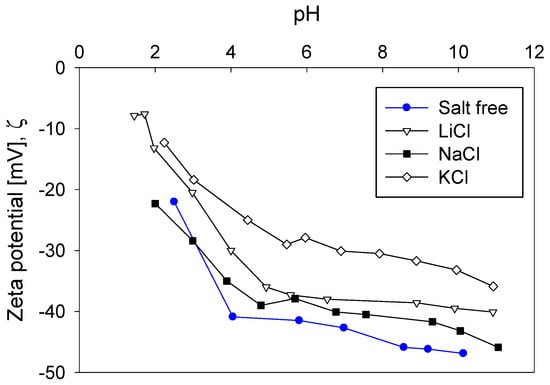
Figure 11.
Impact of salt type (0.01 M) and pH on zeta potential of silica.
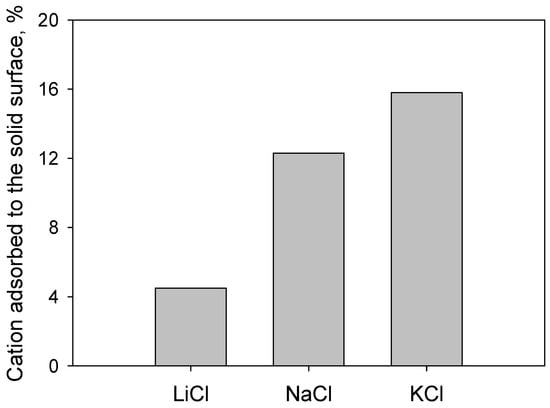
Figure 12.
Percentage of cation adsorbed on silica. Initial salt concentration was 0.01 M.
Dissociated silanol groups determine the negative surface charge of silica above its isoelectric point. At the natural pH of 6.2 used here, the charge density of silica was ca. −0.03 C/m2 (value taken from Kroutil et al. [37] and supported by Goloub et al. [38]). Metal cations, when present, acted as counterions on the silica, adsorbing on the negative sites that dominated the surface. In particular, the surface density of adsorbed alkali metal cations on silica, shown in Figure 12, showed a sustained increase as the size of the cation increased or, alternatively, as the cation was less hydrated. These results compare well with experimental and simulation data for silica and the cations considered here (in particular, see our molecular simulation work [22]). It is important to mention that at a high pH (>6.2), silica has a high surface charge, and Li+ adsorption might level off with the adsorption density of the larger cations [22].
At the natural pH of the quartz suspension (pH 6.2), the absolute value of the particles’ zeta potential was less than 7 mV, regardless of the type of salt. This indicates that electrostatic interactions do not have a significant impact on the pulp rheological behavior. However, the zeta potential obtained at low salinity (0.01 M), as shown in Figure 11, confirms that breaker salts access the particles’ surfaces more easily than maker salts, compressing the ionic cloud better. Considering that hydration phenomena mainly influence both yield stress and electrostatic forces, a relationship was found between both parameters (see Figure 13). Interestingly, it was found that yield stress varies with the known linear relationship between the square of zeta potential and yield stress [39].
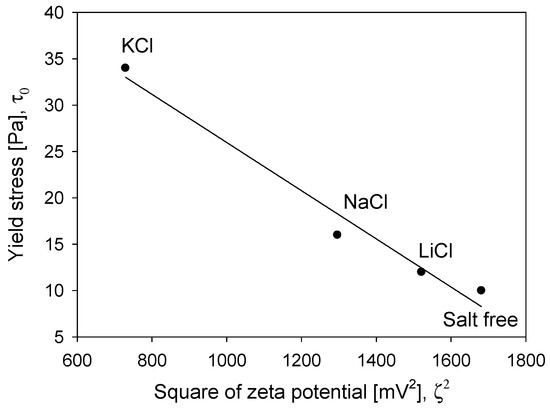
Figure 13.
The relationship between the square of zeta potential (0.01 M) and pulp yield stress (0.5 M) obtained at pH 6.2.
4. Discussion
The electrostatic and hydration phenomena determine the macroscopic characteristics shown by silica pulps in saline medium. Due to the structure of the water surrounding the ions and the silica surface, the larger cations adsorb more easily on the surface of the mineral, achieving a greater decrease in the magnitude of the zeta potential.
All the behaviors observed in this work can be explained according to the “like adsorb like” principle shown by Franks when he analyzed the rheology of silica pulps [9]. In the case of silica, at low pH, the silanol groups are poorly hydrated, which favors the adsorption of cations of higher radius, such as K+. The affinity of the cations for water decreases according to Li+ > Na+ > K+. Specifically, the average quantity of water molecules of coordination of Li+, Na+, and K+ is 5, 4, and 3, respectively [40]. Thus, the larger the cation, the greater its tendency to abandon the bulk solution and to adhere onto the silica surface. Larger ions are better at reducing the electrostatic repulsive force between them and, therefore, the attractive force component of van der Waals acquires a more important relevance.
Although the principle “like adsorb like” helps in understanding the differences of adsorption of cations on silica, another principle or mechanism is needed to explain the different resistances of the particle networks obtained in the presence of different salts. We have seen so far that silica particles smaller than 10 µm in the presence of K+ show the highest tendency to agglomerate, and that the particle networks they form are the most resistant (compared with Li+ and Na+). The invocation of van de Waals long-range forces, although correct, is not sufficient because silica particles partially covered by cations still show a negative zeta potential, indicating residual repulsive forces. The missing mechanism is the formation of salt bridges between silica particles, which is more frequent in the presence of large dehydrated cations such as K+.
The macroscopic consequences observed here in the presence of large cations are higher values of yield stress, complex viscosity, and viscoelastic modules and lower deformations under the application of shear stress. There are also structural changes that are exposed by dynamic oscillatory tests, where the phase angle follows a direct relationship with the size of the bare cation, indicating that the liquid-type proportion of the pulps increases with the size of the bare cation.
5. Conclusions
The effect of the type of salt on the viscoelastic behavior of silica suspensions was analyzed. Measurements of cation adsorption density and zeta potential of silica demonstrate that the presence of large cations promotes adhesion of the cations to the surface of the silica and thus reduces the electrostatic repulsion between silica particles more effectively. Silica particles smaller than 10 µm in the presence of large cations (K+) show the highest tendency to agglomerate, and the particle networks are the most resistant (compared with Li+ and Na+). The invocation of van de Waals long-range forces, although correct, is not sufficient because silica particles partially covered by cations remain anionic, indicating residual repulsive forces. The high resistance of the particle network formed in the presence of large bare cations is partially due to the formation of salt bridges between silica particles, which are more frequent in the presence of large dehydrated cations such as K+. The macroscopic consequences are higher yield stress values, viscoelastic modules, and complex viscosity and lower deformations under shear stress application. Dynamic oscillatory tests revealed structural changes in the silica pulps; in particular, the phase angle follows a direct relationship with the size of the bare cation, indicating that the silica pulps behave less as a solid when the size of the cation increases.
Author Contributions
R.I.J. designed the research and wrote original draft preparation; E.C.P., W.H.L., and J.V. prepared the experimentation; P.G.T. and P.A.R. reviewed and edited the paper; R.I.J. and P.G.T. funding acquisition; P.A.R. supervision; G.R.Q. rheological analysis.
Funding
This research was funded by MINEDUC-UA, ANT 1755; CONICYT Fondecyt 11171036; and Centro CRHIAM Project Conicyt/Fondap/15130015 and the APC was funded by CONICYT Fondecyt 11171036.
Acknowledgments
The authors thank the MINEDUC-UA Project, code ANT 1755; CONICYT Fondecyt 11171036; and the Centro CRHIAM Project Conicyt/Fondap/15130015. Pedro Robles thanks the Pontificia Universidad Católica de Valparaíso for the support provided.
Conflicts of Interest
The authors declare no conflict of interests.
References
- Parsons, D.F.; Boström, M.; Nostro, P.L.; Ninham, B.W. Hofmeister effects: Interplay of hydration, nonelectrostatic potentials, and ion size. Phys. Chem. Chem. Phys. 2011, 13, 12352. [Google Scholar] [CrossRef] [PubMed]
- Lyklema, J. Simple Hofmeister series. Chem. Phys. Lett. 2009, 467, 217–222. [Google Scholar] [CrossRef]
- Yilmaz, H.; Sato, K.; Watari, K. Ion-specific interaction of alumina surfaces. J. Am. Ceram. Soc. 2009, 92, 318–322. [Google Scholar] [CrossRef]
- Azam, M.S.; Weeraman, C.N.; Gibbs-Davis, J.M. Specific cation effects on the bimodal acid-base behavior of the silica/water interface. J. Phys. Chem. Lett. 2012, 3, 1269–1274. [Google Scholar] [CrossRef] [PubMed]
- Oncsik, T.; Trefalt, G.; Borkovec, M.; Szilagyi, I. Specific ion effects on particle aggregation induced by monovalent salts within the Hofmeister series. Langmuir 2015, 31, 3799–3807. [Google Scholar] [CrossRef] [PubMed]
- van der Linden, M.; Conchúir, B.O.; Spigone, E.; Niranjan, A.; Zaccone, A.; Cicuta, P. Microscopic origin of the Hofmeister effect in gelation kinetics of colloidal silica. J. Phys. Chem. Lett. 2015, 6, 2881–2887. [Google Scholar] [CrossRef] [PubMed]
- dos Santos, A.P.; Levin, Y. Ion specificity and the theory of stability of colloidal suspensions. Phys. Rev. Lett. 2011, 106, 167801. [Google Scholar] [CrossRef]
- Hofmeister, F. Zur Lehre von der Wirkung der Salze. Arch. Exp. Pathol. Pharmakol. 1888, 24, 247–260. [Google Scholar] [CrossRef]
- Franks, G.V. Zeta potentials and yield stresses of silica suspensions in concentrated monovalent electrolytes: Isoelectric point shift and additional attraction. J. Colloid Interface Sci. 2002, 249, 44–51. [Google Scholar] [CrossRef]
- Dumont, F.; Verbeiren, P.; Buess-Herman, C. Adsorption sequence of the alkali cations at the tungsten trioxide–water interface. Colloids Surf. A Physicochem. Eng. Asp. 1999, 154, 149–156. [Google Scholar] [CrossRef]
- Dumont, F.; Warlus, J.; Watillon, A. Influence of the point of zero charge of titanium dioxide hydrosols on the ionic adsorption sequences. J. Colloid Interface Sci. 1990, 138, 543–554. [Google Scholar] [CrossRef]
- Sprycha, R. Electrical double layer at alumina/electrolyte interface. J. Colloid Interface Sci. 1989, 127, 12–25. [Google Scholar] [CrossRef]
- Penners, N.H.G.; Koopal, L.K.; Lyklema, J. Interfacial electrochemistry of haematite (α-Fe2O3): Homodisperse and heterodisperse sols. Colloids Surf. 1986, 21, 457–468. [Google Scholar] [CrossRef]
- Zhou, Z.; Franks, G.V. Flocculation mechanism induced by cationic polymers investigated by light scattering. Langmuir 2006, 22, 6775–6786. [Google Scholar] [CrossRef]
- Arinaitwe, E.; Pawlik, M. A role of flocculant chain flexibility in flocculation of fine quartz. Part I. Intrinsic viscosities of polyacrylamide-based flocculants. Int. J. Miner. Process. 2013, 124, 50–57. [Google Scholar] [CrossRef]
- Quezada, G.; Jeldres, R.I.; Goñi, C.; Toledo, P.G.; Stickland, A.D.; Scales, P.J. Viscoelastic behaviour of flocculated silica sediments in concentrated monovalent chloride salt solutions. Miner. Eng. 2017, 110, 131–138. [Google Scholar] [CrossRef]
- Colic, M.; Franks, G.V.; Fisher, M.L.; Lange, F.F. Effect of counterion size on short range repulsive forces at high ionic strengths. Langmuir 1997, 13, 3129–3135. [Google Scholar] [CrossRef]
- Johnson, S.B.; Scales, P.J.; Healy, T.W. The binding of monovalent electrolyte ions on α-alumina. I. Electroacoustic studies at high electrolyte concentrations. Langmuir 1999, 15, 2836–2843. [Google Scholar] [CrossRef]
- Parsons, D.F.; Boström, M.; Maceina, T.J.; Salis, A.; Ninham, B.W. Why direct or reversed Hofmeister series? Interplay of hydration, non-electrostatic potentials, and ion size. Langmuir 2010, 26, 3323–3328. [Google Scholar] [CrossRef]
- Das, M.R.; Borah, J.M.; Kunz, W.; Ninham, B.W.; Mahiuddin, S. Ion specificity of the zeta potential of α-alumina, and of the adsorption of p-hydroxybenzoate at the α-alumina–water interface. J. Colloid Interface Sci. 2010, 344, 482–491. [Google Scholar] [CrossRef]
- Peula-García, J.M.; Ortega-Vinuesa, J.L.; Bastos-González, D. Inversion of Hofmeister series by changing the surface of colloidal particles from hydrophobic to hydrophilic. J. Phys. Chem. C 2010, 114, 11133–11139. [Google Scholar] [CrossRef]
- Quezada, G.R.; Rozas, R.E.; Toledo, P.G. Molecular dynamics simulations of quartz (101)–water and corundum (001)–water interfaces: Effect of surface charge and ions on cation adsorption, water orientation, and surface charge reversal. J. Phys. Chem. C 2017, 121, 25271–25282. [Google Scholar] [CrossRef]
- Morag, J.; Dishon, M.; Sivan, U. The governing role of surface hydration in ion specific adsorption to silica: An AFM-based account of the hofmeister universality and its reversal. Langmuir 2013, 29, 6317–6322. [Google Scholar] [CrossRef]
- Dishon, M.; Zohar, O.; Sivan, U. From repulsion to attraction and back to repulsion: The effect of NaCl, KCl, and CsCl on the force between silica surfaces in aqueous solution. Langmuir 2009, 25, 2831–2836. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Gan, Y.; Wanless, E.J.; Jameson, G.J.; Franks, G.V. Interaction forces between silica surfaces in aqueous solutions of cationic polymeric flocculants: Effect of polymer charge. Langmuir 2008, 24, 10920–10928. [Google Scholar] [CrossRef] [PubMed]
- Goñi, C.; Jeldres, R.I.; Toledo, P.G.; Stickland, A.D.; Scales, P.J. A non-linear viscoelastic model for sediments flocculated in the presence of seawater salts. Colloids Surf. A Physicochem. Eng. Asp. 2015, 482, 500–506. [Google Scholar] [CrossRef]
- Jeldres, R.I.; Piceros, E.C.; Leiva, W.H.; Toledo, P.G.; Herrera, N. Viscoelasticity and yielding properties of flocculated kaolinite sediments in saline water. Colloids Surf. A Physicochem. Eng. Asp. 2017, 529, 1009–1015. [Google Scholar] [CrossRef]
- Torres, C.M.; Taboada, M.E.; Graber, T.A.; Herreros, O.O.; Ghorbani, Y.; Watling, H.R. The effect of seawater based media on copper dissolution from low-grade copper ore. Miner. Eng. 2015, 71, 139–145. [Google Scholar] [CrossRef]
- Jeldres, R.I.; Arancibia-Bravo, M.P.; Reyes, A.; Aguirre, C.E.; Cortes, L.; Cisternas, L.A. The impact of seawater with calcium and magnesium removal for the flotation of copper-molybdenum sulphide ores. Miner. Eng. 2017, 109, 10–13. [Google Scholar] [CrossRef]
- Jeldres, R.I.; Toledo, P.G.; Concha, F.; Stickland, A.D.; Usher, S.P.; Scales, P.J. Impact of seawater salts on the viscoelastic behavior of flocculated mineral suspensions. Colloids Surf. A Physicochem. Eng. Asp. 2014, 461, 295–302. [Google Scholar] [CrossRef]
- Stickland, A.D.; Kumar, A.; Kusuma, T.E.; Scales, P.J.; Tindley, A.; Biggs, S.; Buscall, R. The effect of premature wall yield on creep testing of strongly flocculated suspensions. Rheol. Acta 2015, 54, 337–352. [Google Scholar] [CrossRef]
- Lin, Y.; Phan-Thien, N.; Lee, J.B.P.; Khoo, B.C. Concentration dependence of yield stress and dynamic moduli of kaolinite suspensions. Langmuir 2015, 31, 4791–4797. [Google Scholar] [CrossRef]
- Lim, H.M.; Misni, M. Colloidal and rheological properties of natural rubber latex concentrate. Appl. Rheol. 2016, 26, 15659–15669. [Google Scholar] [CrossRef]
- Michot, L.J.; Baravian, C.; Bihannic, I.; Maddi, S.; Moyne, C.; Duval, J.F.L.; Levitz, P.; Davidson, P. Sol−gel and isotropic/nematic transitions in aqueous suspensions of natural nontronite clay. Influence of particle anisotropy. 2. Gel structure and mechanical properties. Langmuir 2009, 25, 127–139. [Google Scholar] [CrossRef]
- Paineau, E.; Michot, L.J.; Bihannic, I.; Baravian, C. Aqueous suspensions of natural swelling clay minerals. 2. Rheological characterization. Langmuir 2011, 27, 7806–7819. [Google Scholar] [CrossRef]
- Dimitriou, J.C.; Ewoldt, R.H.; McKinley, G.H. Describing and prescribing the constitutive response of yield stress fluids using large amplitude oscillatory shear stress (LAOStress). J. Rheol. 2013, 57, 27–70. [Google Scholar] [CrossRef]
- Kroutil, O.; Chval, Z.; Skelton, A.A.; Predota, M. Computer simulation of quartz(101)-water interface over a range of pH values. J. Phys. Chem. C 2015, 119, 9274–9286. [Google Scholar] [CrossRef]
- Goloub, T.P.; Koopal, L.K.; Bijsterbosch, B.H.; Sidorova, M.P. Adsorption of cationic surfactants on silica. Surface charge effects. Langmuir 1996, 12, 3188–3194. [Google Scholar] [CrossRef]
- Scales, P.J.; Johnson, S.B.; Healy, T.W.; Kapur, P.C. Shear yield stress of partially flocculated colloidal suspensions. AIChE J. 1998, 44, 538–544. [Google Scholar] [CrossRef]
- Israelachvili, J. Intermolecular and Surface Forces, 3rd ed.; Elsevier: Santa Barbara, CA, USA, 2011; ISBN 9780123919274. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).