Application of the Discrete Element Method to Study the Effects of Stream Characteristics on Screening Performance
Abstract
1. Introduction
2. Methodology
2.1. DEM
2.1.1. DEM Contact Model Theory
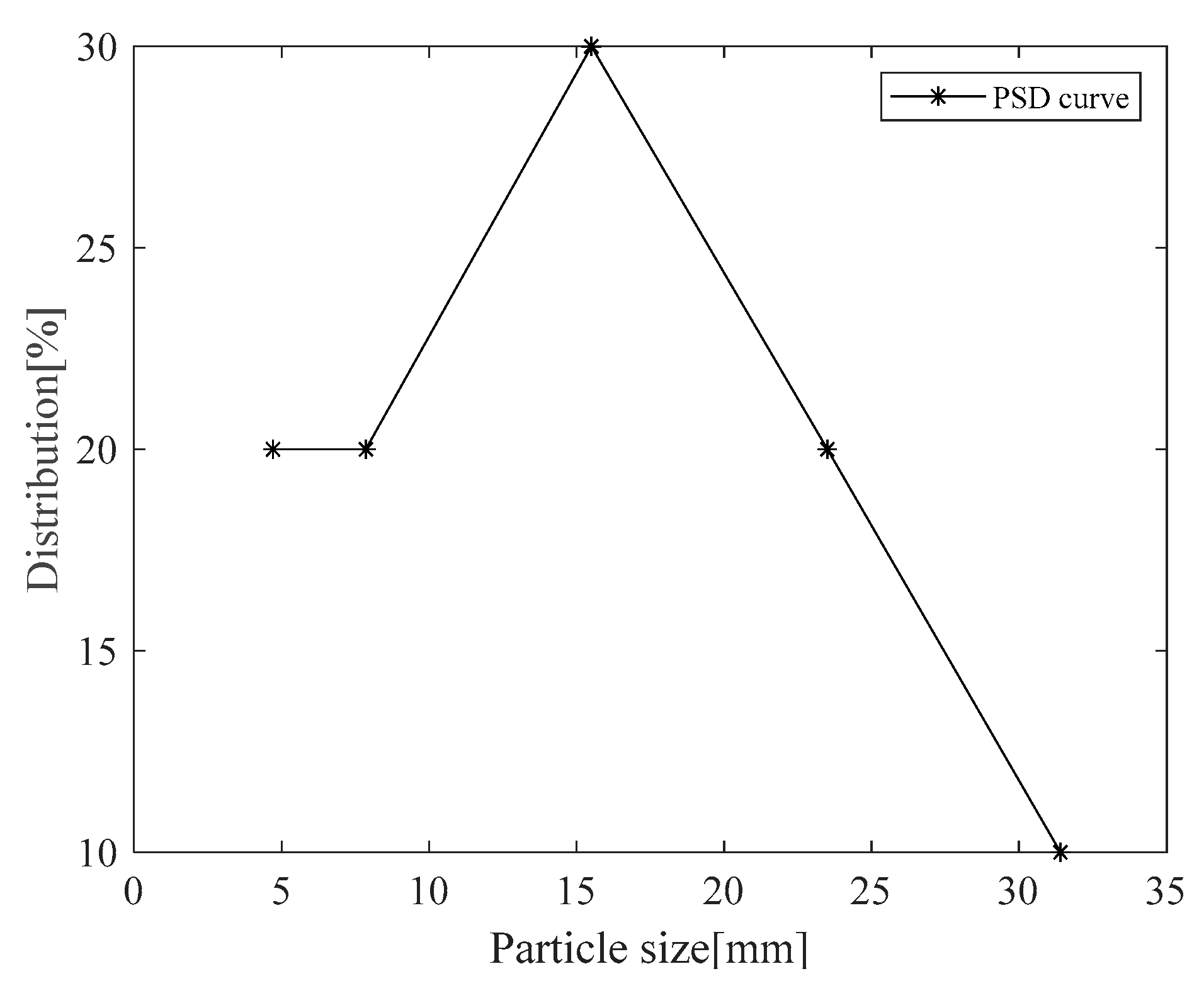
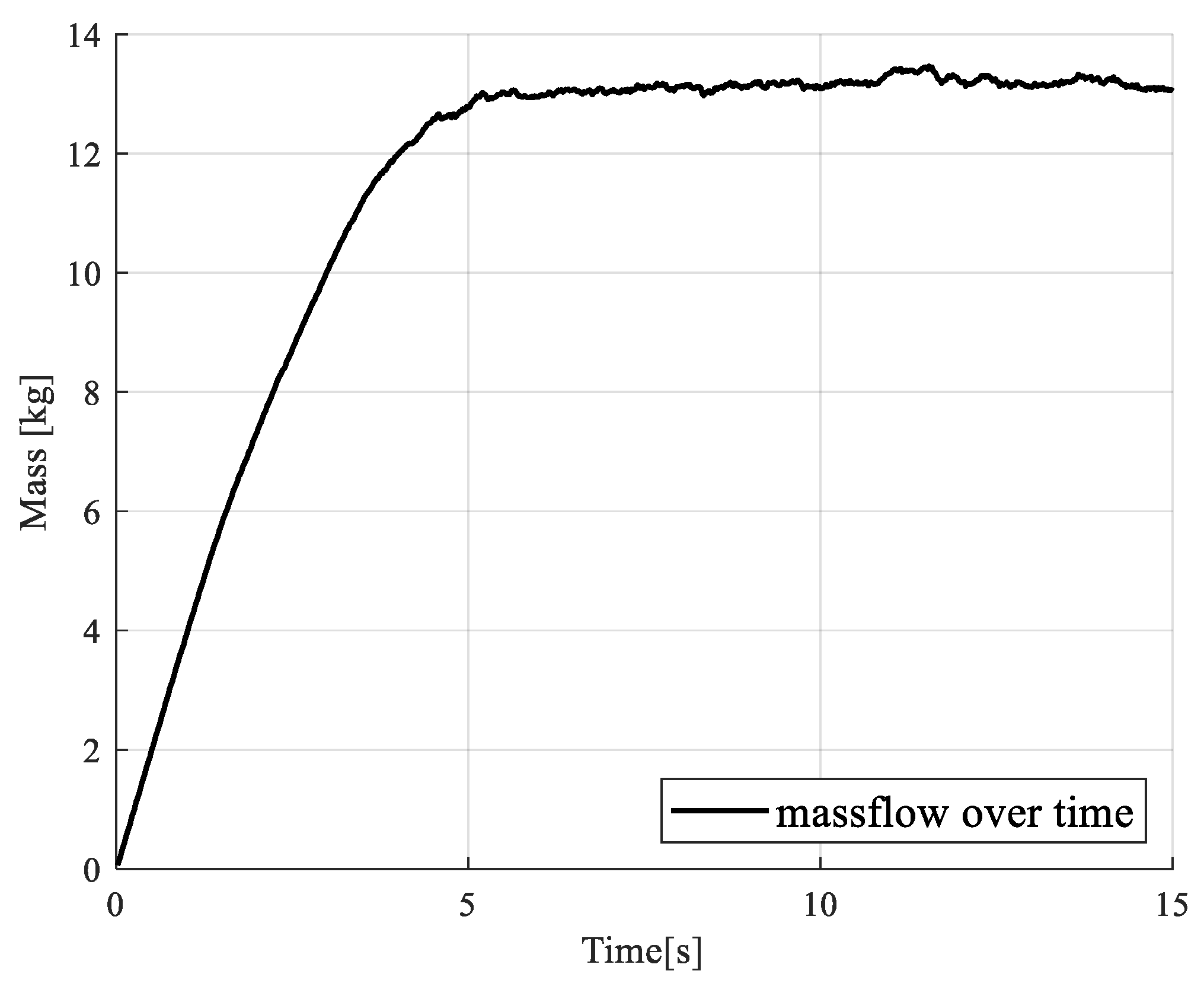
2.1.2. Simulations
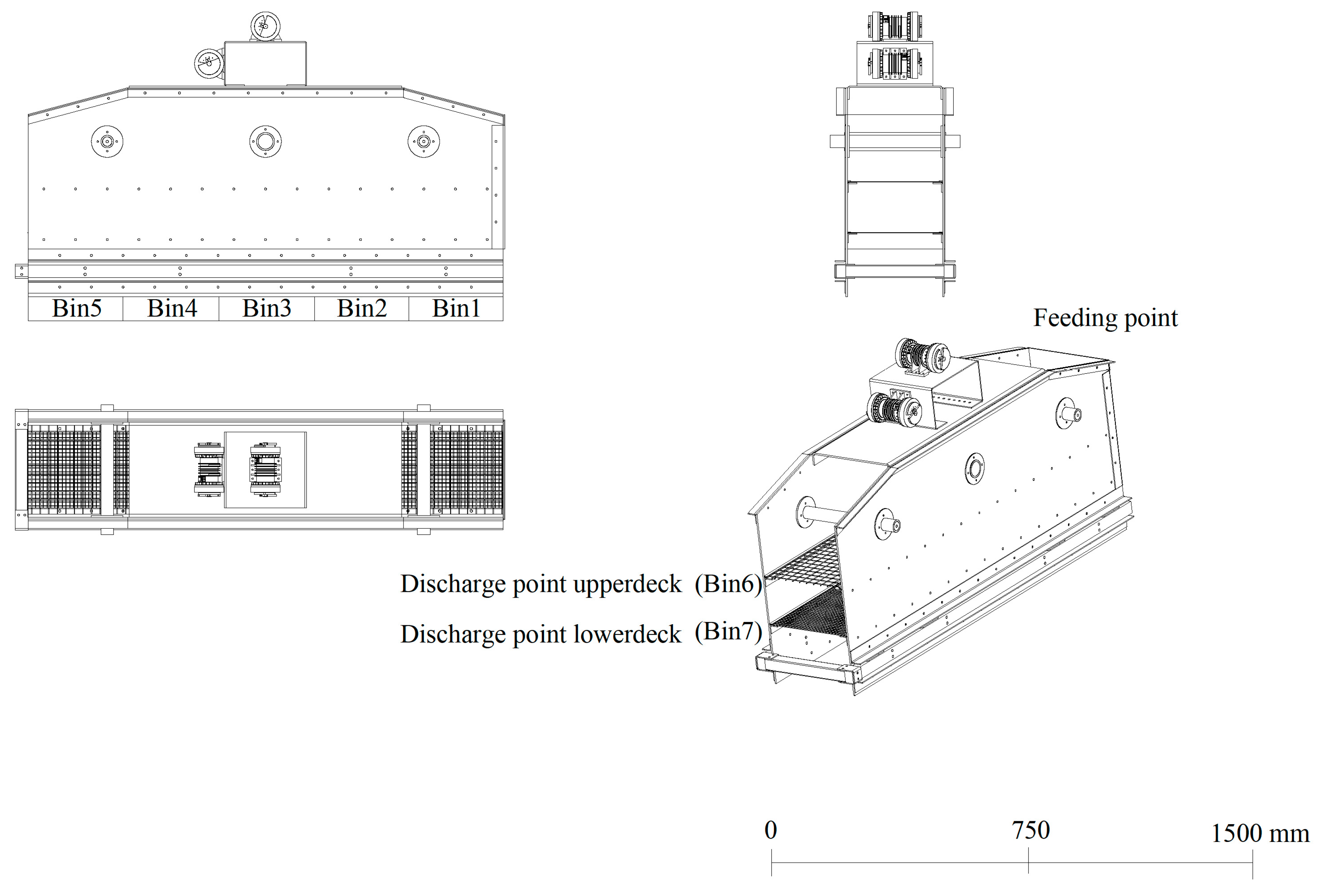
2.2. Laboratory Vibrating Screen
2.3. Modeling
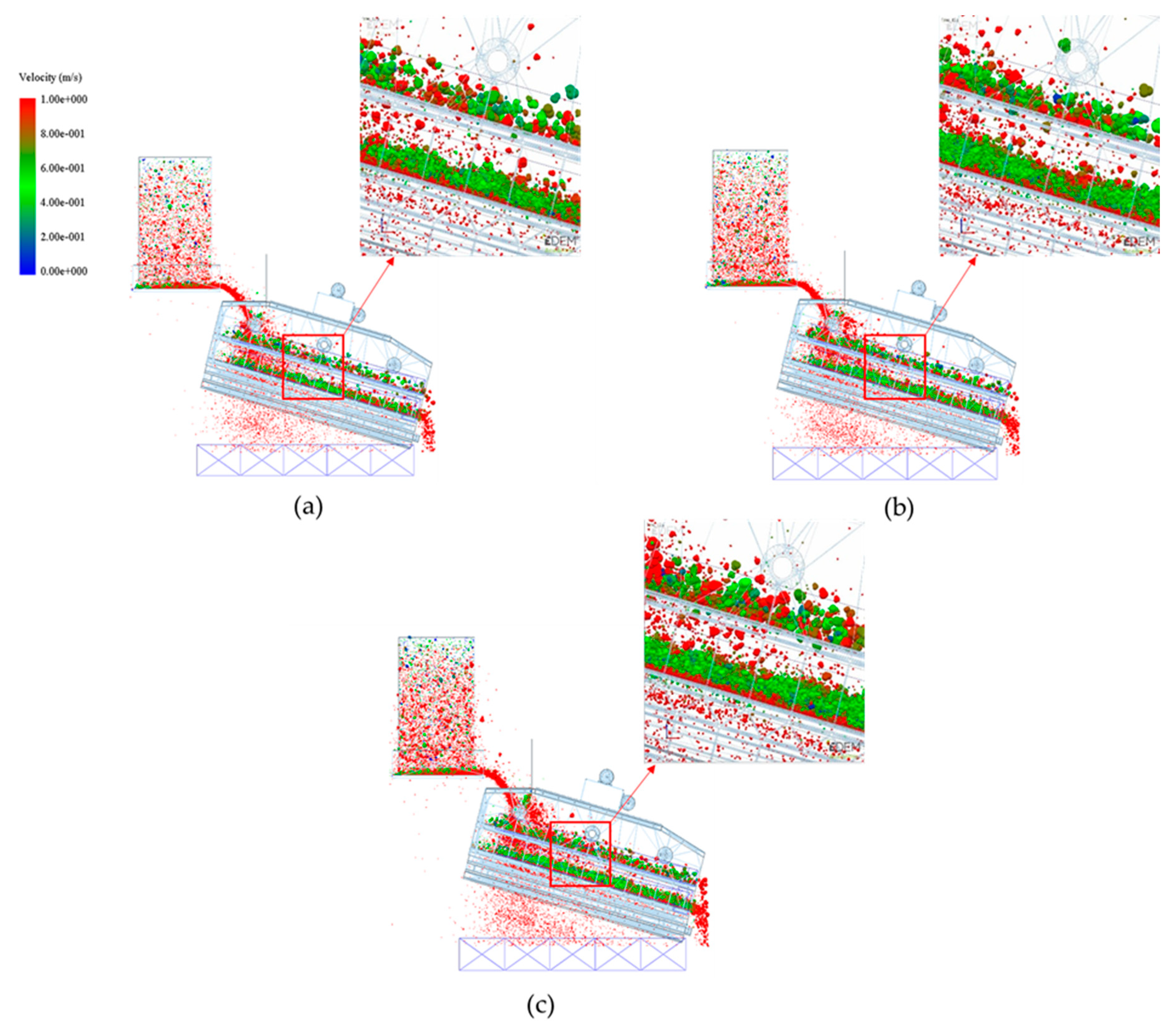
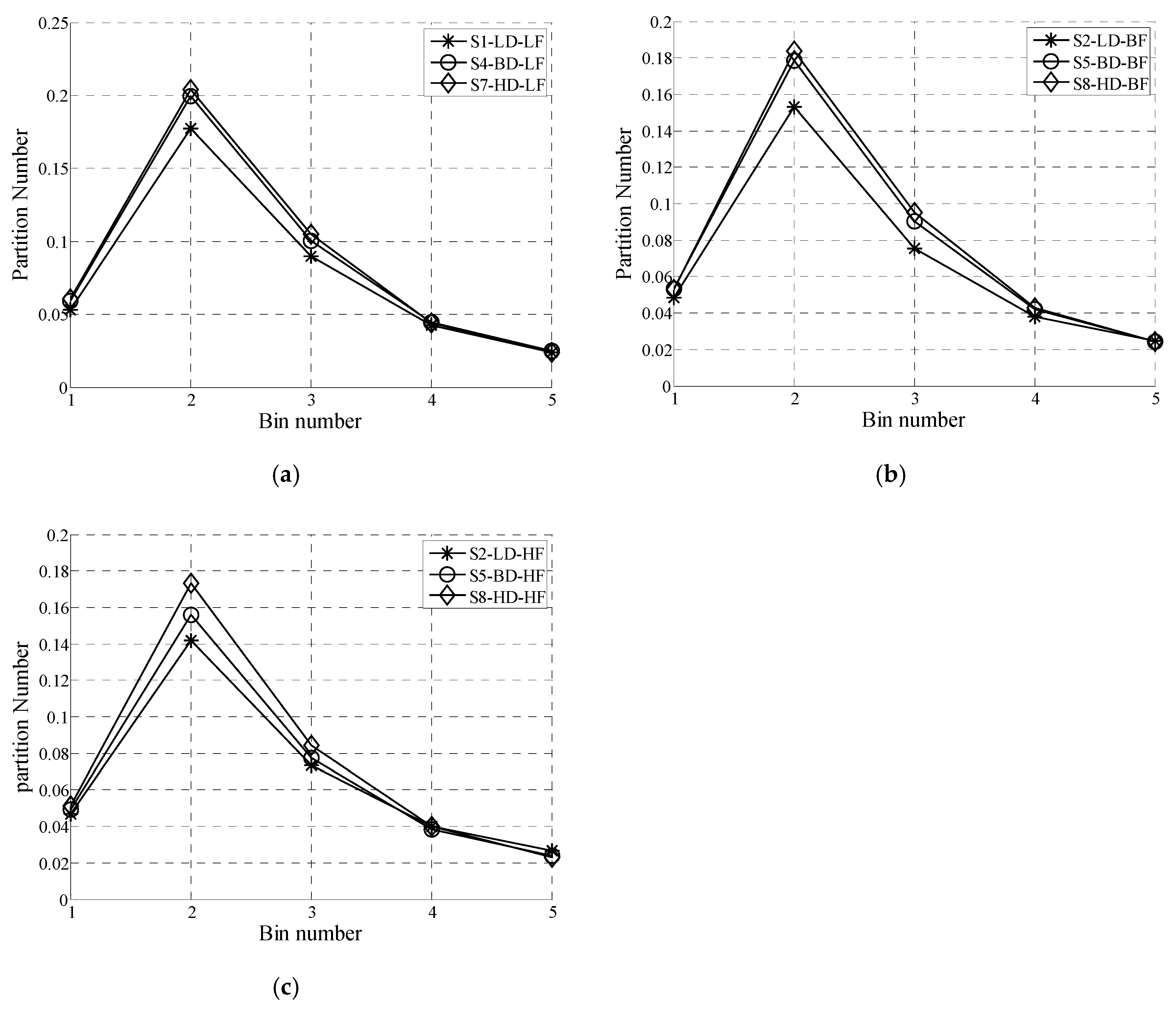
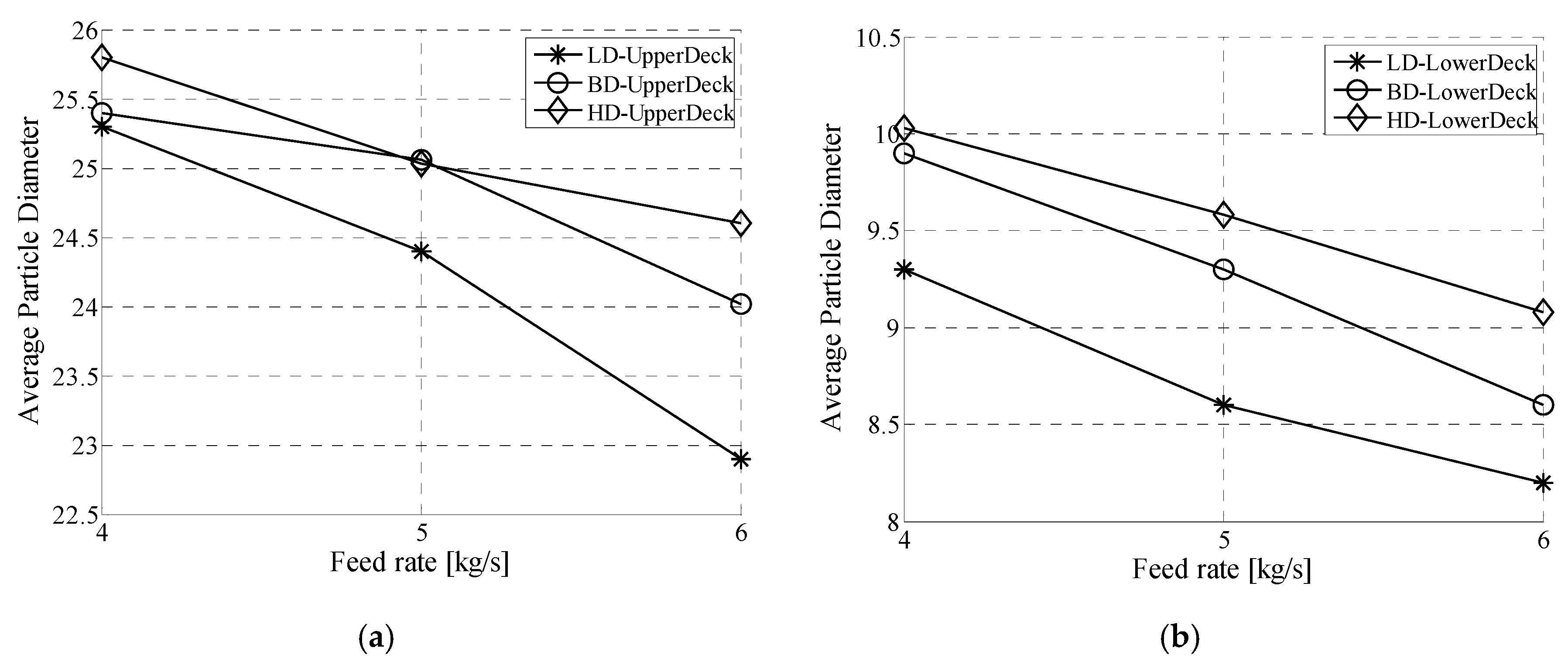
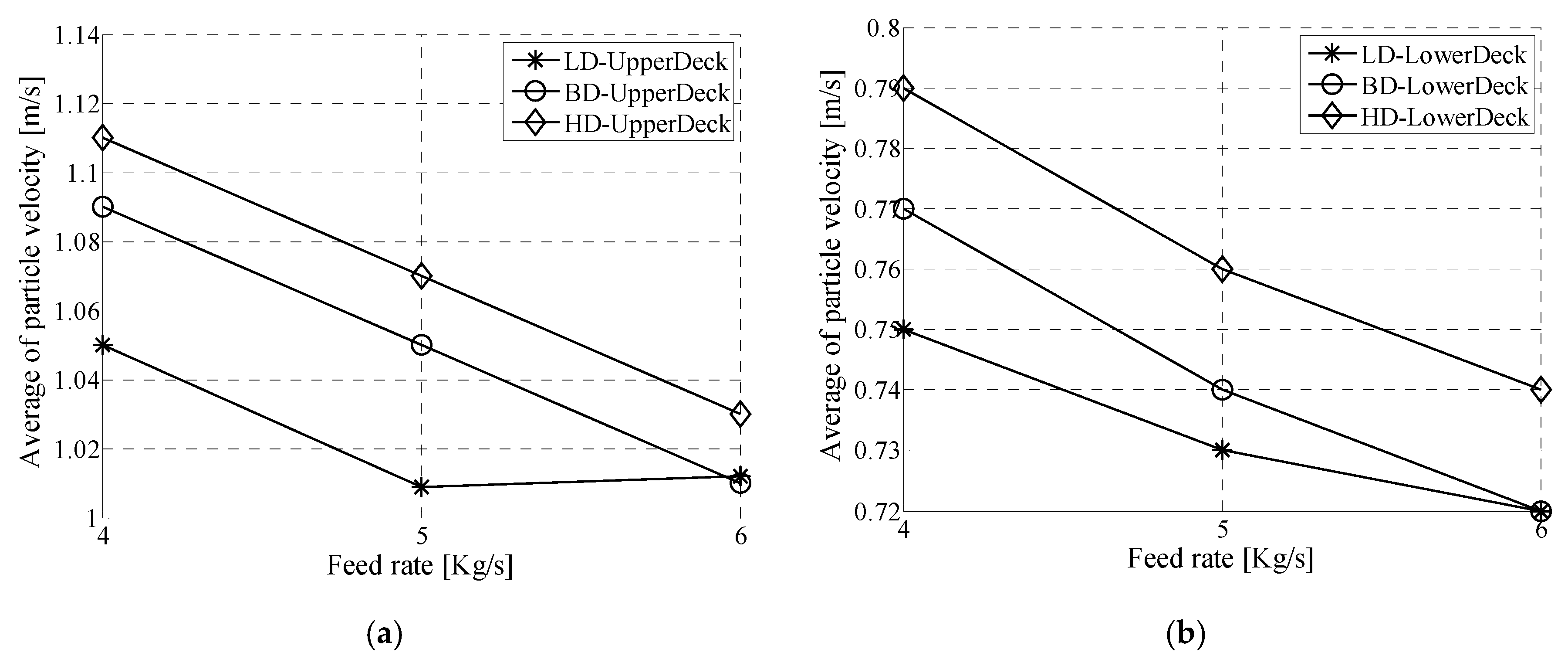
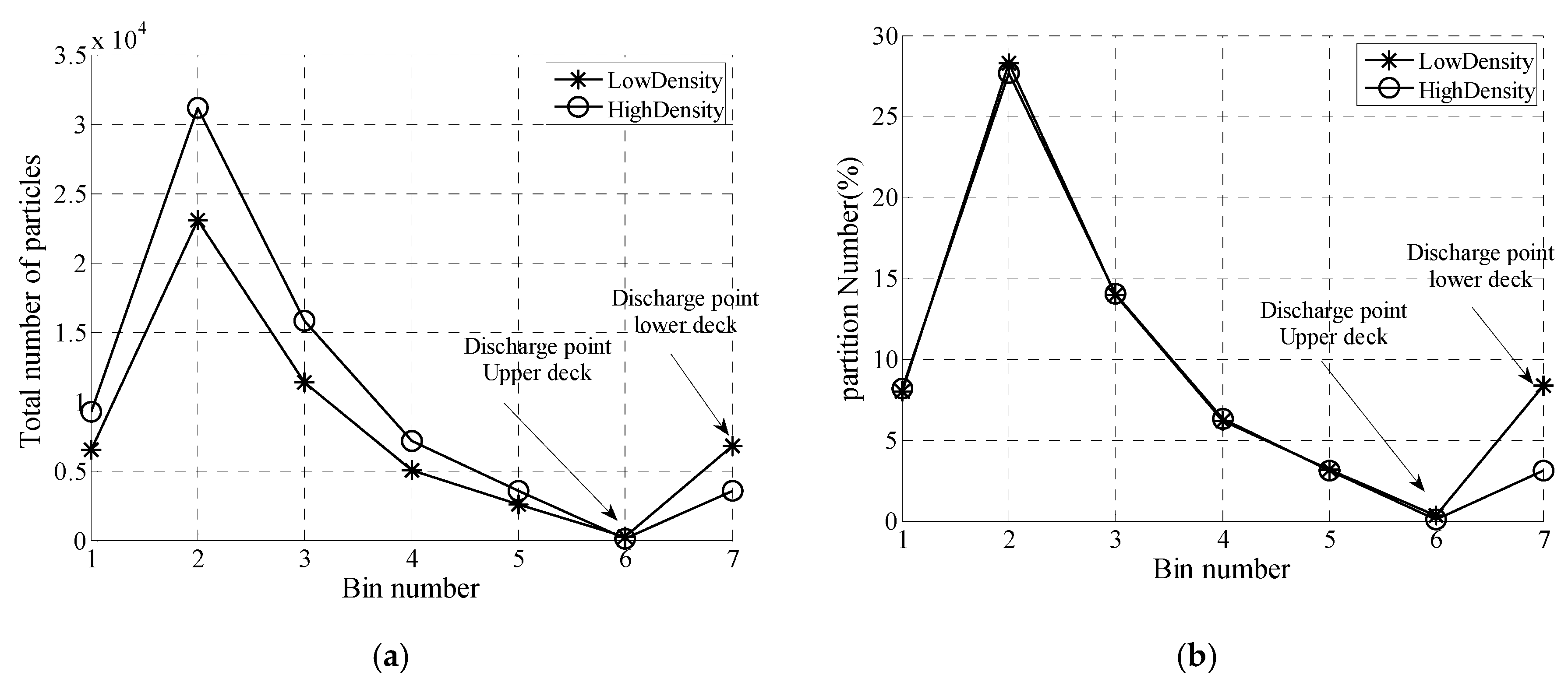
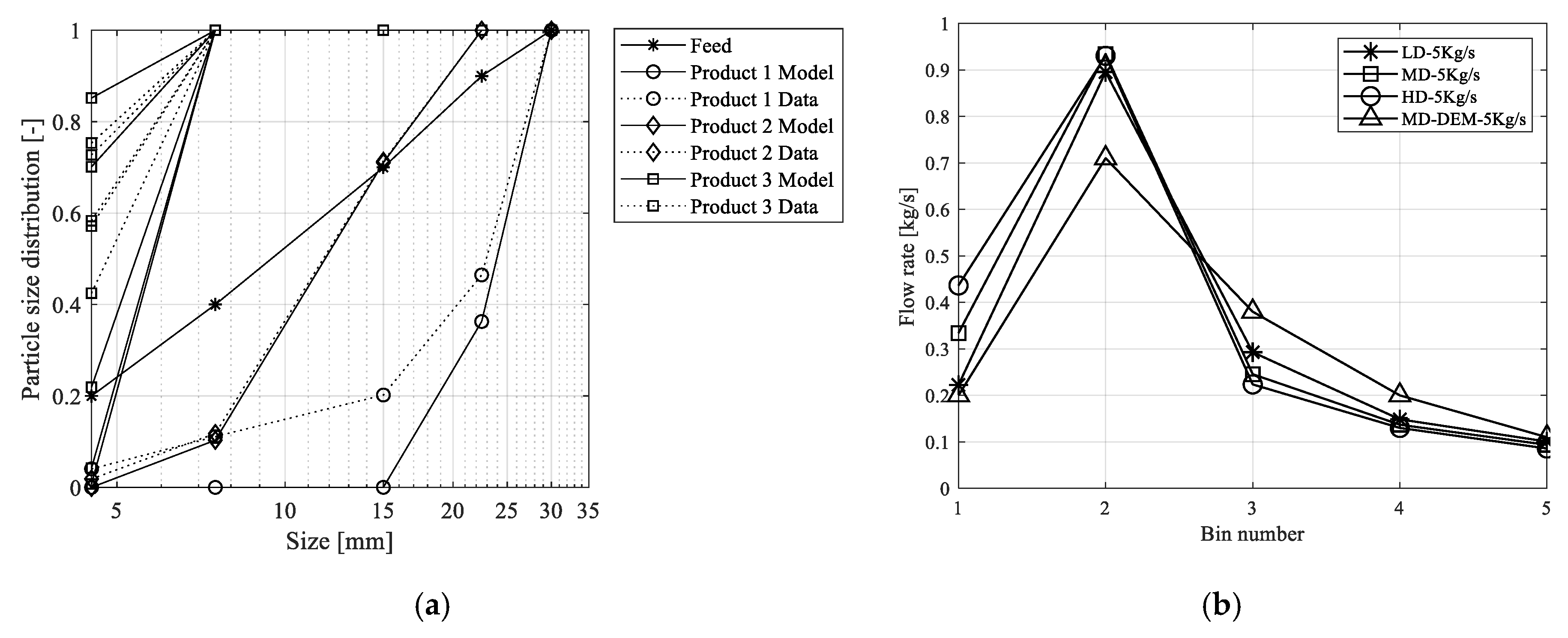
3. Results/Discussion
Model Comparison
4. Conclusions
- DEM is a powerful tool for calculating the overall efficiency and the product size distribution, while also enabling the analysis of important parameters, such as the size fraction (by sampling from any part of the screen); particle tracking; and the observation of bed material, which helps in stratification analysis. Therefore, DEM can provide a better understanding of different process parameters, such as how various particle densities have an effect on the stratification process and screen efficiency.
- The increase in the passing percentage of small undersized particles mainly occurred at the upper deck, and as a result, the particle bed was thicker at the lower deck, which means that the stratification process mainly affects the screen efficiency in the lower deck.
- In the simulations, the passage rate for the low-density material was lower than for the high-density material, since the low-density material had a lower stratification rate compared to the high-density material.
- In the stratification of materials with various densities, it is easier for the high-density material to move vertically through the particle bed. Thus, the high-density material has a higher probability of passage.
5. Future work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wills, B.A. Wills’ Mineral Processing Technology: An Introduction to the Practical Aspects of Ore Treatment and Mineral Recovery; Butterworth-Heinemann: Oxford, UK, 2011. [Google Scholar]
- Asbjörnsson, G.; Bengtsson, M.; Hulthén, E.; Evertsson, M. Model of banana screen for robust performance. Miner. Eng. 2016, 91, 66–73. [Google Scholar] [CrossRef]
- Soldinger, M. Influence of particle size and bed thickness on the screening process. Miner. Eng. 2000, 13, 297–312. [Google Scholar] [CrossRef]
- Soldinger, M. Interrelation of stratification and passage in the screening process. Miner. Eng. 1999, 12, 497–516. [Google Scholar] [CrossRef]
- Drahun, J.A.; Bridgwater, J. The mechanisms of free surface segregation. Powder Technol. 1983, 36, 39–53. [Google Scholar] [CrossRef]
- Khakhar, D.V.; McCarthy, J.J.; Ottino, J.M. Radial segregation of granular mixtures in rotating cylinders. Phys. Fluids 1997, 9, 3600–3614. [Google Scholar] [CrossRef]
- Bridgwater, J.; Foo, W.S.; Stephens, D.J. Particle mixing and segregation in failure zones—theory and experiment. Powder Technol. 1985, 41, 147–158. [Google Scholar] [CrossRef]
- Wang, L.; Ding, Z.; Meng, S.; Zhao, H.; Song, H. Kinematics and dynamics of a particle on a non-simple harmonic vibrating screen. Particuology 2017, 32, 167–177. [Google Scholar] [CrossRef]
- Clément, E.; Rajchenbach, J.; Duran, J. Mixing of a Granular Material in a Bidimensional Rotating Drum. Europhys. Lett. 1995, 30, 7–12. [Google Scholar] [CrossRef]
- Xiao, H.; Umbanhowar, P.B.; Ottino, J.M.; Lueptow, R.M. Modelling density segregation in flowing bidisperse granular materials. Proc. R. Soc. A Math. Phys. Eng. Sci. 2016, 472, 20150856. [Google Scholar] [CrossRef]
- Carvalho, R.; Tavares, L. A mechanistic model of SAG mills. In Proceedings of the IMPC 2014—27th International Mineral Processing Congress, Santiago, Chile, 20–24 October 2014. [Google Scholar]
- Cleary, P.W. Ball motion, axial segregation and power consumption in a full scale two chamber cement mill. Miner. Eng. 2009, 22, 809–820. [Google Scholar] [CrossRef]
- Chen, Y.-h.; Tong, X. Application of the DEM to screening process: A 3D simulation. Min. Sci. Technol. (China) 2009, 19, 493–497. [Google Scholar] [CrossRef]
- Jahani, M.; Farzanegan, A.; Noaparast, M. Investigation of screening performance of banana screens using LIGGGHTS DEM solver. Powder Technol. 2015, 283, 32–47. [Google Scholar] [CrossRef]
- Davoodi, A.; Bengtsson, M.; Hulthén, E.; Evertsson, C.M. Effects of screen decks’ aperture shapes and materials on screening efficiency. Miner. Eng. 2019, 139, 105699. [Google Scholar] [CrossRef]
- Cleary, P.W.; Sinnott, M.D.; Morrison, R.D. Separation performance of double deck banana screens—Part 1: Flow and separation for different accelerations. Miner. Eng. 2009, 22, 1218–1229. [Google Scholar] [CrossRef]
- Teufelsbauer, H.; Wang, Y.; Chiou, M.; Wu, W. Flow–obstacle interaction in rapid granular avalanches: DEM simulation and comparison with experiment. Granul. Matter 2009, 11, 209–220. [Google Scholar] [CrossRef]
- Yan, B.; Regueiro, R.; Sture, S. Three-dimensional ellipsoidal discrete element modeling of granular materials and its coupling with finite element facets. Eng. Comput. 2009, 27. [Google Scholar] [CrossRef]
- Evertsson, J.Q.M. Framework for DEM Model Calibration and Validation. In Proceedings of the 14th European Symposium On Comminution And Classification, Gothenburg, Sweden, 7–11 September 2015. [Google Scholar]
- Soldinger, M. Transport velocity of a crushed rock material bed on a screen. Miner. Eng. 2002, 15, 7–17. [Google Scholar] [CrossRef]
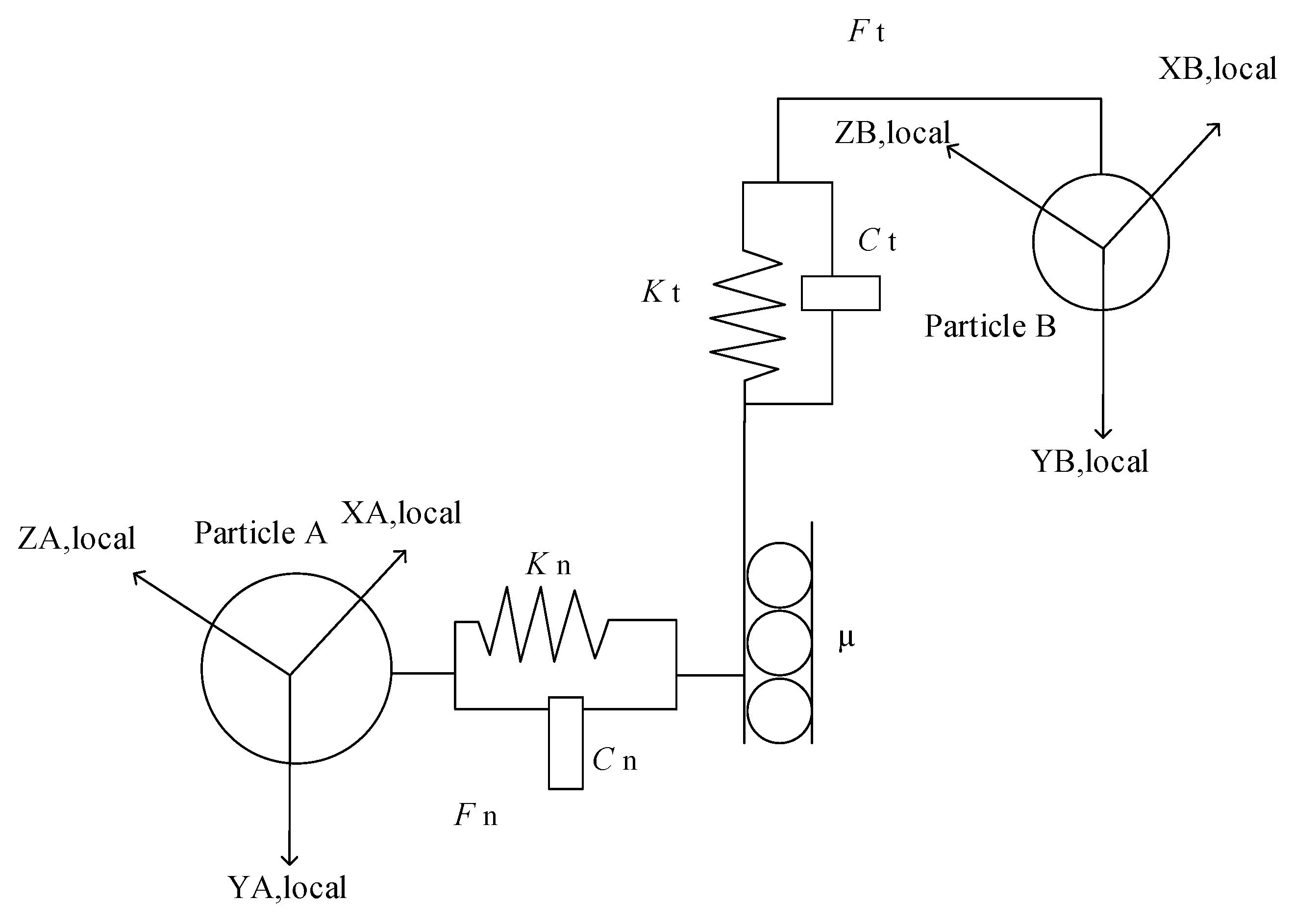

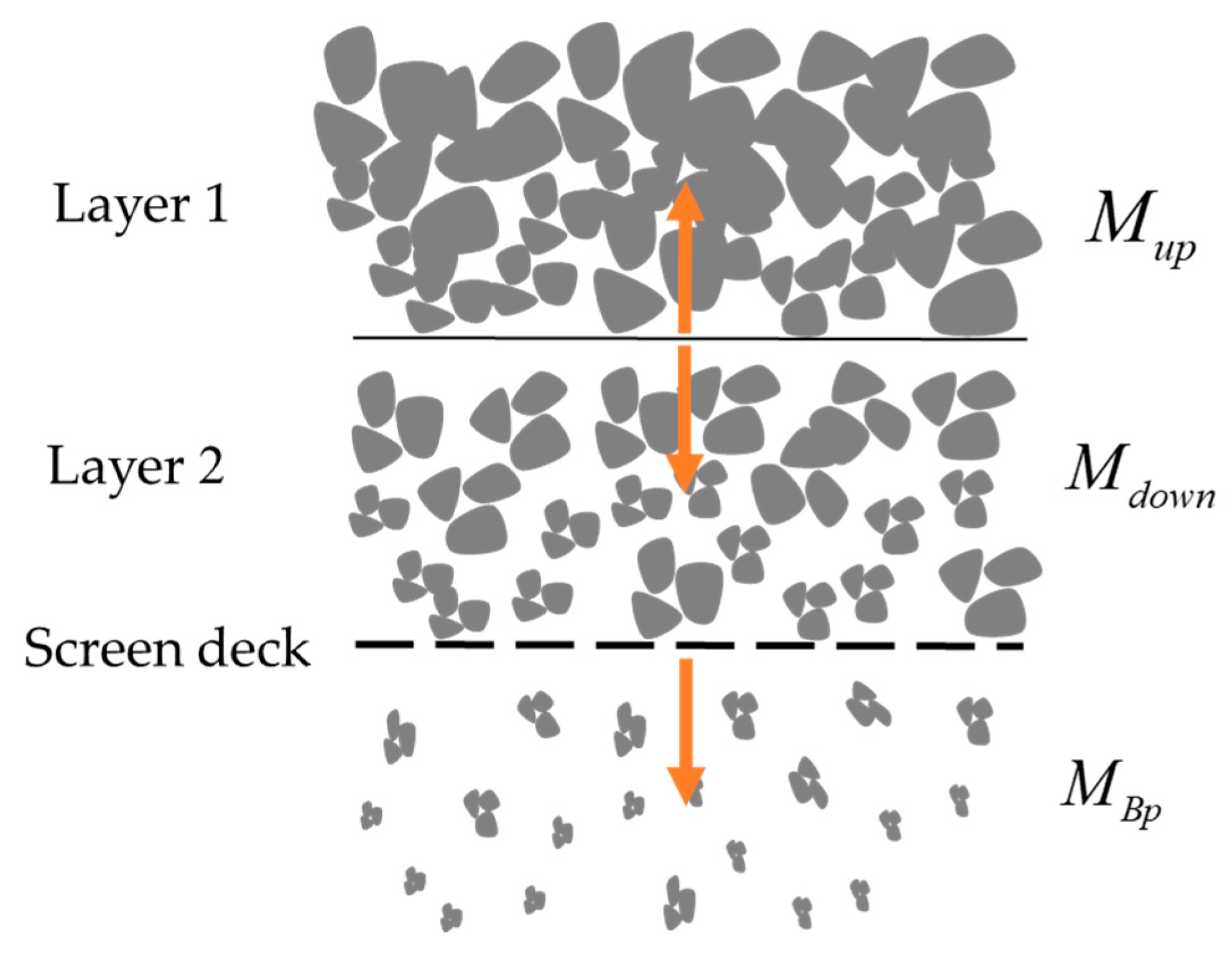
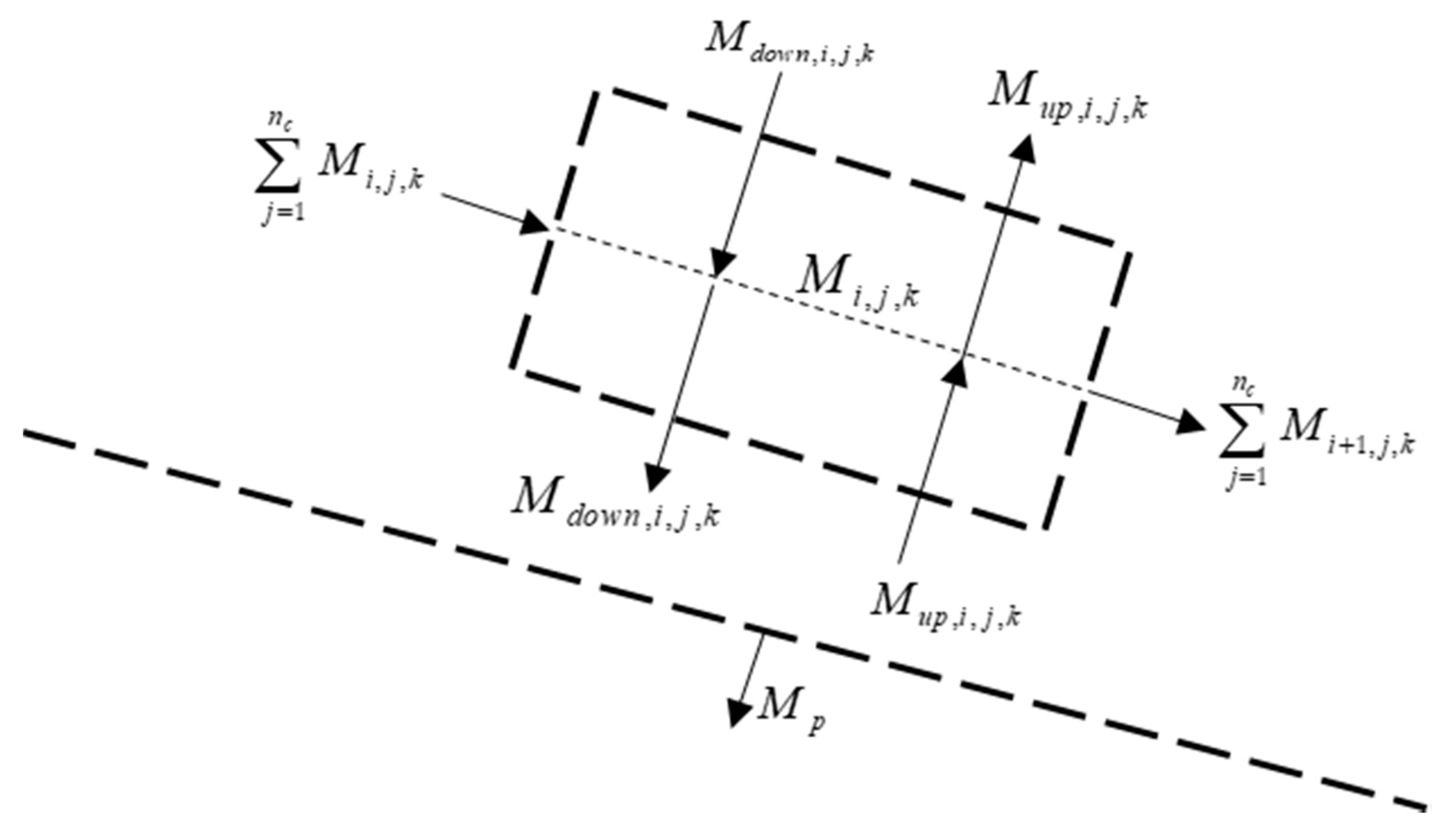
| Normal force, Equation (1), (N) | The mass flow along the screen, Equation (4), (kg) | ||
| Stiffness of the spring, Equation (1), (-) | The downward flow, Equation (4), (kg) | ||
| Viscoelastic damping constant, Equation (1), (m/s) | The upward flow, Equation (4), (kg) | ||
| The relative velocities, Equation (1), (m/s) | Mass flow of the material in the contact layer, Equation (4), (kg) | ||
| Tangential force, Equation (2), (N) | Passage rate parameter, Equation (4), (-) | ||
| Stiffness of the spring, Equation (2), (-) | Time step, Equation (4), (s) | ||
| Viscoelastic damping constant, Equation (2), (-) | Slope of the screen deck, Equation (6), (Angle) | ||
| The relative velocities, Equation (2), (m/s) | Transport velocity of the particle along the screen deck, Equation (6), (m/s) | ||
| Frequency, Equations (3) and (6), (Hz) | Function of stroke, Equation (6), (mm) |
| Material Properties | Poisson’s Ratio | Shear Modulus | Density |
| Particles (Low density) | 0.3 | 24 MPa | 2100 kg/m3 |
| Particles (Medium density) | 0.3 | 24 MPa | 2500 kg/m3 |
| Particles (High density) | 0.3 | 24 MPa | 2900 kg/m3 |
| Screen (Steel) | 0.2 | 79 GPa | 7800 kg/m3 |
| Collision Properties | Coefficient of Restitution | Coefficient of Static Friction | Coefficient of Rolling Friction |
| Particle-particle | 0.2 | 0.6 | 0.01 |
| Particle-screen (Steel) | 0.6 | 0.45 | 0.01 |
| Machine Parameters | |||
| Screen aperture | 25 mm×25 mm and 10 mm×10 mm | ||
| Screen declination | 15° | ||
| Screen vibration | Sinusoidal translation, amplitude 6 mm, and frequency 13 Hz | ||
| Particle generation rate | For particles at 4 kg/s, 5 kg/s, and 6 kg/s | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Davoodi, A.; Asbjörnsson, G.; Hulthén, E.; Evertsson, M. Application of the Discrete Element Method to Study the Effects of Stream Characteristics on Screening Performance. Minerals 2019, 9, 788. https://doi.org/10.3390/min9120788
Davoodi A, Asbjörnsson G, Hulthén E, Evertsson M. Application of the Discrete Element Method to Study the Effects of Stream Characteristics on Screening Performance. Minerals. 2019; 9(12):788. https://doi.org/10.3390/min9120788
Chicago/Turabian StyleDavoodi, Ali, Gauti Asbjörnsson, Erik Hulthén, and Magnus Evertsson. 2019. "Application of the Discrete Element Method to Study the Effects of Stream Characteristics on Screening Performance" Minerals 9, no. 12: 788. https://doi.org/10.3390/min9120788
APA StyleDavoodi, A., Asbjörnsson, G., Hulthén, E., & Evertsson, M. (2019). Application of the Discrete Element Method to Study the Effects of Stream Characteristics on Screening Performance. Minerals, 9(12), 788. https://doi.org/10.3390/min9120788







