Evaluating the Role of Iron-Rich (Mg,Fe)O in Ultralow Velocity Zones
Abstract
1. Introduction
2. Materials and Methods
2.1. X-Ray Diffraction
2.2. Synchrotron Mössbauer Spectroscopy
3. Experimental Results
3.1. Equation of State (B1 Phase)
3.2. Equation of State (Rhombohedral Phase)
3.3. Synchrotron Mössbauer Spectroscopy
4. Modeling Iron-Rich (Mg,Fe)O in the Lowermost Mantle
4.1. Calculating Iron-Rich (Mg,Fe)O Elasticity at CMB Conditions
4.2. Forward Modeling
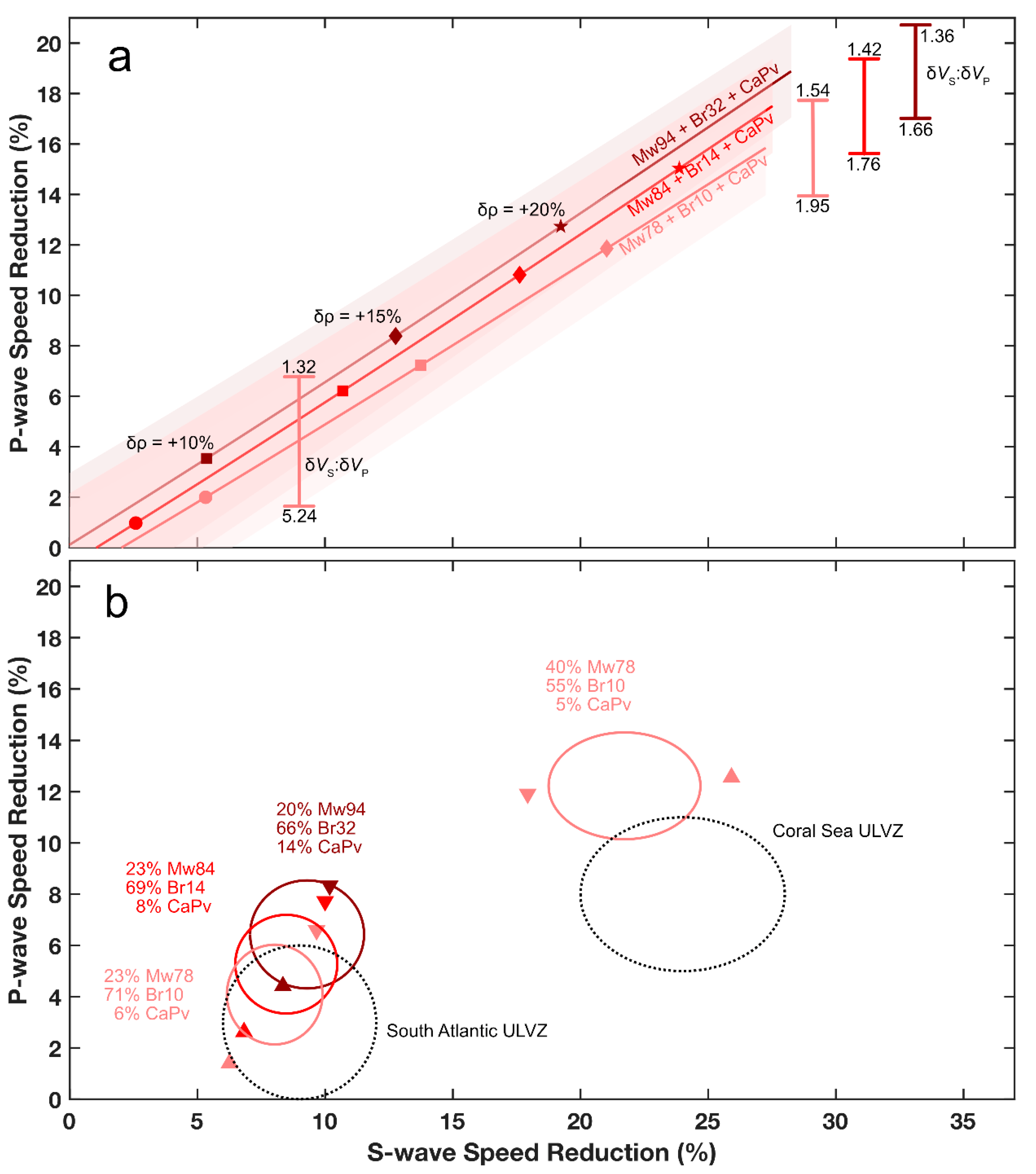
4.3. Inverse Modeling
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Lay, T. Deep Earth Structure: Lower Mantle and D. In Treatise on Geophysics, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2015; Volume 1, pp. 683–723. [Google Scholar] [CrossRef]
- Lay, T.; Helmberger, D.V. A Lower Mantle S-wave Triplication and the Shear Velocity Structure of D″. Geophys. J. R. Astron. Soc. 1983, 75, 799–837. [Google Scholar] [CrossRef]
- Cobden, L.; Thomas, C.; Trampert, J. Seismic Detection of Post-Perovskite inside the Earth. In The Earth’s Heterogeneous Mantle: A Geophysical, Geodynamical, and Geochemical Perspective; Springer: New York, NY, USA, 2015; pp. 391–440. [Google Scholar] [CrossRef]
- Garnero, E.J.; Helmberger, D.V. Further Structural Constraints and Uncertainties of a Thin Laterally Varying Ultralow-Velocity Layer at the Base of the Mantle. J. Geophys. Res. Solid Earth 1998, 103, 12495–12509. [Google Scholar] [CrossRef]
- Thorne, M.S.; Garnero, E.J. Inferences on Ultralow-Velocity Zone Structure from a Global Analysis of SPdKS Waves. J. Geophys. Res. Solid Earth 2004, 1098, 1–22. [Google Scholar] [CrossRef]
- McNamara, A.K.; Garnero, E.J.; Rost, S. Tracking Deep Mantle Reservoirs with Ultra-Low Velocity Zones. Earth Planet. Sci. Lett. 2010, 299, 1–9. [Google Scholar] [CrossRef]
- Yu, S.; Garnero, E.J. Ultralow Velocity Zone Locations: A Global Assessment. Geochem. Geophys. Geosystems 2018, 19, 396–414. [Google Scholar] [CrossRef]
- Manga, M.; Jeanloz, R. Implications of a Metal-Bearing Chemical Boundary Layer in D” for Mantle Dynamics. Geophys. Res. Lett. 1996, 23, 3091–3094. [Google Scholar] [CrossRef]
- Knittle, E.; Jeanloz, R. Earth’s Core-Mantle Boundary: Results of Experiments at High Pressures and Temperatures. Science 1991, 251, 1438–1443. [Google Scholar] [CrossRef]
- Mao, W.L.; Mao, H.K.; Sturhahn, W.; Zhao, J.; Prakapenka, V.B.; Meng, Y.; Shu, J.; Fei, Y.; Hemley, R.J. Iron-Rich Post-Perovskite and the Origin of Ultralow-Velocity Zones. Science 2006, 3123, 564–565. [Google Scholar] [CrossRef]
- Dobson, D.P.; Brodholt, J.P. Subducted Banded Iron Formations as a Source of Ultralow-Velocity Zones at the Core-Mantle Boundary. Nature 2005, 434, 371–374. [Google Scholar] [CrossRef]
- Buffett, B.A.; Garnero, E.J.; Jeanloz, R. Sediments at the Top of Earth’s Core. Science 2000, 290, 1938–1942. [Google Scholar] [CrossRef]
- Andrault, D.; Pesce, G.; Bouhifd, M.A.; Bolfan-Casanova, N.; Heńot, J.M.; Mezouar, M. Melting of Subducted Basalt at the Core-Mantle Boundary. Science 2014, 244, 895. [Google Scholar] [CrossRef]
- Ohtani, E.; Maeda, M. Density of Basaltic Melt at High Pressure and Stability of the Melt at the Base of the Lower Mantle. Earth Planet. Sci. Lett. 2001, 344, 892–895. [Google Scholar] [CrossRef]
- Pradhan, G.K.; Fiquet, G.; Siebert, J.; Auzende, A.L.; Morard, G.; Antonangeli, D.; Garbarino, G. Melting of MORB at Core-Mantle Boundary. Earth Planet. Sci. Lett. 2015, 431, 247–255. [Google Scholar] [CrossRef]
- Liu, J.; Li, J.; Hrubiak, R.; Smith, J.S. Origins of Ultralow Velocity Zones through Slab-Derived Metallic Melt. Proc. Natl. Acad. Sci. USA 2016, 113, 5547–5551. [Google Scholar] [CrossRef]
- Williams, Q.; Garnero, E.J. Seismic Evidence for Partial Melt at the Base of Earth’s Mantle. Science 1996, 273, 1528–1530. [Google Scholar] [CrossRef]
- Berryman, J.G. Seismic Velocity Decrement Ratios for Regions of Partial Melt in the Lower Mantle. Geophys. Res. Lett. 2000, 27, 421–424. [Google Scholar] [CrossRef]
- Sinmyo, R.; Hirose, K.; Nishio-Hamane, D.; Seto, Y.; Fujino, K.; Sata, N.; Ohishi, Y. Partitioning of Iron between Perovskite/Postperovskite and Ferropericlase in the Lower Mantle. J. Geophys. Res. Solid Earth 2008, 113. [Google Scholar] [CrossRef]
- Wicks, J.K.; Jackson, J.M.; Sturhahn, W. Very Low Sound Velocities in Iron-Rich (Mg,Fe)O: Implications for the Core-Mantle Boundary Region. Geophys. Res. Lett. 2010, 37, 1–5. [Google Scholar] [CrossRef]
- Wicks, J.K.; Jackson, J.M.; Sturhahn, W.; Zhang, D. Sound Velocity and Density of Magnesiowüstites: Implications for Ultralow-Velocity Zone Topography. Geophys. Res. Lett. 2017, 44, 2148–2158. [Google Scholar] [CrossRef]
- Bower, D.J.; Wicks, J.K.; Gurnis, M.; Jackson, J.M. A Geodynamic and Mineral Physics Model of a Solid-State Ultralow-Velocity Zone. Earth Planet. Sci. Lett. 2011, 303, 193–202. [Google Scholar] [CrossRef]
- Li, M.; McNamara, A.K.; Garnero, E.J.; Yu, S. Compositionally-Distinct Ultra-Low Velocity Zones on Earth’s Core-Mantle Boundary. Nat. Commun. 2017, 8, 177. [Google Scholar] [CrossRef]
- Brown, S.P.; Thorne, M.S.; Miyagi, L.; Rost, S. A Compositional Origin to Ultralow-Velocity Zones. Geophys. Res. Lett. 2015, 42, 1039–1045. [Google Scholar] [CrossRef]
- Wicks, J.K.; Jackson, J.M.; Sturhahn, W.; Zhuravlev, K.K.; Tkachev, S.N.; Prakapenka, V.B. Thermal Equation of State and Stability of (Mg0.06Fe0.94) O. Phys. Earth Planet. Inter. 2015, 249, 28–42. [Google Scholar] [CrossRef]
- Finkelstein, G.J.; Jackson, J.M.; Sturhahn, W.; Zhang, D.; Ercan Alp, E.; Toellner, T.S. Single-Crystal Equations of State of Magnesiowüstite at High Pressures. Am. Mineral. 2017, 102, 1709–1717. [Google Scholar] [CrossRef]
- Matas, J.; Bass, J.; Ricard, Y.; Mattern, E.; Bukowinski, M.S.T. On the Bulk Composition of the Lower Mantle: Predictions and Limitations from Generalized Inversion of Radial Seismic Profiles. Geophys. J. Int. 2007, 170, 764–780. [Google Scholar] [CrossRef]
- Dewaele, A.; Datchi, F.; Loubeyre, P.; Mezouar, M. High Pressure-High Temperature Equations of State of Neon and Diamond. Phys. Rev. B Condens. Matter Mater. Phys. 2008, 77, 094106. [Google Scholar] [CrossRef]
- Prescher, C.; Prakapenka, V.B. DIOPTAS: A Program for Reduction of Two-Dimensional X-Ray Diffraction Data and Data Exploration. High Press. Res. 2015, 35, 223–230. [Google Scholar] [CrossRef]
- Toby, B.H.; Von Dreele, R.B. GSAS-II: The Genesis of a Modern Open-Source All Purpose Crystallography Software Package. J. Appl. Crystallogr. 2013, 46, 544–549. [Google Scholar] [CrossRef]
- Fei, Y.; Ricolleau, A.; Frank, M.; Mibe, K.; Shen, G.; Prakapenka, V. Toward an Internally Consistent Pressure Scale. Proc. Natl. Acad. Sci. USA 2007, 104, 9182–9186. [Google Scholar] [CrossRef]
- Toellner, T.S. Monochromatization of Synchrotron Radiation for Nuclear Resonant Scattering Experiments. Hyperfine Interact. 2000, 125, 3–28. [Google Scholar] [CrossRef]
- Akahama, Y.; Kawamura, H. Pressure Calibration of Diamond Anvil Raman Gauge to 410 GPa. J. Phys. Conf. Ser. 2010, 215, 1. [Google Scholar] [CrossRef]
- Sturhahn, W. MINUTI Open Source Software, Version 2.0.0. Available online: http://www.nrixs.com (accessed on 10 January 2018).
- Sturhahn, W. CONUSS and PHOENIX: Evaluation of Nuclear Resonant Scattering Data. Hyperfine Interact 2000, 125, 149–172. [Google Scholar] [CrossRef]
- Solomatova, N.V.; Jackson, J.M.; Sturhahn, W.; Wicks, J.K.; Zhao, J.; Toellner, T.S.; Kalkan, B.; Steinhardt, W.M. Equation of State and Spin Crossover of (Mg,Fe)O at High Pressure, with Implications for Explaining Topographic Relief at the Core-Mantle Boundary. Am. Mineral. 2016, 101, 1084–1093. [Google Scholar] [CrossRef]
- Sturhahn, W.; Jackson, J.M.; Lin, J.F. The Spin State of Iron in Minerals of Earth’s Lower Mantle. Geophys. Res. Lett. 2005, 32, 1–5. [Google Scholar] [CrossRef]
- Tsuchiya, T.; Wentzcovitch, R.M.; da Silva, C.R.S.; de Gironcoli, S. Spin Transition in Magnesiowüstite in Earth’s Lower Mantle. Phys. Rev. Lett. 2006, 96, 198501. [Google Scholar] [CrossRef]
- Wu, Z.; Wentzcovitch, R.M. Spin Crossover in Ferropericlase and Velocity Heterogeneities in the Lower Mantle. Proc. Natl. Acad. Sci. USA 2014, 111, 10468–10472. [Google Scholar] [CrossRef]
- Wentzcovitch, R.M.; Wu, Z.; Carrier, P. First Principles Quasiharmonic Thermoelasticity of Mantle Minerals. Rev. Mineral. Geochem. 2010, 71, 99–128. [Google Scholar] [CrossRef]
- Gréaux, S.; Irifune, T.; Higo, Y.; Tange, Y.; Arimoto, T.; Liu, Z.; Yamada, A. Sound Velocity of CaSiO3 Perovskite Suggests the Presence of Basaltic Crust in the Earth’s Lower Mantle. Nature 2019, 565, 218–221. [Google Scholar] [CrossRef]
- Duffy, T.S.; Anderson, D.L. Seismic Velocities in Mantle Minerals and the Mineralogy of the Upper Mantle. J. Geophys. Res. 1989, 94, 1895–1912. [Google Scholar] [CrossRef]
- Li, B.; Zhang, J. Pressure and Temperature Dependence of Elastic Wave Velocity of MgSiO3 Perovskite and the Composition of the Lower Mantle. Phys. Earth Planet. Inter. 2005, 151, 143–154. [Google Scholar] [CrossRef]
- Dorfman, S.M.; Meng, Y.; Prakapenka, V.B.; Duffy, T.S. Effects of Fe-Enrichment on the Equation of State and Stability of (Mg,Fe)SiO3 Perovskite. Earth Planet. Sci. Lett. 2013, 361, 249–257. [Google Scholar] [CrossRef]
- Wolf, A.S.; Jackson, J.M.; Dera, P.; Prakapenka, V.B.; Al, W.E.T. Solid Earth The Thermal Equation of State of (Mg, Fe) SiO3 Bridgmanite (Perovskite) and Implications for Lower Mantle Structures. J. Geophys. Res. 2015, 120, 7460–7489. [Google Scholar] [CrossRef]
- Dziewonski, A.M.; Anderson, D.L. Preliminary Reference Earth Model. Phys. Earth Planet. Inter. 1981, 25, 297–356. [Google Scholar] [CrossRef]
- Simmons, N.A.; Grand, S.P. Partial Melting in the Deepest Mantle. Geophys. Res. Lett. 2002, 29, 1552. [Google Scholar] [CrossRef]
- Rost, S.; Garnero, E.J.; Williams, Q. Fine-Scale Ultralow-Velocity Zone Structure from High-Frequency Seismic Array Data. J. Geophys. Res. 2006, 111, B09310. [Google Scholar] [CrossRef]
- Yuan, K.; Romanowicz, B. Seismic Evidence for Partial Melting at the Root of Major Hot Spot Plumes. Science 2017, 357, 1–5. [Google Scholar] [CrossRef]
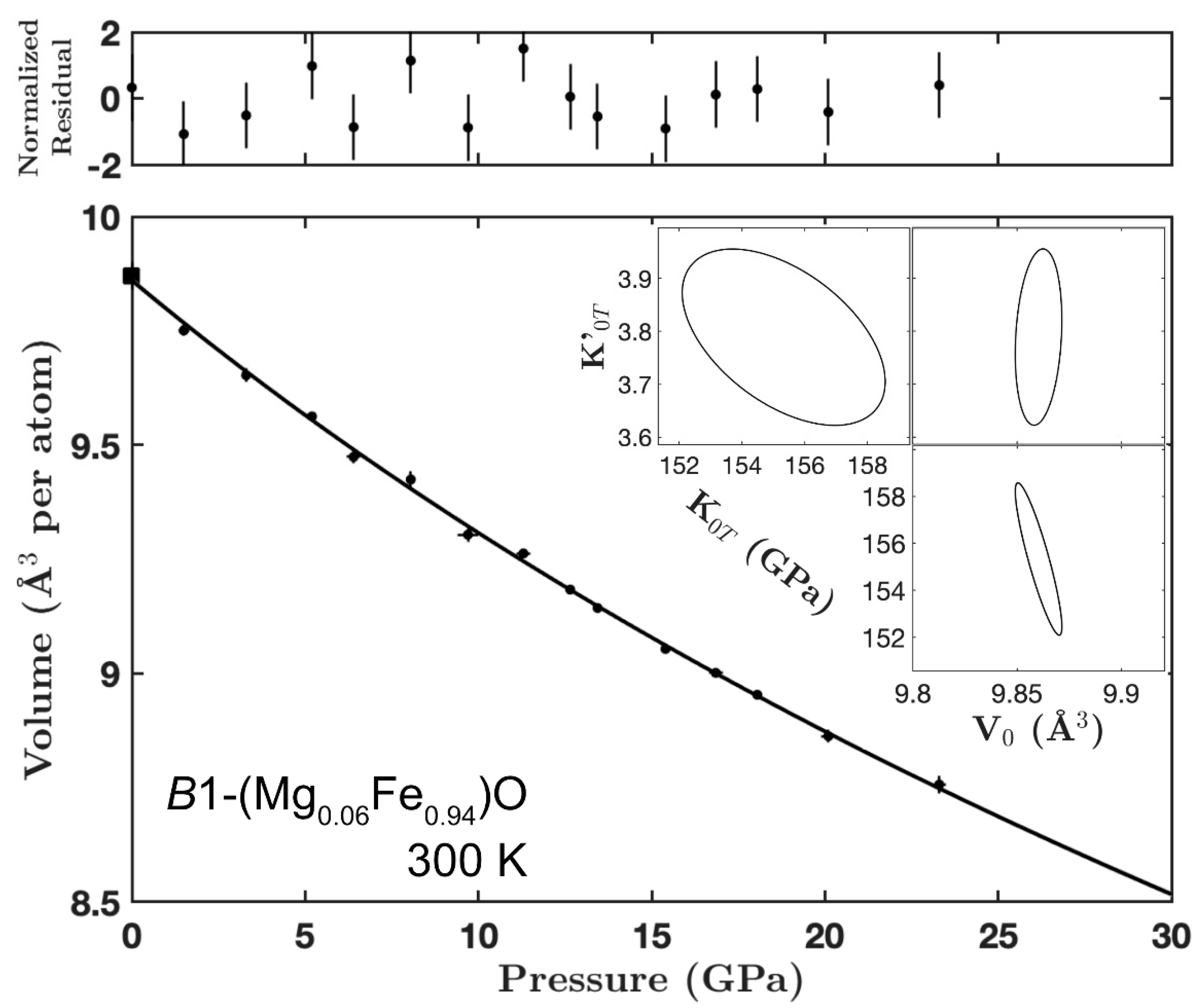
| Parameters | B1–Mw94 | r–Mw94 | Mw94 Model a | Mw84 Model b | Mw78 Model c |
|---|---|---|---|---|---|
| V0 (Å3 /atom) | 9.860 ± 0.007 | 9.59 ± 0.10 | 9.860 ± 0.007 | 9.79 ± 0.04 | 9.86 ± 0.02 |
| K0T (GPa) | 155.3 ± 2.2 | 217 ± 19 | 155.3 ± 2.2 | 155.3 ± 2.2 | 148 ± 3 |
| K’0T | 3.79 ± 0.11 | 2.06 ± 0.22 | 3.79 ± 0.11 | 3.79 ± 0.11 | 4.09 ± 0.12 |
| θ0 (K) | — | — | 426 | 426 | 426 |
| γ0 | — | — | 1.17 | 1.17 | 1.17 |
| q | — | — | 0.5 | 0.5 | 0.5 |
| Reduced χ2 | 0.70 ± 0.23 | 1.37 ± 0.37 | — | — | — |
| Result | δVP (%)a | δVS (%) | δρ (%) | Mw# | XMw (%) | XBr (%) | XCaPv (%) | Reduced χ2 |
|---|---|---|---|---|---|---|---|---|
| ULVZ: S. Atlantic b | −3 ± 3 | −9 ± 3 | +10 ± 10 | |||||
| Fit: Voigt | −8.3 ± 3.4 | −10.2 ± 3.9 | +17.2 ± 2.6 | 94 | 29.0 ± 11 | 59.9 ± 13 | 11.1 | 0.58 ± 0.54 |
| Reuss | −4.4 ± 2.3 | −8.3 ± 2.0 | +8.2 ± 0.6 | 94 | 11.6 ± 1.8 | 72.1 ± 5.6 | 16.3 | 0.09 ± 0.21 |
| Hill | −6.4 ± 2.1 | −9.3 ± 1.7 | +12.7 ± 2.2 | 94 | 20.3 ± 5.6 | 66.0 ± 7.1 | 13.7 | |
| Fit: Voigt | −7.7 ± 2.9 | −10.0 ± 3.1 | +15.3 ± 1.7 | 84 | 34.1 ± 8.6 | 64.5 ± 9.9 | 1.4 | 0.32 ± 0.40 |
| Reuss | −1.6 ± 2.6 | −6.1 ± 2.6 | +2.4 ± 0.6 | 84 | 11.4 ± 2.7 | 73.0 ± 9.2 | 15.6 | 0.22 ± 0.33 |
| Hill | −5.3 ± 1.9 | −8.5 ± 2.0 | +9.7 ± 0.9 | 84 | 22.7 ± 4.5 | 68.7 ± 6.7 | 8.6 | |
| Fit: Voigt c | −6.6 ± 2.6% | −9.7 ± 2.7 | +12.8 ± 1.3 | 78 | 34.4 ± 7.7 | 63 ± 11 | 2.6 | 0.15 ± 0.27 |
| Reussc | −1.4 ± 2.9 | −6.3 ± 2.6 | +2.8 ± 0.7 | 78 | 11.8 ± 4.1 | 80 ± 19 | 8.2 | 0.28 ± 0.37 |
| Hill | −4.1 ± 1.9 | −8.0 ± 1.9 | +7.8 ± 0.8 | 78 | 23.1 ± 4.4 | 71 ± 11 | 5.9 | |
| ULVZ: Coral Sea d | −8 ± 3 | −24 ± 4 | +8 ± 6 | |||||
| Fit: Voigt e | −11.9 ± 3.6 | −17.9 ± 5.2 | +18.3 ± 2.4 | 78 | 46.7 ± 14 | 48.4 ± 17 | 4.9 | 3.5 ± 1.1 |
| Reuss e | −12.6 ± 2.1 | −25.9 ± 2.4 | +12.7 ± 1.5 | 78 | 34.1 ± 4.0 | 61.1 ± 6.3 | 7.9 | 0.41 ± 0.37 |
| Hill | −12.2 ± 2.1 | −21.7 ± 3.0 | +15.5 ± 1.3 | 78 | 40.4 ± 7.3 | 54.7 ± 9.1 | 4.9 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dobrosavljevic, V.V.; Sturhahn, W.; Jackson, J.M. Evaluating the Role of Iron-Rich (Mg,Fe)O in Ultralow Velocity Zones. Minerals 2019, 9, 762. https://doi.org/10.3390/min9120762
Dobrosavljevic VV, Sturhahn W, Jackson JM. Evaluating the Role of Iron-Rich (Mg,Fe)O in Ultralow Velocity Zones. Minerals. 2019; 9(12):762. https://doi.org/10.3390/min9120762
Chicago/Turabian StyleDobrosavljevic, Vasilije V., Wolfgang Sturhahn, and Jennifer M. Jackson. 2019. "Evaluating the Role of Iron-Rich (Mg,Fe)O in Ultralow Velocity Zones" Minerals 9, no. 12: 762. https://doi.org/10.3390/min9120762
APA StyleDobrosavljevic, V. V., Sturhahn, W., & Jackson, J. M. (2019). Evaluating the Role of Iron-Rich (Mg,Fe)O in Ultralow Velocity Zones. Minerals, 9(12), 762. https://doi.org/10.3390/min9120762





