Next Article in Journal
Mg-Rich Authigenic Carbonates in Coastal Facies of the Vtoroe Zasechnoe Lake (Southwest Siberia): First Assessment and Possible Mechanisms of Formation
Next Article in Special Issue
Ultimate Mechanical Properties of Forsterite
Previous Article in Journal / Special Issue
My Career as a Mineral Physicist at Stony Brook: 1976–2019
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Minerals
Volume 9
Issue 12
10.3390/min9120762
minerals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Evaluating the Role of Iron-Rich (Mg,Fe)O in Ultralow Velocity Zones

by
Vasilije V. Dobrosavljevic
*,
Wolfgang Sturhahn
and
Jennifer M. Jackson
Seismological Laboratory, California Institute of Technology, Pasadena, CA 91125, USA
*
Author to whom correspondence should be addressed.
Minerals 2019, 9(12), 762; https://doi.org/10.3390/min9120762
Submission received: 12 November 2019 / Revised: 4 December 2019 / Accepted: 6 December 2019 / Published: 8 December 2019
(This article belongs to the Special Issue Mineral Physics—In Memory of Orson Anderson)
Browse Figures
Review Reports Versions Notes

Abstract

:
The composition of ultralow velocity zones (ULVZs) remains an open question, despite advances in both seismology and experimental work. We investigate the hypothesis of iron-rich (Mg,Fe)O (magnesiowüstite) as a cause of ULVZ seismic signatures. We report new quasi-hydrostatic X-ray diffraction measurements to constrain the equation of state of (Mg0.06Fe0.94)O with fit parameters V0 = 9.860 ± 0.007 Å3, K0T = 155.3 ± 2.2 GPa, K’0T = 3.79 ± 0.11, as well as synchrotron Mössbauer spectroscopy measurements to characterize the high-pressure magnetic and spin state of magnesiowüstite. We combine these results with information from previous studies to calculate the elastic behavior at core–mantle boundary conditions of magnesiowüstite, as well as coexisting bridgmanite and calcium silicate perovskite. Forward models of aggregate elastic properties are computed, and from these, we construct an inverse model to determine the proportions of magnesiowüstite that best reproduce ULVZ observations within estimated mutual uncertainties. We find that the presence of magnesiowüstite can explain ULVZ observations exhibiting 1:2 VP:VS reduction ratios relative to the Preliminary Reference Earth Model (PREM), as well as certain 1:3 VP:VS reductions within estimated uncertainty bounds. Our work quantifies the viability of compositionally distinct ULVZs containing magnesiowüstite and contributes to developing a framework for a methodical approach to evaluating ULVZ hypotheses.

1. Introduction

The boundary layer separating the iron-dominant liquid outer core from the silicate-rich mantle is a region of great complexity, where extreme contrasts in material properties promote the persistence of multiscale structural heterogeneities (e.g., [1,2,3]). The thermo-elastic variations at the lowermost mantle play a dominant role in the evolutionary history of the Earth through regulation of heat flow and consequent influence over the dynamics of both the mantle and the core. Despite the centrality of this region in the development of the solid Earth system, many open questions remain regarding the characteristics, origins, and dynamic interactions of observed heterogeneities, such as large thermochemical piles, ultralow velocity zones, subducted former oceanic material, and small seismic scatterers. As individual observational studies of such features and experimental investigations into candidate compositions continue to develop, synthesis of results from seismology and mineral physics provides quantitative and systematic avenues for revealing new insights into this complex region.
Advances in seismological observation over the past several decades have provided increasing evidence for the existence of ultralow velocity zones (ULVZs)—Small (<50 km in height) localized seismic anomalies at the base of the mantle that are characterized by significant reductions in velocities (up to 25% and 50% for P and S waves, respectively) and likely increases in density (up to 20%) relative to the surrounding mantle ([4,5,6], see also [7] for a recent review). To date, less than 20% of the core–mantle boundary (CMB) has been explored by seismic studies investigating ULVZs, yet the existing observations of ULVZs reveal a large variety of elastic properties, locations, and structural geometries (e.g., [7]). Nevertheless, the growing set of seismic studies observing diverse ULVZ properties can inform us of the causes of such significant velocity reductions. Whether all ULVZs share common characteristics and/or origins and what dynamical links may exist between them and other multi-scale features like slabs or slab debris, large thermochemical piles, and upwelling mantle plumes is the subject of current multidisciplinary research.
The very existence of ULVZs poses the question of their origin and dynamics and has attracted a variety of proposed explanations, including an iron-bearing layer of FeO and FeSi [8,9], iron-enriched postperovskite (Mg,Fe)SiO3 [10], subducted banded iron formations [11], silicate sediments from the core [12], melt within subducted oceanic crust [13,14,15], slab-derived metallic melt [16], and partial melting of mantle material [17,18]. Reports of preferential iron partitioning into ferropericlase coexisting with bridgmanite or postperovskite [19] have motivated recent high-pressure experimental studies on iron-rich compositions of (Mg,Fe)O. These materials show remarkably low sound velocities [20,21], and dynamic modeling work on assemblages containing this material could reproduce the velocities and topography of some observed ULVZs [22]. In addition, recent seismic and dynamic studies have suggested that compositionally distinct origin may be necessary to explain many ULVZs [23,24]. However, quantitative comparisons of such proposed features with seismic observations remain largely unexplored, creating difficulty in evaluating the likelihood of proposed explanations.
With this study, we aim to develop a quantitative approach to assess the role of iron-rich (Mg,Fe)O in ULVZs. First, we present new measurements of the compressional behavior of (Mg0.06Fe0.94)O in a helium pressure medium at ambient temperatures using synchrotron X-ray diffraction and produce a well-constrained equation of state for this material, which had not been done previously [25]. We combine these results with sound velocities and thermo-elastic information from previous studies [21,25,26] to calculate the densities and velocities of iron-rich (Mg,Fe)O compositions at CMB pressure–temperature conditions. Using recent thermoelasticity measurements of bridgmanite and calcium silicate perovskite, we calculate seismic properties of coexisting mineral assemblages containing iron-enriched (Mg,Fe)O and build a linear mixing model that combines uncertainty estimates from both mineral physics and seismic observations to invert for the best-fit concentrations of iron-rich (Mg,Fe)O for select ULVZ observations. While an inversion approach has been used for other applications, such as constraining the composition of the bulk lower mantle [27], this study applies a similar approach to constraining the compositions of ULVZs. Our study quantifies the viability of iron-rich (Mg,Fe)O to account for certain classes of ULVZ seismic observations and, in doing so, contributes to developing a framework for a systematic evaluation of proposed origins of ULVZs.

2. Materials and Methods

A sample of polycrystalline (Mg0.058(1)Fe0.942(1))O, hereafter referred to as Mw94, mixed with NaCl powder, was synthesized at ambient pressure conditions using 95% enriched 57Fe and MgO powders, with ferric iron content capped at 5% by conventional Mössbauer spectroscopy [25]. The powdered sample was loaded inside a rhenium gasket between two beveled diamond anvils of 250 µm diameter within a symmetric diamond-anvil cell. The sample chamber also contained two ruby spheres for use as pressure markers by measurement of their pressure-dependent fluorescence spectra. The chamber was then loaded with compressed helium gas at 170 MPa, explicitly chosen as a pressure-transmitting medium to minimize the nonhydrostatic behavior of the pressure environment (e.g., [26]), using the gas-loading system at Caltech.

2.1. X-Ray Diffraction

High-pressure X-ray diffraction experiments were performed at Beamline 12.2.2 of the Advanced Light Source (ALS) of Lawrence Berkeley National Laboratory (Berkeley, CA, USA). The LaB6 standard was used to calibrate the sample to detector distance. Diffraction patterns at each pressure point were collected using a high-resolution image plate (MAR345) with an incident X-ray energy of 25 keV and a size of about 10 µm × 10 µm (full width at half maximum). Diffraction patterns were collected at a series of 27 compression points across the pressure range of 1.5 to 88.7 GPa. Intervals between pressure steps were limited to ~2 GPa for the range below 30 GPa, in order to finely sample the compressional behavior of the material in the low-pressure regime, a critical step for tightly determining the material’s equation of state.
Measurements of the ruby fluorescence spectra were performed immediately before and after each diffraction measurement, using the pressure scale of [28]. The cell was allowed to rest for 15 min on average after pressure increases, in order to reduce pressure creep during the collection of diffraction patterns. The uncertainty in pressure at each step was estimated as the difference of the pressures measured for the two rubies before and after each diffraction measurement. Diffraction patterns were radially integrated from the 2D image plate using the Dioptas software [29]. Selected diffraction patterns are shown in Figure S1. Peaks for Mw94 and NaCl, as well as for ruby and rhenium, were identified and fit using the GSAS-II software [30] to derive the unit cell volume for Mw94 at each pressure point. The unit cell volumes of NaCl were used as a secondary pressure gauge [31] when present in the diffraction patterns and confirmed pressures determined by ruby fluorescence.

2.2. Synchrotron Mössbauer Spectroscopy

We complement our diffraction data with synchrotron Mössbauer spectroscopy (SMS) performed at Sector 3-ID-B of the Advanced Photon Source (APS) at Argonne National Laboratory (Lemont, IL, USA), using top-up mode of the storage ring with 24 bunches separated by 153 ns. X-rays were focused to an area of about 12 µm × 18 µm and tuned to 14.4125 keV, a nuclear transition energy of 57Fe. A high-resolution monochromator provided an energy bandwidth of 1 meV [32]. A time window of 25 to 125 ns after excitation was used to observe nuclear resonant forward scattering and to fit the data. We performed SMS measurements at three compression points (95.4, 97.0, and 116.4 GPa) on the identical sample used for the diffraction measurements, in order to determine the magnetic ordering and spin state. Pressures were measured before and after SMS data collection using ruby fluorescence [28] and Raman spectroscopy, using the high-frequency edge of the diamond Raman band [33].

3. Experimental Results

The unit cell volume per atom of Mw94 at each compression point was calculated using the following hkl reflections: 111, 200, 220, 311, and 222 for B1; 003, 101, 102, 104, 110, and 105 for the rhombohedral phase (Figure 1 and Figure S2, and Table S1). The splitting of 111 and 220 B1 peaks was observed at 34.5 GPa, suggesting a rhombohedral distortion of the cubic lattice. We bracketed this structural transition from the B1-cubic phase to a rhombohedral phase between 30.1 and 34.5 GPa. The material remains in the rhombohedral phase up to at least 88.7 GPa. We observed a change in the trend of the unit-cell volume as a function of pressure at the two compression points prior to the structural transition (26.8 GPa, 30.1 GPa) and excluded these data in fitting the equation of state.

3.1. Equation of State (B1 Phase)

The pressure–volume data for the B1-cubic phase and for the rhombohedral phase were fit separately with two distinct equations of state using the MINUTI software package [34]. We used a third-order Burch–Murnaghan equation of state and varied the fit parameters V0, K0T, and K’0T representing the zero-pressure unit cell volume per atom, the isothermal zero-pressure bulk modulus, and its pressure derivative, respectively. Due to large tradeoffs between K0T and K’0T and motivated by previous reports of K’0T values for similar compositions (see [26]), we performed the fit using an initial value of 3.8 for K’0T with a prior window of 0.3; given the reduced χ2 value of 0.70 ± 0.23 using this prior and an equivalent value of χ2 = 0.74 ± 0.25 with no prior, we find the prior information to be a good fit to the data. For the B1-cubic phase, the best fit parameters are V0 = 9.860 ± 0.007 Å3 /atom, K0T = 155.3 ± 2.2 GPa, K’0T = 3.79 ± 0.11 (Table 1), which are significantly more compatible with the trends of K0T as a function of iron concentration presented in [26] for the (Mg,Fe)O solid solution, compared with the results from an X-ray diffraction study of Mw94 from the same bulk sample [25]. These results underscore the need to perform measurements using a helium pressure medium in the low pressure regime, which were absent in the experimental range of Wicks et al. [25]. While the choice of neon or helium as the pressure medium can have a significant effect on elastic properties and transition pressure ranges for the (Mg,Fe)O system, the effect may be different for other phases with different crystal structures, such as (Mg,Fe)SiO3 and CaSiO3.

3.2. Equation of State (Rhombohedral Phase)

We fit a third-order Burch–Murnaghan isothermal equation of state to the pressure–volume data for the rhombohedral phase and found best fit parameter values V0 = 9.59 ± 0.10 Å3/atom, K0T = 217 ± 19 GPa, K’0T = 2.06 ± 0.22, with a reduced χ2 value of 1.37 ± 0.37 (data and fit with residuals is shown in Figure S2). While Wicks et al. [25] bracketed the transition pressure for the cubic to rhombohedral transition between 13 and 24 GPa for a sample of Mw94 in a neon pressure medium, we observed a transition pressure in the range of 30.1 to 34.5 GPa for Mw94 in a helium medium. It is likely that a steep increase of non-hydrostaticity at ~20 GPa caused by neon compared to helium [26] induced the rhombohedral distortion at a lower pressure.

3.3. Synchrotron Mössbauer Spectroscopy

In order to explore the possibility of a high-pressure ferrous-iron spin transition in Mw94, we performed synchrotron Mössbauer spectroscopy (SMS) on Mw94 at three compression points (95.4 ± 0.2, 97.0 ± 0.5, and 116.4 ± 0.5 GPa). Pressures were determined by Raman spectroscopy using the high-frequency edge of the diamond Raman band [33], with uncertainties estimated as the difference of pressures before and after SMS measurements and of pressures at two different locations on the anvil. At the two lower pressures, we observed fast oscillations in the time spectra that are caused by magnetic ordering in the sample. At 116.4 GPa, a significant fraction of the fast oscillations was no longer present (Figure S3), suggesting an absence of magnetic ordering that could indicate a high-spin to low-spin transition occurring in the Fe2+ sites of Mw94. In order to evaluate the possibility of a spin transition, we used the CONUSS software version 2.2.0 [35] to fit the 116.4 GPa spectrum. We found that three distinct Fe2+ environments are required to fit the spectrum. One site is characteristic of low-spin Fe2+ and the other two sites are characterized by high-spin Fe2+-like sites: one with no magnetic ordering and one with a magnetic hyperfine field. The best-fit model (Table S2) shows that 37 ± 2% of the iron atoms have transitioned into the low-spin state at 116.4 GPa, with 3% of the iron atoms retaining the magnetic ordering in a high-spin state, and the remaining fraction indicative of a broad high-spin Fe2+-like site with no magnetic ordering. The pressure of the Fe2+ spin transition suggested by this result is consistent with the trend of increasing spin transition pressure with increasing iron content in (Mg,Fe)O (e.g., [20,36]). It should be noted that Mw94 is in the rhombohedral phase at the P–T conditions of these SMS measurements, so the reduced symmetry of the crystal structure compared to the B1 phase may affect the pressure range of the spin transition. The temperature dependence of the spin state in Fe-rich (Mg,Fe)O at CMB conditions has not been thoroughly studied, although the higher temperatures of Earth’s mantle would likely drive the spin transition to higher pressures than those expected within the mantle (e.g., [37,38]). Taken together, these results suggest that, unlike for ferropericlase [39], the fraction of low-spin magnesiowüstite would either be relatively low or negligible at CMB conditions.

4. Modeling Iron-Rich (Mg,Fe)O in the Lowermost Mantle

4.1. Calculating Iron-Rich (Mg,Fe)O Elasticity at CMB Conditions

Mw94 has been reported to remain in the B1-cubic phase along the mantle geotherm up to CMB conditions [25]. We thus combined our results with those from previous studies in order to calculate the densities and sound velocities of iron-rich (Mg,Fe)O compositions at the pressure and temperature of the CMB. We first calculated the bulk sound velocity for Mw94 at 135.8 GPa (CMB pressure given in PREM) and 300 K using our isothermal equation of state. We then used this value and the Debye velocity VD = 4.27 ± 0.09 km/s reported by Wicks et al. [21] for an identical composition at the same pressure–temperature condition in order to calculate a VP and VS for Mw94 at 135.8 GPa and 300 K, following the procedure taken by Wicks et al. [21]. We applied the temperature corrections reported by Wentzcovitch et al. [40] for MgO at CMB conditions to our results and thereby calculated the sound velocities for Mw94 at 135.8 GPa and 3800 K. In addition, we incorporated the thermal parameters reported by Wicks et al. [25] for Mw94 in order to calculate the density of Mw94 at 135.8 GPa and 3800 K. We then repeated this procedure for Mw84 by using the same equation of state except with a zero-pressure volume V0 = 9.79 ± 0.04 Å3 /atom as reported by Wicks et al. [21], and for Mw78 using the isothermal equation of state reported by Finkelstein et al. [26]. In doing so, we computed VP, VS, and density with uncertainties estimated from experimental reports (Table S3) for the behavior of three iron-rich compositions of (Mg,Fe)O at the pressure–temperature conditions of the CMB. We note that while the equation of state for these iron-rich compositions is taken from measurements of the B1 phase that exists at CMB conditions, the measurements reported for the Debye velocity at lower mantle pressures [21] were performed on the rhombohedral phase. Nevertheless, these values reflect the best available understanding of this material’s shear elastic behavior. It is also important to note that Wicks et al. found no discernible compositional dependence of the Debye velocity for Mw84, Mw94, and FeO [21], such that the effect of composition appears primarily in the equations of state used for extrapolation (Table 1).

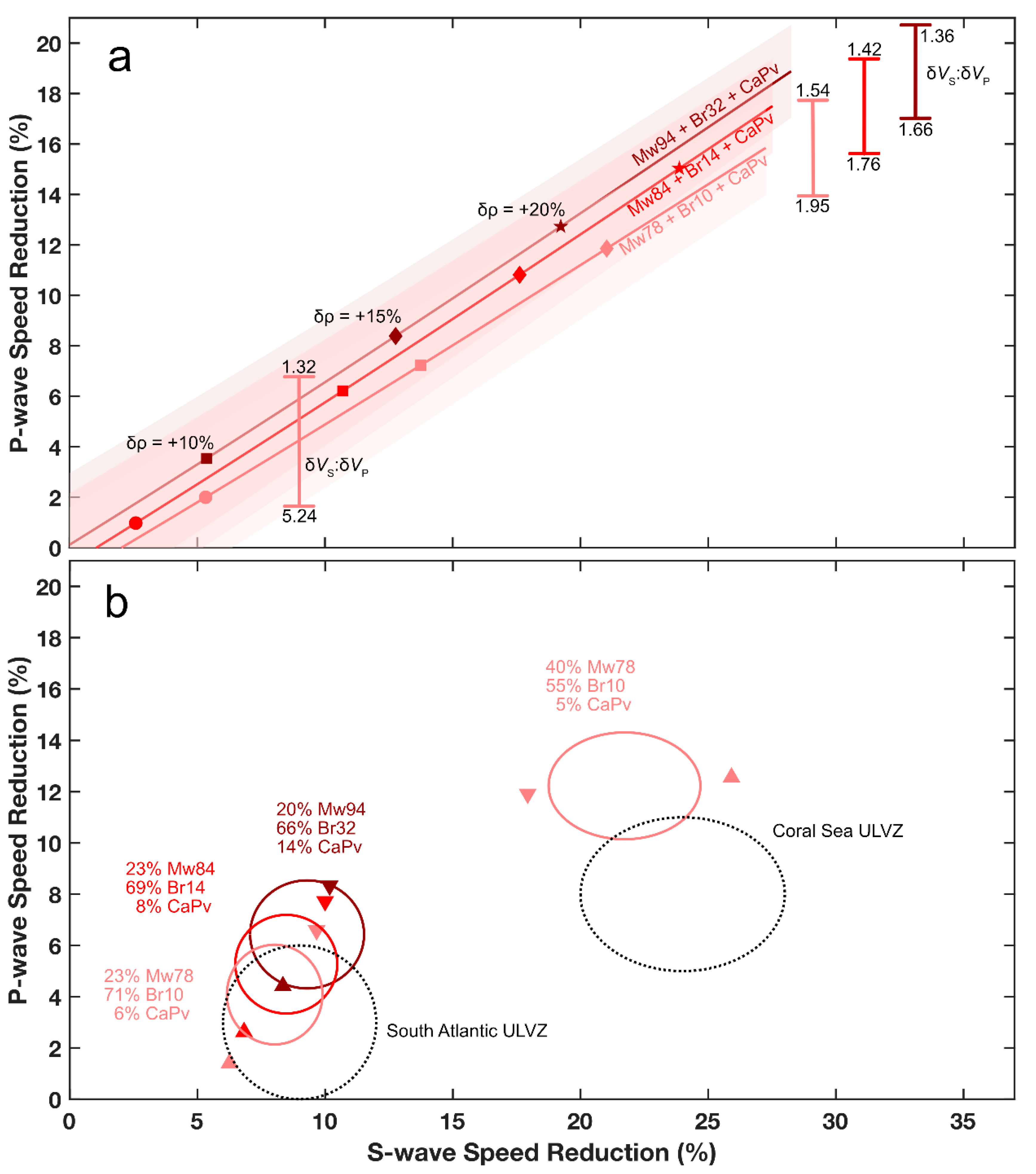
4.2. Forward Modeling

Having calculated sound velocities and densities for three iron-rich compositions of (Mg,Fe)O at the pressure–temperature conditions of the CMB, we next investigated the likelihood of the presence of this material in ULVZs given the range of seismic observations. In order to do so, we first constructed a forward linear mixing model for calculating the sound velocities and densities of mineral aggregates containing iron-rich (Mg,Fe)O mixed with bridgmanite (Br) and calcium silicate perovskite (CaPv). The iron content of Br was determined by the partitioning of iron between Mw and Br using a KD value of 0.03 [21]. For CaPv, we used recent ultrasonic interferometry experiments reported by Gréaux et al. [41] and extrapolated to CMB conditions using finite strain analysis [42]. For modeling Br properties, we used a combination of theoretical and experimental constraints (e.g., [40,43,44,45]) (see Table S3). We calculated properties for aggregates containing concentrations of Mw ranging from 0% to 50% combined with a mixture of Br and CaPv where the concentration of CaPv was controlled by fixing it at 10% of Br concentration, with an uncertainty of 5%. By computing bulk and shear moduli for the minerals we were mixing, we could compute Voigt and Reuss bounds for the aggregate elastic properties in order to determine the range of velocity reductions that can be accounted for by the presence of iron-rich (Mg,Fe)O. The Hill averages for P and S wave velocity reductions relative to PREM for aggregates containing Mw94, Mw84, and Mw78 are shown in Figure 2a, as well as markers indicating density increases relative to PREM. Voigt and Reuss bounds for all three compositions of Mw are shown in Figure S4, with markers indicating Mw concentrations.

4.3. Inverse Modeling

While the forward model demonstrates that a wide array of observed velocity reductions could be caused by the presence of iron-rich (Mg,Fe)O, it does not offer a direct quantitative assessment of the compatibility of ULVZ observations with hypothetical mineral aggregates bearing iron-rich (Mg,Fe)O. To that end, we additionally constructed an inverse linear mixing model that can more comprehensively compare seismic observations with experimental results from mineral physics. The inputs to the inverse model were the bulk and shear moduli and density (computed from reported seismic velocities and density) of an observed ULVZ with estimated uncertainties, as well as these properties for the minerals that were being mixed (e.g., Mw94 + Br32 + CaPv, where Br32 represents (Mg0.68Fe0.32)SiO3), with errors propagated from the relevant experimental results. The model minimizes the difference between the target assemblage elastic properties and the hypothetical assemblage properties, with properties weighted according to the inverse of their observational and experimental uncertainties during the fitting procedure. In this way, the model computes individual mineral concentrations for the assemblage that best fits the observational target, following either the Voigt or Reuss formulation of aggregate mixing. Thus, for a given ULVZ observation, we can compute the concentration (X, in percent) of an iron-rich composition of (Mg,Fe)O for the aggregate that would provide the closest fit of seismic wave velocities and density to the observation. The uncertainty in the resulting (Mg,Fe)O concentration includes uncertainty estimates from both the seismic observation of the ULVZ and from the elastic properties of the constituent minerals. By using the χ2 value to evaluate the quality of the fit, we can compare best-fit assemblages of various mineral compositions to determine which set of minerals with which set of concentrations can best explain a ULVZ observation. More details of the inverse modeling approach can be found in Appendix A.
In order to demonstrate the applicability of this approach, we evaluated two ULVZ seismic observations chosen specifically because the studies report constraints on both VP and VS, as well as density and estimates of uncertainties (Table 2). For the inversions, we report the best-fit assemblages containing magnesiowüstite compositions that result in the lowest χ2 values (Table 2). As part of the inversion process, we can use priors on mineral concentrations to test whether these observed ULVZ properties are compatible with an iron-enriched pyrolitic composition, or whether a non-pyrolitic composition is required to explain the observation. We additionally make use of priors to account for the tradeoffs in concentration between Br and CaPv, which exhibit velocities much closer to PREM than Mw. To that end, for the ULVZ underneath the South Atlantic [47], we impose a prior on the Br concentration of 0.7 with a prior window of 0.2, both due to the trade-off with CaPv and in order to maintain pyrolitic proportions, while for the Mw78 inversion a wider prior window of 0.4 can be used to produce reasonable results. The results demonstrate that an iron-enriched pyrolitic composition is compatible with the South Atlantic ULVZ observation. In contrast, the inversion for the selected seismic observation of a ULVZ beneath the Coral Sea [48] requires more magnesiowüstite than a pyrolitic model would suggest, necessitating a different set of priors. These results suggest that two different formation scenarios may be required for these two ULVZ observations.
The modeling results shown in Figure 2 demonstrate that the presence of iron-rich (Mg,Fe)O results in velocity reductions relative to PREM close to the 1:2 VP:VS ratio. It can additionally be seen that the inversion results suggest that ULVZ observations exhibiting a 1:3 VP:VS reduction ratio can also be explained by the presence of iron-rich (Mg,Fe)O, within the estimated uncertainty bounds. To help clarify this result, the vertical bars on the forward models (Figure 2a and Figure S4) demonstrate the wide range of reduction ratios, particularly at low S-wave speed reductions, that can be produced by the presence of Mw within uncertainty bounds. It is additionally worth noting that the aggregate elastic properties of the inverted ULVZs could in fact be closer to the Reuss or Voigt bounds than the Hill average, depending on the microstructure of the mineral phases. While the observed 1:3 VP:VS reduction ratio is commonly attributed to the presence of partial melt (e.g., [47,49]), the compatibility of solid iron-enriched magnesiowüstite with this reduction ratio, as demonstrated by our results, underscores the necessity of applying a quantitative approach to evaluating ULVZ hypotheses.
By using an inverse linear mixing model, we have shown that the presence of iron-rich (Mg,Fe)O is a viable hypothesis for explaining the seismic anomalies observed within certain ULVZs. The strength of our approach lies in the fact that it incorporates estimated uncertainties from both seismic observations and results from mineral physics, thus permitting a synthesis of information from both fields of study in a quantitative way. We have therefore contributed to the development of a framework for evaluating the likelihood of proposed hypotheses for ULVZs that can be expanded and applied in a systematic way to the growing set of ULVZ observations, in order to develop a comprehensive understanding of heterogeneities in the lowermost mantle.

Supplementary Materials

The following are available online at https://www.mdpi.com/2075-163X/9/12/762/s1, Figure S1: Examples of Integrated XRD Patterns for Mw94, Figure S2: Unit-Cell Volumes and Equation of State for Rhombohedral Mw94, Figure S3: SMS Spectra of Mw94, Figure S4: Forward Modeling the Seismic Signatures of Mw-bearing Aggregates, Table S1: Pressure-Volume Measurements for Mw94, Table S2: Hyperfine Parameters of Mw94 from SMS Measurements, Table S3: Seismic Velocities and Densities of Relevant Phases at CMB Conditions.

Author Contributions

Conceptualization, J.M.J. and V.V.D.; methodology, J.M.J., V.V.D. and W.S.; software, W.S.; validation, J.M.J., V.V.D. and W.S.; formal analysis, V.V.D.; investigation, J.M.J. and V.V.D.; resources, J.M.J. and W.S.; data curation, J.M.J.; writing—original draft preparation, V.V.D.; writing—review and editing, J.M.J., V.V.D. and W.S.; funding acquisition, J.M.J.

Funding

We thank NSF-CSEDI-EAR-1161046 and NSF-EAR-CAREER-0956166 for support of this research. Operations at Sector 3 (APS) and beamline 12.2.2 (ALS) are partially supported by COMPRES. This research used resources of the Advanced Photon Source and of the Advanced Light Source, which are DOE Office of Science User Facilities under contracts DE-AC02-06CH11357 and DE-AC02-05CH11231, respectively.

Acknowledgments

We thank Christine Beavers, as well as Gregory Finkelstein and Natalia Solomatova, for their help with the diffraction experiments. We thank Don Helmberger, Christine Thomas, and Zhongwen Zhan for valuable discussions. We thank June K. Wicks for synthesis of the sample.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

We develop an inverse mixing model with the purpose to determine the mixture of individual minerals with aggregate properties that best match a set of target properties (e.g., velocity reductions and density increase relative to PREM for a given ULVZ observation). The mixture contains ( N + 1 ) individual minerals, e.g., (Mg,Fe)O magnesiowüstite (Mw), (Mg,Fe)SiO3 bridgmanite (Br), CaSiO3 calcium silicate perovskite (CaPv). The concentrations p j ≥ 0 of the minerals in the mixture are normalized by
∑ j = 1 N + 1 p j = 1
The minerals have properties ϕ j k , where j and k are the number of mineral types and properties, respectively. In addition to the density, properties of interest for our inversions are the bulk modulus and shear modulus or their inverse, dependent on Voigt or Reuss mixing, respectively. We calculate these moduli from the compressional and shear velocities. Average properties of the aggregate are then
〈 ϕ k 〉 = ∑ j = 1 N + 1 p j ϕ j k = ϕ N + 1 , k + ∑ j = 1 N p j ( ϕ j , k − ϕ N + 1 , k )
where the concentration p N + 1 is eliminated by use of ∑ j = 1 N + 1 p j = 1 . The measure for matching these average properties and the target properties Φ k is defined as
M ( { p j } ) = ∑ k = 1 n w k ( 〈 ϕ k 〉 − Φ k ) 2 + ∑ j = 1 N ( p j − P j ) 2 δ 2 P j
where n is the number of properties. In order to produce a physically meaningful solution to the inversion, we can introduce priors P j on the mineral concentrations with uncertainties δ 2 P j . The best matching is achieved for the smallest measure. The weights w k are taken as
w k = ( δ Φ k 2 + ∑ j = 1 N + 1 p j 2 δ ϕ j k 2 ) − 1
where δ Φ k 2 and δ ϕ j k 2 are the variances of target properties Φ k and mineral properties ϕ j k , respectively. Because n (number of properties: elastic moduli and density) exceeds the dimensionality of the parameter space N (total minerals minus one), the measure never takes its smallest possible value, zero, but can only be minimized by finding a local minimum of it. The optimal concentrations satisfy N non-linear equations given by
∂ ∂ p j M ( { p j } ) = 0
The non-linearity is caused by the concentration dependence of the weights w k . If the solution does not satisfy p j ≥ 0 for all concentrations, the local minimum of the measure is located outside of the truncated N dimensional parameter space.

References

  1. Lay, T. Deep Earth Structure: Lower Mantle and D. In Treatise on Geophysics, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2015; Volume 1, pp. 683–723. [Google Scholar] [CrossRef]
  2. Lay, T.; Helmberger, D.V. A Lower Mantle S-wave Triplication and the Shear Velocity Structure of D″. Geophys. J. R. Astron. Soc. 1983, 75, 799–837. [Google Scholar] [CrossRef] [Green Version]
  3. Cobden, L.; Thomas, C.; Trampert, J. Seismic Detection of Post-Perovskite inside the Earth. In The Earth’s Heterogeneous Mantle: A Geophysical, Geodynamical, and Geochemical Perspective; Springer: New York, NY, USA, 2015; pp. 391–440. [Google Scholar] [CrossRef]
  4. Garnero, E.J.; Helmberger, D.V. Further Structural Constraints and Uncertainties of a Thin Laterally Varying Ultralow-Velocity Layer at the Base of the Mantle. J. Geophys. Res. Solid Earth 1998, 103, 12495–12509. [Google Scholar] [CrossRef] [Green Version]
  5. Thorne, M.S.; Garnero, E.J. Inferences on Ultralow-Velocity Zone Structure from a Global Analysis of SPdKS Waves. J. Geophys. Res. Solid Earth 2004, 1098, 1–22. [Google Scholar] [CrossRef]
  6. McNamara, A.K.; Garnero, E.J.; Rost, S. Tracking Deep Mantle Reservoirs with Ultra-Low Velocity Zones. Earth Planet. Sci. Lett. 2010, 299, 1–9. [Google Scholar] [CrossRef]
  7. Yu, S.; Garnero, E.J. Ultralow Velocity Zone Locations: A Global Assessment. Geochem. Geophys. Geosystems 2018, 19, 396–414. [Google Scholar] [CrossRef]
  8. Manga, M.; Jeanloz, R. Implications of a Metal-Bearing Chemical Boundary Layer in D” for Mantle Dynamics. Geophys. Res. Lett. 1996, 23, 3091–3094. [Google Scholar] [CrossRef]
  9. Knittle, E.; Jeanloz, R. Earth’s Core-Mantle Boundary: Results of Experiments at High Pressures and Temperatures. Science 1991, 251, 1438–1443. [Google Scholar] [CrossRef]
  10. Mao, W.L.; Mao, H.K.; Sturhahn, W.; Zhao, J.; Prakapenka, V.B.; Meng, Y.; Shu, J.; Fei, Y.; Hemley, R.J. Iron-Rich Post-Perovskite and the Origin of Ultralow-Velocity Zones. Science 2006, 3123, 564–565. [Google Scholar] [CrossRef] [Green Version]
  11. Dobson, D.P.; Brodholt, J.P. Subducted Banded Iron Formations as a Source of Ultralow-Velocity Zones at the Core-Mantle Boundary. Nature 2005, 434, 371–374. [Google Scholar] [CrossRef]
  12. Buffett, B.A.; Garnero, E.J.; Jeanloz, R. Sediments at the Top of Earth’s Core. Science 2000, 290, 1938–1942. [Google Scholar] [CrossRef]
  13. Andrault, D.; Pesce, G.; Bouhifd, M.A.; Bolfan-Casanova, N.; Heńot, J.M.; Mezouar, M. Melting of Subducted Basalt at the Core-Mantle Boundary. Science 2014, 244, 895. [Google Scholar] [CrossRef]
  14. Ohtani, E.; Maeda, M. Density of Basaltic Melt at High Pressure and Stability of the Melt at the Base of the Lower Mantle. Earth Planet. Sci. Lett. 2001, 344, 892–895. [Google Scholar] [CrossRef]
  15. Pradhan, G.K.; Fiquet, G.; Siebert, J.; Auzende, A.L.; Morard, G.; Antonangeli, D.; Garbarino, G. Melting of MORB at Core-Mantle Boundary. Earth Planet. Sci. Lett. 2015, 431, 247–255. [Google Scholar] [CrossRef]
  16. Liu, J.; Li, J.; Hrubiak, R.; Smith, J.S. Origins of Ultralow Velocity Zones through Slab-Derived Metallic Melt. Proc. Natl. Acad. Sci. USA 2016, 113, 5547–5551. [Google Scholar] [CrossRef] [Green Version]
  17. Williams, Q.; Garnero, E.J. Seismic Evidence for Partial Melt at the Base of Earth’s Mantle. Science 1996, 273, 1528–1530. [Google Scholar] [CrossRef] [Green Version]
  18. Berryman, J.G. Seismic Velocity Decrement Ratios for Regions of Partial Melt in the Lower Mantle. Geophys. Res. Lett. 2000, 27, 421–424. [Google Scholar] [CrossRef]
  19. Sinmyo, R.; Hirose, K.; Nishio-Hamane, D.; Seto, Y.; Fujino, K.; Sata, N.; Ohishi, Y. Partitioning of Iron between Perovskite/Postperovskite and Ferropericlase in the Lower Mantle. J. Geophys. Res. Solid Earth 2008, 113. [Google Scholar] [CrossRef] [Green Version]
  20. Wicks, J.K.; Jackson, J.M.; Sturhahn, W. Very Low Sound Velocities in Iron-Rich (Mg,Fe)O: Implications for the Core-Mantle Boundary Region. Geophys. Res. Lett. 2010, 37, 1–5. [Google Scholar] [CrossRef] [Green Version]
  21. Wicks, J.K.; Jackson, J.M.; Sturhahn, W.; Zhang, D. Sound Velocity and Density of Magnesiowüstites: Implications for Ultralow-Velocity Zone Topography. Geophys. Res. Lett. 2017, 44, 2148–2158. [Google Scholar] [CrossRef]
  22. Bower, D.J.; Wicks, J.K.; Gurnis, M.; Jackson, J.M. A Geodynamic and Mineral Physics Model of a Solid-State Ultralow-Velocity Zone. Earth Planet. Sci. Lett. 2011, 303, 193–202. [Google Scholar] [CrossRef] [Green Version]
  23. Li, M.; McNamara, A.K.; Garnero, E.J.; Yu, S. Compositionally-Distinct Ultra-Low Velocity Zones on Earth’s Core-Mantle Boundary. Nat. Commun. 2017, 8, 177. [Google Scholar] [CrossRef]
  24. Brown, S.P.; Thorne, M.S.; Miyagi, L.; Rost, S. A Compositional Origin to Ultralow-Velocity Zones. Geophys. Res. Lett. 2015, 42, 1039–1045. [Google Scholar] [CrossRef]
  25. Wicks, J.K.; Jackson, J.M.; Sturhahn, W.; Zhuravlev, K.K.; Tkachev, S.N.; Prakapenka, V.B. Thermal Equation of State and Stability of (Mg0.06Fe0.94) O. Phys. Earth Planet. Inter. 2015, 249, 28–42. [Google Scholar] [CrossRef] [Green Version]
  26. Finkelstein, G.J.; Jackson, J.M.; Sturhahn, W.; Zhang, D.; Ercan Alp, E.; Toellner, T.S. Single-Crystal Equations of State of Magnesiowüstite at High Pressures. Am. Mineral. 2017, 102, 1709–1717. [Google Scholar] [CrossRef]
  27. Matas, J.; Bass, J.; Ricard, Y.; Mattern, E.; Bukowinski, M.S.T. On the Bulk Composition of the Lower Mantle: Predictions and Limitations from Generalized Inversion of Radial Seismic Profiles. Geophys. J. Int. 2007, 170, 764–780. [Google Scholar] [CrossRef] [Green Version]
  28. Dewaele, A.; Datchi, F.; Loubeyre, P.; Mezouar, M. High Pressure-High Temperature Equations of State of Neon and Diamond. Phys. Rev. B Condens. Matter Mater. Phys. 2008, 77, 094106. [Google Scholar] [CrossRef]
  29. Prescher, C.; Prakapenka, V.B. DIOPTAS: A Program for Reduction of Two-Dimensional X-Ray Diffraction Data and Data Exploration. High Press. Res. 2015, 35, 223–230. [Google Scholar] [CrossRef]
  30. Toby, B.H.; Von Dreele, R.B. GSAS-II: The Genesis of a Modern Open-Source All Purpose Crystallography Software Package. J. Appl. Crystallogr. 2013, 46, 544–549. [Google Scholar] [CrossRef]
  31. Fei, Y.; Ricolleau, A.; Frank, M.; Mibe, K.; Shen, G.; Prakapenka, V. Toward an Internally Consistent Pressure Scale. Proc. Natl. Acad. Sci. USA 2007, 104, 9182–9186. [Google Scholar] [CrossRef] [Green Version]
  32. Toellner, T.S. Monochromatization of Synchrotron Radiation for Nuclear Resonant Scattering Experiments. Hyperfine Interact. 2000, 125, 3–28. [Google Scholar] [CrossRef]
  33. Akahama, Y.; Kawamura, H. Pressure Calibration of Diamond Anvil Raman Gauge to 410 GPa. J. Phys. Conf. Ser. 2010, 215, 1. [Google Scholar] [CrossRef]
  34. Sturhahn, W. MINUTI Open Source Software, Version 2.0.0. Available online: http://www.nrixs.com (accessed on 10 January 2018).
  35. Sturhahn, W. CONUSS and PHOENIX: Evaluation of Nuclear Resonant Scattering Data. Hyperfine Interact 2000, 125, 149–172. [Google Scholar] [CrossRef]
  36. Solomatova, N.V.; Jackson, J.M.; Sturhahn, W.; Wicks, J.K.; Zhao, J.; Toellner, T.S.; Kalkan, B.; Steinhardt, W.M. Equation of State and Spin Crossover of (Mg,Fe)O at High Pressure, with Implications for Explaining Topographic Relief at the Core-Mantle Boundary. Am. Mineral. 2016, 101, 1084–1093. [Google Scholar] [CrossRef]
  37. Sturhahn, W.; Jackson, J.M.; Lin, J.F. The Spin State of Iron in Minerals of Earth’s Lower Mantle. Geophys. Res. Lett. 2005, 32, 1–5. [Google Scholar] [CrossRef] [Green Version]
  38. Tsuchiya, T.; Wentzcovitch, R.M.; da Silva, C.R.S.; de Gironcoli, S. Spin Transition in Magnesiowüstite in Earth’s Lower Mantle. Phys. Rev. Lett. 2006, 96, 198501. [Google Scholar] [CrossRef] [Green Version]
  39. Wu, Z.; Wentzcovitch, R.M. Spin Crossover in Ferropericlase and Velocity Heterogeneities in the Lower Mantle. Proc. Natl. Acad. Sci. USA 2014, 111, 10468–10472. [Google Scholar] [CrossRef] [Green Version]
  40. Wentzcovitch, R.M.; Wu, Z.; Carrier, P. First Principles Quasiharmonic Thermoelasticity of Mantle Minerals. Rev. Mineral. Geochem. 2010, 71, 99–128. [Google Scholar] [CrossRef]
  41. Gréaux, S.; Irifune, T.; Higo, Y.; Tange, Y.; Arimoto, T.; Liu, Z.; Yamada, A. Sound Velocity of CaSiO3 Perovskite Suggests the Presence of Basaltic Crust in the Earth’s Lower Mantle. Nature 2019, 565, 218–221. [Google Scholar] [CrossRef]
  42. Duffy, T.S.; Anderson, D.L. Seismic Velocities in Mantle Minerals and the Mineralogy of the Upper Mantle. J. Geophys. Res. 1989, 94, 1895–1912. [Google Scholar] [CrossRef] [Green Version]
  43. Li, B.; Zhang, J. Pressure and Temperature Dependence of Elastic Wave Velocity of MgSiO3 Perovskite and the Composition of the Lower Mantle. Phys. Earth Planet. Inter. 2005, 151, 143–154. [Google Scholar] [CrossRef]
  44. Dorfman, S.M.; Meng, Y.; Prakapenka, V.B.; Duffy, T.S. Effects of Fe-Enrichment on the Equation of State and Stability of (Mg,Fe)SiO3 Perovskite. Earth Planet. Sci. Lett. 2013, 361, 249–257. [Google Scholar] [CrossRef]
  45. Wolf, A.S.; Jackson, J.M.; Dera, P.; Prakapenka, V.B.; Al, W.E.T. Solid Earth The Thermal Equation of State of (Mg, Fe) SiO3 Bridgmanite (Perovskite) and Implications for Lower Mantle Structures. J. Geophys. Res. 2015, 120, 7460–7489. [Google Scholar] [CrossRef] [Green Version]
  46. Dziewonski, A.M.; Anderson, D.L. Preliminary Reference Earth Model. Phys. Earth Planet. Inter. 1981, 25, 297–356. [Google Scholar] [CrossRef]
  47. Simmons, N.A.; Grand, S.P. Partial Melting in the Deepest Mantle. Geophys. Res. Lett. 2002, 29, 1552. [Google Scholar] [CrossRef]
  48. Rost, S.; Garnero, E.J.; Williams, Q. Fine-Scale Ultralow-Velocity Zone Structure from High-Frequency Seismic Array Data. J. Geophys. Res. 2006, 111, B09310. [Google Scholar] [CrossRef] [Green Version]
  49. Yuan, K.; Romanowicz, B. Seismic Evidence for Partial Melting at the Root of Major Hot Spot Plumes. Science 2017, 357, 1–5. [Google Scholar] [CrossRef] [Green Version]
Minerals 09 00762 g001 550
Figure 1. Unit-cell volumes of B1-(Mg0.058(1)Fe0.942(1))O (Mw94) (solid black circles) and equation of state (solid black line) fit using MINUTI [34]. The uncertainty in pressure at each step was estimated as the difference of the pressures measured by the two rubies before and after each diffraction measurements. We include a zero-pressure measurement of Mw94 (solid black square) from a previous study [25] for comparison. Normalized residuals are shown on the top panel. Error ellipses demonstrate the correlations between fit parameters.
Figure 1. Unit-cell volumes of B1-(Mg0.058(1)Fe0.942(1))O (Mw94) (solid black circles) and equation of state (solid black line) fit using MINUTI [34]. The uncertainty in pressure at each step was estimated as the difference of the pressures measured by the two rubies before and after each diffraction measurements. We include a zero-pressure measurement of Mw94 (solid black square) from a previous study [25] for comparison. Normalized residuals are shown on the top panel. Error ellipses demonstrate the correlations between fit parameters.
Minerals 09 00762 g001
Minerals 09 00762 g002 550
Figure 2. Seismic signatures of iron-rich (Mg,Fe)O in the lowermost mantle relative to PREM [46]. (a) Forward models (Hill average) of three Mw compositions with Mw concentrations ranging from 8.3% (Mw94), 10.2% (Mw84), and 10.6% (Mw78) up to 50%, mixed with bridgmanite and calcium perovskite at a constant Br:CaPv ratio of 10:1. Symbols indicate density increases relative to PREM (circle 5%, square 10%, diamond 15%, star 20%). Vertical bars indicate the range of δVP:δVS for a given Mw composition at a given δVS. (b) Best-fit results of the inverse model for two ULVZ observations: South Atlantic [47] and Coral Sea [48]. Ellipses represent uncertainties for observations (black dotted lines) and uncertainties at the 68% level for Hill average of best-fit Mw-containing assemblages (solid lines), with corresponding concentrations and compositions noted. Downward and upward triangles indicate best-fit assemblage properties for Voigt and Reuss mixing bounds, respectively. The complete inversion results, including the Voigt and Reuss bounds, are reported in Table 2.
Figure 2. Seismic signatures of iron-rich (Mg,Fe)O in the lowermost mantle relative to PREM [46]. (a) Forward models (Hill average) of three Mw compositions with Mw concentrations ranging from 8.3% (Mw94), 10.2% (Mw84), and 10.6% (Mw78) up to 50%, mixed with bridgmanite and calcium perovskite at a constant Br:CaPv ratio of 10:1. Symbols indicate density increases relative to PREM (circle 5%, square 10%, diamond 15%, star 20%). Vertical bars indicate the range of δVP:δVS for a given Mw composition at a given δVS. (b) Best-fit results of the inverse model for two ULVZ observations: South Atlantic [47] and Coral Sea [48]. Ellipses represent uncertainties for observations (black dotted lines) and uncertainties at the 68% level for Hill average of best-fit Mw-containing assemblages (solid lines), with corresponding concentrations and compositions noted. Downward and upward triangles indicate best-fit assemblage properties for Voigt and Reuss mixing bounds, respectively. The complete inversion results, including the Voigt and Reuss bounds, are reported in Table 2.
Minerals 09 00762 g002
Table
Table 1. Isothermal equation of state parameters for the B1 and rhombohedral phases of Mw94, with thermal equation of state models for three iron-rich compositions of Mw.
Table 1. Isothermal equation of state parameters for the B1 and rhombohedral phases of Mw94, with thermal equation of state models for three iron-rich compositions of Mw.
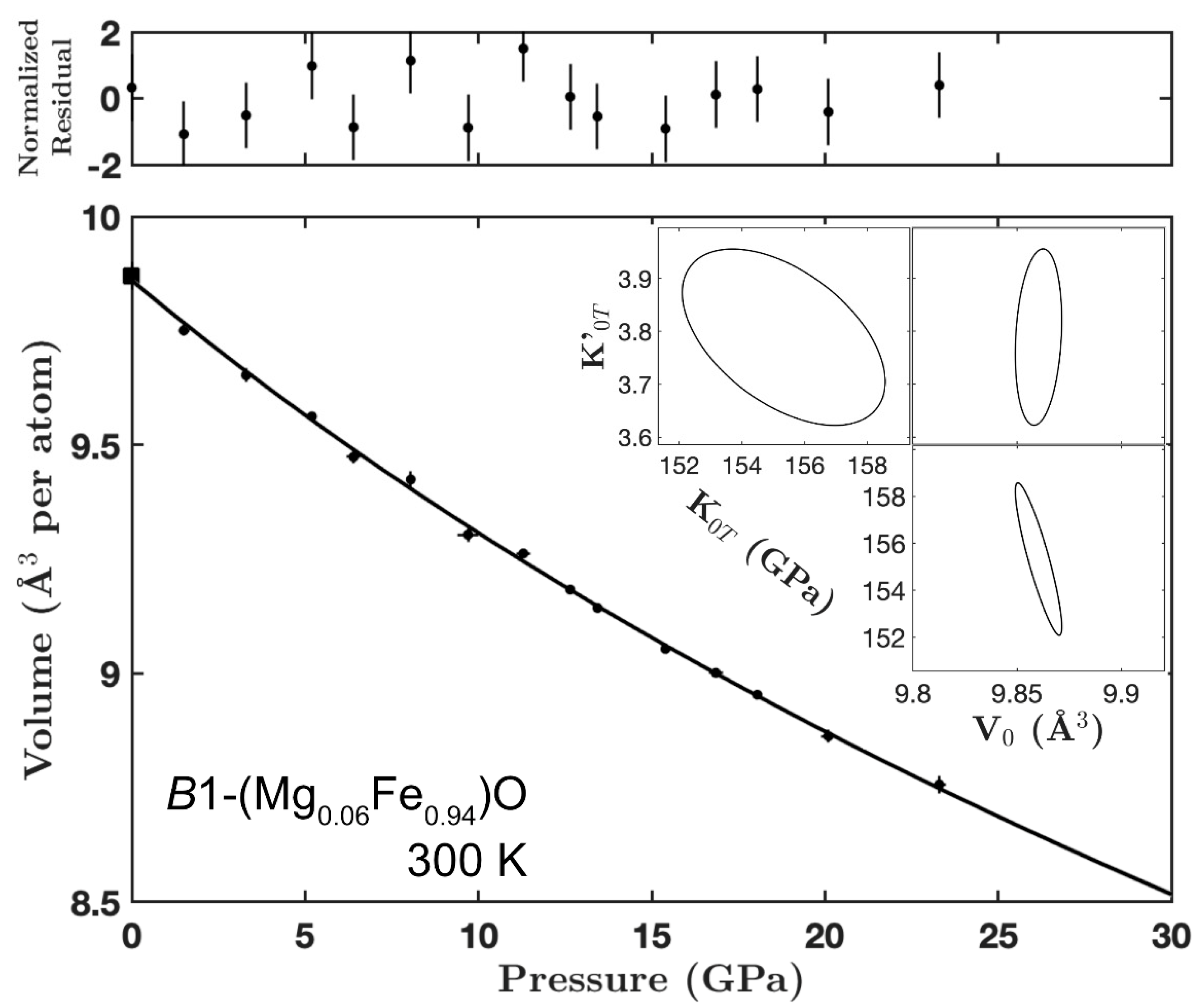
Parameters B1–Mw94r–Mw94Mw94 Model aMw84 Model bMw78 Model c
V0 (Å3 /atom)9.860 ± 0.0079.59 ± 0.109.860 ± 0.0079.79 ± 0.049.86 ± 0.02
K0T (GPa)155.3 ± 2.2217 ± 19155.3 ± 2.2155.3 ± 2.2148 ± 3
K’0T3.79 ± 0.112.06 ± 0.223.79 ± 0.113.79 ± 0.114.09 ± 0.12
θ0 (K)——426426426
γ0——1.171.171.17
q——0.50.50.5
Reduced χ20.70 ± 0.231.37 ± 0.37———
a γ0 and q taken from previously reported values for Mw94 [25]. b Identical to Mw94 model except for V0 taken from Wicks et al. [21]. c Non-thermal parameters from Finkelstein et al. [26].
Table
Table 2. Inversion results for two ULVZ observations showing best-fit assemblages of Mw mixed with Br and CaPv with properties as a percentage relative to PREM at the CMB. See text and Supporting Information for details.
Table 2. Inversion results for two ULVZ observations showing best-fit assemblages of Mw mixed with Br and CaPv with properties as a percentage relative to PREM at the CMB. See text and Supporting Information for details.
Result δVP (%)aδVS (%)δρ (%)Mw#XMw (%)XBr (%)XCaPv (%)Reduced χ2
ULVZ: S. Atlantic b−3 ± 3−9 ± 3+10 ± 10
Fit: Voigt−8.3 ± 3.4−10.2 ± 3.9+17.2 ± 2.69429.0 ± 1159.9 ± 1311.10.58 ± 0.54
Reuss−4.4 ± 2.3−8.3 ± 2.0+8.2 ± 0.69411.6 ± 1.872.1 ± 5.616.30.09 ± 0.21
Hill−6.4 ± 2.1−9.3 ± 1.7+12.7 ± 2.29420.3 ± 5.666.0 ± 7.113.7
Fit: Voigt−7.7 ± 2.9−10.0 ± 3.1+15.3 ± 1.78434.1 ± 8.664.5 ± 9.91.40.32 ± 0.40
Reuss−1.6 ± 2.6−6.1 ± 2.6+2.4 ± 0.68411.4 ± 2.773.0 ± 9.215.60.22 ± 0.33
Hill−5.3 ± 1.9−8.5 ± 2.0+9.7 ± 0.98422.7 ± 4.568.7 ± 6.78.6
Fit: Voigt c−6.6 ± 2.6%−9.7 ± 2.7+12.8 ± 1.37834.4 ± 7.763 ± 112.60.15 ± 0.27
Reussc−1.4 ± 2.9−6.3 ± 2.6+2.8 ± 0.77811.8 ± 4.180 ± 198.20.28 ± 0.37
Hill−4.1 ± 1.9−8.0 ± 1.9+7.8 ± 0.87823.1 ± 4.471 ± 115.9
ULVZ: Coral Sea d−8 ± 3−24 ± 4+8 ± 6
Fit: Voigt e−11.9 ± 3.6−17.9 ± 5.2+18.3 ± 2.47846.7 ± 1448.4 ± 174.93.5 ± 1.1
Reuss e−12.6 ± 2.1−25.9 ± 2.4+12.7 ± 1.57834.1 ± 4.061.1 ± 6.37.90.41 ± 0.37
Hill−12.2 ± 2.1−21.7 ± 3.0+15.5 ± 1.37840.4 ± 7.354.7 ± 9.14.9
Note: Uncertainties are reported at the 68% level. Unless otherwise noted, all inversions use a prior of XBr = 0.7 with a window of 0.2. a Velocity and density changes are reported as a percentage relative to PREM at the CMB. b [47]. c Prior: XBr = 0.7 with a window of 0.4. d [48]. e Priors: XBr = 0.6 and XMw = 0.4, with windows of 0.1 for each.

Share and Cite

MDPI and ACS Style

Dobrosavljevic, V.V.; Sturhahn, W.; Jackson, J.M. Evaluating the Role of Iron-Rich (Mg,Fe)O in Ultralow Velocity Zones. Minerals 2019, 9, 762. https://doi.org/10.3390/min9120762

AMA Style

Dobrosavljevic VV, Sturhahn W, Jackson JM. Evaluating the Role of Iron-Rich (Mg,Fe)O in Ultralow Velocity Zones. Minerals. 2019; 9(12):762. https://doi.org/10.3390/min9120762

Chicago/Turabian Style

Dobrosavljevic, Vasilije V., Wolfgang Sturhahn, and Jennifer M. Jackson. 2019. "Evaluating the Role of Iron-Rich (Mg,Fe)O in Ultralow Velocity Zones" Minerals 9, no. 12: 762. https://doi.org/10.3390/min9120762

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop