The Site Occupancy Assessment in Beryl Based on Bond-Length Constraints
Abstract
1. Introduction
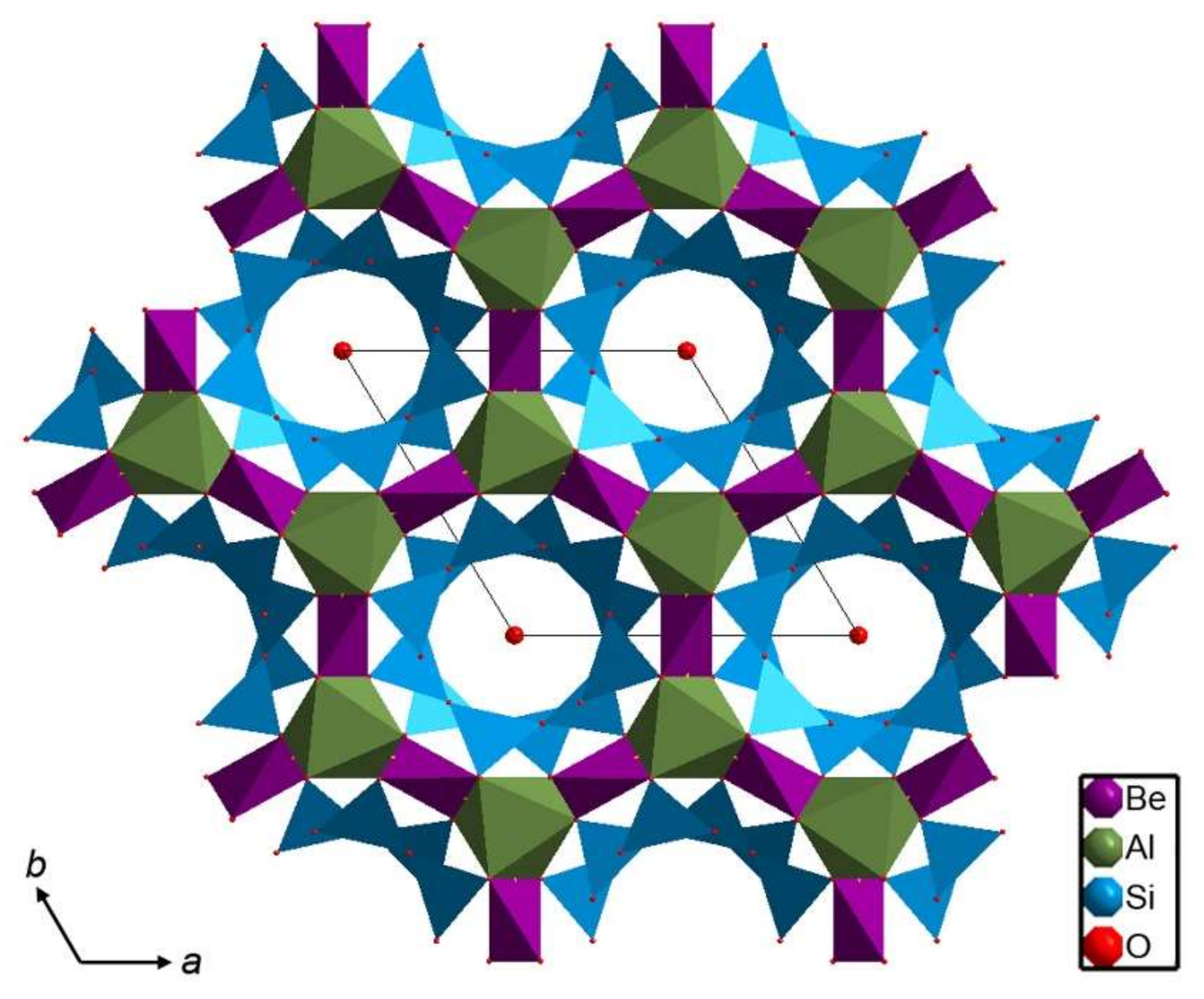
2. Beryl Structure
3. Methods
4. Results
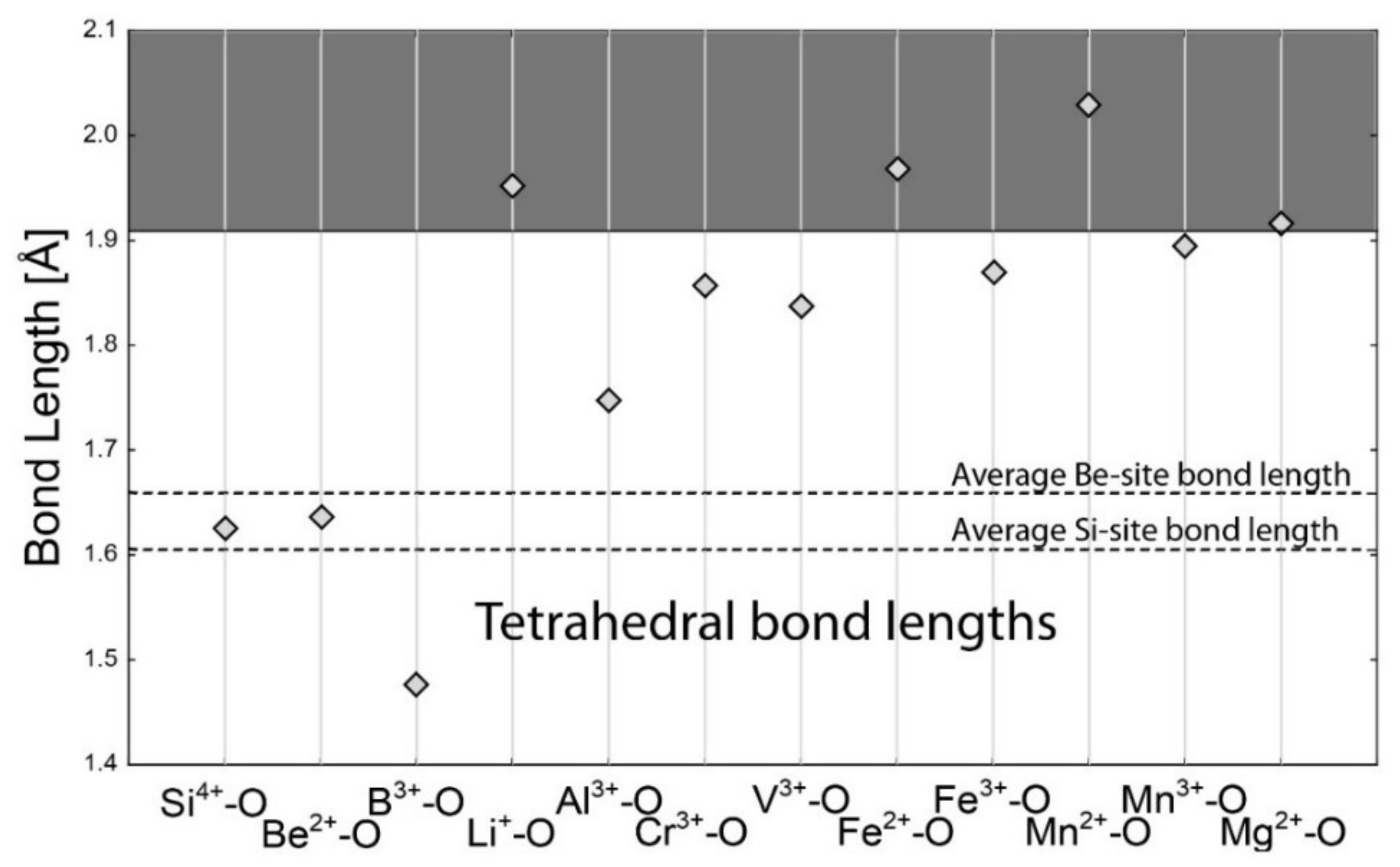
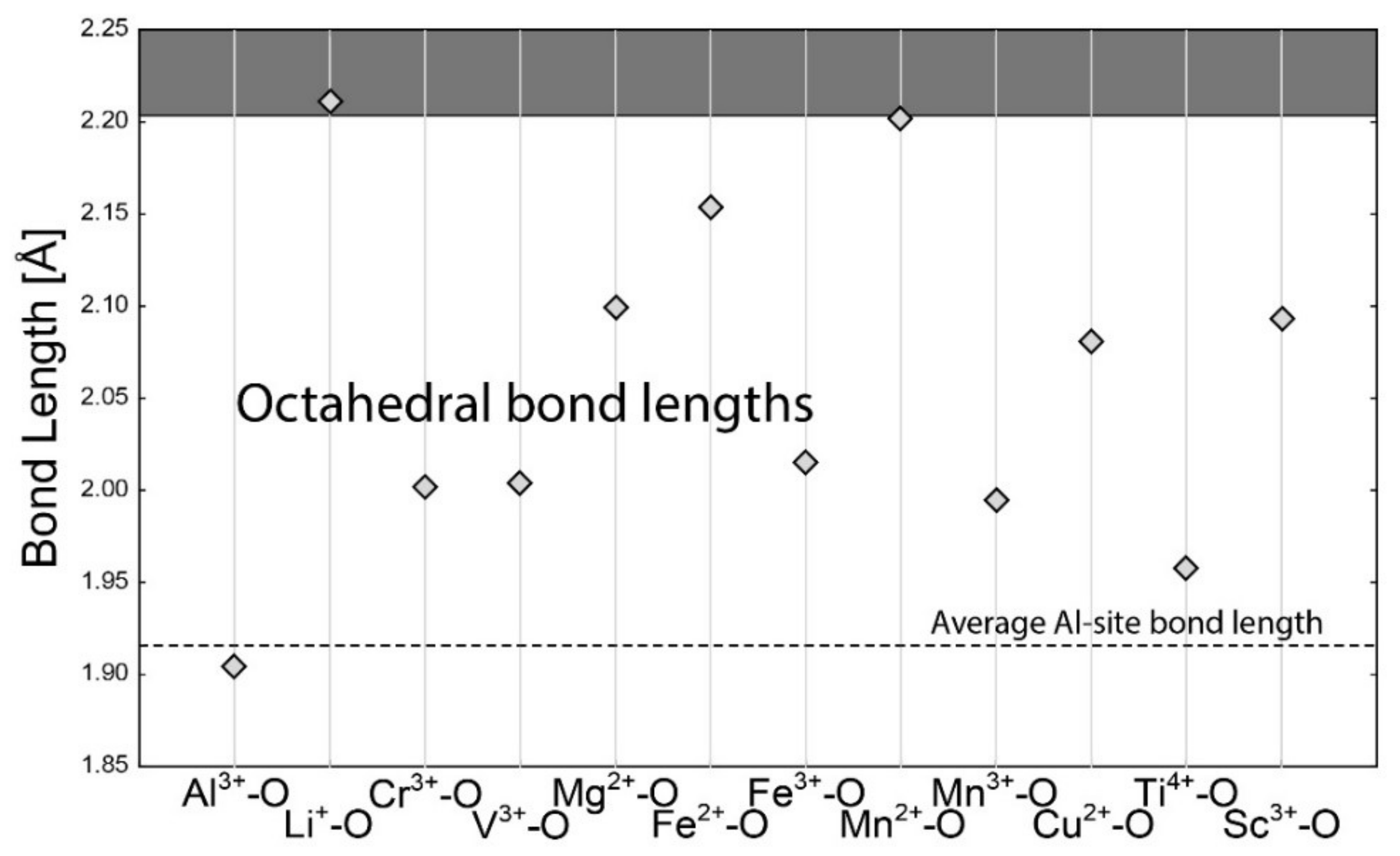
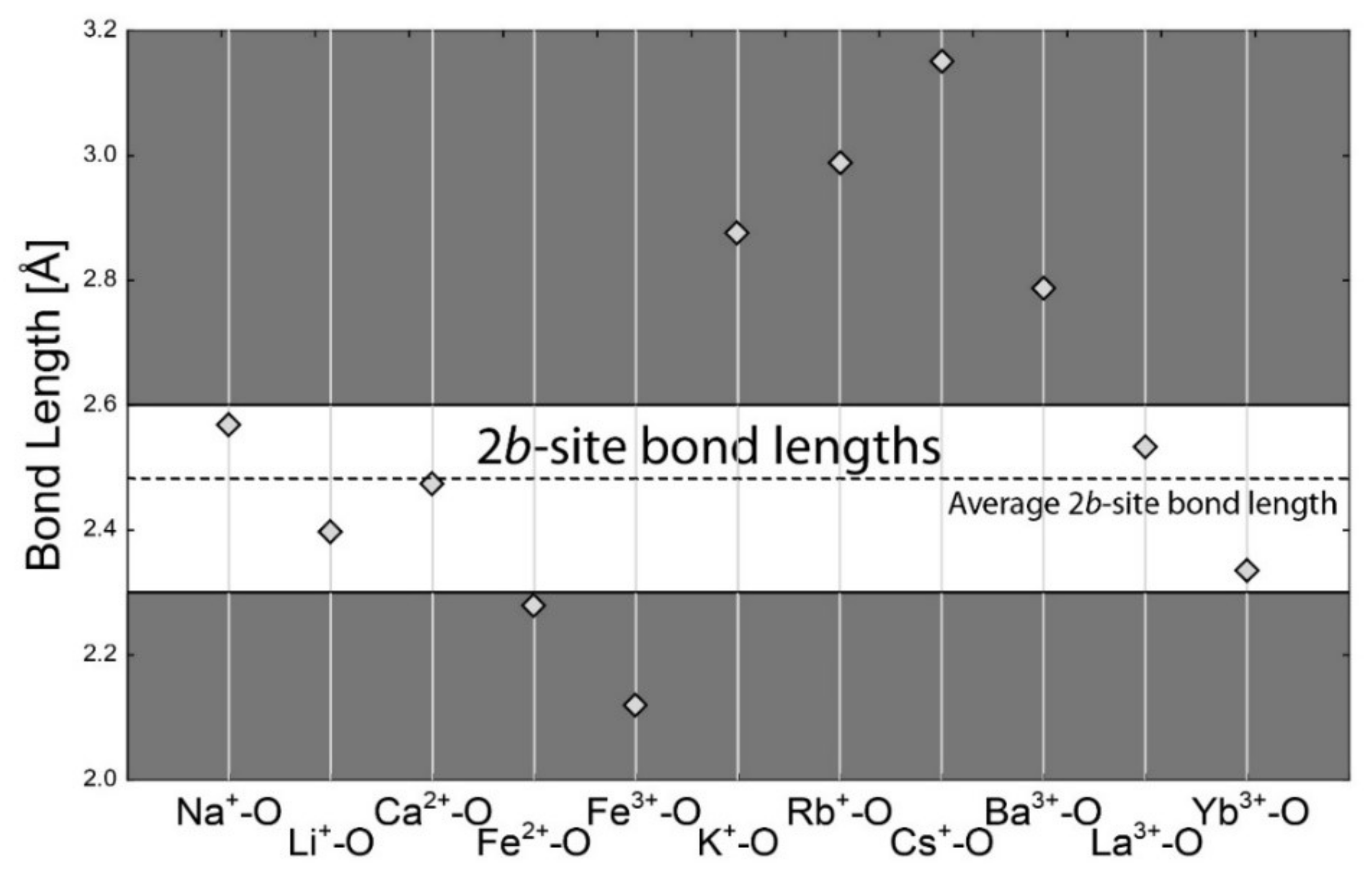
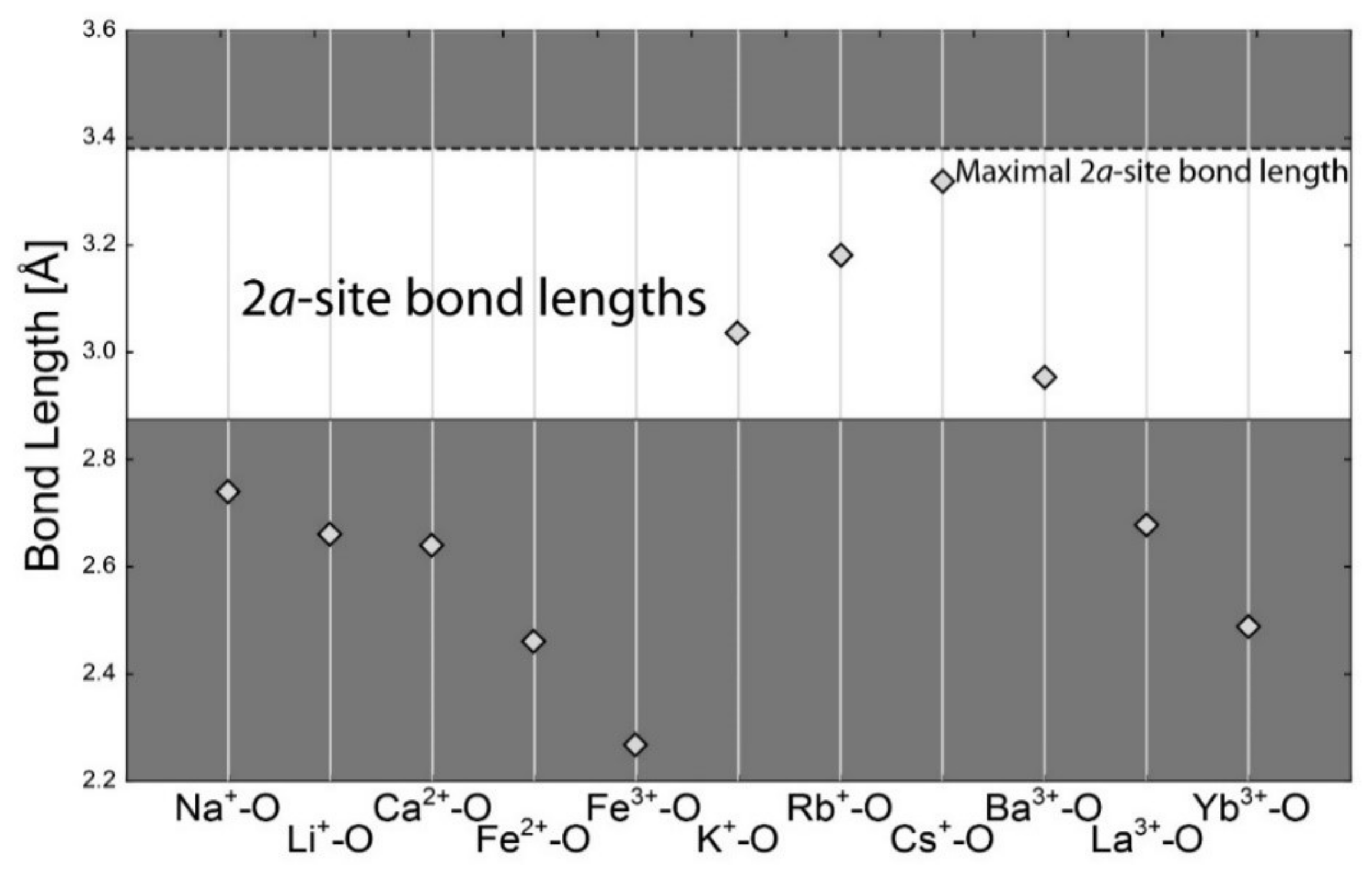
4.1. Bond-Length Calculations
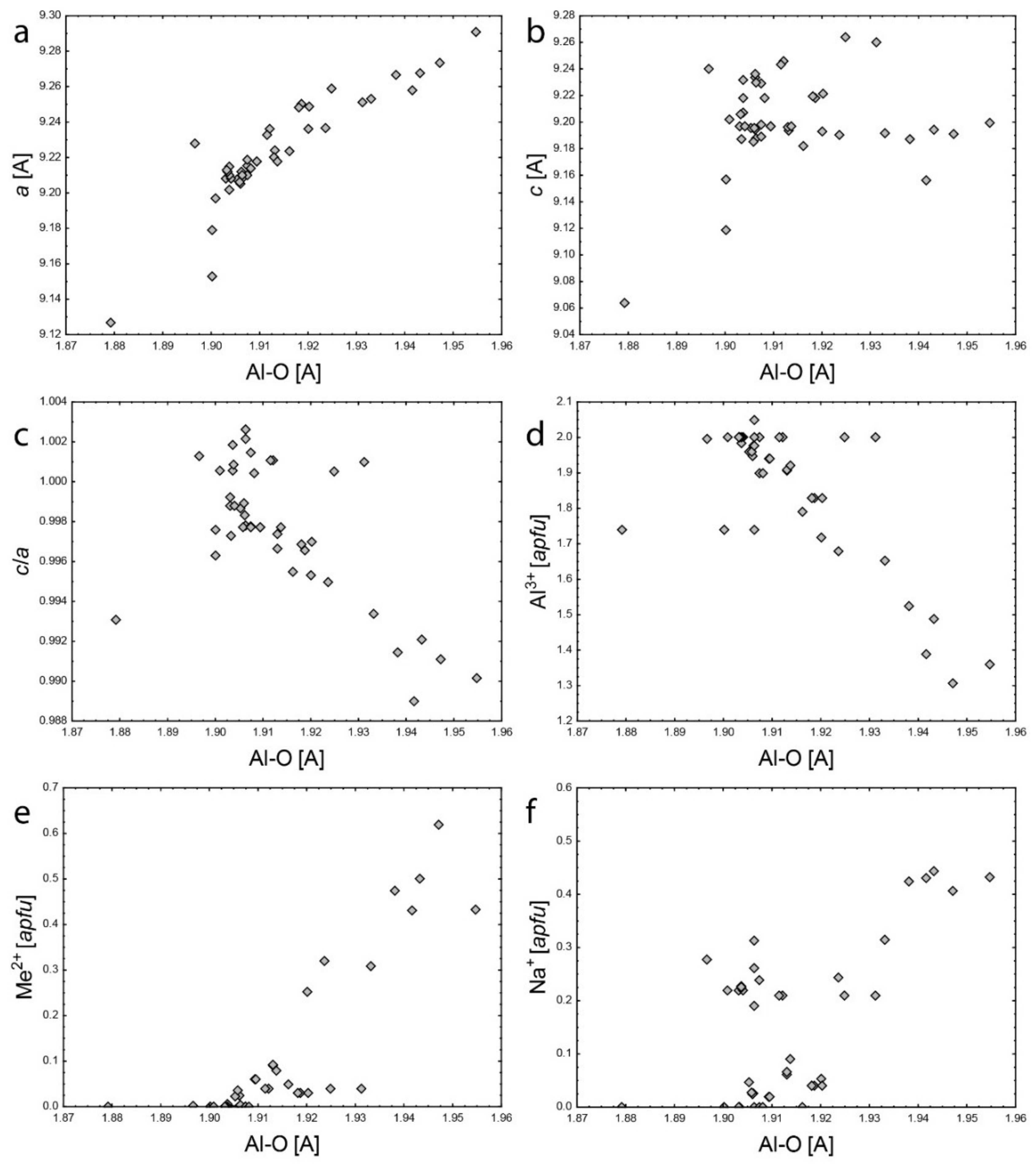
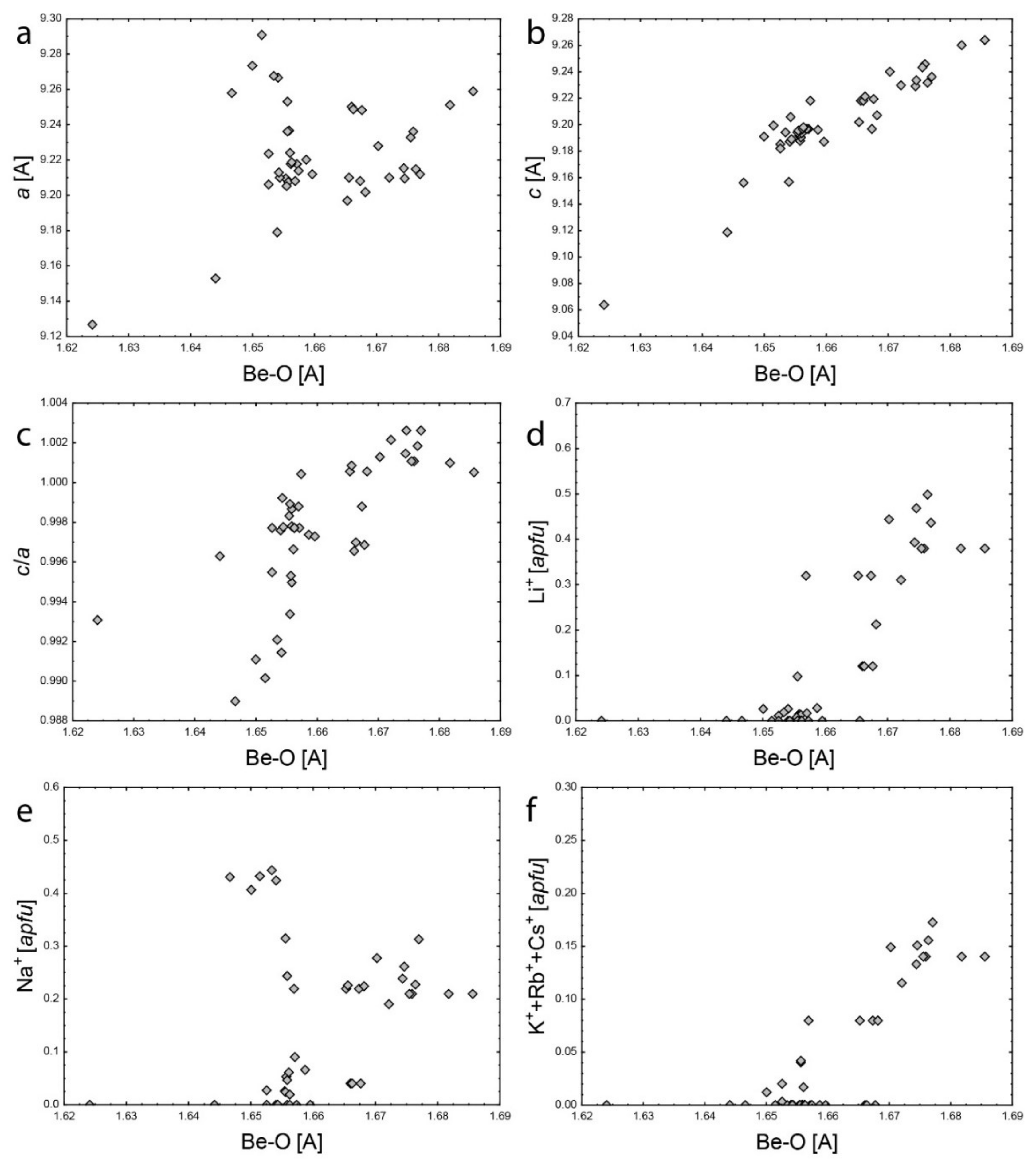
4.2. Empirical Crystal-Chemical Analysis
5. Discussion and Conclusions
5.1. Framework Sites
5.2. Channel Sites
5.3. Compositional Gap
- (1)
- Structural limitations—the rigidity of the 3D structural framework can limit mutual substitutions of larger cations at both Be and Al sites.
- (2)
- Crystal-chemical limitation at the Be and Al sites—substitutions at both sites produce charge deficiency and under-bonding of all O2: −0.25 vu at the Be site with Li+; −0.17 vu at the Al site with Me2+; −0.42 vu in sum. This would increase Si4+–O2 bond valence to 1.42 vu and would induce significant bond shortening to 1.48 Å which would produce a large structural instability.
- (3)
- Channel sites limitations—alkali can charge-balance either octahedral or tetrahedral substitution but not both at the same time. This results from the upper limit for channel sites, which is one apfu (if H2O is not counted) [1], although there are two distinct channel sites. However, the distance between the centers of the 2a and 2b sites is around 2.30 Å [2,4], which disallows the common presence of alkali at both sites. The sum of the most common Na+ and Cs+ ionic radii is 3.06 Å [58]—by far larger than the required 2.30 Å. Only Ca2+ or REE3+ in the channel could be able to charge-balance the combined substitution of Me2+ at the Al site and Li+ at the Be site, but these cations are very rare in beryl. It results from the geochemical properties of the beryl genetic environment. Beryl is the most characteristic and widespread mineral of Be in granitic pegmatites of the LCT (Li–Cs–Ta) suite and is less frequent in the REE-rich NYF (Nb–Y–F) suite [59].
- (4)
- Geochemical limitations—the compositional gap may also result from the chemical composition of the hosting pegmatite environment. The beryl fractionation trend towards a Li-, Cs-rich, and Fe–Mg-poor composition is well documented in rare-element pegmatites worldwide [1,21,60,61,62]. Similarly, the negative correlation between Fe and (Al + Li) and between Fe and Mn in tourmaline is due to fractionation of the pegmatite melt [63]. Other genetic types of beryl are usually Li- and Cs-depleted and, therefore, tend to octahedral or homovalent Me3+Al−1 substitutions.
Author Contributions
Funding
Conflicts of Interest
References
- Aurisicchio, C.; Fioravanti, G.; Grubessi, O.; Zanazzi, P.F. Reappraisal of the crystal chemistry of beryl. Am. Miner. 1988, 73, 826–837. [Google Scholar]
- Brown, G.E.; Mills, B.A. High-temperature structure and crystal chemistry of hydrous alkali-rich beryl from the Harding pegmatite, Taos County, New Mexico. Am. Miner. 1986, 71, 547–556. [Google Scholar]
- Hazen, R.M.; Au, A.Y.; Finger, L.W. High-pressure crystal chemistry of beryl (Be3Al2Si6O18) and euclase (BeAlSiO4OH). Am. Miner. 1986, 71, 977–984. [Google Scholar]
- Artioli, G.; Rinaldi, R.; Stahl, K.; Zanazzi, P.F. Structure refinements of beryl by single-crystal neutron and X-ray diffraction. Am. Miner. 1993, 78, 762–768. [Google Scholar]
- Gatta, G.D.; Nestola, F.; Bromiley, G.D.D.; Mattauch, S. The real topological configuration of the extra-framework content in alkali-poor beryl: A multi-methodological study. Am. Miner. 2006, 91, 29–34. [Google Scholar] [CrossRef]
- Hawthorne, F.C.; Cerny, P. The alkali-metal positions in Cs–Li beryl. Can. Miner. 1977, 15, 414–421. [Google Scholar]
- Sherriff, B.L.; Douglas Grundy, H.; Stephen Hartman, J.; Hawthorne, F.C.; Černý, P. The incorporation of alkalis in beryl: Multi-nuclear MAS NMR and crystal-structure study. Can. Miner. 1991, 29, 271–285. [Google Scholar]
- Groat, L.A.; Rossman, G.R.; Dyar, M.D.; Turner, D.; Piccoli, P.M.B.; Schultz, A.J.; Ottolini, L. Crystal chemistry of dark blue aquamarine from the True Blue showing, Yukon Territory, Canada. Can. Miner. 2010, 48, 597–613. [Google Scholar] [CrossRef]
- Taran, M.N.; Rossman, G.R. Optical spectroscopic study of tuhualite and a re-examination of the beryl, cordierite, and osumilite spectra. Am. Miner. 2001, 86, 973–980. [Google Scholar] [CrossRef]
- Taran, M.N.; Vyshnevskyi, O.A. Be, Fe2+-substitution in natural beryl: an optical absorption spectroscopy study. Phys. Chem. Miner. 2019, 46, 795–806. [Google Scholar] [CrossRef]
- Spinolo, G.; Fontana, I.; Galli, A. Optical absorption spectra of Fe2+ and Fe3+ in beryl crystals. Phys. Status Solidi Basic Res. 2007, 244, 4660–4668. [Google Scholar] [CrossRef]
- Fridrichová, J.; Bačík, P.; Ertl, A.; Wildner, M.; Dekan, J.; Miglierini, M. Jahn-Teller distortion of Mn3+-occupied octahedra in red beryl from Utah indicated by optical spectroscopy. J. Mol. Struct. 2018, 1152, 79–86. [Google Scholar] [CrossRef]
- Fridrichová, J.; Bačík, P.; Rusinová, P.; Antal, P.; Škoda, R.; Bizovská, V.; Miglierini, M. Optical and crystal-chemical changes in aquamarines and yellow beryls from Thanh Hoa province, Vietnam induced by heat treatment. Phys. Chem. Miner. 2015, 42, 287–302. [Google Scholar] [CrossRef]
- Wood, D.L.; Nassau, K. The characterization of beryl and emerald by visible and infrared absorption spectroscopy. Am. Miner. 1968, 53, 777–800. [Google Scholar]
- Viana, R.R.; da Costa, G.M.; De Grave, E.; Stern, W.B.; Jordt-Evangelista, H.; Stern, W.B. Characterization of beryl (aquamarine variety) by Mössbauer spectroscopy. Phys. Chem. Miner. 2002, 29, 78–86. [Google Scholar] [CrossRef]
- Přikryl, J.; Novák, M.; Filip, J.; Gadas, P.; Galiová, M.V. Iron+magnesium-bearing beryl from granitic pegmatites: An EMPA, LA-ICP-MS, Mössbauer spectroscopy, and powder XRD study. Can. Miner. 2014, 52, 271–284. [Google Scholar] [CrossRef]
- Taran, M.N.; Dyar, M.D.; Khomenko, V.M. Spectroscopic study of synthetic hydrothermal Fe3+-bearing beryl. Phys. Chem. Miner. 2018, 45, 489–496. [Google Scholar] [CrossRef]
- Don Goldman, S.; Rossman, G.R.; Parkin, K.M. Channel constituents in beryl. Phys. Chem. Miner. 1978, 3, 225–235. [Google Scholar] [CrossRef]
- Fridrichová, J.; Bačík, P.; Bizovská, V.; Libowitzky, E.; Škoda, R.; Uher, P.; Ozdín, D.; Števko, M. Spectroscopic and bond-topological investigation of interstitial volatiles in beryl from Slovakia. Phys. Chem. Miner. 2016, 43, 419–437. [Google Scholar] [CrossRef]
- Fukuda, J.; Shinoda, K.; Nakashima, S.; Miyoshi, N.; Aikawa, N. Polarized infrared spectroscopic study of diffusion of water molecules along structure channels in beryl. Am. Miner. 2009, 94, 981–985. [Google Scholar] [CrossRef]
- Łodziński, M.; Sitarz, M.; Stec, K.; Kozanecki, M.; Fojud, Z.; Jurga, S. ICP, IR, Raman, NMR investigations of beryls from pegmatites of the Sudety Mts. J. Mol. Struct. 2005, 744, 1005–1015. [Google Scholar] [CrossRef]
- Kolesov, B.A.; Geiger, C.A. The orientation and vibrational states of H2O in synthetic alkali-free beryl. Phys. Chem. Miner. 2000, 27, 557–564. [Google Scholar] [CrossRef]
- Charoy, B.; De Donato, P.; Barres, O.; Pinto-Coelho, C. Channel occupancy in an alkali-poor beryl from Serra Branca (Goias, Brazil): Spectroscopic characterization. Am. Miner. 1996, 81, 395–403. [Google Scholar] [CrossRef]
- Hagemann, H.; Lucken, A.; Bill, H.; Gysler-Sanz, J.; Stalder, H.A.A. Polarized Raman spectra of beryl and bazzite. Phys. Chem. Miner. 1990, 17, 395–401. [Google Scholar] [CrossRef]
- Aurisicchio, C.; Grubessi, O.; Zecchini, P. Infrared spectroscopy and crystal chemistry of the beryl group. Can. Miner. 1994, 32, 55–68. [Google Scholar]
- Wood, D.L.; Nassau, K. Infrared spectra of foreign molecules in beryl. J. Chem. Phys. 1967, 47, 2220–2228. [Google Scholar] [CrossRef]
- Fukuda, J.; Shinoda, K. Water molecules in beryl and cordierite: High-temperature vibrational behavior, dehydration, and coordination to cations. Phys. Chem. Miner. 2011, 38, 469–481. [Google Scholar] [CrossRef]
- Fukuda, J.; Shinoda, K. Coordination of water molecules with Na+ cations in a beryl channel as determined by polarized IR spectroscopy. Phys. Chem. Miner. 2008, 35, 347–357. [Google Scholar] [CrossRef]
- Zavarzina, N.I.; Gabuda, S.P.; Bakakin, V.V.; Rylov, G.M. NMR analysis of water in beryls. J. Struct. Chem. 1970, 10, 696–701. [Google Scholar] [CrossRef]
- Blak, A.R.; Isotani, S.; Watanabe, S. Optical absorption and electron spin resonance in blue and green natural beryl. Phys. Chem. Miner. 1982, 8, 161–166. [Google Scholar] [CrossRef]
- Andersson, L.O. The positions of H+, Li+ and Na+ impurities in beryl. Phys. Chem. Miner. 2006, 33, 403–416. [Google Scholar] [CrossRef]
- Andersson, L.O. The yellow color center and trapped electrons in beryl. Can. Miner. 2013, 51, 15–25. [Google Scholar] [CrossRef]
- Andersson, L.O. Comments on Beryl Colors and on Other Observations Regarding Iron-containing Beryls. Can. Miner. 2019, 57, 551–566. [Google Scholar] [CrossRef]
- Lin, J.; Chen, N.; Huang, D.; Pan, Y. Iron pairs in beryl: New insights from electron paramagnetic resonance, synchrotron X-ray absorption spectroscopy, and ab initio calculations. Am. Miner. 2013, 98, 1745–1753. [Google Scholar] [CrossRef]
- Edgar, A.; Hutton, D.R.R. Exchange-coupled pairs of Fe3+ ions in beryl. Solid State Commun. 1982, 41, 195–198. [Google Scholar] [CrossRef]
- Brown, I.D. The Chemical Bond in Inorganic Chemistry; Oxford University Press: Oxford, UK, 2006; ISBN 9780199298815. [Google Scholar]
- Brown, I.D. Recent developments in the methods and applications of the bond valence model. Chem. Rev. 2009, 109, 6858–6919. [Google Scholar] [CrossRef] [PubMed]
- Brown, I.D. The Chemical Bond in Inorganic Chemistry: The Bond Valence Model; Oxford University Press: Oxford, UK, 2010; Volume 9780199298, ISBN 9780191708879. [Google Scholar]
- Brown, I.D. (IUCr) Bond Valence Parameters. Available online: https://www.iucr.org/resources/data/datasets/bond-valence-parameters (accessed on 7 October 2019).
- Brown, I.D.; Altermatt, D. Bond-valence parameters obtained from a systematic analysis of the Inorganic Crystal Structure Database. Acta Crystallogr. Sect. B 1985, 41, 244–247. [Google Scholar] [CrossRef]
- Gagné, O.C.; Hawthorne, F.C. Comprehensive derivation of bond-valence parameters for ion pairs involving oxygen. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2015, 71, 562–578. [Google Scholar] [CrossRef]
- Gatta, G.D.; Adamo, I.; Meven, M.; Lambruschi, E. A single-crystal neutron and X-ray diffraction study of pezzottaite, Cs(Be2Li)Al2Si6O18. Phys. Chem. Miner. 2012, 39, 829–840. [Google Scholar] [CrossRef]
- Gibbs, G.V.V.; Breck, D.W.W.; Meagher, E.P.P. Structural refinement of hydrous and anhydrous synthetic beryl, Al2(Be3Si6)O18 and emerald, Al1.9Cr0.1(Be3Si6)O18. Lithos 1968, 1, 275–285. [Google Scholar] [CrossRef]
- Meagher, E.P.; Gibbs, G.V. The polymorphism of cordierite. II. The crystal structure of indialite. Can. Miner. 1977, 51, 43–49. [Google Scholar]
- Ferraris, G.; Prencipe, M.; Rossi, P. Stoppaniite, a new member of the beryl group: crystal structure and crystal-chemical implications. Eur. J. Miner. 1998, 10, 491–496. [Google Scholar] [CrossRef]
- Bakakin, V.V.; Rilov, G.M.; Belov, N.V. Crystal structure of a lithium-bearing beryl. Dokl. Akad. Nauk SSSR 1969, 188, 659–662. [Google Scholar]
- De Almeida Sampaio Filho, H.; Sighinolfi, G.; Galli, E. Contribution to crystal chemistry of beryl. Contrib. Miner. Petrol. 1973, 38, 279–290. [Google Scholar] [CrossRef]
- Lehmann, G. Optical absorption and electron spin resonance in blue and green natural beryl: A comment. Phys. Chem. Miner. 1983, 9, 278. [Google Scholar] [CrossRef]
- Viana, R.R.; Jordt-Evangelista, H.; Magela da Costa, G.; Stern, W.B. Characterization of beryl (aquamarine variety) from pegmatites of Minas Gerais, Brazil. Phys. Chem. Miner. 2002, 29, 668–679. [Google Scholar] [CrossRef]
- Meagher, E.P.; Gibbs, G.V. Tetrahedral magnesium in cordierite. Geol. Soc. Am. Spec. Pap. 1968, 115, 146. [Google Scholar]
- Schmetzer, K.; Schwarz, D.; Bernhardt, H.-J.; Häger, T. A new type of Tairus hydrothermally-grown synthetic emerald, coloured by vanadium and copper. J. Gemmol. 2006, 30, 59–74. [Google Scholar] [CrossRef]
- Adamo, I.; Gatta, G.D.; Rotiroti, N.; Diella, V.; Pavese, A. Gemmological investigation of a synthetic blue beryl: a multi-methodological study. Miner. Mag. 2008, 72, 799–808. [Google Scholar] [CrossRef]
- Burns, R.G.; Strens, R.G.J. Structural interpretation of polarized absorption spectra of the Al–Fe–Mn–Cr epidotes. Miner. Mag. J. Miner. Soc. 1967, 36, 204–226. [Google Scholar] [CrossRef]
- Ito, J.; Hafner, S.S. Synthesis and study of gadolinites. Am. Miner. 1974, 59, 700–708. [Google Scholar]
- Bačík, P.; Fridrichová, J.; Uher, P.; Pršek, J.; Ondrejka, M. The crystal chemistry of gadolinite-datolite group silicates. Can. Miner. 2014, 52, 625–642. [Google Scholar] [CrossRef]
- Ertl, A.; Vereshchagin, O.S.; Giester, G.; Tillmanns, E.; Meyer, H.-P.P.; Ludwig, T.; Rozhdestvenskaya, I.V.; Frank-Kamenetskaya, O.V. Structural and chemical investigation of a zoned synthetic Cu-rich tourmaline. Can. Miner. 2015, 53, 209–220. [Google Scholar] [CrossRef]
- Bačík, P. The crystal-chemical autopsy of octahedral sites in Na-dominant tourmalines: Octahedral metrics model unconstrained by the Y, Z-site disorder assignment. J. Geosci. 2018, 63, 137–154. [Google Scholar] [CrossRef]
- Shannon, R.D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallogr. Sect. A 1976, 32, 751–767. [Google Scholar] [CrossRef]
- Černý, P.; Ercit, T.S. The classification of granitic pegmatites revisited. Can. Miner. 2005, 43, 2005–2026. [Google Scholar] [CrossRef]
- Uher, P.; Chudík, P.; Bačík, P.; Vaculovič, T.; Galiová, M. Beryl composition and evolution trends: An example from granitic pegmatites of the beryl-columbite subtype, Western Carpathians, Slovakia. J. Geosci. 2010, 55, 69–80. [Google Scholar] [CrossRef][Green Version]
- London, D.; Evensen, J.M. Beryllium in silicic magmas and the origin of Beryl-bearing pegmatites. In Beryllium: Mineralogy, Petrology, and Geochemistry; De Gruyter: Berlin, Germany, 2019; Volume 50, ISBN 9781501508844. [Google Scholar]
- Bačík, P.; Fridrichová, J.; Uher, P.; Rybár, S.; Bizovská, V.; Luptáková, J.; Vrábliková, D.; Pukančík, L.; Vaculovič, T. Octahedral substitution in beryl from weakly fractionated intragranitic pegmatite Predné Solisko, Tatry Mountains (Slovakia): The indicator of genetic conditions. J. Geosci. 2019, 64, 59–72. [Google Scholar] [CrossRef]
- Selway, J.B.; Smeds, S.A.; Černý, P.; Hawthorne, F.C. Compositional evolution of tourmaline in the petalite-subtype Nyköpingsgruvan pegmatites, Utö, Stockholm Archipelago, Sweden. GFF 2002, 124, 93–102. [Google Scholar] [CrossRef]
| Coordination Number | |||||||
|---|---|---|---|---|---|---|---|
| 4 | 6 | 8 | 12 | ||||
| Bond | dij [Å] | Bond | dij [Å] | Bond | dij [Å] | Bond | dij [Å] |
| Si4+–O | 1.624 | Al3+–O | 1.904 | Na+–O | 2.568 | Na+–O | 2.739 |
| Be2+–O | 1.635 | Li+–O | 2.211 | Li+–O | 2.397 | Li+–O | 2.657 |
| B3+–O | 1.475 | Cr3+–O | 2.002 | Ca2+–O | 2.474 | Ca2+–O | 2.640 |
| Al3+–O | 1.746 | V3+–O | 2.004 | Fe2+–O | 2.278 | Fe2+–O | 2.459 |
| Li+–O | 1.952 | Mg2+–O | 2.099 | Fe3+–O | 2.119 | Fe3+–O | 2.265 |
| Cr3+–O | 1.856 | Fe2+–O | 2.154 | K+–O | 2.875 | K+–O | 3.036 |
| V3+–O | 1.837 | Fe3+–O | 2.016 | Cs+–O | 3.151 | Cs+–O | 3.317 |
| Fe2+–O | 1.968 | Mn2+–O | 2.202 | Rb+–O | 2.987 | Rb+–O | 3.181 |
| Fe3+–O | 1.870 | Mn3+–O | 1.994 | Ba2+–O | 2.786 | Ba2+–O | 2.950 |
| Mn2+–O | 2.029 | Cu2+–O | 2.081 | La3+–O | 2.531 | La3+–O | 2.677 |
| Mn3+–O | 1.894 | Ti4+–O | 1.958 | Yb3+–O | 2.335 | Yb3+–O | 2.486 |
| Mg2+–O | 1.915 | Sc3+–O | 2.093 | ||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bačík, P.; Fridrichová, J. The Site Occupancy Assessment in Beryl Based on Bond-Length Constraints. Minerals 2019, 9, 641. https://doi.org/10.3390/min9100641
Bačík P, Fridrichová J. The Site Occupancy Assessment in Beryl Based on Bond-Length Constraints. Minerals. 2019; 9(10):641. https://doi.org/10.3390/min9100641
Chicago/Turabian StyleBačík, Peter, and Jana Fridrichová. 2019. "The Site Occupancy Assessment in Beryl Based on Bond-Length Constraints" Minerals 9, no. 10: 641. https://doi.org/10.3390/min9100641
APA StyleBačík, P., & Fridrichová, J. (2019). The Site Occupancy Assessment in Beryl Based on Bond-Length Constraints. Minerals, 9(10), 641. https://doi.org/10.3390/min9100641





