Numerical Modeling of REE Fractionation Patterns in Fluorapatite from the Olympic Dam Deposit (South Australia)
Abstract
:1. Introduction
2. Description of the Deposit, Apatite-Group Minerals and Rare Earth Element Behavior
2.1. The Olympic Dam Deposit
2.2. Apatite Mineralogy, Geochemistry and Crystal Structure
2.3. REE Trends in Fluorapatite from the Olympic Dam Deposit
2.4. Fluid Evolution within IOCG Systems, REE Speciation and the Controls on Apatite/Fluid Partitioning
3. Methodology
Numerical Modeling of Apatite/Fluid Partitioning Coefficients
4. Results
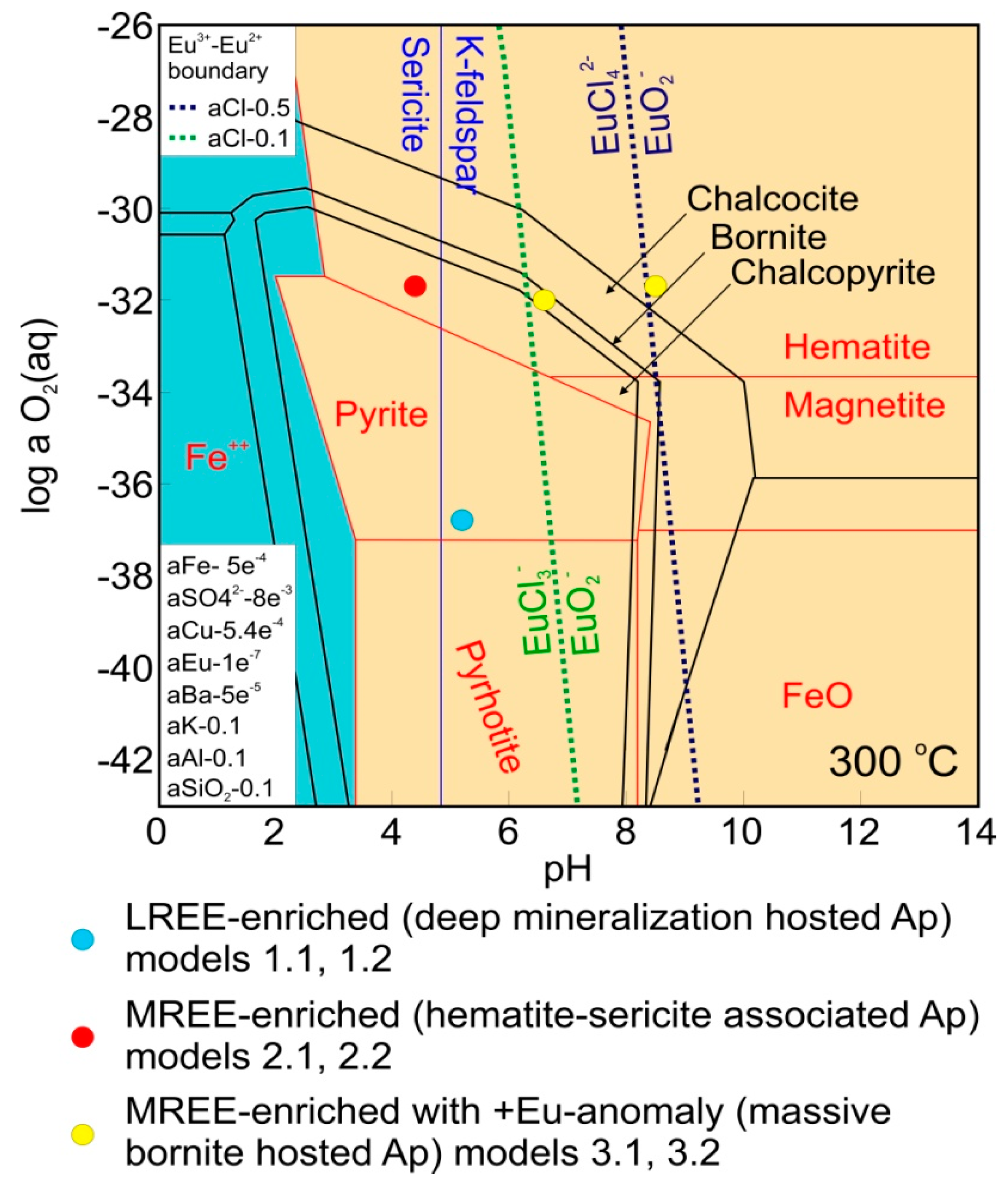
4.1. Study Cases and Determination of Fluid Conditions
4.2. Apatite/Fluid REE Partitioning and the Effects of Evolving Fluid Conditions
5. Discussion
6. Conclusions and Recommendations
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A. Results of Modeling (Models 1.1, 1.2, 2.1, 2.2, 3.1 and 3.2).
| MODEL 1.1 | a (aq.) Total | a (Apatite) | Concentration in Apatite (Mole Fraction) | Concentration Fluid (Modal) | K | Dapatite/fluid | Concentration REE Fluid (ppm) | Model Apatite (ppm) | Model Apatite/Chondrite |
| Ca | 0.141 | 0.974 | 0.974 | 0.195 | |||||
| Na | 3.05 | 0.013 | 0.013 | 4.39 | |||||
| La | 1.35 × 10−4 | 2.25 × 10−3 | 1.51 × 10−3 | 1.58 | 98.4 | 156 | 658 | ||
| Ce | 1.82 × 10−4 | 6.15 × 10−3 | 3.05 × 10−3 | 3.20 | 194 | 622 | 1014 | ||
| Pr | 1.80 × 10−5 | 7.35 × 10−4 | 3.70 × 10−3 | 3.89 | 21.1 | 81.9 | 881 | ||
| Nd | 6.35 × 10−5 | 2.66 × 10−3 | 3.79 × 10−3 | 3.98 | 72.2 | 287 | 629 | ||
| Sm | 1.57 × 10−5 | 4.07 × 10−4 | 2.35 × 10−3 | 2.47 | 13.0 | 32.0 | 216 | ||
| Eu | 1.03 × 10−7 | 3.70 × 10−5 | 0.032 | 0.37 | 1.76 | 0.65 | 11.6 | ||
| Gd | 8.63 × 10−6 | 3.23 × 10−4 | 3.39 × 10−3 | 3.56 | 10.8 | 38.3 | 192 | ||
| Tb | 1.41 × 10−6 | 4.20 × 10−5 | 2.69 × 10−3 | 2.83 | 1.65 | 4.68 | 130 | ||
| Dy | 7.59 × 10−6 | 2.36 × 10−4 | 2.81 × 10−3 | 2.95 | 9.92 | 29.3 | 119 | ||
| Ho | 1.90 × 10−6 | 4.63 × 10−5 | 2.21 × 10−3 | 2.32 | 2.08 | 4.82 | 87.5 | ||
| Er | 7.62 × 10−6 | 1.28 × 10−4 | 1.52 × 10−3 | 1.59 | 5.81 | 9.26 | 57.9 | ||
| Tm | 1.70 × 10−6 | 1.64 × 10−5 | 8.72 × 10−4 | 0.916 | 0.922 | 0.84 | 33.8 | ||
| Yb | 9.21 × 10−6 | 9.90 × 10−5 | 9.72 × 10−4 | 1.02 | 6.04 | 6.17 | 38.3 | ||
| Lu | 1.30 × 10−6 | 1.34 × 10−5 | 9.38 × 10−4 | 0.985 | 0.846 | 0.83 | 33.9 | ||
| Y Eu2+ (aq.) | 7.22 × 10−3 |
| MODEL 1.2 | a (aq.) Total | a (Apatite) | Concentration in Apatite (Mole Fraction) | Concentration Fluid (Modal) | K | Dapatite/fluid | Concentration REE Fluid (ppm) | Model Apatite (ppm) | Model Apatite/Chondrite |
| Ca | 0.789 | 0.974 | 0.974 | 1.05 | |||||
| Na | 3.39 | 0.013 | 0.013 | 4.80 | |||||
| La | 1.59 × 10−4 | 2.25 × 10−3 | 0.036 | 7.68 | 98.4 | 756 | 3189 | ||
| Ce | 2.08 × 10−4 | 6.15 × 10−3 | 0.075 | 16.1 | 194 | 3117 | 5084 | ||
| Pr | 1.89 × 10−5 | 7.35 × 10−4 | 0.099 | 21.1 | 21.1 | 445 | 4785 | ||
| Nd | 6.59 × 10−5 | 2.66 × 10−3 | 0.103 | 22.0 | 72.2 | 1587 | 3473 | ||
| Sm | 1.82 × 10−5 | 4.07 × 10−4 | 0.057 | 12.2 | 13.0 | 158 | 1067 | ||
| Eu | 9.78 × 10−8 | 3.70 × 10−5 | 0.965 | 2.19 | 1.76 | 3.85 | 68.7 | ||
| Gd | 1.10 × 10−5 | 3.23 × 10−4 | 0.075 | 16.0 | 10.8 | 172 | 864 | ||
| Tb | 1.78 × 10−6 | 4.20 × 10−5 | 0.060 | 12.8 | 1.65 | 21.2 | 588 | ||
| Dy | 8.80 × 10−6 | 2.36 × 10−4 | 0.068 | 14.6 | 9.92 | 145 | 589 | ||
| Ho | 2.31 × 10−6 | 4.63 × 10−5 | 0.051 | 10.9 | 2.08 | 22.6 | 412 | ||
| Er | 9.50 × 10−6 | 1.28 × 10−4 | 0.034 | 7.32 | 5.81 | 42.5 | 266 | ||
| Tm | 1.84 × 10−6 | 1.64 × 10−5 | 0.023 | 4.86 | 0.922 | 4.48 | 179 | ||
| Yb | 1.13 × 10−5 | 9.90 × 10−5 | 0.022 | 4.77 | 6.04 | 28.8 | 179 | ||
| Lu | 1.61 × 10−6 | 1.34 × 10−5 | 0.021 | 4.54 | 0.846 | 3.84 | 156 | ||
| Y Eu2+ (aq.) | 6.25 × 10−3 |
| MODEL 2.1 | a (aq.) Total | a (Apatite) | Concentration in Apatite (Mole Fraction) | Concentration Fluid (Modal) | K | Dapatite/fluid | Concentration REE Fluid (ppm) | Model Apatite (ppm) | Model Apatite/Chondrite |
| Ca | 0.068 | 0.996 | 0.996 | 0.105 | |||||
| Na | 1.28 | 1.96 × 10−3 | 1.96 × 10−3 | 1.94 | |||||
| La | 1.42 × 10−4 | 9.31 × 10−5 | 4.73 × 10−6 | 4.10 × 10−3 | 100 | 0.41 | 1.73 | ||
| Ce | 1.49 × 10−4 | 3.27 × 10−4 | 1.58 × 10−5 | 0.014 | 200 | 2.74 | 4.47 | ||
| Pr | 1.62 × 10−5 | 6.56 × 10−5 | 2.93 × 10−5 | 0.025 | 24.0 | 0.61 | 6.54 | ||
| Nd | 3.74 × 10−5 | 4.15 × 10−4 | 8.01 × 10−5 | 0.069 | 80.0 | 5.55 | 12.1 | ||
| Sm | 5.63 × 10−6 | 2.86 × 10−4 | 3.67 × 10−4 | 0.318 | 14.0 | 4.45 | 30.0 | ||
| Eu | 1.60 × 10−7 | 6.52 × 10−5 | 27.9 | 0.199 | 1.90 | 0.38 | 6.76 | ||
| Gd | 4.26 × 10−6 | 4.01 × 10−4 | 6.78 × 10−4 | 0.587 | 11.8 | 6.93 | 34.8 | ||
| Tb | 4.50 × 10−7 | 4.29 × 10−5 | 6.88 × 10−4 | 0.596 | 1.70 | 1.01 | 28.2 | ||
| Dy | 2.89 × 10−6 | 1.66 × 10−4 | 4.15 × 10−4 | 0.359 | 10.3 | 3.70 | 15.0 | ||
| Ho | 5.46 × 10−7 | 2.10 × 10−5 | 2.78 × 10−4 | 0.241 | 2.00 | 0.48 | 8.75 | ||
| Er | 1.37 × 10−6 | 4.14 × 10−5 | 2.17 × 10−4 | 0.188 | 6.10 | 1.15 | 7.18 | ||
| Tm | 1.79 × 10−7 | 4.40 × 10−6 | 1.78 × 10−4 | 0.154 | 0.70 | 0.11 | 4.31 | ||
| Yb | 1.48 × 10−6 | 2.75 × 10−5 | 1.34 × 10−4 | 0.116 | 6.30 | 0.73 | 4.53 | ||
| Lu | 2.48 × 10−7 | 3.10 × 10−6 | 9.03 × 10−5 | 0.078 | 1.10 | 0.086 | 3.50 | ||
| Y Eu2+ (aq.) | 0.012 |
| MODEL 2.2 | a (aq.) Total | a (Apatite) | Concentration in Apatite (Mole Fraction) | Concentration Fluid (Modal) | K | Dapatite/fluid | Concentration REE Fluid (ppm) | Model Apatite (ppm) | Model Apatite/Chondrite |
| Ca | 0.906 | 0.996 | 0.996 | 1.28 | |||||
| Na | 1.48 | 1.96 × 10−3 | 1.96 × 10−3 | 2.19 | |||||
| La | 1.58 × 10−4 | 9.31 × 10−5 | 6.46 × 10−4 | 0.052 | 100 | 5.18 | 21.8 | ||
| Ce | 1.67 × 10−4 | 3.27 × 10−4 | 2.14 × 10−3 | 0.172 | 200 | 34.4 | 56.0 | ||
| Pr | 1.70 × 10−5 | 6.56 × 10−5 | 4.22 × 10−3 | 0.338 | 24.0 | 8.11 | 87.2 | ||
| Nd | 3.85 × 10−5 | 4.15 × 10−4 | 0.012 | 0.946 | 80.0 | 75.7 | 166 | ||
| Sm | 6.55 × 10−6 | 2.86 × 10−4 | 0.048 | 3.83 | 14.0 | 53.6 | 362 | ||
| Eu | 1.27 × 10−7 | 6.52 × 10−5 | 468 | 3.79 | 1.90 | 7.21 | 129 | ||
| Gd | 5.71 × 10−6 | 4.01 × 10−4 | 0.077 | 6.15 | 11.8 | 72.6 | 365 | ||
| Tb | 5.09 × 10−7 | 4.29 × 10−5 | 0.092 | 7.38 | 1.70 | 12.5 | 349 | ||
| Dy | 3.19 × 10−6 | 1.66 × 10−4 | 0.057 | 4.56 | 10.3 | 47.0 | 191 | ||
| Ho | 6.08 × 10−7 | 2.10 × 10−5 | 0.038 | 3.03 | 2.00 | 6.06 | 110 | ||
| Er | 1.31 × 10−6 | 4.14 × 10−5 | 0.035 | 2.78 | 6.10 | 16.9 | 106 | ||
| Tm | 2.30 × 10−7 | 4.40 × 10−6 | 0.021 | 1.67 | 0.70 | 1.17 | 46.9 | ||
| Yb | 1.33 × 10−6 | 2.75 × 10−5 | 0.023 | 1.81 | 6.30 | 11.4 | 70.9 | ||
| Lu | 2.32 × 10−7 | 3.10 × 10−6 | 0.015 | 1.17 | 1.10 | 1.29 | 52.5 | ||
| Y Eu2+ (aq.) | 8.10 × 10−3 |
| MODEL 3.1 | a (aq.) Total | a (Apatite) | Concentration in Apatite (Mole Fraction) | Concentration Fluid (Modal) | K | Dapatite/fluid | Concentration REE Fluid (ppm) | Model Apatite (ppm) | Model Apatite/Chondrite |
| Ca | 0.224 | 0.992 | 0.992 | 0.292 | |||||
| Na | 0.439 | 4.10 × 10−3 | 4.10 × 10−3 | 0.944 | |||||
| La | 3.47 × 10−3 | 1.01 × 10−5 | 1.39 × 10−6 | 2.10 × 10−4 | 120 | 0.252 | 1.06 | ||
| Ce | 4.71 × 10−3 | 6.99 × 10−5 | 7.10 × 10−6 | 1.07 × 10−3 | 170 | 1.82 | 2.98 | ||
| Pr | 3.94 × 10−4 | 2.42 × 10−5 | 2.93 × 10−5 | 4.44 × 10−3 | 150 | 0.665 | 7.16 | ||
| Nd | 1.01 × 10−3 | 2.69 × 10−4 | 1.28 × 10−4 | 0.019 | 393 | 7.58 | 16.6 | ||
| Sm | 1.01 × 10−4 | 8.41 × 10−4 | 3.99 × 10−3 | 0.603 | 41.2 | 24.9 | 168 | ||
| Eu | 2.99 × 10−5 | 5.15 × 10−4 | 8.22 × 10−3 | 1.24 | 12.4 | 15.4 | 275 | ||
| Gd | 6.54 × 10−5 | 1.55 × 10−3 | 0.011 | 1.71 | 28.0 | 47.9 | 241 | ||
| Tb | 7.87 × 10−6 | 1.22 × 10−4 | 7.40 × 10−3 | 1.12 | 3.40 | 3.80 | 106 | ||
| Dy | 3.78 × 10−5 | 4.58 × 10−4 | 5.80 × 10−3 | 0.877 | 16.7 | 14.6 | 59.5 | ||
| Ho | 6.69 × 10−6 | 6.10 × 10−5 | 4.36 × 10−3 | 0.659 | 3.00 | 1.98 | 36.0 | ||
| Er | 2.00 × 10−5 | 1.15 × 10−4 | 2.74 × 10−3 | 0.415 | 9.10 | 3.78 | 23.6 | ||
| Tm | 2.61 × 10−6 | 1.08 × 10−5 | 1.98 × 10−3 | 0.299 | 1.20 | 0.359 | 14.4 | ||
| Yb | 1.83 × 10−5 | 4.82 × 10−5 | 1.26 × 10−3 | 0.191 | 8.60 | 1.64 | 10.2 | ||
| Lu | 2.73 × 10−6 | 5.25 × 10−6 | 9.18 × 10−4 | 0.139 | 1.30 | 0.180 | 7.34 | ||
| Y Eu2+ (aq.) | NA |
| MODEL 3.2 | a (aq.) Total | a (Apatite) | Concentration in Apatite (Mole Fraction) | Concentration Fluid (Modal) | K | Dapatite/fluid | Concentration REE Fluid (ppm) | Model Apatite (ppm) | Model Apatite/Chondrite |
| Ca | 0.645 | 0.992 | 0.992 | 1.05 | |||||
| Na | 0.652 | 4.10 × 10−3 | 4.10 × 10−3 | 1.03 | |||||
| La | 7.37 × 10−3 | 1.01 × 10−5 | 3.63 × 10−6 | 1.66 × 10−4 | 120 | 0.199 | 0.841 | ||
| Ce | 9.16 × 10−3 | 6.99 × 10−5 | 2.03 × 10−5 | 9.29 × 10−4 | 170 | 1.58 | 2.58 | ||
| Pr | 4.88 × 10−4 | 2.42 × 10−5 | 1.32 × 10−4 | 6.03 × 10−3 | 150 | 0.904 | 9.72 | ||
| Nd | 1.23 × 10−3 | 2.69 × 10−4 | 5.81 × 10−4 | 0.027 | 393 | 10.4 | 22.9 | ||
| Sm | 1.10 × 10−4 | 8.41 × 10−4 | 0.020 | 0.933 | 41.2 | 38.4 | 260 | ||
| Eu | 2.99 × 10−5 | 5.15 × 10−4 | 0.046 | 2.10 | 12.4 | 26.0 | 464 | ||
| Gd | 7.01 × 10−5 | 1.55 × 10−3 | 0.059 | 2.69 | 28.0 | 75.3 | 378 | ||
| Tb | 8.49 × 10−6 | 1.22 × 10−4 | 0.038 | 1.75 | 3.40 | 5.93 | 165 | ||
| Dy | 4.02 × 10−5 | 4.58 × 10−4 | 0.030 | 1.39 | 16.7 | 23.2 | 94.3 | ||
| Ho | 7.17 × 10−6 | 6.10 × 10−5 | 0.023 | 1.04 | 3.00 | 3.11 | 56.5 | ||
| Er | 2.11 × 10−5 | 1.15 × 10−4 | 0.014 | 0.661 | 9.10 | 6.01 | 37.6 | ||
| Tm | 2.77 × 10−6 | 1.08 × 10−5 | 0.010 | 0.475 | 1.20 | 0.570 | 22.8 | ||
| Yb | 1.95 × 10−5 | 4.82 × 10−5 | 6.59 × 10−3 | 0.301 | 8.60 | 2.59 | 16.1 | ||
| Lu | 2.89 × 10−6 | 5.25 × 10−6 | 4.83 × 10−3 | 0.221 | 1.30 | 0.287 | 11.7 | ||
| Y Eu2+ (aq.) | NA |
References
- Smith, M.; Henderson, P.; Jeffries, T.; Long, J.; Williams, C. The rare earth elements and uranium in garnets from the Beinn an Dubhaich Aureole, Skye, Scotland, UK: Constraints on processes in a dynamic hydrothermal system. J. Pet. 2004, 45, 457–484. [Google Scholar] [CrossRef]
- Brugger, J.; Etschmann, B.; Pownceby, M.; Liu, W.; Grundler, P.; Brewe, D. Oxidation state of europium in scheelite: Tracking fluid-rock interaction in gold deposits. Chem. Geol. 2008, 257, 26–33. [Google Scholar] [CrossRef]
- van Hinsberg, V.J.; Migdisov, A.A.; Williams-Jones, A.E. Reading the mineral record of fluid composition from element partitioning. Geology 2010, 38, 847–850. [Google Scholar] [CrossRef]
- Haas, J.R.; Shock, E.L.; Sassani, D.C. Rare earth elements in hydrothermal systems: Estimates of standard partial molal thermodynamic properties of aqueous complexes of the rare earth elements at high pressures and temperatures. Geochim. Cosmochim. Acta 1995, 59, 4329–4350. [Google Scholar] [CrossRef]
- Bau, M. Rare-earth element mobility during hydrothermal and metamorphic fluid-rock interaction and the significance of the oxidation state of europium. Chem. Geol. 1991, 93, 219–230. [Google Scholar] [CrossRef]
- Migdisov, A.A.; Williams-Jones, A.E. Hydrothermal transport and deposition of the rare earth elements by fluorine-bearing aqueous liquids. Miner. Deposita 2014, 49, 987–997. [Google Scholar] [CrossRef]
- Migdisov, A.A.; Williams-Jones, A.E.; Brugger, J.; Caporuscio, F.A. Hydrothermal transport, deposition, and fractionation of the REE: Experimental data and thermodynamic calculations. Chem. Geol. 2016, 439, 13–42. [Google Scholar] [CrossRef]
- Brugger, J.; Lahaye, Y.; Costa, S.; Lambert, D.; Bateman, R. Inhomogenous distribution of REE in scheelite and dynamics of Archean hydrothermal systems (Mt. Charlotte and Drysdale gold deposits, Western Australia). Contrib. Miner. Pet. 2000, 139, 251–264. [Google Scholar] [CrossRef]
- Harlov, D.E. Apatite: A fingerprint for metasomatic processes. Elements 2015, 11, 171–176. [Google Scholar] [CrossRef]
- Belousova, E.A.; Walters, S.; Griffin, W.L.; O’Reilly, S.Y. Trace-element signatures of apatites in granitoids from the Mt Isa Inlier, northwestern Queensland. Aust. J. Earth Sci. 2001, 48, 603–619. [Google Scholar] [CrossRef]
- Belousova, E.A.; Griffin, W.L.; O’Reilly, S.Y.; Fisher, N.I. Apatite as an indicator mineral for mineral exploration: Trace-element compositions and their relationship to host rock type. J. Geochem. Explor. 2002, 76, 45–69. [Google Scholar] [CrossRef]
- Cao, M.; Li, G.; Qin, K.; Seitmuratova, E.Y.; Liu, Y. Major and Trace element characteristics of apatites in granitoids from Central Kazakhstan: Implications for petrogenesis and mineralization. Res. Geol. 2012, 62, 63–83. [Google Scholar] [CrossRef]
- Teiber, H.; Marks, M.A.W.; Arzamastsev, A.A.; Wenzel, T.; Markl, G. Compositional variation in apatite from various host rocks: Clues with regards to source composition and crystallization conditions. J. Miner. Geochem. 2015, 192, 151–167. [Google Scholar] [CrossRef]
- Mao, M.; Rukhlov, A.S.; Rowins, S.M.; Spence, J.; Coogan, L.A. Apatite trace element compositions: A robust new tool for mineral exploration. Econ. Geol. 2016, 111, 1187–1222. [Google Scholar] [CrossRef]
- Krneta, S.; Ciobanu, C.L.; Cook, N.J.; Ehrig, K.; Kontonikas-Charos, A. Apatite at Olympic Dam, South Australia: A petrogenetic tool. Lithos 2016, 262, 470–485. [Google Scholar] [CrossRef]
- Krneta, S.; Ciobanu, C.L.; Cook, N.J.; Ehrig, K.; Kontonikas-Charos, A. The Wirrda Well and Acropolis prospects Gawler Craton, South Australia: Insights into evolving fluid conditions through apatite chemistry. J. Geochem. Explor. 2017, 181, 276–291. [Google Scholar] [CrossRef]
- Krneta, S.; Ciobanu, C.L.; Cook, N.J.; Ehrig, K.; Kontonikas-Charos, A. Rare earth element behaviour in apatite from the Olympic Dam Cu-U-Au-Ag deposit, South Australia. Minerals 2017, 7, 135. [Google Scholar] [CrossRef]
- Ismail, R.; Ciobanu, C.L.; Cook, N.J.; Teale, G.S.; Giles, D.; Schmidt Mumm, A.; Wade, B. Rare earths and other trace elements in minerals from skarn assemblages, Hillside iron oxide–copper–gold deposit, Yorke Peninsula, South Australia. Lithos 2014, 184–187, 456–477. [Google Scholar] [CrossRef]
- Ehrig, K.; Kamenetsky, V.S.; McPhie, J.; Apukhtina, O.; Ciobanu, C.L.; Cook, N.J.; Kontonikas-Charos, A.; Krneta, S. The IOCG-IOA Olympic Dam Cu-U-Au-Ag deposit and nearby prospects, South Australia. In Proceedings of the 14th SGA Biennial Meeting, Quebec City, QC, Canada, 20–23 August 2017; pp. 823–826. [Google Scholar]
- Ehrig, K.; McPhie, J.; Kamenetsky, V.S. Geology and mineralogical zonation of the Olympic Dam iron oxide Cu-U-Au-Ag deposit, South Australia. In Geology and Genesis of Major Copper Deposits and Districts of the World, a Tribute to Richard Sillitoe; Hedenquist, J.W., Harris, M., Camus, F., Eds.; Society of Economic Geologists: Littleton, CO, USA, 2012; pp. 237–268. [Google Scholar]
- Oreskes, M.; Einaudi, M.T. Origin of Hydrothermal Fluids at Olympic Dam: Preliminary Results from Fluid Inclusions and Stable Isotopes. Econ. Geol. 1992, 87, 64–90. [Google Scholar] [CrossRef]
- Bastrakov, E.N.; Skirrow, R.G.; Davidson, G.J. Fluid evolution and origins of iron oxide Cu-Au prospects in the Olympic Dam District, Gawler Craton, South Australia. Econ. Geol. 2007, 102, 1415–1440. [Google Scholar] [CrossRef]
- BHP Billiton. Available online: https://www.bhp.com/-/media/bhp/documents/investors/annual-reports/2016/bhpbillitonannualreport2016.pdf?la=en (accessed on 8 August 2018).
- Reeve, J.S.; Cross, K.C.; Smith, R.N.; Oreskes, N. Olympic Dam copper-uranium-gold-silver deposit. In Geology of the Mineral. Deposits of Australia and Papua New Guinea; Hughes, F.E., Ed.; Australasian Institute of Mining and Metallurgy Monograph: Melbourne, Australia, 1990; pp. 1009–1035. [Google Scholar]
- Creaser, R.A. The Geology and Petrology of Middle Proterozoic Felsic Magmatism of the Stuart Shelf, South Australia. Unpublished Ph.D. Thesis, La Trobe University, Melbourne, Australia, 1989. [Google Scholar]
- Kontonikas-Charos, A.; Ciobanu, C.L.; Cook, N.J.; Ehrig, K.; Krneta, S.; Kamenetsky, V.S. Feldspar evolution in the Roxby Downs Granite, host to Fe-oxide Cu-Au-(U) mineralisation at Olympic Dam, South Australia. Ore Geol. Rev. 2017, 80, 838–859. [Google Scholar] [CrossRef]
- Jagodzinski, E.A. The age of magmatic and hydrothermal zircon at Olympic Dam. In Proceedings of the 2014 Australian Earth Sciences Convention (AESC), Sustainable Australia, Newcastle, Australia, 7–10 July 2014; Volume 110, p. 260. [Google Scholar]
- Ciobanu, C.L.; Wade, B.; Cook, N.J.; Schmidt Mumm, A.; Giles, D. Uranium-bearing hematite from the Olympic Dam Cu-U-Au deposit, South Australia; a geochemical tracer and reconnaissance Pb-Pb geochronometer. Precambr. Res. 2013, 238, 129–147. [Google Scholar] [CrossRef]
- Courtney-Davies, L.; Zhu, Z.; Ciobanu, C.L.; Wade, B.P.; Cook, N.J.; Ehrig, K.; Cabral, A.R.; Kennedy, A. Matrix-matched iron-oxide laser ablation ICP-MS U-Pb geochronology using mixed solutions standards. Minerals 2016, 6, 85. [Google Scholar] [CrossRef]
- Pasero, M.; Kampf, A.; Ferraris, C.; Pekov, I.V.; Rakovan, J.; White, T. Nomenclature of the apatite supergroup minerals. Eur. J. Miner. 2010, 22, 163–179. [Google Scholar] [CrossRef]
- White, T.J.; Dong, Z.L. Structural derivation and crystal chemistry of apatites. Acta Cryst. 2002, B59, 1–16. [Google Scholar] [CrossRef]
- Hughes, J.M.; Rakovan, J.F. Structurally robust, chemically diverse: Apatite and apatite supergroup minerals. Elements 2015, 11, 165–170. [Google Scholar] [CrossRef]
- Hughes, J.M.; Rakovan, J.F. The crystal structure of apatite, Ca5(PO4)3(F,OH,Cl). Rev. Miner. Geochem. 2002, 48, 1–12. [Google Scholar] [CrossRef]
- Goldschmidt, V.M. The principles of distribution of chemical elements in minerals and rocks. The seventh Hugo Müller Lecture, delivered before the Chemical Society on 17th March 1937. J. Chem Soc. (Resumed) 1937, 655–673. [Google Scholar] [CrossRef]
- Pan, Y.; Fleet, M.E. Compositions of the apatite-group minerals: Substitution mechanisms and controlling factors. Rev. Miner. Geochem. 2002, 48, 13–49. [Google Scholar] [CrossRef]
- Rønsbo, J.G. Coupled substitutions involving REE’s and Na and Si in apatites in alkaline rocks from Ilimaussaq, South Greenland, and the petrological implications. Am. Miner. 1989, 74, 896–901. [Google Scholar]
- Hughes, J.M. The many facets of apatite. Am. Miner. 2015, 100, 1033–1039. [Google Scholar] [CrossRef]
- Luo, Y.; Rakovan, J.; Tang, Y.; Lupulescu, M.; Hughes, J.M.; Pan, Y. Crystal chemistry of Th in fluorapatite. Am. Mineral. 2011, 96, 23–33. [Google Scholar] [CrossRef]
- Verdugo-Ihl, M.R.; Ciobanu, C.L.; Cook, N.J.; Ehrig, K.; Courtney-Davies, L.; Gilbert, S. Textures and U-W-Sn-Mo signatures in hematite from the Cu-U-Au-Ag orebody at Olympic Dam, South Australia: Defining the archetype for IOCG deposits. Ore Geol. Rev. 2017, 91, 173–195. [Google Scholar] [CrossRef]
- Morales Ruano, S.; Both, R.A.; Golding, S.D. A fluid inclusion and stable isotope study of the Moonta copper-gold deposits, South Australia: Evidence for fluid immiscibility in a magmatic hydrothermal system. Chem. Geol. 2002, 192, 211–226. [Google Scholar] [CrossRef]
- Schlegel, T.U. The Prominent Hill Iron Oxide-Cu-Au Deposit in South. Australia. A Deposit Formation Model Based on Geology, Geochemistry and Stable Isotopes and Fluid Inclusions. Unpublished Ph.D. Thesis, ETH Zurich, Zürich, Switzerland, 2015. [Google Scholar]
- Chiaradia, M.; Banks, D.; Cliff, R.; Marschik, R.; de Haller, A. Origin of fluids in iron oxide–copper–gold deposits: Constraints from δ37Cl, 87Sr/Sr, and Cl/Br. Miner. Deposita 2006, 41, 565–573. [Google Scholar] [CrossRef]
- Baker, T.; Mustard, R.; Fu, B.; Williams, P.J.; Dong, G.; Fisher, L.; Mark, G.; Ryan, C.G. Mixed messages in iron oxide-copper-gold systems of the Cloncurry district, Australia: Insights from PIXE analysis of halogens and copper in fluid inclusions. Miner. Deposita 2008, 43, 599–608. [Google Scholar] [CrossRef]
- Gleeson, S.A.; Smith, M.P. The sources and evolution of mineralising fluids in iron oxide–copper–gold systems, Norrbotten, Sweden: Constraints from Br/Cl ratios and stable Cl isotopes of fluid inclusion leachates. Geochim. Cosmochim. Acta 2009, 73, 5658–5672. [Google Scholar] [CrossRef]
- Haynes, D.W.; Cross, K.C.; Bills, R.T.; Reed, M.H. Olympic Dam Ore Genesis: A Fluid-Mixing Model. Econ. Geol. 1995, 90, 281–307. [Google Scholar] [CrossRef]
- Cook, N.J.; Ciobanu, C.L.; O’Reilly, D.; Wilson, R.; Das, K.; Wade, B. Mineral chemistry of rare earth element (REE) mineralization, Browns Range, Western Australia. Lithos 2013, 172, 192–213. [Google Scholar] [CrossRef]
- Weng, Z.; Jowitt, S.M.; Mudd, G.M.; Haque, N. A detailed assessment of global Rare Earth Element resources: Opportunities and challenges. Econ. Geol. 2015, 110, 1925–1952. [Google Scholar] [CrossRef]
- GWB Essentials Guide. Available online: https://www.gwb.com/pdf/GWB11/GWBessentials.pdf (accessed on 22 July 2017).
- Migdisov, A.A.; Williams-Jones, A.E.; Wagner, T. An experimental study of the solubility and speciation of the Rare Earth Elements (III) in fluoride- and chloride-bearing aqueous solutions at temperatures up to 300 °C. Geochim. Cosmochim. Acta 2009, 73, 7087–7109. [Google Scholar] [CrossRef]
- van Dongen, M.; Weinberg, R.F.; Tomkins, A.G. REE-Y, Ti, and P Remobilization in Magmatic Rocks by Hydrothermal Alteration during Cu-Au Deposit Formation. Econ. Geol. 2010, 105, 763–776. [Google Scholar] [CrossRef]
- Schmandt, D.S.; Cook, N.J.; Ciobanu, C.L.; Ehrig, K.; Wade, B.P.; Gilbert, S.; Kamenetsky, V.S. Rare earth element fluorocarbonate minerals from the Olympic Dam Cu-U-Au-Ag deposit, South Australia. Minerals 2017, 7, 202. [Google Scholar] [CrossRef]
- Ciobanu, C.L.; Kontonikas-Charos, A.; Slattery, A.; Cook, N.J.; Ehrig, K.; Wade, B.P. Short-range stacking disorder in mixed-layer compounds: A HAADF STEM study of bastnäsite-parisite intergrowths. Minerals 2017, 7, 227. [Google Scholar] [CrossRef]
- Kontonikas-Charos, A.; Ciobanu, C.L.; Cook, N.J.; Ehrig, K.; Ismail, R.; Krneta, S.; Basak, A. Feldspar mineralogy and rare earth element (re)mobilization in iron-oxide copper gold systems from South Australia: A nanoscale study. Miner. Mag. 2018, 82, S173–S197. [Google Scholar] [CrossRef]
- Kolonin, G.R.; Shironosova, G.P. Influence of acidity–alkalinity of solutions On REE distribution during ore formation: Thermodynamic modeling. Dokl. Earth Sci. 2012, 443, 502–505. [Google Scholar] [CrossRef]
- Shironosova, G.P.; Kolonin, G.R. Thermodynamic modeling of REE partitioning between monazite, fluorite, and apatite. Dokl. Earth Sci. 2013, 450, 628–632. [Google Scholar] [CrossRef]
- Shironosova, G.P.; Kolonin, G.R.; Borovikov, A.A.; Borisenko, A.S. Thermodynamic modeling of REE behavior in oxidized hydrothermal fluids of high sulfate sulfur concentrations. Dokl. Earth Sci. 2016, 469, 855–859. [Google Scholar] [CrossRef]
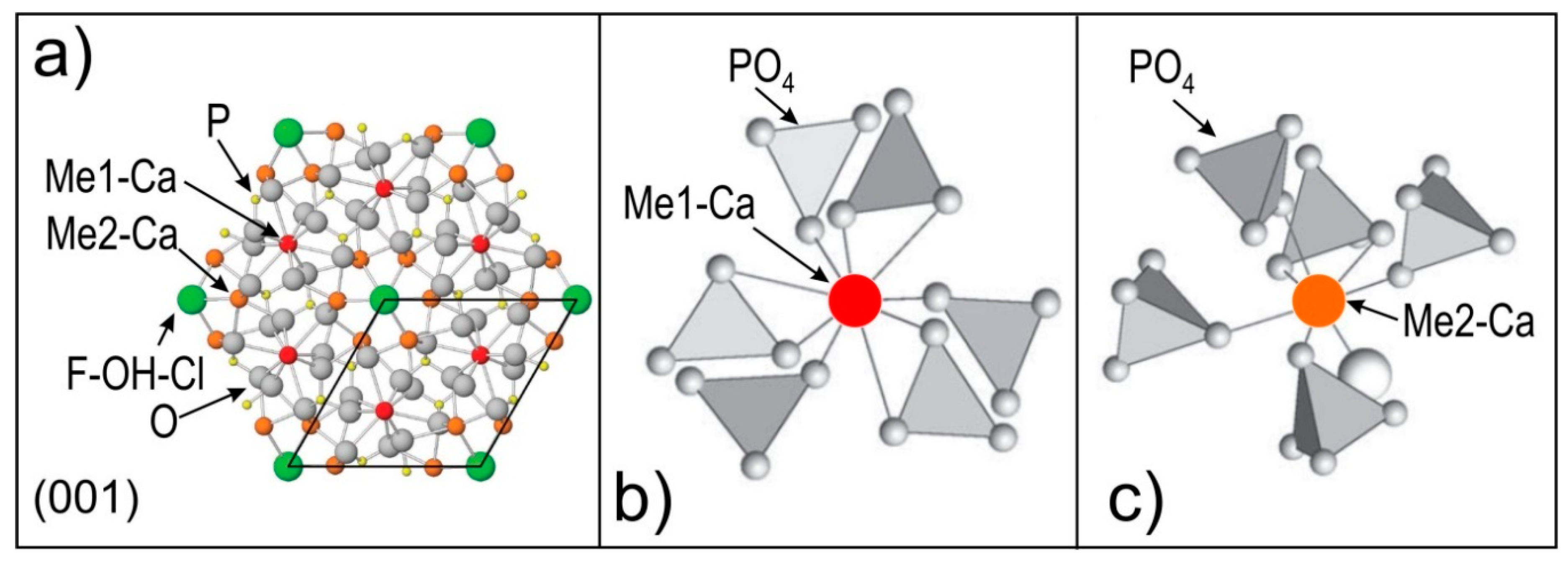
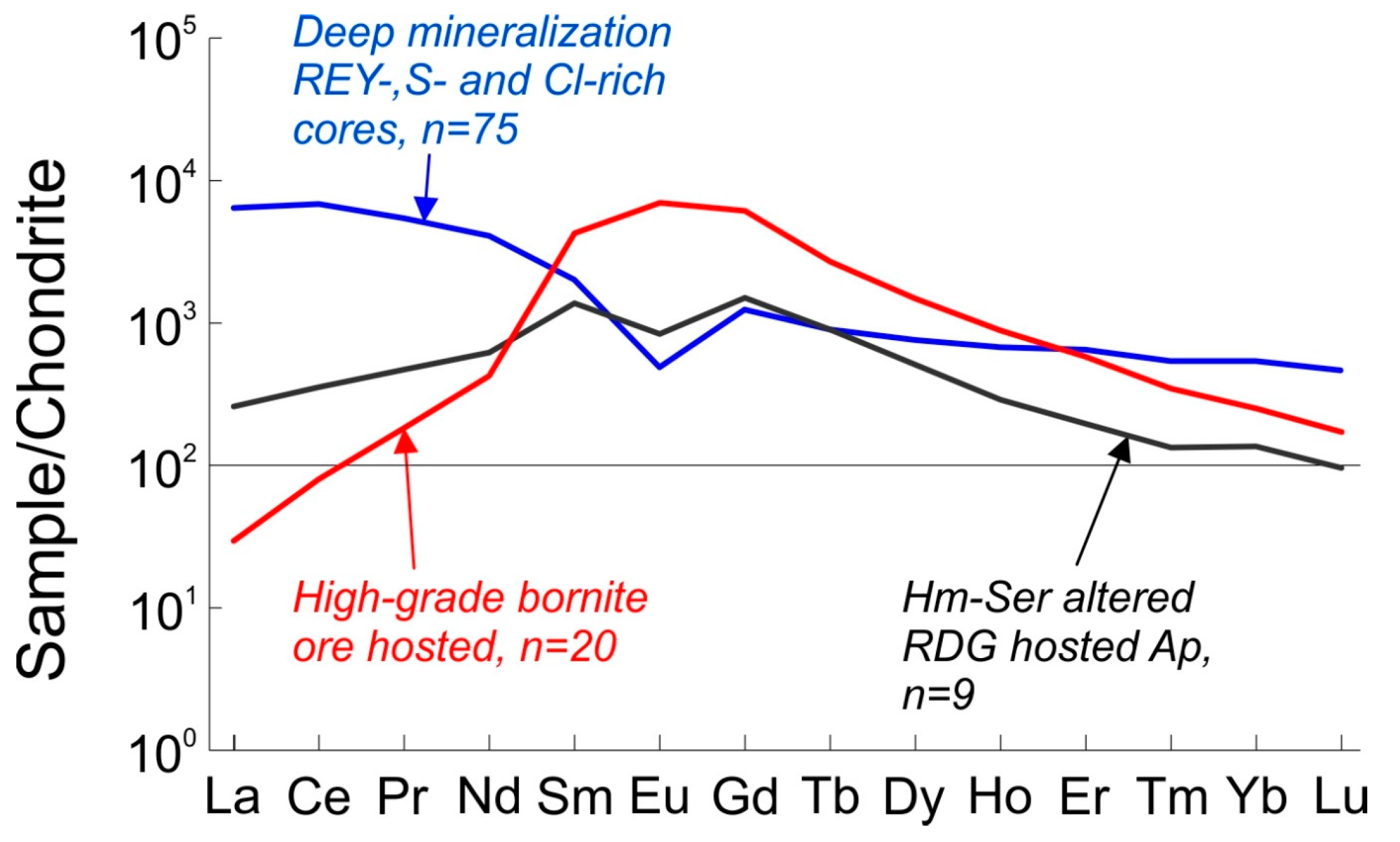

| Apatite in Altered Granite | Ore-Hosted Apatite | ||
|---|---|---|---|
| Deep Mineralization REE + Y-, S- and Cl-rich cores | Hematite-Sericite Altered | High-Grade Bornite Ore | |
| La | 1520 | 84 | 7 |
| Ce | 4192 | 258 | 49 |
| Pr | 504 | 47 | 17 |
| Nd | 1868 | 280 | 194 |
| Sm | 298 | 195 | 631 |
| Eu | 27 | 45 | 391 |
| Gd | 247 | 290 | 1217 |
| Tb | 32 | 32 | 97 |
| Dy | 187 | 125 | 365 |
| Ho | 37 | 16 | 49 |
| Er | 104 | 33 | 92 |
| Tm | 13 | 4 | 9 |
| Yb | 83 | 24 | 39 |
| Lu | 11 | 3 | 4 |
| Case 1 Mt + Py + Cp K-Feldspar Stable | Case 2 Hm + Py + Cp Sericite Stable | Case 3 Hm + Bn Silicates Absent | ||||
|---|---|---|---|---|---|---|
| Model | 1.1 | 1.2 | 2.1 | 2.2 | 3.1 | 3.2 |
| O2 aq (log g) | −36.8 | −36.8 | −31.7 | −31.7 | −31.7 | −32 |
| H+ (pH) | 5.2 | 5.2 | 4.4 | 4.4 | 8.5 | 6.6 |
| NaCl (wt %) | 20 | 20 | 10 | 10 | 5 | 5 |
| Ca (wt %) | 0.61 | 3 | 0.37 | 4 | 1.06 | 3.5 |
| HCO3− (wt %) | 0.37 | 0.37 | 0.94 | 0.94 | 2.40 | 2.40 |
| F- (wt %) | 0.005 | 0.005 | 0.005 | 0.005 | 0.005 | 0.005 |
| SO4− (wt %) | 0.15 | 0.15 | 0.15 | 0.15 | 2.00 | 2.00 |
| Temperature (°C) | 300 | 300 | 300 | 300 | 300 | 300 |
| La (ppm) | 100 | 100 | 100 | 100 | 1200 | 1200 |
| Ce (ppm) | 200 | 200 | 200 | 200 | 1700 | 1700 |
| Pr (ppm) | 21 | 21 | 24 | 24 | 150 | 150 |
| Nd (ppm) | 70 | 70 | 80 | 80 | 393 | 393 |
| Sm (ppm) | 12.4 | 12.4 | 14 | 14 | 41.2 | 41.2 |
| Eu (ppm) | 1.7 | 1.7 | 1.9 | 1.9 | 12.4 | 12.4 |
| Gd (ppm) | 10.3 | 10.3 | 11.8 | 11.8 | 28 | 28 |
| Tb (ppm) | 1.6 | 1.6 | 1.7 | 1.7 | 3.4 | 3.4 |
| Dy (ppm) | 9.5 | 9.5 | 10.3 | 10.3 | 16.7 | 16.7 |
| Ho (ppm) | 1.9 | 1.9 | 2 | 2 | 3 | 3 |
| Er (ppm) | 5.7 | 5.7 | 6.1 | 6.1 | 9.1 | 9.1 |
| Tm (ppm) | 0.5 | 0.5 | 0.7 | 0.7 | 1.2 | 1.2 |
| Yb (ppm) | 5.6 | 5.6 | 6.3 | 6.3 | 8.6 | 8.6 |
| Lu (ppm) | 0.9 | 0.9 | 1.1 | 1.1 | 1.3 | 1.3 |
| % of REE Activity as Cl Complexes | Proportion of REE Activity as Oxide and OH− Complexes | |||||||||||
| Model | 1.1 | 1.2 | 2.1 | 2.2 | 3.1 | 3.2 | 1.1 | 1.2 | 2.1 | 2.2 | 3.1 | 3.2 |
| La | 91.9 | 94.0 | 97.5 | 99.1 | 0 | 3.5 × 10−3 | 6.21 | 4.57 | 0.20 | 0.11 | 100 | 100 |
| Ce | 63.7 | 70.8 | 93.8 | 97.1 | 1.2 × 10−10 | 4.9 × 10−4 | 31.7 | 27.0 | 1.89 | 1.09 | 100 | 100 |
| Pr | 67.0 | 73.6 | 96.1 | 98.2 | 0 | 1.6 × 10−4 | 29.6 | 25.0 | 1.67 | 0.97 | 100 | 100 |
| Nd | 30.7 | 36.9 | 84.6 | 92.6 | 0 | 2.9 × 10−5 | 65.3 | 61.9 | 6.01 | 4.39 | 100 | 100 |
| Sm | 10.2 | 13.1 | 64.5 | 79.7 | 0 | 1.7 × 10−6 | 85.5 | 84.8 | 12.9 | 10.4 | 100 | 100 |
| Eu | 100 | 100 | 100 | 100 | 0 | 0 | 0 | 0 | 0 | 0 | 100 | 100 |
| Gd | 13.3 | 18.3 | 57.3 | 77.1 | 0 | 1.7 × 10−6 | 72.4 | 73.9 | 7.40 | 5.32 | 100 | 100 |
| Tb | 5.04 | 7.65 | 34.4 | 58.8 | 0 | 7.4 × 10−7 | 79.4 | 83.8 | 8.49 | 8.37 | 100 | 100 |
| Dy | 5.96 | 2.02 | 30.3 | 56.0 | 0 | 5.1 × 10−7 | 69.3 | 83.4 | 5.36 | 5.05 | 100 | 100 |
| Ho | 7.82 | 6.79 | 31.2 | 56.5 | 0 | 4.7 × 10−7 | 75.2 | 83.8 | 7.85 | 7.24 | 100 | 100 |
| Er | 1.06 | 1.47 | 16.4 | 34.7 | 0 | 0 | 89.1 | 93.3 | 12.3 | 13.6 | 100 | 100 |
| Tm | 1.30 | 1.80 | 3.72 | 36.0 | 0 | 8.4 × 10−8 | 91.8 | 95.2 | 17.8 | 47.9 | 100 | 100 |
| Yb | 0.60 | 0.82 | 11.2 | 26.7 | 0 | 0 | 93.4 | 97.2 | 20.5 | 24.5 | 100 | 100 |
| Lu | 0.18 | 0.25 | 3.01 | 6.51 | 0 | 0 | 88.7 | 94.1 | 14.0 | 30.7 | 100 | 100 |
| % of REE Activity as F Complexes | Proportion of REE Activity as SO4 Complexes | |||||||||||
| Model | 1.1 | 1.2 | 2.1 | 2.2 | 3.1 | 3.2 | 1.1 | 1.2 | 2.1 | 2.2 | 3.1 | 3.2 |
| La | 1.85 | 1.38 | 1.94 | 0.74 | 2.3 × 10−8 | 0 | 0 | 0 | 0.38 | 0.10 | 3.3 × 10−9 | 1.5 × 10−4 |
| Ce | 4.54 | 2.21 | 4.28 | 1.76 | 3.1 × 10−9 | 7.9 × 10−10 | 0 | 0 | 0 | 0 | 0 | 0 |
| Pr | 3.44 | 1.42 | 2.19 | 0.83 | 4.2 × 10−10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Nd | 4.02 | 1.20 | 5.76 | 2.00 | 1.5 × 10−10 | 1.2 × 10−10 | 0 | 0 | 3.59 | 1.04 | 7.5 × 10−11 | 1.3 × 10−5 |
| Sm | 4.34 | 2.09 | 18.4 | 8.57 | 1.9 × 10−11 | 0 | 0 | 0 | 4.17 | 1.34 | 6.5 × 10−12 | 1.4 × 10−6 |
| Eu | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Gd | 14.3 | 7.77 | 35.3 | 17.5 | 7.5 × 10−11 | 2.9 × 10−10 | 0 | 0 | 0 | 0 | 0 | 0 |
| Tb | 15.5 | 8.60 | 53.8 | 32.8 | 8.5 × 10−11 | 4.4 × 10−10 | 0 | 0 | 3.38 | 0 | 2.9 × 10−12 | 0 |
| Dy | 24.7 | 14.6 | 62.7 | 38.9 | 1.1 × 10−10 | 3.5 × 10−10 | 0 | 0 | 1.73 | 0 | 1.7 × 10−12 | 0 |
| Ho | 17.0 | 9.41 | 59.2 | 36.3 | 8.6 × 10−11 | 1.1 × 10−10 | 0 | 0 | 1.76 | 0 | 1.5 × 10−12 | 0 |
| Er | 9.81 | 5.19 | 69.7 | 51.7 | 2.5 × 10−11 | 7.2 × 10−11 | 0 | 0 | 1.59 | 0 | 3.5 × 10−13 | 7.7 × 10−8 |
| Tm | 6.89 | 2.96 | 74.2 | 10.7 | 2.7 × 10−11 | 8.2 × 10−11 | 0 | 0 | 4.32 | 5.34 | 4.0 × 10−13 | 8.7 × 10−8 |
| Yb | 5.96 | 1.96 | 66.6 | 48.8 | 1.7 × 10−11 | 5.5 × 10−10 | 0 | 0 | 1.69 | 0 | 3.5 × 10−13 | 7.7 × 10−8 |
| Lu | 11.1 | 5.68 | 82.3 | 62.8 | 3.1 × 10−11 | 1.2 × 10−10 | 0 | 0 | 0.68 | 0 | 0 | 2.8 × 10−8 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krneta, S.; Ciobanu, C.L.; Cook, N.J.; Ehrig, K.J. Numerical Modeling of REE Fractionation Patterns in Fluorapatite from the Olympic Dam Deposit (South Australia). Minerals 2018, 8, 342. https://doi.org/10.3390/min8080342
Krneta S, Ciobanu CL, Cook NJ, Ehrig KJ. Numerical Modeling of REE Fractionation Patterns in Fluorapatite from the Olympic Dam Deposit (South Australia). Minerals. 2018; 8(8):342. https://doi.org/10.3390/min8080342
Chicago/Turabian StyleKrneta, Sasha, Cristiana L. Ciobanu, Nigel J. Cook, and Kathy J. Ehrig. 2018. "Numerical Modeling of REE Fractionation Patterns in Fluorapatite from the Olympic Dam Deposit (South Australia)" Minerals 8, no. 8: 342. https://doi.org/10.3390/min8080342
APA StyleKrneta, S., Ciobanu, C. L., Cook, N. J., & Ehrig, K. J. (2018). Numerical Modeling of REE Fractionation Patterns in Fluorapatite from the Olympic Dam Deposit (South Australia). Minerals, 8(8), 342. https://doi.org/10.3390/min8080342






