1. Introduction
Modeling heterogeneous reactions at the interface between mineral surfaces and natural waters provides information about processes such as pollutant transport, transformation, bioavailability, and fate. However, owing to the structural and compositional variety of real mineral surfaces, as well as variable ion concentrations and pH in natural waters, it is difficult to find a favorable balance between model accuracy and complexity. As such, it is necessary to study analog systems in which the structure, composition, and other properties of interest can be precisely controlled and examined in detail. Transition metal oxide surfaces have been long-standing model systems for this purpose [
1,
2]. Building on earlier work on clean single-crystal mineral surfaces studied under ultra-high vacuum conditions [
3,
4,
5,
6], experimental studies of hydrated surfaces have emerged to address questions, such as how exposed surfaces transform under geochemical conditions [
7,
8,
9,
10]. Experimental studies of Al and Fe (hydr)oxide surfaces are prolific [
11,
12,
13,
14,
15,
16,
17], as these materials have a natural abundance and reactivity towards aqueous contaminants. As an example, numerous studies conducted by Catalano and co-workers can be mentioned [
18,
19,
20,
21]. In one study, the (012) plane of the α-Al
2O
3-water interface [
18] was probed through high-resolution X-ray reflectivity experiments and fitting analysis. These experiments concluded that the most probable surface structure has a stoichiometric termination, on which dangling Al bonds are capped with hydroxyl groups (from dissociative water adsorption). In another work, Trainor et al. reported the termination of this surface as being dominated by a “missing-Al” layer structure [
22]. In this surface termination, the five-fold Al layer of the defect-free surface, as proposed by Catalano et al. is removed. Mason et al. later addressed the discrepancy between the two accounts, by using first-principles calculations and thermodynamics [
23]. The modeling work demonstrated that the two different terminations are both thermodynamically favorable, and that surface preparation conditions and measurement settings likely give rise to observations of the two terminations. Experimental and theoretical studies of the isostructural hematite surfaces have also been carried out, resulting in similar conclusions [
24,
25]. More recently, experimental and theoretical studies are building up from the mineral–water interface, in order to obtain structural information about interfacial water ordering [
19,
26].
The robust structural models for mineral–water interfaces, such as the (012) and (001) planes of corundum α-Al
2O
3 and hematite α-Fe
2O
3, form a basis for detailed studies of aqueous contaminant adsorption. As a case study, inner-sphere complexation of divalent Pb on single crystal surfaces has been characterized using grazing-incidence X-ray absorption spectroscopy (GI-XAS). In a series of studies by Bargar and co-workers [
27], the binding of Pb(II) on the (001) and (012) planes of alumina and hematite were interpreted using a bond–valence analysis of the experimental structures. Based on bonding principles proposed by Pauling [
28,
29,
30,
31,
32], and later modeled by Brown [
29], the bond–valence terms
between atoms
i and
j are defined as:
In this formalism,
is a measure of bond strength between two species
i and
j,
B is an empirical parameter, and
is the separation between hypothetical atoms
i and
j. Further,
denotes the tabulated value for the internuclear distance between
i and
j when the bond strength is 1. Some parameters have been previously reported by Brown and Altermatt [
29]. Based on the bond–valence (BV) model, the parameters are determined such that the sum of all
values is equal to the absolute value of the oxidation number for that ion. While there is no rigorous way to relate valence sums to bond energies, it is assumed that structures which yield BV sums close to ideal values are more stable than those in which the sums deviate from ideal values. The way in which the BV model is applied to geochemical surface science is to first consider the hydrated surface structure in the absence of adsorbates (other than water and water dissociation products). The terminal oxygen functional groups of the mineral are the potential reactive sites. Atomic distances between oxygen and its nearest neighbor pairing ions (either the cation(s) of the mineral or hydrogen, the latter using a modified BV form [
1]) are used in the bulk parametrized model to arrive at BV sums. The BV sums then reveal whether the oxygen functional group is under-saturated—and thus likely or plausible to form additional bonds—or saturated. The analysis can be repeated with the addition of adsorbates, and by considering (de)protonation events. The coordination of surface oxygen to a cation or cations is often denoted using Roman numerals, such as O(I) for a singly-coordinated functional group, and protonation can be written in such as O(I)H for a singly-coordinated hydroxyl group. In this fashion, Bargar and co-workers were able to use GI-XAS bond distance information and BV modeling to conclude that, for the case of Pb(II) inner-sphere adsorption on Al
2O
3, the following ranking in sorption complex geometry is expected: O(III)-Pb > O(I)H-Pb > O(II)-Pb. O(II)H-Pb is expected to be over-saturated and thus unlikely to occur.
The BV-based rationalization of sorption complex stability has been used in conjunction with the well-vetted structural models of (012) and (001) alumina–water interfaces, in order to interpret observed differences in reactivity as a function of surface structure. For example, the stoichiometric (012) surface structure exposes O(III)H and O(I)H groups, expected to be reactive, based on BV analysis. The (001) surface is terminated solely by O(II)H groups, which are expected to be saturated and unreactive towards inner-sphere complex formation. In this example, the BV predictions by functional group type offers a plausible interpretation for the experimentally observed trend that the (001) plane is relatively inert (forming mostly outer-sphere complexes with Pb(II)) relative to the (012) plane, which forms inner-sphere complexes.
As recently summarized by Xu and Catalano [
20], the reactivity of oxygen functional groups in aluminum hydroxides can be thought of in terms of interactions with water as well as adsorbates. The pKa values associated with protonation and deprotonation events of O(I)H compared to O(II)H groups supports the inert nature of O(II)H groups, again attributed to saturation arguments. The study went on to use the aluminum hydroxide polymorphs of gibbsite, terminated by O(II)H groups, and bayerite, terminated by a mixture of O(II)H/O(I)H groups, to directly assess reactivity towards arsenate, in terms of surface functional group type. The macroscopic adsorption studies show that the O(I)H-rich bayerite adsorbs more arsenate per normalized surface area than the O(II)H-terminated gibbsite. The results support the idea that reactivity (in terms of tendency to form inner-sphere complexes with adsorbates) tracks with functional group distribution, and that these trends can be conceptualized in terms of oxygen functional group coordination and protonation.
The success of BV-based structure–reactivity relationships has provided a basis for geochemical surface complexation models, such as the charge distribution multisite complexation CD-MUSIC model, to interpret ionic adsorption on mineral–water interfaces [
33]. However, the advent of tractable first-principles modeling of sorption processes has provided a means for electronic structure analysis and interpretation, as well as more details about sorption complex geometry than can be obtained experimentally. Aspects of mineral–water interface reactivity that can be described accurately by first-principles calculations include dynamic bonding, adsorption-induced surface relaxations, and bonding interpretations based on chemical orbital descriptions. For example, in a first-principles molecular dynamics study of the silica water, Leung and co-workers [
34] identified changes in oxygen functional group protonation states over the course of the simulations, which offered a new interpretation of the acid–base behavior of the surface [
34]. Further discussion of recent quantum mechanical modeling contributions to geochemical surface science can be found in the literature [
16,
35,
36,
37,
38].
While computational chemistry approaches to the mineral–water interface structure–reactivity relationship enable a detailed molecular-level understanding of sorption bonds, the use of these methods requires convergence studies with regard to computational parameters and the structural model chosen to represent the system. Density functional theory (DFT) modeling that employs the pseudopotential approach and periodic boundary conditions to model a hydrated metal surface requires preliminary testing in advance of research calculations. Examples include the need to test the pseudopotentials used to represent electron–nucleus interactions, convergence with respect to the energy sampling in
k-space, and how the choice of exchange–correlation function affects the structural and electronic properties of the system. As recently reviewed [
39], some online pseudopotential libraries are not reliable, while others, such as the GBRV [
40] have been shown to enable highly reproducible results.
In terms of the choice of model geometry, so-called cluster models and periodic repeat slab models are two popular categories. When clusters are used to represent metal (hydr)oxide surfaces, the model usually contains an average of two metal atoms with approximately 10–14 oxygen atoms of varying protonation state, often to achieve neutrality. Paul et al. has modeled sulfate adsorption onto Fe clusters. They used Fe clusters that contained two Fe atoms, ten O atoms, and a varying number of hydrogen atoms [
16]. They concluded that both the cluster models and the surface had acceptable bond agreement, using Extended X-ray Absorption Fine Structure (EXAFS) data. However, the long-range interactions are not and cannot be present in the Fe cluster models due to the size constraints. Baltrusaitis et al. have used iron and aluminum clusters to study bicarbonate adsorption [
41]. In their study, two tetrahedral metal atoms were linked by one bridging oxygen atom, and different configurations of bicarbonate were modelled. Another study by Watts et al. employed a tri-nuclear Fe cluster structure, to model As adsorption [
15]. In this Fe structure, two Fe atoms are octahedrally coordinated, while one Fe atom only has five bonds. These authors compared the extended Fe structure, as well as an Fe surface, to EXAFS studies, and concluded that while both systems matched bonding patterns to the EXAFS data, the surface showed precise bond distance agreement compared to the cluster. Another study that questions the reliability of such cluster models is performed by Pierre-Louis et al. These authors used Al, Fe and, Al/Fe structures to model CO
2 adsorption [
42]. This study has modelled monodentate and bidentate CO
2 adsorption on Al
2 clusters, Fe
2 clusters, and Al/Fe clusters (one Al atom and one Fe atom). Upon comparing the results of these computational models with EXAFS data, the authors recognized that these small metal clusters do not correctly mimic the Al/Fe surface adsorption process. However, they are sufficient in determining the bonding interactions of adsorbents. In another study, Pahlavan and Pakiari [
43] have investigated the adsorption of ethylene atop iron surfaces, using mono- and bi-nuclear Fe clusters. The study also focuses on the effect of chlorine addition on the adsorption strength of small organic specimen on iron surfaces. Whilst the small cluster approach has fared successfully for nanoparticle simulations and more [
44], it does not include certain crucial effects, such as surface-mediated lateral interactions and other coverage-dependent behaviors. Neglecting these effects can potentially skew the results unfavorably. Overall, the approach appears to be excessively facile and lacks the elements required to provide a meaningful and realistic insight into the adsorption phenomenon as a whole. It is noteworthy that the justification for the use of small clusters to simulate surface adsorption properties is given rise to by the same rationale that assumes that the surface effects can be considered local, as approximated in the BV model. In other words, the BV model implicitly assumes that the local effects are the only variable that can influence the bonding between the surface and the adsorbate. As such, comparing the cluster model and the periodic model can be advantageous, in the sense that the comparison will provide us with insight as to whether or not this is a valid approximation.
The aim of this study is to further develop the fundamental understanding of arsenate adsorption on hydrated alumina surfaces through first-principles DFT calculations. By choosing a system that is both highly relevant and well-studied, it is possible to assess and compare the DFT results with experimental information and long-standing BV arguments about reactivity. This work also compares the results of periodic slab models and cluster models of aluminum hydroxide-arsenate complexes, which offer the modeling community an assessment of the strengths and weaknesses of the two model geometries. Our small aluminum cluster contains two Al atoms, ten O atoms, and enough H atoms to maintain the charge neutrality principle. We hypothesize that the adsorption energy cannot be the same on both the surface and the clusters, due to their inherent structural differences.
Arsenic (As) contamination of ground water is a global problem of high profile. It is considered to have influenced more than 137 million people in 70 countries. As is one of the most toxic ions found in drinking water [
45,
46]. Arsenic poisoning is more commonplace in continents from Southeast Asia, such as Bangladesh, Vietnam, and India [
47,
48,
49,
50]. Negative health impacts caused by As include respiratory issues, cardiovascular disease, diabetes, and skin and lungs cancers, and As poisoning is potentially fatal [
51,
52,
53,
54]. As can exist in a range of oxidation states, depending on the environmental systems. It is most commonly found in the form of a +3 or +5 cation, with the former cation being more toxic than the latter [
55]. Water in nature tends to have a pH range of 4–9. In water, As(V) is more stable than As(III). Wilson et al. have reported that within a pH range of about 2–7, H
2AsO
4− is the stable form of As(V), whereas at a pH above 7, HAsO
42− is the most stable form [
55].
There is a consensus in literature as to how arsenate binds to aluminum or iron surfaces, based on EXAFS data [
11,
12,
13,
14]. When arsenate binds to α-alumina, γ-alumina, and gibbsite, these studies reveal that arsenate preferentially binds to the aluminum surface in a bidentate, binuclear manner (which can also be called corner-sharing). This means that the As binds to two oxygen atoms, which are bound to two separate Al atoms. This type of configuration will be referenced as bidentate binuclear (BB) throughout this paper. Arsenate adsorption onto iron oxide surfaces is also found to be more favorable in a bidentate binuclear configuration [
15,
16,
17]. In a comprehensive study done by Watts and colleagues, the adsorption of arsenic atop mineral substrates and its current state in the literature has been reviewed. Part of this work is devoted to systematically analyzing the influence of surface charge, hydration, and oxidation states on adsorption geometries and energetics of arsenic onto iron-(oxyhydr)oxide models [
15]. The work has concluded that properties such as reaction rates, thermodynamics, and structural results are biased towards the choice of the DFT method and should be further validated. On the experimental end of the spectrum, Catalano and co-workers have investigated the adsorption of arsenate on the (012) planes of alumina and hematite using X-ray scattering measurements [
21]. Their work concludes that arsenate adsorption on the aforementioned surfaces is bimodal, namely, inner- and outer-sphere complexes. However, the authors have also commented that it is experimentally difficult to determine whether or not the outer-sphere arsenate is occurring in the presence of inner-sphere effects. Nonetheless, it has suggested that the inner-sphere adsorption takes place through bridging bidentate ligation, in agreement with the pertinent literature. The study has also revealed that the average Al–As distance for the inner-sphere adsorption is ~3.2 Å. EXAFS studies show that the As(V)–O
surf bond distance on α-alumina, gibbsite, and γ-alumina are 1.69 ± 0.005 Å, 1.68 ± 0.02 Å and 1.69 ± 0.01 Å, respectively. For all these surfaces, the coordination number of As is ~4 [
12,
13,
14]. Using bond geometry analysis, we modelled a variety of configurations for As adsorption in order to compare EXAFS bond distances with our computational studies.
2. Materials and Methods
Structural calculations of α-Al
2O
3 (012) and small Al clusters were carried out using DFT, as implemented in the DMol
3 code developed by Delley [
56,
57]. Aperiodic all-electron DFT calculations were performed using the generalized gradient approximation (GGA) of Perdew, Burke, and Ernzerhof (PBE) [
58], with a double-numeric-plus polarization atom-centered basis set. A real-space basis set cutoff of 4.50 Å was used. Lattice optimizations for the bulk α-Al
2O
3 were converged with respect to
k-points using a Monkhorst-Pack (MP) grid of 4 × 4 × 4 to sample the Brillouin zone. The optimized lattice constants are 4.821 Å (+1.3%) and 13.111 Å (+0.9%) for alumina. These values are in excellent agreement with experimental data (as indicated in parentheses) [
59]. Our lattice parameter values are also consistent with previously-reported DFT-GGA results [
60,
61,
62,
63,
64].
All surface and cluster geometry optimization calculations were carried out with aqueous effects, accounted for through the Conductor-like Screening Model (COSMO). This scheme applies the dielectric constant chosen to model water that can simulate environmental conditions [
65]. When using COSMO, the cluster is placed into a cavity within the implicit water, as determined by the solvent dielectric constant. The charge distribution of the cluster polarizes the dielectric continuum. The response to the medium is described by screening charges on the cavity’s exterior. The structural optimizations used a convergence criterion of 0.03 eV/Å.
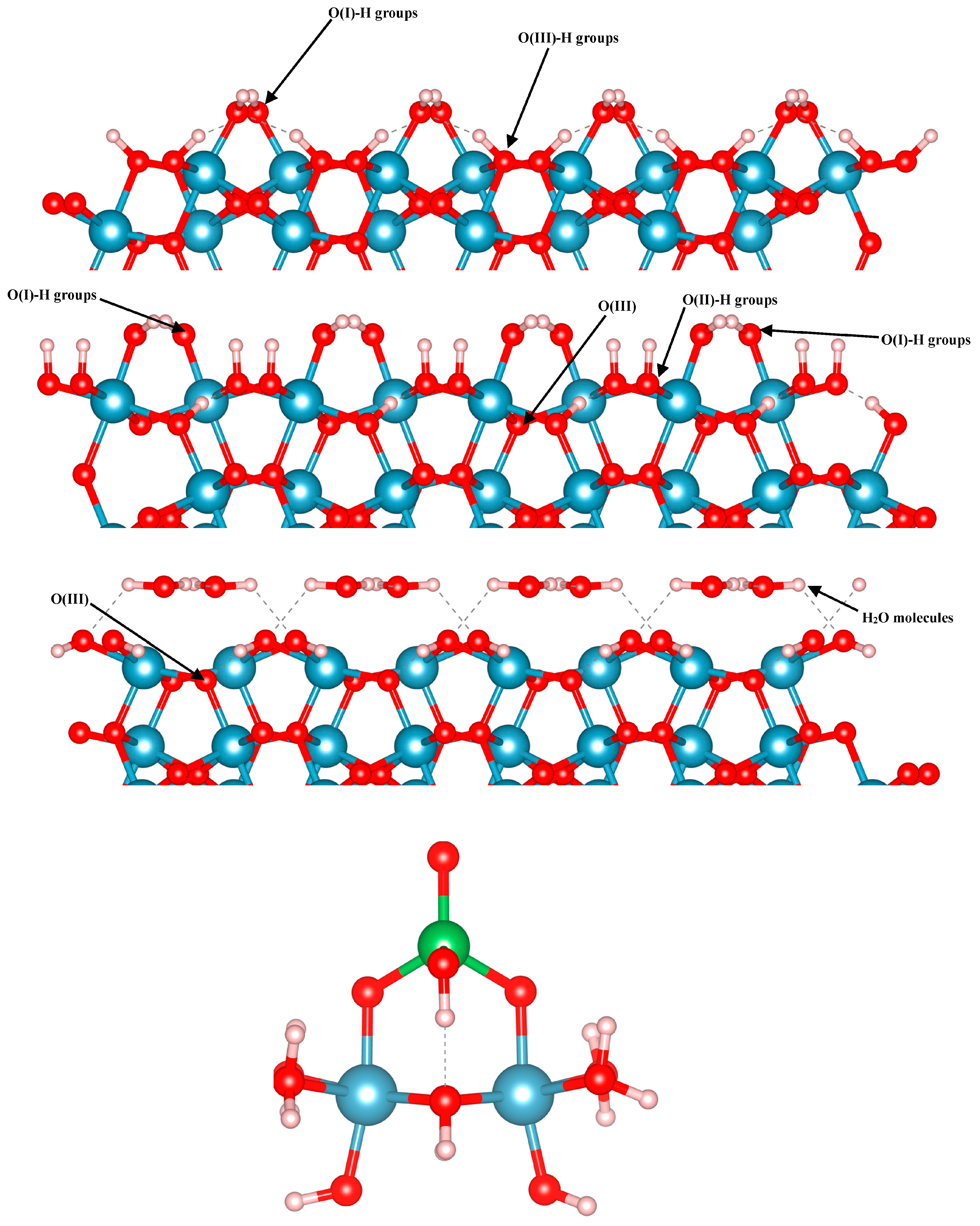
In the present work, we focused on arsenate adsorption binding to three different terminations of the (012) alumina surfaces, as well as on small Al clusters in multiple configurations. Using the alpha-numeric surface stoichiometry naming scheme of Lo et al. [
24], we modelled arsenate on the C3, C4, and A3 terminations of the (
) surface (
Figure 1). For the slab calculations, 2 × 2 supercells were used, and the
k-point density was appropriately reduced to 2 × 2 × 1. With a surface area of approximately 100 Å
2, this rectangle-shaped slab accommodates a surface coverage of 0.06 atoms/Å
2. The three surface terminations are shown in
Figure 1. These surfaces differ in terms of the type(s) of exposed oxygen functional groups. The C4 and C3 surfaces have a missing layer of Al cations compared to the A3 surface. The A3 and C3 surfaces are capped with hydroxyls, while the C4 surface contains water groups on its top and bottom. With these differences, the C3, C4, and A3 slabs consist of 12, 12, and 14 O layers, and 6, 6, and 8 Al layers, respectively. In its bare form, A3 termination has singly- and triply-coordinated O (O(I) and O(III), respectively) atoms on its outermost layer. C3 and C4 however, have singly-, doubly- and triply-coordinated O atoms on their topmost layer (O(I), O(II) and O(III), respectively). These surfaces are ideal for examining the adsorption of arsenate onto the (012) facet of Al
2O
3, due to their stabilities and range of exposed oxygen functional groups. These three surfaces are the most energetically favored terminations of the (012) facet in the aqueous environment, as per Mason et al. [
23]. For all these three surfaces, 25 Å of vacuum space was added to separate the periodic images along the
c direction. We modelled arsenate adsorption in three different configurations on each surface. Each surface contained inversion symmetry, so there was one arsenate ion bound to each side of the surface, as recently demonstrated to be appropriate for an accurate representation of surface electronic structure [
66].
The small aluminum hydroxide cluster models are composed of two Al octahedra, which contain bound hydroxyl and bound water groups so that the clusters remain neutral. This structure was based on cluster model figures in previously-reported literature, and is also shown in
Figure 1 [
16,
42,
67]. We modelled arsenate adsorption in multiple configurations to compare with the surface complex models, and in all cases the cluster models are overall charge neutral.
In the periodic slab model, on each surface, As(V) surface complex geometries were initiated to explore different possible adsorption configurations, and to span bonding environments involving the various types of oxygen functional groups. Following the language in current literature, arsenate can bind in a bidentate mononuclear (BM) fashion or a bidentate binuclear (BB) one [
12,
13,
14]. A BM adsorption occurs when the two oxygen atoms bound to the arsenate are bound to the same Al atom. This configuration can also be labeled as edge-sharing. A BB adsorption occurs when the two oxygen atoms bound to the arsenate are bound to two different Al atoms. For the cluster models, we tested three different BM and one BB conformers. For all three surface models, we examined two different BB configurations and one BM configuration. For the single protonation surfaces and the cluster calculations, we used Equations (1a) and (1b), respectively. The adsorption energy,
Eads, is determined using the DFT total energy information, appropriately weighted by stoichiometric coefficients, and reported per As(V) surface complex.
3. Results and Discussion
The modeled adsorption results are analyzed in terms of optimized geometry, energetics, and electronic structure. Truncated side views of the optimized structures are shown in
Figure 2 (A3),
Figure 3 (C3), and
Figure 4 (C4). The local geometry of the most favorable As configuration on the A3, C3, and C4 structures is shown in
Figure 2,
Figure 3 and
Figure 4. In
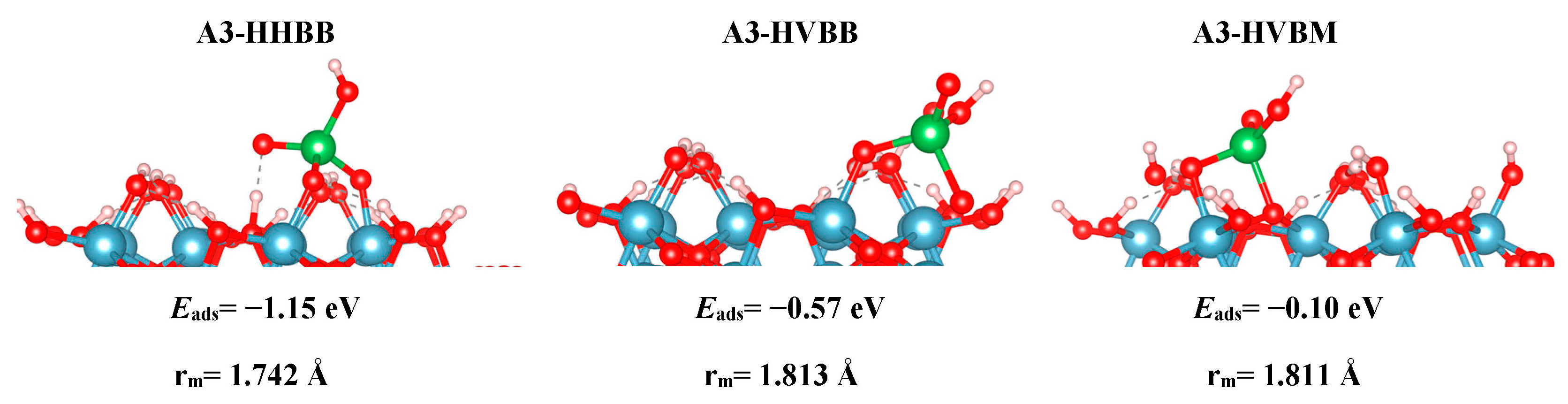
Table 1, we report the adsorption energies for all modeled surfaces using Equations (1a) and (1b). We use a naming scheme for all our structures that will now be described. For the three A3 structures, we use the names HHBB, HVBB, and HVBM, which represent a hill–hill bidentate binuclear structure, a hill–valley bidentate binuclear structure, and a hill–valley bidentate mononuclear structure, where a hill signifies an O atom from the top surface O layer, and valley signifies an O atom from the second O surface layer.
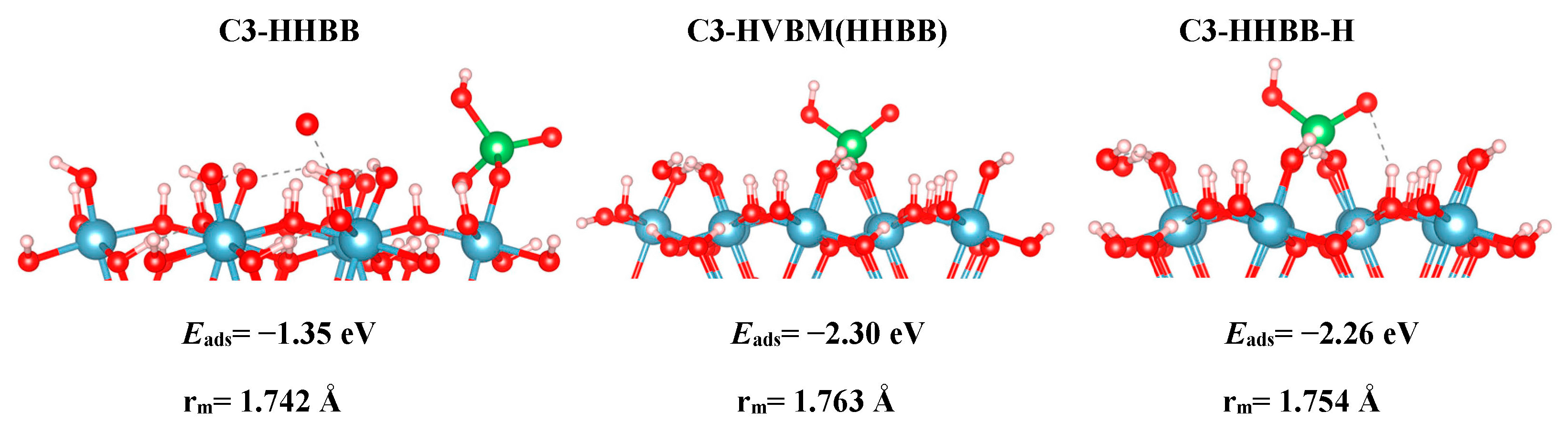
For the C3 surface, we modelled an HHBB and HVBM structure, which represent a hill–hill bidentate binuclear structure and a hill–valley bidentate mononuclear structure. The HVBM structure optimizes to a HHBB (hill–hill bidentate binuclear) configuration. Thus, we call the HVBM structure HVBM (HHBB). After optimization, the major difference between C3 HHBB and C3 HVBM (HHBB) is the location of certain H atoms. When the HVBM (HHBB) structure optimizes, proton rearrangement occurs and ultimately makes the C3 HVBM (HHBB) structure more favorable than C3 HHBB. This is evident from their respective adsorption energies. The C3 HVBM (HHBB) has an adsorption energy of −2.30 eV, while the adsorption energy for the C3 HHBB configuration is −2.26 eV. We rearranged the protons on the C3 HHBB surface to better resemble the C3 HVBM (HHBB) surface. We call this surface C3 HHBB-H, for a hill–hill bidentate binuclear structure with a proton rearrangement.
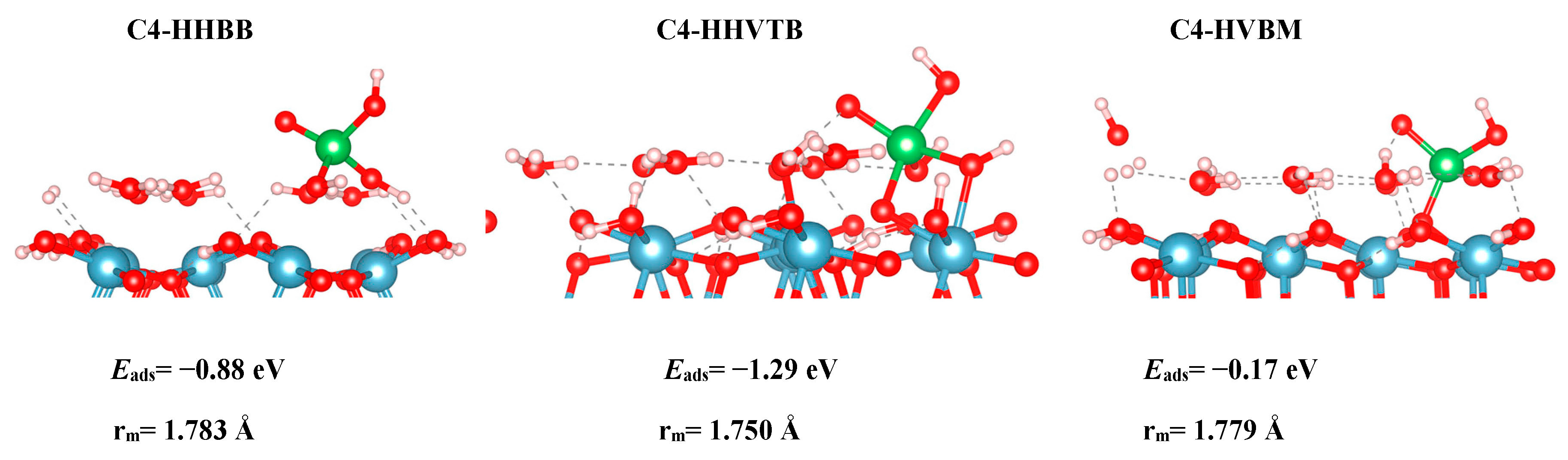
Initially, we chose to model two As(V) complexes on the C4 surface, HHBB and HVBM, which represents hill–hill bidentate binuclear and hill–valley bidentate mononuclear configurations. We realized that the way in which the arsenate is situated on top of two surface waters for the HHBB configuration will result in a bidentate or tridentate bonding to the surface. We denoted the HHBB structure that resulted in a tridentate configuration on the C4 surface as HHVTB. This structure represents a hill–hill–valley tridentate binuclear configuration. The distance between the hill O and O valley is 2.39 Å in the optimized C4-HHVTB configuration. In this configuration, arsenate is experiencing a significant amount of distortion. The coordination number for arsenate is almost 5 in a trigonal bipyramidal environment. This can be observed in the As–Osurf–As angle being 92.6°, which is far from the ideal tetrahedral angle of 109.5°.
Based on the DFT results, we can note reactivity trends in the As(V)/Al
2O
3 surface models. The reaction energies, as reported in
Table 1 for all systems, suggest that a BB configuration is more favorable than a BM configuration. For the A3 surface, the two BB configurations are 0.47 eV and 1.05 eV lower in energy, respectively, than the HVBM structure. For the C3 surface, the BM configuration optimized to a BB configuration, thus resulting in a BM configuration not being stable for the C3 surface. For the C4 surface, the two BB configurations are 0.71 eV and 1.12 eV lower in energy than in the BM configuration, respectively.
We also found a trend between the hill–hill (HH) and the hill–valley (HV) configurations, with the HH configurations being more favorable than the HV configurations. For the A3 structure, the HHBB structure was the most favorable by at least 0.58 eV, compared to the HV structures. For the C3 surface, once again, an HV configuration could not be optimized. The HV configuration optimized to a HH configuration. For the C4 surface, the HH configuration is more favorable than the HV configuration by 0.71 eV. However, the most favorable C4 surface was seen as the arsenate forms a tridentate configuration and binds to two hill oxygen atoms as well as one valley oxygen atom.
Even though
Table 1 shows that there is a significant energy difference between the BB and BM, as well as the HH and HV configurations, we do not see a significant difference in the bond lengths between the surface/cluster O atom and the As atom. We label this as As–O
surf distance. We report our findings in
Table 2. For A3, we find that the most favorable structure (HHBB) has the shortest As–O
surf bond length by 0.071 Å. For the most favorable C3 structure, the As–O
surf bond length is longer by only 0.021 Å. It is hard to compare the separations in the bonding of the C4 structure, since one structure forms three bonds to the surface, while two structures only form two bonds to the surface. The structure that binds in a tridentate fashion has longer bond lengths than the bidentate configurations.
The As–O
surf distances range from 1.718 Å to 1.870 Å for the most favorable structures. All these distances are in agreement with the experimental value of 1.69 Å [
13]. Although this value is measured for a microscopic sample spanning planes other than the (012), the agreement is reasonable.
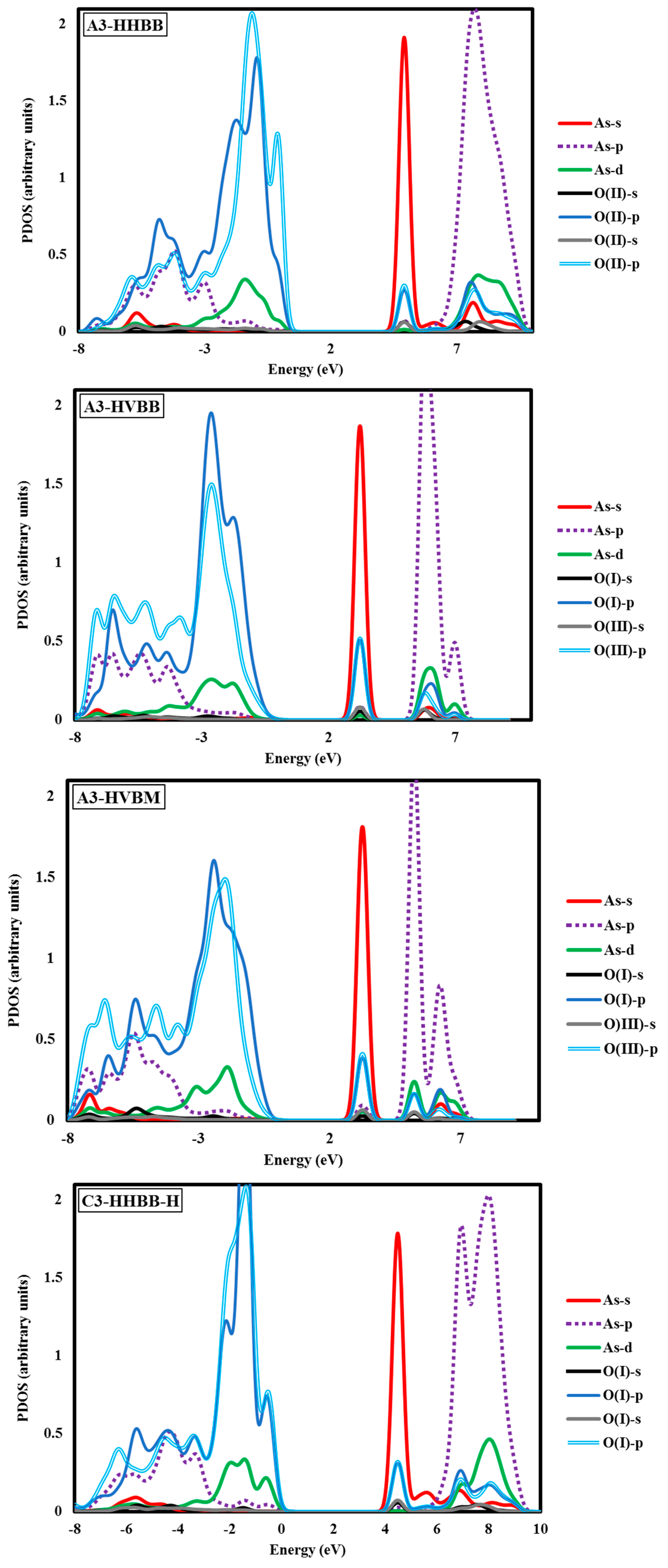
Electronic structure analyses were carried out for arsenate-adsorbed surface terminations in their most energetically-preferred forms, namely, A3-HHBB, C3-HHBB-H, and C4-HHVTB. The analyses were done to characterize the bonding nature between the adsorbate and the surfaces. Projected density of states (PDOS) calculations were performed to examine the As–O bonding. Covalent interactions can be inspected by means of PDOS calculations, by noting the intensity of projections onto different states (such as the oxygen p states and arsenate d states) over common energy ranges. The fractional fillings of states can also be deduced from the PDOS, by considering the relative area under the PDOS, below the Fermi level, relative to the total area, providing information about ionization. The hybridization of As in AsO
43− is sp
3d. As such, we have plotted the s, p, and d states of As and the s and p states of the O atom of the surface attached to the As. The PDOS graphs of the optimized configurations of arsenate atop alumina are plotted with respect to their intensities in
Figure 5 It should be kept in mind that the A3-HHBB, C3-HHBB-H, and C4-HHVTB plots are for singly-protonated structures, and the Fermi level is offset to 0.00 eV. The Fermi energy level is offset to 0.00 to obtain the relative energy changes of various states more easily and clearly.
The A3-HHBB As(V)/Al2O3 complex is the most favorable on the A3 surface, with Eads = −1.15 eV. Only singly-coordinated oxygen functional groups form bonds to As in this corner-sharing configuration, with distances of 1.718 Å and 1.766 Å.
Based on the relatively favorable adsorption energy, common functional group type through which As binds, and similar bond distances, we expect that the PDOS of the two oxygen atoms will reflect favorable, similar bonding patterns. As shown in
Figure 5, the HOMO state has a significant contribution from As d orbitals between −4.10 eV and +0.68 eV. Also, the LUMO states have a certain degrees of d orbitals between 6.80 eV and 9.52 eV. This is consistent with a partially-filled As d-band. Two sharp intense peaks were observed at ~−9.52 eV and ~+5.44 eV. We interpret these peaks as the result of an overlap between As s and O p orbitals. The superposition of As and O p states was observed over broader energy ranges between −8.16 eV and 0.0 eV, as well as between 6.80 eV and 10.89 eV. The latter peak was of higher intensity as compared to the former.
Another noticeable aspect of this chart is the interaction between the As d and O p orbitals that occurs between 6.80 and 10.89 eV. Examining the C3-HHBB-H PDOS (
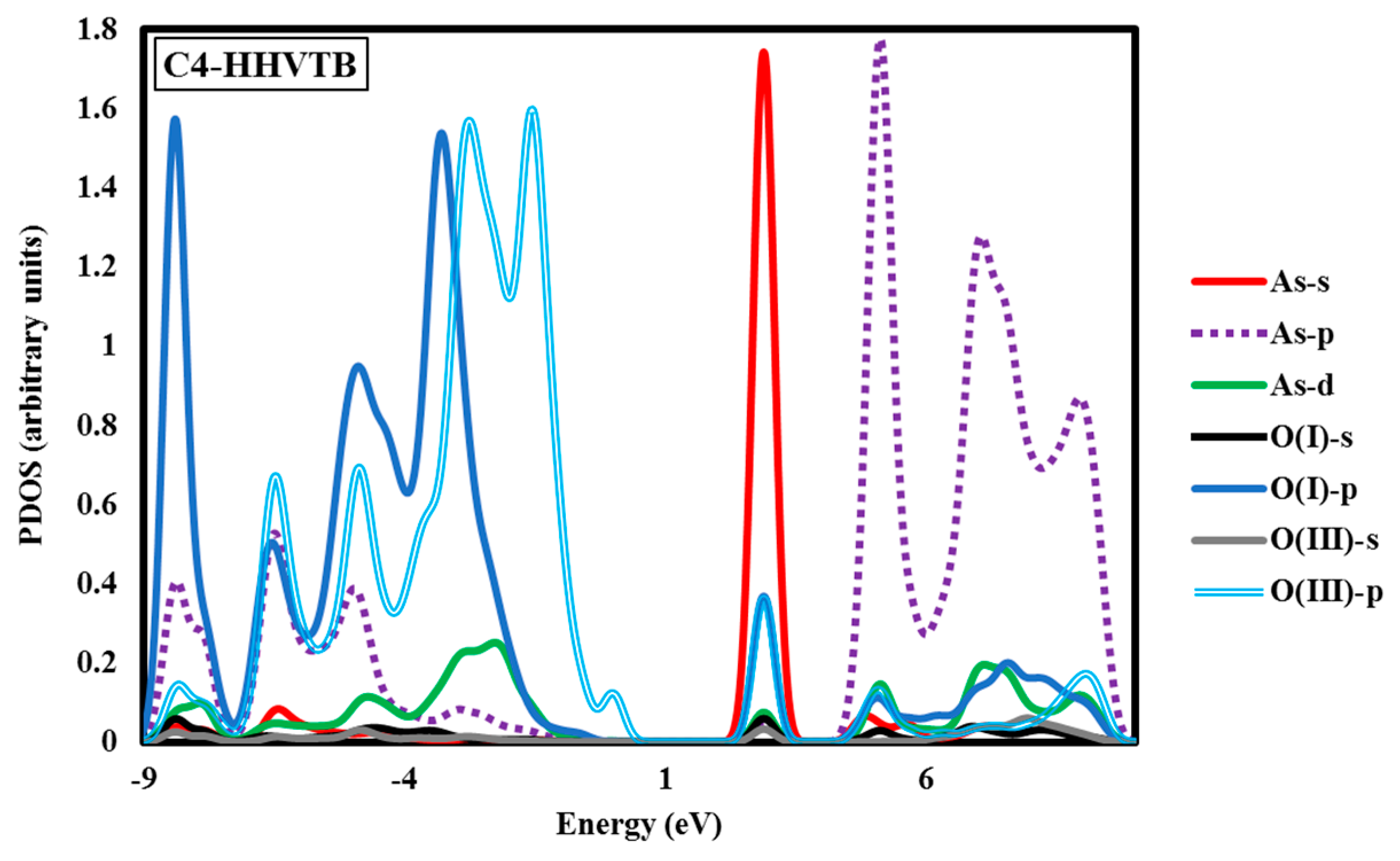
Figure 5), we see that the overlap of the p states of O and As occurs within the range of −8.16 eV to 0.00 eV, and to a far lesser extent between 5.44 eV and 10.89 eV. The overlap between O p and As d states falls within the same range as As p and O p, as well as within 2.72 eV and 0.00 eV. Overall, the PDOS for the C3-HHBB-H configuration follows the same general trends, as compared to the one for A3-HHBB. However, the C4-HHVTB structure is different from the A3-HHBB and C3-HHBB-H, in that the As is bound to two different types of surface O atoms. Hereafter, the surface O atoms of C4-HHVTB will be labeled as O(I) (for lower-layer surface O) and O(II) (for upper-layer surface O). Therefore, acronyms O(II)-s and O(I)-p stand for the s state of upper-layer surface O and, p states of lower-layer surface O, respectively. Interestingly, O(II)-p and O(I)-p superimpose on one another in several regimes, such as at 2.72 eV and 5.44 eV. As p and O(II) p show the same behavior at −6.80 eV. On the other hand, except for the region close to −6.53 eV, the remainder of the bonding regime (below the Fermi level) exhibits different levels of overlap between the As p states and those of O(I), compared to As p states and O(III) p states. In other words, whenever the peaks of As p states are close to that of O(II) p states, they are far less similar to peaks of O(I) p states, and vice versa. This is due to the fact that O(I) and O(II) are situated in two different coordination environments (singly-coordinated for O(I) while doubly-coordinated for O(II)). Comparing these three structures, it can be concluded that the energy matching found between the surface oxygen states and those of the As adsorbate states supports the fact that these three structures are the most energetically-favorable adsorption configurations.
The DFT values of
Eads for the As(V)/Al
2O
3 complexes, modeled on the A3 surface, span more than 1 eV. We inspected the PDOS and sorption complex geometries to find an explanation for this wide energy range. However, the PDOS plots for A3-HHBB, A3-HVBB, and A3-HVBM show no major differences (see
Figure 5). As previously noted, the As–O bond distances did not display variations to explain the trend in the values of
Eads. However, the geometry of the adsorption complexes does show that the tetrahedrally coordinated As(V) undergoes significant distortions in the less-favorable configurations. We interpret the adsorption-induced perturbations in the As(V) tetrahedral angles to be the root cause for noticeable fluctuation in values of
Eads. For instance, the O
surf–As–O
surf angle is very close to its ideal value of 104.5° for the A3-HHBB structure (105°), which is energetically preferred. The same angles for A3-HVBB and A3-HVBM are 101.5° and 88.5°, respectively. Thus, while the PDOS shows that ultimately the favorable As–O overlap is achieved, doing so requires distortion from the ideal T
d symmetry, and thus the adsorption becomes less energetically favorable.
The above case study demonstrates that As(V)/Al
2O
3 structures with significantly varying
Eads can have similar PDOS. This suggests that arsenate can form covalent bonding interactions with surface oxygen atoms, even when distorted considerably from ideal T
d geometry. We also wanted to analyze the PDOS for incidents in which As–O bonding gives rise to distinct PDOS features. Owing to the variety of oxygen functional groups involved in As bonding, we chose the C4-HHVTB structure with one acidic H atom on the adsorbate. The PDOS plot for this structure is shown in
Figure 5. The C4-HHVTB conformer is bound to two different surface O atoms, two doubly-coordinated and one triply-coordinated. In the PDOS plot, we have only included the overlap between the charge densities of the non-hydrated, singly-coordinated O and the doubly-coordinated O on the surface of the As atom of the arsenate. The separation between the As atom and the O(II) (i.e., the doubly-coordinated O) is 1.840 Å, whereas the distance between the As and the O(I) (the singly-coordinated O) is 1.755 Å. Interestingly, the PDOS shows an energy shift of approximately 0.60 eV towards the more positive regime of the energy spectrum for O(I), as compared to O(II). In other words, although BV theory would dictate that the longer bond (As–O(II)) is thought to be weaker than the shorter bond (As–O(I)), the PDOS diagram shows more destabilization for the shorter bond (As–O(I)) as compared to the longer one (As–O(II)). This finding is in line with the results of an earlier work reported by Ramadugu and Mason [
68], regarding the violation of direct bond length–bond strength arguments in Sb(V)/Al
2O
3 structures.
Another interesting aspect of this PDOS is the distribution of the As d states. The relatively small amount of d in the bonding states is due to the presence of d states in the sp
3d hybridized atomic orbitals, and the remainder of the d states in the anti-bonding region is attributable to empty d states of the As atom. Using literature parameter values [
27], we computed the BV sums for As in all of the DFT-optimized geometries. These values are collected in
Table 3. As it can be seen in
Table 3, the BV sum values are notably smaller than the oxidation state of the As (i.e., +5). Based on the BV approach, this outcome will mean that As is under-saturated. This can be due to the fact that GGA-PBE method systematically underestimates the bond energy, which will in turn result in overestimating the bond lengths [
69,
70,
71]. Another possibility for the underestimation of the As BV sum is the fact that the chemical environment of As(V) in the surface complex is unlike that of bulk As(V) oxides used to parametrize the BV model.
However, even taking into account a possible systematic error, due to differences between experimentally determined bulk parameters and DFT surface results, there is no direct correlation between the adsorption energies and the BV sums for As.
The present study can be compared to previous work in which the adsorption of Sb(V) on the same alumina surfaces was investigated using the same DFT methods [
69].
Based on the results of this study, the adsorption of Sb is energetically preferred for bidentate and tridentate conformers. While Sb(V) and As(V) have a common electron configuration of sp3d, the higher coordination number of the antimony means that the surface complex maintains more distal ligands. While both adsorbed species exhibit considerable distortions from ideal angles, as discussed, the impact is different. In the case of Sb(V)/Al2O3, the Sb–Osurf bonds are not able to achieve desirable overlap in the distorted structures, as confirmed by the PDOS analysis. In the case of As(V)/Al2O3, the overlap is ultimately comparable, regardless of distortion of the As coordination environment in the surface complex. We interpret this disparity in terms of the differences in coordination number. The adsorption of arsenate, a tetrahedrally-coordinated oxyanion, creates an adsorption environment with a lower symmetry as compared to Sb.
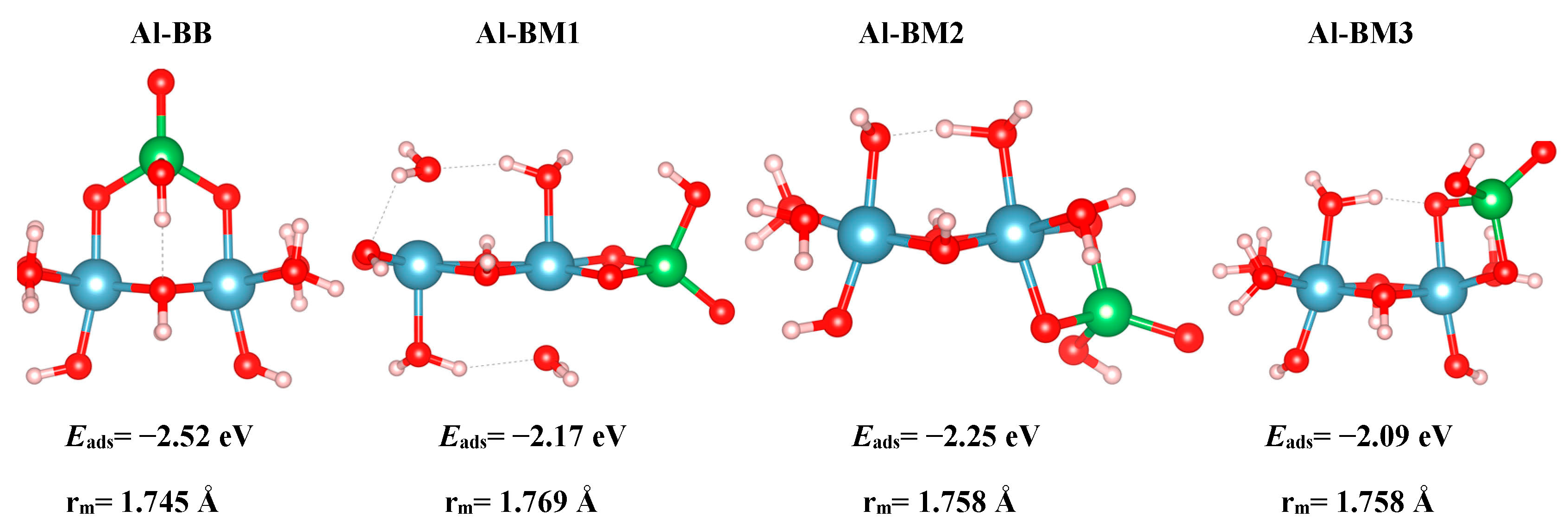
Finally, we discuss the results of the cluster models. One BB As(V) configuration and three BM As(V) configurations for the Al clusters are modelled, and the optimized geometries are shown in
Figure 6. Inspection of the As–O bond distances in
Table 2 shows that for the cluster model, the distances are generally longer than for the slab model. In both the small cluster model and the periodic slab model, the Al–O
surf distance for the adsorbate-free species is shorter than that of arsenate-adsorbed one. The Al–O
cluster axial separation is 1.816 Å for the freestanding cluster, whereas the same distance for the As-adsorbed complex is 1.882 Å. The Al–O(I) distance for the A3 bare surface is 1.815 Å. The same distance for the A3-HHBB configuration is 1.867 Å and 1.827 Å for the two surface O(I) atoms involved in the inner-sphere adsorption environment. This bond elongation upon adsorption is consistent with what is observed for the slab model. However, the bond elongation in the cluster model is greater than that of the surface. We attribute this to the fact that the slab model is more rigid than the flexible small cluster model.
The results of As(V) adsorption to the cluster models also provides an opportunity to compare the results quantitatively and qualitatively to those calculated for the surface. In this sense, we note that the Al-BB cluster model is most similar to the A3HHBB surface model, in that both can be described as corner sharing or bridging bidentate complexes. The Al–BM1-3 are all edge sharing, and thus comparable to the A3-HVBM surface complex. While both the cluster and surface models predict BB-type complexes to be energetically favorable, relative to the edge-sharing BM type, the absolute and relative values of Eads vary considerably. Specifically, while the A3HHBB complex is favored by 1.05 eV relative to the AsHVBM complex, the cluster A1BB complex is only favored by 0.27–0.43 eV. Furthermore, the values of Eads for the A3HHBB is −1.15 eV, while that of the analogous Al-BB is −2.52 eV, or more than twice as large in magnitude. The Ocluster–As–Ocluster angle was found to be very similar to that of a freestanding Td structure (104.6°) in the BB configuration, for which the adsorption energy was computed to be −2.52 eV. This configuration was also found to be the most stable one amongst our various clusters. On the other hand, the least energetically favorable structure, BM3, with an adsorption energy of −2.09 eV, exhibited an Ocluster–As–Ocluster angle of 92.14°. This steric hindrance has resulted in the lack of energetic favorability of this configuration.
For the Al clusters, the BB configuration has the shortest A–O
cluster bond length of 1.745 Å. Our As–O
cluster separations are between 1.744 Å and 1.772 Å. Hence, all of our calculated As–O
cluster distances are not only in agreement with their experimental counterpart [
13], but also are similar to our computed As–O
surf separations. In an arsenate-free cluster, the Al–O distance is 1.816 Å, whereas in an arsenate-adsorbed Al-BB cluster, this distance is 1.882 Å.
The agreement between the bond distances for the cluster model and the experimental result is also observed in the results of the work done by Watts et al. [
16]. Based on their study, different configurations of the arsenate on a binuclear Fe cluster and a periodic α-goethite (010) surface have been investigated. In both cases, the As–O separations matched well with their experimental counterpart (1.62–1.64 Å). Their surface model predicted this distance to be 1.63 Å, whereas their cluster model assumed an As–O
cluster distance of 1.67 Å.