3D Modeling of the Epembe (Namibia) Nb-Ta-P-(LREE) Carbonatite Deposit: New Insights into Geometry Related to Rare Metal Enrichment
Abstract
1. Introduction
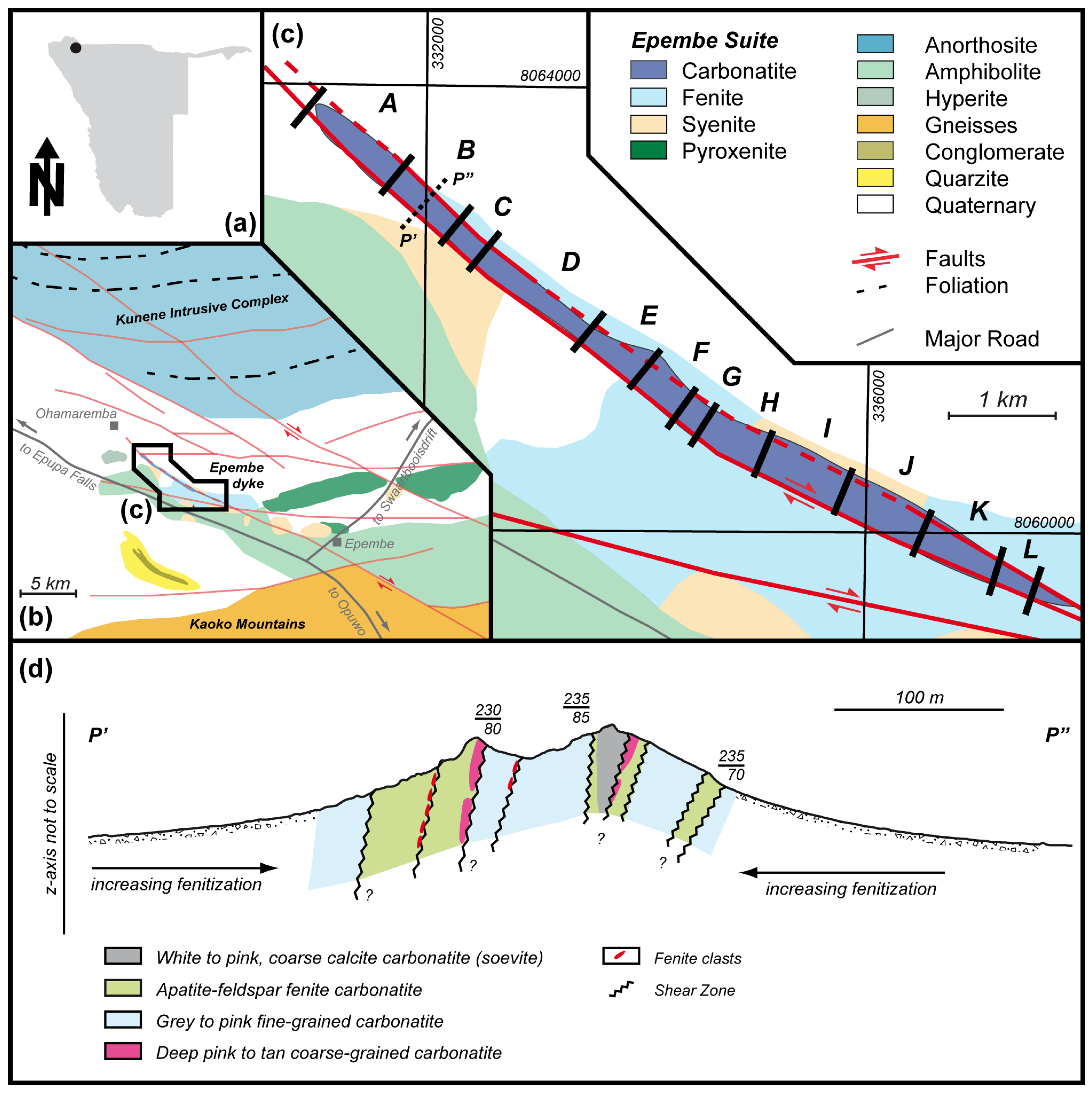
2. Geological Setting
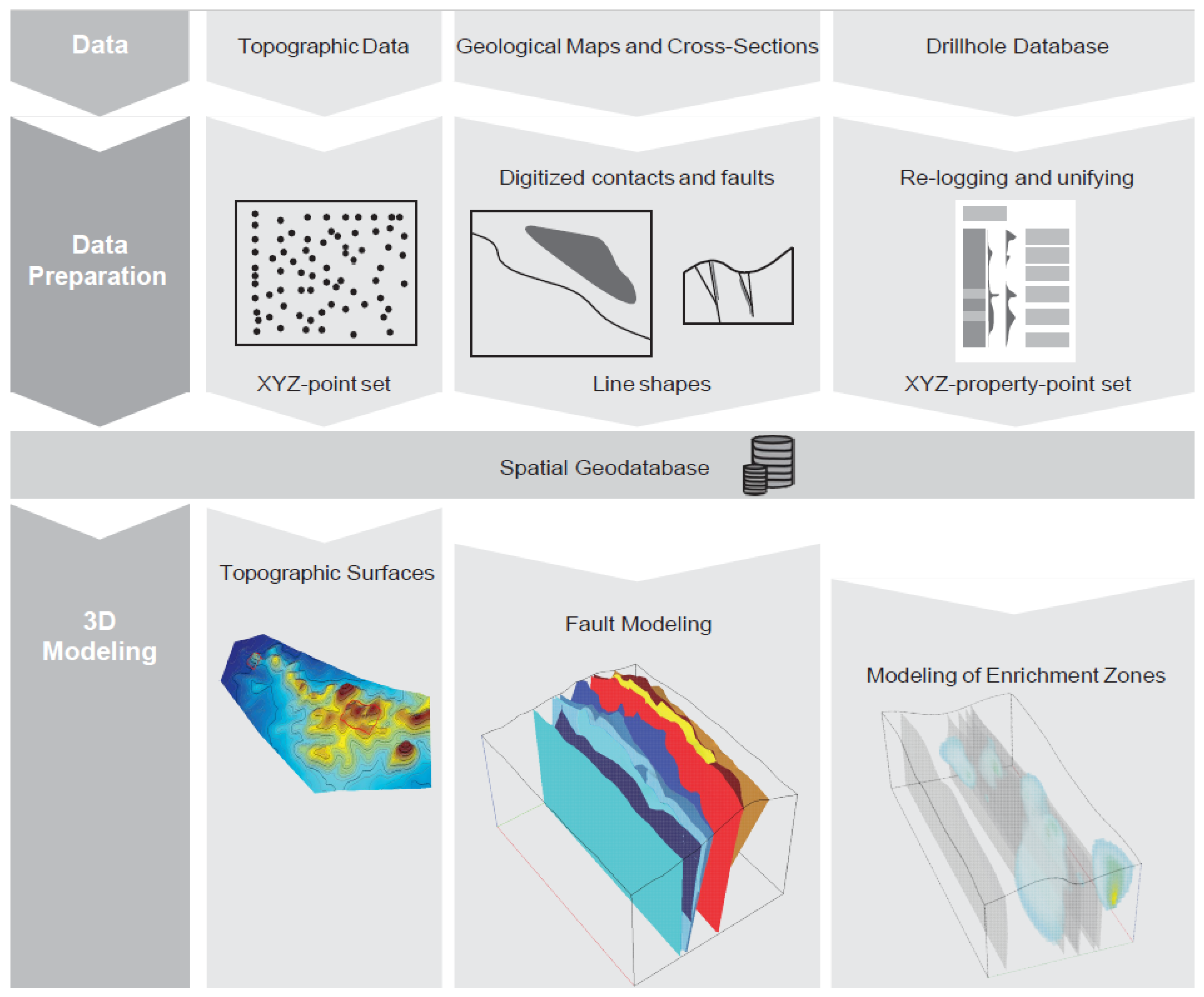
3. Input Data for 3D Modeling
- Surface topography:The surface topography was modeled based on one-arc-second SRTM data (Shuttle Radar Topography Mission with 30-m spatial resolution [33]). In addition, available elevation information (e.g., Sector B) was densified using well locations, points of surface sampling, and GPS tracks from our own observation. All information was merged to a point (XYZ) layer and imported into the 3D modeling software.
- Geological maps and cross-sections:Previous investigations of Bull [26] and Swinden [32] resulted in geological maps and cross-sections at scales of 1:10,000–1:15,000 for selected areas (Sectors B and K). The maps were digitized, and information on surface lithology, fault indicators, and structural constraints was extracted. The respective cross-sections were referenced and digitized in the modeling software. Information on the surface expression of the fault system in the area of investigation was compiled from satellite data [27]. Fault information was stored as 2D polylines and later draped on surface topography in the 3D models.
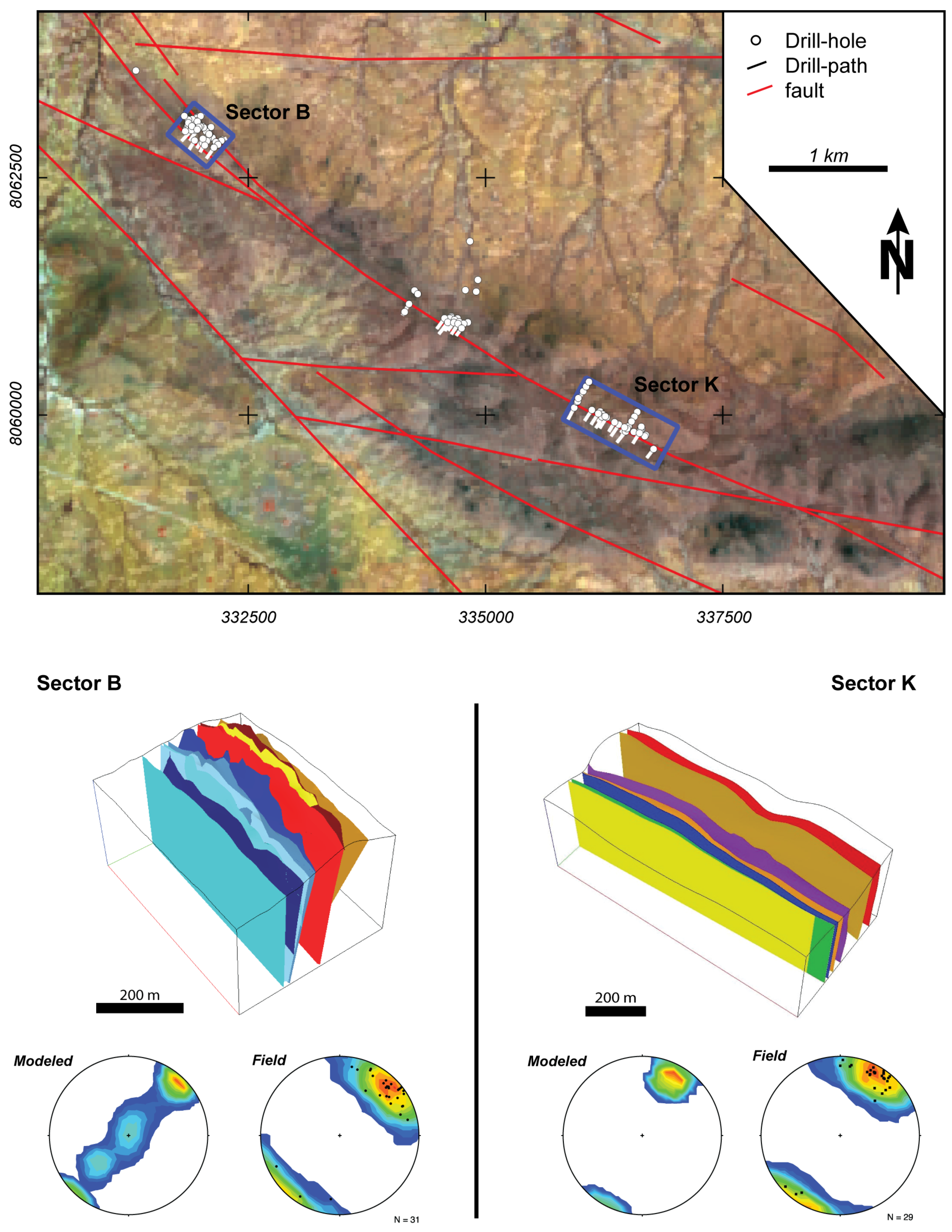
- Drill-hole database:Drill-hole assay data were first re-logged and unified in terms of lithology by using the drillhole logging results. Similar rock types and transition zones were combined based on modal mineralogy, appearance, and color to match the description of surface rock types from Swinden [32]. Markers and descriptions with indications of shearing (mylonites, breccias, rock loss, flow bands) were marked for later fault modeling. The drill core data basis for the model was 117 variably-inclined reverse circulation (RC) and a few diamond-drilled boreholes with a sampling interval of 1 m. In total, a length of 7400 m, including 2900 m of diamond cores, was drilled until 2014 [28]. The boreholes were drilled at shallow angles, perpendicular to the average strike direction of the lithology. Most of them were located in Sectors B and K (Figure 3). The average depth of the drillholes was 150 m, which also corresponds to the model depth. Bulk geochemical analysis of all core sections of both host rock and carbonatite was conducted by WD-XRF and ICP-MS. Geochemical data were retrieved from percussion sample chips and averaged over one-meter intervals. Several files were created and imported to SKUA-GoCad including: (1) drill paths, (2) fault markers, and (3) geochemical data.
4. 3D and Property Modeling Methodology
4.1. SKUA-GoCad and the DSI Algorithm
4.2. Modeling Approach
- Faults are sub-parallel to the tectonic foliation (Sector B mean dip direction/dip: 226/75; Sector K mean dip direction/dip: 210/80 according to field data) and planes dipping sub-vertically (80 to S).
- The fault system is converging into a common detachment at the sub-surface.
5. Results
5.1. Fault System
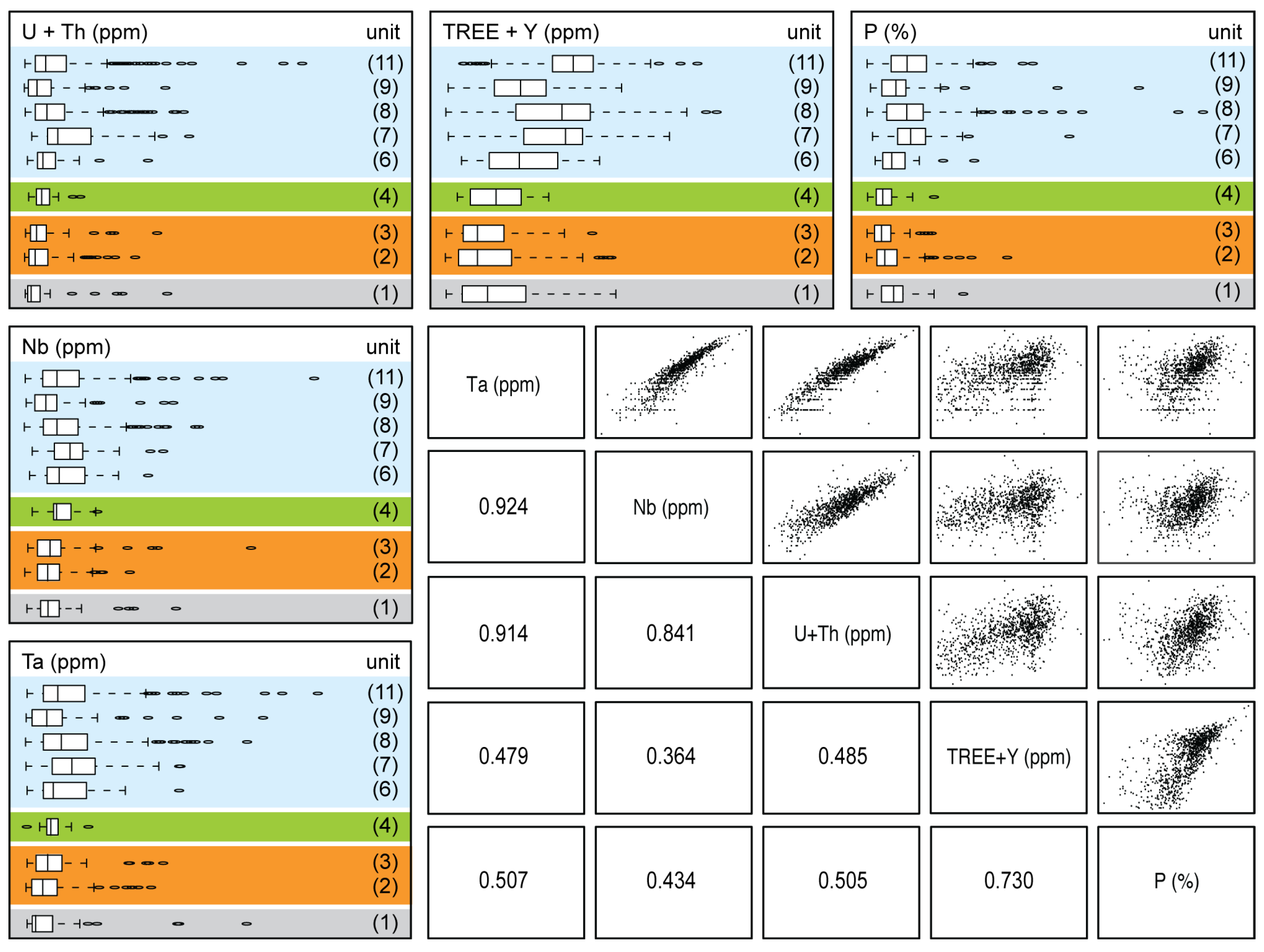
5.2. Lithological Analysis
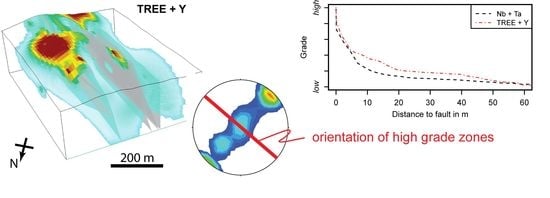
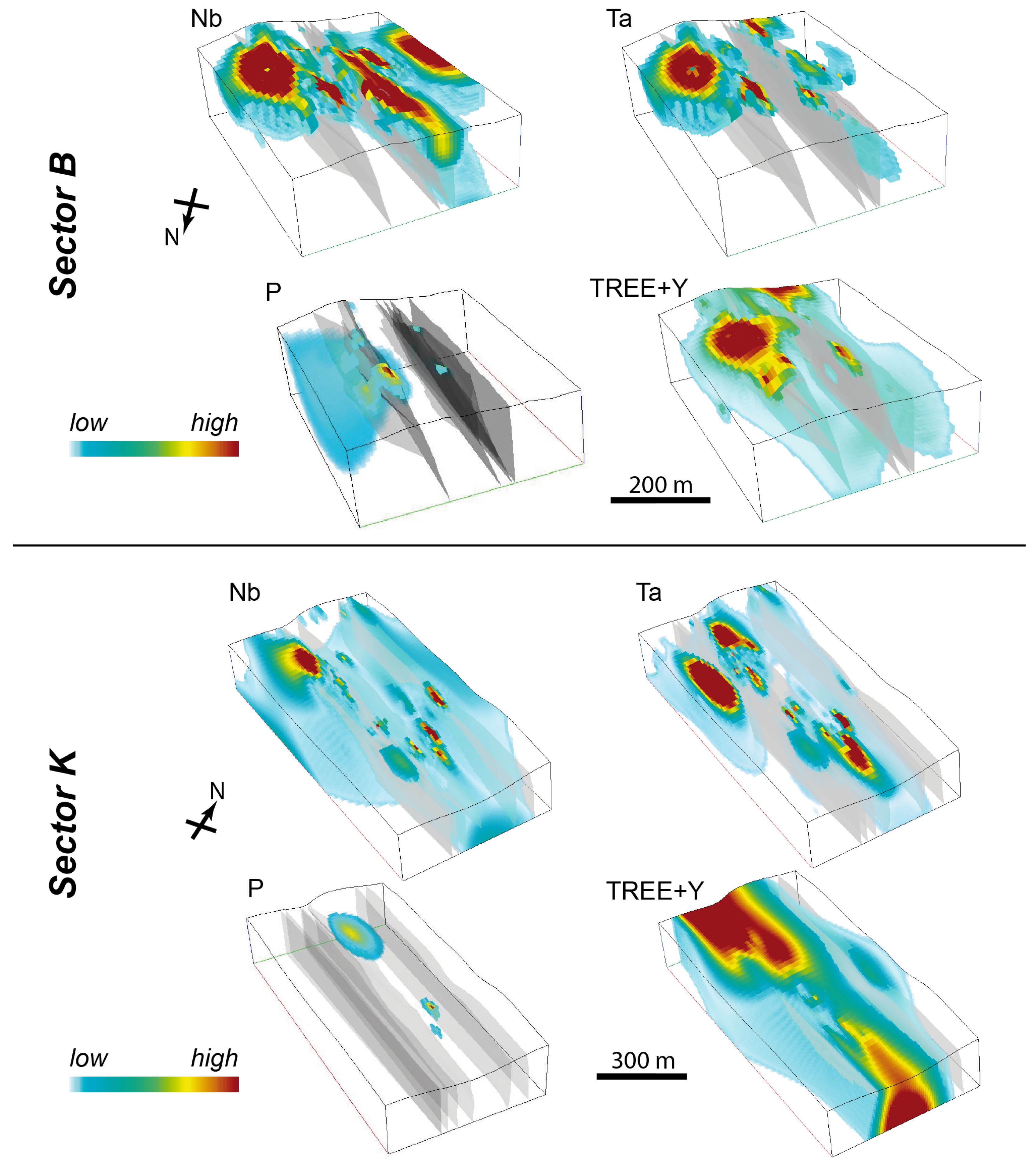
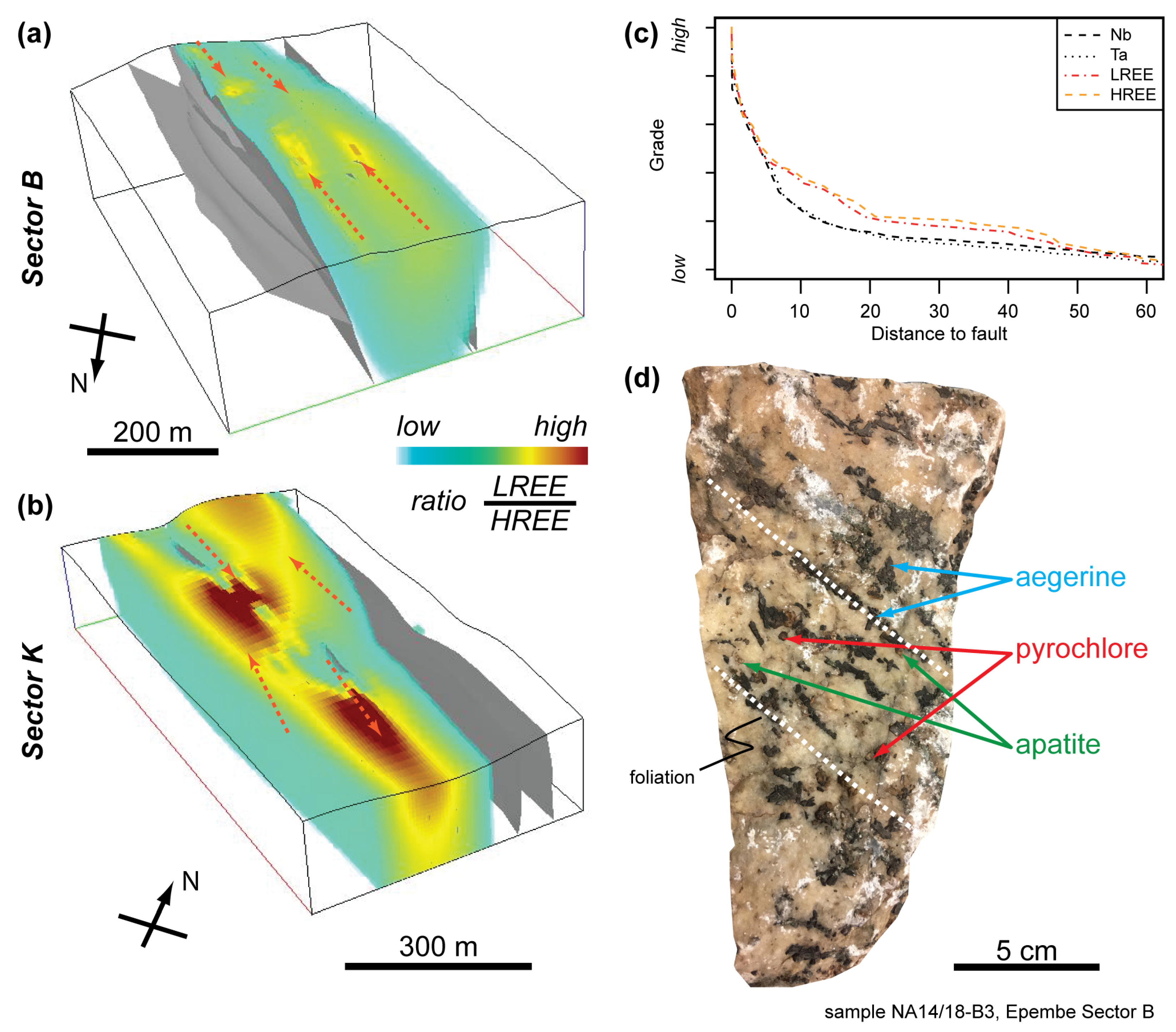
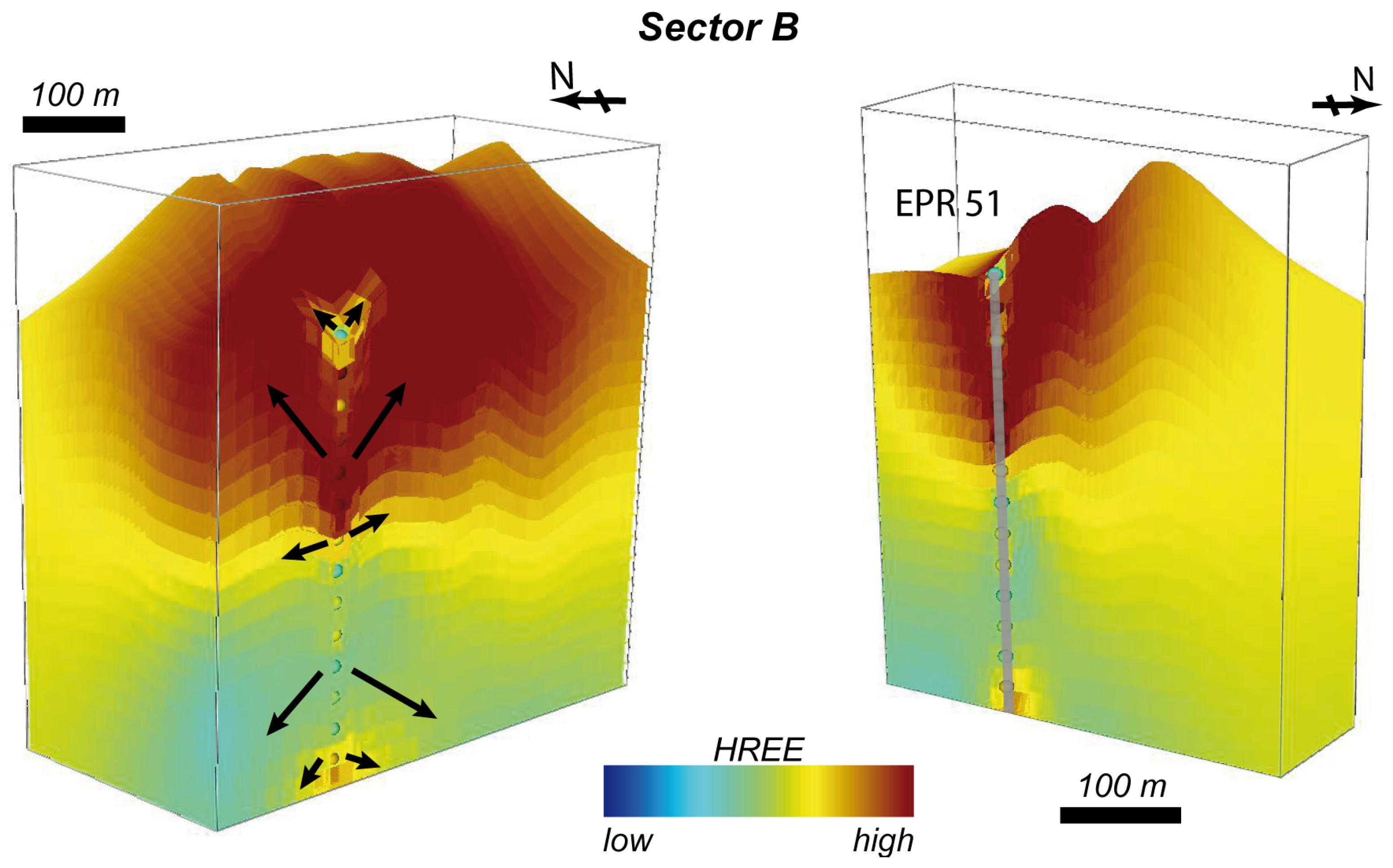
5.3. Enrichment Zones
6. Discussion
6.1. Methodological Aspects
6.2. Consequences of the 3D Model for the Nb, Ta, and REE Enrichment
6.3. Enrichment during the Late Stage
7. Conclusions
- There is a distinct correlation between enrichment in Nb, Ta, P, REE, U, and Th and sheared lithological units, as well as the concentration of high-grade zones along faults. This is further supported by element concentration in 3D distance to faults (75% quantile 10 m and median at 4.5 m) and field evidence of shear-bands showing enrichment of apatite, pyrochlore, and pyroxene.
- The complex fault system geometry affects the whole dyke and, thus, creates fluid pathways for the remobilization of the incompatible elements (HFSE).
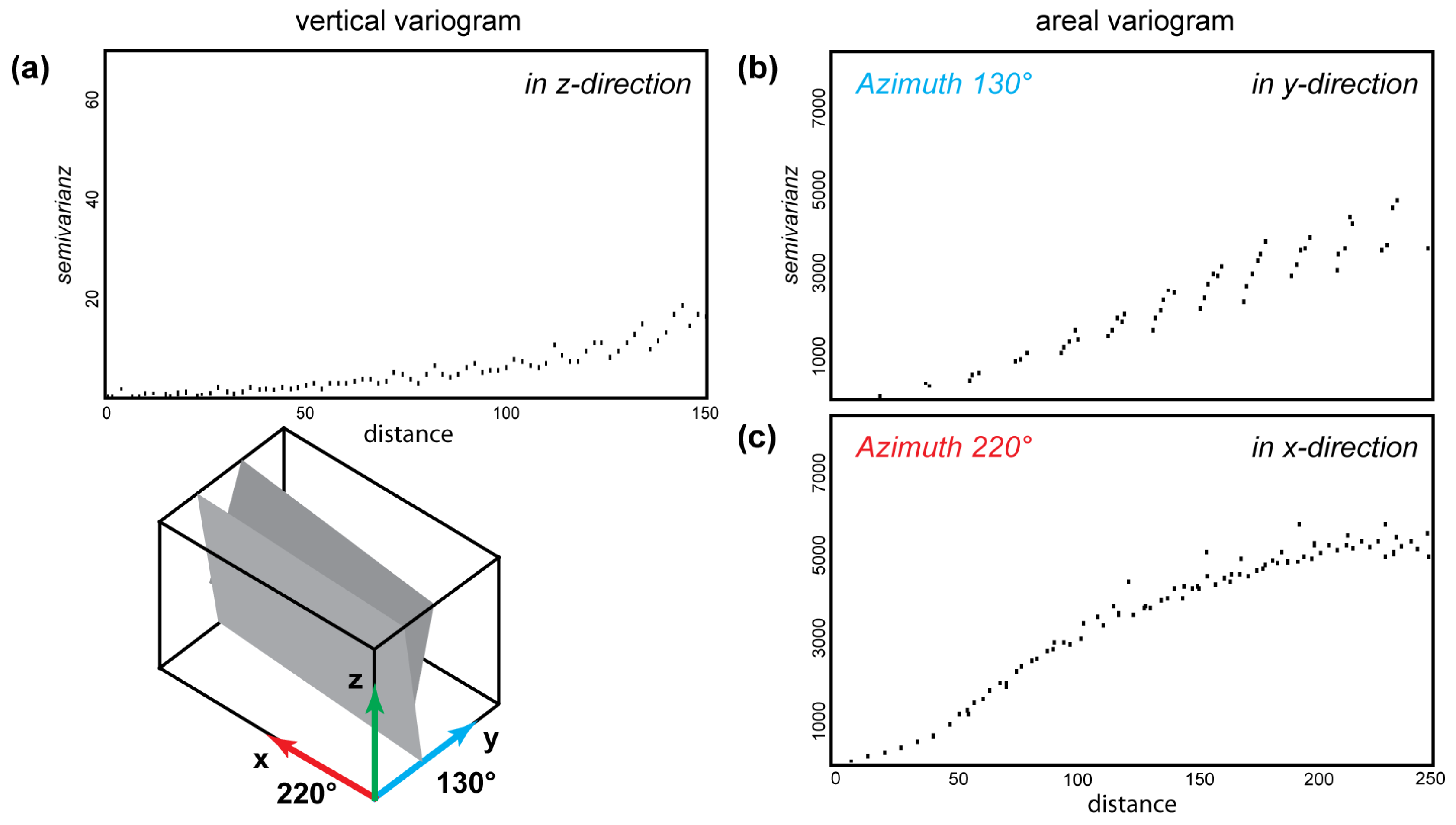
- Oscillating 3D variograms that indicate focused enrichment along faults.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- European Union. Study on the Review of the List of Critical Raw Materials, Final Report; Publications Office of the European Union: Brussels, Belgium, 2017. [Google Scholar]
- Kynicky, J.; Smith, M.; Xu, C. Diversity of Rare Earth Deposits: The Key Example of China. Elements 2012, 8, 361–367. [Google Scholar] [CrossRef]
- Calas, G. Mineral Resources and Sustainable Development. Elements 2017, 13, 301–306. [Google Scholar] [CrossRef]
- Mariano, A.N. Nature of economic mineralization in carbonatites and related rocks. In Carbonatites—Genesis and Evolution; Bell, K., Ed.; Unwin Hyman Ltd.: Boston, MA, USA, 1989; pp. 149–176. [Google Scholar]
- Wallace, M.; Green, H. An experimental determination of primary carbonatite magma composition. Nature 1988, 335, 343–346. [Google Scholar] [CrossRef]
- Woolley, A.R. Alkaline Rocks and Carbonatites of the World, Part 3: Africa; British Museum (Natural History): London, UK, 2001; Chapter Namibia. [Google Scholar]
- Verplanck, P.L.; Van Gosen, B.S.; Seal, R.R.; McCafferty, A.E. A Deposit Model for Carbonatite and Peralkaline Intrusion-Related Rare Earth Element Deposits; U.S. Geological Survey Scientific Investigations Report; USGS: Denver, CO, USA, 2014.
- Williams-Jones, A.E.; Migdisov, A.A.; Samson, I.M. Hydrothermal Mobilisation of the Rare Earth Elements—A Tale of “Ceria” and “Yttria”. Elements 2012, 8, 355–360. [Google Scholar] [CrossRef]
- Broom-Fendley, S.; Styles, M.; Appleton, J.; Gunn, G.; Wall, F. Evidence for dissolution-reprecipitation of apatite and preferential LREE mobility in carbonatite-derived late-stage hydrothermal processes. Am. Mineral. 2016, 101, 596–611. [Google Scholar] [CrossRef]
- Andersson, M.; Malehmir, A.; Troll, V.R.; Dehghannejad, M.; Juhlin, C.; Ask, M. Carbonatite ring-complexes explained by caldera-style volcanism. Sci. Rep. 2013, 3, 1677. [Google Scholar] [CrossRef]
- Simandl, G.J.; Paradis, S. Carbonatites: Related ore deposits, resources, footprint, and exploration methods. Appl. Earth Sci. 2018, 127, 123–152. [Google Scholar] [CrossRef]
- Feltrin, L.; McLellan, J.; Oliver, N. Modelling the Giant, Zn–Pb–Ag Century Deposit, Queensland, Australia; Technical Report; Predictive Mineral Discovery Cooperative Research Centre, School of Earth Sciences, James Cook University: Douglas, Australia, 2007. [Google Scholar]
- Kaufmann, O.; Martin, T. 3D geological modeling from boreholes, cross-sections and geological maps, application over former natural gas storages in coal mines. Comput. Geosci. 2008, 34, 278–290. [Google Scholar] [CrossRef]
- Schetselaar, E.M. Mapping the 3D lithofacies architecture of a VMS ore system on a curvilinear-faulted grid: A case study from the Flin Flon mining camp, Canada. Ore Geol. Rev. 2013, 53, 261–275. [Google Scholar] [CrossRef]
- Martin-Izard, A.; Arias, D.; Arias, M.; Gumiel, P.; Sanderson, D.J.; Castañon, C.; Lavandeira, A.; Sanchez, J. A new 3D geological model and interpretation of structural evolution of the world-class Rio Tinto VMS deposit, Iberian Pyrite Belt (Spain). Ore Geol. Rev. 2015, 71, 457–476. [Google Scholar] [CrossRef]
- Saalmann, K.; Laine, E. Structure of the Outokumpu ore district and ophiolite-hosted Cu-Co-Zn- Ni-Ag-Au sulfide deposits revealed from 3D modeling and 2D high-resolution seismic reflection data. Ore Geol. Rev. 2014, 62, 156–180. [Google Scholar] [CrossRef]
- Renard, R.; Courrioux, G. Three-dimensional geometric modeling of a faulted domain: The Soultz Horst example (Alsace, France). Comput. Geosci. 1994, 20, 1379–1390. [Google Scholar] [CrossRef]
- Bistacchi, A.; Massironi, M.; Piaz, G.V.D.; Piaz, G.D.; Monopoli, B.; Schiavo, A.; Toffolon, G. 3D fold and fault reconstruction with an uncertainty model: An example from an Alpine tunnel case study. Comput. Geosci. 2008, 34, 351–372. [Google Scholar] [CrossRef]
- Caumon, G.; Collon-Drouaillet, P.; Le Carlier De Veslud, C.; Viseur, S.; Sausse, J. Surface-based 3D modeling of geological structures. Math. Geosci. 2009, 41, 927–945. [Google Scholar] [CrossRef]
- Zanchi, A.; Francesca, S.; Stefano, Z.; Simone, S.; Graziano, G. 3D reconstruction of complex geological bodies: Examples from the Alps. Comput. Geosci. 2009, 35, 49–69. [Google Scholar] [CrossRef]
- Cherpeaua, N.; Caumon, G.; Lévy, B. Stochastic simulations of fault networks in 3D structural modeling. C. R. Geosci. 2010, 34, 687–694. [Google Scholar] [CrossRef]
- Arndt, D.; Bär, K.; Fritsche, J.G.; Kracht, M.; Sass, I.; Hoppe, A. 3D structural model of the Federal State of Hesse (Germany) for geopotential evaluation. Zeitschrift der Deutschen Gesellschaft für Geowissenschaften 2011, 162, 353–369. [Google Scholar] [CrossRef]
- Caumon, G.; Gray, G.; Antoine, C.; Titeux, M.O. Three-dimensional implicit stratigraphic model building from remote sensing data on tetrahedral meshes: Theory and application to a regional model of la Popa Basin, NE Mexico. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1613–1621. [Google Scholar] [CrossRef]
- Royer, J.-J.; Mejia-Herrera, P.; Caumon, G.; Collon, P. 3D and 4D Geomodeling Applied to Mineral Resources Exploration—An Introduction. In 3D, 4D and Predictive Modelling of Major Mineral Belts in Europe; Weihed, P., Ed.; Springer: Berlin, Germany, 2015; pp. 73–89. [Google Scholar]
- Falshaw, S. The Geology and Rare Metal Metallogenesis of the Epembe Carbonatite Dyke, North West Namibia. Master’s Thesis, Camborne School of Mines, Penryn, UK, 2012. [Google Scholar]
- Bull, J. Detailed Geological Mapping and Petrological Study of the Ta-Na ± U Epembe Carbonatite-Syenite Complex in North-West Namibia. Master’s Thesis, Camborne School of Mines, Penryn, UK, 2013. [Google Scholar]
- Zimmermann, R.; Brandmeier, M.; Andreani, L.; Mhopjeni, K.; Gloaguen, R. Remote Sensing Exploration of Nb-Ta-LREE-Enriched Carbonatite (Epembe/Namibia). Remote Sens. 2016, 8, 620. [Google Scholar] [CrossRef]
- Ellmies, R.; Kunene Resources (pty) Ltd., Klein-Windhoek, Namibia. Personal communication, 2014.
- Salomon, E.; Koehn, D.; Passchier, C. Brittle reactivation of ductile shear zone in NW Namibia in relation to South Atlantic rifting. Tectonics 2015, 34, 70–85. [Google Scholar] [CrossRef]
- Brandt, S.; Will, T.M.; Klemd, R. Magmatic loading in the proterozoic Epupa Complex, NW Namibia, as evidenced by ultrahigh-temperature sapphirine-bearing orthopyroxene–sillimanite–quartz granulites. Precambrian Res. 2007, 153, 143–178. [Google Scholar] [CrossRef]
- Maier, W.; Rasmussen, B.; Flechtner, I.; Li, C.; Barnes, S.J.; Huhma, H. The Kunene Anorthosite Complex, Namibia, and its Satellite Intrusions: Geochemistry, Geochronology and Economic Potential. Econ. Geol. 2013, 108, 953–986. [Google Scholar] [CrossRef]
- Swinden, S. (Swinden Geoscience Consultants Ltd., Wolfville, Canada). Personal communication, 2014.
- NASA JPL. NASA Shuttle Radar Topography Mission Global 1 Arc Second Number S18E013V3; NASA EOSDIS Land Processes DAAC: Sioux Falls, SD, USA, 2013.
- Stoch, B.; Anthonissen, C.J.; McCall, M.-J.; Basson, I.J.; Deacon, J.; Cloete, E.; Botha, J.; Britz, J.; Strydom, M.; Nel, D.; et al. 3D implicit modeling of the Sishen Mine: New resolution of the geometry and origin of Fe mineralization. Miner. Depos. 2018, 53, 835–853. [Google Scholar] [CrossRef]
- Mallet, J.L. Gocad: A computer aided design program for geological applications. In Three-Dimensional Modeling with Geoscientific Information Systems; Turner, A.K., Ed.; AS1 Series; Springer: Dordrecht, The Netherlands, 1992; pp. 123–141. [Google Scholar]
- Mallet, J.L. Discrete smooth interpolation in geometric modeling. Comput. Aided Des. 1992, 24, 178–191. [Google Scholar] [CrossRef]
- Mallet, J.L. Discrete smooth interpolation. ACM Trans. Gr. 1989, 8, 121–144. [Google Scholar] [CrossRef]
- Royse, K. Combining numerical and cognitive 3D modeling approaches in order to determine the structure of the Chalk in the London Basin. Comput. Geosci. 2010, 36, 500–511. [Google Scholar] [CrossRef]
- Bühn, B. The role of the volatile phase for REE and Y fractionation in low-silica carbonate magmas: Implications from natural carbonatites, Namibia. Mineral. Petrol. 2008, 92, 453–470. [Google Scholar] [CrossRef]
- Andersson, M.; Almqvist, B.S.; Burchardt, S.; Troll, V.R.; Malehmir, A.; Snowball, I.; Kübler, L. Magma transport in sheet intrusions of the Alnö carbonatite complex, central Sweden. Sci. Rep. 2016, 6, 27635. [Google Scholar] [CrossRef]
- Andersson, M.; Malehmir, A. Unravelling the internal architecture of the Alnö alkaline and carbonatite complex (central Sweden) using 3D models of gravity and magnetic data. Solid Earth Discuss. 2017, 1–35. [Google Scholar] [CrossRef]
- Jones, A.P.; Genge, M.; Carmody, L. Carbonate Melts and Carbonatites. Rev. Mineral. Geochem. 2013, 75, 289–322. [Google Scholar] [CrossRef]
- Wall, F.; Niku-Paavola, V.N.; Storey, C.; Müller, A.; Jeffries, T. Xenotime-(Y) from carbonatite dykes at Lofdal, Namibia: Unusually low LREE:HREE ratio in carbonatite, and the first dating of xenotime overgrowths on zircon. Can. Mineral. 2008, 46, 861–877. [Google Scholar] [CrossRef]
- Bodeving, S.; Williams-Jones, A.E.; Swinden, S. Carbonate–silicate melt immiscibility, REE mineralizing fluids, and the evolution of the Lofdal Intrusive Suite, Namibia. Lithos 2017, 268–271, 383–398. [Google Scholar] [CrossRef]
- Cook, N.J.; Ciobanu, C.L.; O’Rielly, D.; Wilson, R.; Das, K.; Wade, B. Mineral chemistry of Rare Earth Element (REE) mineralization, Browns Ranges, Western Australia. Lithos 2013, 172–173, 192–213. [Google Scholar] [CrossRef]
- Richter, L.; Diamond, L.W.; Atanasova, P.; Banks, D.A.; Gutzmer, J. Hydrothermal formation of heavy rare earth element (HREE)—Enotime deposits at 100 °C in a sedimentary basin. Geology 2018, 26, 263–266. [Google Scholar] [CrossRef]
- Mott, A.V.; Bird, D.K.; Grove, M.; Rose, N.; Bernstein, S.; Mackay, H.; Krebs, J. Karrat Isfjord: A newly discovered Paleoproterozoic carbonatite-sourced REE deposit, Central West Greenland. Econ. Geol. 2013, 108, 1471–1488. [Google Scholar] [CrossRef]
| Lithofacies Class | Description | Genetic Interpretation | |
|---|---|---|---|
| 1 | fenite, gneisses, and mica-schist | metamorphosed (chlorite, epidote) and fenitized rock | host rock |
| 2 | grey nepheline-bearing syenite | grey, medium-grained, mesocratic nepheline-bearing syenite | unaltered syenite |
| 3 | red highly fenitized syenite | fenitized rock, less mafic minerals | hydrothermally-altered syenite |
| 4 | lamprophyre dykes | dark, 2–20 m-long, 0.1–0.5 m-wide porphyritic dykes | mafic dykes, related to late-stage magmatism |
| 5 | coarse-grained fenite breccia | carbonatic matrix with fragments of syenites or fenite | alteration aureole around the carbonatite complex |
| 6 | mixture zones | only observed in drillcores, mixing of various lithologies | breccia? |
| 7 | deep-pink px-carbonatite | large aeg crystals within flow bands, rich in U/Th/K | shear zone-related carbonatite |
| 8 | grey ap-fsp-fenite- carbonatite | little px, fenitized rock | late-stage carbonatite, hydrothermal overprint |
| 9 | grey ap-fsp-aeg- carbonatite | flow bands with K-fsp, aeg, ap; syenite xenoliths | shear zone-related carbonatite |
| 10 | foliated, deformed grey ap-fsp-aeg-carbonatite | same as (9), but with a strong deformation | intensely-sheared carbonatite, hydrothermally overprinted |
| 11 | white coarse-grained sövite | non- to weakly-foliated, heterogeneous sövite | weakly-deformed (primary?) carbonatite |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Unger, G.; Zimmermann, R.; Gloaguen, R. 3D Modeling of the Epembe (Namibia) Nb-Ta-P-(LREE) Carbonatite Deposit: New Insights into Geometry Related to Rare Metal Enrichment. Minerals 2018, 8, 600. https://doi.org/10.3390/min8120600
Unger G, Zimmermann R, Gloaguen R. 3D Modeling of the Epembe (Namibia) Nb-Ta-P-(LREE) Carbonatite Deposit: New Insights into Geometry Related to Rare Metal Enrichment. Minerals. 2018; 8(12):600. https://doi.org/10.3390/min8120600
Chicago/Turabian StyleUnger, Gabriel, Robert Zimmermann, and Richard Gloaguen. 2018. "3D Modeling of the Epembe (Namibia) Nb-Ta-P-(LREE) Carbonatite Deposit: New Insights into Geometry Related to Rare Metal Enrichment" Minerals 8, no. 12: 600. https://doi.org/10.3390/min8120600
APA StyleUnger, G., Zimmermann, R., & Gloaguen, R. (2018). 3D Modeling of the Epembe (Namibia) Nb-Ta-P-(LREE) Carbonatite Deposit: New Insights into Geometry Related to Rare Metal Enrichment. Minerals, 8(12), 600. https://doi.org/10.3390/min8120600