Economic Block Model Development for Mining Seafloor Massive Sulfides
Abstract
1. Introduction
2. Background
3. Theory
3.1. Revenues
3.2. Costs
3.3. Mining Time and Specific Energy
3.3.1. Mining Time
- is the specific energy (in kWh/m3 or MPa)
- is the available cutting power (in kW), i.e., the portion of the machine total power dedicated to the cutting machinery
- is the achieved excavation rate (in m3/h)
3.3.2. Specific Energy
- The cutting parameters: w, , the blade angle, , and the friction angle between the blade and the rock, ;
- The rock parameters: the cohesive strength of the rock, , and the internal friction angle of the rock, .
- The hyperbaric forces function of the environmental pressure (calculated using the ambient pressure at the work site, , and the level of cavitation ).
- To summarize:
- , no cavitation occurs, ,
- , cavitation partially occurs,
- full cavitation is established,
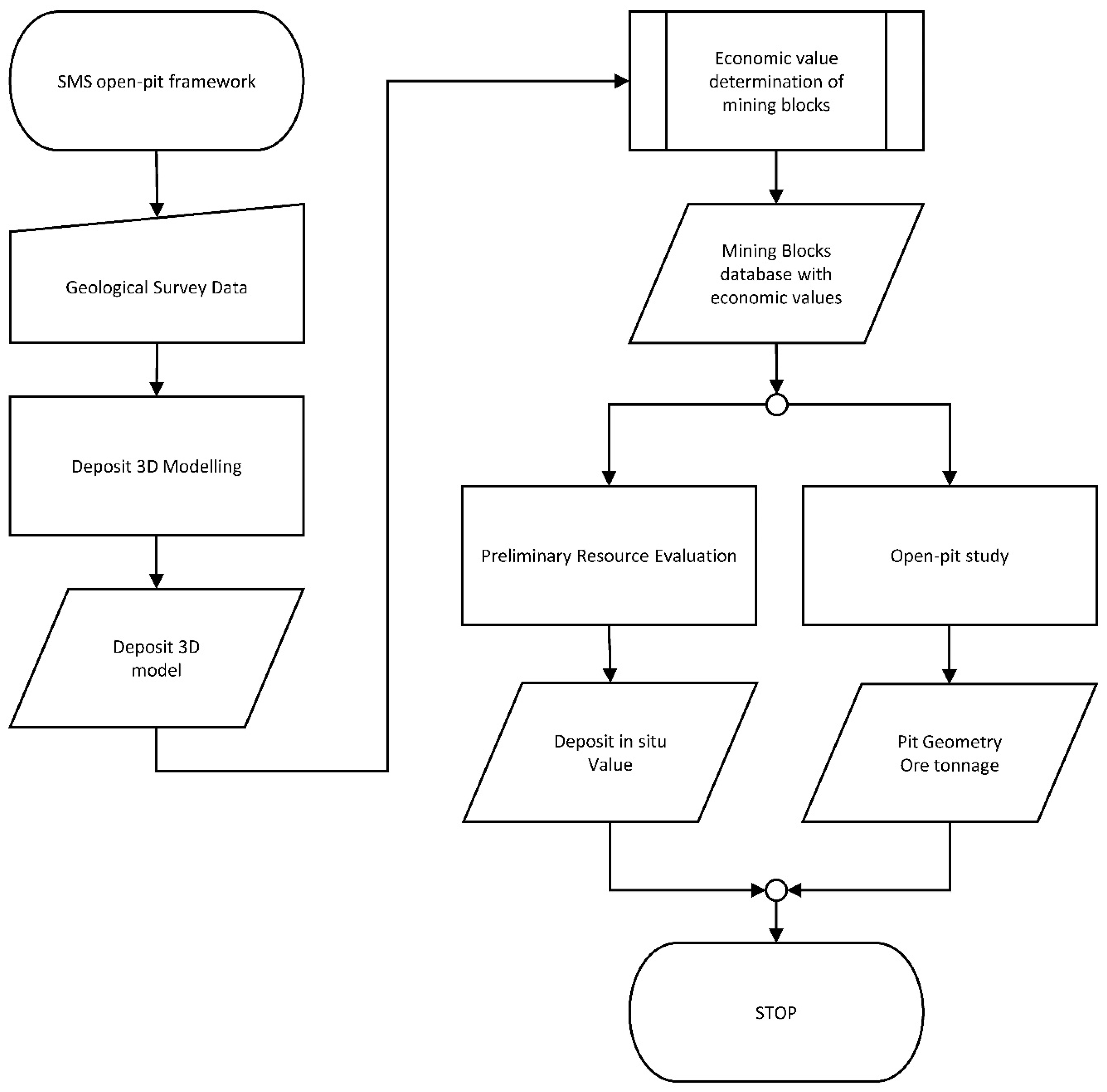
4. Methodology
4.1. Description of the Proposed Framework
4.2. Determination of the Block Model Parameters
- -
- either the parameter will be calculated using known relationships with one or several of the previously simulated parameters,
- -
- or arbitrarily attributed using a typical value from the literature.
4.2.1. Grades
4.2.2. Porosity, Grain Density, Bulk Density and Permeability
4.2.3. Pore Fluid Dynamic Viscosity, Compressibility and Local Pressure
4.2.4. Cohesive Strength and Internal Friction Angle
4.2.5. Metal Prices, Payable Metal Contents and Cost of Assets
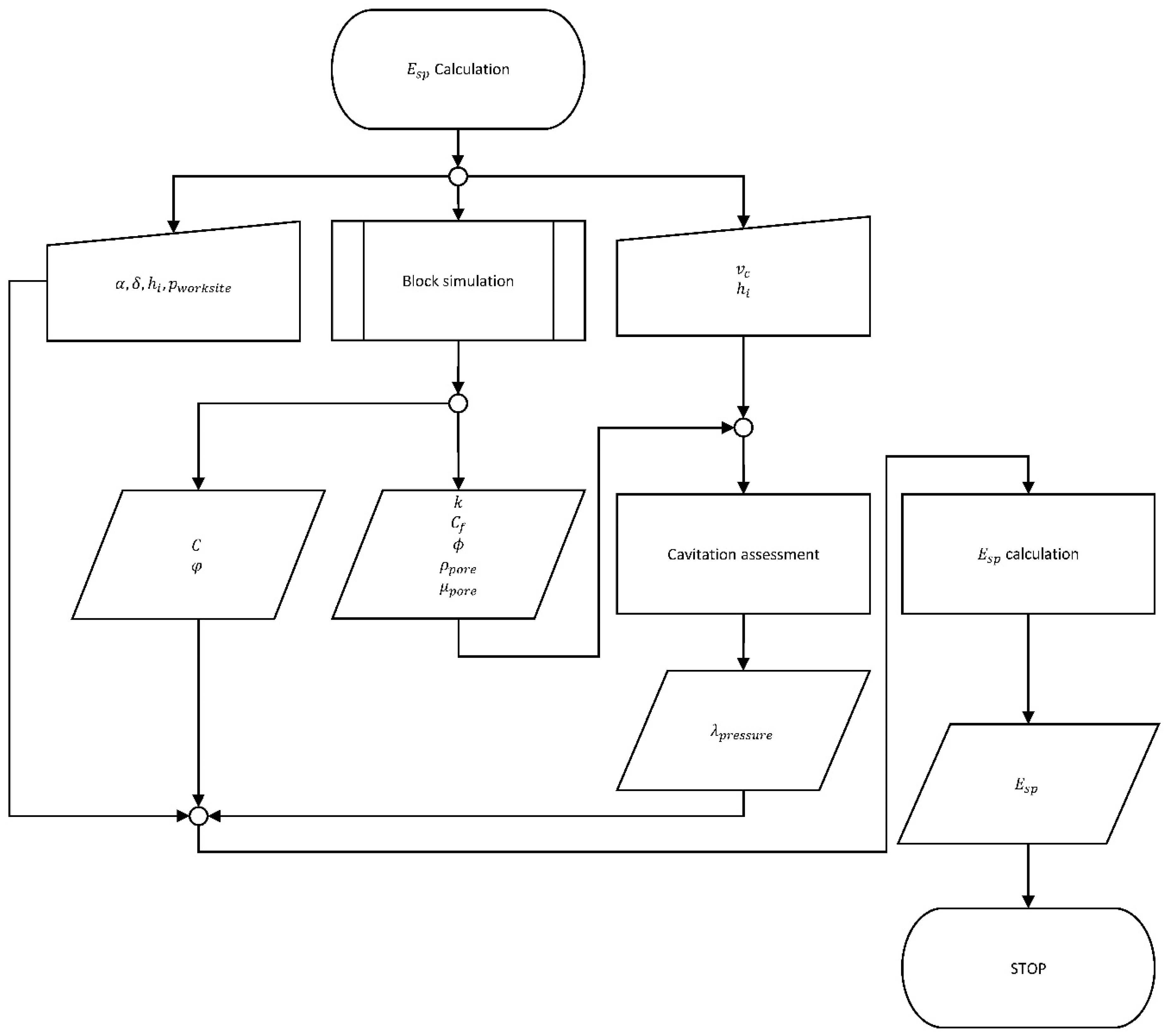
4.3. Determination of Specific Energy
4.4. Sensitivity Study
5. Materials and Data
5.1. Fixed Parameters
5.1.1. Cutting Parameters
5.1.2. Mining Costs
5.1.3. Commodity Prices
5.1.4. Mining Recovery Rate
5.1.5. Net Smelter Return
5.2. Grades
5.3. Porosity and Grain Density
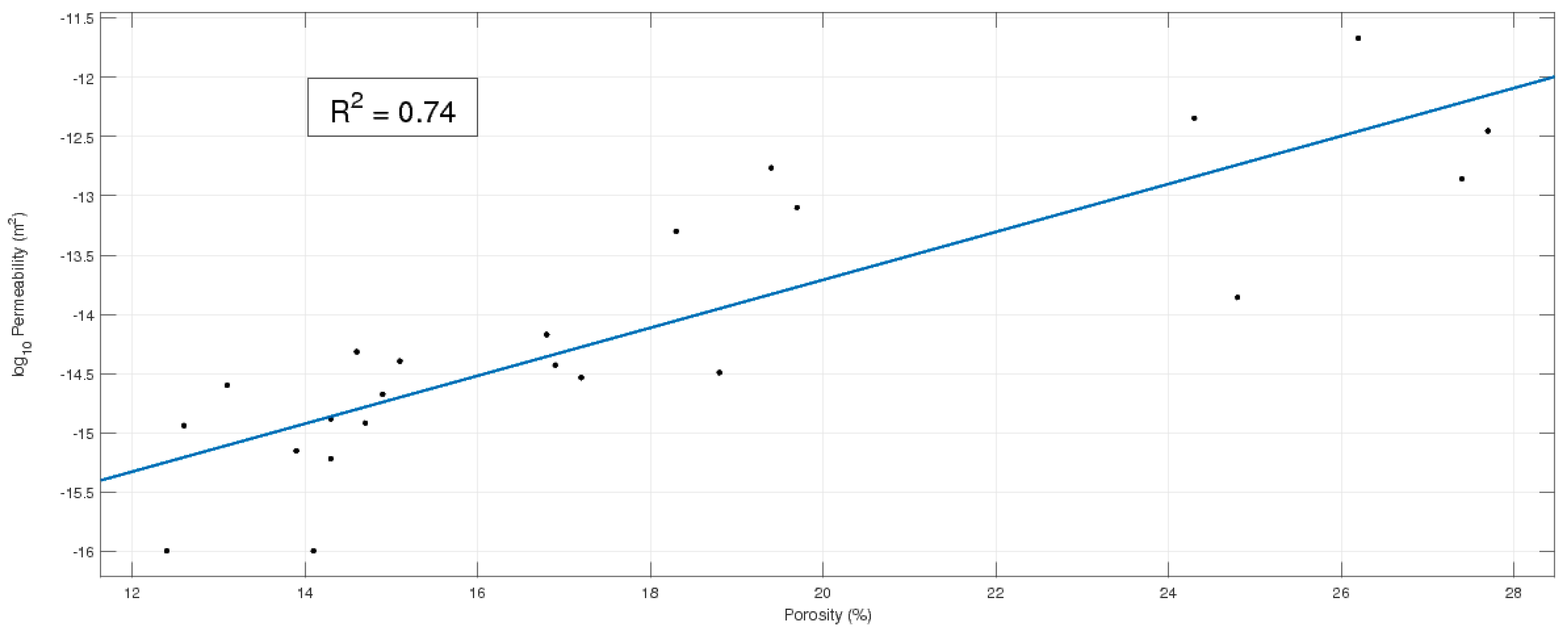
5.4. Permeability
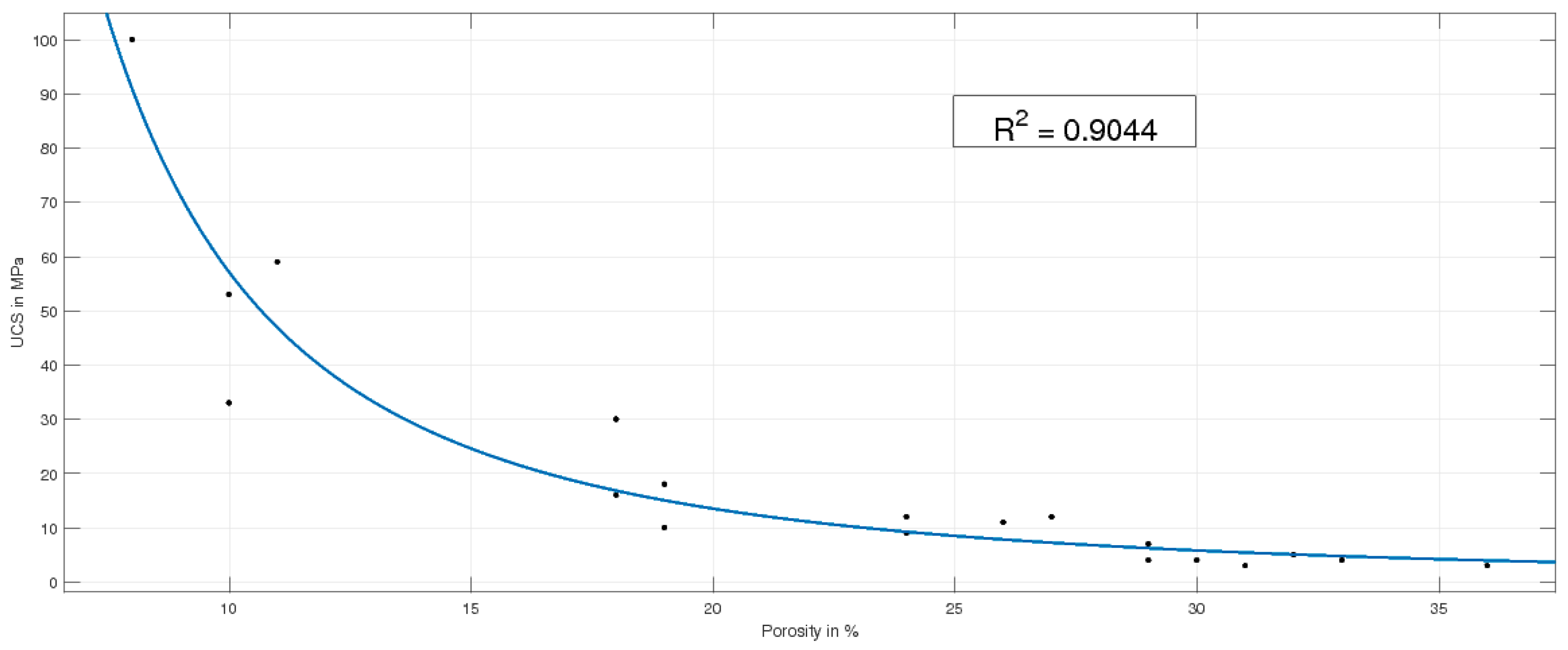
5.5. UCS and BTS
5.6. Pore Fluid Dynamic Viscosity and Compressibility, Local Pressure
- ,
- .
5.7. Processing Costs
6. Results
6.1. Grades and Tonnages
6.2. Economic Sensitivity Analysis and Relation to Specific Energy
6.2.1. Specific Energy and Cut Trench Height
- A reduced mining time for the excavation of the deposit from 596 days to 439 days; this is a 26% reduction of the total mining time; and
- An increased economic value of the deposit from approximately −69.6 M$ to approximately −32.5 M$, equivalent to an approximate 53% decrease of the deficit economic value of the deposit.
6.2.2. Assets’ Availability Factor
6.2.3. Available Cutting Power
6.2.4. Processing Costs
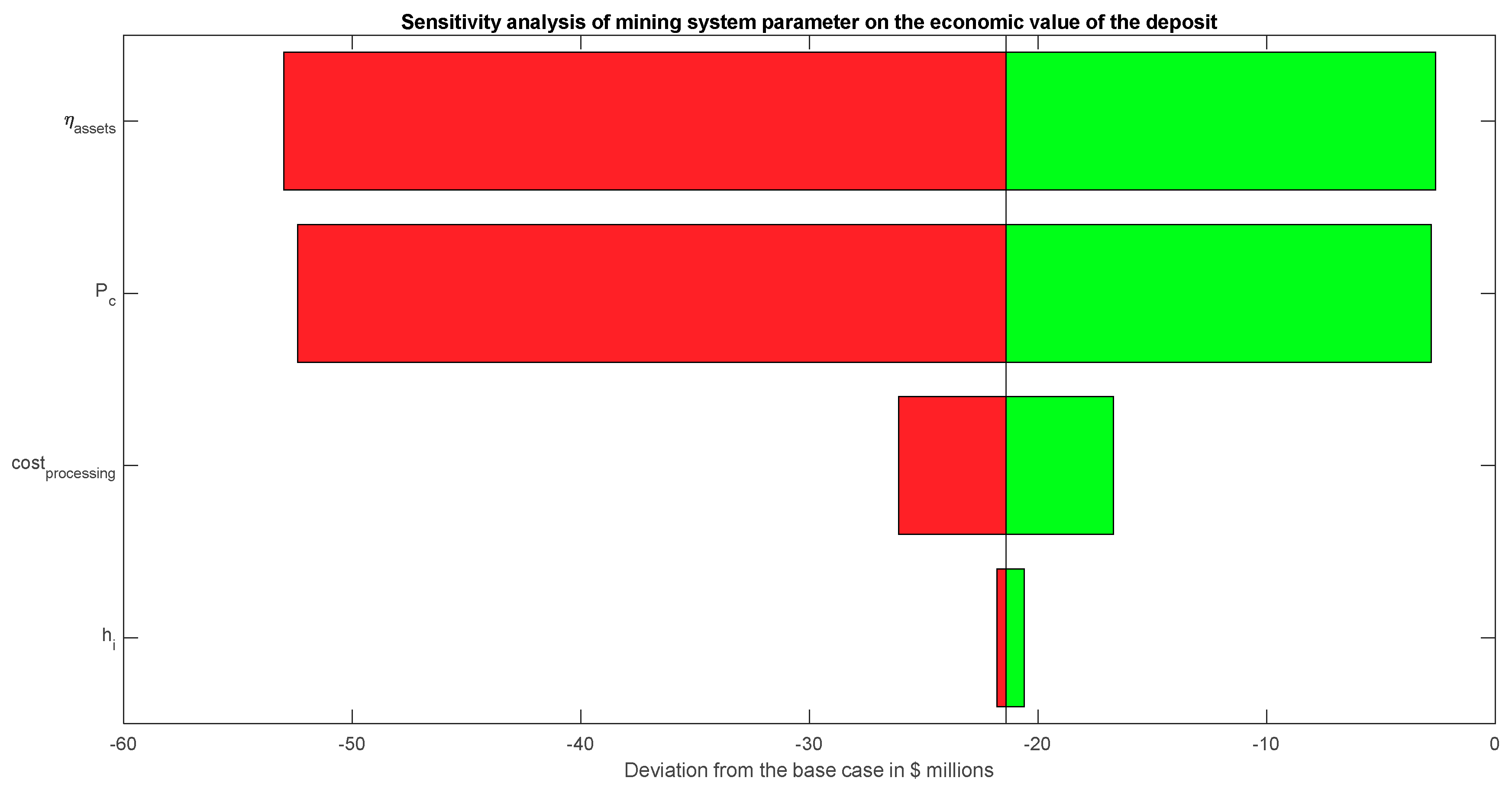
6.2.5. Multi-Parameter Sensitivity Study
7. Discussion
7.1. Geological Uncertainties
7.2. Specific Energy
7.3. Assets Availability Factor
7.4. Available Cutting Power
7.5. Process Route
7.6. Capabilities of the Framework
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Block Model Development Methodology, Flowchart
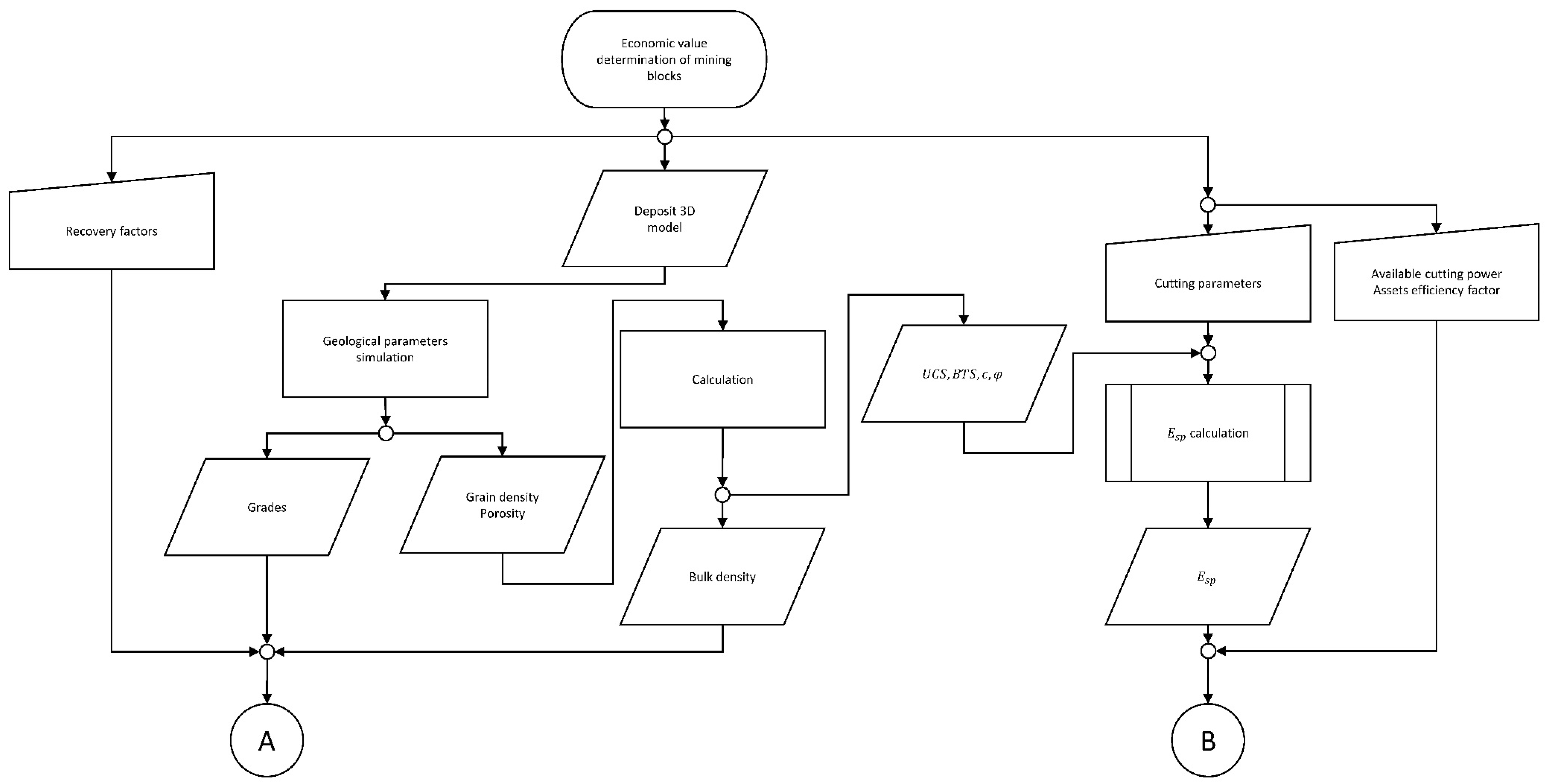
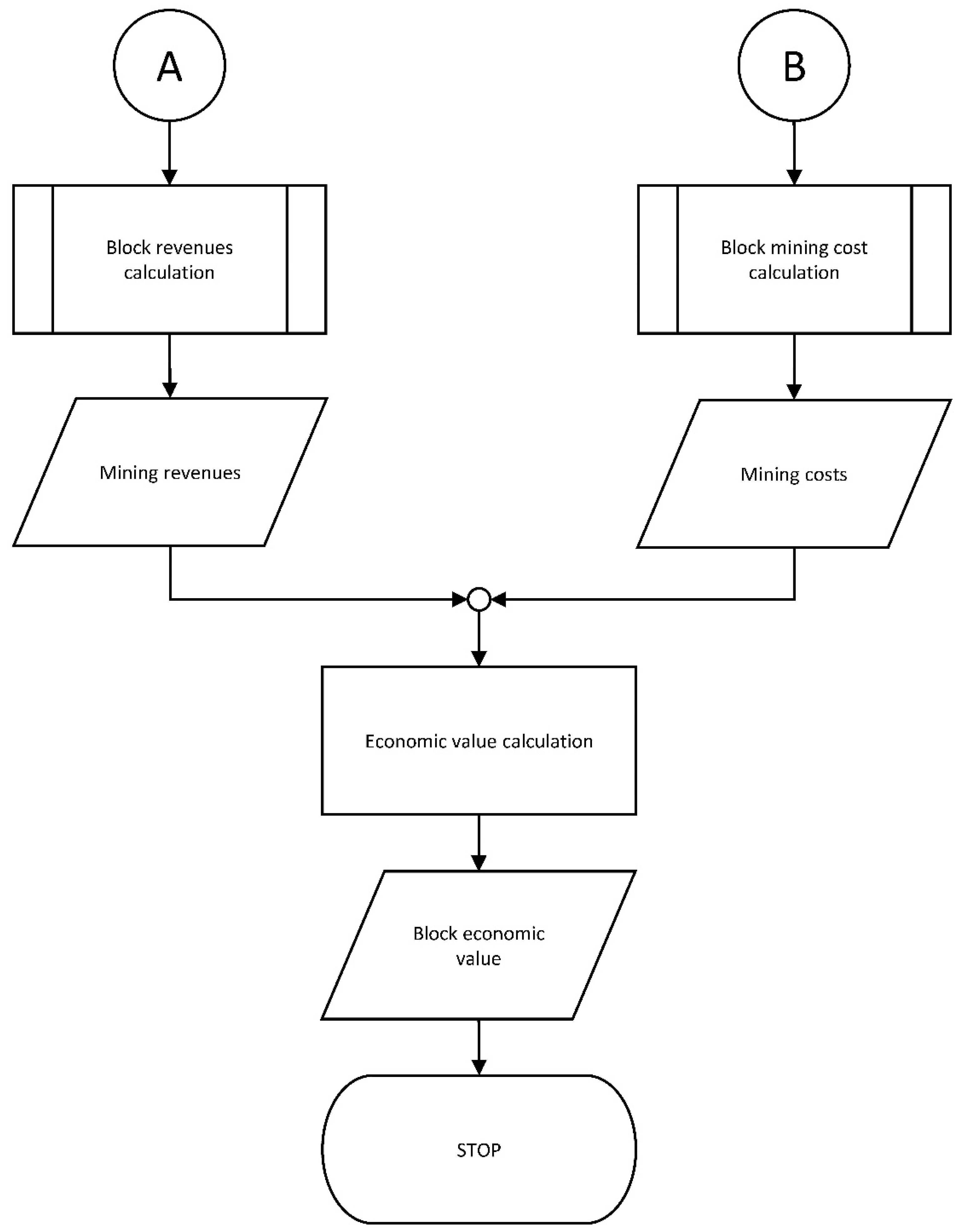
Appendix B. Flowcharts’ Legend
References
- Mero, J.L. The Mineral Resources of the Sea, 1st ed.; Oceanography Series; Elsevier: Amsterdam, The Netherlands; London, UK; New York, NY, USA, 1965; Volume 1, ISBN 978-0-08-087037-3. [Google Scholar]
- Nautilus Minerals Press Release Number 2017-21. Available online: http://www.nautilusminerals.com/irm/PDF/1930_0/Nautilusprovidesprojectupdate (accessed on 21 December 2017).
- METI; JOGMEC World’s First Success in Continuous Ore Lifting Test for Seafloor Polymetallic Sulphides. Available online: http://www.meti.go.jp/english/press/2017/0926_004.html (accessed on 21 December 2017).
- Brekke, H. Seabed Search for Metals Surging Ahead. Available online: http://www.npd.no/en/Publications/Norwegian-Continental-Shelf/No-1-2017/Minerals/ (accessed on 21 December 2017).
- Pedersen, R.B.; Rapp, H.T.; Thorseth, I.H.; Lilley, M.D.; Barriga, F.J.A.S.; Baumberger, T.; Flesland, K.; Fonseca, R.; Früh-Green, G.L.; Jorgensen, S.L. Discovery of a black smoker vent field and vent fauna at the Arctic Mid-Ocean Ridge. Nat. Commun. 2010, 1, 126. [Google Scholar] [CrossRef] [PubMed]
- Runge Picock Minarko. Minimum Engineering Study Requirements. Available online: https://www.rpmglobal.com/wp-content/uploads/mp/files/resources/files/rpm-perspectives-2015-128.pdf (accessed on 10 October 2017).
- CIM NI 43-101 Standards of Disclosure for Mineral Projects 2011. Available online: http://web.cim.org/standards/documents/block484_doc111.pdf (accessed on 10 October 2017).
- AusIMM, T. M. I. JORC Code, 2012 Edition 2012. Available online: http://www.jorc.org/docs/JORC_code_2012.pdf (accessed on 10 October 2017).
- Alvarez, F.; Amaya, J.; Griewank, A.; Strogies, N. A continuous framework for open pit mine planning. Math. Methods Oper. Res. 2011, 73, 29–54. [Google Scholar] [CrossRef]
- Caccetta, L. Application of optimisation techniques in open pit mining. In Handbook of Operations Research in Natural Resources; Springer: Boston, MA, USA, 2007; pp. 547–559. ISBN 978-0-387-71815-6. [Google Scholar]
- Caccetta, L.; Hill, S.P. An Application of Branch and Cut to Open Pit Mine Scheduling. J. Glob. Optim. 2003, 27, 349–365. [Google Scholar] [CrossRef]
- Lerchs, H.; Grossmann, I.F. Optimum Design of Open-Pit Mines. In Transactions CIM; Canadian Institute of Mining and Metallurgy: Montreal, QC, Canada, 1965; Volume 58, pp. 17–24. [Google Scholar]
- Picard, J.-C. Maximal Closure of a Graph and Applications to Combinatorial Problems. Manag. Sci. 1976, 22, 1268–1272. [Google Scholar] [CrossRef]
- Rona, P.A.; Klinkhammer, G.; Nelsen, T.A.; Trefry, J.H.; Elderfield, H. Black smokers, massive sulphides and vent biota at the Mid-Atlantic Ridge. Nature 1986, 321, 33. [Google Scholar] [CrossRef]
- Humphris, S.E.; Kleinrock, M.C. Detailed morphology of the TAG Active Hydrothermal Mound: Insights into its formation and growth. Geophys. Res. Lett. 1996, 23, 3443–3446. [Google Scholar] [CrossRef]
- Ludvigsen, M.; Aasly, K.; Ellefmo, S.L.; Hilário, A.; Ramirez-Llodra, E.; Søreide, F.X.; Falcon-Suarez, I.; Juliani, C.J.; Kieswetter, A.; Lim, A.; et al. MarMine Cruise Report—Arctic Mid-Ocean Ridge 15.08.2016–05.09.2016. 2016. Available online: https://brage.bibsys.no/xmlui/handle/11250/2427715 (accessed on 10 October 2017).
- Hannington, M.D.; Galley, A.G.; Herzig, P.M.; Petersen, S. 28. Comparison of the TAG mound and stockwork complex with Cyprus-type massive sulfide deposits. In Proceedings of the Ocean Drilling Program, Scientific Results; Texas A & M University: College Station, TX, USA, 1998; Volume 158, pp. 389–415. [Google Scholar] [CrossRef]
- Hustrulid, W.A.; Kuchta, M.; Martin, R.K. Open Pit Mine Planning and Design, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2013; Volume 1, ISBN 978-1-4822-2117-6. [Google Scholar]
- Wellmer, F.-W.; Dalheimer, M.; Wagner, M. Economic Evaluations in Exploration, 2nd ed.; Springer: Berlin, Germany; New York, NY, USA, 2008; ISBN 978-3-540-73557-1. [Google Scholar]
- Allen, P.A.; Allen, J.R. Basin Analysis: Principles and Applications, 2nd ed.; Blackwell Publishing Ltd.: Oxford, UK, 2005; ISBN 0-632-05207-4. [Google Scholar]
- Rigzone Weekly Offshore Rig Review: More Day Rates & Durations. Available online: https://www.rigzone.com/news/oil_gas/a/45027/weekly_offshore_rig_review_more_day_rates_durations/ (accessed on 18 October 2018).
- SRK Consulting. Offshore Production System Definition and Cost Study 2010. Available online: http://actnowpng.org/sites/default/files/Solwara%201%20Production%20System%20Definition%20and%20Cost%20Study%202010.pdf (accessed on 10 October 2017).
- Darling, P. SME Mining Engineering Handbook, 3rd ed.; SME: Littleton, CO, USA, 2011; ISBN 978-0-87335-264-2. [Google Scholar]
- Alvarez Grima, M.; Miedema, S.A.; van de Ketterij, R.G.; Yenigül, N.B.; van Rhee, C. Effect of high hyperbaric pressure on rock cutting process. Eng. Geol. 2015, 196, 24–36. [Google Scholar] [CrossRef]
- Van Os, A.G.; van Leussen, W. Basic research on cutting forces in saturated sand. J. Geotech. Eng. 1987, 113, 1501–1516. [Google Scholar] [CrossRef]
- SMD Deliver Deep Sea Mining Vehicles. Available online: https://www.smd.co.uk/smd-deliver-deep-sea-mining-vehicles/ (accessed on 18 October 2018).
- Miedema, S.A. The Delft Sand, Clay and Rock Cutting Model, 3rd ed.; IOS Press: Amsterdam, The Netherlands, 2014; ISBN 978-94-6186-539-7. [Google Scholar]
- Helmons, R.L.J.; Miedema, S.A.; Alvarez Grima, M.; van Rhee, C. Modeling fluid pressure effects when cutting saturated rock. Eng. Geol. 2016, 211, 50–60. [Google Scholar] [CrossRef]
- Helmons, R.L.J.; Miedema, S.A.; van Rhee, C. Simulating hydro mechanical effects in rock deformation by combination of the discrete element method and the smoothed particle method. Int. J. Rock Mech. Min. Sci. 2016, 86, 224–234. [Google Scholar] [CrossRef]
- Helmons, R.L.J. Excavation of Hard Deposits and Rocks: On the Cutting of Saturated Rock. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2017. [Google Scholar]
- Spagnoli, G.; Miedema, S.A.; Herrmann, C.; Rongau, J.; Weixler, L.; Denegre, J. Preliminary Design of a Trench Cutter System for Deep-Sea Mining Applications Under Hyperbaric Conditions. IEEE J. Ocean. Eng. 2016, 41, 930–943. [Google Scholar] [CrossRef]
- Detournay, E.; Atkinson, C. Influence of pore pressure on the drilling response in low-permeability shear-dilatant rocks. Int. J. Rock Mech. Min. Sci. 2000, 37, 1091–1101. [Google Scholar] [CrossRef]
- Copper Prices—45 Year Historical Chart. Available online: https://www.macrotrends.net/1476/copper-prices-historical-chart-data (accessed on 18 October 2018).
- Zinc—Monthly Price—Commodity Prices—Price Charts, Data, and News—IndexMundi. Available online: https://www.indexmundi.com/commodities/?commodity=zinc&months=300 (accessed on 18 October 2018).
- Market Index: Gold. Available online: https://www.marketindex.com.au/gold (accessed on 18 October 2018).
- Market Index: Silver. Available online: https://www.marketindex.com.au/silver (accessed on 18 October 2018).
- Ludwig, R.J.; Iturrino, G.J.; Rona, P.A. 23. Seismic velocity-porosity relationship of sulfide, sulfate, and basalt samples from the TAG hydrothermal mound. In Proceedings of the Ocean Drilling Program, Scientific Results; Texas A & M University: College Station, TX, USA, 1998; Volume 158, pp. 313–328. [Google Scholar] [CrossRef]
- Zhu, W.; Tivey, M.K.; Gittings, H.; Craddock, P.R. Permeability-porosity relationships in seafloor vent deposits: Dependence on pore evolution processes. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef]
- Waquet, B.; Fouquet, Y. Evolution of geotechnical properties in hydrothermal sulfide mounds: A maturation threshold. In SME Annual Meeting; SME: Denver, CO, USA, 2011. [Google Scholar]
- Yamazaki, T.; Park, S.-H. Relationships between Geotechnical Engineering Properties and Assay of Seafloor Massive Sulfides. In Proceedings of the Thirteenth (2003) International Offshore and Polar Engineering Conference, Honolulu, HI, USA, 25–30 May 2003; pp. 310–316. [Google Scholar]
- Nayar, K.G.; Sharqawy, M.H.; Banchik, L.D.; Lienhard, V.J.H. Thermophysical properties of seawater: A review and new correlations that include pressure dependence. Desalination 2016, 390, 1–24. [Google Scholar] [CrossRef]
- Golder Associates. Scoping Study of Proposed Mining of Nussir Copper Prospect; W. Finnmark: Vadsø, Norway, 2009; p. 118. [Google Scholar]
- InfoMine USA, Cost Models. Available online: http://costs.infomine.com/costdatacenter/miningcostmodel.aspx (accessed on 10 October 2017).
- Yamazaki, T.; Takeda, Y.; Arai, R.; Nakatani, N. Economic Seafloor Massive Sulfide Mining by Japan’s Model. In Proceedings of the ASME 2016 35th International Conference on Ocean, Offshore and Arctic Engineering, Busan, Korea, 19–24 June 2016. [Google Scholar]
- Eyyuboglu, E.M.; Bolukbasi, N. Effects of circumferential pick spacing on boom type roadheader cutting head performance. Tunn. Undergr. Space Technol. 2005, 20, 418–425. [Google Scholar] [CrossRef]
- Li, X.Y.; Lv, Y.G.; Jiang, S.B.; Zeng, Q.L. Effects of spiral line for pick arrangement on boom type roadheader cutting load. Int. J. Simul. Modell. 2016, 15, 170–180. [Google Scholar] [CrossRef]
- Van der Wal, R.J.; de Boer, G. Downtime Analysis Techniques for Complex Offshore and Dredging Operations. In Proceedings of the 23rd International Conference on Offshore Mechanics and Arctic Engineering, Vancouver, BC, Canada, 20–25 June 2004; Volume 2, pp. 93–101. [Google Scholar]
- DNV GL DNV-OS-H101: Marine Operations, General October 2011. Available online: https://rules.dnvgl.com/docs/pdf/DNV/codes/docs/2011-10/Os-H101.pdf (accessed on 18 October 2018).
- Gintautas, T.; Sørensen, J. Improved Methodology of Weather Window Prediction for Offshore Operations Based on Probabilities of Operation Failure. J. Mar. Sci. Eng. 2017, 5, 20. [Google Scholar] [CrossRef]
- Natvig, B.J.; Johnsen, O.; Grimsrud, G.; Smith, D. Weather-Dependent Operability for Offshore Single Lift Jacket Deck Removals. In Proceedings of the Eleventh (2001) International Offshore and Polar Engineering Conference, Stavanger, Norway, 17–22 June 2001; The International Society of Offshore and Polar Engineers: Stavanger, Norway, 2001; Volume 1, pp. 129–135. [Google Scholar]
- Sandvik, E.; Gutsch, M.; Asbjørnslett, B.E. A simulation-based ship design methodology for evaluating susceptibility to weather-induced delays during marine operations. Ship Technol. Res. 2018, 65, 137–152. [Google Scholar] [CrossRef]
- Tekle Muhabie, Y.; Rigo, P.; Cepeda, M.; de Almeida D’Agosto, M.; Caprace, J.-D. A discrete-event simulation approach to evaluate the effect of stochastic parameters on offshore wind farms assembly strategies. Ocean Eng. 2018, 149, 279–290. [Google Scholar] [CrossRef]
- Dekker, R. Applications of maintenance optimization models: A review and analysis. Reliab. Eng. Syst. Saf. 1996, 51, 229–240. [Google Scholar] [CrossRef]
- Lazakis, I.; Turan, O.; Alkaner, S.; Olcer, A. Effective ship maintenance strategy using a risk and criticality based approach. In Proceedings of the 13th International Congress of the International Maritime Association of the Mediterranean (IMAM 2009), Istanbul, Turkey, 12–15 October 2009; p. 9. [Google Scholar]
- Barlow, R.; Hunter, L. Optimum Preventive Maintenance Policies. Oper. Res. 1960, 8, 90–100. [Google Scholar] [CrossRef]
- Warrington, L.; Jones, J.A.; Davis, N. Modelling of maintenance, within discrete event simulation. In Proceedings of the Annual Reliability and Maintainability Symposium, Seattle, WA, USA, 28–31 January 2002; pp. 260–265. [Google Scholar]
- Alrabghi, A.; Tiwari, A. A novel approach for modelling complex maintenance systems using discrete event simulation. Reliab. Eng. Syst. Saf. 2016, 154, 160–170. [Google Scholar] [CrossRef]
- Cao, D.; Sun, Y.; Guo, H. Optimizing maintenance policies based on discrete event simulation and the OCBA mechanism. In Proceedings of the Annual Reliability and Maintainability Symposium (RAMS), Orlando, FL, USA, 28–31 January 2013; pp. 1–6. [Google Scholar]
- Stahlbock, R.; Voß, S. Operations research at container terminals: A literature update. OR Spectr. 2008, 30, 1–52. [Google Scholar] [CrossRef]
- Legato, P.; Mazza, R.M. Berth planning and resources optimisation at a container terminal via discrete event simulation. Eur. J. Oper. Res. 2001, 133, 537–547. [Google Scholar] [CrossRef]
- Bichou, K.; Bell, M.G.H.; Evans, A. (Eds.) Risk Management in Port Operations, Logistics and Supply-Chain Security, 1st ed.; Informa: London, UK, 2007; ISBN 978-1-84311-655-4. [Google Scholar]
- Chahar, K.; Cheng, C.; Pranoto, Y. Strategic crew planning tool in railroad: A discrete event simulation. In Proceedings of the 2011 Winter Simulation Conference (WSC), Phoenix, AZ, USA, 11–14 December 2011; pp. 3688–3698. [Google Scholar]
- Fatnassi, E.; Chaouachi, J. Discrete Event Simulation of Loading Unloading Operations in a Specific Intermodal Transportation Context. In Software Engineering Perspectives and Application in Intelligent Systems; Silhavy, R., Senkerik, R., Oplatkova, Z.K., Silhavy, P., Prokopova, Z., Eds.; Advances in Intelligent Systems and Computing; Springer International Publishing: Cham, Switzerland, 2016; pp. 435–444. [Google Scholar]
- Riley, L.A. Discrete-event Simulation Optimization: A Review of Past Approaches and Propositions for Future Direction. In Proceedings of the 2013 Summer Computer Simulation Conference, Toronto, ON, Canada, 7–10 July 2013; Society for Modeling & Simulation International: Vista, CA, USA, 2013; pp. 47:1–47:8. [Google Scholar]
| Size of Block | 2 m × 2 m × 2 m |
|---|---|
| Cu-rich number of blocks | 4654 |
| Zn-rich number of blocks | 4231 |
| Si-rich number of blocks | 26,191 |
| Total deposit blocks | 35,076 |
| Deposit volume | 280,608 m3 |
| Parameter | Value |
|---|---|
| Cutting speed, | 1 m/s |
| Blade width, w | 0.1 m |
| Blade angle, | |
| External friction angle, |
| Parameter | Total Daily Cost in USD |
|---|---|
| Production Support Vessel | 144,796 |
| Seafloor Mining Equipment | 20,130 |
| Work-class ROV’s | 20,190 |
| RALS | 23,184 |
| Support Services | 15,235 |
| Barging | 12,694 |
| TOTAL | 236,949 |
| Commodity | Price in USD/t |
|---|---|
| Cu [33] | 6215 |
| Zn [34] | 2270 |
| Au [35] | 40,877,880 |
| Ag [36] | 592,733 |
| Commodity | NF | |
|---|---|---|
| Cu | 65% | 90% |
| Zn | 50% | 90% |
| Au | 98% | 80% |
| Ag | 95% | 80% |
| Element | Mean | Standard Deviation | Maximum Value | Minimum Value |
|---|---|---|---|---|
| Cu-Rich | ||||
| Cu | 2.69 wt% | 2.13 wt% | 8.8 wt% | 0.10 wt% |
| Zn | 0.37 wt% | 0.93 wt% | 3.9 wt% | 0.01 wt% |
| Au | 406.25 ppb | 490.93 ppb | 2160 ppb | 20 ppb |
| Ag | 18.3 ppm | 15.5 ppm | 105 ppm | 0.5 ppm |
| Zn-Rich | ||||
| Cu | 3.26 wt% | 1.57 wt% | 8.8 wt% | 0.1 wt% |
| Zn | 1.12 wt% | 0.39 wt% | 3.4 wt% | 0.7 wt% |
| Au | 765.1 ppb | 179.1 ppb | 2160 ppb | 3.4 ppb |
| Ag | 26.1 ppm | 14.8 ppm | 105 ppm | 8.0 ppm |
| Si-Rich | ||||
| Cu | 2.16 wt% | 0.7 wt% | 3.8 wt% | 0.03 wt% |
| Zn | 0.0128 wt% | 0.0017 wt% | 0.02 wt% | 0.01 wt% |
| Au | 174.8 ppb | 53.2 ppb | 350 ppb | 60 ppb |
| Ag | 0.724 ppm | 0.093 ppm | 1 ppm | 0.5 ppm |
| Element | Mean | Standard Deviation | Maximum Value | Minimum Value |
|---|---|---|---|---|
| Cu-rich | 7.97% | 3.45% | 15.95% | 3.42% |
| Zn-rich | 7.82% | 3.83% | 15.95% | 3.59% |
| Si-rich | 3.46% | 2.09% | 6.48% | 1.17% |
| Element | Mean | Standard Deviation | Maximum Value | Minimum Value |
|---|---|---|---|---|
| Cu-rich | 3.84 g/cm3 | 0.37 g/cm3 | 4.96 g/cm3 | 2.98 g/cm3 |
| Zn-rich | 3.87 g/cm3 | 0.27 g/cm3 | 4.96 g/cm3 | 3.39 g/cm3 |
| Si-rich | 3.37 g/cm3 | 0.27 g/cm3 | 4.43 g/cm3 | 2.90 g/cm3 |
| Salinity in g/kg | ||
|---|---|---|
| 35 | 120 | |
| 0 | 1.906 × 10−3 | 2.328 × 10−3 |
| 10 | 1.397 × 10−3 | 1.714 × 10−3 |
| Salinity in g/kg | |||
|---|---|---|---|
| 30 | 40 | 120 | |
| 0 | 43.5 | 44.5 | 34.9 |
| 10 | 42.6 | 41.7 | 33.5 |
| Processing Plant Capacity in Mtpa (Million Tonnes per Annum) | Processing Costs in USD/t |
|---|---|
| Nussir [42] (Section 10.6 therein) | |
| 0.6 | 13 |
| 1 | 11.5 |
| InfoMine [43] (CM 132, Table 4 therein) | |
| 0.7 | 19.47 |
| 1.8 | 14.83 |
| Element | Grade | In-Situ Tonnage, Pure Metal |
|---|---|---|
| Cu | 2.29 wt% | 21,305.46 |
| Zn | 0.18 wt% | 1832.03 |
| Au | 271.00 ppb | 0.26 |
| Ag | 6.07 ppm | 5.98 |
| Designation | Mean | Standard Deviation |
|---|---|---|
| 4.17% | 2.67% | |
| Grain density | 3.44 g/cm3 | 0.52 g/cm3 |
| Bulk density | 3.29 g/cm3 | 0.48 g/cm3 |
| k | 5.79 × 10−17 m2 | 2.03 × 10−16 m2 |
| UCS | 95.84 MPa | 13.96 MPa |
| BTS | 4.13 MPa | 0.10 MPa |
| c | 22.35 MPa | 3.23 MPa |
| Total Mining Time in Days | |||
|---|---|---|---|
| 0.10 | 0.98 | 183.53 | 596.06 |
| 0.09 | 0.98 | 183.29 | 595.28 |
| 0.08 | 0.97 | 183.01 | 594.36 |
| 0.07 | 0.97 | 182.59 | 593.00 |
| 0.06 | 0.97 | 182.08 | 591.35 |
| 0.05 | 0.96 | 181.35 | 589.00 |
| 0.04 | 0.94 | 179.86 | 584.14 |
| 0.03 | 0.93 | 178.24 | 578.89 |
| 0.02 | 0.86 | 171.80 | 557.96 |
| 0.01 | 0.50 | 135.31 | 439.45 |
| Blocks | |||
| in m | Number of blocks with positive economic value | Number of blocks with negative economic value | Ratio positive/negative |
| 0.10 | 3413 | 31,663 | 0.11 |
| 0.01 | 5776 | 29,300 | 0.20 |
| Economic Values | |||
| in m | Mean block value in USD | Standard deviation block value in USD | Deposit value in USD |
| 0.10 | −1983.9 | 1485.8 | −69,587,650 |
| 0.01 | −926.0 | 1400.6 | −32,479,093 |
| Blocks | |||
| Number of blocks with positive economic value | Number of blocks with negative economic value | Ratio positive/negative | |
| 1 | 5776 | 29,300 | 0.20 |
| 0.75 | 3422 | 31,654 | 0.11 |
| 0.5 | 1255 | 33,821 | 0.04 |
| Economic values | |||
| Mean block value in USD | Standard deviation block value in USD | Deposit value in USD | |
| 1 | −926 | 1401 | −32,479,093 |
| 0.75 | −1916 | 1444 | −67,188,222 |
| 0.5 | −3895 | 1546 | −136,606,480 |
| Blocks | |||
| in MW | Number of blocks with positive economic value | Number of blocks with negative economic value | Ratio positive/negative |
| 1 | 5776 | 29,300 | 0.20 |
| 2 | 20,930 | 14,146 | 1.48 |
| 3 | 30,117 | 4959 | 6.07 |
| Economic values | |||
| in MW | Mean block value in $ | Standard deviation block value in $ | Deposit value in $ |
| 1 | −926 | 1401 | −32,479,093 |
| 2 | 558 | 1345 | 19,584,601 |
| 3 | 1053 | 1329 | 36,939,166 |
| Blocks | |||
| in $/t | Number of blocks with positive economic value | Number of blocks with negative economic value | Ratio positive/negative |
| 14.60 | 31,823 | 3253 | 9.78 |
| 19.47 | 30,117 | 4959 | 6.07 |
| 24.34 | 28,054 | 7022 | 4.00 |
| Economic values | |||
| in $/t | Mean block value in $ | Standard deviation block value in $ | Deposit value in $ |
| 14.60 | 1187 | 1339 | 41,641,513 |
| 19.47 | 1053 | 1329 | 36,939,166 |
| 24.34 | 919 | 1320 | 32,236,818 |
| Base Case | ||
|---|---|---|
| Parameter | Value | |
| 2 MW | ||
| 0.75 | ||
| 0.05 m | ||
| 19.47 $/t | ||
| High and low scenarios | ||
| Low | High | |
| 1.5 MW | 2.5 MW | |
| 0.56 | 0.94 | |
| 0.06 m | 0.04 m | |
| 24.34 $/t | 14.60 $/t | |
| Base Case | ||
|---|---|---|
| Deposit’s economic value | −$21.4 m | |
| High and low scenarios | ||
| Low | High | |
| −$52.4 m | −$2.8 m | |
| −$53.0 m | −$2.6 m | |
| −$21.8 m | −$20.6 m | |
| −$26.1 m | −$16.7 m | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lesage, M.; Juliani, C.; Ellefmo, S.L. Economic Block Model Development for Mining Seafloor Massive Sulfides. Minerals 2018, 8, 468. https://doi.org/10.3390/min8100468
Lesage M, Juliani C, Ellefmo SL. Economic Block Model Development for Mining Seafloor Massive Sulfides. Minerals. 2018; 8(10):468. https://doi.org/10.3390/min8100468
Chicago/Turabian StyleLesage, Maxime, Cyril Juliani, and Steinar L. Ellefmo. 2018. "Economic Block Model Development for Mining Seafloor Massive Sulfides" Minerals 8, no. 10: 468. https://doi.org/10.3390/min8100468
APA StyleLesage, M., Juliani, C., & Ellefmo, S. L. (2018). Economic Block Model Development for Mining Seafloor Massive Sulfides. Minerals, 8(10), 468. https://doi.org/10.3390/min8100468





