CO2 Absorption and Magnesium Carbonate Precipitation in MgCl2–NH3–NH4Cl Solutions: Implications for Carbon Capture and Storage
Abstract
1. Introduction
1.1. CO2 Mineral Sequestration
1.2. Chemistry and Kinetics of the CO2–MgCl2–NH3–NH4Cl System
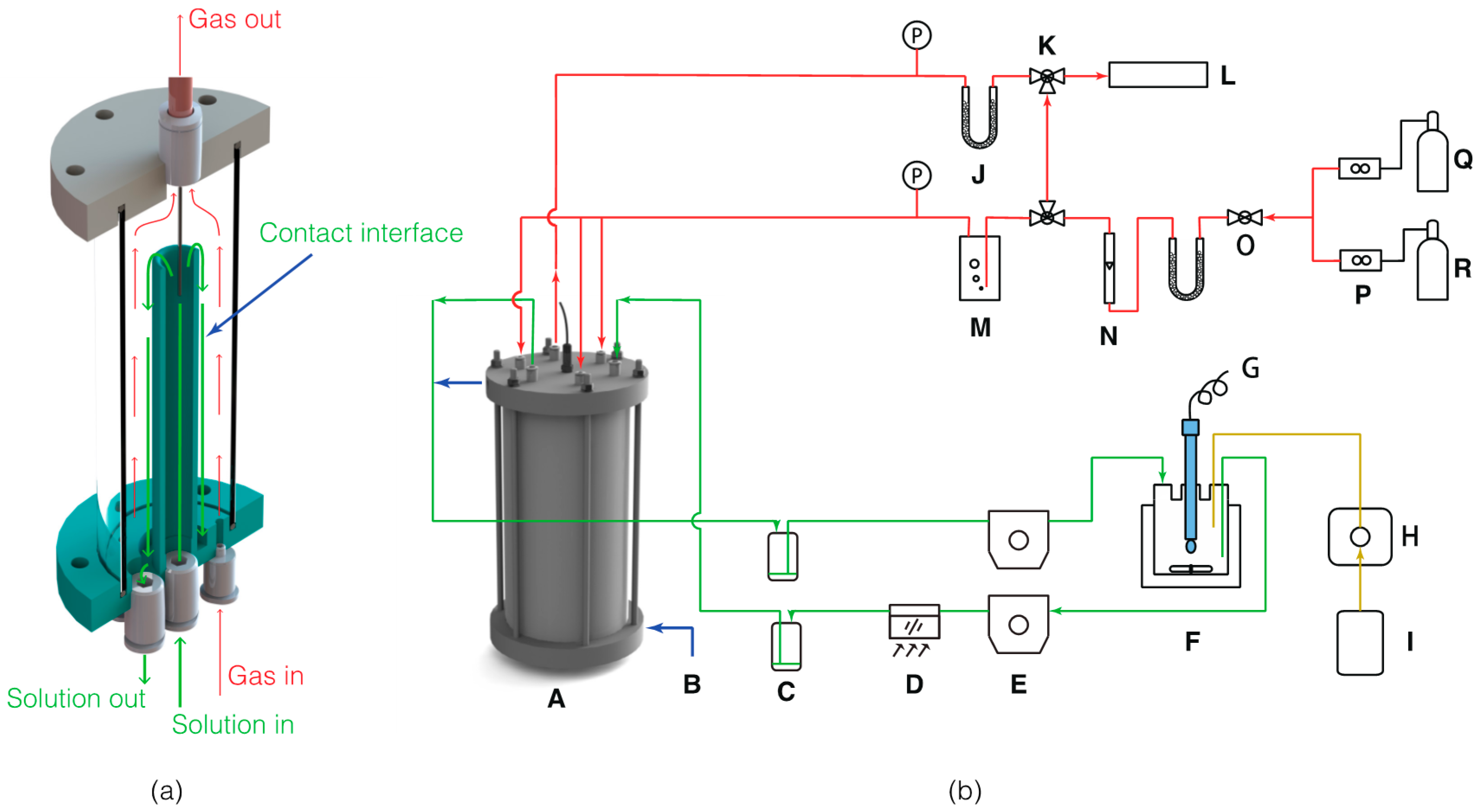
2. Materials and Methods
2.1. Reagents
2.2. Absorption Experiments
2.3. Mg-Carbonate Precipitation and Phase Transformation Experiments
2.4. Theoretical Modeling of Solution Chemistry
3. Results
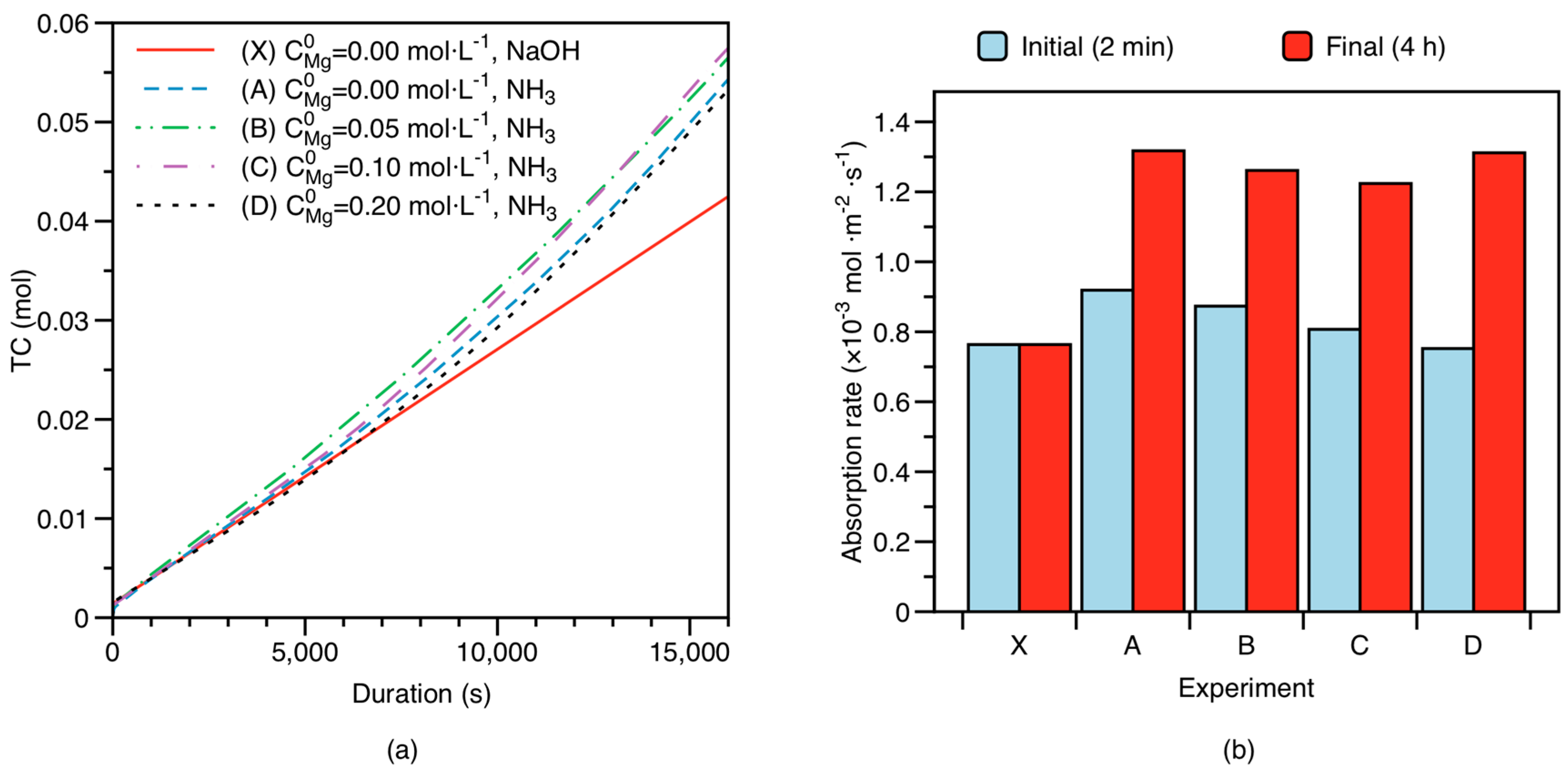
3.1. CO2 Absorption under Changing Mg Initial Concentration
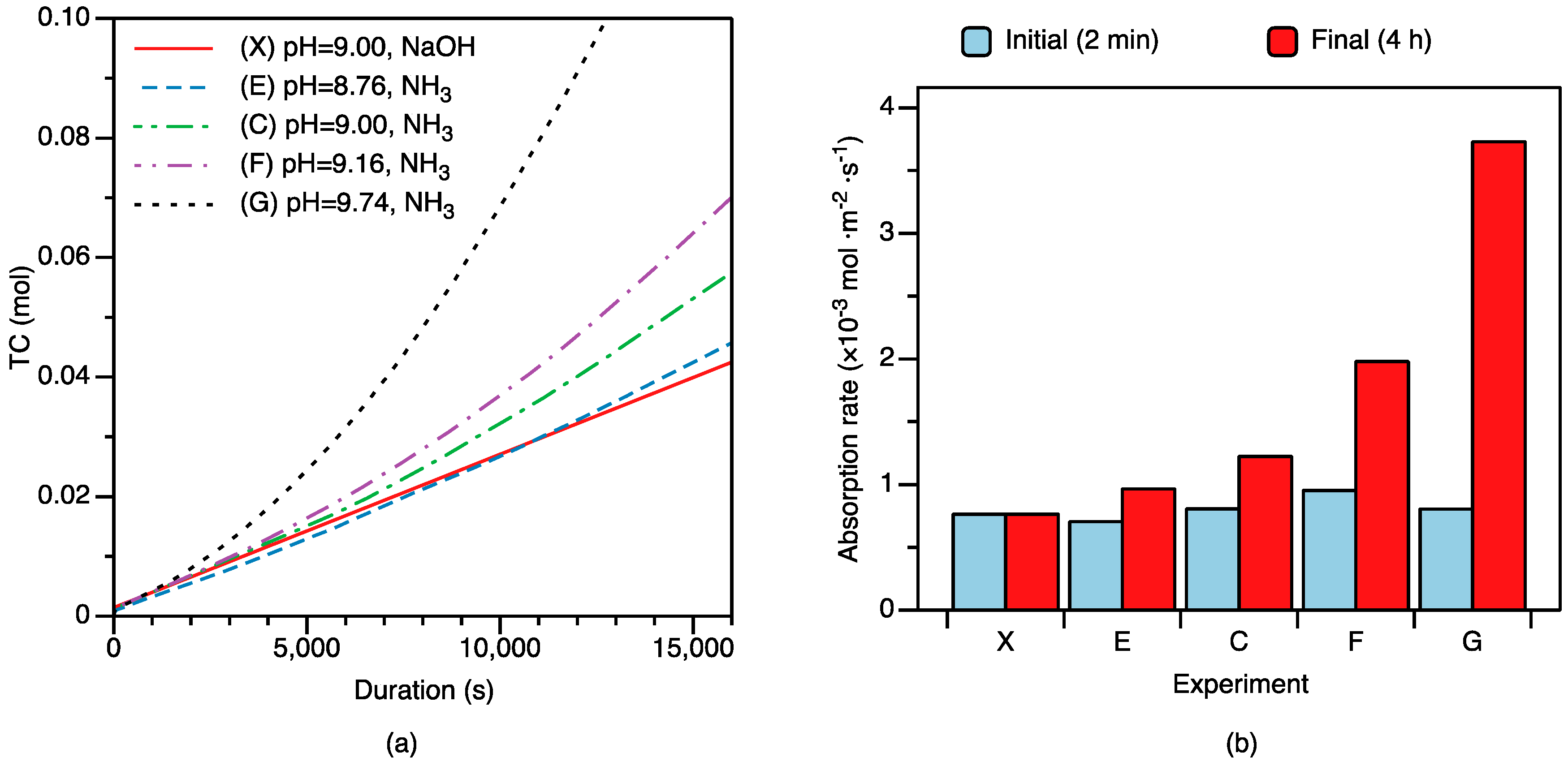
3.2. CO2 Absorption under Changing Solution pH
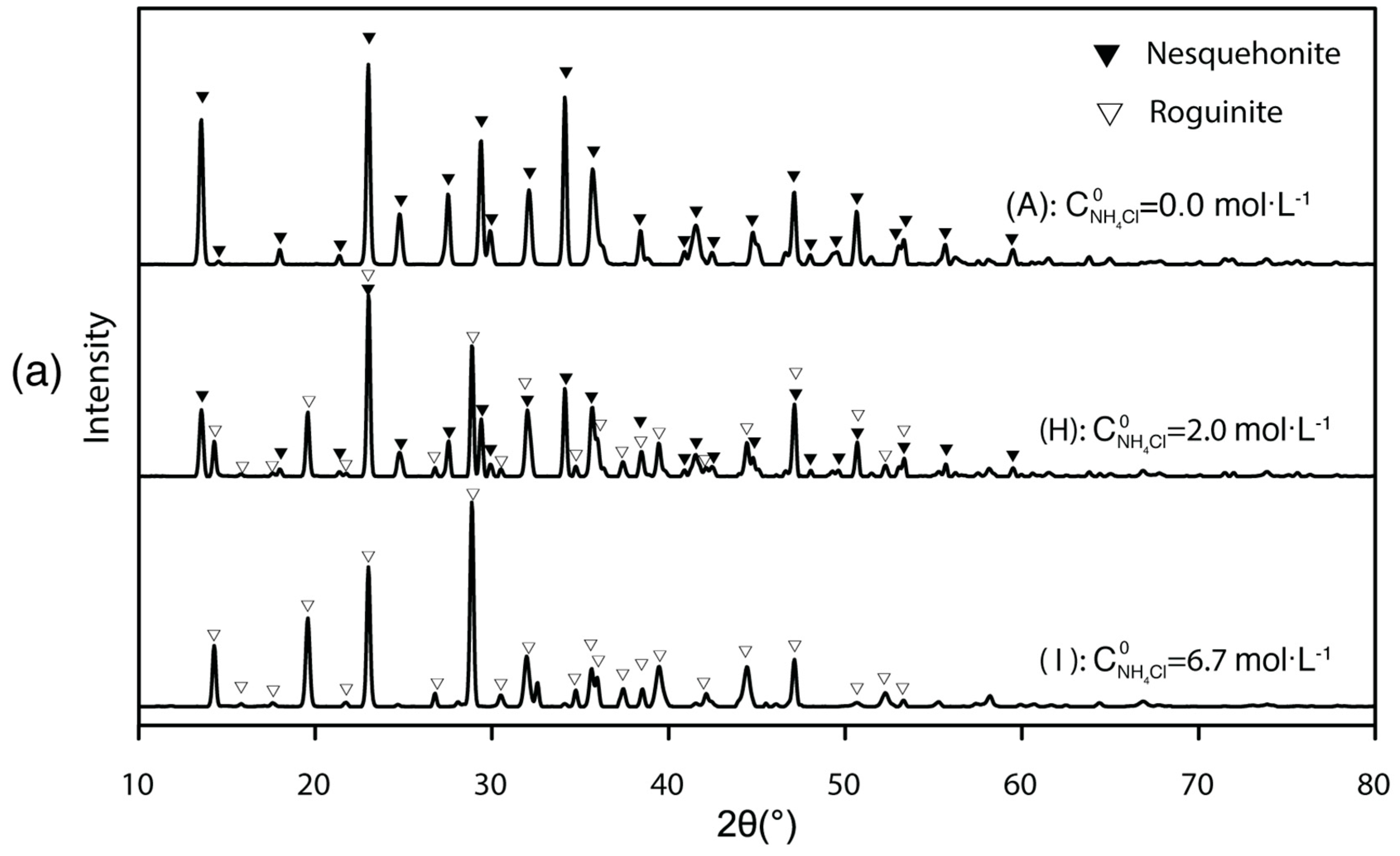
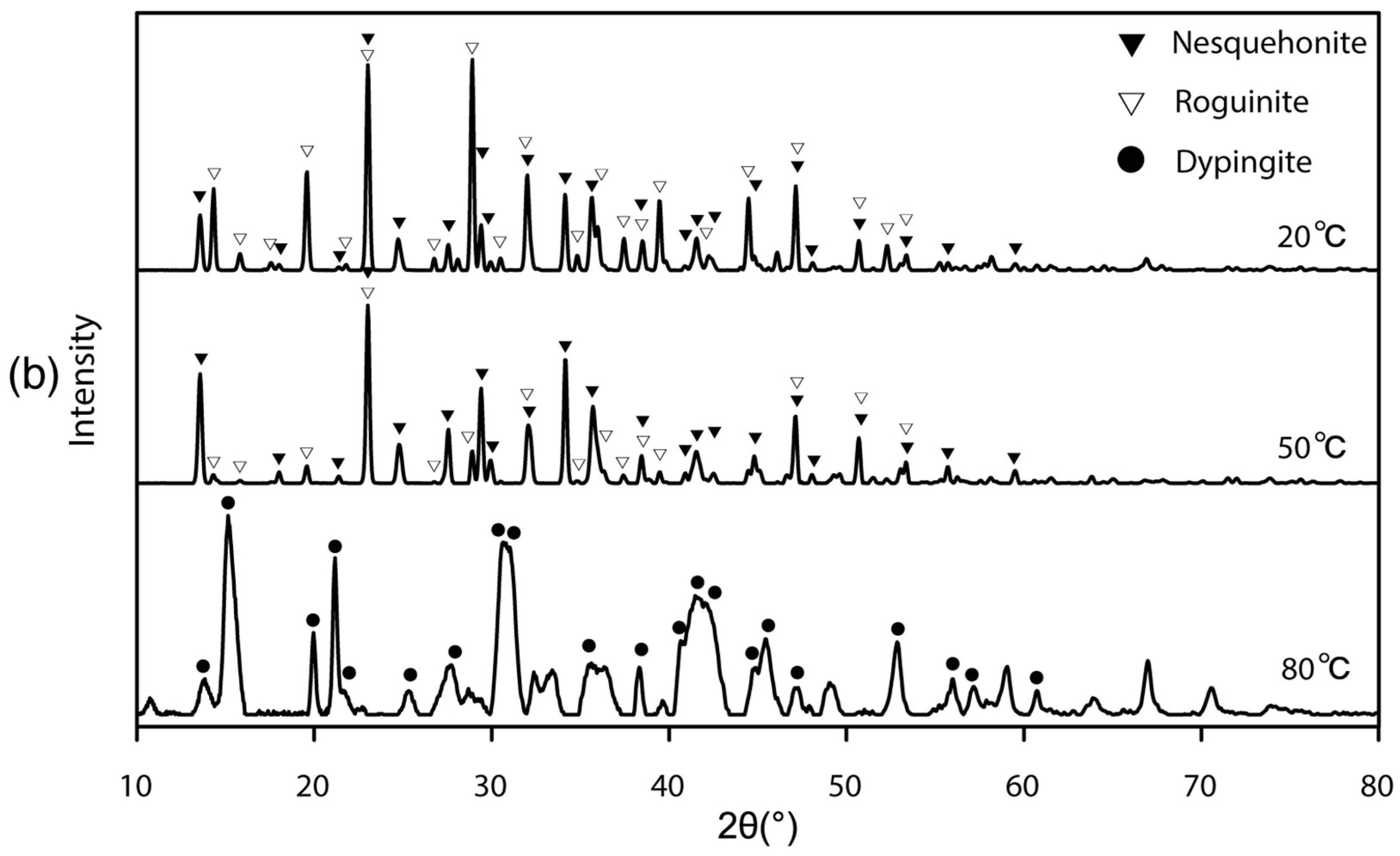
3.3. Mg-Carbonate Precipitated under Changing Ammonium Concentration and Its Purification
4. Discussion
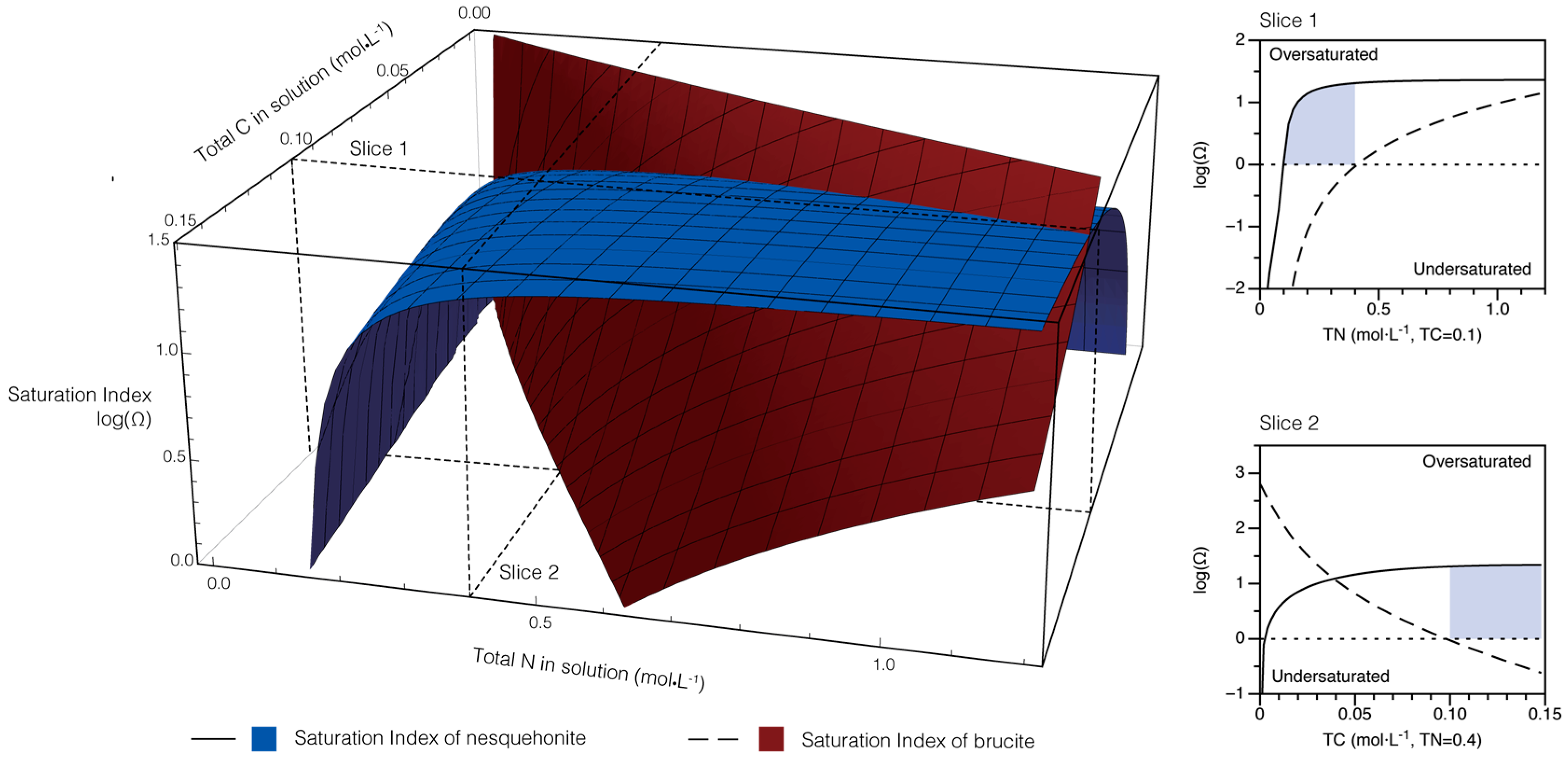
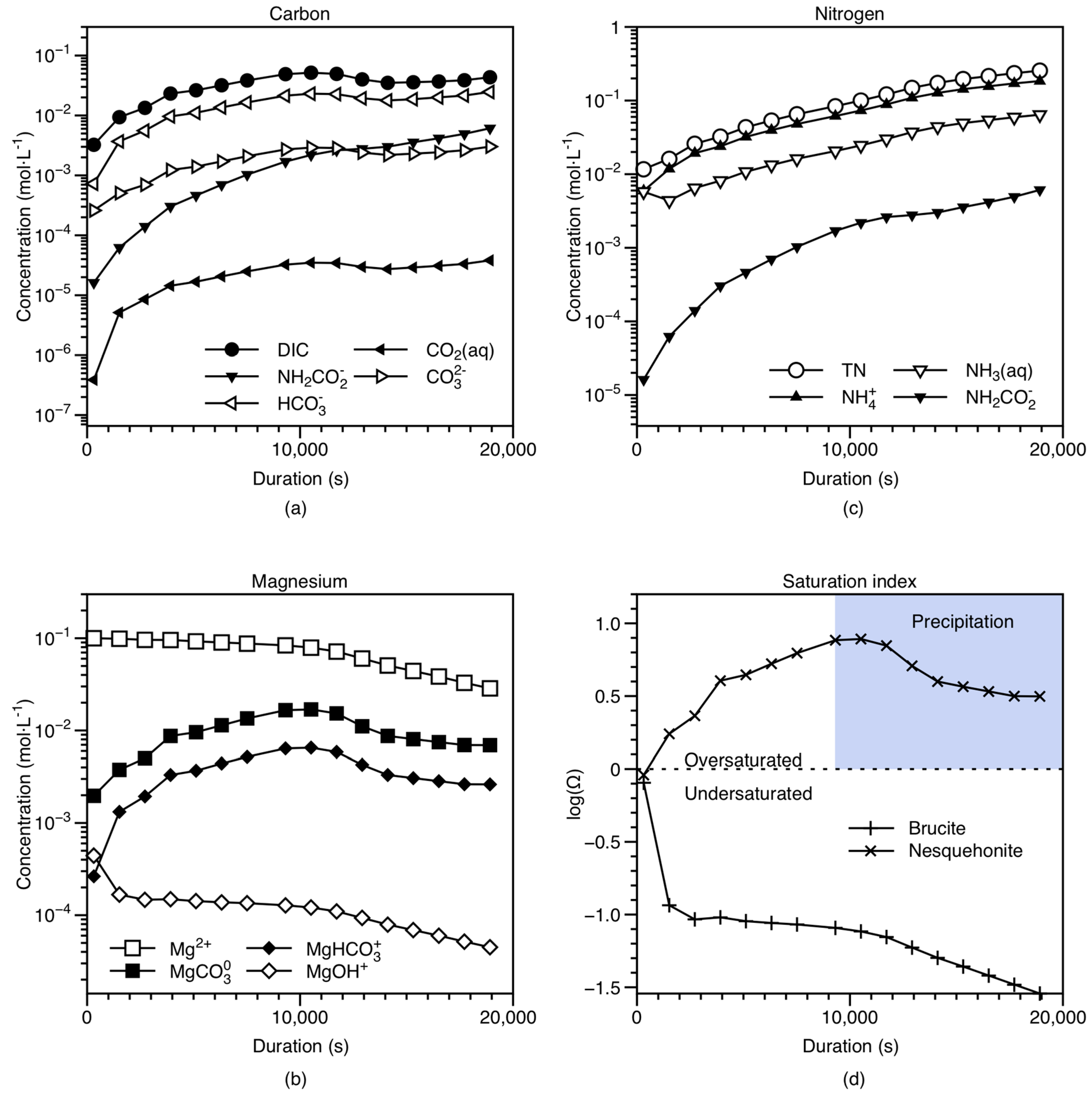
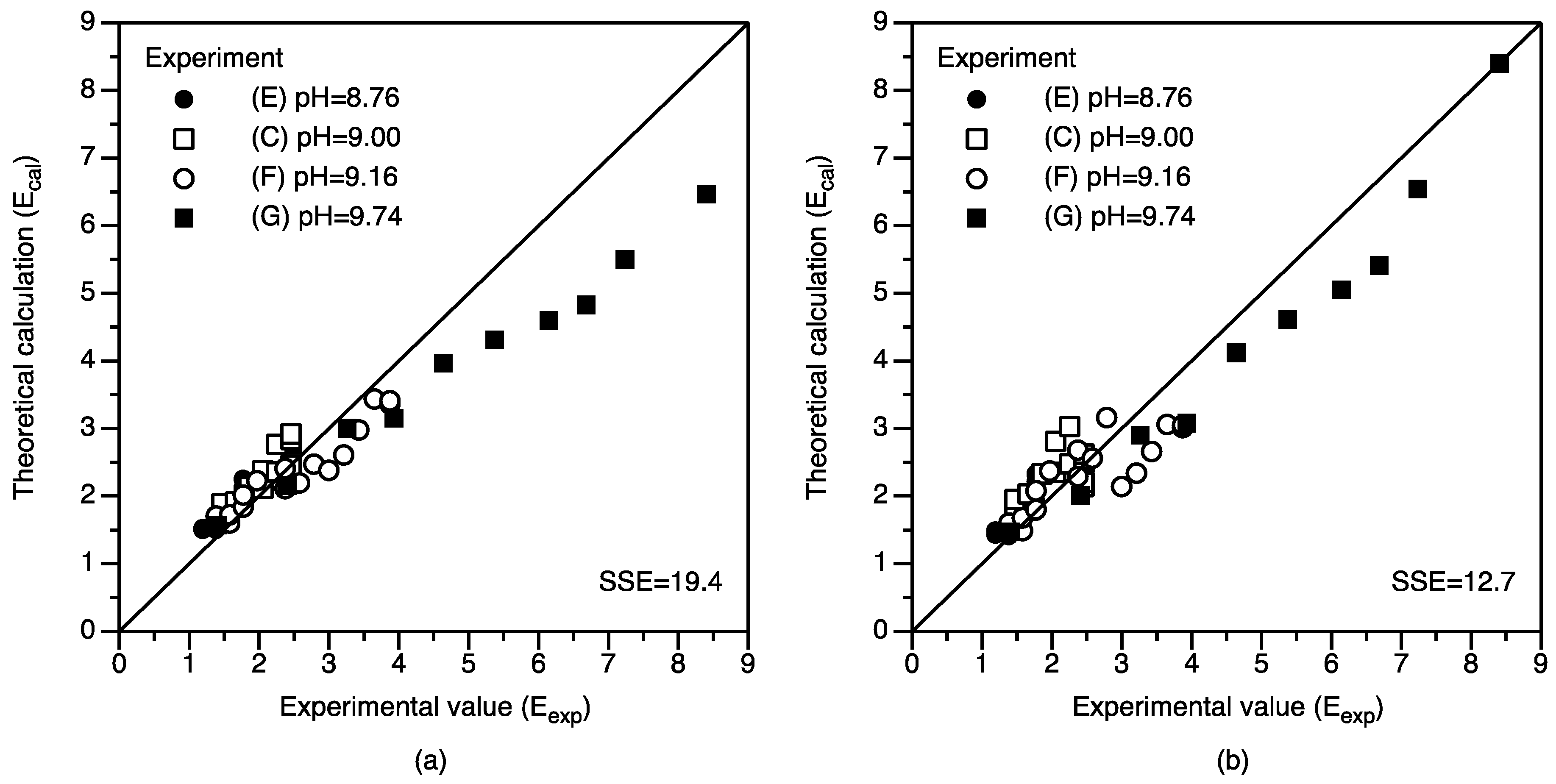
4.1. Modeling of Solution Chemistry and Temporal Evolution
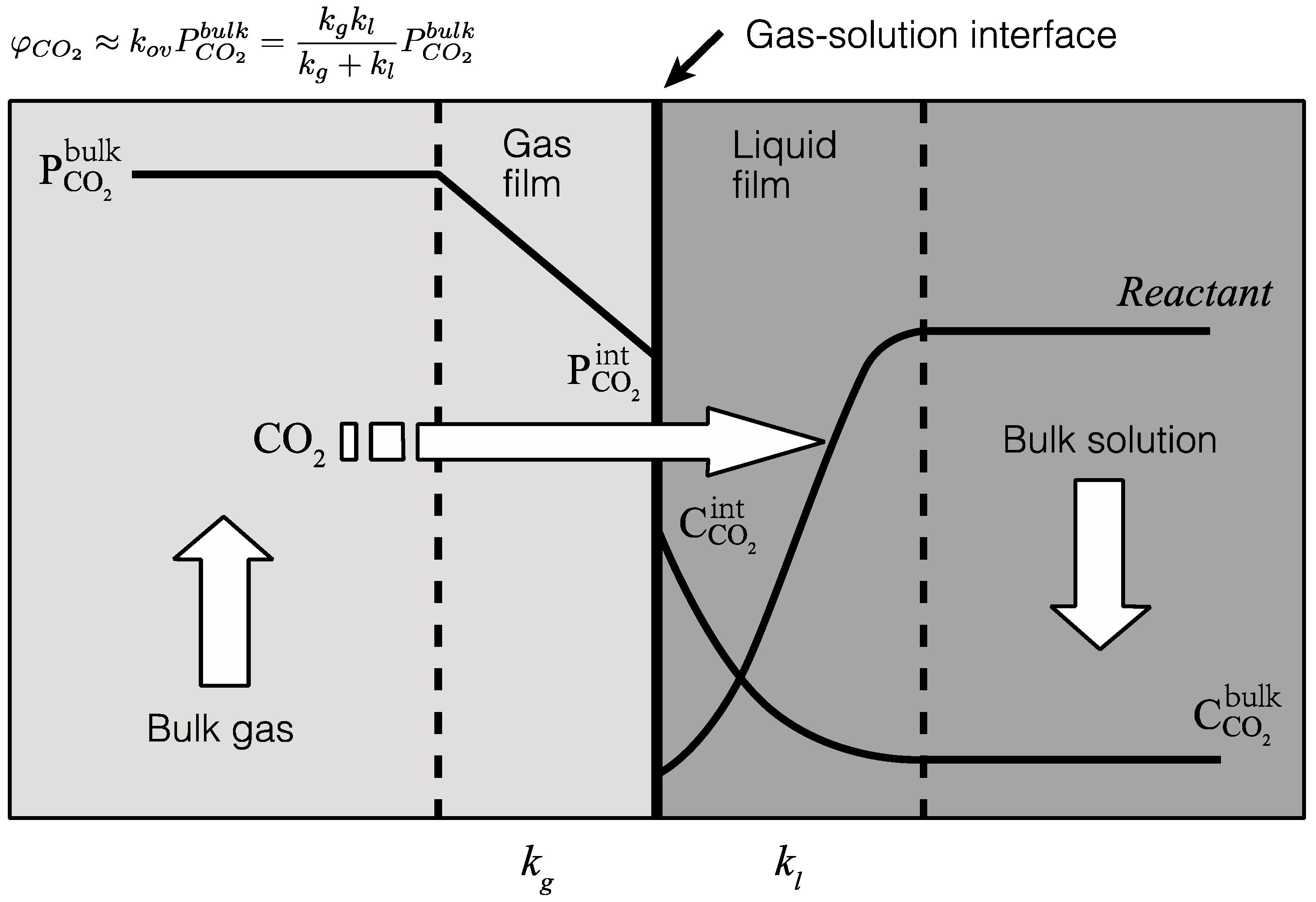
4.2. Gas-Solution Interface Kinetics
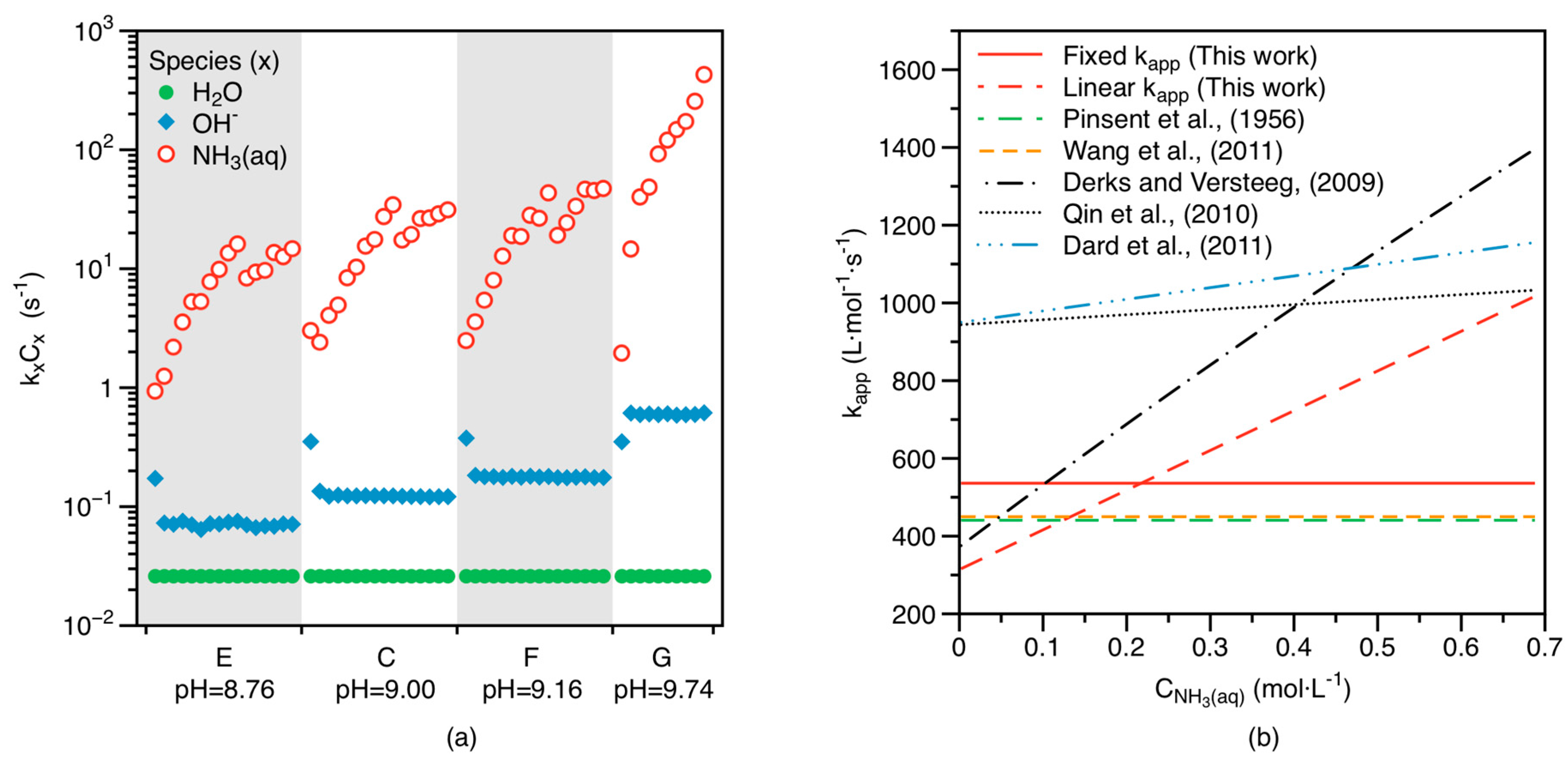
4.2.1. Reaction Kinetics between CO2 and NH3
4.2.2. Factors Controlling CO2 Absorption
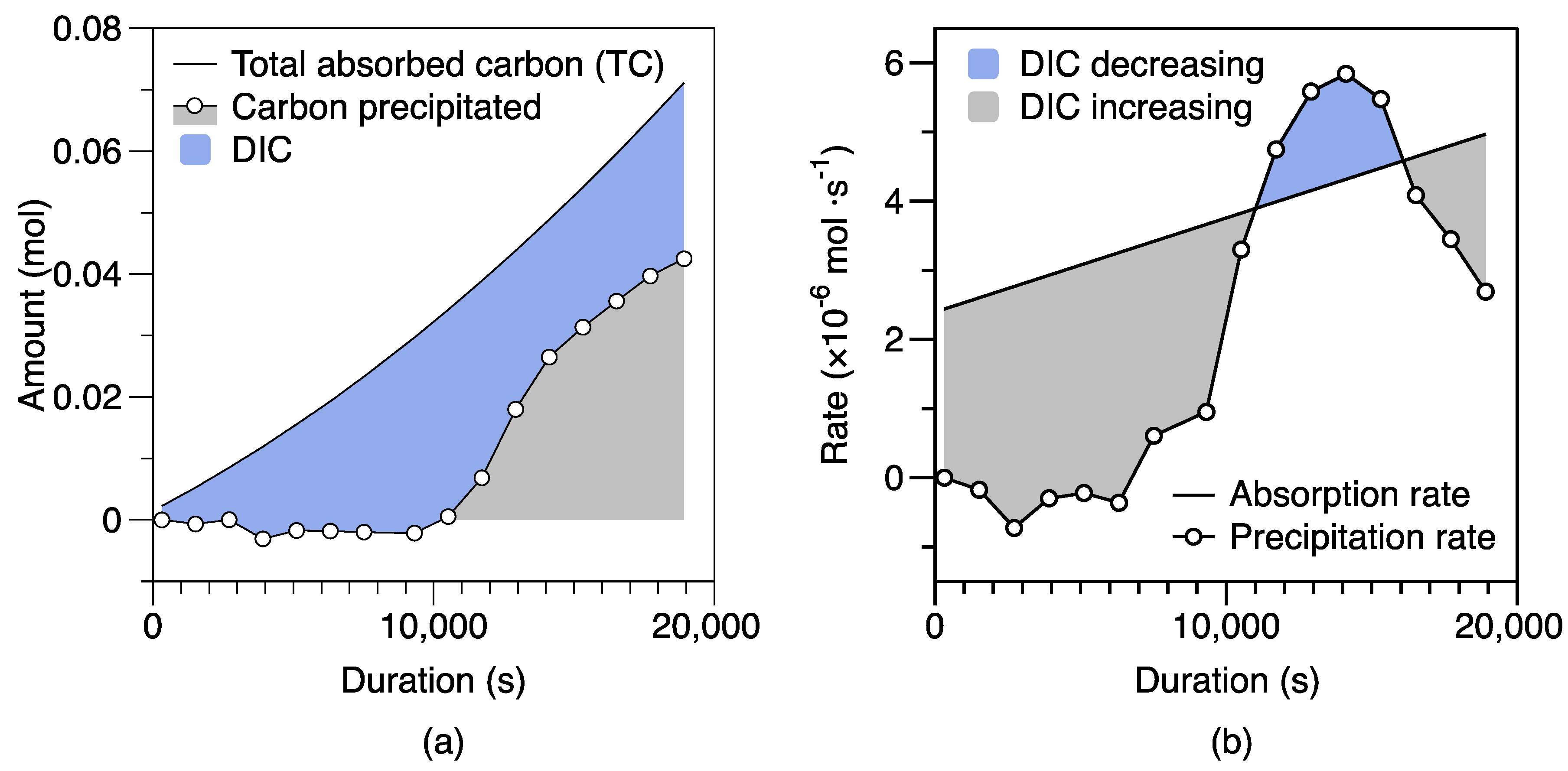
4.3. Mg-carbonate Precipitation and Phase Transformation
4.3.1. Nesquehonite Precipitation Kinetics
4.3.2. Phase Transformation of Less Stable to More Stable Carbonation Products
4.4. Implications for Industrial Applications
5. Conclusions
- (1)
- Careful design and theoretical modeling of solution chemistry led to the precipitation of high-purity nesquehonite in NH4Cl-free experiments.
- (2)
- The gas-side and liquid-side mass transfer coefficients were estimated through combining experimental data and a two-film mass transfer model. Notably, the CO2 mass transfer resistance on the liquid side was found to be greater than the gas side, suggesting that the liquid-side reaction is the major limiting step in the overall reaction and that a higher liquid-side mass transfer coefficient should promote CO2 absorption.
- (3)
- Interaction of CO2(aq) with NH3(aq) is a critical process controlling CO2 mass transfer from the gas to the solid phase. Based on the zwitterion mechanism, NH3(aq) concentration correlates closely with the apparent rate constant of the CO2–NH3(aq) reaction (), pointing to the importance of NH3 in the overall reaction. Together with the literature data, our results suggest that increasing temperature, pH, and NH3(aq) concentration would facilitate CO2 absorption.
- (4)
- The solid products are sensitive to ambient conditions and treatments. If the initial ammonium nitrogen concentration is low ( < 2), only nesquehonite would precipitate; if > 2, roguinite would appear. High pH value and high Mg concentration could help nesquehonite overcome the nucleation energy barrier and facilitate carbonation. Thus, besides adjusting pH, adding dissolved Mg is likely an effective way to enhance the precipitation rate of Mg-carbonate.
- (5)
- Industrially useful and more stable materials could be obtained with designed treatments of the solid products. Specifically, washing nesquehonite and roguinite in hot water (>50 °C) could convert those minerals to more basic forms of Mg-carbonate (e.g., dypingite).
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Seifritz, W. CO2 disposal by means of silicates. Nature 1990, 345, 486. [Google Scholar] [CrossRef]
- Park, A.-H.A.; Fan, L.-S. Mineral sequestration: Physically activated dissolution of serpentine and pH swing process. Chem. Eng. Sci. 2004, 59, 5241–5247. [Google Scholar] [CrossRef]
- Béarat, H.; McKelvy, M.J.; Chizmeshya, A.V.G.; Gormley, D.; Nunez, R.; Carpenter, R.W.; Squires, K.; Wolf, G.H. Carbon Sequestration via Aqueous Olivine Mineral Carbonation: Role of Passivating Layer Formation. Environ. Sci. Technol. 2006, 40, 4802–4808. [Google Scholar] [CrossRef] [PubMed]
- Intergovernmental Panel on Climate Change (IPCC). IPCC Special Report on Carbon Dioxide Capture and Storage; Cambridge University Press: Cambridge, UK, 2006; ISBN 978-0-521-68551-1. [Google Scholar]
- White, A.F.; Brantley, S.L. The effect of time on the weathering of silicate minerals: Why do weathering rates differ in the laboratory and field? Chem. Geol. 2003, 202, 479–506. [Google Scholar] [CrossRef]
- O’Connor, W.K.; Dahlin, D.C.; Nilsen, D.N.; Gerdemann, S.J.; Rush, G.E.; Penner, L.R.; Walters, R.P.; Turner, P.C. Continuing Studies on Direct Aqueous Mineral Carbonation of CO2 Sequestration; Albany Research Center: Albany, OR, USA, 2002.
- O’Connor, W.K.; Dahlin, D.C.; Rush, G.E.; Gedermann, S.J.; Penner, L.R.; Nilsen, D.N. Aqueous Mineral Carbonation; Albany Research Center: Albany, OR, USA, 2005.
- Rigopoulos, I.; Vasiliades, M.A.; Ioannou, I.; Efstathiou, A.M.; Godelitsas, A.; Kyratsi, T. Enhancing the rate of ex situ mineral carbonation in dunites via ball milling. Adv. Powder Technol. 2016, 27, 360–371. [Google Scholar] [CrossRef]
- Park, A.-H.A.; Jadhav, R.; Fan, L.-S. CO2 Mineral Sequestration: Chemically Enhanced Aqueous Carbonation of Serpentine. Can. J. Chem. Eng. 2003, 81, 885–890. [Google Scholar] [CrossRef]
- Andreani, M.; Luquot, L.; Gouze, P.; Godard, M.; Hoisé, E.; Gibert, B. Experimental Study of Carbon Sequestration Reactions Controlled by the Percolation of CO2-Rich Brine through Peridotites. Environ. Sci. Technol. 2009, 43, 1226–1231. [Google Scholar] [CrossRef] [PubMed]
- Huijgen, W.J.J.; Comans, R.N.J. Carbon Dioxide Sequestration by Mineral Carbonation: Literature Review; Energy Research Centre of the Netherlands ECN: Petten, The Netherlands, 2003. [Google Scholar]
- Azdarpour, A.; Asadullah, M.; Junin, R.; Manan, M.; Hamidi, H.; Daud, A.R.M. Carbon Dioxide Mineral Carbonation Through pH-swing Process: A Review. Energy Procedia 2014, 61, 2783–2786. [Google Scholar] [CrossRef]
- Azdarpour, A.; Asadullah, M.; Mohammadian, E.; Hamidi, H.; Junin, R.; Karaei, M.A. A review on carbon dioxide mineral carbonation through pH-swing process. Chem. Eng. J. 2015, 279, 615–630. [Google Scholar] [CrossRef]
- Rudnick, R.L.; Gao, S. Composition of the Continental Crust. Treatise Geochem. 2003, 3, 659. [Google Scholar] [CrossRef]
- Van Essendelft, D.T.; Schobert, H.H. Kinetics of the Acid Digestion of Serpentine with Concurrent Grinding. 1. Initial Investigations. Ind. Eng. Chem. Res. 2009, 48, 2556–2565. [Google Scholar] [CrossRef]
- Van Essendelft, D.T.; Schobert, H.H. Kinetics of the Acid Digestion of Serpentine with Concurrent Grinding. 2. Detailed Investigation and Model Development. Ind. Eng. Chem. Res. 2009, 48, 9892–9901. [Google Scholar] [CrossRef]
- Van Essendelft, D.T.; Schobert, H.H. Kinetics of the Acid Digestion of Serpentine with Concurrent Grinding. 3. Model Validation and Prediction. Ind. Eng. Chem. Res. 2010, 49, 1588–1590. [Google Scholar] [CrossRef]
- Hariharan, S.B.; Werner, M.; Zingaretti, D.; Baciocchi, R.; Mazzotti, M. Dissolution of Activated Serpentine for Direct Flue-Gas Mineralization. Energy Procedia 2013, 37, 5938–5944. [Google Scholar] [CrossRef]
- Farhang, F.; Rayson, M.; Brent, G.; Hodgins, T.; Stockenhuber, M.; Kennedy, E. Insights into the dissolution kinetics of thermally activated serpentine for CO2 sequestration. Chem. Eng. J. 2017, 330, 1174–1186. [Google Scholar] [CrossRef]
- Yoo, K.; Kim, B.-S.; Kim, M.-S.; Lee, J.; Jeong, J. Dissolution of Magnesium from Serpentine Mineral in Sulfuric Acid Solution. Mater. Trans. 2009, 50, 1225–1230. [Google Scholar] [CrossRef]
- Lacinska, A.M.; Styles, M.T.; Bateman, K.; Wagner, D.; Hall, M.R.; Gowing, C.; Brown, P.D. Acid-dissolution of antigorite, chrysotile and lizardite for ex situ carbon capture and storage by mineralisation. Chem. Geol. 2016, 437, 153–169. [Google Scholar] [CrossRef]
- Teir, S.; Kuusik, R.; Fogelholm, C.-J.; Zevenhoven, R. Production of magnesium carbonates from serpentinite for long-term storage of CO2. Int. J. Miner. Process. 2007, 85, 1–15. [Google Scholar] [CrossRef]
- Wang, X.; Maroto-Valer, M.M. Dissolution of serpentine using recyclable ammonium salts for CO2 mineral carbonation. Fuel 2011, 90, 1229–1237. [Google Scholar] [CrossRef]
- Zhu, C.; Zhao, L.; Gao, X.; Ji, J.; Chen, J. CO2 sequestration based study of reaction kinetics of brucite. Quat. Sci. 2011, 31, 438–446. (In Chinese) [Google Scholar] [CrossRef]
- Krevor, S.C.M.; Lackner, K.S. Enhancing serpentine dissolution kinetics for mineral carbon dioxide sequestration. Int. J. Greenh. Gas Control 2011, 5, 1073–1080. [Google Scholar] [CrossRef]
- Power, I.M.; Dipple, G.M.; Southam, G. Bioleaching of Ultramafic Tailings by Acidithiobacillus spp. for CO2 Sequestration. Environ. Sci. Technol. 2010, 44, 456–462. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Xu, J.; Teng, H.H.; Liu, L.; Chen, J.; Chen, Y.; Zhao, L.; Ji, J. Bioleaching of Lizardite by Magnesium- and Nickel-Resistant Fungal Isolate from Serpentinite Soils—Implication for Carbon Capture and Storage. Geomicrobiol. J. 2015, 32, 181–192. [Google Scholar] [CrossRef]
- Chen, P.-C.; Kou, K.L.; Tai, H.K.; Jin, S.L.; Lye, C.L.; Lin, C.Y. Removal of carbon dioxide by reactive crystallization in a scrubber—Kinetics of barium carbonate crystals. J. Cryst. Growth 2002, 237, 2166–2171. [Google Scholar] [CrossRef]
- Chen, P.-C.; Chen, C.; Fun, M.; Liao, O.Y.; Jiang, J.; Wang, Y.; Chen, C. Mixing and Crystallization Kinetics in Gas-liquid Reactive Crystallization. Chem. Eng. Technol. 2004, 27, 519–528. [Google Scholar] [CrossRef]
- Chen, P.-C.; Shi, W.; Du, R.; Chen, V. Scrubbing of CO2 Greenhouse Gases, Accompanied by Precipitation in a Continuous Bubble-Column Scrubber. Ind. Eng. Chem. Res. 2008, 47, 6336–6343. [Google Scholar] [CrossRef]
- Kotaki, Y.; Tsuge, H. Reactive crystallization of calcium carbonate by gas-liquid and liquid-liquid reactions. Can. J. Chem. Eng. 1990, 68, 435–442. [Google Scholar] [CrossRef]
- Tamura, K.; Tsuge, H. Characteristics of multistage column crystallizer for gas–liquid reactive crystallization of calcium carbonate. Chem. Eng. Sci. 2006, 61, 5818–5826. [Google Scholar] [CrossRef]
- Ferrini, V.; De Vito, C.; Mignardi, S. Synthesis of nesquehonite by reaction of gaseous CO2 with Mg chloride solution: Its potential role in the sequestration of carbon dioxide. J. Hazard. Mater. 2009, 168, 832–837. [Google Scholar] [CrossRef] [PubMed]
- Harrison, A.L.; Power, I.M.; Dipple, G.M. Accelerated Carbonation of Brucite in Mine Tailings for Carbon Sequestration. Environ. Sci. Technol. 2013, 47, 126–134. [Google Scholar] [CrossRef] [PubMed]
- Han, B.; Qu, H.; Niemi, H.; Sha, Z.; Louhi-Kultanen, M. Mass Transfer and Kinetics Study of Heterogeneous Semi-Batch Precipitation of Magnesium Carbonate. Chem. Eng. Technol. 2014, 37, 1363–1368. [Google Scholar] [CrossRef]
- Hopkinson, L.; Rutt, K.; Cressey, G. The transformation of nesquehonite to hydromagnesite in the system CaO-MgO-H2O-CO2: An experimental spectroscopic study. J. Geol. 2008, 116, 387–400. [Google Scholar] [CrossRef]
- Ballirano, P.; De Vito, C.; Mignardi, S.; Ferrini, V. Phase transitions in the Mg-CO2-H2O system and the thermal decomposition of dypingite, Mg5(CO3)4(OH)2·5H2O: Implications for geosequestration of carbon dioxide. Chem. Geol. 2013, 340, 59–67. [Google Scholar] [CrossRef]
- Kristova, P.; Hopkinson, L.J.; Rutt, K.J.; Hunter, H.M.A.; Cressey, G. Carbonate mineral paragenesis and reaction kinetics in the system MgO-CaO-CO2-H2O in presence of chloride or nitrate ions at near surface ambient temperatures. Appl. Geochem. 2014, 50, 16–24. [Google Scholar] [CrossRef]
- Derks, P.W.J.; Versteeg, G.F. Kinetics of absorption of carbon dioxide in aqueous ammonia solutions. Energy Procedia 2009, 1, 1139–1146. [Google Scholar] [CrossRef]
- Darde, V.; Van Well, W.J.M.; Fosboel, P.L.; Stenby, E.H.; Thomsen, K. Experimental measurement and modeling of the rate of absorption of carbon dioxide by aqueous ammonia. Int. J. Greenh. Gas Control 2011, 5, 1149–1162. [Google Scholar] [CrossRef]
- Zeng, Q.; Guo, Y.; Niu, Z.; Lin, W. The absorption rate of CO2 by aqueous ammonia in a packed column. Fuel Process. Technol. 2013, 108, 76–81. [Google Scholar] [CrossRef]
- Pinsent, B.R.W.; Pearson, L.; Roughton, F.J.W. The kinetics of combination of carbon dioxide with hydroxide ions. Trans. Faraday Soc. 1956, 52, 1512–1520. [Google Scholar] [CrossRef]
- Hänchen, M.; Prigiobbe, V.; Baciocchi, R.; Mazzotti, M. Precipitation in the Mg-carbonate system—Effects of temperature and CO2 pressure. Chem. Eng. Sci. 2008, 63, 1012–1028. [Google Scholar] [CrossRef]
- Montes-Hernandez, G.; Renard, F.; Chiriac, R.; Findling, N.; Toche, F. Rapid Precipitation of Magnesite Microcrystals from Mg(OH)2-H2O-CO2 Slurry Enhanced by NaOH and a Heat-Aging Step (from ∼20 to 90 °C). Cryst. Growth Des. 2012, 12, 5233–5240. [Google Scholar] [CrossRef]
- Swanson, E.J.; Fricker, K.J.; Sun, M.; Park, A.-H.A. Directed precipitation of hydrated and anhydrous magnesium carbonates for carbon storage. Phys. Chem. Chem. Phys. 2014, 16, 23440–23450. [Google Scholar] [CrossRef] [PubMed]
- Sayles, F.L.; Fyfe, W.S. The crystallization of magnesite from aqueous solution. Geochim. Cosmochim. Acta 1973, 37, 87–99. [Google Scholar] [CrossRef]
- Königsberger, E.; Königsberger, L.-C.; Gamsjäger, H. Low-temperature thermodynamic model for the system Na2CO3-MgCO3-CaCO3-H2O. Geochim. Cosmochim. Acta 1999, 63, 3105–3119. [Google Scholar] [CrossRef]
- Braithwaite, C.J.R.; Zedef, V. Living hydromagnesite stromatolites from Turkey. Sediment. Geol. 1994, 92, 1–5. [Google Scholar] [CrossRef]
- Schroll, E. Genesis of magnesite deposits in the view of isotope geochemistry. Bol. Parana. Geocienc. 2002, 50, 59–68. [Google Scholar] [CrossRef]
- Parente, C.V.; Ronchi, L.H.; Sial, A.N.; Guillou, J.J.; Arthaud, M.H.; Fuzikawa, K.; Veríssimo, C.U.V. Geology and geochemistry of paleoproterozoic magnesite deposits (∼1.8Ga), State of Ceará, Northeastern Brazil. Carbonates Evaporites 2004, 19, 28–50. [Google Scholar] [CrossRef]
- Jull, A.J.T.; Cheng, S.; Gooding, J.L.; Velbel, M.A. Rapid growth of magnesium-carbonate weathering products in a stony meteorite from antarctica. Science 1988, 242, 417–419. [Google Scholar] [CrossRef] [PubMed]
- Power, I.M.; Wilson, S.A.; Thom, J.M.; Dipple, G.M.; Southam, G. Biologically induced mineralization of dypingite by cyanobacteria from an alkaline wetland near Atlin, British Columbia, Canada. Geochem. Trans. 2007, 8, 13. [Google Scholar] [CrossRef] [PubMed]
- Fischbeck, R.; Müller, G. Monohydrocalcite, hydromagnesite, nesquehonite, dolomite, aragonite, and calcite in speleothems of the Fränkische Schweiz, Western Germany. Contrib. Mineral. Petrol. 1971, 33, 87–92. [Google Scholar] [CrossRef]
- Davies, P.J.; Bubela, B. The Transformation of Nesquehonite to Hydromagnesite; Bureau of Mineral Resources, Geology and Geophysics; Bureau of Mineral Resources and Baas, Becking Geobiological Laboratory, Division of Mineralogy: Canberra, Australia, 1973; p. 31.
- Hopkinson, L.; Kristova, P.; Rutt, K.; Cressey, G. Phase transitions in the system MgO–CO2–H2O during CO2 degassing of Mg-bearing solutions. Geochim. Cosmochim. Acta 2012, 76, 1–13. [Google Scholar] [CrossRef]
- Zhang, Z.; Zheng, Y.; Ni, Y.; Liu, Z.; Chen, J.; Liang, X. Temperature- and pH-Dependent Morphology and FT−IR Analysis of Magnesium Carbonate Hydrates. J. Phys. Chem. B 2006, 110, 12969–12973. [Google Scholar] [CrossRef] [PubMed]
- Zhu, C.; Yao, X.; Zhao, L.; Teng, H.H. A composite reactor with wetted-wall column for mineral carbonation study in three-phase systems. Rev. Sci. Instrum. 2016, 87, 115115. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Zhu, C.; Ji, J.; Chen, J.; Teng, H.H. Thermodynamic and kinetic effect of organic solvent on the nucleation of nesquehonite. Geochim. Cosmochim. Acta 2013, 106, 192–202. [Google Scholar] [CrossRef]
- Zhu, C.; Wang, Z.; Zhao, L. The effect of solution chemistry on nucleation of nesquehonite. Am. J. Sci. 2016, 316, 1027–1053. [Google Scholar] [CrossRef]
- Schulz, K.G.; Riebesell, U.; Rost, B.; Thoms, S.; Zeebe, R.E. Determination of the rate constants for the carbon dioxide to bicarbonate inter-conversion in pH-buffered seawater systems. Mar. Chem. 2006, 100, 53–65. [Google Scholar] [CrossRef]
- Mani, F.; Peruzzini, M.; Stoppioni, P. CO2 absorption by aqueous NH3 solutions: Speciation of ammonium carbamate, bicarbonate and carbonate by a 13C NMR study. Green Chem. 2006, 8, 995. [Google Scholar] [CrossRef]
- Wang, X.; Conway, W.; Fernandes, D.; Lawrance, G.; Burns, R.; Puxty, G.; Maeder, M. Kinetics of the Reversible Reaction of CO2(aq) with Ammonia in Aqueous Solution. J. Phys. Chem. A 2011, 115, 6405–6412. [Google Scholar] [CrossRef] [PubMed]
- Clegg, S.L.; Whitfield, M. A chemical model of seawater including dissolved ammonia and the stoichiometric dissociation constant of ammonia in estuarine water and seawater from −2 to 40 °C. Geochim. Cosmochim. Acta 1995, 59, 2403–2421. [Google Scholar] [CrossRef]
- Earnshaw, A.; Greenwood, N. Chemistry of the Elements, Second Edition, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 1997; ISBN 0-7506-3365-4. [Google Scholar]
- Hostetler, P.B. The degree of saturation of magnesium and calcium carbonate minerals in natural waters. Int. Assoc. Sci. Hydrol. Commun. Subterr. Waters Publ. 1964, 64, 34–49. [Google Scholar]
- Marion, G.M. Carbonate mineral solubility at low temperatures in the Na-K-Mg-Ca-H-Cl-SO4-OH-HCO3-CO3-CO2-H2O system. Geochim. Cosmochim. Acta 2001, 65, 1883–1896. [Google Scholar] [CrossRef]
- Blake, S.; Cuff, C. Preparation and Use of Cationic Halides, Sequestration of Carbon Dioxide 2007. Patent WO2007003013A1, 11 January 2007. [Google Scholar]
- Cheng, W.; Li, Z. Nucleation kinetics of nesquehonite (MgCO3·3H2O) in the MgCl2−Na2CO3 system. J. Cryst. Growth 2010, 312, 1563–1571. [Google Scholar] [CrossRef]
- Wang, D.; Li, Z. Gas–Liquid Reactive Crystallization Kinetics of Hydromagnesite in the MgCl2-CO2-NH3-H2O System: Its Potential in CO2 Sequestration. Ind. Eng. Chem. Res. 2012, 51, 16299–16310. [Google Scholar] [CrossRef]
- Haynes, W.M. CRC Handbook of Chemistry and Physics, 95th ed.; CRC press: Boca Raton, FL, USA, 2014. [Google Scholar]
- DeCoursey, W.J. Absorption with chemical reaction: Development of a new relation for the Danckwerts model. Chem. Eng. Sci. 1974, 29, 1867–1872. [Google Scholar] [CrossRef]
- Pinsent, B.R.W.; Pearson, L.; Roughton, F.J.W. The kinetics of combination of carbon dioxide with ammonia. Trans. Faraday Soc. 1956, 52, 1594–1598. [Google Scholar] [CrossRef]
- Qin, F.; Wang, S.; Hartono, A.; Svendsen, H.F.; Chen, C. Kinetics of CO2 absorption in aqueous ammonia solution. Int. J. Greenh. Gas Control 2010, 4, 729–738. [Google Scholar] [CrossRef]
- Crooks, J.E.; Donnellan, J.P. Kinetics and mechanism of the reaction between carbon dioxide and amines in aqueous solution. J. Chem. Soc. Perkin Trans. 2 1989, 0, 331–333. [Google Scholar] [CrossRef]
- Liu, J.; Wang, S.; Zhao, B.; Tong, H.; Chen, C. Absorption of carbon dioxide in aqueous ammonia. Energy Procedia 2009, 1, 933–940. [Google Scholar] [CrossRef]
- Zhao, L.; Sang, L.; Chen, J.; Ji, J.; Teng, H.H. Aqueous Carbonation of Natural Brucite: Relevance to CO2 Sequestration. Environ. Sci. Technol. 2010, 44, 406–411. [Google Scholar] [CrossRef] [PubMed]
- Highfield, J.; Lim, H.; Fagerlund, J.; Zevenhoven, R. Mechanochemical processing of serpentine with ammonium salts under ambient conditions for CO2 mineralization. RSC Adv. 2012, 2, 6542–6548. [Google Scholar] [CrossRef]
- Dell, R.M.; Weller, S.W. The thermal decomposition of nesquehonite MgCO3·3H2O and magnesium ammonium carbonate MgCO3·(NH4)2CO3·4H2O. Trans. Faraday Soc. 1959, 55, 2203–2220. [Google Scholar] [CrossRef]
- Power, I.M.; Harrison, A.L.; Dipple, G.M. Accelerating Mineral Carbonation Using Carbonic Anhydrase. Environ. Sci. Technol. 2016, 50, 2610–2618. [Google Scholar] [CrossRef] [PubMed]
- Levenspiel, O. Chemical Reaction Engineering, 3rd ed.; Wiley: New York, NY, USA, 1999; ISBN 0-471-25424-X. [Google Scholar]
- Hollingbery, L.A.; Hull, T.R. The fire retardant behaviour of huntite and hydromagnesite—A review. Polym. Degrad. Stab. 2010, 95, 2213–2225. [Google Scholar] [CrossRef]
- Hollingbery, L.A.; Hull, T.R. The fire retardant effects of huntite in natural mixtures with hydromagnesite. Polym. Degrad. Stab. 2012, 97, 504–512. [Google Scholar] [CrossRef]
- Hull, T.R.; Witkowski, A.; Hollingbery, L. Fire retardant action of mineral fillers. Polym. Degrad. Stab. 2011, 96, 1462–1469. [Google Scholar] [CrossRef]
- Glasser, F.P.; Jauffret, G.; Morrison, J.; Galvez-Martos, J.-L.; Patterson, N.; Imbabi, M.S.-E. Sequestering CO2 by Mineralization into Useful Nesquehonite-Based Products. Front. Energy Res. 2016, 4. [Google Scholar] [CrossRef]
- Walling, S.A.; Provis, J.L. Magnesia-Based Cements: A Journey of 150 Years, and Cements for the Future? Chem. Rev. 2016, 116, 4170–4204. [Google Scholar] [CrossRef] [PubMed]
- Jones, B.F.; Deocampo, D.M. Geochemistry of Saline Lakes. In Treatise on Geochemistry; Elsevier: Amsterdam, The Netherlands, 2003; pp. 393–424. ISBN 978-0-08-043751-4. [Google Scholar]
- Zhang, B. Development and Countermeasures of Magnesium Salt Industry in Salt Lakes of Qaidam Basin. Sea Lake Salt Chem. Ind. 2001, 17–21. (In Chinese) [Google Scholar] [CrossRef]
| ID | Base | pH 1 | 2 | Duration | Mg-Carbonate Phase 3 | tind 4 | |
|---|---|---|---|---|---|---|---|
| s | s | ||||||
| A | NH3 | 9.00 | 0.00 | 0.0 | 16,532 | N/A | - |
| B | NH3 | 9.00 | 0.05 | 0.0 | 22,728 | Nes | 12,792 |
| C | NH3 | 9.00 | 0.10 | 0.0 | 19,117 | Nes | 9302 |
| D | NH3 | 9.00 | 0.20 | 0.0 | 22,416 | Nes | 7899 |
| E | NH3 | 8.76 | 0.10 | 0.0 | 20,000 | Nes | 11,222 |
| F | NH3 | 9.16 | 0.10 | 0.0 | 18,380 | Nes | 8036 |
| G | NH3 | 9.74 | 0.10 | 0.0 | 18,839 | Nes | 4185 |
| H | NH3 | 9.20 | 0.20 | 2.0 | 28,800 | Nes + Rog | - |
| I | NH3 | 9.63 | 0.20 | 6.7 | 19,740 | Rog | - |
| X | NaOH | 9.00 | 0.00 | 0.0 | 16,353 | N/A | - |
| Equation | pK 1 | Source |
|---|---|---|
| (1) | 5.86 | [60] |
| (2) | −8.03 | Calculated 2 |
| (3) | −3.29 | [61,62] |
| (12) | −9.24 | [63] |
| (13) | 10.32 | [64] |
| (14) | −6.37 | [64] |
| (15) | −5.34 | [65,66,67,68,69] 3 |
| ID | Time | pH | TN | DIC | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| s | ||||||||||
| E | 406 | 9.146 | 0.007 | 0.002 | 0.003 | 0.103 | 0.51 | 0.52 | 1.38 | 1.50 |
| 2206 | 8.771 | 0.017 | 0.003 | 0.008 | 0.102 | 0.44 | 0.45 | 1.19 | 1.50 | |
| 4006 | 8.761 | 0.027 | 0.004 | 0.015 | 0.102 | 0.44 | 0.45 | 1.19 | 1.53 | |
| 5806 | 8.786 | 0.041 | 0.007 | 0.022 | 0.101 | 0.58 | 0.60 | 1.57 | 1.60 | |
| 7606 | 8.755 | 0.058 | 0.009 | 0.030 | 0.101 | 0.58 | 0.60 | 1.57 | 1.68 | |
| 9406 | 8.715 | 0.059 | 0.009 | 0.041 | 0.105 | 0.58 | 0.60 | 1.57 | 1.64 | |
| 11,206 | 8.763 | 0.075 | 0.012 | 0.046 | 0.102 | 0.58 | 0.60 | 1.57 | 1.72 | |
| 12,406 | 8.760 | 0.092 | 0.015 | 0.051 | 0.102 | 0.58 | 0.60 | 1.57 | 1.81 | |
| 13,606 | 8.776 | 0.110 | 0.018 | 0.055 | 0.099 | 0.65 | 0.67 | 1.77 | 1.90 | |
| 14,806 | 8.784 | 0.109 | 0.018 | 0.060 | 0.099 | 0.65 | 0.67 | 1.77 | 1.87 | |
| 16,006 | 8.753 | 0.130 | 0.020 | 0.065 | 0.098 | 0.65 | 0.67 | 1.77 | 1.95 | |
| 17,206 | 8.731 | 0.151 | 0.023 | 0.062 | 0.089 | 0.65 | 0.67 | 1.77 | 2.01 | |
| 18,406 | 8.747 | 0.149 | 0.023 | 0.057 | 0.078 | 0.65 | 0.67 | 1.77 | 1.98 | |
| 19,606 | 8.746 | 0.212 | 0.033 | 0.054 | 0.068 | 0.65 | 0.67 | 1.77 | 2.25 | |
| 20,806 | 8.766 | 0.184 | 0.030 | 0.053 | 0.062 | 0.65 | 0.67 | 1.77 | 2.13 | |
| 22,006 | 8.765 | 0.217 | 0.035 | 0.051 | 0.056 | 0.65 | 0.67 | 1.77 | 2.25 | |
| C | 316 | 9.456 | 0.015 | 0.007 | 0.003 | 0.102 | 0.54 | 0.56 | 1.47 | 1.71 |
| 1516 | 9.038 | 0.020 | 0.005 | 0.009 | 0.103 | 0.54 | 0.56 | 1.47 | 1.62 | |
| 2716 | 8.996 | 0.033 | 0.008 | 0.013 | 0.102 | 0.54 | 0.56 | 1.47 | 1.70 | |
| 3916 | 9.004 | 0.039 | 0.010 | 0.023 | 0.107 | 0.54 | 0.56 | 1.47 | 1.72 | |
| 5116 | 8.999 | 0.059 | 0.015 | 0.026 | 0.105 | 0.54 | 0.56 | 1.47 | 1.89 | |
| 6316 | 8.999 | 0.068 | 0.017 | 0.032 | 0.105 | 0.61 | 0.63 | 1.66 | 1.91 | |
| 7516 | 9.000 | 0.098 | 0.024 | 0.038 | 0.105 | 0.68 | 0.71 | 1.86 | 2.14 | |
| 9316 | 8.999 | 0.107 | 0.026 | 0.049 | 0.105 | 0.75 | 0.78 | 2.05 | 2.12 | |
| 10,516 | 8.999 | 0.149 | 0.036 | 0.052 | 0.101 | 0.75 | 0.78 | 2.05 | 2.38 | |
| 11,716 | 9.000 | 0.156 | 0.038 | 0.049 | 0.092 | 0.82 | 0.86 | 2.25 | 2.36 | |
| 12,916 | 8.999 | 0.169 | 0.042 | 0.040 | 0.075 | 0.90 | 0.93 | 2.46 | 2.39 | |
| 14,116 | 9.000 | 0.186 | 0.047 | 0.035 | 0.062 | 0.90 | 0.93 | 2.46 | 2.46 | |
| 15,316 | 9.000 | 0.254 | 0.063 | 0.036 | 0.054 | 0.90 | 0.93 | 2.46 | 2.79 | |
| 16,516 | 8.998 | 0.255 | 0.064 | 0.037 | 0.048 | 0.82 | 0.86 | 2.25 | 2.77 | |
| 17,716 | 9.000 | 0.273 | 0.069 | 0.039 | 0.042 | 0.90 | 0.93 | 2.46 | 2.84 | |
| 18,916 | 9.000 | 0.297 | 0.074 | 0.043 | 0.038 | 0.90 | 0.93 | 2.46 | 2.92 | |
| F | 263 | 9.485 | 0.012 | 0.006 | 0.003 | 0.102 | 0.58 | 0.60 | 1.58 | 1.60 |
| 1463 | 9.172 | 0.024 | 0.008 | 0.008 | 0.102 | 0.51 | 0.53 | 1.39 | 1.70 | |
| 2663 | 9.161 | 0.034 | 0.011 | 0.014 | 0.102 | 0.58 | 0.60 | 1.58 | 1.72 | |
| 3863 | 9.161 | 0.048 | 0.016 | 0.019 | 0.102 | 0.65 | 0.67 | 1.77 | 1.84 | |
| 5063 | 9.155 | 0.069 | 0.022 | 0.025 | 0.102 | 0.65 | 0.67 | 1.77 | 2.02 | |
| 6263 | 9.164 | 0.096 | 0.031 | 0.031 | 0.101 | 0.72 | 0.75 | 1.97 | 2.23 | |
| 7463 | 9.155 | 0.090 | 0.029 | 0.041 | 0.104 | 0.87 | 0.90 | 2.37 | 2.11 | |
| 8663 | 9.164 | 0.130 | 0.042 | 0.047 | 0.102 | 0.87 | 0.90 | 2.37 | 2.41 | |
| 9863 | 9.157 | 0.110 | 0.035 | 0.056 | 0.102 | 0.94 | 0.98 | 2.58 | 2.19 | |
| 11,063 | 9.162 | 0.151 | 0.048 | 0.058 | 0.096 | 1.01 | 1.06 | 2.78 | 2.47 | |
| 12,263 | 9.154 | 0.145 | 0.046 | 0.056 | 0.084 | 1.08 | 1.14 | 3.00 | 2.38 | |
| 13,463 | 9.155 | 0.183 | 0.059 | 0.052 | 0.069 | 1.16 | 1.22 | 3.21 | 2.61 | |
| 14,663 | 9.160 | 0.250 | 0.080 | 0.052 | 0.060 | 1.23 | 1.30 | 3.43 | 2.98 | |
| 15,863 | 9.165 | 0.347 | 0.111 | 0.054 | 0.050 | 1.30 | 1.39 | 3.65 | 3.43 | |
| 17,063 | 9.158 | 0.341 | 0.108 | 0.059 | 0.044 | 1.38 | 1.47 | 3.87 | 3.37 | |
| 18,263 | 9.158 | 0.356 | 0.112 | 0.067 | 0.039 | 1.38 | 1.47 | 3.87 | 3.41 | |
| G | 179 | 9.460 | 0.009 | 0.005 | 0.002 | 0.091 | 0.52 | 0.53 | 1.40 | 1.57 |
| 1979 | 9.703 | 0.052 | 0.033 | 0.010 | 0.089 | 0.88 | 0.91 | 2.40 | 2.16 | |
| 3779 | 9.690 | 0.130 | 0.081 | 0.026 | 0.091 | 1.17 | 1.24 | 3.26 | 3.01 | |
| 4979 | 9.696 | 0.152 | 0.095 | 0.035 | 0.089 | 1.40 | 1.49 | 3.93 | 3.15 | |
| 6179 | 9.690 | 0.260 | 0.161 | 0.043 | 0.084 | 1.63 | 1.76 | 4.63 | 3.97 | |
| 7379 | 9.700 | 0.315 | 0.197 | 0.042 | 0.068 | 1.87 | 2.04 | 5.37 | 4.31 | |
| 8579 | 9.689 | 0.370 | 0.229 | 0.045 | 0.054 | 2.11 | 2.34 | 6.14 | 4.60 | |
| 9779 | 9.693 | 0.417 | 0.257 | 0.055 | 0.045 | 2.28 | 2.54 | 6.68 | 4.83 | |
| 10,979 | 9.693 | 0.557 | 0.338 | 0.067 | 0.037 | 2.45 | 2.75 | 7.24 | 5.50 | |
| 13,979 | 9.699 | 0.815 | 0.477 | 0.110 | 0.024 | 2.79 | 3.19 | 8.41 | 6.47 | |
| T | 1 | 2 | Sources | |
|---|---|---|---|---|
| °C | ||||
| 0.027–0.19 | 0–40 | 0.44 | - | [72] |
| 0.002–0.016 | 15–45 | 0.45 | - | [62] |
| 0.1–7 | 5–25 | 0.37–1.30 | [39] | |
| 0.9–5.4 | 25–49 | 0.94–0.95 | [73] | |
| 0.6–5.6 | 6–31 | 0.95–1.14 | [40] | |
| 0.002–0.62 | 25 | 0.32–0.95 | - | This work |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, C.; Wang, H.; Li, G.; An, S.; Ding, X.; Teng, H.H.; Zhao, L. CO2 Absorption and Magnesium Carbonate Precipitation in MgCl2–NH3–NH4Cl Solutions: Implications for Carbon Capture and Storage. Minerals 2017, 7, 172. https://doi.org/10.3390/min7090172
Zhu C, Wang H, Li G, An S, Ding X, Teng HH, Zhao L. CO2 Absorption and Magnesium Carbonate Precipitation in MgCl2–NH3–NH4Cl Solutions: Implications for Carbon Capture and Storage. Minerals. 2017; 7(9):172. https://doi.org/10.3390/min7090172
Chicago/Turabian StyleZhu, Chen, Han Wang, Gen Li, Siyu An, Xiaofeng Ding, Hui Henry Teng, and Liang Zhao. 2017. "CO2 Absorption and Magnesium Carbonate Precipitation in MgCl2–NH3–NH4Cl Solutions: Implications for Carbon Capture and Storage" Minerals 7, no. 9: 172. https://doi.org/10.3390/min7090172
APA StyleZhu, C., Wang, H., Li, G., An, S., Ding, X., Teng, H. H., & Zhao, L. (2017). CO2 Absorption and Magnesium Carbonate Precipitation in MgCl2–NH3–NH4Cl Solutions: Implications for Carbon Capture and Storage. Minerals, 7(9), 172. https://doi.org/10.3390/min7090172





