Yield Stress Prediction of Filling Slurry Based on Rheological Experiments and Machine Learning
Abstract
1. Introduction
2. Experiments and Results
2.1. Materials and Experimental Procedures
2.2. Experimental Setup
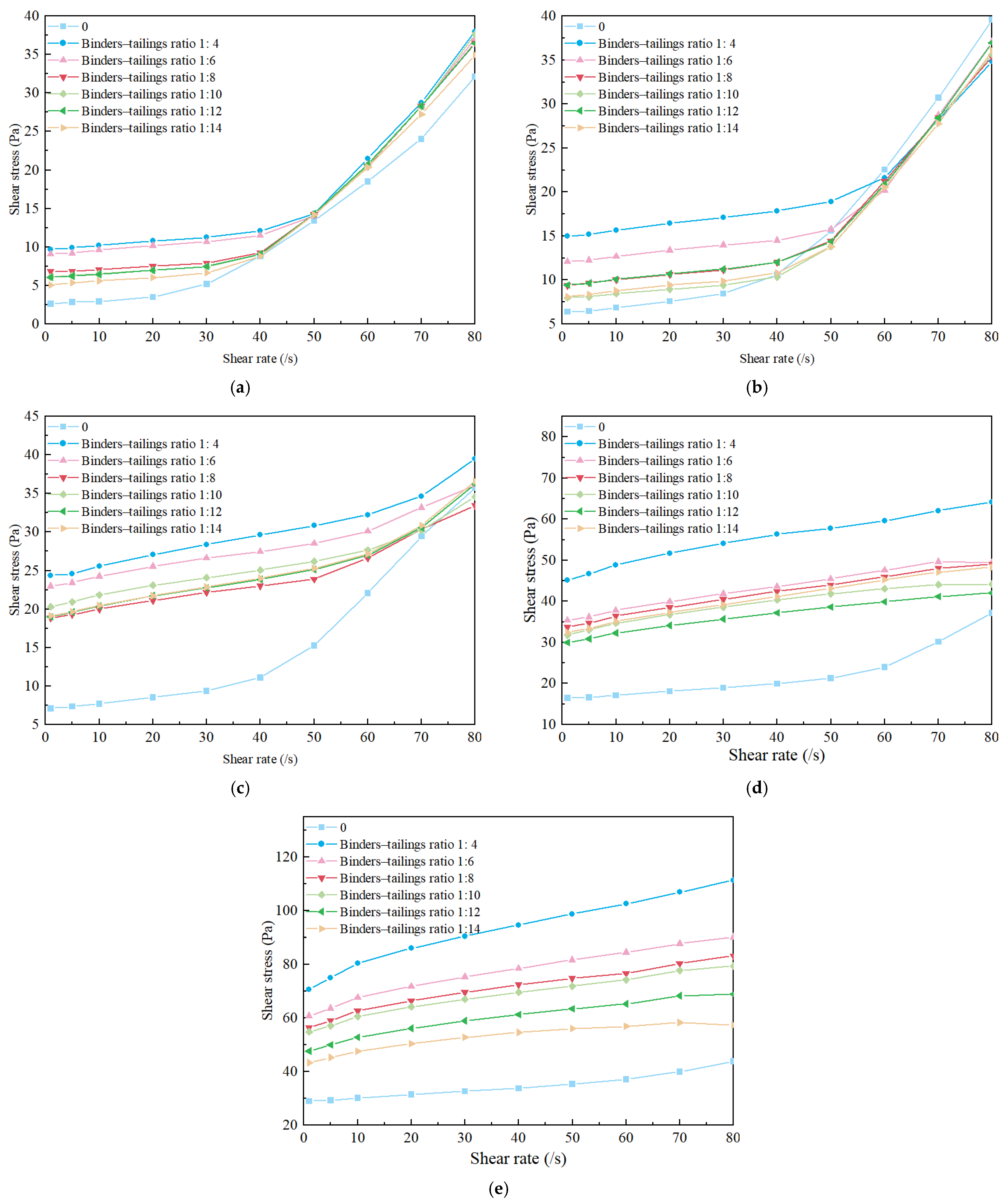
2.3. Experimental Results
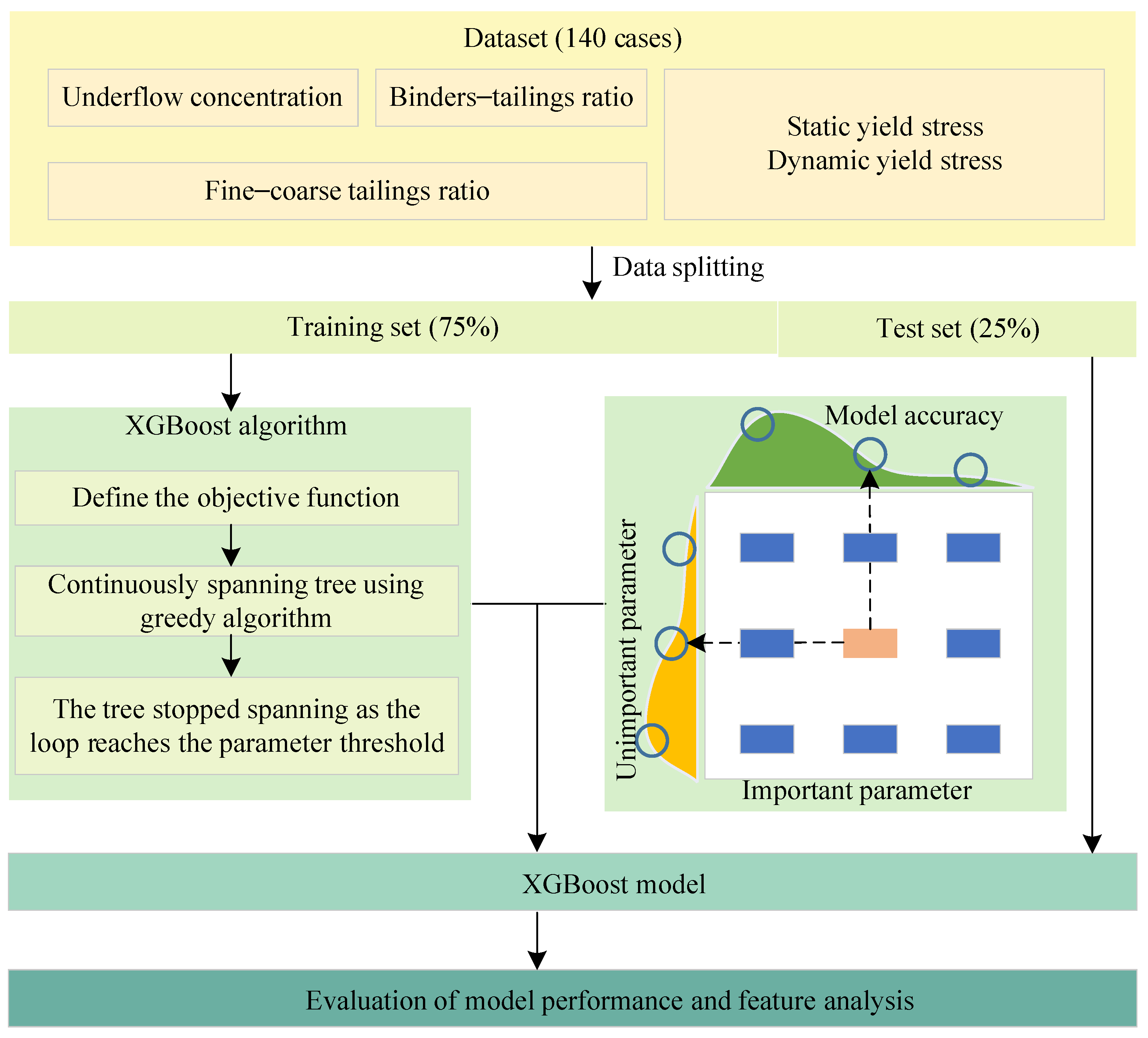
3. Construction and Implementation of the Model
3.1. XGBoost Methodology
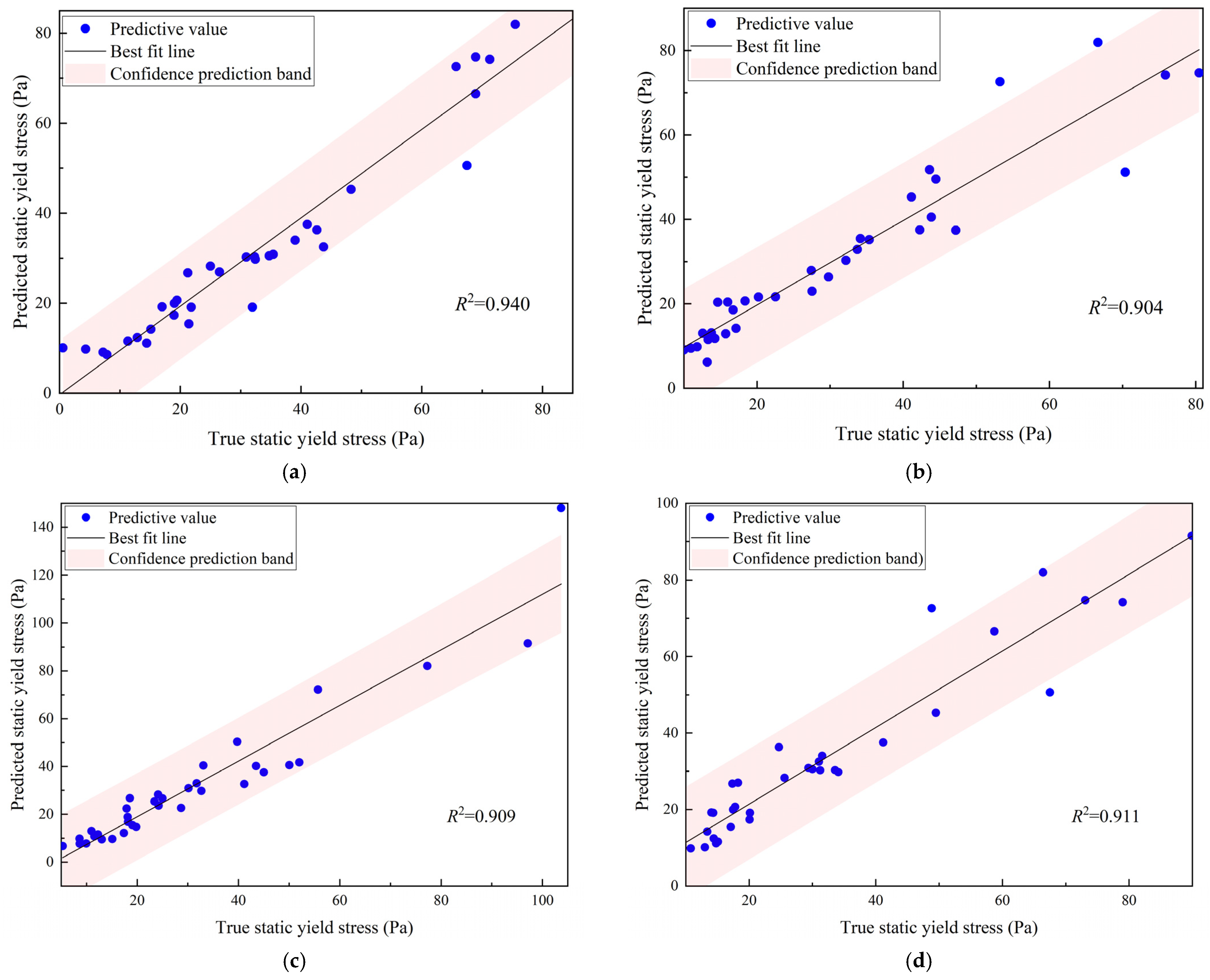
3.2. Model Evaluation
3.3. Hyperparameter Tuning
3.4. Comparison Analysis of Models
4. Results and Discussions
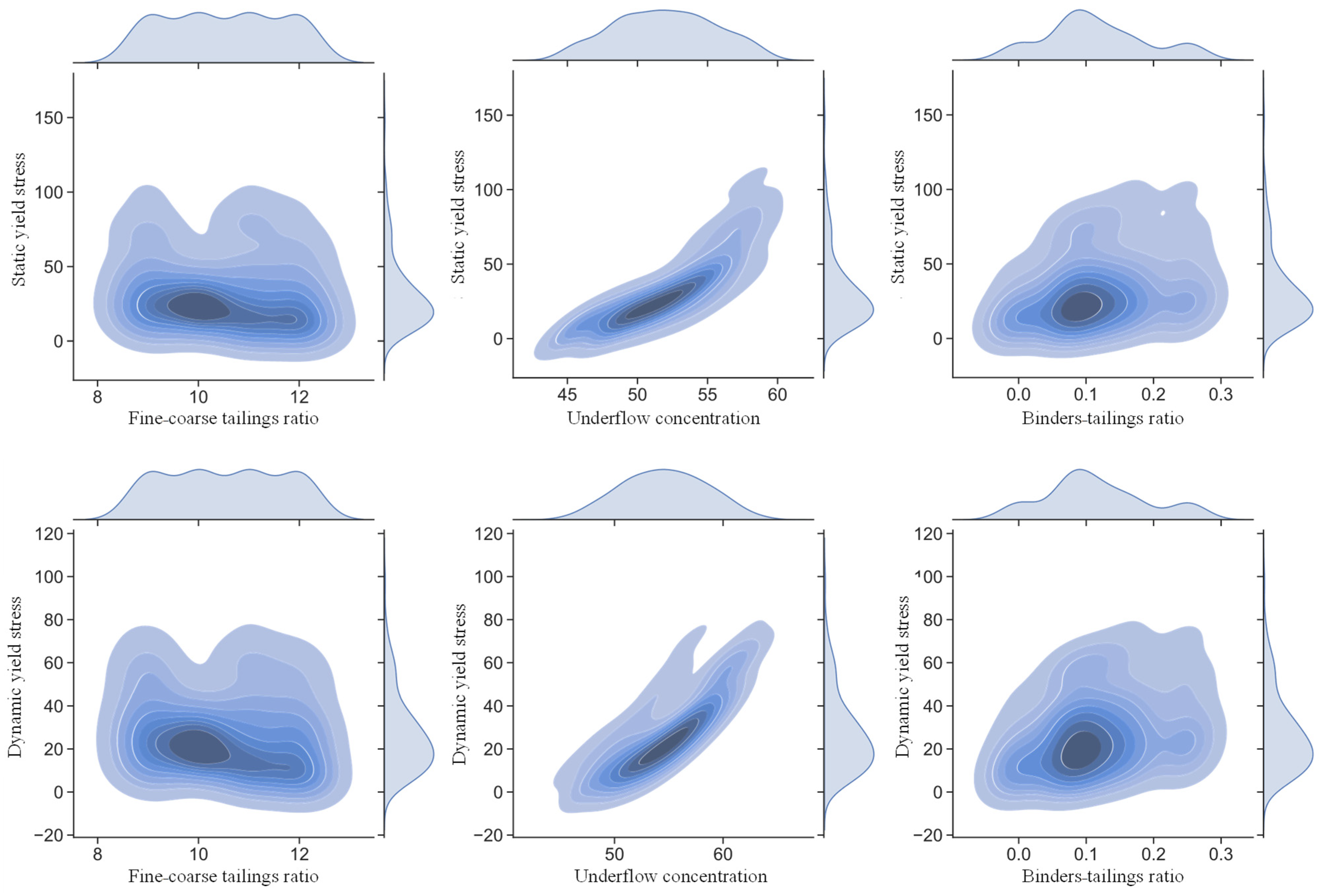
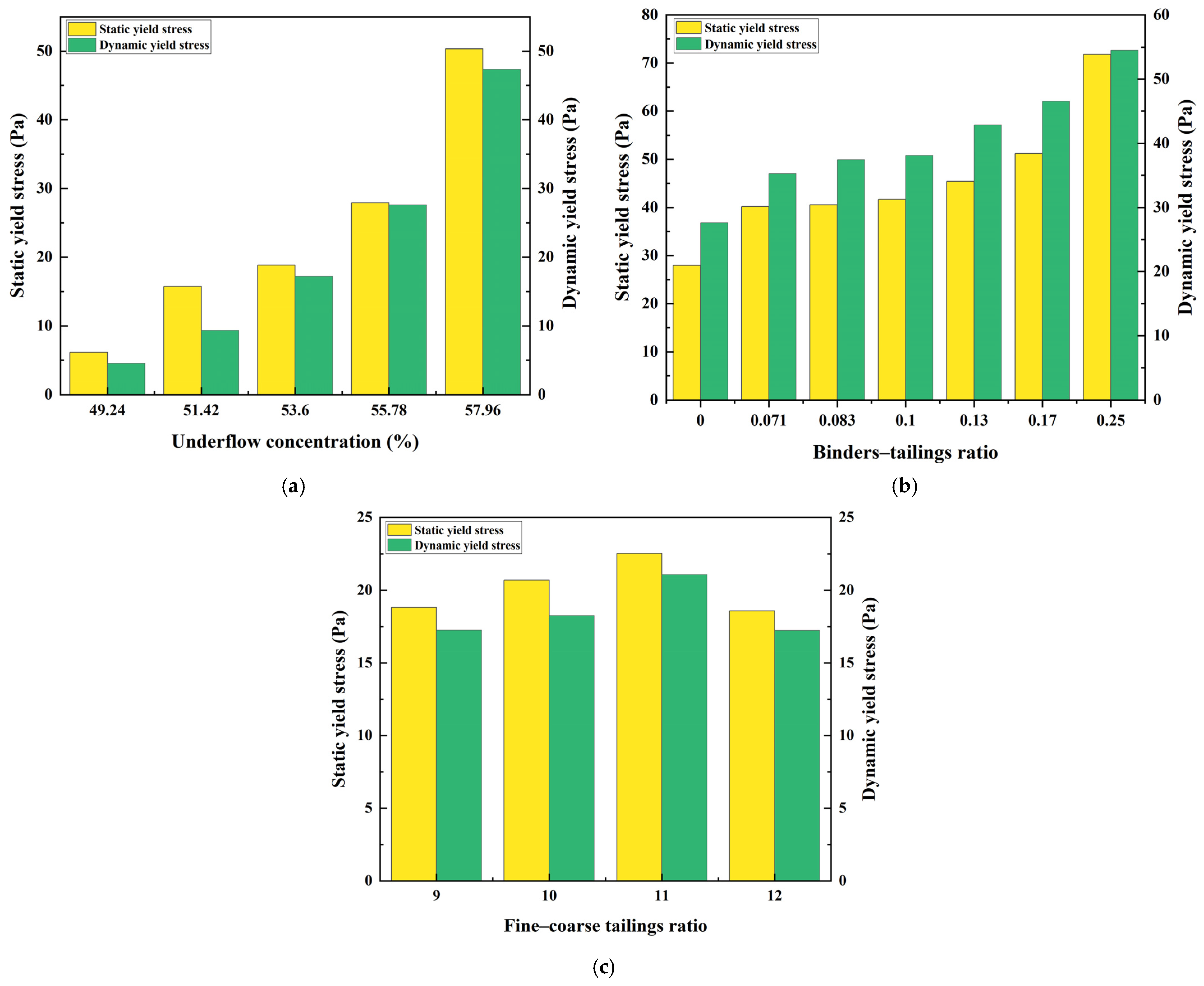
4.1. Effect of a Single Feature on the Yield Stress
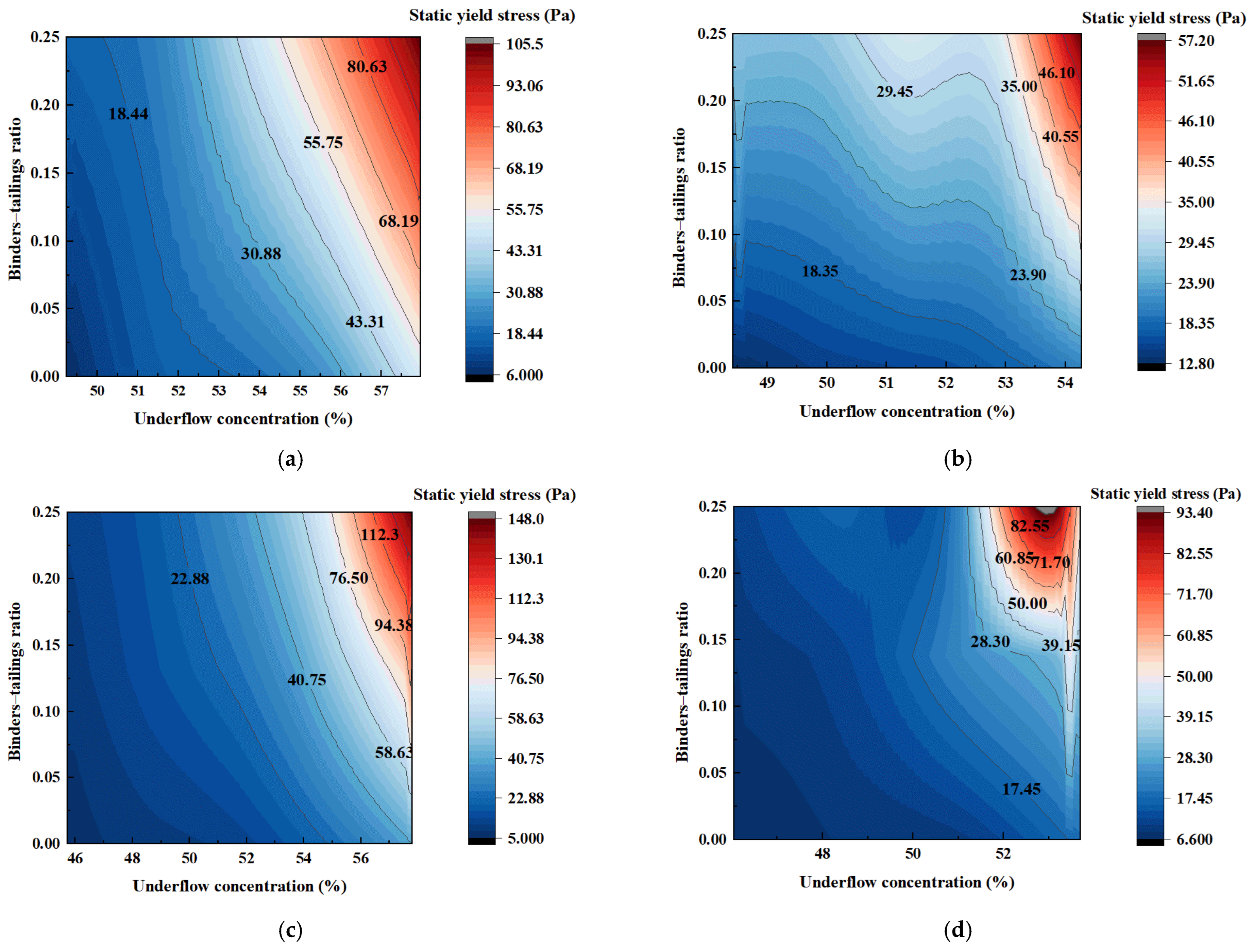
4.2. Effect of Feature Coupling on the Yield Stress
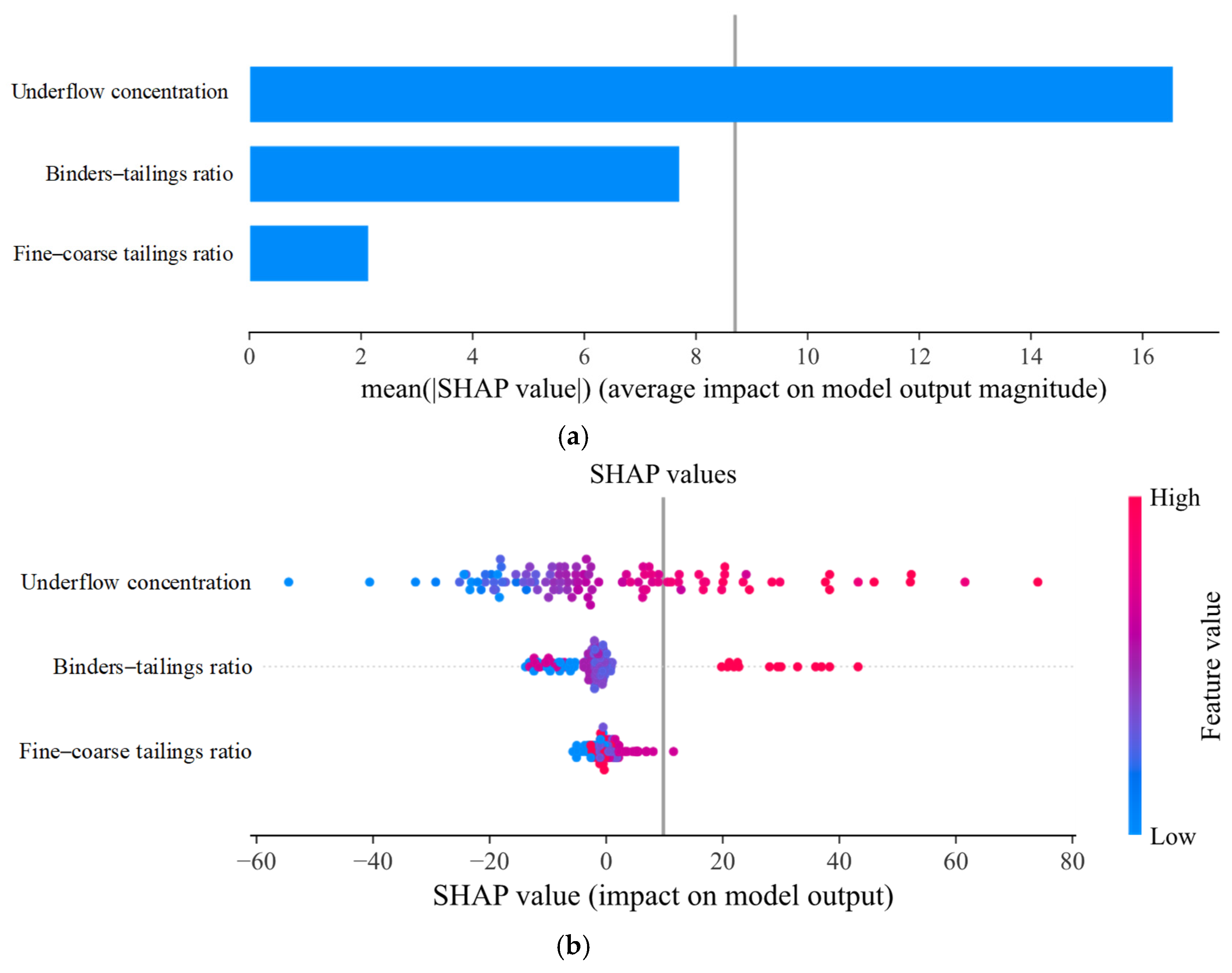
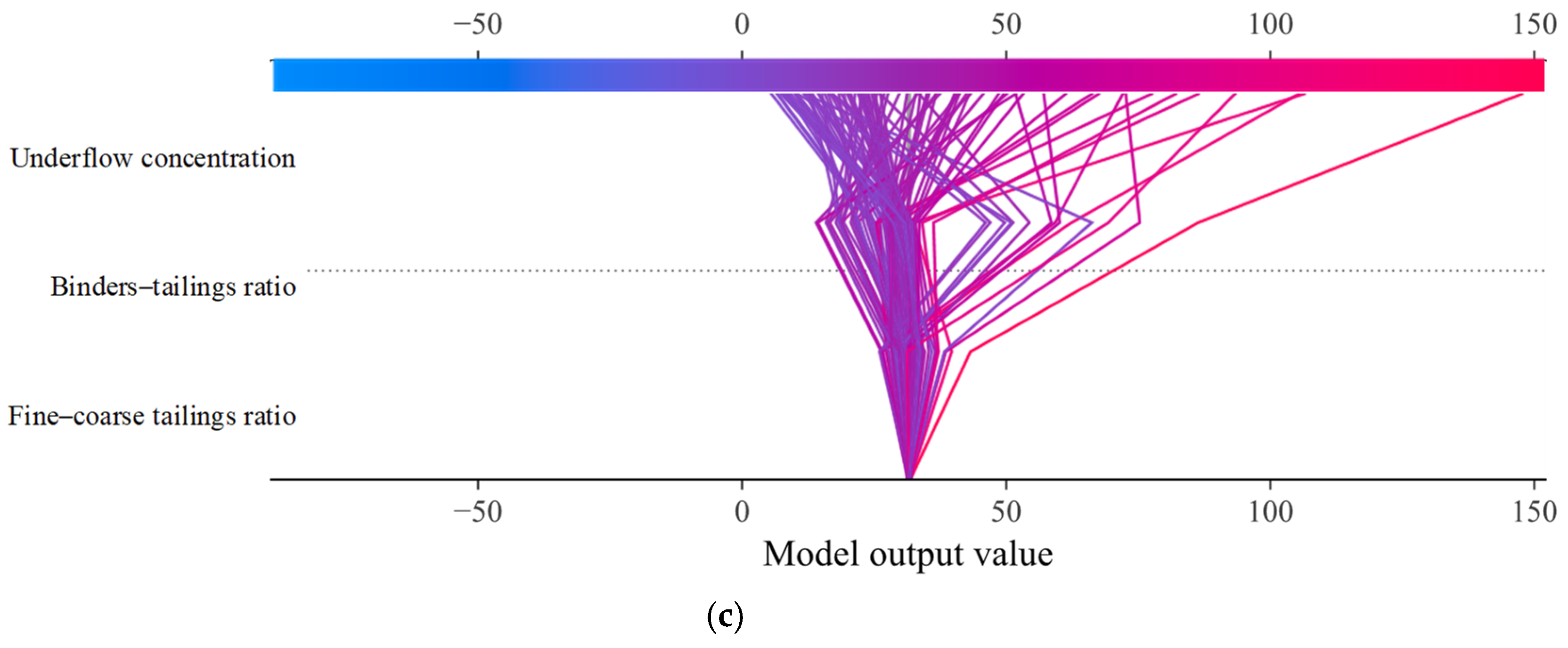
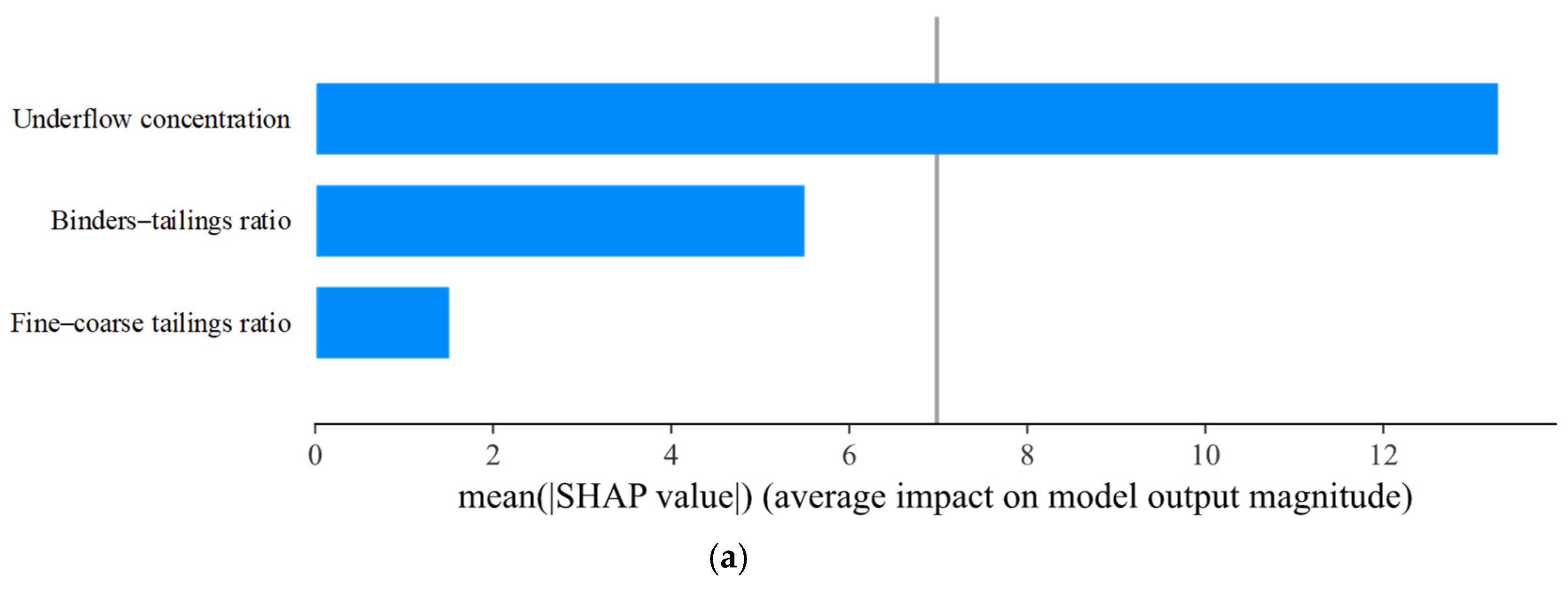
4.3. Feature Importance Analysis
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cai, M.F.; Xue, D.L.; Ren, F.H. Current status and development strategy of metal mines. Chin. J. Eng. 2019, 41, 417–426. [Google Scholar] [CrossRef]
- Nguyen, Q.D.; Boger, D.V. Application of rheology to solving tailings disposal problems. Int. J. Miner. Process. 1998, 54, 217–233. [Google Scholar] [CrossRef]
- Wang, C.; Harbottle, D.; Liu, Q.; Xu, Z. Current state of fine mineral tailings treatment: A critical review on theory and practice. Miner. Eng. 2014, 58, 113–131. [Google Scholar] [CrossRef]
- Hui, Y.H.; Cai, L.B.; Liu, W.; Qin, W.Q.; Jiao, F.; Yang, C.R. Current status and development of comprehensive utilization of waste rock in metal mines in China. Chin. J. Nonferrous Met. 2021, 31, 1649–1660. [Google Scholar]
- Santamarina, J.C.; Torres-Cruz, L.A.; Bachus, R.C. Why did the tailings dam at Brumadinho fail? Eng. Geol. 2021, 294, 106339. [Google Scholar] [CrossRef]
- Ministry of Industry and Information Technology (MIIT). Management Measures for the Prevention and Control of Environmental Pollution by Tailings; MIIT: Beijing, China, 2022. Available online: https://www.gov.cn/gongbao/content/2022/content_5697980.htm (accessed on 6 April 2022).
- Landriault, D.; Verburg, R.; Cincilla, W.; Welch, D. Paste technology for underground backfill and surface tailings disposal applications. In Short Course Notes; Technical Workshop œ April; Canadian Institute of Mining and Metallurgy: Westmount, QC, USA, 1997; p. 121. [Google Scholar]
- Chen, H.J.; Liu, Q.J. Harms and Resource-like Treatment of the Solid Wastes from Metal Mines. Met. Mine 2009, 4, 154–156+167. [Google Scholar] [CrossRef]
- Yin, S.; Shao, Y.; Wu, A.; Wang, H.; Liu, X.; Wang, Y. A systematic review of paste technology in metal mines for cleaner production in China. J. Clean. Prod. 2020, 247, 119590. [Google Scholar] [CrossRef]
- Yang, K.; Zhao, X.; Wei, Z.; Zhang, J. Development overview of paste backfill technology in China’s coal mines: A review. Environ. Sci. Pollut. Res. 2021, 28, 67957–67969. [Google Scholar] [CrossRef]
- Wu, A.X.; Yang, Y.; Cheng, H.Y.; Chen, S.M.; Han, Y. Status and prospects of paste technology in China. Chin. J. Eng. 2018, 40, 517–525. [Google Scholar] [CrossRef]
- Zhou, Z.; Liu, J.; Zhou, Q.; Wu, A.; Wang, H. A New High Charge Density Superplasticizer Regulates the Rheological Properties of Tailings Slurry and Cemented Paste Backfill Materials. Min. Metall. Explor. 2022, 39, 749–759. [Google Scholar] [CrossRef]
- Yang, L.H.; Wang, H.J.; Wu, A.X.; Gao, W.H. Status and Development Tendency of the Full-tailings Paste Mixing Technology. Met. Mine 2016, 7, 34–41. [Google Scholar]
- Wu, A.X.; Li, H.; Cheng, H.Y.; Wang, Y.M.; Li, C.P.; Ruan, Z.E. Status and prospects of researches on rheology of paste backfill using unclassified tailings (Part 1): Concepts, characteristics and models. Chin. J. Eng. 2020, 42, 803–813. [Google Scholar] [CrossRef]
- Wang, S.; Song, X.; Wei, M.; Liu, W.; Wang, X.; Ke, Y.; Tao, T.; Liu, H. Flow Characteristics of Fresh Cemented Paste Backfill Containing Flocculant under Variable Shear Rate Based on Water Migration. Min. Metall. Explor. 2022, 39, 1189–1203. [Google Scholar] [CrossRef]
- Hu, C.F.; Li, C.P.; Yan, B.H.; Chen, G.Z. Effect of water reducing agent on rheological property of fine-grained tailings paste. Chin. J. Nonferrous Met. 2022, 32, 2458–2468. [Google Scholar] [CrossRef]
- Chen, F.B.; Su, R.; Yang, L.H.; Jiao, H.Z.; Wu, A.X.; Yin, S.H.; Wang, H.J.; Gao, Y.; Kou, Y.P.; Wang, Z.J. Effect of mixing speed on rheological properties of cemented paste backfill. Chin. J. Nonferrous Met. 2022, 32, 3541–3552. [Google Scholar] [CrossRef]
- Zhang, X.X.; Qiao, D.P. Rheological properties and yield stress prediction model of waste rock-tailings high concentration slurry. J. Saf. Environ. 2015, 15, 278–283. [Google Scholar]
- Zhang, Q.L.; Liu, W.J.; Wang, X.M.; Chen, Q.S. Optimal prediction model of backfill paste rheological parameters. J. Cent. South Univ. Sci. Technol. 2018, 49, 124–130. [Google Scholar]
- Yan, B.H.; Li, C.P.; Wang, S.Y.; Hou, H.Z. Measurement of Rheological Parameters for the Whole-tailing Paste and Optimization of the Rheological Models. Met. Mine 2017, 12, 44–48. [Google Scholar]
- Liu, X.H.; Wu, A.X.; Wang, H.J.; Wang, Y.M. Influence mechanism and calculation model of CPB rheological parameters. Chin. J. Eng. 2017, 39, 190–195. [Google Scholar]
- Qi, C.C.; Fourie, A. Cemented paste backfill for mineral tailings management: Review and future perspectives. Miner. Eng. 2019, 144, 106025. [Google Scholar] [CrossRef]
- Sun, Y.; Li, G.; Zhang, J.; Sun, J.; Xu, J. Development of an Ensemble Intelligent Model for Assessing the Strength of Cemented Paste Backfill. Adv. Civ. Eng. 2020, 2020, 1–6. [Google Scholar] [CrossRef]
- Du, K.; Liu, M.; Zhou, J.; Khandelwal, M. Investigating the Slurry Fluidity and Strength Characteristics of Cemented Backfill and Strength Prediction Models by Developing Hybrid GA-SVR and PSO-SVR, Mining. Metall. Explor. 2022, 39, 433–452. [Google Scholar] [CrossRef]
- Farooq, F.; Ahmed, W.; Akbar, A.; Aslam, F.; Alyousef, R. Predictive modeling for sustainable high-performance concrete from industrial wastes: A comparison and optimization of models using ensemble learners. J. Clean. Prod. 2021, 292, 126032. [Google Scholar] [CrossRef]
- Ramzi, M.; Kashaninejad, M.; Salehi, F.; Sadeghi Mahoonak, A.R.; Ali Razavi, S.M. Modeling of rheological behavior of honey using genetic algorithm–artificial neural network and adaptive neuro-fuzzy inference system. Food Biosci. 2015, 9, 60–67. [Google Scholar] [CrossRef]
- Ghaffarkhah, A.; Bazzi, A.; Dijvejin, Z.A.; Talebkeikhah, M.; Moraveji, M.K.; Agin, F. Experimental and numerical analysis of rheological characterization of hybrid nano-lubricants containing COOH-Functionalized MWCNTs and oxide nanoparticles. Int. Commun. Heat Mass Transf. 2019, 101, 103–115. [Google Scholar] [CrossRef]
- Shahsavar, A.; Jamei, M.; Karbasi, M. Experimental evaluation and development of predictive models for rheological behavior of aqueous Fe3O4 ferrofluid in the presence of an external magnetic field by introducing a novel grid optimization based-Kernel ridge regression supported by sensitivity analysis. Powder Technol. 2021, 393, 1–11. [Google Scholar] [CrossRef]
- Asadi, A.; Alarifi, I.M.; Nguyen, H.M.; Moayedi, H. Feasibility of least-square support vector machine in predicting the effects of shear rate on the rheological properties and pumping power of MWCNT–MgO/oil hybrid nanofluid based on experimental data. J. Therm. Anal. Calorim. 2021, 143, 1439–1454. [Google Scholar] [CrossRef]
- Gomaa, E.; Han, T.; ElGawady, M.; Huang, J.; Kumar, A. Machine learning to predict properties of fresh and hardened alkali-activated concrete. Cem. Concr. Compos. 2021, 115, 103863. [Google Scholar] [CrossRef]
- Nehdi, M.; Al Martini, S. Estimating time and temperature dependent yield stress of cement paste using oscillatory rheology and genetic algorithms. Cem. Concr. Res. 2009, 39, 1007–1016. [Google Scholar] [CrossRef]
- Nguyen, T.-D.; Tran, T.-H.; Hoang, N.-D. Prediction of interface yield stress and plastic viscosity of fresh concrete using a hybrid machine learning approach. Adv. Eng. Inform. 2020, 44, 101057. [Google Scholar] [CrossRef]
- Chen, T.Q.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Shehadeh, A.; Alshboul, O.; Al Mamlook, R.E.; Hamedat, O. Machine learning models for predicting the residual value of heavy construction equipment: An evaluation of modified decision tree, LightGBM, and XGBoost regression. Autom. Constr. 2021, 129, 103827. [Google Scholar] [CrossRef]
- Nguyen, N.-H.; Abellán-García, J.; Lee, S.; Garcia-Castano, E.; Vo, T.P. Efficient estimating compressive strength of ultra-high performance concrete using XGBoost model. J. Build. Eng. 2022, 52, 104302. [Google Scholar] [CrossRef]
- Li, C.; Yan, B.; Wang, S.; Hou, H.; Chen, G. Variability behavior of yield stress for unclassified tailings pasted under measurement time–velocity double factors. Chin. J. Eng. 2020, 42, 1308–1317. [Google Scholar] [CrossRef]
- Huang, Z.; Li, C.; Li, X.; Ruan, Z.; Wang, S. Volume Concentration Effect on Rheology of Filling Slurry with Different Material Ratios. Mater. Rep. 2023, 37, 102–110. [Google Scholar]
- Jiao, D.; Shi, C.; Yuan, Q. Time-dependent rheological behavior of cementitious paste under continuous shear mixing. Constr. Build. Mater. 2019, 226, 591–600. [Google Scholar] [CrossRef]
- Mahaut, F.; Mokéddem, S.; Chateau, X.; Roussel, N.; Ovarlez, G. Effect of coarse particle volume fraction on the yield stress and thixotropy of cementitious materials. Cem. Concr. Res. 2008, 38, 1276–1285. [Google Scholar] [CrossRef]
- Li, H.; Cao, Y.; Li, S.; Zhao, J.; Sun, Y. XGBoost model and its application to personal credit evaluation. IEEE Intell. Syst. 2020, 35, 52–61. [Google Scholar] [CrossRef]
- Qi, C.; Fourie, A.; Chen, Q.; Zhang, Q. A strength prediction model using artificial intelligence for recycling waste tailings as cemented paste backfill. J. Clean. Prod. 2018, 183, 566–578. [Google Scholar] [CrossRef]
- Cao, J.; Gao, J.; Nikafshan Rad, H.; Mohammed, A.S.; Hasanipanah, M.; Zhou, J. A novel systematic and evolved approach based on XGBoost-firefly algorithm to predict Young’s modulus and unconfined compressive strength of rock. Eng. Comput. 2021, 38 (Suppl. S5), 3829–3845. [Google Scholar] [CrossRef]
- Duan, J.; Asteris, P.G.; Nguyen, H.; Bui, X.-N.; Moayedi, H. A novel artificial intelligence technique to predict compressive strength of recycled aggregate concrete using ICA-XGBoost model. Eng. Comput. 2021, 37, 3329–3346. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. arXiv 2017, arXiv:1705.07874. [Google Scholar] [CrossRef]
- Parsa, A.B.; Movahedi, A.; Taghipour, H.; Derrible, S.; Mohammadian, A.K. Toward safer highways, application of XGBoost and SHAP for real-time accident detection and feature analysis. Accid. Anal. Prev. 2020, 136, 105405. [Google Scholar] [CrossRef]
- Chang, I.; Park, H.; Hong, E.; Lee, J.; Kwon, N. Predicting effects of built environment on fatal pedestrian accidents at location-specific level: Application of XGBoost and SHAP. Accid. Anal. Prev. 2022, 166, 106545. [Google Scholar] [CrossRef]





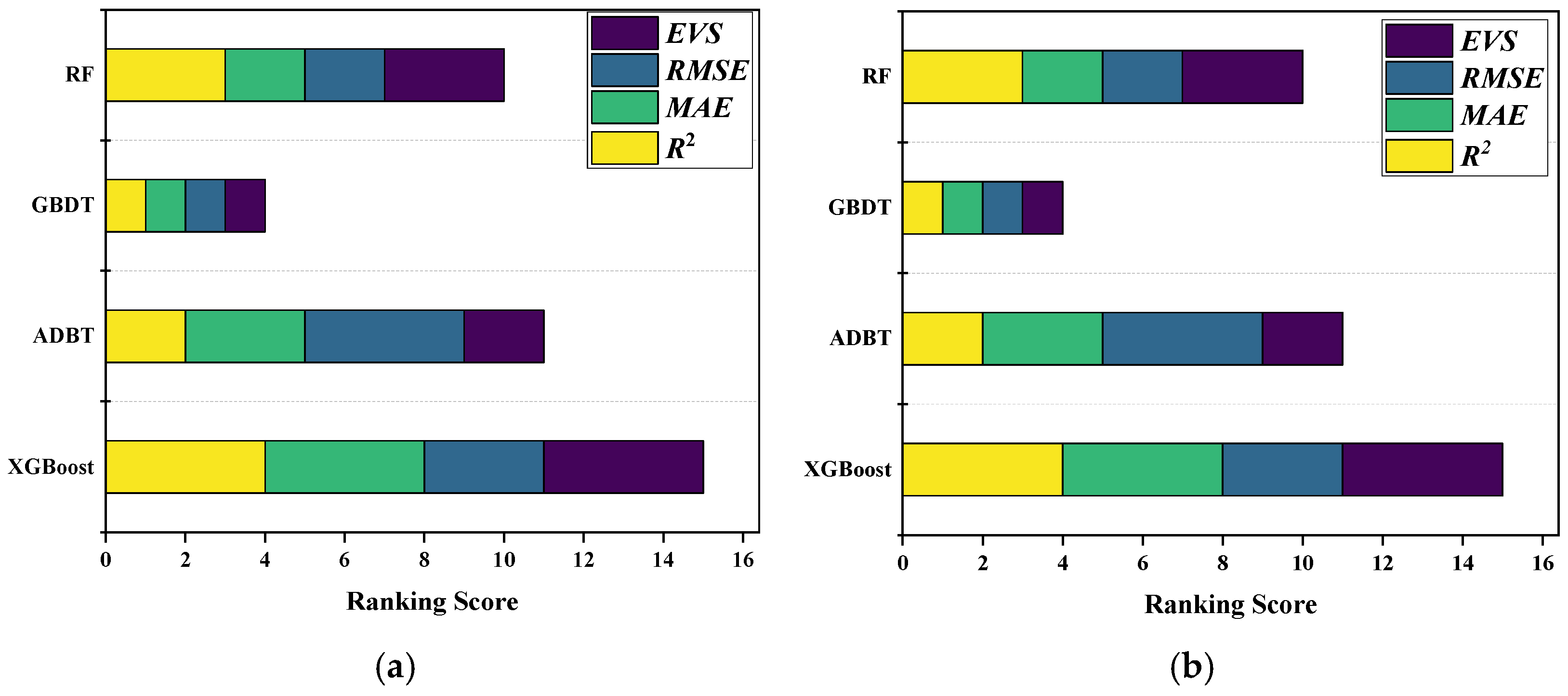


| Particle Size | 150–220 μm | 220–400 μm | 400–500 μm | 500–630 μm | 630–800 μm | 800–1000 μm |
|---|---|---|---|---|---|---|
| Percentage | 20.61% | 20.52% | 8.89% | 13.86% | 28.18% | 7.85% |
| Material | Oxide (wt%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| SiO2 | MgO | Fe2O3 | Al2O3 | CaO | P2O5 | K2O | SO3 | Others | |
| Tailing | 41.25 | 15.00 | 12.60 | 12.03 | 10.02 | 3.18 | 3.11 | 0.82 | 1.99 |
| Binders | 29.76 | 5.36 | 1.43 | 15.97 | 37.95 | - | 0.50 | 7.2 | 1.20 |
| Influence Factors | Experimental Level | |
|---|---|---|
| Fine–coarse tailings ratio | 9:1, 10:1, 11:1, 12:1 | |
| Binders–tailings ratio | 0, 1:14, 1:12, 1:10, 1:8, 1:6, 1:4 | |
| Underflow concentration | Fine–coarse tailings ratio 9:1 | 49.24%, 51.42%, 53.6%, 55.78%, 57.96% |
| Fine–coarse tailings ratio 10:1 | 48.43%, 49.89%, 51.35%, 52.81%, 54.27% | |
| Fine–coarse tailings ratio 11:1 | 45.72%, 48.74%, 51.76%, 54.78%, 57.8% | |
| Fine–coarse tailings ratio 12:1 | 46.04%, 48.59%, 51.14%, 53.69%, 56.24% | |
| Indicator | Description | Equation |
|---|---|---|
| R2 | Describes regression model variance score, with a range of from (0, 1], with larger values indicating higher accuracy of the prediction model | |
| MAE | Evaluates how close the predictions are to the true dataset; the smaller the value, the better the fit | |
| RMSE | Explains distribution of forecast errors, with smaller values of RMSE indicating less variation in forecast distribution | |
| EVS | Defines a model variance score in the range of (0, 1], with larger values being more effective |
| Parameter Classification | Parameter | Initial Setting | Static Yield Stress Model Results | Dynamic Yield Stress Model Results |
|---|---|---|---|---|
| Tree booster | Eta | 0.05–0.3 | 0.15 | 0.16 |
| Min_child_weight | 1 | 1 | 1 | |
| Max_depth | [3, 10] | 4 | 5 | |
| Gamma | [0, 0.2] | 0.1 | 0.1 | |
| Subsample | [0.5, 0.9] | 0.8 | 0.72 | |
| Colsample_bytree | [0, 1] | 0.76 | 0.78 | |
| Alpha | 1 | 0 | 0 | |
| Lambda | 1 | 2 | 2 | |
| Learning Task | Objective | LinearRegression | LinearRegression | LinearRegression |
| Eval_metric | RMSE | RMSE | RMSE | |
| Command line | Num_round | 500 | 400 | 300 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Qian, K.; Tian, R.; Xiong, Z.; Chang, X.; Du, H. Yield Stress Prediction of Filling Slurry Based on Rheological Experiments and Machine Learning. Minerals 2025, 15, 931. https://doi.org/10.3390/min15090931
Li X, Qian K, Tian R, Xiong Z, Chang X, Du H. Yield Stress Prediction of Filling Slurry Based on Rheological Experiments and Machine Learning. Minerals. 2025; 15(9):931. https://doi.org/10.3390/min15090931
Chicago/Turabian StyleLi, Xue, Kailong Qian, Rui Tian, Zhipeng Xiong, Xinke Chang, and Hairui Du. 2025. "Yield Stress Prediction of Filling Slurry Based on Rheological Experiments and Machine Learning" Minerals 15, no. 9: 931. https://doi.org/10.3390/min15090931
APA StyleLi, X., Qian, K., Tian, R., Xiong, Z., Chang, X., & Du, H. (2025). Yield Stress Prediction of Filling Slurry Based on Rheological Experiments and Machine Learning. Minerals, 15(9), 931. https://doi.org/10.3390/min15090931









