Hyperspectral Lithological Classification of 81 Rock Types Using Deep Ensemble Learning Algorithms
Abstract
1. Introduction
- ①
- Inadequate dataset foundations: Existing datasets exhibit critical constraints in lithological diversity. For instance, the Okada Mineral Set [31] covers only five mineral types, while the Galdames dataset [32] expands coverage to thirteen rock types—including andesite, tourmaline breccia, and travertine breccia. Nevertheless, the persistent lack of spectral variability analysis fundamentally restricts their applicability to complex rock identification and classification scenarios.
- ②
- Small-sample generalization deficit: Data scarcity induces severe overfitting and accuracy degradation, especially for metamorphic rocks. As evidenced by Li et al. [33], the ShufflNetV2 model misclassified 46 metamorphic rock samples as volcanic rocks when using deep learning to classify thin rock section images, while the overall accuracy (OA) of metamorphic rocks was the lowest (67%).
- ③
- Spectral confusion: Spectral Homogeneity with Material Heterogeneity (SHMH) and Spectral Heterogeneity for Compositionally Similar Deposits (MCSD) disrupt the spectral-lithological correspondence, significantly compromising the recognition accuracy of mainstream classification models. SHMH refers to the spectral uniformity arising from the overlapping of key mineral absorption features in different lithologies. For instance, Zhang et al. [34] discovered spectral overlap in certain mineral assemblages. Barbey et al. [35] observed that the reflection curves of cordierite hornfels and granite converge in the 2200–2400 nm band due to overlapping Fe2+ absorption features. Regmi [36] confirmed that metamorphic hornfels and granite exhibit similarities in Al-OH absorption due to their shared ferromagnesian minerals.
2. Hardware and Dataset
2.1. Hyperspectral Imaging System
2.2. Hyperspectral Rock Standard Dataset HSRD-1.0
2.3. Spectral Characteristics of Dataset HSRD-1.0
3. Method
3.1. Related Work
3.1.1. Two-Dimensional CNN
3.1.2. Recurrent Neural Network
3.2. Proposed Algorithm
3.2.1. A Framework for Hyperspectral Rock Classification Based on Bimodal Feature Synergy
3.2.2. Two-Dimensional Convolutional Recurrent Neural Network
3.2.3. AdaBoost Algorithm Integrated with Deep Learning Frameworks
4. Results and Discussion
4.1. Experimental Design
4.1.1. Datasets
4.1.2. Experimental Environment and Evaluation Criteria
4.1.3. Experimental Setup
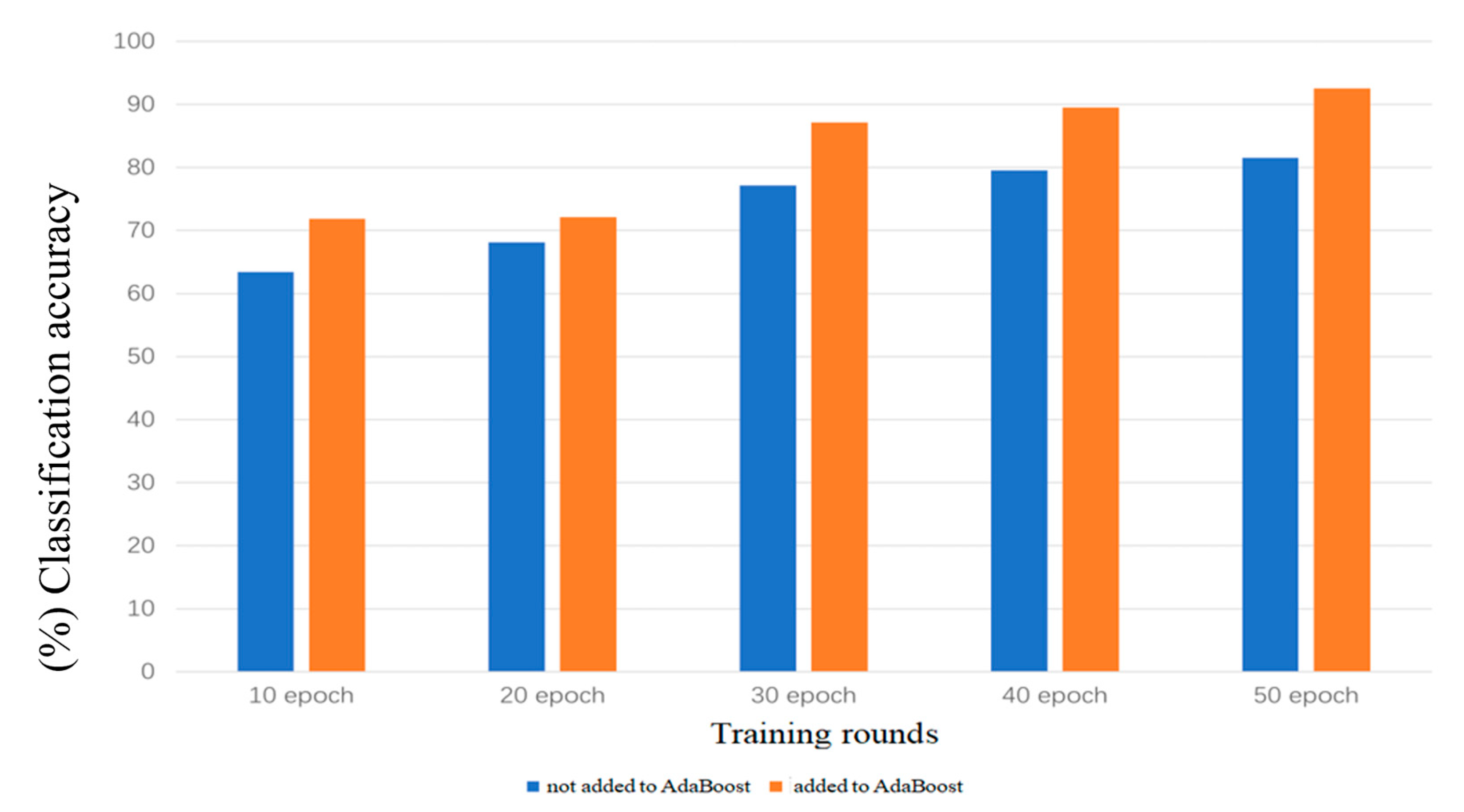
4.1.4. Effect of the Number of Training Rounds on Classification Accuracy
4.1.5. Effect of the Number of Weak Classifiers on Classification Accuracy
4.1.6. Effect of RNN Branch on Classification Accuracy
4.2. Comparison and Discussion of Experimental Results
4.3. Analysis and Discussion of Typical Samples of Metamorphic Rock
4.3.1. Identification of Typical and Easily Confused Metamorphic Rock
4.3.2. Class Identification of Typical Metamorphic Rock
- ①
- Spectral curve similarity: Cordierite formation is intrinsically linked to biotite dehydration melting reactions. This petrogenetic process induces significant spectral overlap between cordierite-dominant hornfels and granite in the 2200–2400 nm range, where overlapping hydroxyl (OH−) and ferrous iron (Fe2+) absorption features create nearly identical reflectance curve morphologies. Additionally, these lithologies show comparable full width at half maximum (FWHM) values for their broad absorption features in the 1000–1300 nm region. Such spectral convergence hinders deep learning models from resolving diagnostic mineralogical signatures, leading to blurred classification boundaries and a significant increase in error rates.
- ②
- Mineralogical composition overlap: Both rock types share common components such as quartz and mafic minerals (e.g., cordierite and biotite), leading to similar spectral responses due to Fe2+ and Al-OH absorption features. Quantitative analyses reveal over 20% error in mineral abundance estimation between them. Weathered secondary minerals (e.g., limonite and kaolinite) and mixed image element interference (>40% mixing probability at 30 m resolution) further confound the primary spectral-compositional correlation.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Karimpouli, S.; Tahmasebi, P. Segmentation of digital rock images using deep convolutional autoencoder networks. Comput. Geosci. 2019, 126, 142–150. [Google Scholar] [CrossRef]
- Guo, W.; Dong, C.; Lin, C.; Wu, Y.; Zhang, X.; Liu, J. Rock physical modeling of tight sandstones based on digital rocks and reservoir porosity prediction from seismic data. Front. Earth Sci. 2022, 10, 932929. [Google Scholar] [CrossRef]
- Houshmand, N.; Goodfellow, S.; Esmaeili, K.; Calderón, J.C.O. Rock type classification based on petrophysical, geochemical, and core imaging data using machine and deep learning techniques. Appl. Comput. Geosci. 2022, 16, 100104. [Google Scholar] [CrossRef]
- Li, W.; Yin, G.; Yu, H.; Liu, X. The Yanshanian granites and associated Mo-polymetallic mineralization in the Xiangcheng-Luoji area of the Sanjiang-Yangtze conjunction zone in Southwest China. Acta Geol. Sin.—Engl. Ed. 2014, 88, 1742–1756. [Google Scholar] [CrossRef]
- Ferrero, S.; Bartoli, O.; Cesare, B.; Salvioli-Mariani, E.; Acosta-Vigil, A.; Cavallo, A.; Groppo, C.; Battiston, S. Microstructures of melt inclusions in anatectic metasedimentary rocks. J. Metamorph. Geol. 2012, 30, 303–322. [Google Scholar] [CrossRef]
- Xu, Y.; Ma, H.; Peng, S. Study on identification of altered rock in hyperspectral imagery using spectrum of field object. Ore Geol. Rev. 2014, 56, 584–595. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, G.; Zhou, B.; Ying, J.; Liu, J. Exploring an application-oriented land-based hyperspectral target detection framework based on 3D–2D CNN and transfer learning. EURASIP J. Adv. Signal Process. 2024, 2024, 37. [Google Scholar] [CrossRef]
- Transon, J.; D’Andrimont, R.; Maugnard, A.; Defourny, P. Survey of Hyperspectral Earth Observation Applications from Space in the Sentinel-2 Context. Remote Sens. 2018, 10, 157. [Google Scholar] [CrossRef]
- Jakob, S.; Zimmermann, R.; Gloaguen, R. The need for accurate geometric and radiometric corrections of drone-borne hyperspectral data for mineral exploration: MEPHySTo—A toolbox for pre-processing drone-borne hyperspectral data. Remote Sens. 2017, 9, 88. [Google Scholar] [CrossRef]
- Paoletti, M.E.; Haut, J.M.; Plaza, J.; Plaza, A. Deep&Dense Convolutional Neural Network for Hyperspectral Image Classification. Remote Sens. 2018, 10, 1454. [Google Scholar] [CrossRef]
- Zhang, X.; Li, P. Lithological mapping from hyperspectral data by improved use of spectral angle mapper. Int. J. Appl. Earth Obs. Geoinf. 2014, 31, 95–109. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Kanungo, T.; Mount, D.M.; Netanyahu, N.S.; Piatko, C.D.; Silverman, R.; Wu, A.Y. An efficient k-means clustering algorithm: Analysis and implementation. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 881–892. [Google Scholar] [CrossRef]
- Ghezelbash, R.; Maghsoudi, A.; Shamekhi, M.; Pradhan, B.; Daviran, M. Genetic algorithm to optimize the SVM and K-means algorithms for mapping of mineral prospectivity. Neural Comput. Appl. 2023, 35, 719–733. [Google Scholar] [CrossRef]
- Tessier, J.; Duchesne, C.; Bartolacci, G. A machine vision approach to on-line estimation of run-of-mine ore composition on conveyor belts. Miner. Eng. 2007, 20, 1129–1144. [Google Scholar] [CrossRef]
- Tripathi, P.; Garg, R.D. Potential of DESIS and PRISMA hyperspectral remote sensing data in rock classification and mineral identification: A case study for Banswara in Rajasthan, India. Environ. Monit. Assess. 2023, 195, 575. [Google Scholar] [CrossRef] [PubMed]
- Hughes, G. On the mean accuracy of statistical pattern recognizers. IEEE Trans. Inf. Theory 1968, 14, 55–63. [Google Scholar] [CrossRef]
- Kilickaya, S.; Ahishali, M.; Sohrab, F.; Ince, T.; Gabbouj, M. Hyperspectral image analysis with subspace learning-based one-class classification. In Proceedings of the 2023 Photonics & Electromagnetics Research Symposium (PIERS), Prague, Czech Republic, 3–6 July 2023; pp. 953–959. [Google Scholar] [CrossRef]
- Güler, E.; Kakız, M.T.; Günay, F.B.; Şanal, B.; Çavdar, T. Kapalı mekan ortamında 1D-CNN kullanarak yapılan doluluk tespiti sınıflandırması. Karadeniz Fen Bilim. Derg. 2023, 13, 60–71. [Google Scholar] [CrossRef]
- Yang, J.; Chang, B.; Zhang, Y.; Luo, W.; Ge, S.; Wu, M. CNN coal and rock recognition method based on hyperspectral data. Int. J. Coal Sci. Technol. 2022, 9, 63. [Google Scholar] [CrossRef]
- Zhang, C.; Yi, M.; Ye, F.; Xu, Q.; Li, X.; Gan, Q. Application and Evaluation of Deep Neural Networks for Airborne Hyperspectral Remote Sensing Mineral Mapping: A Case Study of the Baiyanghe Uranium Deposit in Northwestern Xinjiang, China. Remote Sens. 2022, 14, 5122. [Google Scholar] [CrossRef]
- Jiang, T.; Wang, X.J. Hyperspectral images classification based on fusion features derived from 1D and 2D convolutional neural network. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 42, 335–341. [Google Scholar] [CrossRef]
- Sinaice, B.B.; Kawamura, Y.; Kim, J.; Okada, N.; Kitahara, I.; Jang, H. Application of deep learning approaches in igneous rock hyperspectral imaging. In Proceedings of the 28th International Symposium on Mine Planning and Equipment Selection—MPES 2019, Perth, Australia, 2–4 December 2019; Topal, E., Ed.; Springer: Cham, Switzerland, 2020; pp. 347–356. [Google Scholar] [CrossRef]
- Ge, W.; Cheng, Q.; Tang, Y.; Jing, L.; Gao, C. Lithological classification using Sentinel-2A data in the Shibanjing ophiolite complex in Inner Mongolia, China. Remote Sens. 2018, 10, 638. [Google Scholar] [CrossRef]
- Bozga, M.; Maler, O.; Tripakis, S. Efficient verification of timed automata using dense and discrete time semantics. In Correct Hardware Design and Verification Methods; Pierre, L., Kropf, T., Eds.; Springer: Berlin/Heidelberg, Germany, 1999; pp. 125–141. [Google Scholar] [CrossRef]
- Dang, L.; Pang, P.; Zuo, X.; Liu, Y.; Lee, J. A Dual-Path Small Convolution Network for Hyperspectral Image Classification. Remote Sens. 2021, 13, 3411. [Google Scholar] [CrossRef]
- Hussain, M.; Bird, J.J.; Faria, D.R. A study on CNN transfer learning for image classification. In Advances in Computational Intelligence Systems: UKCI 2018; Lotfi, A., Bouchachia, H., Gegov, A., Langensiepen, C., McGinnity, M., Eds.; Springer: Cham, Switzerland, 2019; Volume 84, pp. 199–212. [Google Scholar] [CrossRef]
- Zhao, H.; Deng, K.; Li, N.; Wang, Z.; Wei, W. Hierarchical Spatial-Spectral Feature Extraction with Long Short Term Memory (LSTM) for Mineral Identification Using Hyperspectral Imagery. Sensors 2020, 20, 6854. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, N.; Govil, H. A deep residual convolutional neural network for mineral classification. Adv. Space Res. 2023, 71, 3186–3202. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, X.; Teng, Q.; He, H. Mineral identification of rock thin section images based on improved SKnet and Bi-GRU. Intell. Comput. Appl. 2023, 13, 104–111. [Google Scholar] [CrossRef]
- Okada, N.; Maekawa, Y.; Owada, N.; Haga, K.; Shibayama, A.; Kawamura, Y. Automated Identification of Mineral Types and Grain Size Using Hyperspectral Imaging and Deep Learning for Mineral Processing. Minerals 2020, 10, 809. [Google Scholar] [CrossRef]
- Galdames, F.J.; Perez, C.A.; Estévez, P.A.; Adams, M. Rock lithological instance classification by hyperspectral images using dimensionality reduction and deep learning. Chemom. Intell. Lab. Syst. 2022, 224, 104538. [Google Scholar] [CrossRef]
- Li, D.; Zhao, J.; Ma, J. Experimental studies on rock thin-section image classification by deep learning-based approaches. Mathematics 2022, 10, 2317. [Google Scholar] [CrossRef]
- Zhang, Z.; Zheng, C.; Liang, C.; Santosh, M.; Hao, J.; Dong, L.; Hou, J.; Hou, F.; Li, M. Metamorphism and P-T Evolution of High-Pressure Granulites from the Fuping Complex, North China Craton. Minerals 2024, 14, 138. [Google Scholar] [CrossRef]
- Barbey, P.; Marignac, C.; Montel, J.M.; Macaudière, J.; Gasquet, D.; Jabbori, J. Cordierite growth textures and the conditions of genesis and emplacement of crustal granitic magmas: The Velay granite complex (Massif Central, France). J. Petrol. 1999, 40, 1425–1441. [Google Scholar] [CrossRef]
- Regmi, K.R. Petrogenesis of the augen gneisses from Mahesh Khola section, Central Nepal. Bull. Dep. Geol. 2008, 11, 13–22. [Google Scholar] [CrossRef]
- Karimzadeh, Z.; Tangestani, M.H. Application of WorldView-3 data in alteration mineral mapping in Chadormalu area, central Iran. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, 42, 589–596. [Google Scholar] [CrossRef]
- LeCun, Y.; Boser, B.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D. Backpropagation applied to handwritten zip code recognition. Neural Comput. 1989, 1, 541–551. [Google Scholar] [CrossRef]
- Zaremba, W.; Sutskever, I.; Vinyals, O. Recurrent neural network regularization. arXiv 2014. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Dey, R.; Salem, F.M. Gate-variants of gated recurrent unit (GRU) neural networks. In Proceedings of the 2017 IEEE 60th International Midwest Symposium on Circuits and Systems (MWSCAS), Boston, MA, USA, 6–9 August 2017; pp. 1597–1600. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv 2014. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. A decision-theoretic generalization of on-line learning and an application to boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- Schuster, M.; Paliwal, K.K. Bidirectional recurrent neural networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef]
- Alrebdi, N.; Al-Shargabi, A.A. Emotional state prediction based on EEG signals using ensemble methods. Int. J. Adv. Comput. Sci. Appl. 2023, 14, 123. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Shen, Q. Spectral–Spatial Classification of Hyperspectral Imagery with 3D Convolutional Neural Network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef]
- Liu, Q.; Zhou, F.; Hang, R.; Yuan, X. Bidirectional-convolutional LSTM based spectral-spatial feature learning for hyperspectral image classification. Remote Sensing 2017, 9, 1330. [Google Scholar] [CrossRef]
- Zhong, Z.; Li, J.; Luo, Z.; Chapman, M. Spectral–spatial residual network for hyperspectral image classification: A 3-D deep learning framework. IEEE Trans. Geosci. Remote Sens. 2018, 56, 847–858. [Google Scholar] [CrossRef]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2261–2269. [Google Scholar] [CrossRef]


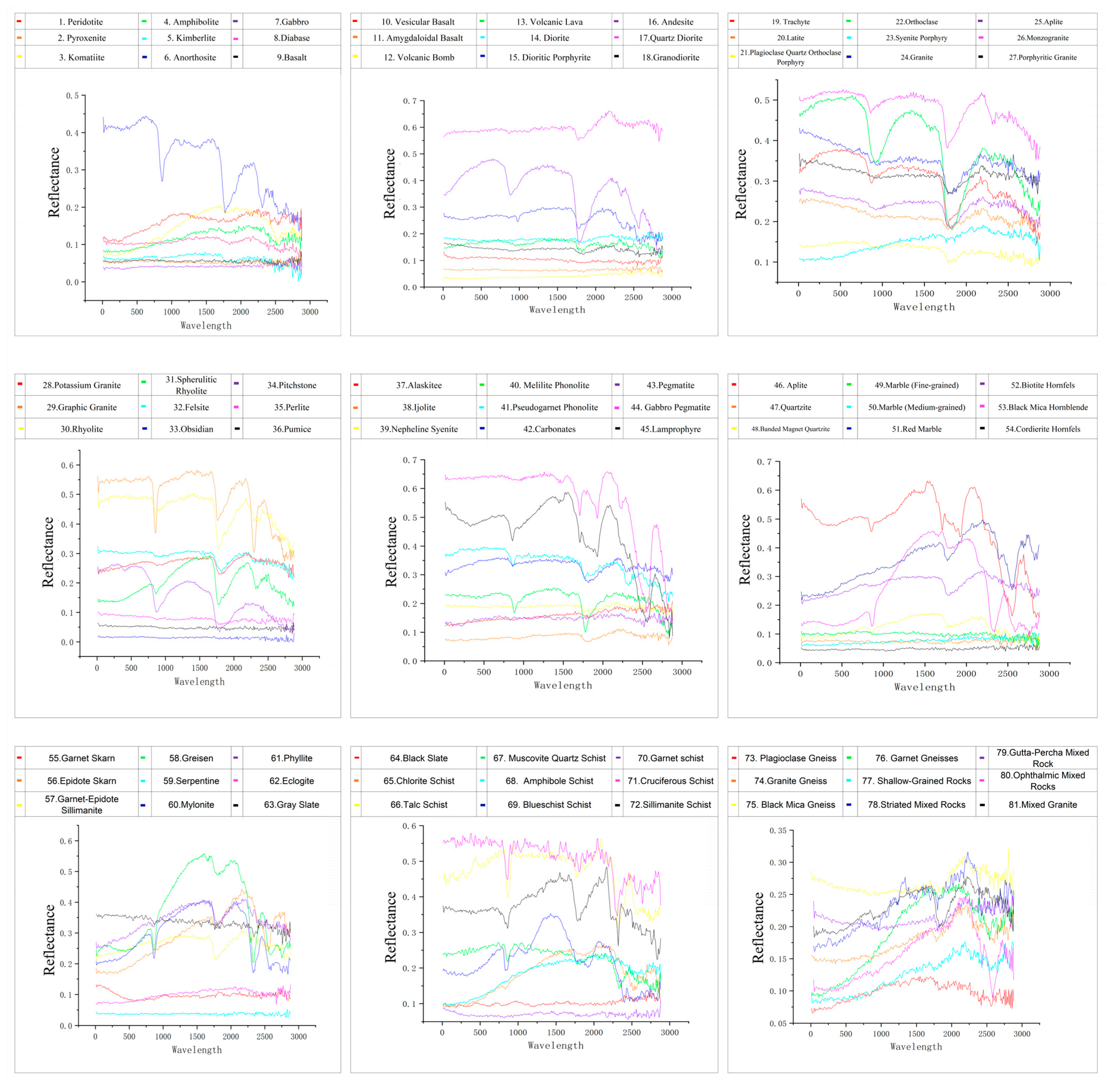







| Rock Name | Class | Samples | Rock Name | Class | Samples |
|---|---|---|---|---|---|
| Peridotite |  1 1 | 4986 | Pseudoleucite Phonolite |  41 41 | 5014 |
| Pyroxenite |  2 2 | 5519 | Carbonatite |  42 42 | 4576 |
| Komatiite |  3 3 | 5740 | Pegmatite |  43 43 | 6018 |
| Amphibolite |  4 4 | 4837 | Gabbroic Pegmatite |  44 44 | 4631 |
| Kimberlite |  5 5 | 6548 | Lamprophyre |  45 45 | 5078 |
| Anorthosite |  6 6 | 5404 | Aplite |  46 46 | 5045 |
| Gabbro |  7 7 | 5472 | Quartzite |  47 47 | 4175 |
| Diabase |  8 8 | 4166 | Banded Magnetite Quartzite |  48 48 | 4722 |
| Basalt |  9 9 | 3747 | Marble (Fine-grained) |  49 49 | 2771 |
| Vesicular Basalt |  10 10 | 4296 | Marble (Medium-grained) |  50 50 | 5699 |
| Amygdaloidal Basalt |  11 11 | 2906 | Red Marble |  51 51 | 5551 |
| Volcanic Bomb |  12 12 | 4739 | Andalusite Hornfels |  52 52 | 3969 |
| Volcanic Lava |  13 13 | 2945 | Biotite Hornfels |  53 53 | 4983 |
| Diorite |  14 14 | 6163 | Cordierite Hornfels |  54 54 | 3479 |
| Diorite Porphyry |  15 15 | 4923 | Garnet Skarn |  55 55 | 4842 |
| Andesite |  16 16 | 4238 | Epidote Skarn |  56 56 | 4256 |
| Quartz Diorite |  17 17 | 4251 | Garnet-Epidote Skarn |  57 57 | 3819 |
| Granodiorite |  18 18 | 5359 | Greisen |  58 58 | 4183 |
| Trachyte |  19 19 | 5239 | Serpentinite |  59 59 | 3221 |
| Latite |  20 20 | 4717 | Mylonite |  60 60 | 3670 |
| Pyroxene-Quartz Syenite Porphyry |  21 21 | 4492 | Phyllite |  61 61 | 3120 |
| Orthoclase |  22 22 | 5110 | Eclogite |  62 62 | 4857 |
| Syenite Porphyry |  23 23 | 3914 | Gray Slate |  63 63 | 4485 |
| Granite |  24 24 | 5384 | Black Slate |  64 64 | 4931 |
| Aplite |  25 25 | 5126 | Chlorite Schist |  65 65 | 5440 |
| Monzogranite |  26 26 | 3477 | Talc schist |  66 66 | 4998 |
| Porphyritic Granite |  27 27 | 4656 | Muscovite Quartz Schist |  67 67 | 5207 |
| Potassic Granite |  28 28 | 4782 | Amphibole Schist |  68 68 | 4012 |
| Graphic Granite |  29 29 | 5186 | Kyanite Schist |  69 69 | 4664 |
| Rhyolite |  30 30 | 4263 | Pyroxene Amphibolite |  70 70 | 4660 |
| Spherulitic Rhyolite |  31 31 | 4529 | Staurolite Schist |  71 71 | 4192 |
| Felsite |  32 32 | 3906 | Sillimanite Schist |  72 72 | 4604 |
| Obsidian |  33 33 | 4107 | Plagioclase Amphibole Schist |  73 73 | 5170 |
| Pitchstone |  34 34 | 4035 | Granitic Gneiss |  74 74 | 5596 |
| Perlite |  35 35 | 3009 | Biotite Gneiss |  75 75 | 5370 |
| Pumice |  36 36 | 5155 | Garnet Granulite |  76 76 | 5789 |
| Alaskite |  37 37 | 4365 | Leptynite |  77 77 | 6215 |
| Ijolite |  38 38 | 4118 | Banded Migmatite |  78 78 | 6082 |
| Nepheline Syenite |  39 39 | 4892 | Ptygmatic Migmatite |  79 79 | 4715 |
| Melilite Phonolite |  40 40 | 3648 | Augen Migmatite |  80 80 | 4781 |
| Mixed Granite |  81 81 | 4638 | |||
| Total | 377,577 | ||||
| Model | OA (%) | Kappa × 100 |
|---|---|---|
| AdaBoost | 53.837 ± 1.461 | 53.2 ± 1.5 |
| C-RNN | 81.493 ± 32.850 | 81.2 ± 33.3 |
| Number of Classifiers | OA (%) | AA (%) | Kappa × 100 | Average Training Duration (Seconds) |
|---|---|---|---|---|
| 1 | 88.513 ± 5.323 | 88.348 ± 4.993 | 88.40 ± 5.1 | 1838.816 |
| 3 | 92.554 ± 7.442 | 92.250 ± 7.861 | 92.50 ± 7.5 | 4374.326 |
| 5 | 91.927 ± 4.298 | 92.016 ± 5.134 | 92.10 ± 4.3 | 6402.439 |
| 7 | 89.365 ± 5.611 | 89.131 ± 5.309 | 89.20 ± 5.2 | 7129.034 |
| Model | OA (%) | AA (%) | Kappa × 100 | Parameter Quantity |
|---|---|---|---|---|
| 2D-BRNN-AdaBoost | 83.914 ± 1.579 | 83.350 ± 1.700 | 83.70 ± 1.6 | 16,342,941 |
| 2D-LSTM-AdaBoost | 89.796 ± 2.842 | 89.298 ± 3.194 | 89.70 ± 2.9 | 8,229,085 |
| 2D-1D CNN-AdaBoost | 91.118 ± 5.227 | 90.670 ± 5.461 | 91.10 ± 5.3 | 36,670,263 |
| Proposed CRNN-AdaBoost | 92.554 ± 7.442 | 92.250 ± 7.861 | 92.50 ± 7.5 | 1,012,632 |
| Model | OA (%) | AA (%) | Kappa × 100 |
|---|---|---|---|
| 3D CNN | 87.129 ± 6.439 | 88.235 ± 6.873 | 87.10 ± 6.5 |
| Bi-CLSTM | 89.476 ± 3.316 | 89.038 ± 3.128 | 88.20 ± 3.0 |
| SSRN | 91.012 ± 4.734 | 91.989 ± 4.325 | 90.90 ± 4.9 |
| DenseNet | 90.301 ± 3.213 | 90.991 ± 3.052 | 90.80 ± 3.1 |
| Proposed CRNN-AdaBoost | 92.554 ± 7.442 | 92.250 ± 7.861 | 92.50 ± 7.5 |
| Class Name | Classification Results of the Four Classes |
|---|---|
| 49–50 | 99.5% |
| 56–57 | 99.4% |
| 68/73 | 98.6% |
| 70/72 | 99.8% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, S.; Qiu, Y.; Cao, S.; Wu, W. Hyperspectral Lithological Classification of 81 Rock Types Using Deep Ensemble Learning Algorithms. Minerals 2025, 15, 844. https://doi.org/10.3390/min15080844
Xie S, Qiu Y, Cao S, Wu W. Hyperspectral Lithological Classification of 81 Rock Types Using Deep Ensemble Learning Algorithms. Minerals. 2025; 15(8):844. https://doi.org/10.3390/min15080844
Chicago/Turabian StyleXie, Shanjuan, Yichun Qiu, Shixian Cao, and Wenyuan Wu. 2025. "Hyperspectral Lithological Classification of 81 Rock Types Using Deep Ensemble Learning Algorithms" Minerals 15, no. 8: 844. https://doi.org/10.3390/min15080844
APA StyleXie, S., Qiu, Y., Cao, S., & Wu, W. (2025). Hyperspectral Lithological Classification of 81 Rock Types Using Deep Ensemble Learning Algorithms. Minerals, 15(8), 844. https://doi.org/10.3390/min15080844





